Elastoplastic Mechanical Properties and Kinematic Hardening Model of 35CrNi3MoVR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Introduction of the Experimental Material
2.2. Explanations of the Uniaxial Mechanical Property Tests
3. Construction of the Constitutive Modeling
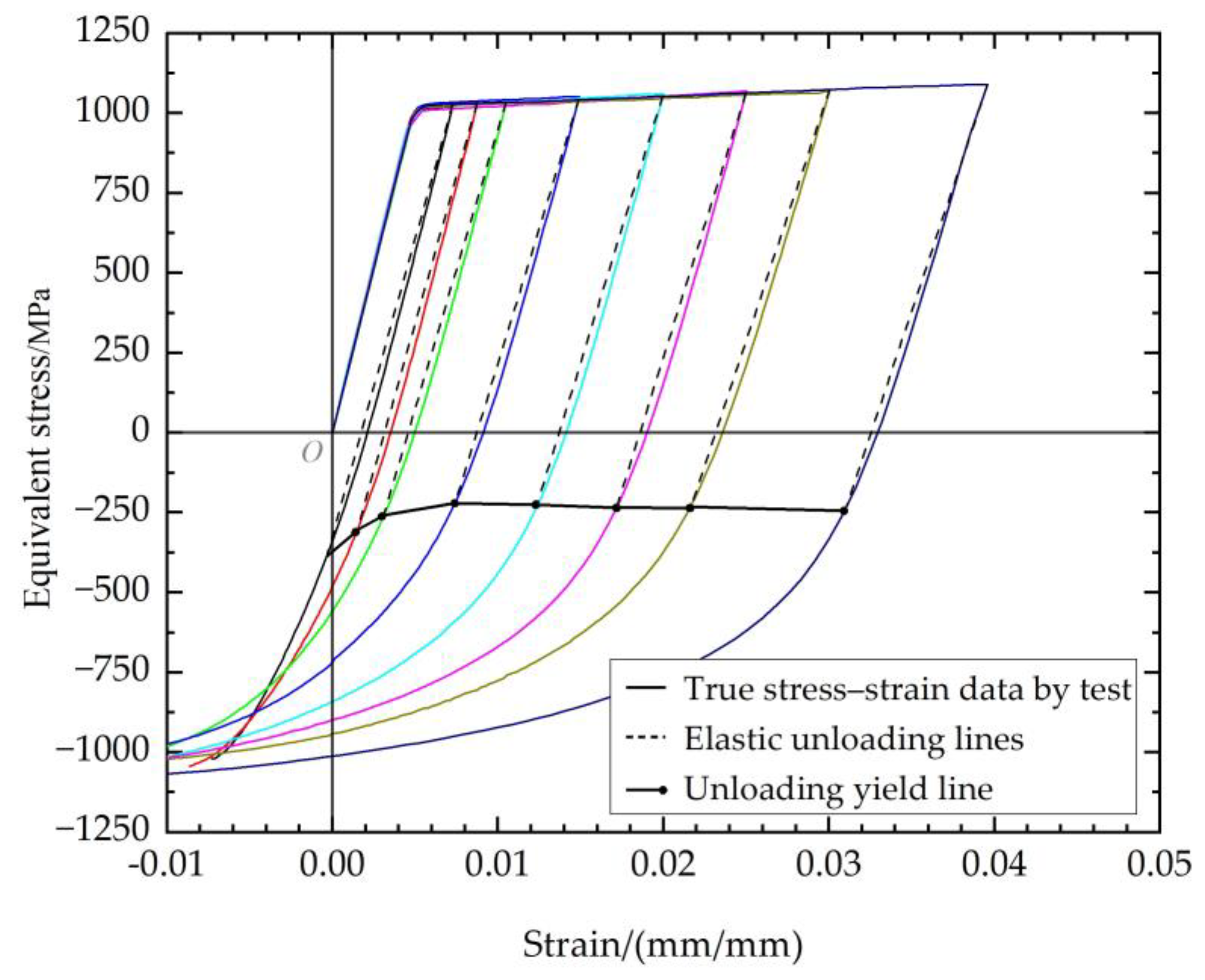
3.1. Processing of Experimental Data
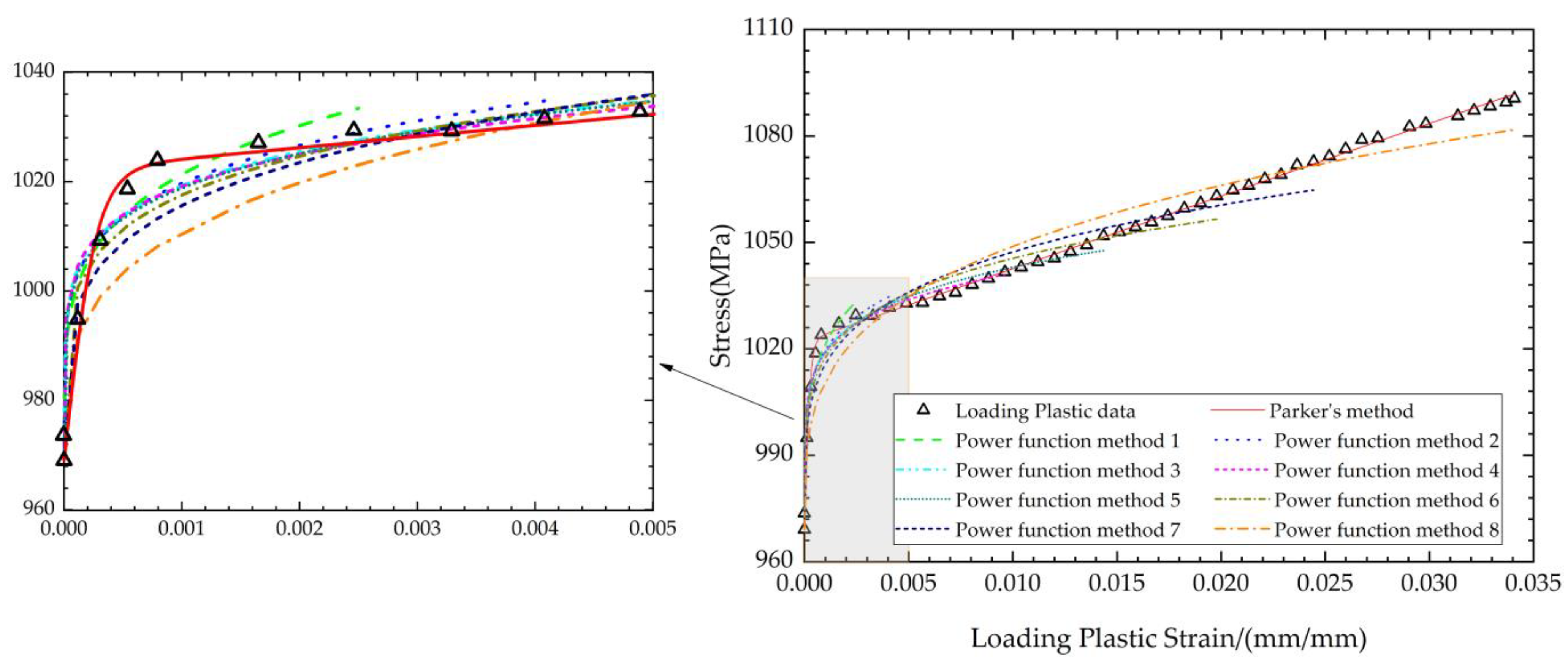
3.2. Fitting of the Equations
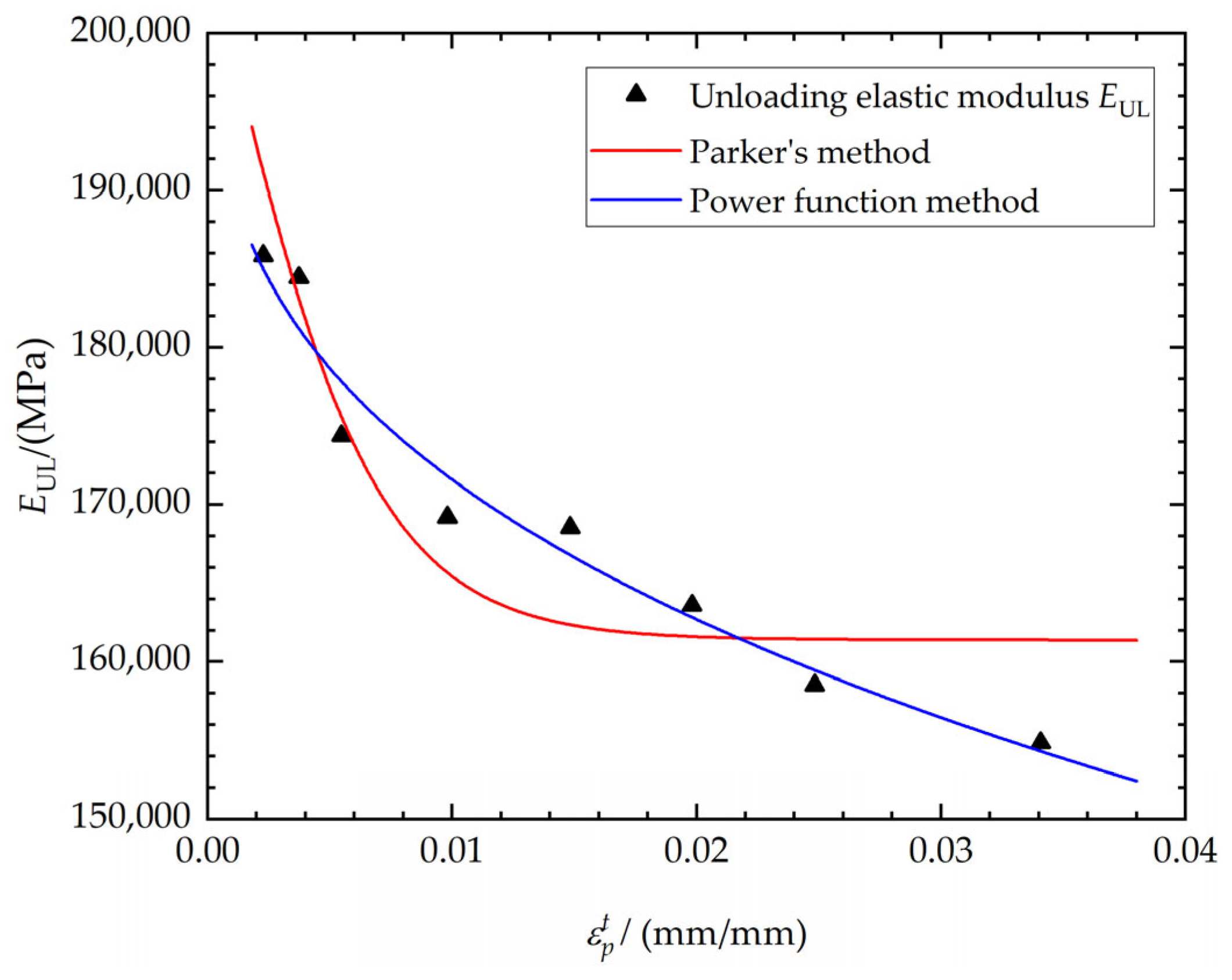
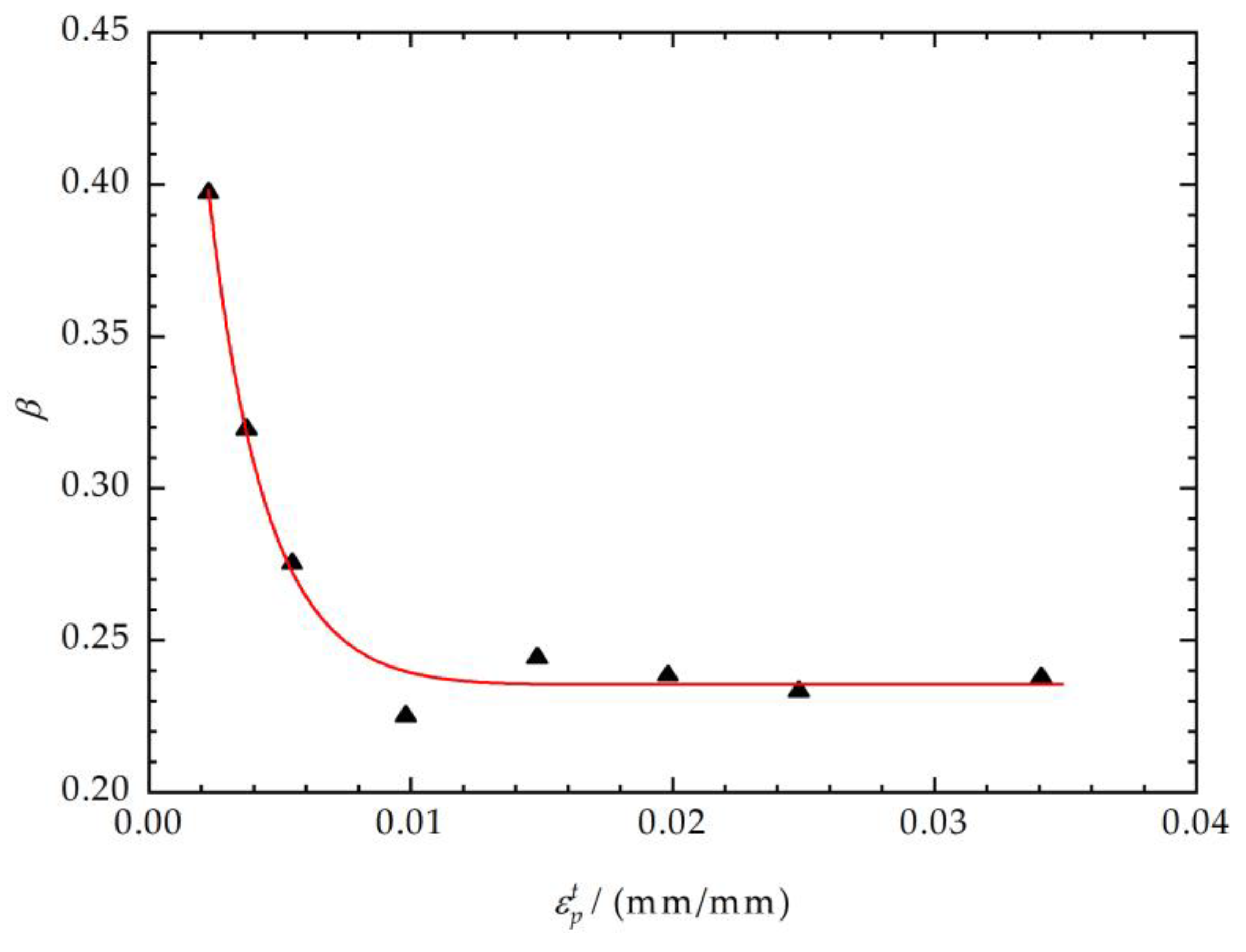
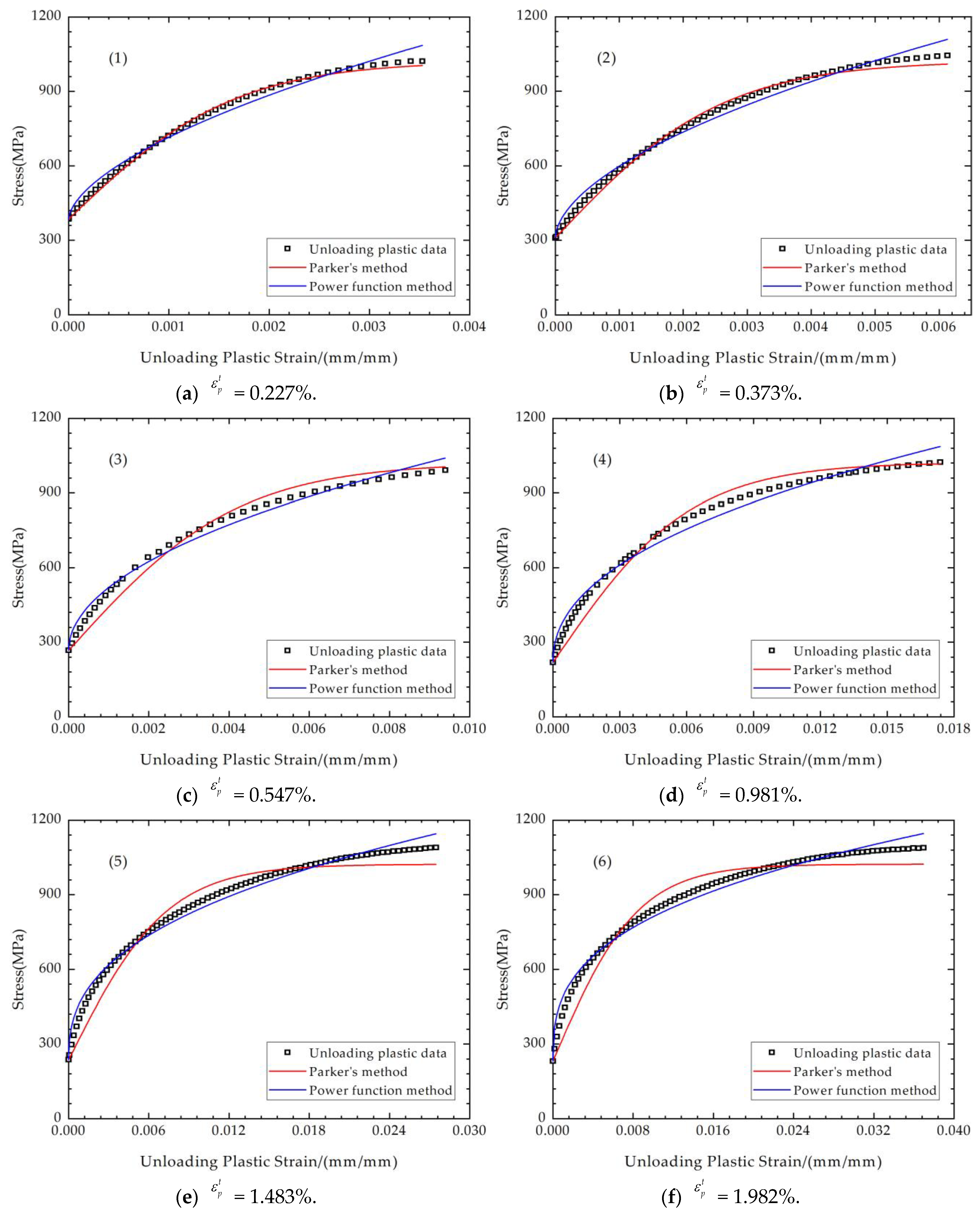
3.3. Discussion of the Fitting Results
- (a)
- Loading elastic region:
- (b)
- Loading plastic region:
- (c)
- Unloading elastic region:
- (d)
- Unloading plastic region:
3.4. Power Function Kinematic Hardening Model of 35CrNi3MoVR Steel
4. Finite Element Method of the Elastoplastic Constitutive Model
5. Implementation of Experimental Research and Finite Element Method Calculation
5.1. Introduction of the Autofrettage Experiment
5.2. Issues with Autofrettage Calculation by the Finite Element Method
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rees, D.W.A. The Fatigue Life of Thick-Walled Autofrettaged Cylinders with Closed Ends. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 51–68. [Google Scholar] [CrossRef]
- Alegre, J.M.; Bravo, P.; Preciado, M. Design of an Autofrettaged High-Pressure Vessel, Considering the Bauschinger Effect. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2006, 220, 7–16. [Google Scholar] [CrossRef]
- Dixit, U.S.; Shufen, R. 2—Finite Element Method Modeling of Hydraulic and Thermal Autofrettage Processes. In Mechanics of Materials in Modern Manufacturing Methods and Processing Techniques; Silberschmidt, V.V., Ed.; Elsevier Series in Mechanics of Advanced Materials; Elsevier: Amsterdam, The Netherlands, 2020; pp. 31–69. ISBN 978-0-12-818232-1. [Google Scholar]
- Davidson, T.E.; Barton, C.S.; Reiner, A.N.; Kendall, D.P. Overstrain of High-Strength Open-End Cylinders of Intermediate Diameter Ratio. In Experimental Mechanics; Rossi, B.E., Ed.; Pergamon: Oxford, UK, 1963; pp. 335–352. ISBN 978-0-08-013346-1. [Google Scholar]
- Shufen, R.; Dixit, U.S. A Review of Theoretical and Experimental Research on Various Autofrettage Processes. J. Press. Vessel Technol. 2018, 140, 050802. [Google Scholar] [CrossRef]
- Hu, Z.; Parker, A.P. Swage Autofrettage Analysis—Current Status and Future Prospects. Int. J. Press. Vessel. Pip. 2019, 171, 233–241. [Google Scholar] [CrossRef]
- Perl, M.; Perry, J.; Aharon, T.; Kolka, O. Is There an “Ultimate” Autofrettage Process? J. Press. Vessel Technol. 2012, 134, 041001. [Google Scholar] [CrossRef]
- Roy, A.K.; Kamal, S.M.; Patil, R.U.; Rao, V.V. Practicing Hydraulic Autofrettage for Strengthening a Gun Barrel: Critical Issues and Challenges. In Engineering Pedagogy: A Collection of Articles in Honor of Prof. Amitabha Ghosh; Dixit, U.S., Echempati, R., Dey, S., Eds.; Springer Nature: Singapore, 2023; pp. 163–184. ISBN 978-981-19801-6-9. [Google Scholar]
- Vullo, V. Thick-Walled Circular Cylinders in the Linear Elastic-Perfectly Plastic State After Loading Beyond the Elastic Range. In Circular Cylinders and Pressure Vessels: Stress Analysis and Design; Vullo, V., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 179–210. ISBN 978-3-319-00690-1. [Google Scholar]
- Alexandrov, S.; Lyamina, E.; Aoh, J.-N.; Jeng, Y.-R. Description of Residual Stresses in Autofrettaged Open-Ended Cylinders Made of High-Strength Steel. Materials 2020, 13, 2940. [Google Scholar] [CrossRef] [PubMed]
- Shim, W.S.; Kim, J.H.; Lee, Y.S.; Cha, K.U.; Hong, S.K. A Study on Hydraulic Autofrettage of Thick-Walled Cylinders Incorporating Bauschinger Effect. Exp. Mech. 2010, 50, 621–626. [Google Scholar] [CrossRef]
- Çandar, H.; Filiz, İ.H. Experimental Study on Residual Stresses in Autofrettaged Thick-Walled High Pressure Cylinders. High Press. Res. 2017, 37, 516–528. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, S.Y.; Yang, J.; Zhang, P. Neutron Diffraction, Finite Element and Analytical Investigation of Residual Strains of Autofrettaged Thick-Walled Pressure Vessels. Int. J. Press. Vessel. Pip. 2022, 200, 104786. [Google Scholar] [CrossRef]
- Maleki, M.; Farrahi, G.H.; Haghpanah Jahromi, B.; Hosseinian, E. Residual Stress Analysis of Autofrettaged Thick-Walled Spherical Pressure Vessel. Int. J. Press. Vessel. Pip. 2010, 87, 396–401. [Google Scholar] [CrossRef]
- Chen, P.C.T. The Bauschinger and Hardening Effect on Residual Stresses in an Autofrettaged Thick-Walled Cylinder. J. Press. Vessel Technol. 1986, 108, 108–112. [Google Scholar] [CrossRef]
- Livieri, P.; Lazzarin, P. Autofrettaged Cylindrical Vessels and Bauschinger Effect: An Analytical Frame for Evaluating Residual Stress Distributions. J. Press. Vessel Technol. 2001, 124, 38–46. [Google Scholar] [CrossRef]
- Milligan, R.V.; Koo, W.H.; Davidson, T.E. The Bauschinger Effect in a High-Strength Steel. J. Basic Eng. 1966, 88, 480–488. [Google Scholar] [CrossRef]
- Megahed, M.M.; Abbas, A.T. Influence of Reverse Yielding on Residual Stresses Induced by Autofrettage. Int. J. Mech. Sci. 1991, 33, 139–150. [Google Scholar] [CrossRef]
- Troiano, E.; Parker, A.P.; Underwood, J.; Mossey, C. Experimental Data, Numerical Fit and Fatigue Life Calculations Relating to the Bauschinger Effect in High Strength Armament Steels. J. Press. Vessel Technol. 2003, 125, 330–334. [Google Scholar] [CrossRef]
- Huang, X.P. A General Autofrettage Model of a Thick-Walled Cylinder Based on Tensile-Compressive Stress-Strain Curve of a Material. J. Strain Anal. Eng. Des. 2005, 40, 599–607. [Google Scholar] [CrossRef]
- De Swardt, R.R. Material Models for the Finite Element Analysis of Materials Exhibiting a Pronounced Bauschinger Effect. J. Press. Vessel Technol. 2006, 128, 190–195. [Google Scholar] [CrossRef]
- Parker, A.P. Assessment and Extension of an Analytical Formulation for Prediction of Residual Stress in Autofrettaged Thick Cylinders. In Proceedings of the PVP2005 High Pressure Technology, Nondestructive Evaluation, Pipeline Systems, Student Paper Competition, Denver, CO, USA, 17–21 July 2005; Volume 5, pp. 67–71. [Google Scholar]
- Parker, A.P. Autofrettage of Open-End Tubes—Pressures, Stresses, Strains, and Code Comparisons. J. Press. Vessel Technol. 2000, 123, 271–281. [Google Scholar] [CrossRef]
- Parker, A.P.; Underwood, J.H.; Kendall, D.P. Bauschinger Effect Design Procedures for Autofrettaged Tubes Including Material Removal and Sachs’ Method. J. Press. Vessel Technol. 1999, 121, 430–437. [Google Scholar] [CrossRef]
- Parker, A.P.; Troiano, E.; Underwood, J.H.; Mossey, C. Characterization of Steels Using a Revised Kinematic Hardening Model Incorporating Bauschinger Effect. J. Press. Vessel Technol. 2003, 125, 277–281. [Google Scholar] [CrossRef]
- Faghih, S.; Jahed, H.; Behravesh, S.B. Variable Material Properties Approach: A Review on Twenty Years of Progress. J. Press. Vessel Technol. 2018, 140, 050803. [Google Scholar] [CrossRef]
- Troiano, E.; Parker, A.P.; Underwood, J.H. Mechanisms and Modeling Comparing HB7 and A723 High Strength Pressure Vessel Steels. J. Press. Vessel Technol. 2004, 126, 473–477. [Google Scholar] [CrossRef]
- Farrahi, G.H.; Voyiadjis, G.Z.; Hoseini, S.H.; Hosseinian, E. Residual Stress Analysis of the Autofrettaged Thick-Walled Tube Using Nonlinear Kinematic Hardening. J. Press. Vessel Technol. 2013, 135, 021204. [Google Scholar] [CrossRef]
- Troiano, E.; Underwood, J.H.; Parker, A.P. Finite Element Investigation of Bauschinger Effect in High-Strength A723 Pressure Vessel Steel. J. Press. Vessel Technol. 2006, 128, 185–189. [Google Scholar] [CrossRef]
- Gibson, M.C. Determination of Residual Stress Distributions in Autofrettaged Thick Cylinders; Cranfield University: Bedford, UK, 2008. [Google Scholar]
- Hu, Z.; Gibson, M.C.; Parker, A.P. Swage Autofrettage FEA Incorporating a User Function to Model Actual Bauschinger Effect. Int. J. Press. Vessel. Pip. 2021, 191, 104372. [Google Scholar] [CrossRef]
- Hu, Z.; Puttagunta, S. Computer Modeling of Internal Pressure Autofrettage Process of a Thick-Walled Cylinder with the Bauschinger Effect. Am. Trans. Eng. Appl. Sci. 2012, 1, 143–161. [Google Scholar]
- Loffredo, M. Measurement and Modelling of Bauschinger Effect for Low-Level Plastic Strains on AISI 4140 Steel. Procedia Struct. Integr. 2018, 8, 265–275. [Google Scholar] [CrossRef]
- Molaie, M.; Darijani, H.; Bahreman, M.; Hosseini, S.M. Autofrettage of Nonlinear Strain-Hardening Cylinders Using the Proposed Analytical Solution for Stresses. Int. J. Mech. Sci. 2018, 141, 450–460. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Pan, M.; Cao, W.; Ma, X.; Li, Y. Fatigue Life Analysis of High-Pressure Seamless Steel Cylinder for Hydrogen Using Autofrettage Design. Int. J. Press. Vessel. Pip. 2023, 206, 105065. [Google Scholar] [CrossRef]
- Shufen, R.; Singh, N.P.; Dixit, U.S. Thermally Assisted Rotational Autofrettage of Long Cylinders with Free Ends. J. Press. Vessel Technol. 2023, 145, 051303. [Google Scholar] [CrossRef]
- Hu, Z.; Parker, A.P. Fluid End Blocks: Numerical Analysis of Autofrettage and Reautofrettage Based Upon a True Material Model. J. Press. Vessel Technol. 2023, 145, 021503. [Google Scholar] [CrossRef]
- GB/T 34019-2017; Ultra-High Pressure Vessels General. Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China & Standardization Administration of the People’s Republic of China: Beijing, China, 2017. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=CE0C7DC1368FEB304FC01EBB4CB2FB00 (accessed on 30 May 2024).
- Dunne, F.; Petrinic, N. Introduction to Computational Plasticity; Oxford University Press: Oxford, UK, 2005; ISBN 978-0-19-856826-1. [Google Scholar]
- Zhu, R.; Yang, J. Autofrettage of Thick Cylinders. Int. J. Press. Vessel. Pip. 1998, 75, 443–446. [Google Scholar] [CrossRef]
- Sachs, G. Der Nachweis Innerer Spannungen in Stangen Und Rohren. Zeits Zeitshrift Met. 1927, 19, 352–357. [Google Scholar]
- De Swardt, R.R. Finite Element Simulation of the Sachs Boring Method of Measuring Residual Stresses in Thick-Walled Cylinders. J. Press. Vessel Technol. 2003, 125, 274–276. [Google Scholar] [CrossRef]
- Parker, A.P. A Critical Examination of Sachs’ Material-Removal Method for Determination of Residual Stress. J. Press. Vessel Technol. 2004, 126, 234–236. [Google Scholar] [CrossRef]

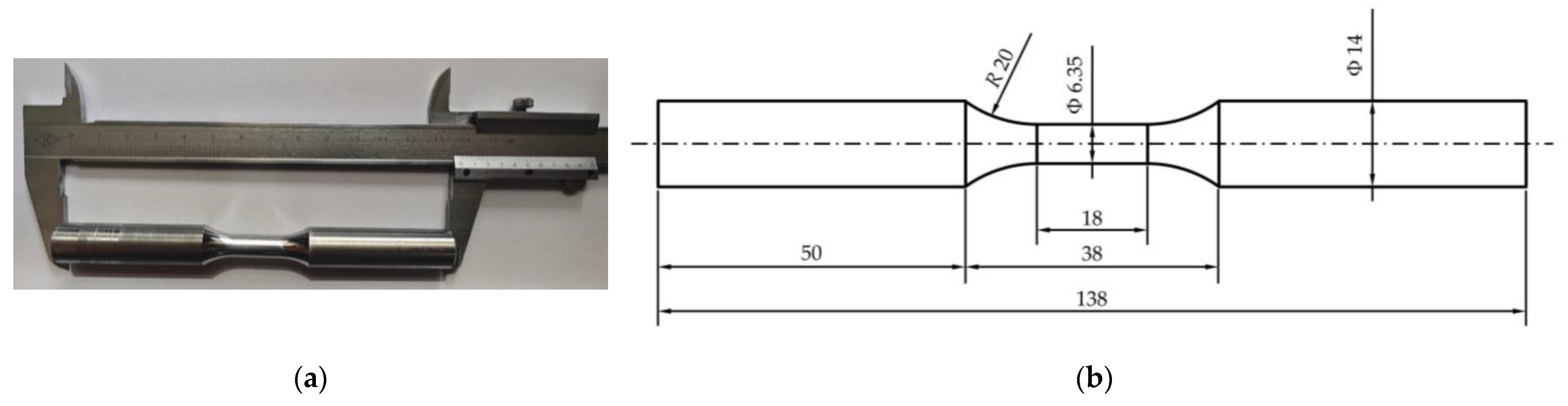








| Element | C | Mn | Si | Cr | Ni | Mo | V | S |
|---|---|---|---|---|---|---|---|---|
| Standard weight percent/% | 0.30~0.40 | 0.20~0.80 | 0.10~0.35 | 0.50~1.20 | 2.50~3.30 | 0.40~0.70 | 0.10~0.25 | ≤0.005 |
| Test weight percent/% | 0.38 | 0.47 | 0.18 | 1.07 | 2.84 | 0.50 | 0.17 | 0.0009 |
| Yield Stress Rp0.2/MPa | UTS Rm/MPa | Elongation A/% | Young’s Modulus E/MPa | POISSON’S RATIO |
|---|---|---|---|---|
| ≥960 | 1070~1230 | ≥16 | 206,000 | 0.3 |
| No. | 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# |
|---|---|---|---|---|---|---|---|---|
| Nominal total tensile strain | 0.7% | 0.85% | 1.0% | 1.50% | 2.0% | 2.5% | 3.0% | 4.0% |
| Tensile plastic strain | 0.227% | 0.373% | 0.547% | 0.981% | 1.483% | 1.982% | 2.483% | 3.407% |
| 0.227% | 0.373% | 0.547% | 0.981% | 1.483% | 1.982% | 2.483% | 3.407% | Average (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Parker A.A. | 0.99915 | 0.99813 | 0.99323 | 0.99341 | 0.99159 | 0.99030 | 0.98980 | 0.98797 | 0.99295 |
| Power function | 0.99521 | 0.99571 | 0.99587 | 0.99488 | 0.99652 | 0.99626 | 0.99007 | 0.99378 | 0.99479 |
| Region | Function | Parameter |
|---|---|---|
| (a) | ||
| (b) | ||
| (c) | ||
| (d) |
| Model | Autofrettage Pressure/MPa | Mises Stress/MPa | Error |
|---|---|---|---|
| Experimental result | 680 | 351.43 | - |
| Power function model | 344.14 | 2.07% | |
| Parker’s model | 332.56 | 5.37% | |
| Huang’s model | 391.52 | 11.41% | |
| Ideal E-P model | 499.45 | 42.12% | |
| Experimental result | 780 | 443.41 | -- |
| Power function model | 452.21 | 1.98% | |
| Parker’s model | 396.40 | 10.60% | |
| Huang’s model | 507.02 | 14.35% | |
| Ideal E-P model | 713.07 | 60.82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, X.; Chen, Q. Elastoplastic Mechanical Properties and Kinematic Hardening Model of 35CrNi3MoVR. Materials 2024, 17, 3223. https://doi.org/10.3390/ma17133223
Zhang Z, Wang X, Chen Q. Elastoplastic Mechanical Properties and Kinematic Hardening Model of 35CrNi3MoVR. Materials. 2024; 17(13):3223. https://doi.org/10.3390/ma17133223
Chicago/Turabian StyleZhang, Zhao, Xuesheng Wang, and Qinzhu Chen. 2024. "Elastoplastic Mechanical Properties and Kinematic Hardening Model of 35CrNi3MoVR" Materials 17, no. 13: 3223. https://doi.org/10.3390/ma17133223
APA StyleZhang, Z., Wang, X., & Chen, Q. (2024). Elastoplastic Mechanical Properties and Kinematic Hardening Model of 35CrNi3MoVR. Materials, 17(13), 3223. https://doi.org/10.3390/ma17133223





