A VMD-BP Model to Predict Laser Welding Keyhole-Induced Pore Defect in Al Butt–Lap Joint
Abstract
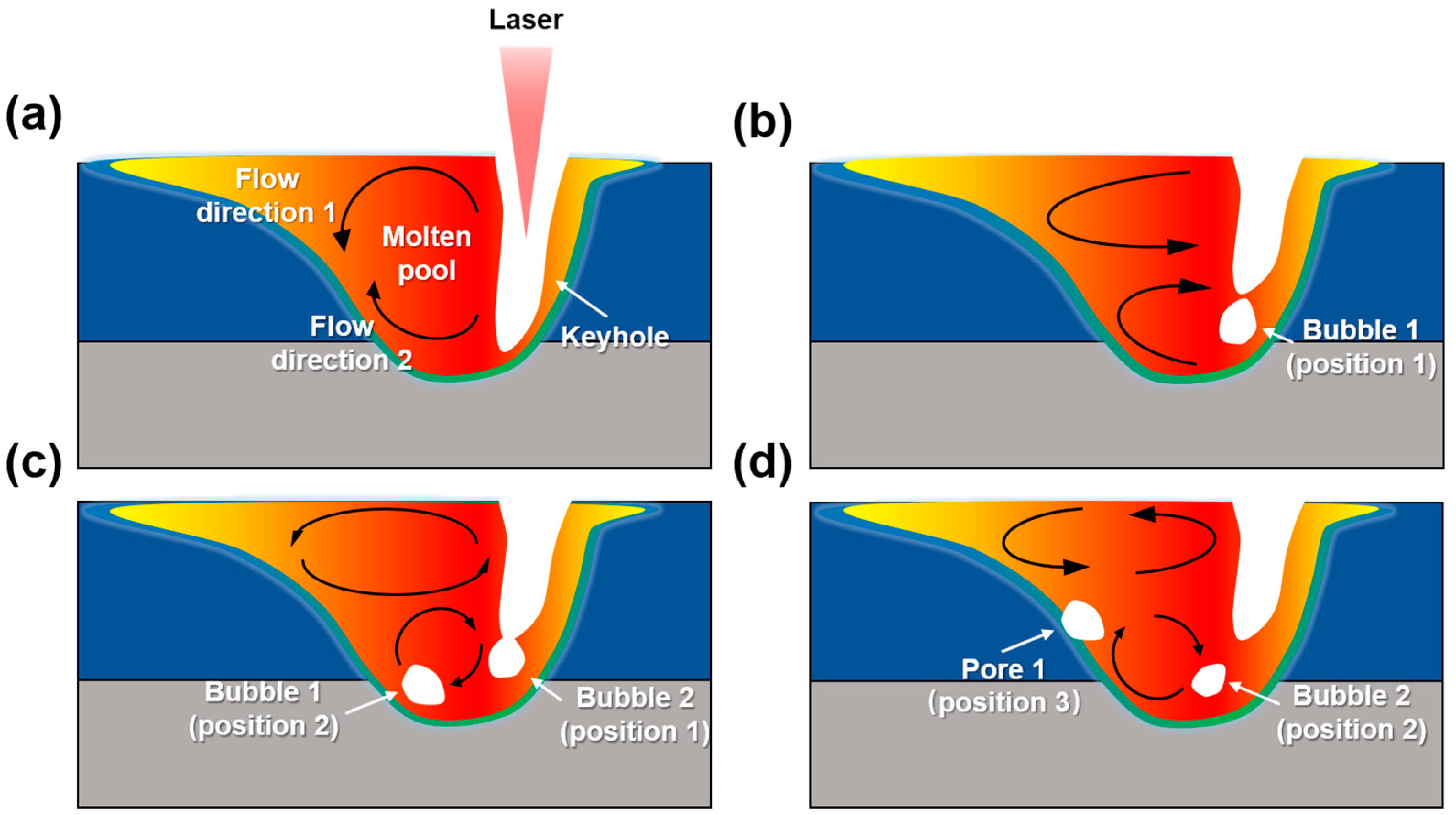
:1. Introduction
- The integration of VMD with BP neural networks enabled adaptive adjustment of the decomposition layers and demonstrated remarkable performance in signal decomposition and the prediction of porosity.
- The temporal information was considered to mitigate the effects of porosity migration, and the influence of signal segment length was evaluated.
- Widening the application of this model in the welding of high-speed trins, significantly improving manufacturing efficiency and ensuring the safety and reliability of high-speed trains.
2. Materials and Method
2.1. Materials and Reagents
2.2. Welding Procedures and Dataset Setting
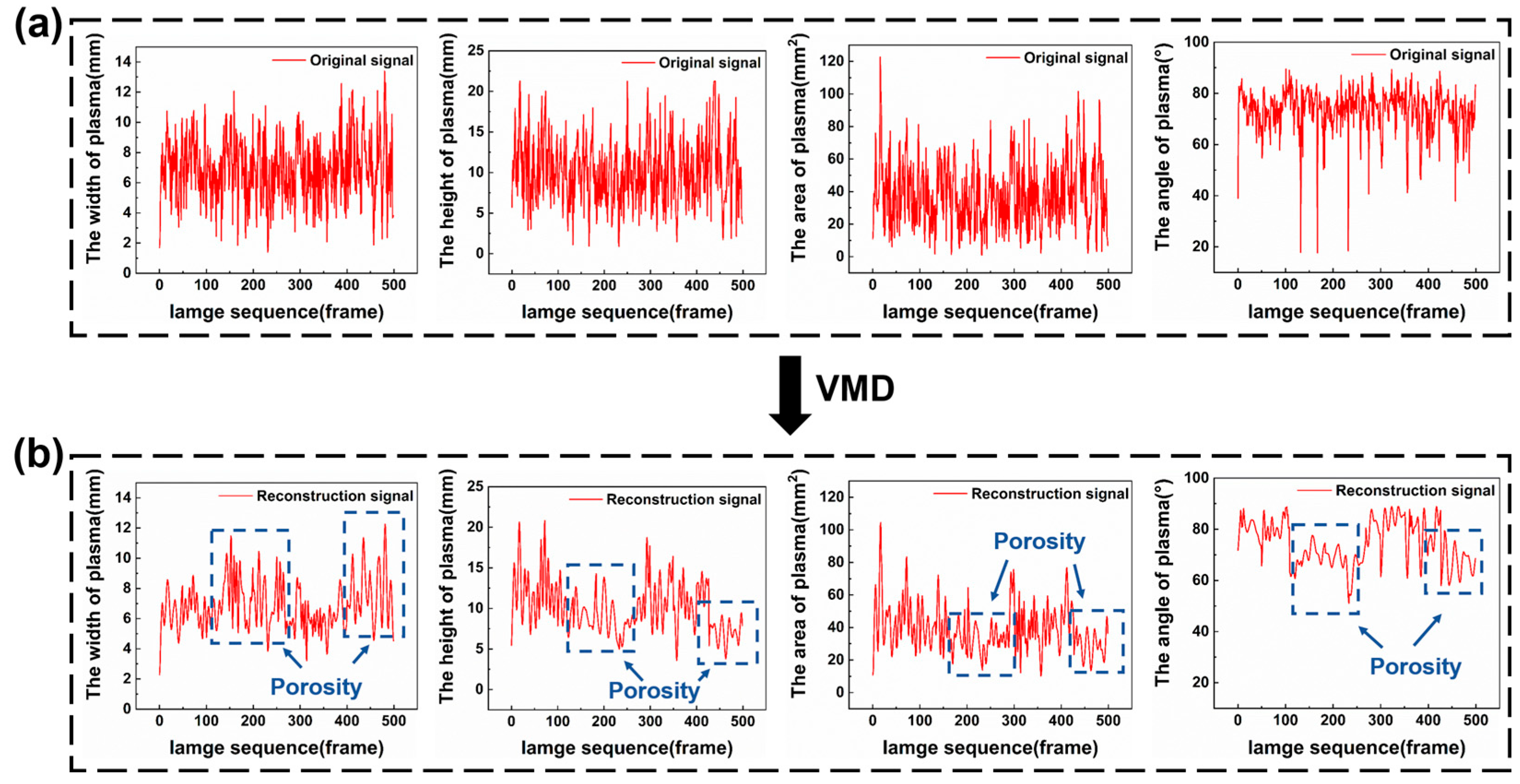
2.3. Data Preprocessing
2.3.1. Image Process
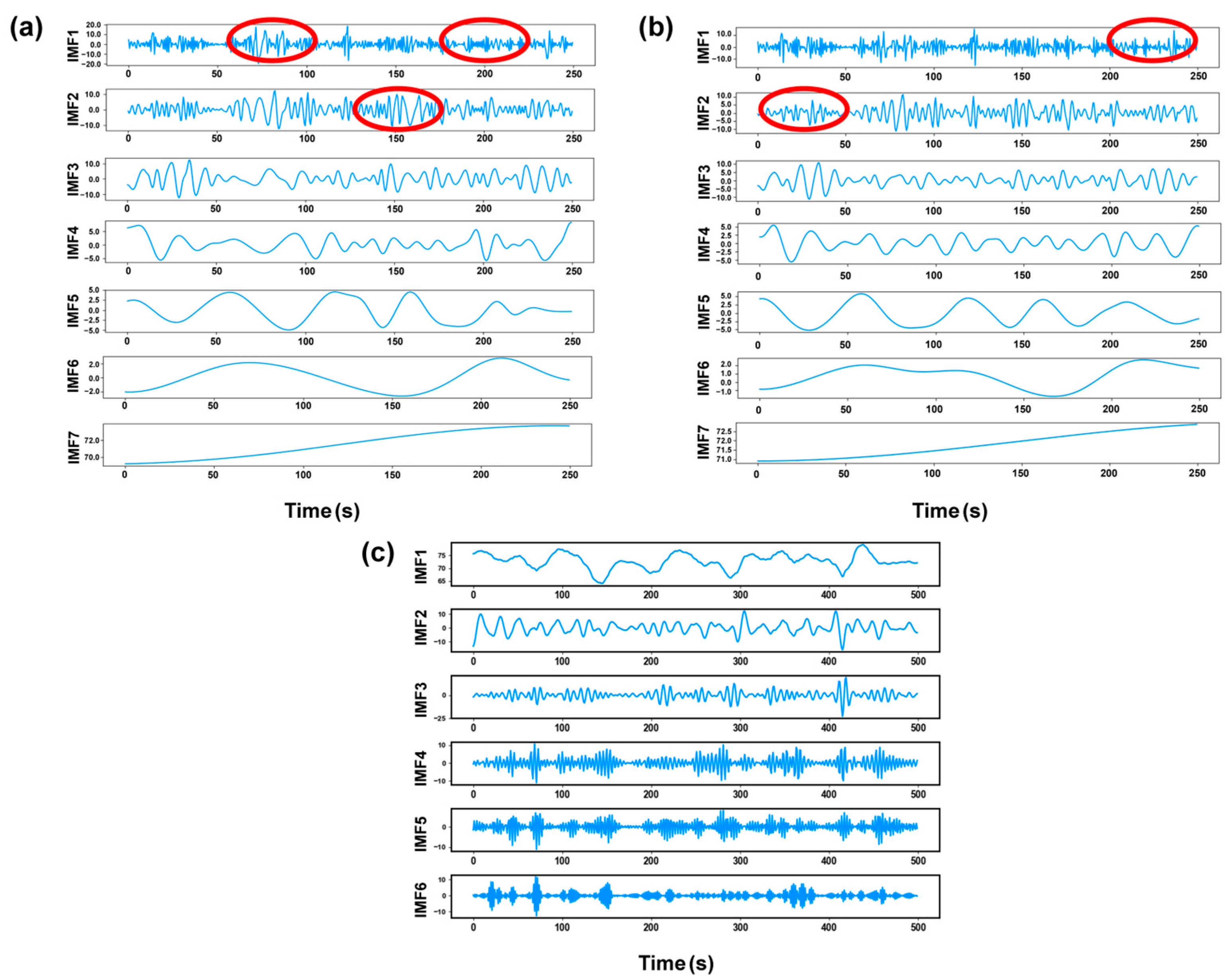
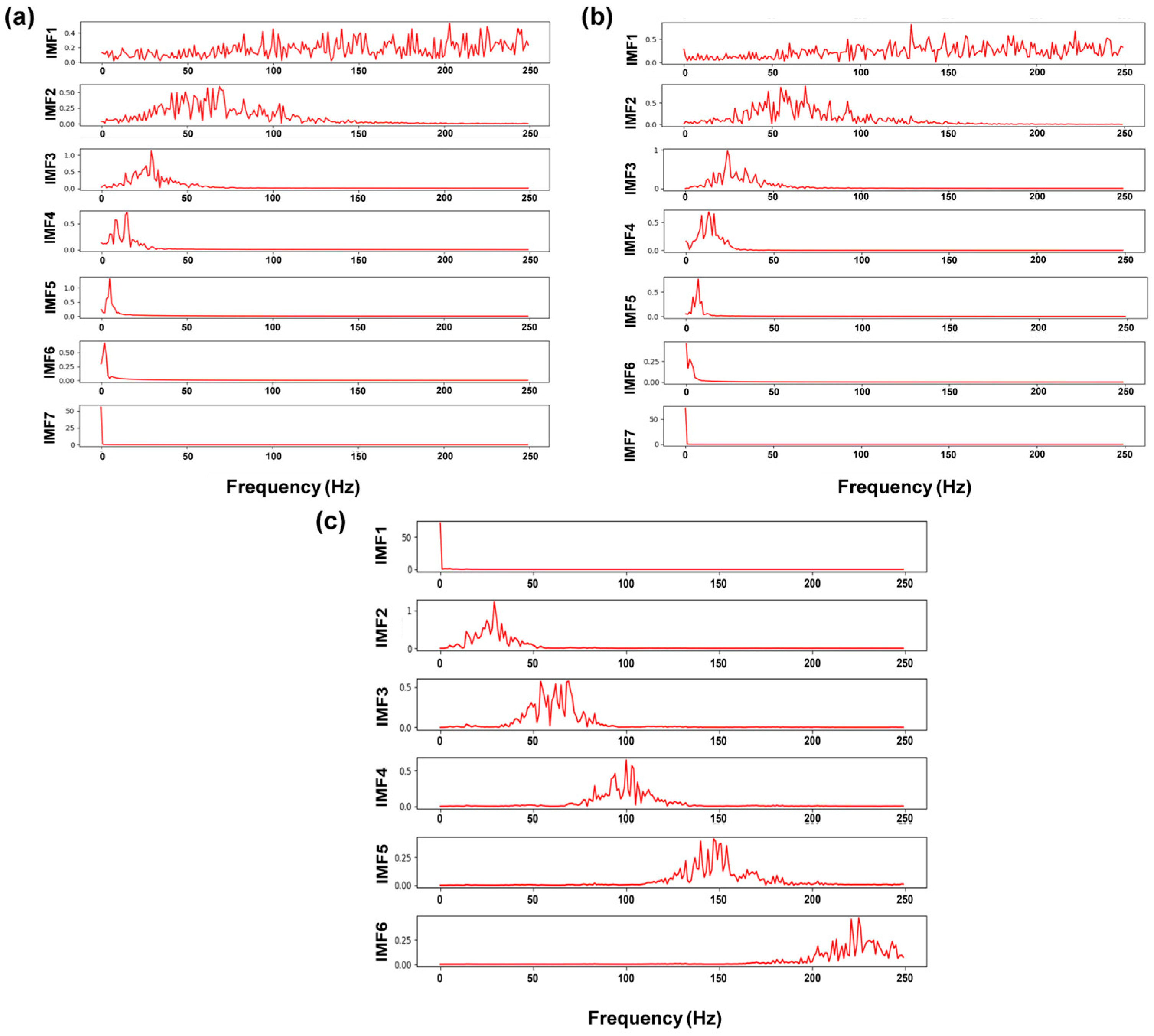
2.3.2. Signal Decomposition
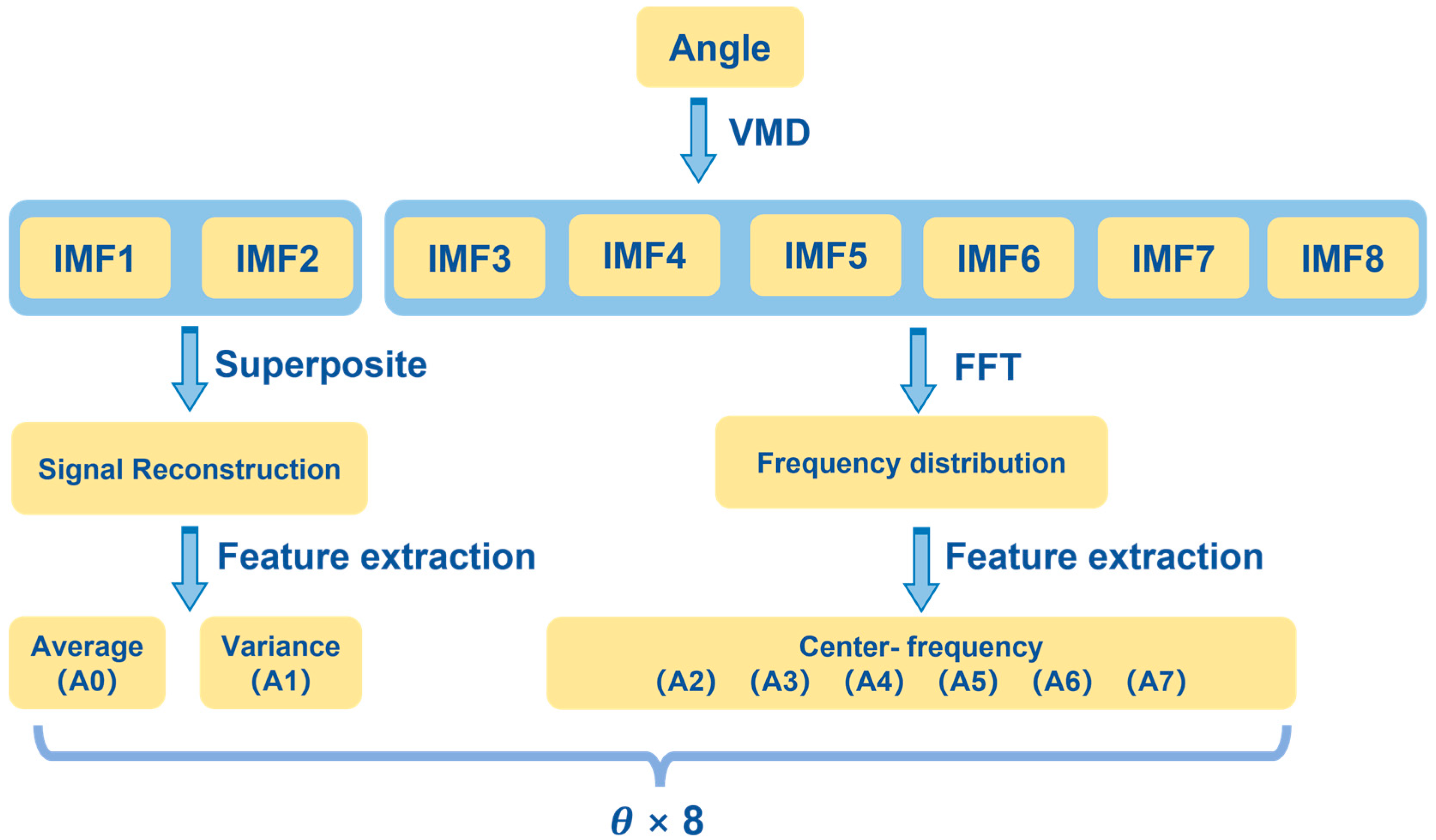
2.3.3. Feature Extraction
2.3.4. Division of Signal Segments
2.4. Calculations and Modelling
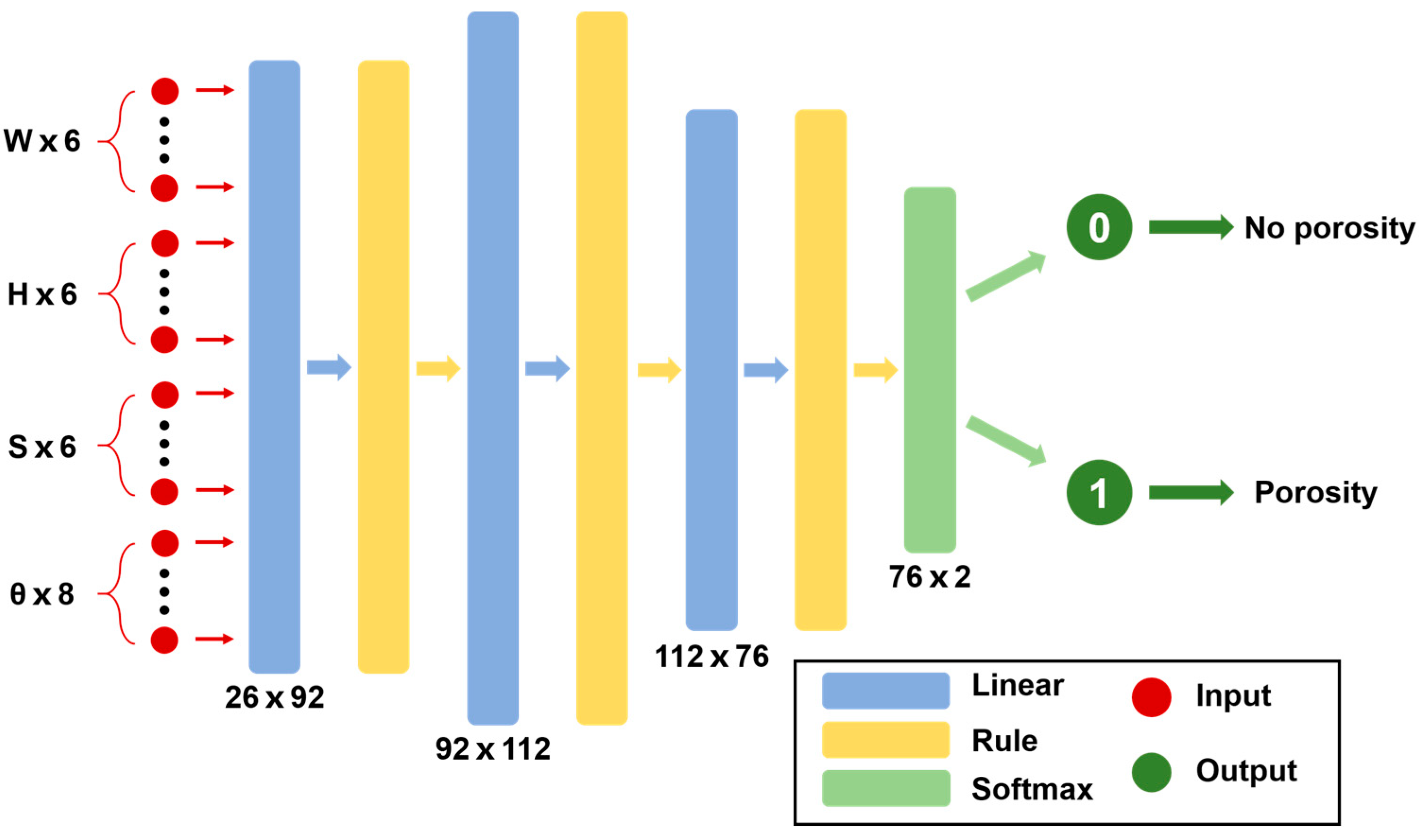
2.4.1. Architecture of BP Neural Network
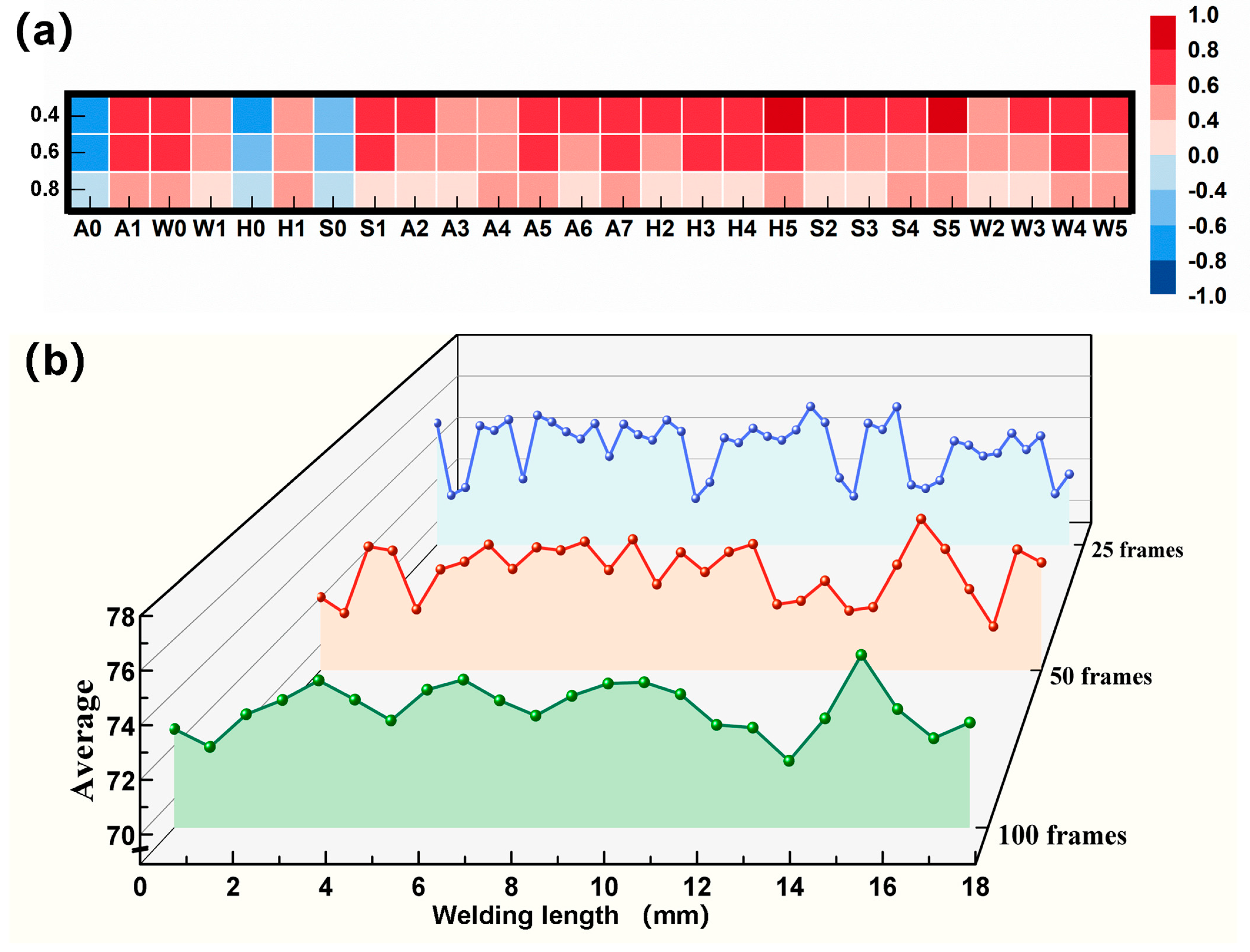
2.4.2. Correlation Analysis of BP Neural Network
3. Results and Discussion
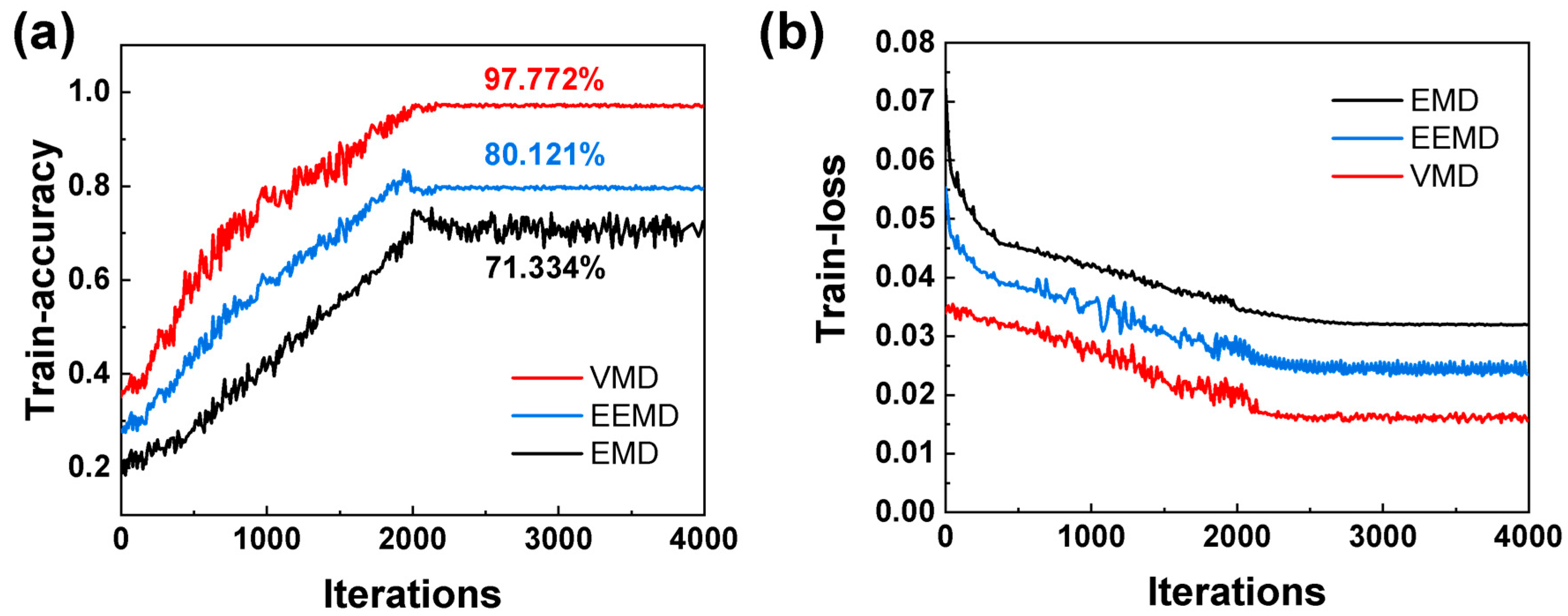
3.1. The Performance of Different Decomposition Methods
3.2. The Performance of Neural Network Prediction
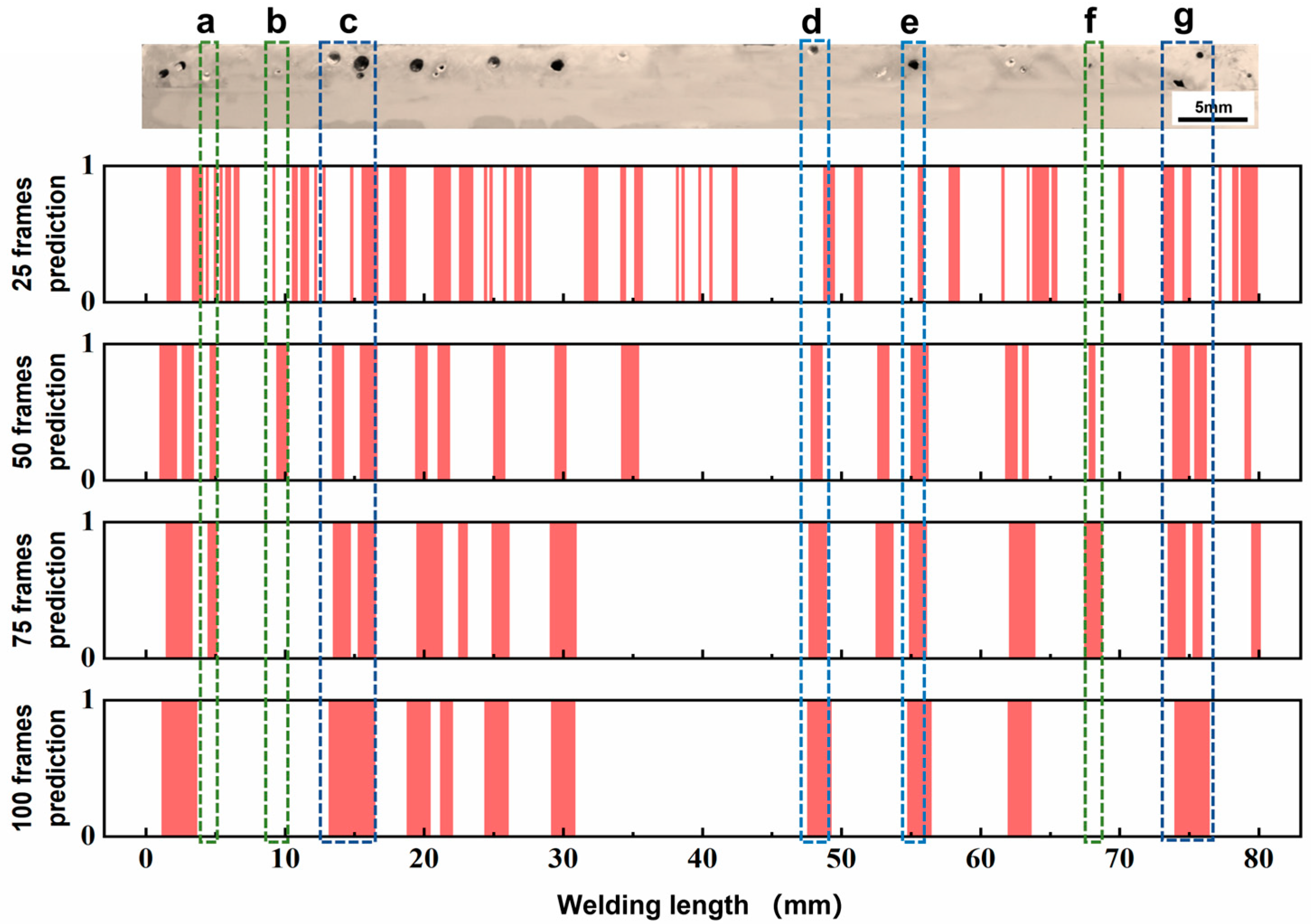
3.3. Influence Mechanism of Signal Segment Length
4. Conclusions
- (1)
- The VMD method was newly utilized to process the morphological signals of the laser plume in this study. More high-frequency components existed in the decomposition results, corresponding to the presence of keyhole-induced pores. By comparing with the EMD and EEMD methods, VMD had better robustness in processing the nonlinear and non-smooth welding signal. The decomposed signals had lower orthogonal coefficients, indicating that the mode mixing was sufficiently suppressed.
- (2)
- The time–frequency-domain feature extraction method is based on the signals after being decomposed by VMD. The feature dataset consisted of frequency-domain features from high-frequency components and time-domain features from low-frequency components. A BP neural network was developed and achieved 97.77% accuracy in pore prediction.
- (3)
- The length of the signal segment was a key parameter affecting the BP neural network accuracy. The best signal segment length was 0.4 mm. The reduction in the signal segment length failed to escape the prediction errors due to pore migration. Excessively long signal segments ignored the position of small-sized pores and the distinguishing dense pores, which was attributed to the decrease in correlation between features and defects caused by the feature dilution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Yin, X.; Liao, W.; Xiang, Y.; Gao, M.; Zhang, Y. Microstructure and properties of 6061/2A12 dissimilar aluminum alloy weld by laser oscillation scanning. J. Mater. Res. Technol. 2021, 14, 2789–2798. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.; Xiong, L.; Zhang, X.; Mi, G. Microstructural, porosity and mechanical properties of lap joint laser welding for 5182 and 6061 dissimilar aluminum alloys under different place configurations. Mater. Des. 2020, 191, 108625. [Google Scholar] [CrossRef]
- Tan, C.; Liu, Y.; Xu, B.; Wang, H.; Liu, F.; Gong, X.; Zeng, Z.; Chen, B.; Song, X. Numerical and experimental study of thermal fluid flow and keyhole dynamic in laser welding of aluminum alloy assisted by electromagnetic field. Opt. Laser Technol. 2023, 157, 108718. [Google Scholar] [CrossRef]
- Huang, L.; Hua, X.; Wu, D.; Fang, L.; Cai, Y.; Ye, Y. Effect of magnesium content on keyhole-induced porosity formation and distribution in aluminum alloys laser welding. J. Manuf. Process. 2018, 33, 43–53. [Google Scholar] [CrossRef]
- Huang, S.; Xu, L.; Lou, M.; Chen, H.; Zhang, K.; Li, Y. Keyhole-induced pore formation mechanism in laser-MIG hybrid welding of aluminum alloy based on experiment and multiphase numerical model. J. Mater. Process. Technol. 2023, 314, 117903. [Google Scholar] [CrossRef]
- Kim, H.; Nam, K.; Kim, Y.; Ki, H. Analysis of laser-beam absorptance and keyhole behavior during laser keyhole welding of aluminum alloy using a deep-learning-based monitoring system. J. Manuf. Process. 2022, 80, 75–86. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, P.; Yu, Z.; Gao, Y.; Zhang, H.; Chen, H.; Chen, S.; Tian, Y. Progress and perspectives of in-situ optical monitoring in laser beam welding: Sensing, characterization and modeling. J. Manuf. Process. 2022, 75, 767–791. [Google Scholar] [CrossRef]
- Luo, M.; Shin, Y.C. Estimation of keyhole geometry and prediction of welding defects during laser welding based on a vision system and a radial basis function neural network. Int. J. Adv. Manuf. Technol. 2015, 81, 263–276. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, K.-M.; Shin, Y.C. Deep-learning-based porosity monitoring of laser welding process. Manuf. Lett. 2020, 23, 62–66. [Google Scholar] [CrossRef]
- Geng, S.; Yang, W.; Jiang, P.; Han, C.; Ren, L. Numerical study of keyhole dynamics and porosity formation during high-power oscillating laser welding of medium-thick aluminum alloy plates. Int. J. Heat Mass Transf. 2022, 194, 123084. [Google Scholar] [CrossRef]
- Ma, D.; Jiang, P.; Shu, L.; Geng, S. Multi-sensing signals diagnosis and CNN-based detection of porosity defect during Al alloys laser welding. J. Manuf. Syst. 2022, 62, 334–346. [Google Scholar] [CrossRef]
- Xu, H.; Huang, H. In situ monitoring in laser melt injection based on fusion of infrared thermal and high-speed camera images. J. Manuf. Process. 2023, 92, 466–478. [Google Scholar] [CrossRef]
- Fan, X.; Gao, X.; Zhang, N.; Ye, G.; Liu, G.; Zhang, Y. Monitoring of 304 austenitic stainless-steel laser-MIG hybrid welding process based on EMD-SVM. J. Manuf. Process. 2022, 73, 736–747. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Zhang, Z.; Chen, H.; Chen, S. EMD-based pulsed TIG welding process porosity defect detection and defect diagnosis using GA-SVM. J. Mater. Process. Technol. 2017, 239, 92–102. [Google Scholar] [CrossRef]
- Hu, X.; Peng, S.; Hwang, W.-L. EMD Revisited: A New Understanding of the Envelope and Resolving the Mode-Mixing Problem in AM-FM Signals. IEEE Trans. Signal Process. 2012, 60, 1075–1086. [Google Scholar] [CrossRef]
- Qiao, N.; Wang, L.; Liu, Q.; Zhai, H. Multi-scale eigenvalues Empirical Mode Decomposition for geomagnetic signal filtering. Measurement 2019, 146, 885–891. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, B.; Han, X.; Tan, C.; Liu, F.; Zeng, Z.; Chen, B.; Song, X. Predicting laser penetration welding states of high-speed railway Al butt-lap joint based on EEMD-SVM. J. Mater. Res. Technol. 2022, 21, 1316–1330. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.; Chen, S.; Wang, J.; Zhang, X. Optimised ensemble empirical mode decomposition with optimised noise parameters and its application to rolling element bearing fault diagnosis. Insight 2016, 58, 494–501. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, D.; Lu, Y.; Kong, L.; Ma, Z. Online chatter detection in milling process based on fast iterative VMD and energy ratio difference. Measurement 2022, 194, 111060. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, Z.; Wang, Y.; Chen, H. Machined surface defects monitoring through VMD of acoustic emission signals. J. Manuf. Process. 2022, 79, 587–599. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Xiang, J. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement 2021, 168, 108402. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Z.; He, K.; Liu, Y.; Lu, Q.; Li, Q.; Liu, L.; Luo, R. Quality monitoring of aluminum alloy DPMIG welding based on broadband mode decomposition and MMC-FCH. Measurement 2020, 158, 107683. [Google Scholar] [CrossRef]
- Jahn, M. Artificial neural network regression models in a panel setting: Predicting economic growth. Econ. Model. 2020, 91, 148–154. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, C.; Cheng, J.; Chen, Z.; Wang, L.; Wang, K. Research of surface oxidation defects in copper alloy wire arc additive manufacturing based on time-frequency analysis and deep learning method. J. Mater. Res. Technol. 2023, 25, 511–521. [Google Scholar] [CrossRef]
- Koopman, B.O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Rockafellar, R.T. Lagrange Multipliers and Optimality. SIAM Rev. 1993, 35, 183–238. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, X.; Chen, Y.; Tao, W. Mitigation of porosity defects in fiber laser welding under low vacuum. J. Mater. Process. Technol. 2020, 276, 116385. [Google Scholar] [CrossRef]
- Lei, Z.; Wu, S.; Cao, B.; Li, B.; Liang, J.; Hu, X.; Chen, Y. Role of thermal fluid dynamics in alloying element distribution and weld porosity in powder feeding-based laser welding of Al alloy. Appl. Therm. Eng. 2020, 171, 115081. [Google Scholar] [CrossRef]
- Li, S.; Jiang, P.; Gao, Y.; Song, M.; Shu, L. A penetration depth monitoring method for Al-Cu laser lap welding based on spectral signals. J. Mater. Process. Technol. 2023, 317, 117972. [Google Scholar] [CrossRef]
- XuanRui, Y.; Feng, Z.G.; Hua, J.H.; Xiang, S.A. A data driven model for estimating the fatigue life of 7075-T651 aluminum alloy based on the updated BP model. J. Mater. Res. Technol. 2023, 24, 1252–1263. [Google Scholar] [CrossRef]
- Hahnloser, R.H.R.; Sarpeshkar, R.; Mahowald, M.A.; Douglas, R.J.; Seung, H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947–951. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A Comparative Study of Empirical Mode Decomposition-Based Short-Term Wind Speed Forecasting Methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise- assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]



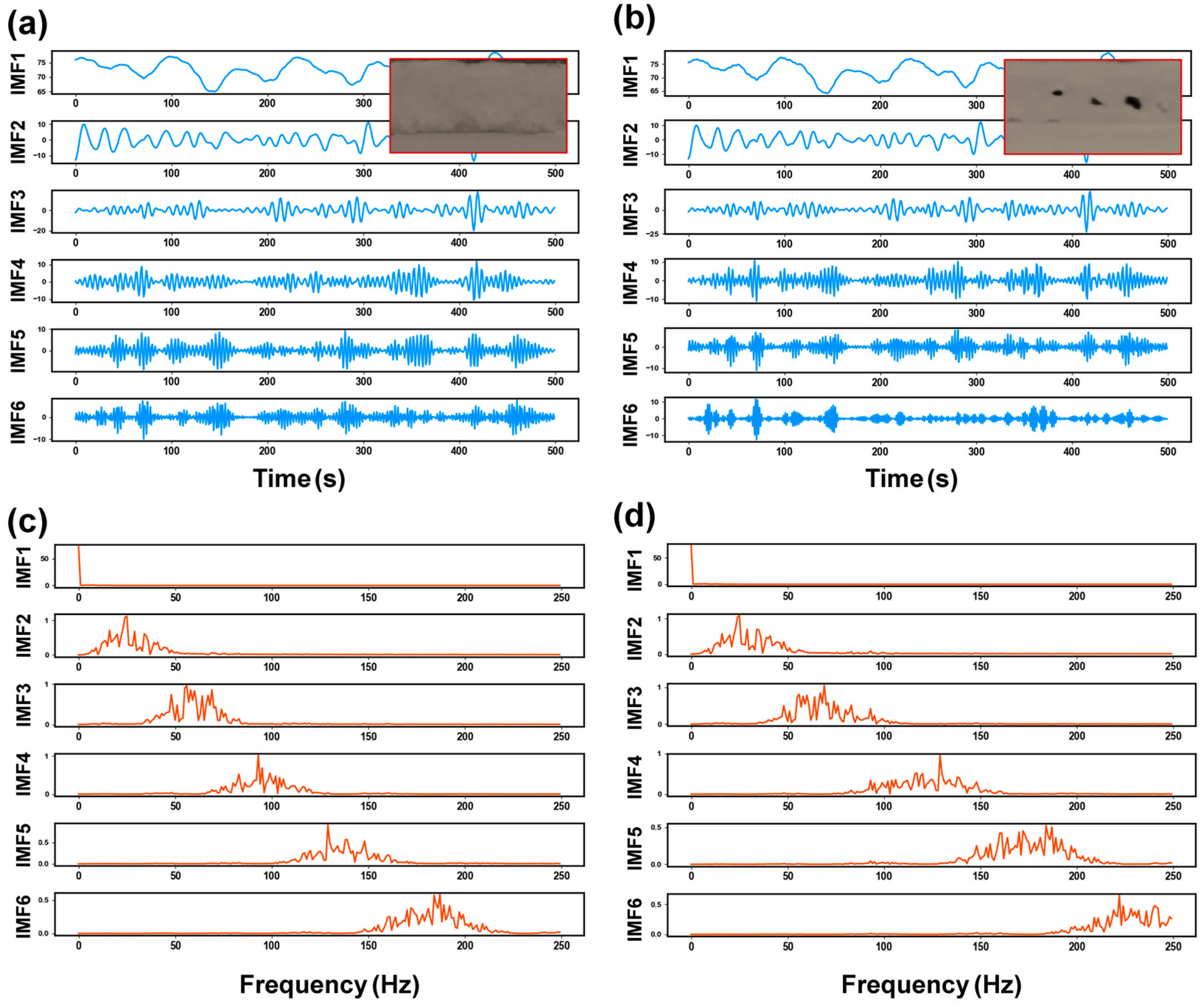

| Components | SampEn |
|---|---|
| Raw data | 0.358 |
| IMF1 | 0.357 |
| IMF2 | 0.362 |
| IMF3 | 0.652 |
| IMF4 | 0.542 |
| IMF5 | 0.674 |
| IMF6 | 0.598 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Dong, Y.; Liu, F.; Yang, B.; Han, X.; Wei, L.; Song, X.; Tan, C. A VMD-BP Model to Predict Laser Welding Keyhole-Induced Pore Defect in Al Butt–Lap Joint. Materials 2024, 17, 3270. https://doi.org/10.3390/ma17133270
Wang W, Dong Y, Liu F, Yang B, Han X, Wei L, Song X, Tan C. A VMD-BP Model to Predict Laser Welding Keyhole-Induced Pore Defect in Al Butt–Lap Joint. Materials. 2024; 17(13):3270. https://doi.org/10.3390/ma17133270
Chicago/Turabian StyleWang, Wei, Yang Dong, Fuyun Liu, Biao Yang, Xiaohui Han, Lianfeng Wei, Xiaoguo Song, and Caiwang Tan. 2024. "A VMD-BP Model to Predict Laser Welding Keyhole-Induced Pore Defect in Al Butt–Lap Joint" Materials 17, no. 13: 3270. https://doi.org/10.3390/ma17133270
APA StyleWang, W., Dong, Y., Liu, F., Yang, B., Han, X., Wei, L., Song, X., & Tan, C. (2024). A VMD-BP Model to Predict Laser Welding Keyhole-Induced Pore Defect in Al Butt–Lap Joint. Materials, 17(13), 3270. https://doi.org/10.3390/ma17133270







