Proposal for New Method for Calculating Sedimentation Process Efficiency in Water Treatment Plants
Abstract
:1. Introduction
1.1. Sizes of Particles of Irregular Shapes
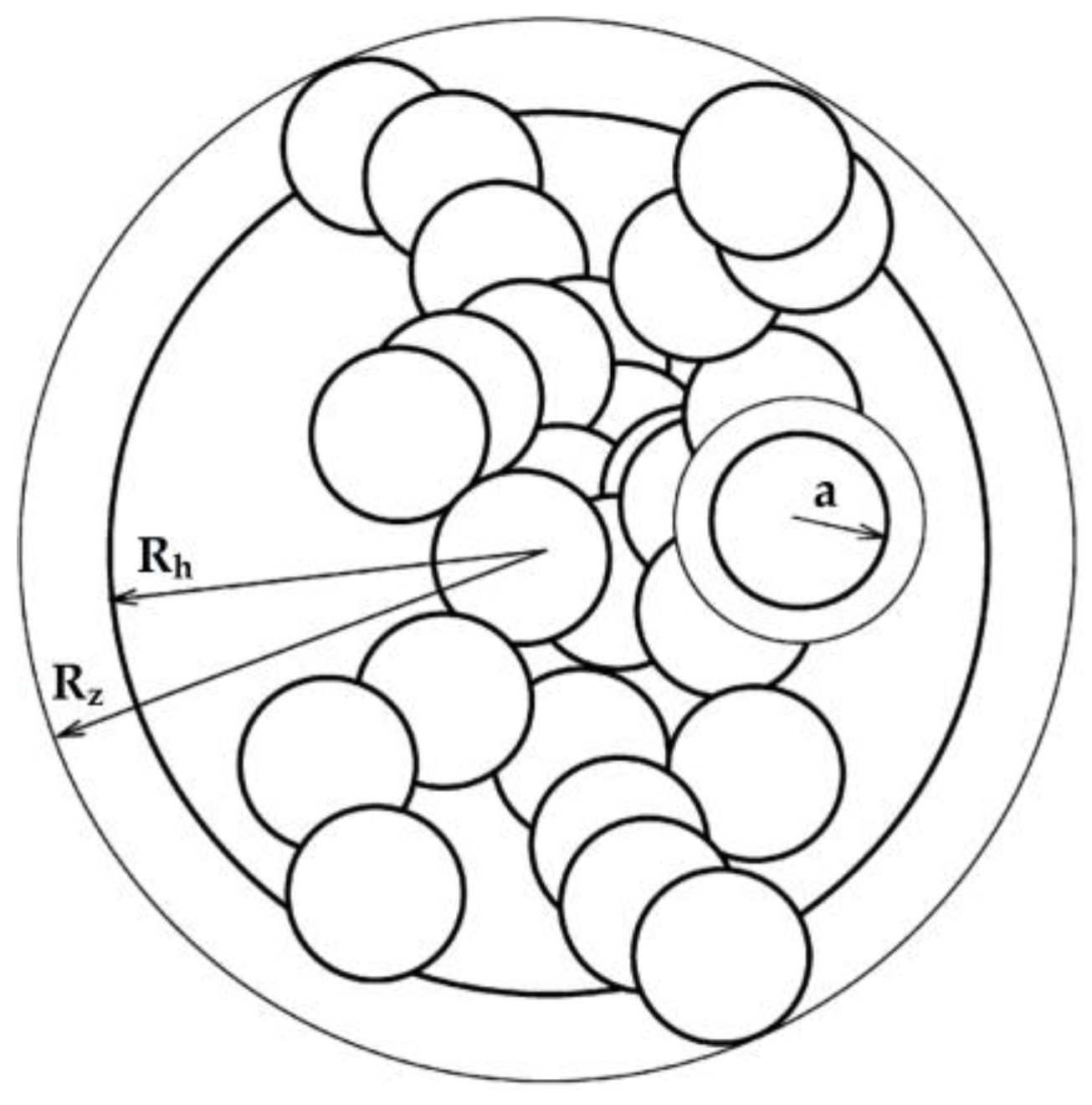
- The radius of the basic particle (primary particle)— or —for the presented model in Figure 1. For simplification, it is assumed that all of the basic particles in the aggregate have the same radius and have the shape of a sphere. An additional assumption is that the density of the basic particles is isotropic and constant for all of them.
- Outer radius——the radius of the smallest ball, in which the floc under investigation can be inserted—the radius of the bounding (circumscribed) sphere on the agglomerate. It can be determined by several direct (optic) methods, such as optical microscopy. An alternate name for the outer radius is the collision radius.
- Stokes–Einstein radius (hydrodynamic radius)——the radius of a sphere that has the same hydrodynamic drag as the floc under investigation. One important assumption is that the equivalent sphere is impermeable and only the drag of the flow is taken under consideration. The influence of advection flow through the volume of the particle is ignored. The Stokes radius allows us to determine the behaviour of the agglomerate as it is freefalling in the fluid.
- Radius of gyration—; this radius describes the distribution of mass of basic particles around the centre of gravity of the aggregate. It is defined as the mean square of the distance of the basic particles from the centre of mass of the aggregate, weighted against the mass of these particles.
1.2. Sedimentation Process
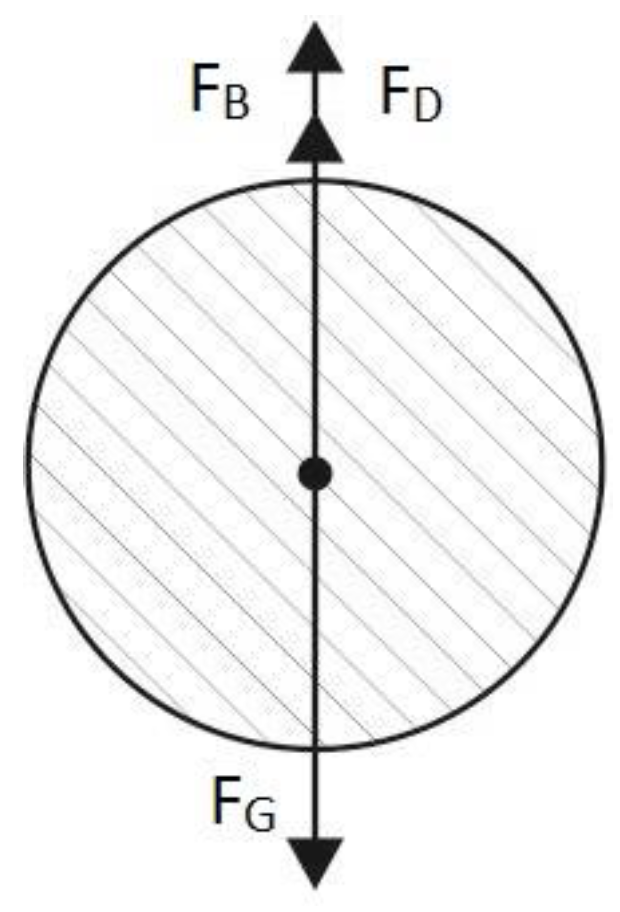
1.3. Phase Separation Efficiency—The Classical Model
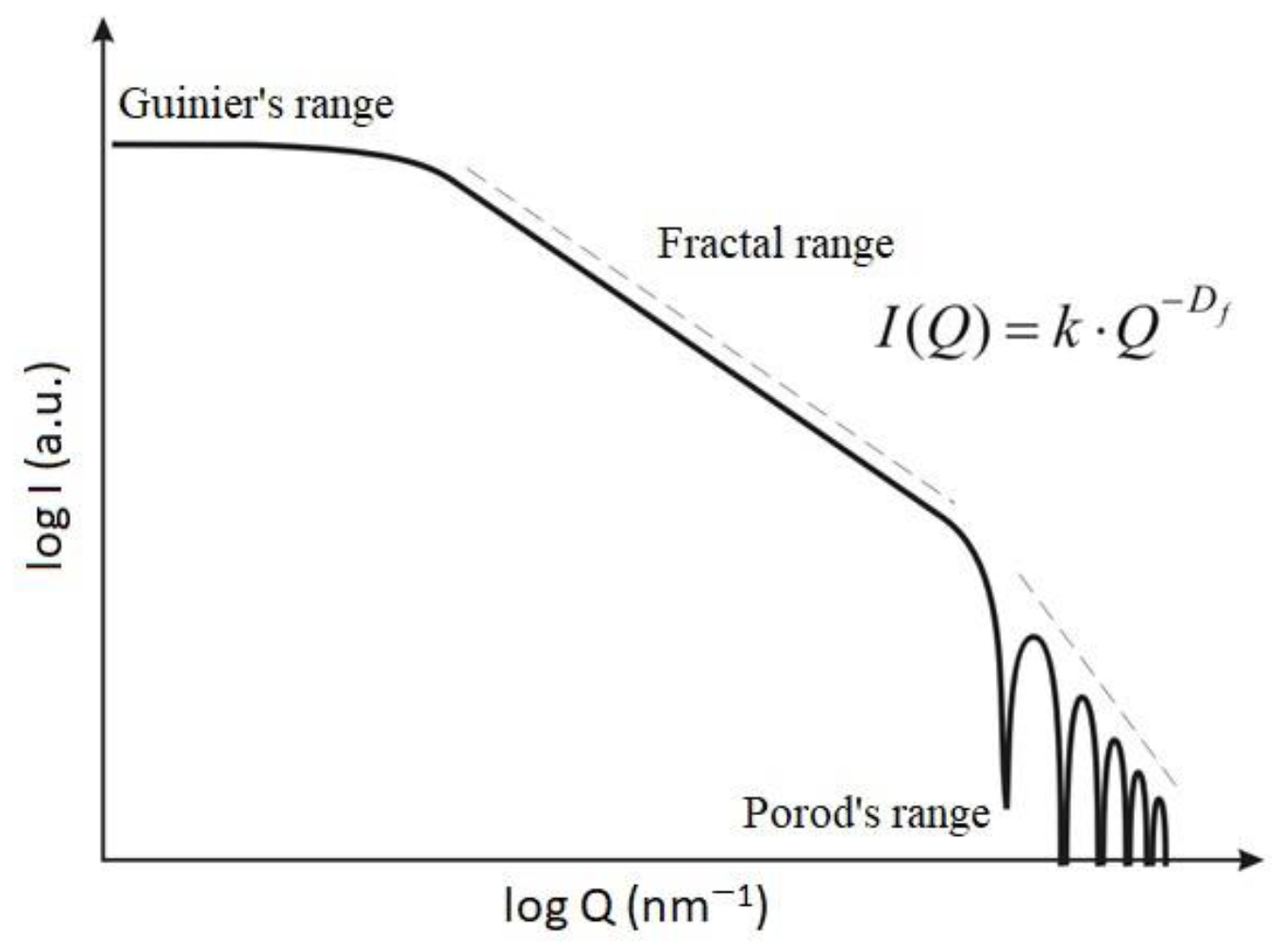
1.4. The Fractal Model
2. Materials and Methods
2.1. Materials
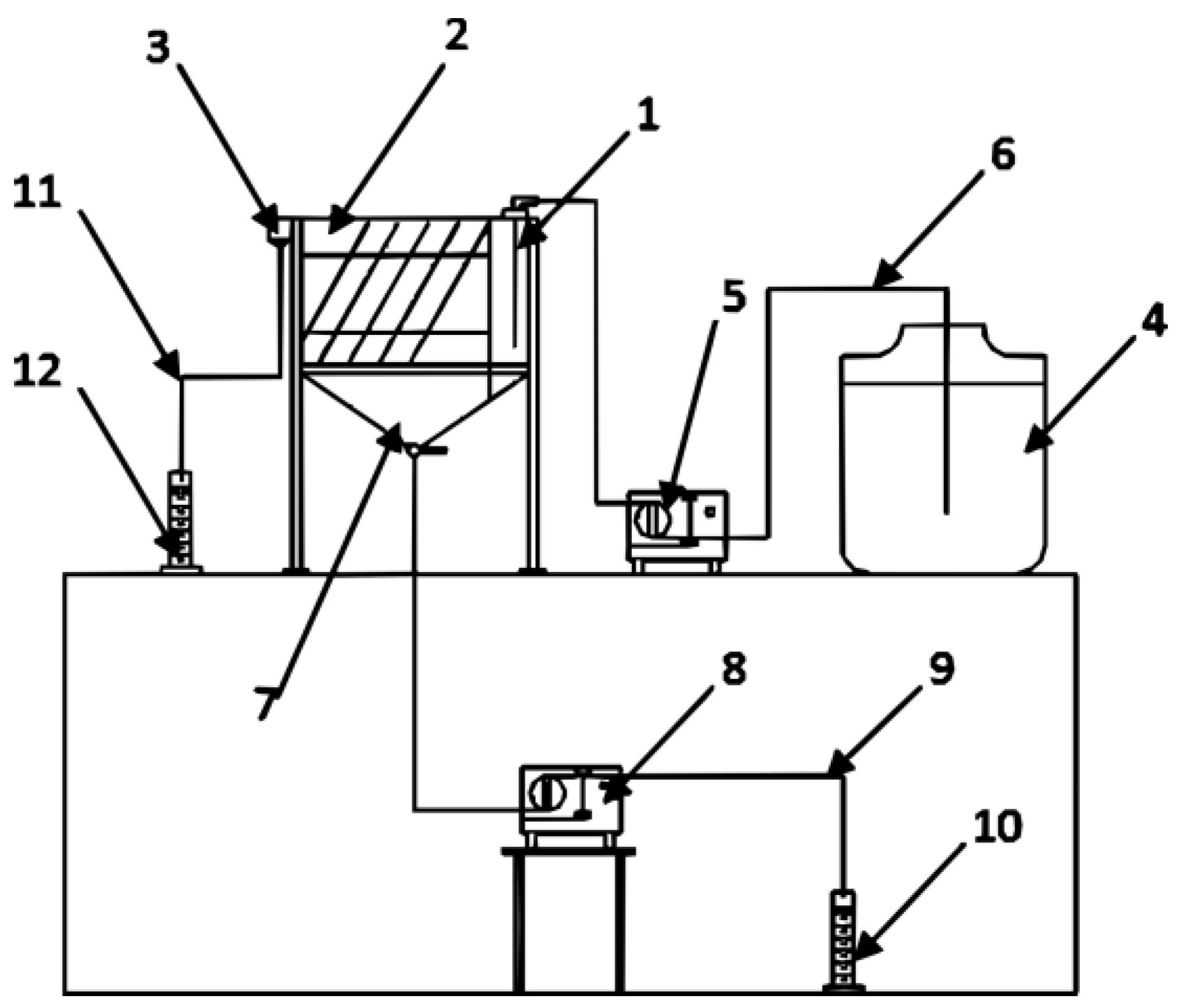
2.2. Methods and Procedures
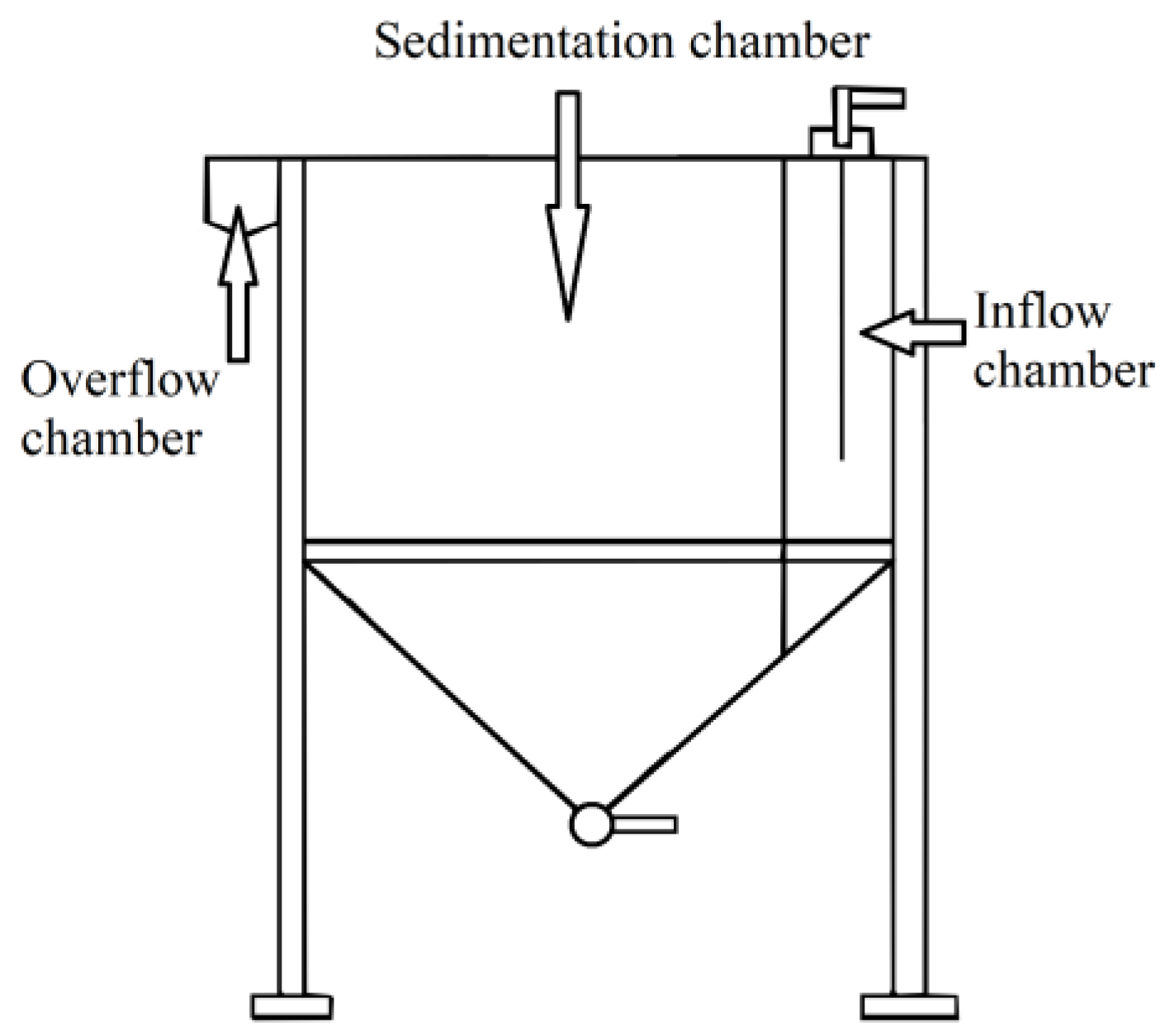
- Priming chamber—the chamber where tested suspension is supplied. In the priming chamber, uniform distribution of the suspension is obtained through a feed tube located over the entire height of the priming chamber and perforated baffle.
- Sedimentation chamber—the space where the multiflux lamella packet is placed. The precipitate is discharged outside the tank through a collector in the shape of funnel, which is located in the lower part of the sedimentation chamber.
- Overflow chamber—the chamber in which clear water after the sedimentation process is obtained through V-notch overflow into the overflow connector.
3. Results
- Measurement of several characteristic properties of solid-phase particles in suspension:
- The particle size distribution of aggregates/flocs in the form of parameters of the log-normal distribution (m and σ);
- The density of the solid phase of the suspension (and, from the information of the temperature during tests, the values of the density and viscosity of the fluid phase);
- The size of the basic (primary) particles and the value of the fractal dimension of aggregates/flocs in the suspension.
- Calculation of the diameter of the terminal particles by using a selected equation between the velocity of the free-falling particles and physico-chemical properties of the particles under consideration (the modified Stokes’ formula—Equation (28)—is used in the proposed method).
- Calculation of sedimentation efficiency with the use of information on terminal velocity and granulometric properties of the suspension (Equation (26) is used in the proposed method).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kowalski, W.P. Lamella Sedimentation—The State of Art and Directions of Development. Inżynieria Chem. I Proces. 2004, 25, 1163–1170. [Google Scholar]
- Turlej, T. Modern Sedimentation Techniques. In Proceedings of the Ecology, Economics, Education and Legislation, Conference Proceedings, SGEM 2018, Albena, Bulgaria, 2–8 July 2018; Volume 18, pp. 549–556. [Google Scholar]
- Hilger, B.; Banaś, M.; Wisła-Walsh, E.; Warzecha, P. Purification Efficiency for Selected Bentonites in Laboratory Settling Tank. In Proceedings of the Water Resources Forest, Marine and Ocean Ecosystems, Conference Proceedings, SGEM 2016, Vienna, Austria, 2 November 2016; Volume 3, pp. 227–234. [Google Scholar]
- WHO. Guidelines for Drinking-Water Quality; Fourth Edition Incorporating the First and Second Addenda; World Health Organization: Geneva, Switzerland, 2022; ISBN 978-92-4-004506-4. [Google Scholar]
- Nadella, M.; Sharma, R.; Chellam, S. Fit-for-Purpose Treatment of Produced Water with Iron and Polymeric Coagulant for Reuse in Hydraulic Fracturing: Temperature Effects on Aggregation and High-Rate Sedimentation. Water Res. 2020, 170, 115330. [Google Scholar] [CrossRef] [PubMed]
- Maggi, F. Experimental Evidence of How the Fractal Structure Controls the Hydrodynamic Resistance on Granular Aggregates Moving through Water. J. Hydrol. 2015, 528, 694–702. [Google Scholar] [CrossRef]
- Sharma, G.; Ray, B. Numerical Simulation of Square Shaped Particle Sedimentation. Particuology 2024, 84, 107–116. [Google Scholar] [CrossRef]
- Choe, Y.; An, J.; Won, J. Sedimentation Kinetics of Kaolinitic and Illitic Clay: Impact of Cation Valence, Ionic Concentration, and Water Content. Appl. Clay Sci. 2024, 253, 107351. [Google Scholar] [CrossRef]
- Wang, S.; Gao, H.; Jia, S.; Gu, M.; Shi, F.; Yao, X. Settling Velocity of Atmospheric Particles in Seawater: Based on Hydrostatic Sedimentation Method Using Video Imaging Techniques. Mar. Pollut. Bull. 2024, 203, 116472. [Google Scholar] [CrossRef] [PubMed]
- Jin, B.; Wilén, B.-M.; Lant, P. A Comprehensive Insight into Floc Characteristics and Their Impact on Compressibility and Settleability of Activated Sludge. Chem. Eng. J. 2003, 95, 221–234. [Google Scholar] [CrossRef]
- Yokojima, S.; Takashima, R.; Asada, H.; Miyahara, T. Impacts of Particle Shape on Sedimentation of Particles. Eur. J. Mech. B/Fluids 2021, 89, 323–331. [Google Scholar] [CrossRef]
- Turlej, T. Parametric Modeling of Recording Sedimentation Curve. Przemysł Chem. 2020, 1, 115–117. [Google Scholar] [CrossRef]
- Bushell, G.C.; Yan, Y.D.; Woodfield, D.; Raper, J.; Amal, R. On Techniques for the Measurement of the Mass Fractal Dimension of Aggregates. Adv. Colloid Interface Sci. 2002, 95, 1–50. [Google Scholar] [CrossRef]
- Jarvis, P.; Jefferson, B.; Parsons, S.A. Measuring Floc Structural Characteristics. Rev. Env. Sci. Biotechnol. 2005, 4, 1–18. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundation and Applications, 2003rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2003. [Google Scholar]
- Gmachowski, L. Fractal Aggregate Model of Sedimenting Macromolecules. Polymer 2005, 46, 10443–10449. [Google Scholar] [CrossRef]
- Błażejewski, R. Sedymentacja Cząstek Ciała Stałego; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2015. [Google Scholar]
- Gregory, J. Particles in Water: Properties and Processes; CRC Press: Boca Raton, FL, USA, 2006; ISBN 978-1-58716-085-1. [Google Scholar]
- Lin, M.Y.; Lindsay, H.M.; Weitz, D.A.; Ball, R.C.; Klein, R.; Meakin, P. Universality in Colloid Aggregation. Nature 1989, 339, 360. [Google Scholar] [CrossRef]
- Miyahara, K.; Adachi, Y.; Nakaishi, K.; Ohtsubo, M. Settling Velocity of a Sodium Montmorillonite Floc under High Ionic Strength. Colloids Surf. A Physicochem. Eng. Asp. 2002, 196, 87–91. [Google Scholar] [CrossRef]
- Adachi, Y.; Tanaka, Y. Settling Velocity of an Aluminium-Kaolinite Floc. Water Res. 1997, 31, 449–454. [Google Scholar] [CrossRef]
- Winterwerp, J.C. A Simple Model for Turbulence Induced Flocculation of Cohesive Sediment. J. Hydraul. Res. 1998, 36, 309–326. [Google Scholar] [CrossRef]
- Khelifa, A.; Hill, P.S. Models for Effective Density and Settling Velocity of Flocs. J. Hydraul. Res. 2006, 44, 390–401. [Google Scholar] [CrossRef]
- Gmachowski, L. Aggregate Structure and Hydrodynamics of Aggregated Systems. Colloids Surf. A Physicochem. Eng. Asp. 2005, 255, 105–110. [Google Scholar] [CrossRef]
- Kowalski, W.P. Osadniki Wielostrumieniowe; Wydawnictwa AGH: Kraków, Poland, 2004. [Google Scholar]
- Warzecha, P.; Kowalski, W.P. Badania Przepływu Zawiesiny i Efektywności Sedymentacji w Modelu Wielostrumieniowego Osadnika Prostopadłoprądowego—[Research of Suspension Flow and Efficiency of Sedimentation in Cross-Current Settling Tank Model]; Wydział Inżynierii Mechanicznej i Robotyki AGH. Katedra Systemów Energetycznych i Urządzeń Ochrony Środowiska: Kraków, Poland, 2017. [Google Scholar]
- Mouzon, J.; Bhuiyan, I.U.; Hedlund, J. The Structure of Montmorillonite Gels Revealed by Sequential Cryo-XHR-SEM Imaging. J. Colloid Interface Sci. 2016, 465, 58–66. [Google Scholar] [CrossRef]
- ISO 7027-1:2016; Water Quality—Determination of Turbidity. Part 1: Quantitative Methods. ISO: Geneva, Switzerland, 2016.
- Warzecha, P.; Hilger, B. Coagulation Behaviour of Bentonite Clay Suspensions; SGEM: Mogadishu, Somalia, 2018; Volume 18, pp. 235–244. [Google Scholar]
- Kowalski, W.; Banaś, M. Obtaining Parameters of Granulometric Characteristics of Suspension with Usage Computer Controlled Sedimentation Balance. Vìsnik Nacìonal’nogo Unìversitetu “L’vìvs’ka Polìtehnìka” 2004, 501, 62–68. [Google Scholar]
- Besra, L.; Sengupta, D.K.; Roy, S.K. Particle Characteristics and Their Influence on Dewatering of Kaolin, Calcite and Quartz Suspensions. Int. J. Miner. Process. 2000, 59, 89–112. [Google Scholar] [CrossRef]
- Kerry, R.; Rawlins, B.G.; Oliver, M.A.; Lacinska, A.M. Problems with Determining the Particle Size Distribution of Chalk Soil and Some of Their Implications. Geoderma 2009, 152, 324–337. [Google Scholar] [CrossRef]
- Wang, Q.; Cui, Y.-J.; Minh Tang, A.; Xiang-Ling, L.; Wei-Min, Y. Time- and Density-Dependent Microstructure Features of Compacted Bentonite. Soils Found. 2014, 54, 657–666. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Zhang, X.-X.; Liu, X.-M.; Ye, W.-M.; Wang, Q. Effects of Graphene Content and Dry Density on Swelling Pressure of Graphene-Modified GMZ Bentonite. Constr. Build. Mater. 2022, 342, 128066. [Google Scholar] [CrossRef]

| Name | Description | Formula |
|---|---|---|
| Perimeter diameter | Diameter of a circle with the same perimeter as the considered particle | |
| Projection area diameter | Diameter of a disk with the same projected cross-sectional surface as the considered particle | |
| Surface diameter | Diameter of a sphere with the same surface as the considered particle | |
| Volumetric diameter (equivalent spherical diameter) | Diameter of a sphere with the same volume as considered the particle | |
| Surface volume diameter or Sauter mean diameter | Diameter of a sphere with the same ratio of surface area to volume as the considered particle | |
| Free-falling diameter | Diameter of a sphere with the same density and free-falling velocity that the considered particle has in the same fluid medium (at the same density and viscosity) | |
| Stokes diameter | As above, but with Reynolds number Re < 0.2 | |
| Feret diameter | Distance between the two parallel planes restricting the object perpendicular to that direction | |
| Martin diameter | Length of the chord parallel to a fixed direction, which splits the particle projected area into two equal parts | |
| Circumscribing diameter | Diameter of the smallest circle that circumscribes the outline of the particle | |
| Inscribing diameter | Diameter of the biggest circle which fits inside the outline of the projected particle. |
| Correction Factor | Description | Formula |
|---|---|---|
| Form factor (FF) | Deviation of an object from a circle; it is especially well used for describing “rough” particles. For circular particles, FF assumes the value of one. | |
| Three-dimensional aspect ratio (aspect ratio) (AR) | It is very sensitive to the extension of an object, where the more elongated the object is, the larger the value of this coefficient; as above, circles have the AR of one. | |
| Elongation factor | The more elongated the shape of a particle, the higher its elongation factor. | |
| Roundness (RD) | It is mainly influenced by the elongation of an object, and it varies between 1 (circle) and 0. | |
| Heywood circularity factor | Perimeter divided by the circumference of a circle with the same area. The closer the shape of a particle is to a disk, the closer the Heywood circularity factor is to 1. | |
| Feret factor | Ratio of Feret diameters (horizontal and vertical). | |
| Malinowska factor | Relationship between perimeter and cross-sectional area of particle. | |
| Elongated shape factor | Square root of the two second moments of the particle around its principal axis. | |
| Compactness shape factor | Function of the polar second moment of a particle and a circle of equal area. | |
| Wadell’s spherical factor (sphericity) | Surface area of a sphere of the same volume as the particle divided by the actual surface area of the particle. | |
| Brockmann’s dynamic shape factor | Flow resistance of particle and flow resistance of equivalent diameter of a sphere with the same mass as the particle. |
| Author/s | Comments | Formula |
|---|---|---|
| Lin and Lindsay [19] | Number of basic particles, permeability and hydrodynamic radius are used for calculation. fragment results from permeability and provides information about the degree of filling of the aggregate with basic particles. | |
| Miyahara [20] | Number of basic particles and density of fractal aggregate are used for calculation. describes the density of the fractal aggregate. | |
| Adachi and Tanaka [21] | Similar method to Miyahara’s, where the additional factor α describes the permeability and the shape of the non-grainy particle. | |
| Witnterwerp [22] | Flow resistance coefficient from function of Reynolds number and shape factors, which are assumed a priori. α, β—shape factors, where for spheres, α=β=1. Re—Reynolds number. | |
| Khelifa [23] | Similar method to Winterwerp’s, it works well with polydisperse suspensions. θ—shape factor, where for spheres, it has value1. d50—median of polydispersed particles. ϕ—value of dispersion of basic particles. | |
| Gmachowski [24] | Dependences between value of hydrodynamic radius Rh and radius of the aggregate R (radius of circumscribed sphere), where rp—radius of basic particle. | |
| Bushell [13] | This formula includes flow resistance, permeability of particle and the fact that due to permeability of the particle, its flow resistance coefficient is smaller. k—structural coefficient of fractal aggregate. kcorr—correctional coefficient which includes shape of particle and influence of permeability on flow resistance coefficient. |
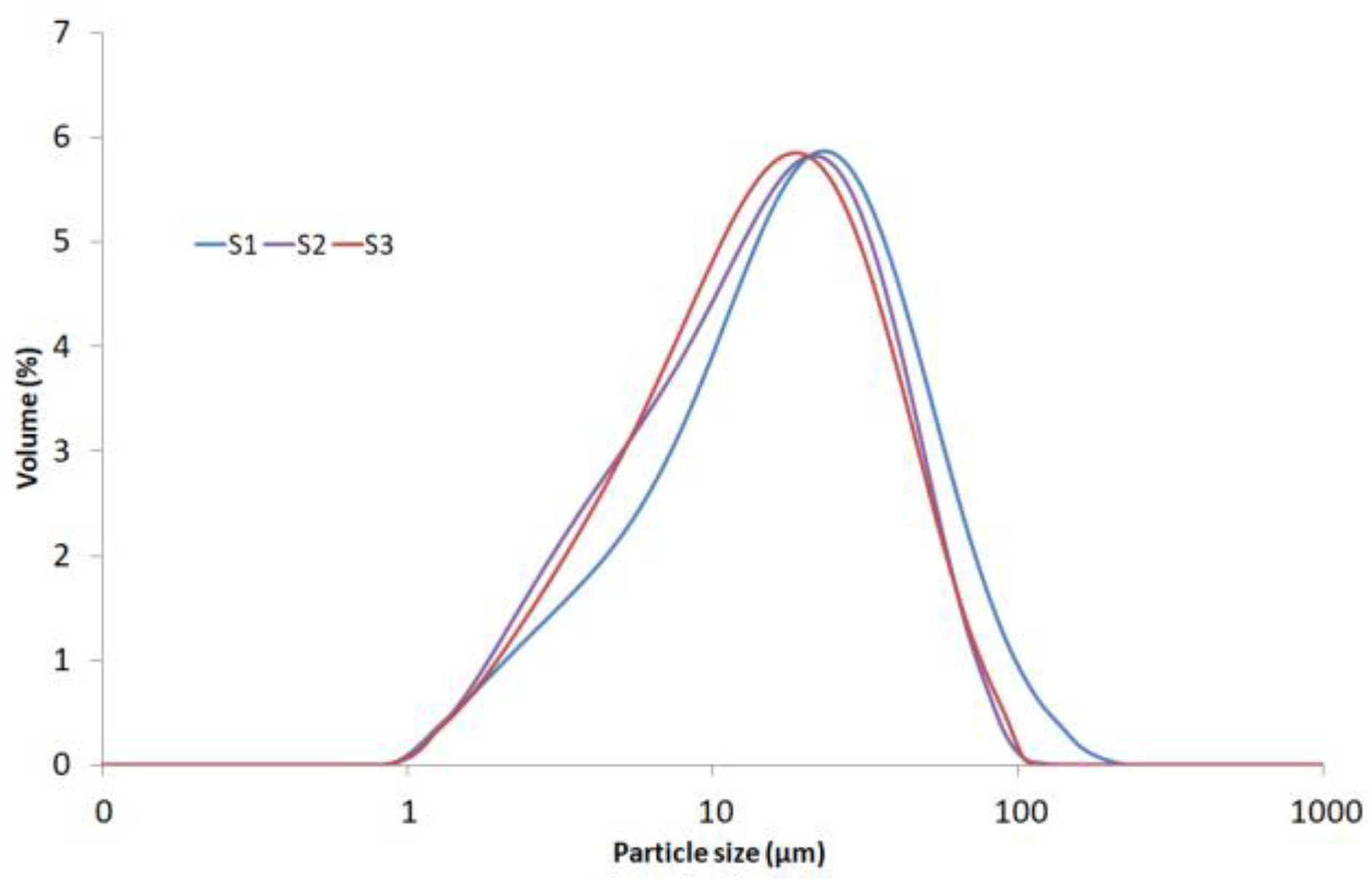
| Kind of Bentonite | Parameters of Log-Normal Distribution | Median (μm) | |||
|---|---|---|---|---|---|
| m | σ | R2 | Sedimentation Balance | Laser Diffraction Analyser | |
| S1 | 2.84 | 0.56 | 0.993 | 17.1 | 17.5 |
| S2 | 2.83 | 0.47 | 0.990 | 16.9 | 14.2 |
| S3 | 2.65 | 0.77 | 0.990 | 14.2 | 13.8 |
| Bentonite | Weight (g) | Average Volume (cm3) | Average Density (g/cm3) |
|---|---|---|---|
| S1 | 2.0256 | 0.7601 | 2.6650 |
| S2 | 1.6959 | 0.6397 | 2.6511 |
| S3 | 2.3590 | 0.8431 | 2.7980 |
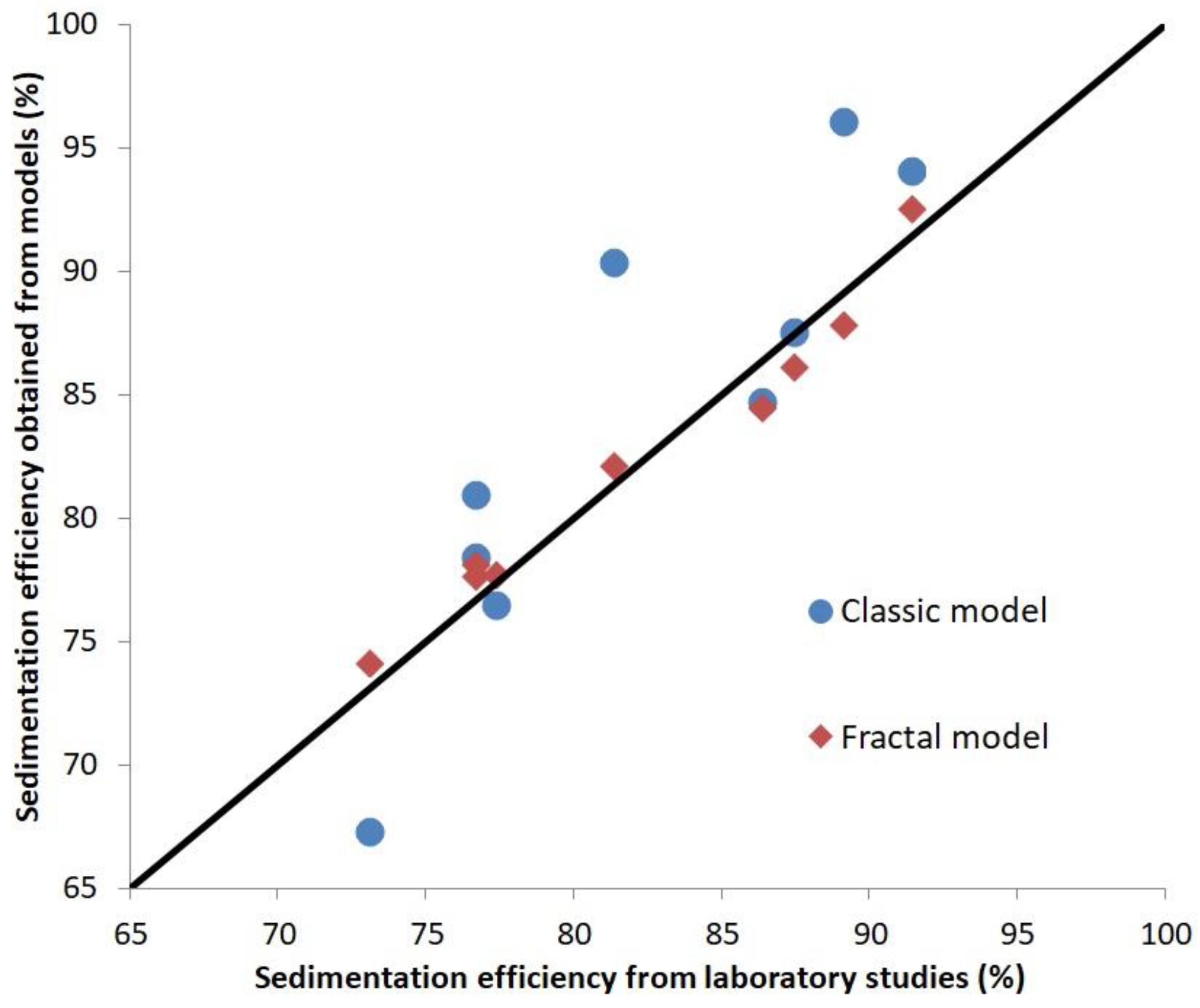
| Sample | Surface Load | Sedimentation Efficiency | Differences in Efficiency of Sedimentation | |||
|---|---|---|---|---|---|---|
| Data from Sedimentation Test | Classical Model of Sedimentation | Fractal Model of Sedimentation | ||||
| ηb | ηmk | ηmf | ηb − ηmk | ηb − ηmf | ||
| m3/m2h | % | % | % | p.p. | p.p. | |
| S1 | 0.3 | 91.42 | 94.12 | 92.62 | −2.70 | −1.20 |
| S1 | 0.5 | 87.47 | 87.62 | 86.20 | −0.15 | 1.47 |
| S1 | 0.8 | 76.67 | 78.46 | 78.19 | −1.79 | −1.52 |
| S2 | 0.3 | 89.12 | 96.17 | 87.88 | −7.05 | 1.24 |
| S2 | 0.5 | 81.37 | 90.46 | 82.18 | −9.09 | −0.81 |
| S2 | 0.8 | 76.67 | 81.00 | 77.70 | −4.33 | −1.03 |
| S3 | 0.3 | 86.38 | 84.78 | 84.52 | 1.60 | 1.86 |
| S3 | 0.5 | 77.39 | 76.56 | 77.73 | 0.83 | −0.34 |
| S3 | 0.8 | 73.07 | 67.35 | 74.18 | 5.72 | −1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banaś, M.; Hilger, B. Proposal for New Method for Calculating Sedimentation Process Efficiency in Water Treatment Plants. Materials 2024, 17, 3285. https://doi.org/10.3390/ma17133285
Banaś M, Hilger B. Proposal for New Method for Calculating Sedimentation Process Efficiency in Water Treatment Plants. Materials. 2024; 17(13):3285. https://doi.org/10.3390/ma17133285
Chicago/Turabian StyleBanaś, Marian, and Bartłomiej Hilger. 2024. "Proposal for New Method for Calculating Sedimentation Process Efficiency in Water Treatment Plants" Materials 17, no. 13: 3285. https://doi.org/10.3390/ma17133285





