USAF Characteristic K Approach: A Robust Tool for Predicting Fatigue Crack Growth under Various Underload Spectra
Abstract
:1. Introduction
- USAF MIL-STD-1530Dc stipulates that the airworthiness certification of military aircraft necessitates a durability analysis. This analysis should follow a building block approach, where the equation describing crack growth under constant amplitude loads must demonstrate its capability to handle more intricate, real-world load spectra;
- While the 2014 review paper [7] notes, that several crack growth equations are typically employed for assessing the damage tolerance of conventionally manufactured metals, their effectiveness in accurately forecasting the growth of small, naturally occurring cracks in AM components and cold spray repairs has not yet been confirmed.
2. The USAF Characteristic K Approach
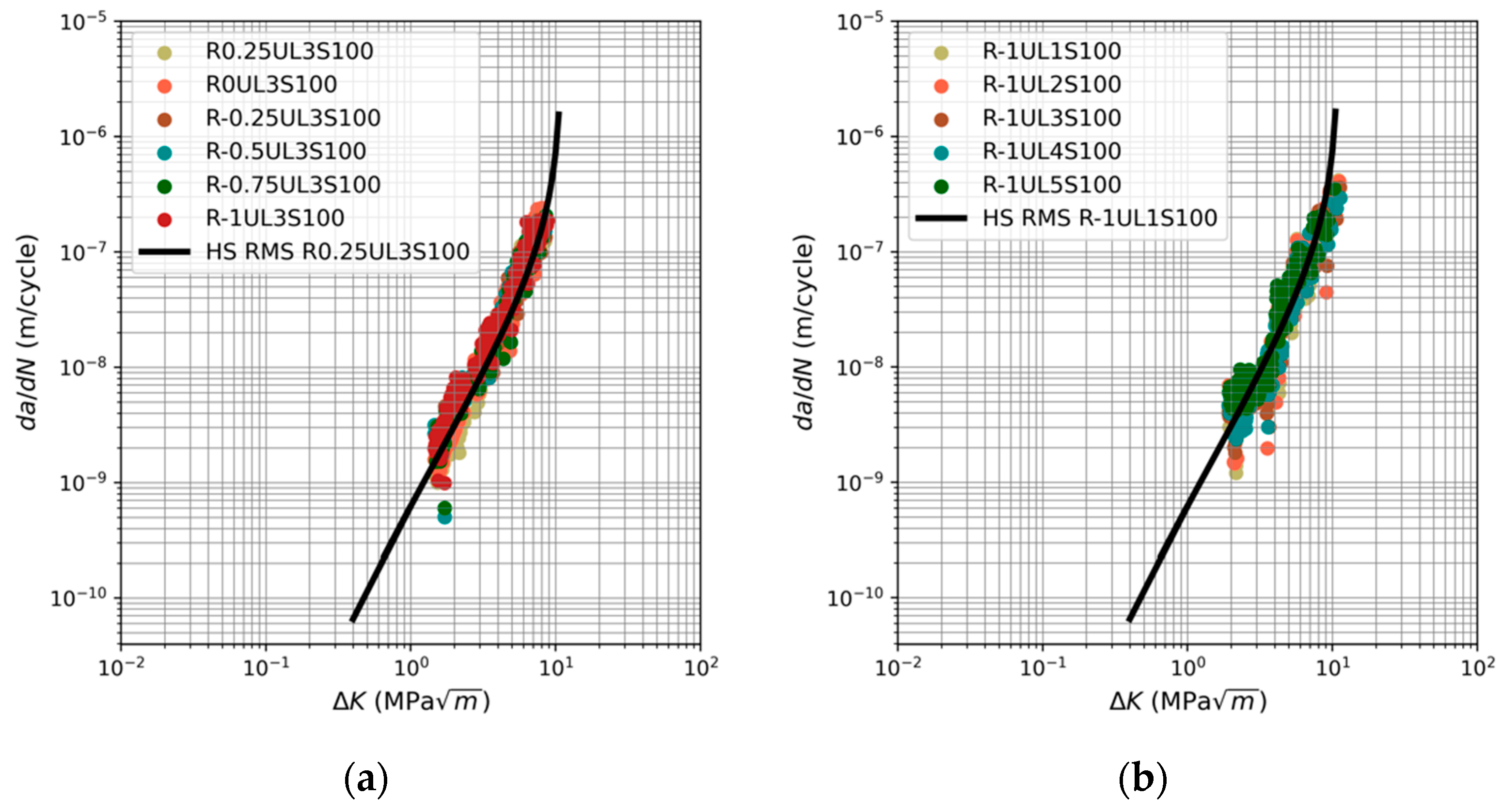
3. Fatigue Crack Growth under a Range of Underload Spectra
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | crack length |
| D,m | constants in the Hartman–Schijve and Nasgro crack growth equations |
| AM | additive manufacturing |
| da/dN | rate of fatigue crack growth |
| β | beta (geometry) factor |
| K | stress intensity factor |
| Kmax | maximum stress intensity factor |
| Kchar | characteristic stress intensity factor |
| ΔKchar | characteristic stress intensity factor range |
| ΔKchar,thr | fatigue threshold associated with ΔKchar |
| Krms | the rms value of stress intensity factor |
| ΔKrms | the rms value of stress intensity factor range |
| ΔKrms,thr | fatigue threshold associated with ΔKrms |
| σchar | characteristic stress |
| σrms | rms value of stress |
| A | cyclic fracture toughness |
| DADT | durability and damage tolerance |
| LEFM | linear elastic fracture mechanics |
| NASA | North American Space Administration |
| DoD | Department of Defense |
| USAF | United States Air Force |
References
- Under Secretary of Defense. Acquisition and Sustainment, Directive-Type Memorandum (DTM)-19-006-Interim Policy and Guidance for the Use of Additive Manufacturing (AM) in Support of Material Sustainment. Pentagon: Washington, DC, USA. Available online: https://oldcc.gov/sites/default/files/news/Directive-type-Memorandum.pdf (accessed on 13 April 2024).
- US Army Directive 2019-29. Enabling Readiness and Modernization through Advanced Manufacturing. Secretary of the Army, Pentagon: Washington, DC, USA. Available online: https://armypubs.army.mil/epubs/DR_pubs/DR_a/pdf/web/ARN19451_AD2019-29_Web_Final.pdf (accessed on 13 April 2024).
- Structures Bulletin EZ-SB-19-01. Durability and Damage Tolerance Certification for Additive Manufacturing of Aircraft Structural Metallic Parts. Available online: https://daytonaero.com/usaf-structures-bulletins-library/ (accessed on 15 February 2024).
- McMichael, E.; Frazier, W.; NAVAIR Additive Manufacturing. Joint Federal Aviation Administration–Air Force Workshop on Qualification/Certification of Additively Manufactured Parts (DOT/FAA/TC-16/15). Available online: http://www.tc.faa.gov/its/worldpac/techrpt/tc16-15.pdf (accessed on 4 January 2024).
- MIL-STD-1530D; Department of Defense Standard Practice Aircraft Structural Integrity Program (ASIP). Military and Government Specs & Standards (Naval Publications and Form Center) (NPFC): Philadelphia, PA, USA, 2016. Available online: http://everyspec.com/MIL-STD/MIL-STD-1500-1599/MIL-STD-1530D_55392/ (accessed on 2 January 2024).
- Molent, L. Aircraft Fatigue Management; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar] [CrossRef]
- Jones, R. Fatigue crack growth and damage tolerance. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 463–483. [Google Scholar] [CrossRef]
- Kundu, S.; Jones, R.; Peng, D.; Matthews, N.; Alankar, A.; Raman, S.R.K.; Huang, P. Review of requirements for the durability and damage tolerance certification of additively manufactured aircraft structural parts and AM repairs. Materials 2020, 13, 1341. [Google Scholar] [CrossRef] [PubMed]
- E647-13a; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM: Montgomery County, PA, USA, 2013. [CrossRef]
- Champagne, V.K. The Cold Spray Materials Deposition Process: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2007; p. 362. Available online: https://search.worldcat.org/title/191557639 (accessed on 13 April 2024).
- Matthews, N. Additive Metal Technologies for Aerospace Sustainment. In Aircraft Sustainment and Repair; Butterworth-Heinemann: Oxford, UK, 2018; pp. 845–862. [Google Scholar] [CrossRef]
- Peng, D.; Tang, C.; Matthews, N.; Jones, R.; Kundu, S.; Raman, R.K.S.; Alankar, A. Computing the Fatigue Life of Cold Spray Repairs to Simulated Corrosion Damage. Materials 2021, 14, 4451. [Google Scholar] [CrossRef] [PubMed]
- Champagne, V.; Matthews, N.; Champagne, V. Introduction to Supersonic Particle Deposition. In Aircraft Sustainment and Repair; Butterworth-Heinemann: Oxford, UK, 2018; pp. 799–844. [Google Scholar] [CrossRef]
- JSSG-2006; Joint Service Specification Guide: Aircraft Structures. DoD: Arlington County, VI, USA, 1998.
- NASA-HDBK-5010; Fracture Control Handbook for Payloads, Experiments, And Similar Hardware. NASA: Washington, DC, USA, 2007.
- Wanhill, R.; Barter, S.; Molent, L. Fatigue Crack Growth Failure and Lifing Analyses for Metallic Aircraft Structures and Components; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Lo, M.; Jones, R.; Bowler, A.; Dorman, M.; Edwards, D. Crack growth at fastener holes containing intergranular cracking. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1664–1675. [Google Scholar] [CrossRef]
- Huang, P.; Peng, D.; Jones, R. The USAF characteristic K approach for cracks growing from small material discontinuities under combat aircraft and civil aircraft load spectra. Eng. Fail. Anal. 2017, 80, 39–48. [Google Scholar] [CrossRef]
- Virkler, D.A.; Hillberry, B.M.; Goel, P.K. The statistical nature of fatigue crack propagation. Trans. ASME 1979, 101, 148–153. [Google Scholar] [CrossRef]
- Hassanipour, M.; Verreman, Y.; Lanteigne, J.; Chen, J.Q. Effect of periodic underloads on fatigue crack growth in three steels used in hydraulic turbine runners. Int. J. Fatigue 2016, 85, 40–48. [Google Scholar] [CrossRef]
- Iranpour, M.; Taheri, F. On the effect of stress intensity factor in evaluating the fatigue crack growth rate of aluminum alloy under the influence of compressive stress cycles. Int. J. Fatigue 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Silva, F.S. Fatigue crack propagation after overloading and underloading at negative stress ratios. Int. J. Fatigue 2007, 29, 1757–1771. [Google Scholar] [CrossRef]
- Silva, F.S. The importance of compressive stresses on fatigue crack propagation rate. Int. J. Fatigue 2005, 27, 1441–1452. [Google Scholar] [CrossRef]
- Zitounis, V.; Irving, P.E. Fatigue crack acceleration effects during tensile underloads in 7010 and 8090 aluminium alloys. Int. J. Fatigue 2007, 29, 108–118. [Google Scholar] [CrossRef]
- Gallagher, J.P.; Giessler, F.J.; Berens, A.P.; Engle, R.M. USAF Damage Tolerant Design Handbook: Guidelines for the Analysis and Design of Damage Tolerant Aircraft Structures; AFWAL-TR-82-3073; Air Force Research Laboratory, Wright-Patterson Air Force Base: Dayton, OH, USA, 1985. [Google Scholar]
- Miedlar, P.C.; Berens, A.P.; Gunderson, A.; Gallagher, J.P. Analysis and Support Initiative for Structural Sechnology (ASIST) AFRL-VA-WP-TR-2003-3002.2003. Available online: https://apps.dtic.mil/sti/pdfs/ADA411872.pdf (accessed on 2 January 2024).
- Kim, S.T.; Tadjiev, D.; Yang, H.T. Fatigue Life Prediction under Random Loading Conditions in 7475-T7351 Aluminum Alloy using the RMS Model. Int. J. Damage Mech. 2006, 15, 89–102. [Google Scholar] [CrossRef]
- Gallagher, J.P.; Molent, L. The equivalence of EPS and EIFS based on the same crack growth life data. Int. J. Fatigue 2015, 80, 162–170. [Google Scholar] [CrossRef]
- Zhuang, W.Z.; McDonald, M.; Phillips, M.; Molent, L. Effective Block Approach for Aircraft Damage Tolerance Analyses. Int. J. Damage Mech. 2012, 46, 1660–1666. [Google Scholar] [CrossRef]
- Gallagher, J.P.; Miedlar, P.C.; Juarez, V. Rapid repair DTA technology for F-16 aircraft. In Proceedings of the 1989 Structural Integrity Program Conference, San Antonio, TX, USA, 5–7 December 1989; Cooper, T.D., Lincoln, W., Eds.; WRDC-TR-90-4051. Wright-Patterson AFB: Dayton, OH, USA, 1990. [Google Scholar]
- Barsom, J.; Rolfe, S. Fracture and Fatigue Control in Structures: Applications of Fracture Mechanics, 3rd ed.; Butterworth-Heinemann Press: Oxford, UK, 1999. [Google Scholar] [CrossRef]
- Peng, D.; Jones, R.; Ang, A.S.; Michelson, A.; Champagne, V.; Birt, A.; Pinches, S.; Kundu, S.; Alankar, A.; Singh, R.R.K. Computing the durability of WAAM 18Ni 250 maraging steel specimens. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 3535–3545. [Google Scholar] [CrossRef]
- Peng, D.; Champagne, V.K.; Ang, A.S.M.; Birt, A.; Michelson, A.; Pinches, S.; Jones, R. Computing the Durability of WAAM 18Ni-250 Maraging Steel Specimens with Surface Breaking Porosity. Crystals 2023, 13, 443. [Google Scholar] [CrossRef]
- Han, S.; Dinh, T.D.; De Baere, I.; Boone, M.; Josipovic, I.; Van Paepegem, W. Study of the effect of defects on fatigue life prediction of additive manufactured Ti-6Al-4V by combined use of micro-computed tomography and fracture-mechanics-based simulation. Int. J. Fatigue 2024, 180, 108110. [Google Scholar] [CrossRef]
- Shamir, M.; Zhang, X.; Syed, A.K. Characterising and representing small crack growth in an additive manufactured titanium alloy. Eng. Fract. Mech. 2021, 253, 107876. [Google Scholar] [CrossRef]
- Shamir, M.; Zhang, X.; Syed, A.K.; Sadler, W. Predicting the Effect of Surface Waviness on Fatigue Life of a Wire + Arc Additive Manufactured Ti-6Al-4V Alloy. Materials 2023, 16, 5355. [Google Scholar] [CrossRef]
- Dastgerdi, J.N.; Jaberi, O.; Remes, H.; Lehto, P.; Hosseini Toudeshky, H.; Kuva, J. Fatigue damage process of additively manufactured 316 L steel using X-ray computed tomography imaging. Addit. Manuf. 2023, 70, 103559. [Google Scholar] [CrossRef]
- Markham, M.J.; Fatemi, A. Multiaxial fatigue life predictions of additively manufactured metals using a hybrid of linear elastic fracture mechanics and a critical plane approach. Int. J. Fatigue 2024, 178, 107979. [Google Scholar] [CrossRef]
- Main, B.; Jones, M.; Dixon, B.; Barter, S. On small fatigue crack growth rates in AA7085-T7452. Int. J. Fatigue 2022, 156, 106704. [Google Scholar] [CrossRef]
- Tamboli, D.; Barter, S.; Jones, R. On the growth of cracks from etch pits and the scatter associated with them under a miniTWIST spectrum. Int. J. Fatigue 2018, 109, 10–16. [Google Scholar] [CrossRef]
- Jones, R.; Molent, L.; Barter, S.A. Calculating crack growth from small discontinuities in 7050-T7451 under combat aircraft spectra. Int. J. Fatigue 2013, 55, 178–182. [Google Scholar] [CrossRef]
- Jones, R.; Kovarik, O.; Cizek, J.; Ang, A.; Lang, J. Crack growth in conventionally manufactured pure nickel, titanium and aluminum and the cold spray additively manufactured equivalents. Addit. Manuf. Lett. 2022, 3, 100043. [Google Scholar] [CrossRef]
- Jones, R.; Kovarik, O.; Bagherifard, S.; Cizek, J.; Lang, J. Damage tolerance assessment of AM 304L and cold spray fabricated 316L steels and its implications for attritable aircraft. Eng. Fract. Mech. 2021, 254, 107916. [Google Scholar] [CrossRef]
- Field, I.; Kandare, E.; Dixon, B.; Tian, J.; Barter, S. Effect of underloads in small fatigue crack growth. Int. J. Fatigue 2022, 157, 106706. [Google Scholar] [CrossRef]
- Molent, L.; Barter, S.A.; Wanhill, R.J.H. The lead crack fatigue lifing framework. Int. J. Fatigue 2011, 33, 323–331. [Google Scholar] [CrossRef]
- Berens, A.; Hovey, P.W.; Skinn, D.A. Risk Analysis for Aging Aircraft Fleets—Volume 1: Analysis; WL-TR-91-3066; Flight Dynamics Directorate, Wright Laboratory, Air Force Systems Command, Wright-Patterson Air Force Base: Dayton, OH, USA, 2019. [Google Scholar]
- ASM Material Data Sheet. Available online: https://asm.matweb.com/search/SpecificMaterial.asp?bassnum=ma7050t745 (accessed on 13 April 2024).




| Nomenclature of Load Spectra | Loading Pattern |
|---|---|
| R0.25UL3S100 | 3 cycles @ R = 0.25 + 100 cycles @ R = 0.5 |
| R-1UL1S100 | 1 cycle @ R = −1.0 + 100 cycles @ R = 0.5 |
| R-1UL3S50 | 3 cycles @ R = −1.0 + 50 cycles @ R = 0.5 |
| R-0.5UL3S150 | 3 cycles @ R = −0.5 + 150 cycles @ R = 0.5 |
| Load Spectra | frms | |
|---|---|---|
| R0.25:-1UL3S100 | R0.25UL3S100 | 0.345 |
| R0UL3S100 | 0.348 | |
| R-0.25UL3S100 | 0.348 | |
| R-0.5UL3S100 | 0.348 | |
| R-0.75UL3S100 | 0.348 | |
| R-1UL3S100 | 0.348 | |
| R-1UL1:5S100 | R-1UL1S100 | 0.344 |
| R-1UL2S100 | 0.346 | |
| R-1UL3S100 | 0.348 | |
| R-1UL4S100 | 0.350 | |
| R-1UL5S100 | 0.352 | |
| R-0.5UL1:5S100 | R-0.5UL1S100 | 0.344 |
| R-0.5UL2S100 | 0.346 | |
| R-0.5UL3S100 | 0.348 | |
| R-0.5UL4S100 | 0.350 | |
| R-0.5UL5S100 | 0.352 | |
| R-1UL3S50:300 | R-1UL3S50 | 0.331 |
| R-1UL3S100 | 0.348 | |
| R-1UL3S150 | 0.362 | |
| R-1UL3S200 | 0.373 | |
| R-1UL3S250 | 0.383 | |
| R-1UL3S300 | 0.391 | |
| R-0.5UL3S50:300 | R-0.5UL3S50 | 0.331 |
| R-0.5UL3S100 | 0.348 | |
| R-0.5UL3S150 | 0.362 | |
| R-0.5UL3S200 | 0.373 | |
| R-0.5UL3S250 | 0.383 | |
| R-0.5UL3S300 | 0.391 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, K.; Alankar, A.; Singh Raman, R.K.; Jones, R. USAF Characteristic K Approach: A Robust Tool for Predicting Fatigue Crack Growth under Various Underload Spectra. Materials 2024, 17, 3303. https://doi.org/10.3390/ma17133303
Tiwari K, Alankar A, Singh Raman RK, Jones R. USAF Characteristic K Approach: A Robust Tool for Predicting Fatigue Crack Growth under Various Underload Spectra. Materials. 2024; 17(13):3303. https://doi.org/10.3390/ma17133303
Chicago/Turabian StyleTiwari, Kushagra, Alankar Alankar, R. K. Singh Raman, and Rhys Jones. 2024. "USAF Characteristic K Approach: A Robust Tool for Predicting Fatigue Crack Growth under Various Underload Spectra" Materials 17, no. 13: 3303. https://doi.org/10.3390/ma17133303
APA StyleTiwari, K., Alankar, A., Singh Raman, R. K., & Jones, R. (2024). USAF Characteristic K Approach: A Robust Tool for Predicting Fatigue Crack Growth under Various Underload Spectra. Materials, 17(13), 3303. https://doi.org/10.3390/ma17133303









