A 3D Elastoplastic Constitutive Model Considering Progressive Damage Behavior for Thermoplastic Composites of T700/PEEK
Abstract
:1. Introduction
2. Experiment Design and Results Analysis
2.1. Material and Specimen
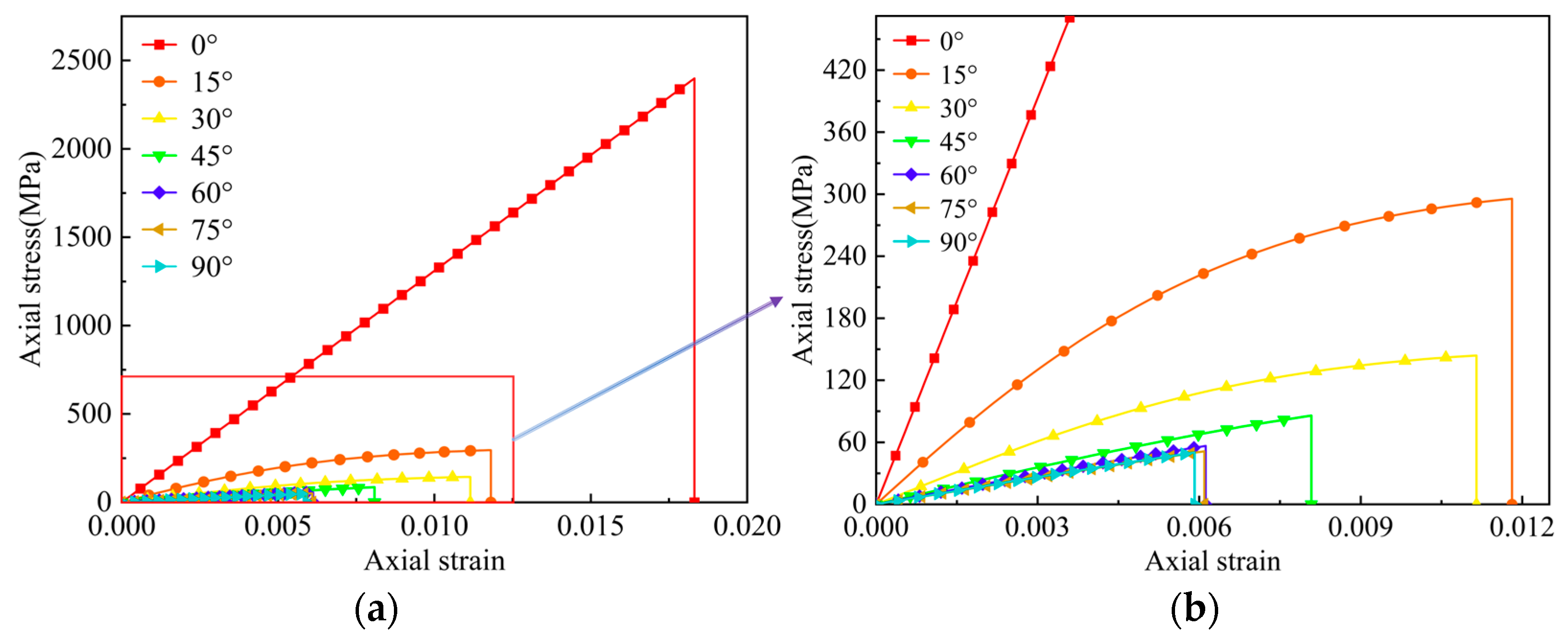
2.2. Off-Axis Testing and Results
3. Constitutive Model Coupling with 3D Elastoplastic Damage
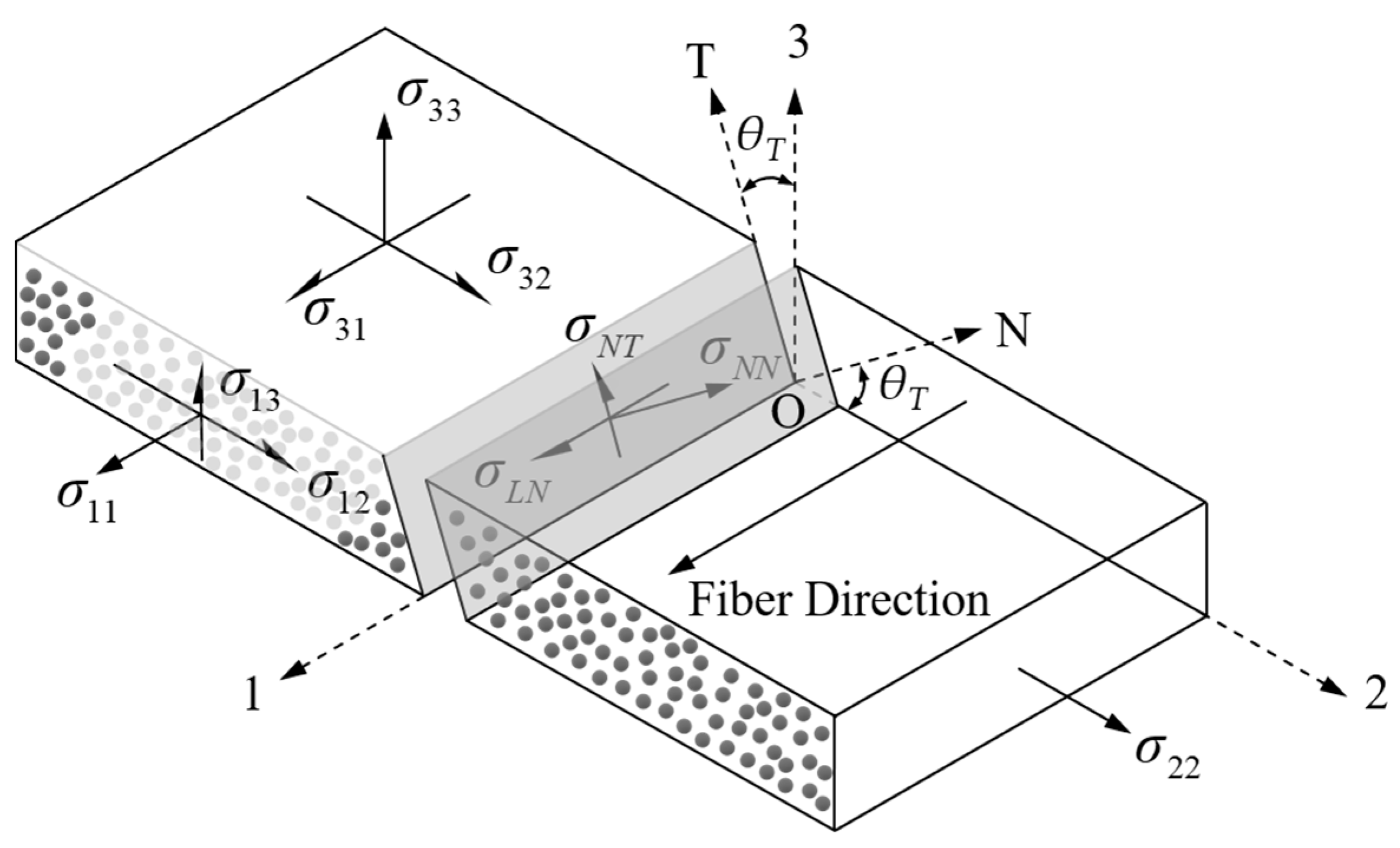
3.1. Elasticity Description
3.2. Plasticity Description
3.3. Damage Description
3.3.1. Damage Initiation Criteria
- (1)
- Failure of the fiber tension (Fft ≥ 1, σ11 > 0):
- (2)
- Failure of the matrix tension (Fmt ≥ 1, σn(θT) > 0):
3.3.2. Damage Evolution Law
- (1)
- Fiber Tensile Failure:
- (2)
- Matrix tensile failure:
4. Model Validation
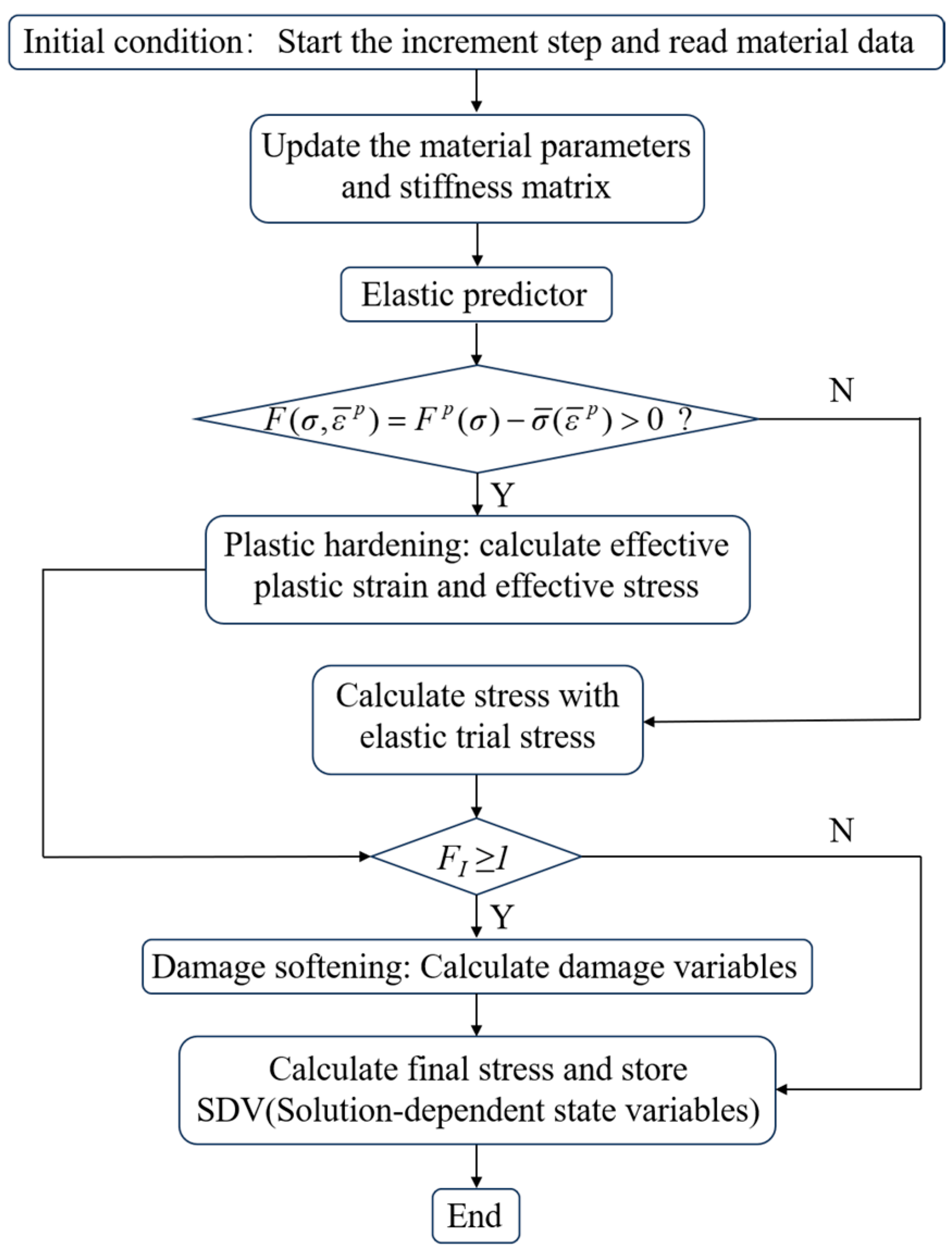
4.1. Implementation of the Numerical Simulation
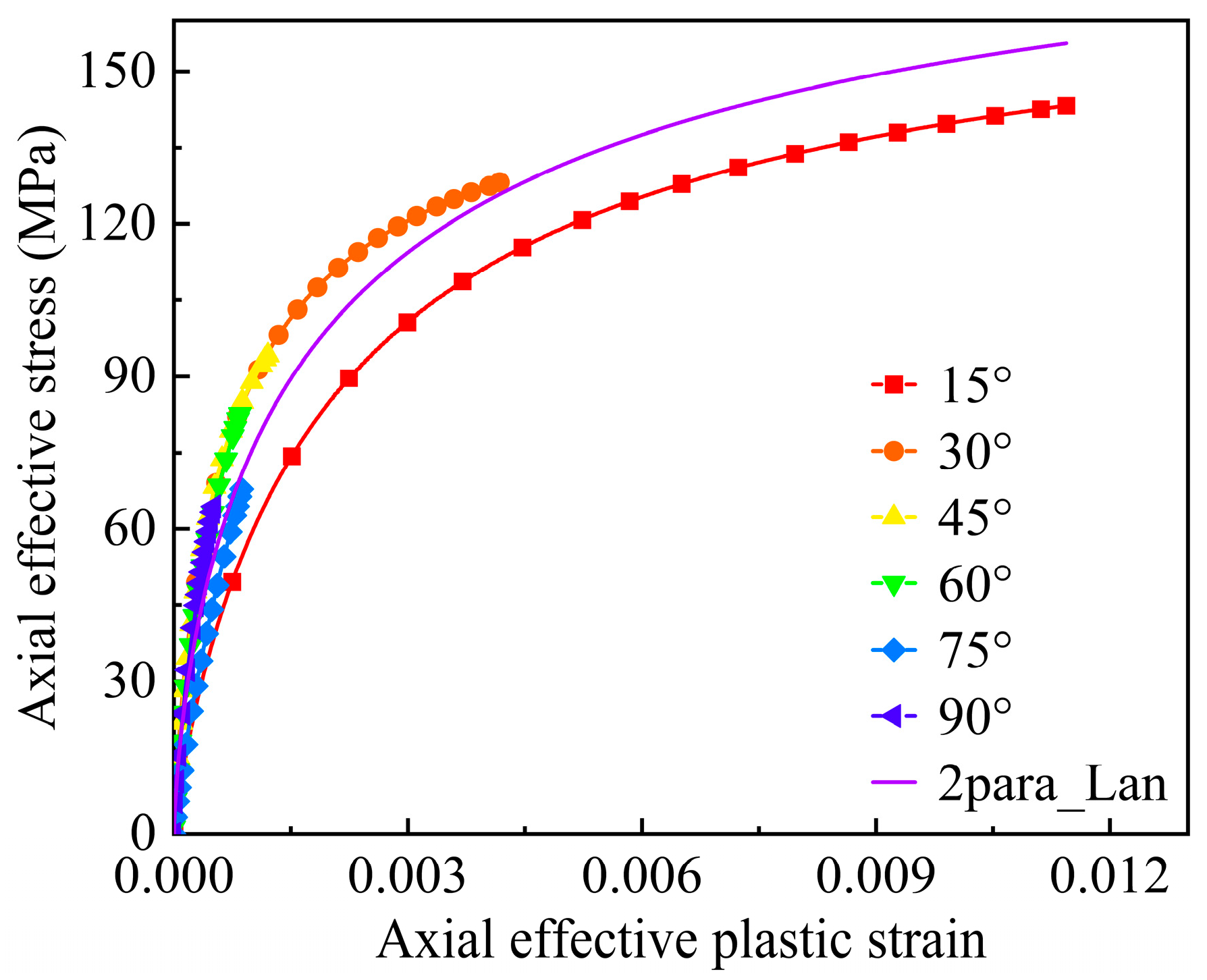
4.2. Determination of the Plasticity Parameters
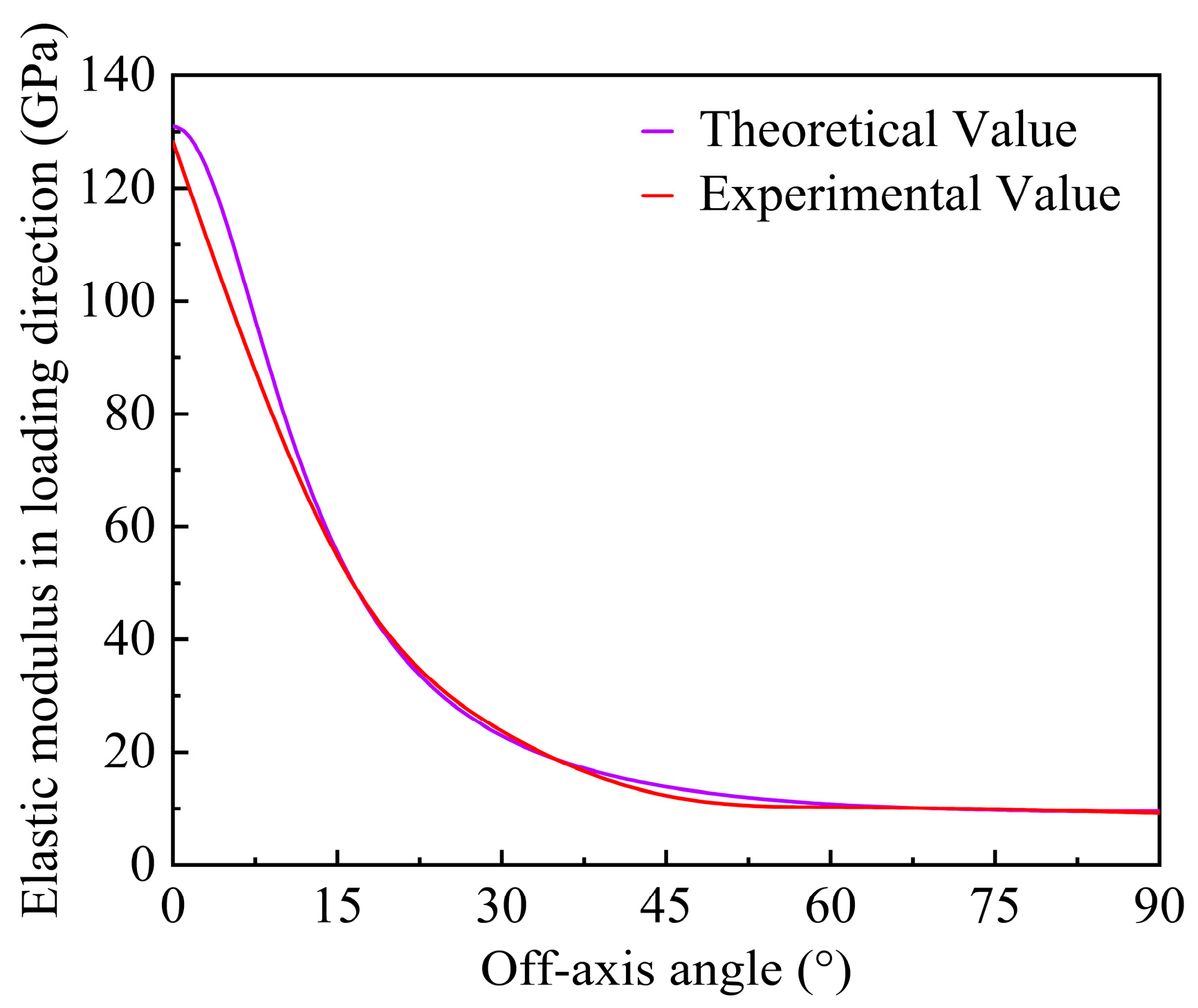
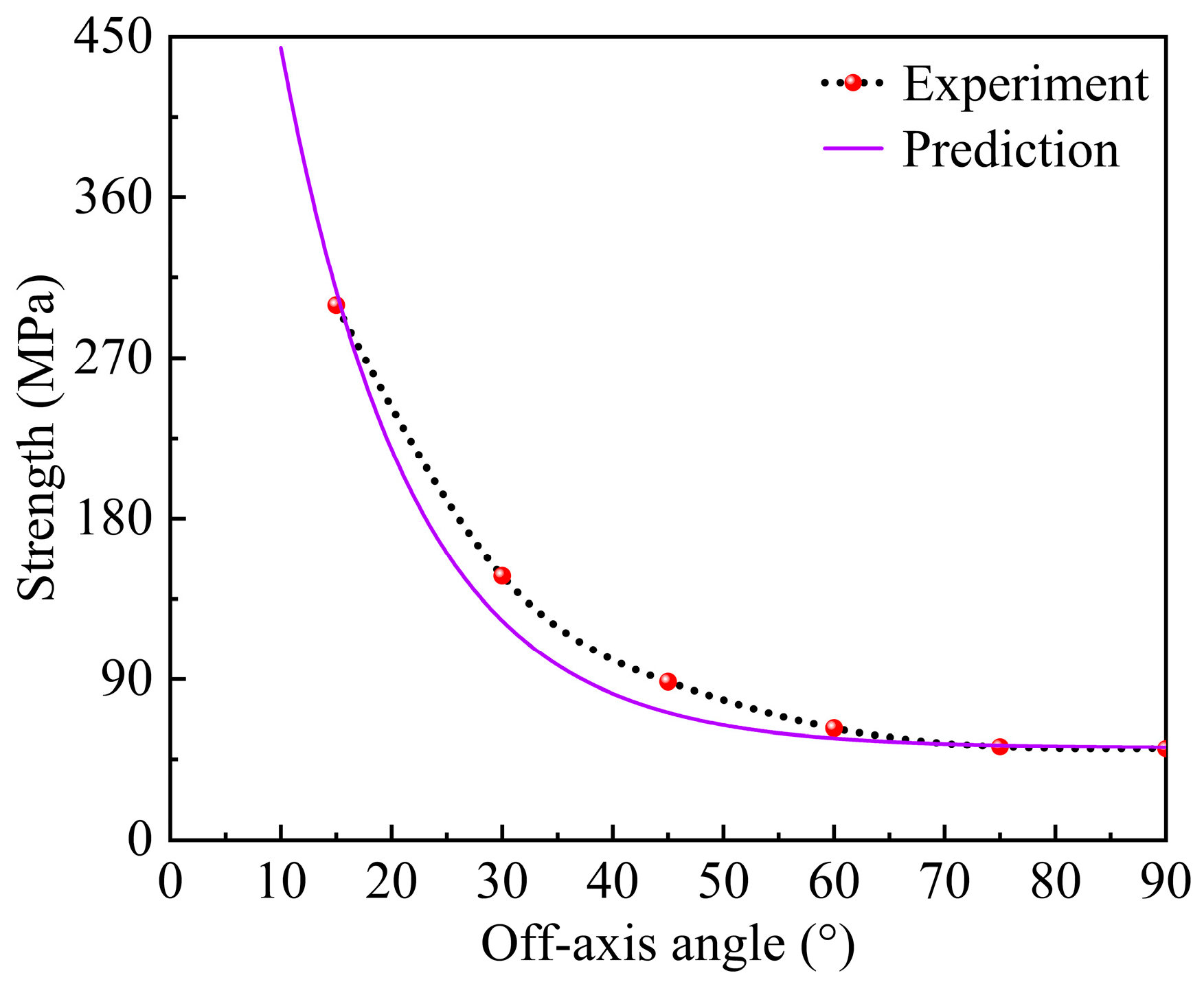
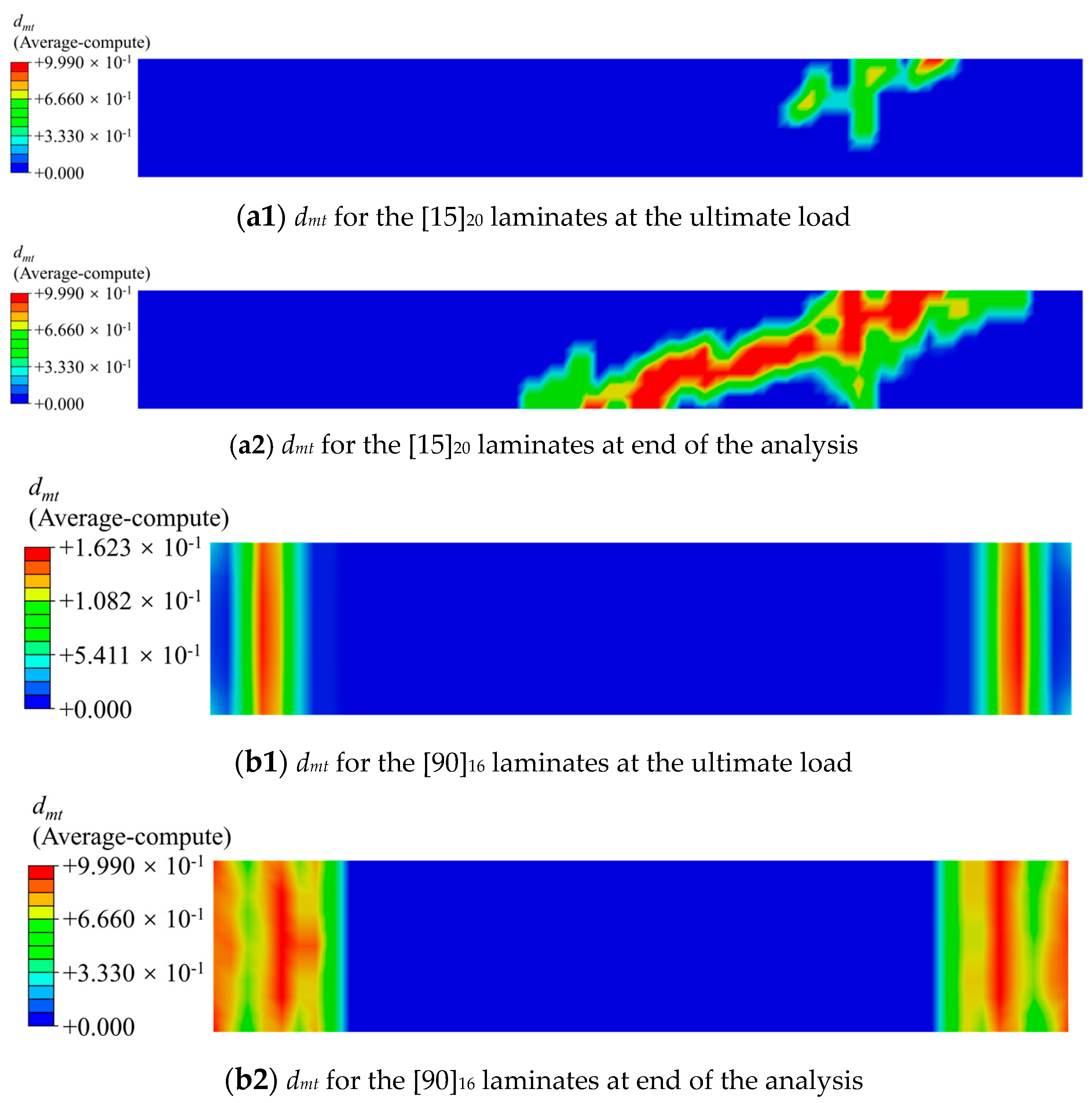
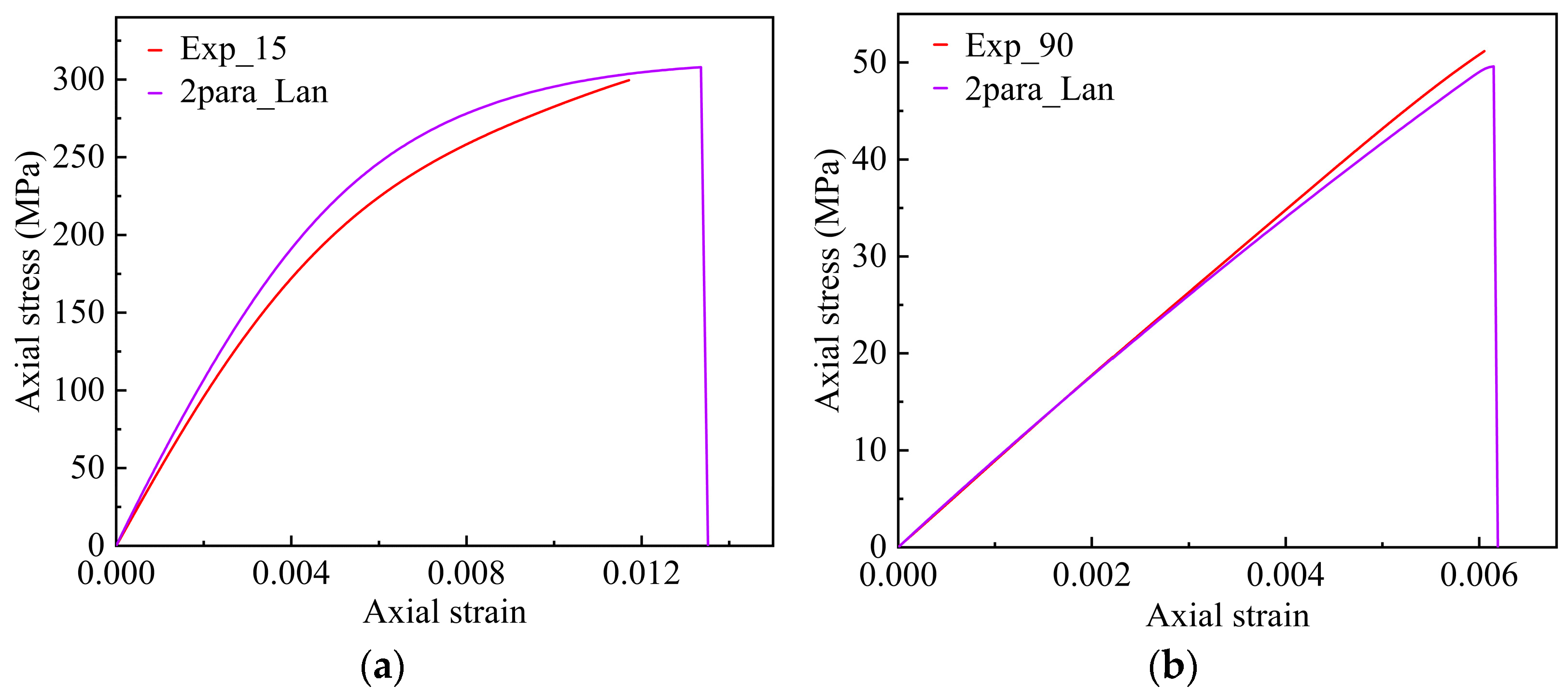
4.3. Prediction of the Results and Verification
5. Conclusions
- (1)
- By conducting off-axis tensile tests on seven types of samples, namely [0]8, [15]20, [30]20, [45]20, [60]20, [75]20, and [90]16, the corresponding axial stress–strain curves, elastic modulus, and tensile strengths were obtained. The fracture surface angles of the specimens for different off-axis angles were measured by using a high-precision digital angle gauge, and the difference between the measured fracture surface angle and the off-axis angle of each specimen was within −2°~3°. This difference is small and acceptable, and it may be caused by the manufacturing defects of the unidirectional T700/PEEK specimen.
- (2)
- A two-parameter 3D plastic potential was developed by incorporating both deviatoric and dilatation deformations. The plastic parameters in the proposed plastic potential are determined using the quasi-Newton algorithm to optimize an objective function related to these plastic parameters. The Langmuir function was initially employed to fit the effective stress–strain relationships of the composites for hardening behavior, providing a precise prediction of the nonlinear mechanical response in CFRPs with thermoplastic resins.
- (3)
- The two-parameter 3D plastic potential was integrated with the Langmuir function of plastic hardening to model the constitutive behavior for unidirectional T700/PEEK Laminates. Based on the proposed constitutive model, a user-defined subroutine (VUMAT), based on ABAQUS, has been developed. This subroutine incorporates the maximum stress criterion for fiber failure and the LaRC05 criterion for matrix failure, allowing for the simulation of 3D elastoplastic damage behavior during tensile loading tests. This work constructs a two-parameter 3D elastoplastic damage constitutive model considering the material plasticity, damage evolution, and dilatational deformation.
- (4)
- Applying the 3D elastoplastic damage constitutive model to simulate the off-axis tensile behavior of unidirectional T700/PEEK laminates, the predicted stress–strain curves align closely with experimental data. This suggests that the model effectively captures the plastic behavior of unidirectional T700/PEEK thermoplastic laminates. The analysis of plastic strain in various directions indicates that shear plastic strain in the 1–2 plane governs plastic deformation. Nevertheless, this effect diminishes as the off-axis angle increases. The comparison between the numerically simulated and experimentally measured tensile strengths under identical loading planes reveals a gradual decrease in ultimate tensile strength with an increasing off-axis angle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Zou, B.; Ding, S.; Huang, C.; Shi, Z.; Ma, Y.; Yao, P. Preparation of short CF/GF reinforced PEEK composite filaments and their comprehensive properties evaluation for FDM-3D printing. Compos. Part B Eng. 2020, 198, 108175. [Google Scholar] [CrossRef]
- Guo, L.; Qi, H.; Zhang, G.; Wang, T.; Wang, Q. Distinct tribological mechanisms of various oxide nanoparticles added in PEEK composite reinforced with carbon fibers. Compos. Part A Appl. Sci. Manuf. 2017, 97, 19–30. [Google Scholar] [CrossRef]
- Oladapo, B.I.; Zahedi, S.A. Improving bioactivity and strength of PEEK composite polymer for bone application. Mater. Chem. Phys. 2021, 266, 124485. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Rashid, A.A.; Arif, Z.U.; Akram, N.; Arshad, H.; García Márquez, F.P. Characterization of failure strain in fiber reinforced composites: Under on-axis and off-axis loading. Crystals 2021, 11, 216. [Google Scholar] [CrossRef]
- Kawai, M.; Saito, S. Off-axis strength differential effects in unidirectional carbon/epoxy laminates at different strain rates and predictions of associated failure envelopes. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1632–1649. [Google Scholar] [CrossRef]
- Chen, J.F.; Morozov, E.V.; Shankar, K. A combined elastoplastic damage model for progressive failure analysis of composite materials and structures. Compos. Struct. 2012, 94, 3478–3489. [Google Scholar] [CrossRef]
- Liao, B.B.; Liu, P.F. Finite element analysis of dynamic progressive failure of plastic composite laminates under low velocity impact. Compos. Struct. 2017, 159, 567–578. [Google Scholar] [CrossRef]
- Sun, C.T.; Chen, J.L. A simple flow rule for characterizing nonlinear behavior of fiber composites. J. Compos. Mater. 1989, 23, 1009–1020. [Google Scholar] [CrossRef]
- Sato, Y.; Okabe, T.; Higuchi, R.; Yoshioka, K. Multiscale approach to predict crack initiation in unidirectional off-axis laminates. Adv. Compos. Mater. 2014, 23, 461–475. [Google Scholar] [CrossRef]
- Alyavuz, B.; Anil, Ö.; Bulut, N. Nonlinear finite element analysis of masonry wall strengthened with CFRP strips. Adv. Compos. Mater. 2016, 25, 159–175. [Google Scholar] [CrossRef]
- Ogasawara, T.; Ishikawa, T. A simple test method, NAL-II, to evaluate the strength and elastic modulus of polymer matrix composite laminates. Adv. Compos. Mater. 2016, 25 (Suppl. S1), 131–145. [Google Scholar] [CrossRef]
- Chen, J.L.; Sun, C.T. A plastic potential function suitable for anisotropic fiber composites. J. Compos. Mater. 1993, 27, 1379–1390. [Google Scholar] [CrossRef]
- Weeks, C.A.; Sun, C.T. Modeling non-linear rate-dependent behavior in fiber-reinforced composites. Compos. Sci. Technol. 1998, 58, 603–611. [Google Scholar] [CrossRef]
- Cho, J.; Fenner, J.; Werner, B.; Daniel, I. A constitutive model for fiber-reinforced polymer composites. J. Compos. Mater. 2010, 44, 3133–3150. [Google Scholar] [CrossRef]
- Chen, G.; Suo, X. Constitutive modeling of nonlinear compressive behavior of fiber reinforced polymer composites. Polym. Compos. 2020, 41, 182–190. [Google Scholar] [CrossRef]
- Yao, C.; Qi, Z.; Chen, W.; Zhang, C. Effect of CF/PEEK plasticity behavior on the mechanical performance of interference-fit joint. Polym. Compos. 2021, 42, 2574–2588. [Google Scholar] [CrossRef]
- Chen, J.F.; Morozov, E.V.; Shankar, K. Simulating progressive failure of composite laminates including in-ply and delamination damage effects. Compos. Part A Appl. Sci. Manuf. 2014, 61, 185–200. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ding, Y.; Zhou, J.; Kong, X.; Harper, L.T.; Blackman, B.R.; Falzon, B.G.; Dear, J.P. Modelling damage in fibre-reinforced thermoplastic composite laminates subjected to three-point bend loading. Compos. Struct. 2020, 236, 111889. [Google Scholar] [CrossRef]
- Ding, S.; Tong, J.W.; Shen, M.; Huo, Y. Three-dimensional elastic-plastic analysis of the interlaminar stresses for the AS4/PEEK composite laminate with a circular hole. Mech. Adv. Mater. Struct. 2010, 17, 406–418. [Google Scholar] [CrossRef]
- Mandal, B.; Chakrabarti, A. Elasto-plastic damage model considering cohesive matrix interface layers for composite laminates. J. Mech. Sci. Technol. 2018, 32, 121–127. [Google Scholar] [CrossRef]
- Vyas, G.M.; Pinho, S.T.; Robinson, P. Constitutive modelling of fibre-reinforced composites with unidirectional plies using a plasticity-based approach. Compos. Sci. Technol. 2011, 71, 1068–1074. [Google Scholar] [CrossRef]
- Ren, R.; Le, G.; Zhong, J.; Ma, D.; He, Q. Numerical research on elasto-plastic behaviors of fiber-reinforced polymer based composite laminates. Compos. Struct. 2019, 207, 364–372. [Google Scholar] [CrossRef]
- Zhang, D.; Cen, X.; Wen, H.; Wang, H.; Deng, J.; Tang, R.; Shu, C.-M. Effect of particle size on CO adsorption and thermodynamic analysis. J. Loss Prev. Process Ind. 2023, 84, 105127. [Google Scholar] [CrossRef]
- Glatz, G.; Alafnan, S.; Raza, A.; Mahmoud, M. Multicomponent gas adsorption behavior of kerogen: A molecular investigation. Energy Fuels 2022, 36, 6695–6710. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Liu, D.; Fu, Q.; Hou, R.; Li, Q.; Cui, S.; Li, M. Research on the adsorption mechanism of Cu and Zn by biochar under freeze-thaw conditions. Sci. Total Environ. 2021, 774, 145194. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, S.S.; Hale, F.; Taufique, M.F.N.; Soulami, A.; Devanathan, R. Investigation of Crashworthiness of Carbon Fiber-Based Electric Vehicle Battery Enclosure Using Finite Element Analysis. Appl. Compos. Mater. 2023, 30, 1689–1715. [Google Scholar] [CrossRef]
- Guo, Q.; Yao, W.; Li, W.; Gupta, N. Constitutive models for the structural analysis of composite materials for the finite element analysis: A review of recent practices. Compos. Struct. 2021, 260, 113267. [Google Scholar] [CrossRef]
- Din, I.U.; Hao, P.; Franz, G.; Panier, S. Elastoplastic CDM model based on Puck’s theory for the prediction of mechanical behavior of Fiber Reinforced Polymer (FRP) composites. Compos. Struct. 2018, 201, 291–302. [Google Scholar] [CrossRef]
- Singh, H.; Mahajan, P. Modeling damage induced plasticity for low velocity impact simulation of three dimensional fiber reinforced composite. Compos. Struct. 2015, 131, 290–303. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Ji, Y.; Hu, H.; Cao, D.; Zheng, K.; Liu, H.; Li, S. Modeling Progressive Damage and Failure of Single-Lap Thin-Ply-Laminated Composite-Bolted Joint Using LaRC Failure Criterion. Materials 2022, 15, 8123. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Liu, L. Off-Axis Compressive Behaviour of Fibre Reinforced Thermoplastic Composites. Materials 2022, 15, 5547. [Google Scholar] [CrossRef] [PubMed]
- ASTM D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2017. Available online: https://www.astm.org (accessed on 7 May 2024).
- Völkerink, O.; Petersen, E.; Koord, J.; Huehne, C. A pragmatic approach for a 3D material model considering elasto-plastic behaviour, damage initiation by Puck or Cuntze and progressive failure of fibre-reinforced plastics. Comput. Struct. 2020, 236, 106280. [Google Scholar] [CrossRef]
- Ogi, K.; Takeda, N. Effects of moisture content on nonlinear deformation behavior of CF/epoxy composites. J. Compos. Mater. 1997, 31, 530–551. [Google Scholar] [CrossRef]
- Pinho, S.; Darvizeh, R.; Robinson, P.; Schuecker, C.; Camanho, P. Material and structural response of polymer-matrix fibre-reinforced composites. J. Compos. Mater. 2012, 46, 2313–2341. [Google Scholar] [CrossRef]
- Pinho, S.T.; Vyas, G.M.; Robinson, P. Material and structural response of polymer-matrix fibre-reinforced composites: Part B. J. Compos. Mater. 2013, 47, 679–696. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 2002, 62, 1633–1662. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ding, Y.; Zhou, J.; Kong, X.; Blackman, B.R.; Kinloch, A.J.; Falzon, B.G.; Dear, J.P. Effects of impactor geometry on the low-velocity impact behaviour of fibre-reinforced composites: An experimental and theoretical investigation. Appl. Compos. Mater. 2020, 27, 533–553. [Google Scholar] [CrossRef]
- Zhang, C.; Li, N.; Wang, W.; Binienda, W.K.; Fang, H. Progressive damage simulation of triaxially braided composite using a 3D meso-scale finite element model. Compos. Struct. 2015, 125, 104–116. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matériaux Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ding, Y.; Hall, Z.E.; Kong, X.; Zhou, J.; Blackman, B.R.K.; Kinloch, A.J.; Dear, J.P. A three-dimensional elastic-plastic damage model for predicting the impact behaviour of fibre-reinforced polymer-matrix composites. Compos. Part B Eng. 2020, 201, 108389. [Google Scholar] [CrossRef]
- Jen, M.H.R.; Lee, C.H. Strength and life in thermoplastic composite laminates under static and fatigue loads. Part II: Formulation. Int. J. Fatigue 1998, 20, 617–629. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Ai, S.; He, C.; Tao, Y.; Yang, Y.; Fang, D. A constitutive model for elastoplastic-damage coupling effect of unidirectional fiber-reinforced polymer matrix composites. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105736. [Google Scholar] [CrossRef]
- Yokozeki, T.; Ogihara, S.; Yoshida, S.; Ogasawara, T. Simple constitutive model for nonlinear response of fiber-reinforced composites with loading-directional dependence. Compos. Sci. Technol. 2007, 67, 111–118. [Google Scholar] [CrossRef]







| Sample Number | Layup | ||||||
|---|---|---|---|---|---|---|---|
| [0]8 | [15]20 | [30]20 | [45]20 | [60]20 | [75]20 | [90]16 | |
| Fracture Surface Angles/° | |||||||
| Sample 1 | 0 | 15.06 | 29.35 | 47.45 | 60.05 | 75.90 | 90.05 |
| Sample 2 | 0 | 14.95 | 30.03 | 43.45 | 61.35 | 75.45 | 92.00 |
| Sample 3 | 0 | 15.70 | 29.45 | 46.10 | 60.32 | 75.54 | 89.70 |
| Sample 4 | 0 | 14.75 | 29.65 | 44.90 | 60.45 | 74.00 | 89.55 |
| Sample 5 | 0 | 15.35 | 30.30 | 45.60 | 60.24 | 76.35 | 89.25 |
| Average value | 0 | 15.16 | 29.76 | 45.50 | 60.48 | 75.45 | 90.11 |
| Standard deviation | 0 | 0.33 | 0.36 | 1.32 | 0.45 | 0.79 | 0.98 |
| E11 (GPa) * | E22 (GPa) * | E33 (GPa) * | G12 (GPa) * | G13 (GPa) * | v12 * |
| 130 | 10.1 | 10.1 | 5.77 | 5.77 | 0.32 |
| v13 * | XT (MPa) * | XC (MPa) * | YT (MPa) * | YC (MPa) [43] | SL (MPa) [43] |
| 0.32 | 2419 | 1094 | 50.2 | 205.9 | 133 |
| Gft (KJ/m2) [30] | GI (KJ/m2) [42] | GII (KJ/m2) [42] | GIII (KJ/m2) [42] | ||
| 133 | 1.7 | 2.0 | 2.0 |
| Parameter | Plastic Potential | |
|---|---|---|
| Single-Parameter | Two-Parameter | |
| a | 3.0727 | 1.2612 |
| b | - | 0.0252 |
| Objective function value | 31,926.5522 | 18,491.6292 |
| Computational time/s | 0.5690 | 0.9793 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, W.; Xiong, H.; Liao, Z.; Ma, J.; Fu, Y.; Wang, B. A 3D Elastoplastic Constitutive Model Considering Progressive Damage Behavior for Thermoplastic Composites of T700/PEEK. Materials 2024, 17, 3317. https://doi.org/10.3390/ma17133317
Fu W, Xiong H, Liao Z, Ma J, Fu Y, Wang B. A 3D Elastoplastic Constitutive Model Considering Progressive Damage Behavior for Thermoplastic Composites of T700/PEEK. Materials. 2024; 17(13):3317. https://doi.org/10.3390/ma17133317
Chicago/Turabian StyleFu, Weigang, Huanjie Xiong, Zhe Liao, Junchi Ma, Yaoming Fu, and Bin Wang. 2024. "A 3D Elastoplastic Constitutive Model Considering Progressive Damage Behavior for Thermoplastic Composites of T700/PEEK" Materials 17, no. 13: 3317. https://doi.org/10.3390/ma17133317
APA StyleFu, W., Xiong, H., Liao, Z., Ma, J., Fu, Y., & Wang, B. (2024). A 3D Elastoplastic Constitutive Model Considering Progressive Damage Behavior for Thermoplastic Composites of T700/PEEK. Materials, 17(13), 3317. https://doi.org/10.3390/ma17133317







