An Adaptive Elastic Support Seat-Based Magnetorheological Elastomer for Human Body Vibration Reduction
Abstract
:1. Introduction
2. Simulation Calculation
2.1. Stiffness and Damping of the MRE Electromagnetic Structure
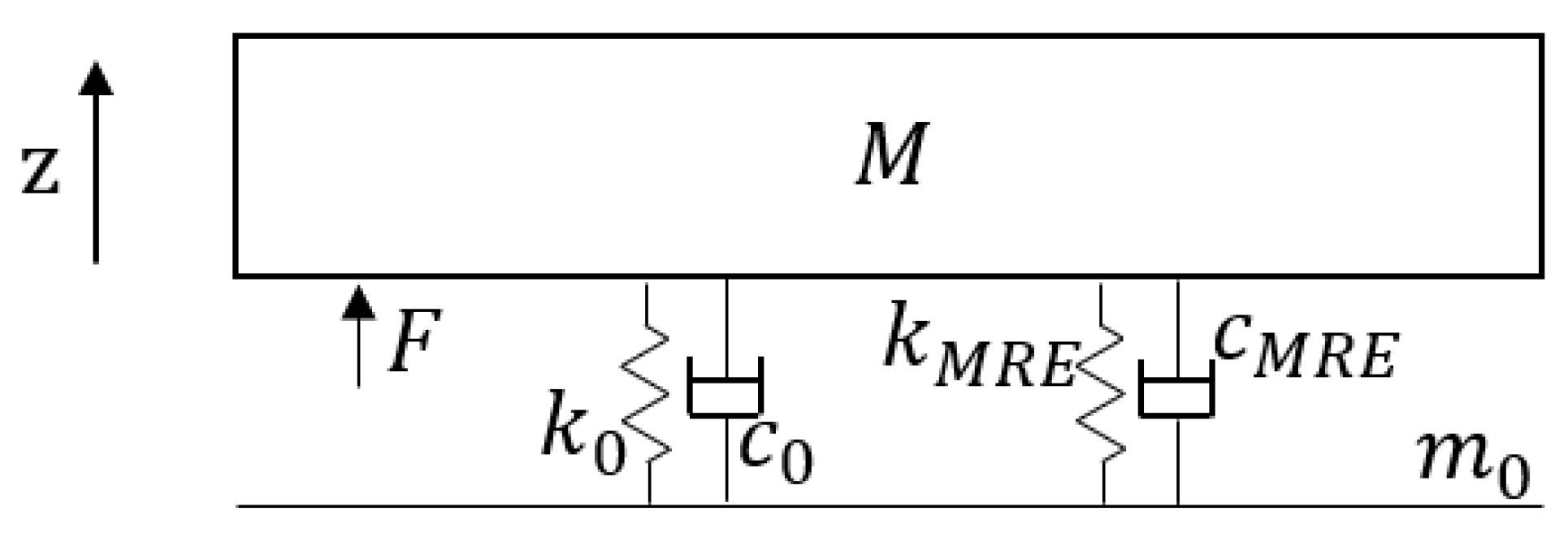
2.2. Vibrating Seat Model
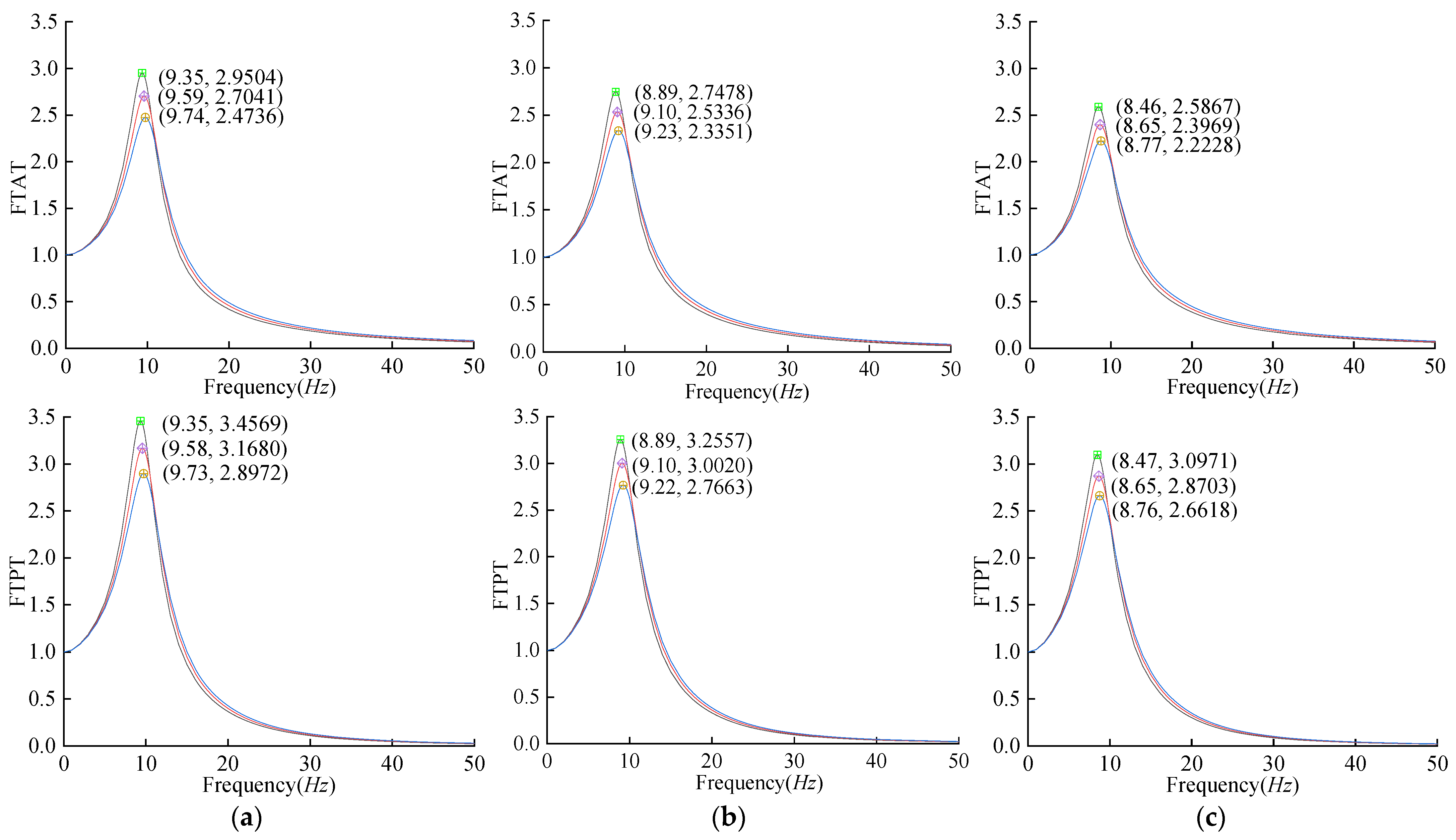
2.3. Calculation Results
3. Vibration Experiment
3.1. Experimental Equipment
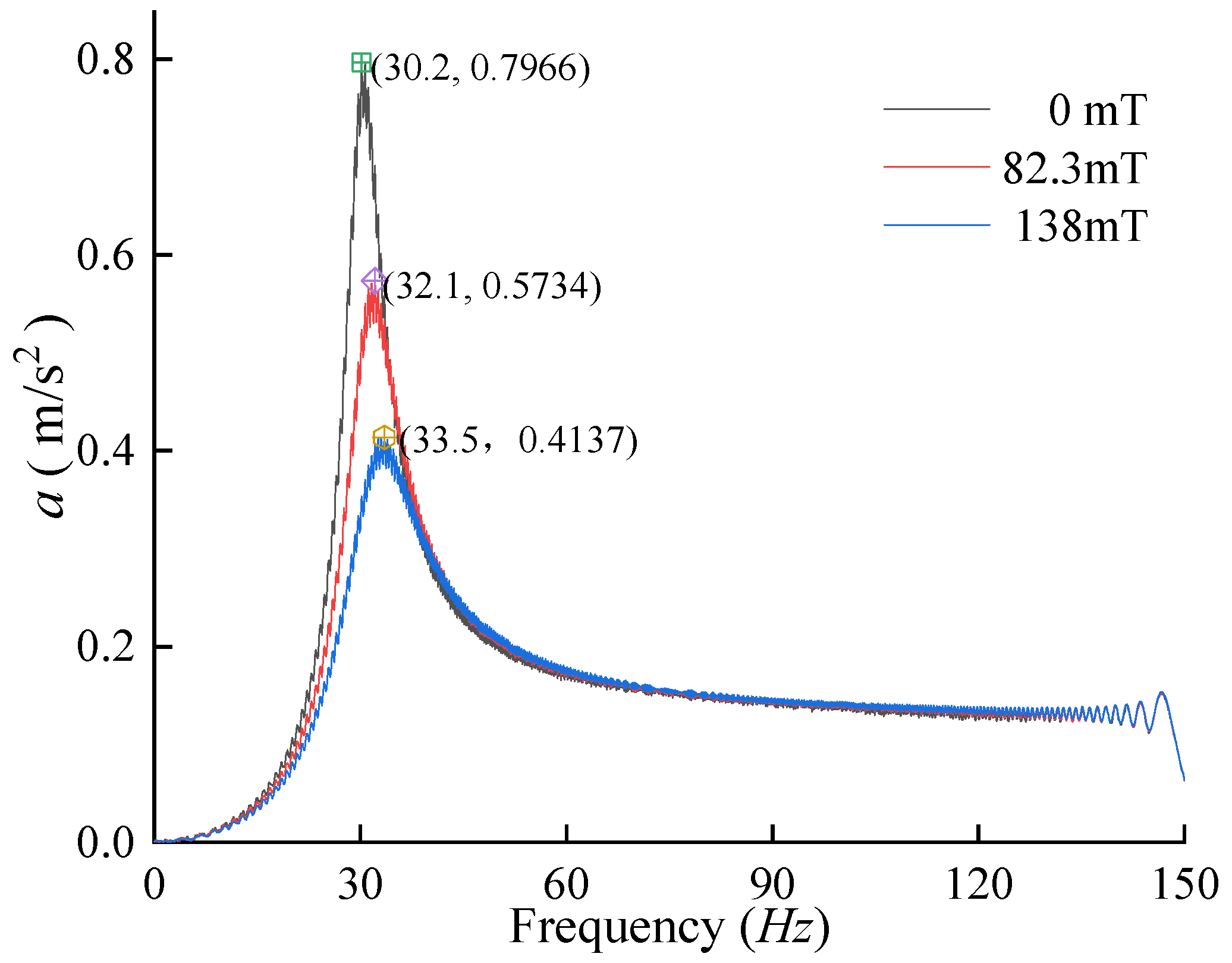
3.2. Results
- No current in the MRE electromagnetic structure;
- MRE electromagnetic structure at a current of 3 A with a magnetic flux of 138 mT;
- MRE electromagnetic structure at a current of 5 A with a magnetic flux of 180 mT.
4. Discussion
4.1. Analysis of Vibration Reduction
- (1)
- Despite efforts in the experiment to allow the internal stress of the MRE to stabilize before measuring vibration response, Figure 1 shows that the stress curves of the MRE under a magnetic field stabilized only to a certain extent. The rubber softened under pressure, and the material hardened due to CIP under the magnetic field, but these effects could not reach equilibrium in the vibrating environment, resulting in dynamic changes in the actual stiffness and damping of the adaptive elastic foundation.
- (2)
- The experimental setup’s structure deviated from a purely single-mass configuration; the guide sliders introduced additional rolling friction, dissipating some energy. Moreover, slight angular deviations in the I-beam folding angle from 90° caused vertical misalignment of the four strut rails, resulting in discrepancies between the actual and simulated stiffness and damping.
- (3)
- The post-processing software used for analyzing the experimental spectrograms employed a frequency resolution of 0.5 Hz, which may have led to an inadequate frequency resolution.
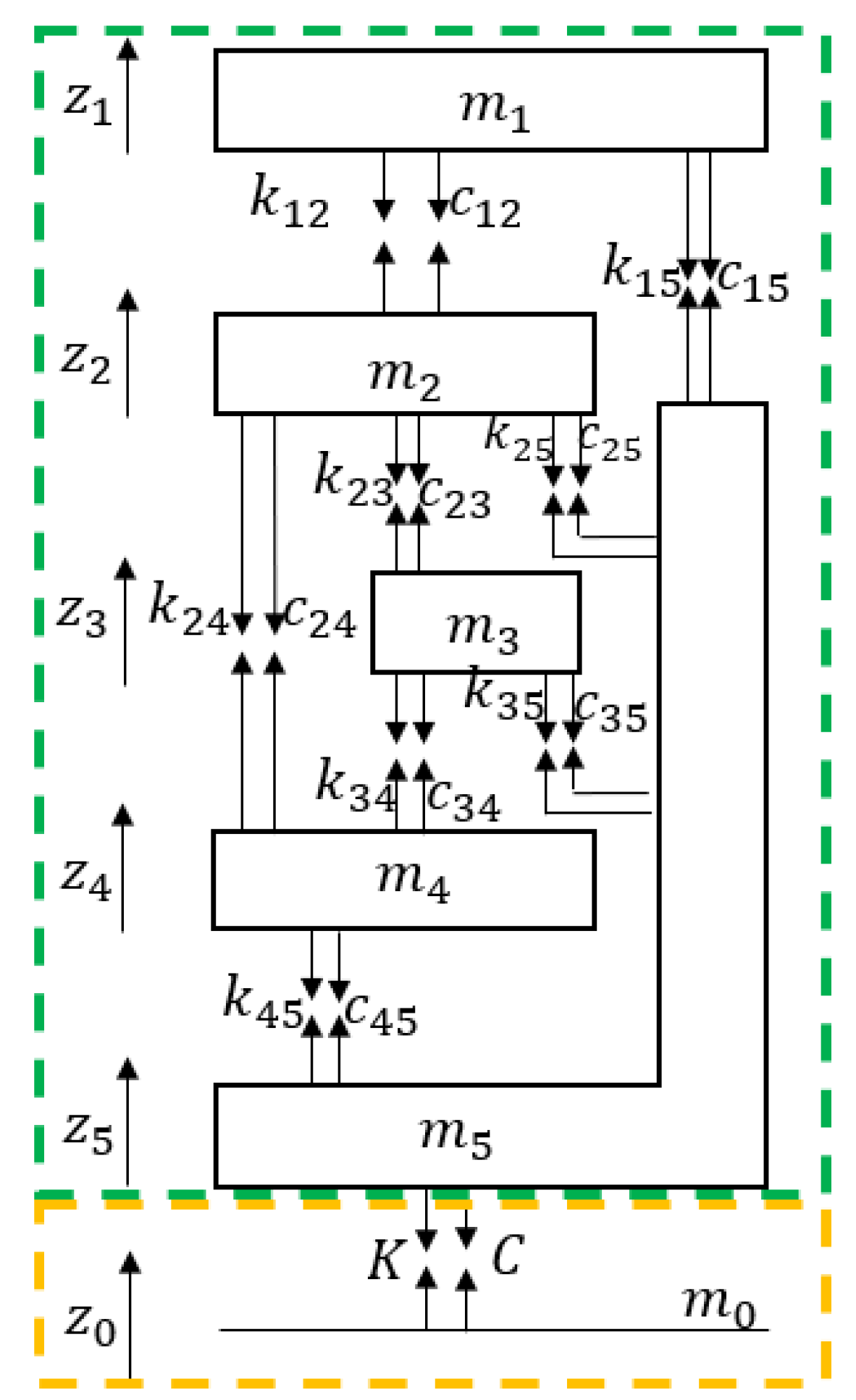
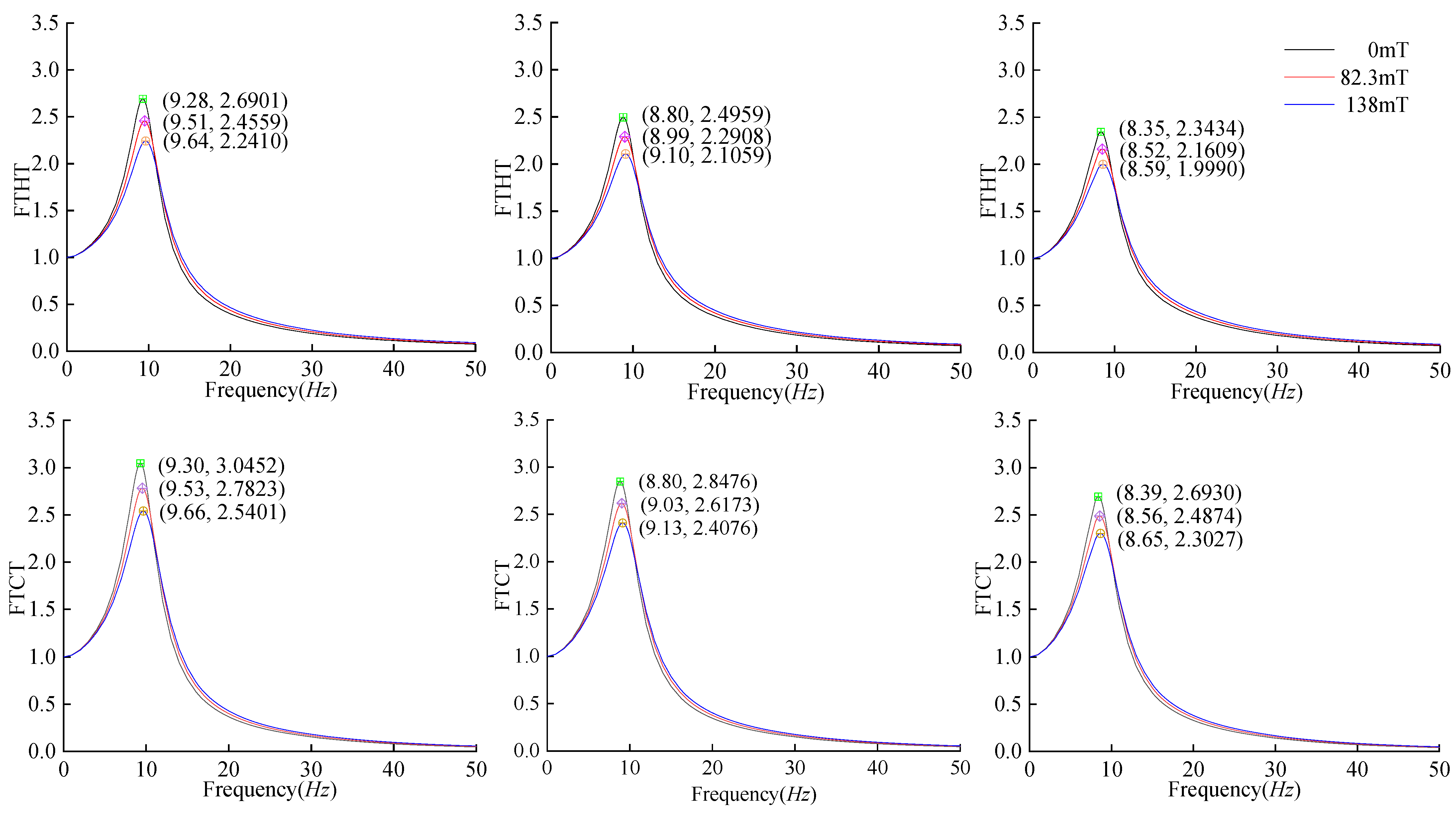
4.2. Vibration Reduction in a Seated Human Body
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, B.B.; Bigelow, P.L.; Wells, R.P.; Davies, H.W.; Hall, P.; Johnson, P.W. The impact of different seats and whole-body vibration exposures on truck driver vigilance and discomfort. Ergonomics 2018, 61, 528–537. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, N.J.; MacMull, S.J.; Singla, G.; Rimell, A.N. Relative influence of sitting duration and vibration magnitude on sitting discomfort in a car seat. In Proceedings of the 42nd United Kingdom Conference on Human Responses to Vibration, Southampton, UK, 10–12 September 2007. [Google Scholar]
- Morioka, M.; Griffin, M.J. Difference thresholds for intensity perception of whole-body vertical vibration: Effect of frequency and magnitude. J. Acoust. Soc. Am. 2000, 107, 620–624. [Google Scholar] [CrossRef] [PubMed]
- Griffin, M.J. Handbook of Human Vibration; Academic Press Limited: London, UK, 1991. [Google Scholar]
- Kjellberg, A. Psychological aspects of occupational vibration. Scand. J. Work. Environ. Health 1990, 16, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Leizhi, W.; Zhao, C.; Hongrui, A.; Hui, Y. Vibration reduction of human body biodynamic response in sitting posture under vibration environment by seat backrest support. Sci. Rep. 2024, 14, 6427. [Google Scholar]
- Bai, X.-X.; Wereley, N.M.; Choi, Y.-T. Magnetorheological energy absorber with dual concentric annular valves. J. Intell. Mater. Syst. Struct. 2016, 27, 944–958. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Qi, S.; Wang, T.; Liang, Y. Development of a magnetorheological isolator with variable damping and variable stiffness for broadband vibration suppression. Smart Mater. Struct. 2021, 30, 025023. [Google Scholar] [CrossRef]
- Ubaidillah, U.; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent progress on magnetorheological solids: Materials, fabrication, testing, and applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part B Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Borin, D.; Saphiannikova, M.; Heinrich, G. Mechanical properties of magneto-sensitive elastomers in a homogeneous magnetic field: Theory and experiment. Macromol. Symp. 2014, 338, 96–107. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Gong, X.L. An effective permeability model to predict field-dependent modulus of magnetorheological elastomers. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1910–1916. [Google Scholar] [CrossRef]
- Feng, J.; Xuan, S.; Liu, T.; Ge, L.; Yan, L.; Zhou, H.; Gong, X. The prestress-dependent mechanical response of magnetorheological elastomers. Smart Mater. Struct. 2015, 24, 085032. [Google Scholar] [CrossRef]
- Shen, Y.; Golnaraghi, M.F.; Heppler, G.R. Experimental Research and Modeling of Magnetorheological Elastomers. J. Intell. Mater. Syst. Struct. 2004, 15, 27–35. [Google Scholar] [CrossRef]
- Ponte Castañeda, P.; Galipeau, E. Homogenization-based constitutive models for magnetorheological elastomers at finite strain. J. Mech. Phys. Solids 2011, 59, 194–215. [Google Scholar] [CrossRef]
- Agirre-Olabide, I.; Elejabarrieta, M.J. A new magneto-dynamic compression technique for magnetorheological elastomers at high frequencies. Polym. Test. 2018, 66, 114–121. [Google Scholar] [CrossRef]
- Vatandoost, H.; Rakheja, S.; Sedaghati, R. Effects of iron particles’ volume fraction on compression mode properties of magnetorheological elastomers. J. Magn. Magn. Mater. 2021, 522, 167552. [Google Scholar] [CrossRef]
- Vatandoost, H.; Hemmatian, M.; Sedaghati, R.; Rakheja, S. Dynamic characterization of isotropic and anisotropic magnetorheological elastomers in the oscillatory squeeze mode superimposed on large static pre-strain. Compos. Part B Eng. 2019, 182, 107648. [Google Scholar] [CrossRef]
- Chen, S.W.; Li, R.; Zhang, Z.; Wang, X.J. Micromechanical analysis on tensile modulus of structured magneto-rheological elastomer. Smart Mater. Struct. 2016, 25, 035001. [Google Scholar] [CrossRef]
- Gong, X.; Wang, Y.; Hu, T.; Xuan, S. Mechanical property and conductivity of a flax fibre weave strengthened magnetorheological elastomer. Smart Mater. Struct. 2017, 26, 075013. [Google Scholar] [CrossRef]
- Schubert, G.; Harrison, P. Large-strain behaviour of Magneto-Rheological Elastomers tested under uniaxial compression and tension, and pure shear deformations. Polym. Test. 2015, 42, 122–134. [Google Scholar] [CrossRef]
- Vatandoost, H.; Hemmatian, M.; Sedaghati, R.; Rakheja, S. Effect of shape factor on compression mode dynamic properties of magnetorheological elastomers. J. Intell. Mater. Syst. Struct. 2021, 32, 1678–1699. [Google Scholar] [CrossRef]
- Vatandoost, H.; Rakheja, S.; Sedaghati, R.; Hemmatian, M. Compensation of magnetic force of an electromagnet for compression mode characterization of magnetorheological elastomers. IEEE Trans. Magn. 2021, 57, 2500114. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L. Dot-patterned hybrid magnetorheological elastomer developed by 3D printing. J. Magn. Magn. Mater. 2020, 494, 165825. [Google Scholar] [CrossRef]
- Yarali, E.; Baniasadi, M.; Zolfagharian, A.; Chavoshi, M.; Arefi, F.; Hossain, M.; Bastola, A.; Ansari, M.; Foyouzat, A.; Dabbagh, A.; et al. Magneto-/ electro-responsive polymers toward manufacturing, characterization, and biomedical/ soft robotic applications. Appl. Mater. Today 2022, 26, 101306. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, Y.; Wang, Q.; Peng, L. Study on the fluctuating wind responses of constructing bridge towers with magnetorheological elastomer variable stiffness tuned mass damper. J. Intell. Mater. Syst. Struct. 2022, 33, 290–308. [Google Scholar] [CrossRef]
- Hu, T.; Xuan, S.; Ding, L.; Gong, X. Liquid metal circuit based magnetoresistive strain sensor with discriminating magnetic and mechanical sensitivity. Sens. Actuators B Chem. 2020, 314, 128095. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Bunoiu, M.; Vatzulik, B.; Juganaru, I. Hybrid magnetorheological elastomer: Influence of magnetic field and compression pressure on its electrical conductivity. J. Ind. Eng. Chem. 2014, 20, 3994–3999. [Google Scholar] [CrossRef]
- Zhang, P.; Kamezaki, M.; He, Z.; Sakamoto, H.; Sugano, S. EPM–MRE: Electropermanent magnet–magnetorheological elastomer for soft actuation system and its application to robotic grasping. IEEE Robot. Autom. Lett. 2021, 6, 8181–8188. [Google Scholar] [CrossRef]
- Liu, S.; Wang, S.; Xuan, S.; Zhang, S.; Fan, X.; Jiang, H.; Song, P.; Gong, X. Highly flexible multilayered e-skins for thermal-magnetic-mechanical triple sensors and intelligent grippers. ACS Appl. Mater. Interfaces 2020, 12, 15675–15685. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Z.; Jiang, L.; Cheng, L. Magneto-mechanical properties of anisotropic magnetorheological elastomers with tilt angle of magnetic chain under compression mode. J. Magn. Magn. Mater. 2023, 570, 170441. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, K.; Ding, W.; Chen, Z.; Hou, L. Adaptive beam with elastic support based on magnetorheological elastomers for modal modulation and vibration suppression. Smart Mater. Struct. 2024, 33, 035013. [Google Scholar] [CrossRef]
- GB/T 2089-2009; Cylindrical Coiled Compression Spring Dimensions and Parameters. Standards Press of China: Beijing, China, 2009.
- Zhu, M.; Yu, M.; Qi, S.; Fu, J. Investigations on response time of magnetorheological elastomer under compression mode. Smart Mater. Struct. 2018, 27, 055017. [Google Scholar] [CrossRef]
- Pheasant, S.; Haslegrave, C.M.; Ebrary, I. Bodyspace: Anthropometry, Ergonomics, and the Design of Work; Taylor and Francis: Abingdon, UK, 1998. [Google Scholar]




| B | −5 | 61 | 0 |
| E | −3026 | 93,820 | 1,612,000 |
| c | 3.7 | 18.46 | 59.56 |
| Mass/(kg) | Stiffness/(103 N/m) | Damping/(102 Ns/m) | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.170 | 15.00 | 5.500 | 36.00 | 32.40 | 134.4 | 10.00 | 20.00 | 49.34 | 192.0 | 49.34 | 49.34 | 49.34 | 2.500 | 2.00 | 3.300 | 24.75 | 9.091 | 24.75 | 24.75 | 24.75 |
| Body Part | Absolute | Percentage | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Head | Chest | Abdomen | Pelvis | Head | Chest | Abdomen | Pelvis | ||
| Peak reduction | 82.3 mT | 0.2051 | 0.2303 | 0.2142 | 0.2537 | 8.217% | 8.088% | 7.795% | 7.792% |
| 138 mT | 0.3900 | 0.4400 | 0.4127 | 0.4894 | 15.63% | 15.45% | 15.02% | 15.03% | |
| Increase in frequency | 82.3 mT | 0.19 | 0.23 | 0.21 | 0.21 | 2.2% | 2.6% | 2.4% | 2.4% |
| 138 mT | 0.30 | 0.33 | 0.34 | 0.33 | 3.4% | 3.8% | 3.8% | 3.7% | |
| Mass Coefficient | Absolute | Percentage | |||||
|---|---|---|---|---|---|---|---|
| 0.9 | 1.0 | 1.1 | 0.9 | 1.0 | 1.1 | ||
| Peak reduction | 82.3 mT | 0.2342 | 0.2051 | 0.1825 | 8.706% | 8.217% | 7.788% |
| 138 mT | 0.4491 | 0.3900 | 0.3444 | 16.69% | 15.63% | 14.70% | |
| Increase in frequency | 82.3 mT | 0.23 | 0.19 | 0.17 | 2.5% | 2.2% | 2.0% |
| 138 mT | 0.36 | 0.30 | 0.24 | 3.9% | 3.4% | 2.9% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Wang, L.; Chen, Z.; Ao, H.; Yan, H. An Adaptive Elastic Support Seat-Based Magnetorheological Elastomer for Human Body Vibration Reduction. Materials 2024, 17, 3330. https://doi.org/10.3390/ma17133330
Ding W, Wang L, Chen Z, Ao H, Yan H. An Adaptive Elastic Support Seat-Based Magnetorheological Elastomer for Human Body Vibration Reduction. Materials. 2024; 17(13):3330. https://doi.org/10.3390/ma17133330
Chicago/Turabian StyleDing, Wei, Leizhi Wang, Zhaobo Chen, Hongrui Ao, and Hui Yan. 2024. "An Adaptive Elastic Support Seat-Based Magnetorheological Elastomer for Human Body Vibration Reduction" Materials 17, no. 13: 3330. https://doi.org/10.3390/ma17133330
APA StyleDing, W., Wang, L., Chen, Z., Ao, H., & Yan, H. (2024). An Adaptive Elastic Support Seat-Based Magnetorheological Elastomer for Human Body Vibration Reduction. Materials, 17(13), 3330. https://doi.org/10.3390/ma17133330






