Are Critical Fluctuations Responsible for Glass Formation?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methodology
2.3. Data Analysis
3. Results and Discussion
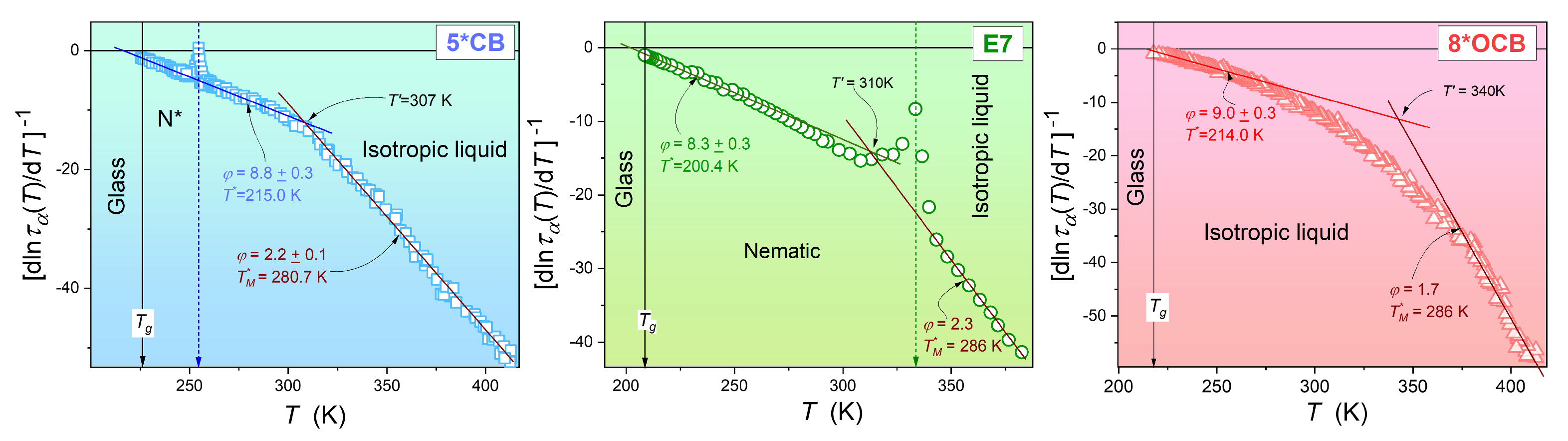
3.1. Previtreous Behavior of the Primary Relaxation Time
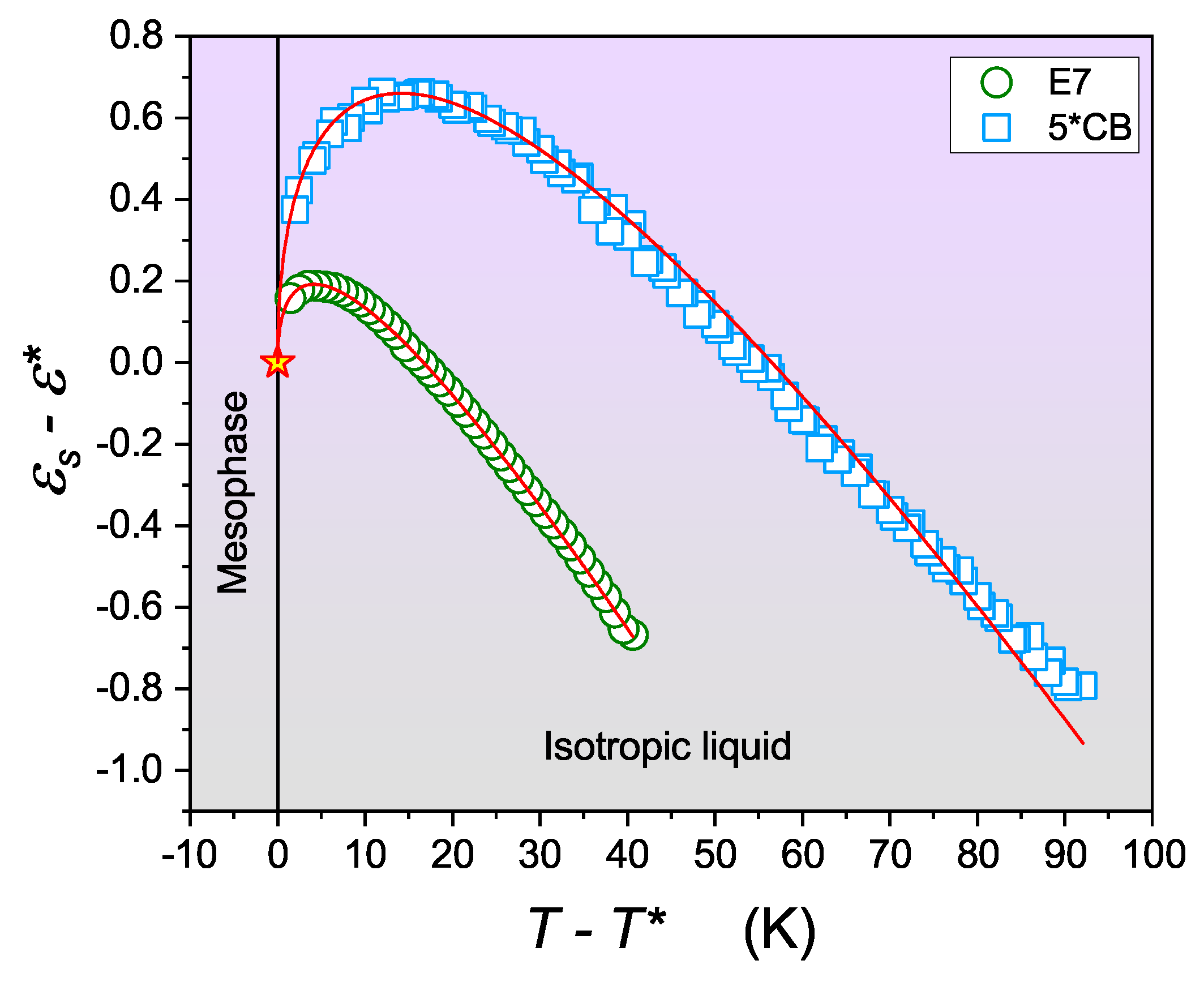
3.2. Pretranstional Anomalies in the Isotropic Phase
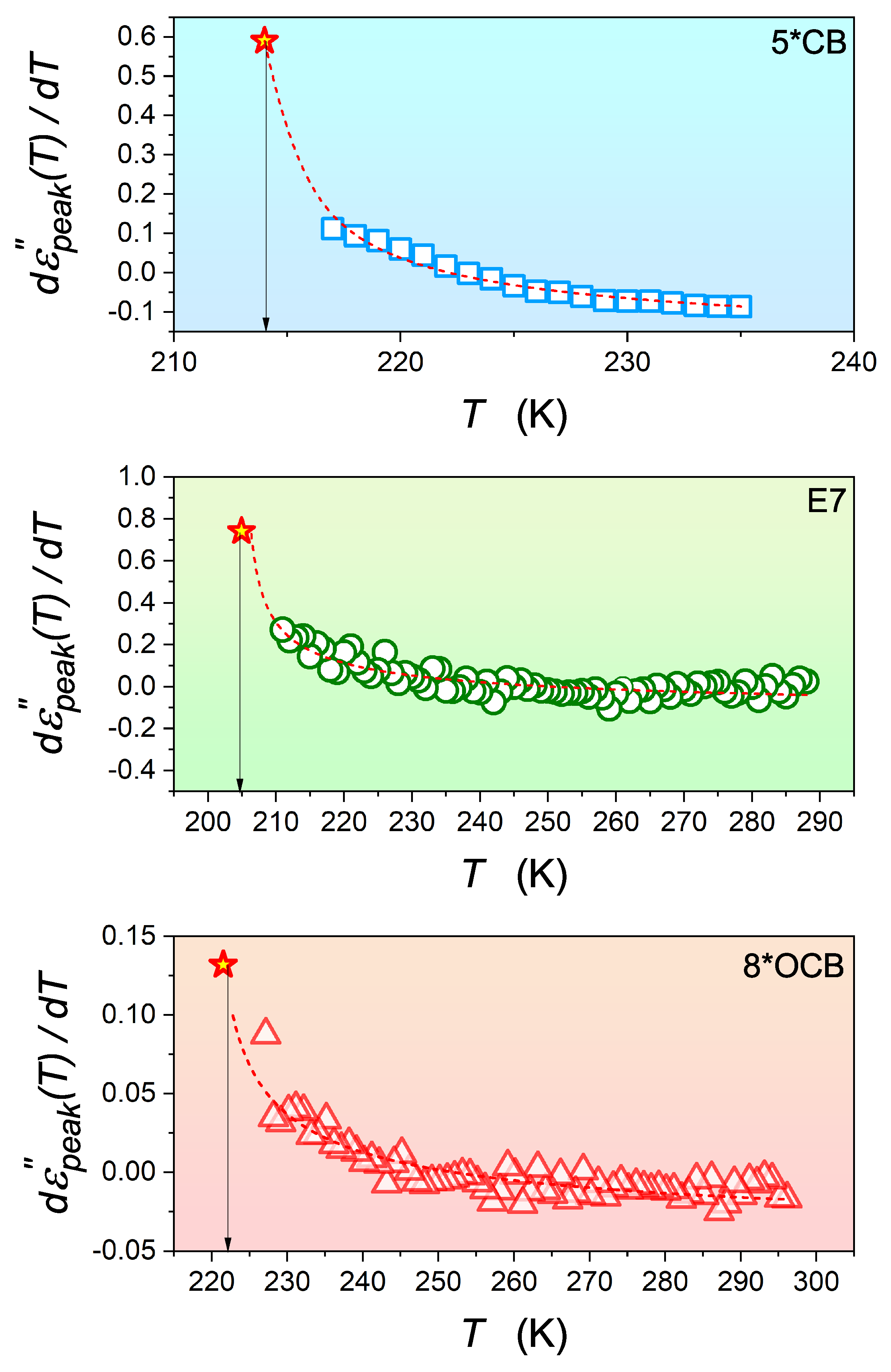
3.3. Critical-like Behavior near the Glass Transition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NDE | nonlinear dielectric effect |
| BDS | broadband dielectric spectroscopyu |
| 5*CB | (S)-4-(2-methylbutyl)-4’-cyanobiphenyl |
| 8*OCB | (S)-4-(1-methylheptyloxy)-4’-cyanobiphenyl |
| E7 | eutectic mixture of liquid crystals |
References
- Kennedy, D.; Norman, C. What don’t we know? Science 2005, 309, 75. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L.; Ediger, M. Facets of the glass transition. Phys. Today 2016, 69, 40–44. [Google Scholar] [CrossRef]
- McKenna, G.B.; Simon, S.L. 50th Anniversary Perspective: Challenges in the Dynamics and Kinetics of Glass-Forming Polymers. Macromolecules 2017, 50, 6333–6361. [Google Scholar] [CrossRef]
- McKenna, G.B. Glass transition: Challenges of extreme time scales and other interesting problems. Rubber Chem. Technol. 2020, 93, 79–120. [Google Scholar] [CrossRef]
- Yue, Y. Shadow glass transition in glass. Nat. Sci. Rev. 2021, 8, nwab160. [Google Scholar] [CrossRef]
- Tanaka, H. Roles of liquid structural ordering in glass transition, crystallization, and water’s anomalies. J. Non-Cryst. Solids X 2022, 13, 100076. [Google Scholar] [CrossRef]
- Skripov, V.P.; Faizulin, M.Z. Crystal-Liquid-Gas Phase Transitions and Thermodynamic Similarity; Wiley-VCH: Berlin, Germany, 2006; ISBN 978-3-527-40576-3. [Google Scholar]
- Anisimov, M.A. Critical Phenomena in Liquids and Liquid Crystals Gordon and Breach; CRC Press: Reading, UK, 1992. [Google Scholar]
- Rzoska, S.J.; Drozd-Rzoska, A.; Mukherjee, P.K.; Lopez, D.O.; Martinez-Garcia, J.C. Distortions-sensitive analysis of pretransional behaviour in n-octyloxycyanobiphenyl (8OCB). J. Phys. Cond. Matter 2013, 25, 245105. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Starzonek, S.; Drozd-Rzoska, A.; Czupryński, K.; Chmiel, K. Impact of nanoparticles on pretransitional effects in liquid crystalline dodecylcyanobiphenyl. Phys. Rev. 2016, 93, 020701. [Google Scholar]
- Starzonek, S.; Rzoska, S.J.; Drozd-Rzoska, A.; Czupryński, K.; Kralj, S. Impact of ferroelectric and superparaelectric nanoparticles on phase transitions and dynamics in nematic liquid crystals. Phys. Rev. E 2017, 96, 022705. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.J.; Kralj, S. Nanoparticle-controlled glassy dynamics in nematogen-based nanocolloids. Phys. Rev. E 2019, 99, 052703. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Starzonek, S.; Łoś, J.; Drozd-Rzoska, A.; Kralj, S. Dynamics and Pretransitional Effects in C60 Fullerene Nanoparticles and Liquid Crystalline Dodecylcyanobiphenyl (12CB) Hybrid System. Nanomaterials 2020, 10, 2343. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Pawlus, S.; Tamarit, J.L. Dynamics crossover and dynamic scaling description in vitrification of orientationally disordered crystal. Phys. Rev. B 2006, 73, 224205. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Pawlus, S.; Tamarit, J.L. Dielectric relaxation in compressed glassy and orientationally disordered mixed crystal. Phys. Rev. B 2006, 74, 064201. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.J.; Łoś, J.; Kutnjak, Z.; Kralj, S. Pretransitional effects of the isotropic liquid–plastic crystal transition. Molecules 2021, 26, 429. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Szpakiewicz-Szatan, A.; Łoś, J.; Starzonek, S. Supercritical anomalies in liquid ODIC-forming cyclooctanol under the strong electric field. J. Mol. Liq. 2022, 345, 1178491. [Google Scholar] [CrossRef]
- Kremer, F.; Loidl, A. Scaling of Relaxation Processes; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Ramirez, R. An Introduction to Glass Transition; Nova Sci Pub: London, UK, 2019. [Google Scholar]
- Angell, C.A. Strong and fragile liquids. In Relaxations in Complex Systems; Ngai, K.L., Wright, G.B., Eds.; NRL: Washington, DC, USA, 1985; pp. 13–42. [Google Scholar]
- Angell, C.A. Structural instability and relaxation in liquid and glassy phases near the fragile liquid limit. J. Non-Cryst. Solids 1988, 102, 205–221. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass-formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Drozd-Rzoska, A. Dual field nonlinear dielectric spectroscopy in a glass forming EPON 828 epoxy resin. J. Phys. Condens. Matter 2011, 24, 035101. [Google Scholar] [CrossRef] [PubMed]
- Selevus, A.; Papamokos, G.; Yildrim, T.; Duran, H.; Steinhart, M.; Floudas, G. Eutectic liquid crystal mixture E7 in nanoporous alumina. Effects of confinement on the thermal and concentration fluctuations. RSC Adv. 2019, 9, 37846. [Google Scholar] [CrossRef]
- Ghanadzadeh, A.; Beevers, M.S. The electro-optical Kerr effect in eutectic nematic mixtures of E7 and E8. J. Mol. Liq. 2001, 92, 217–225. [Google Scholar] [CrossRef]
- Vogel, H. Temperaturabhängigkeitsgesetz der viskosität von flüssigkeiten. Phys. Zeit. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G. Glasses as supercooled liquids. J. Soc. Glass Technol. 1925, 9, 166–185. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New scaling paradigm for dynamics in glass-forming systems. Prog. Mater. Sci. 2023, 134, 101074. [Google Scholar] [CrossRef]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glassforming liquids. Proc. Natl. Acad. Sci. USA 2009, 24, 19780–19784. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A. A universal behaviour of the apparent fragility in ultraslow glass forming systems. Sci. Rep. 2019, 9, 6816. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Paluch, M. Universal critical-like scaling of dynamic properties in symmetry-selected glass-formers. J. Chem. Phys. 2008, 129, 184509. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Pawlus, S.; Martinez-Garcia, J.C.; Tamarit, J.L. Evidence for critical-like behaviour in ultraslowing glass-forming systems. Phys. Rev. E 2010, 82, 031501. [Google Scholar] [CrossRef] [PubMed]
- Garcia, J.C.M.; Tamarit, J.L.; Rzoska, S.J. Enthalpy space analysis of the evolution of the primary relaxation time in ultraslowing systems. J. Chem. Phys. 2011, 134, 024512. [Google Scholar] [CrossRef]
- Colby, R.H. Dynamic scaling approach to glass formation. Phys. Rev. E 2000, 61, 1783–1792. [Google Scholar] [CrossRef]
- Erwin, B.M.; Colby, R.H. Temperature dependence of relaxation times and the length scale of cooperative motion for glass-forming liquids. J. Non-Cryst. Solids 2002, 307–310, 225–232. [Google Scholar] [CrossRef]
- Rzoska, S.; Drozd-Rzoska, A.; Mazur, V. Metastable Systems under Pressure; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New paradigm for configurational entropy in glass forming liquids. Sci. Rep. 2022, 12, 3058. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drozd-Rzoska, A.; Martinez-Garcia, J. A universal description of ultraslow glass dynamics. Nat. Comm. 2013, 4, 1823. [Google Scholar] [CrossRef] [PubMed]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Berthier, L.; Ozawa, M.; Scaillet, C. Configurational entropy of glass-forming liquids. J. Chem. Phys. 2019, 150, 160902. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J.; Drozd-Rzoska, A.; Górny, M.; Jadżyn, J.; Zioło, J. Nonlinear dielectric effect in superpressed chiral isopentylcyanobiphenyl (5*CB). J. Non-Cryst. Solids 2002, 307–310, 311–316. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Paluch, M.; Pawlus, S.; Drozd-Rzoska, A.; Ziolo, J.; Jadzyn, J.; Czupryński, K.; Dabrowski, R. Complex dielectric relaxation in supercooling and superpressing liquid-crystalline chiral isopentylcyanobiphenyl. Phys. Rev. E 2003, 68, 031705. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Paluch, M.; Pawlus, S.; Ziolo, J.; Santangelo, P.G.; Roland, C.M.; Czupryński, K.; Dąbrowski, R. Mode coupling behaviour in glass-forming liquid crystalline isopentylcyanobiphenyl. Phys. Rev. E 2005, 71, 011508. [Google Scholar] [CrossRef] [PubMed]
- Fragiadakis, D.; Urban, S.; Massalska-Arodz, M.; Bogoslovov, R.B.; Czub, J.; Roland, C.M. Phase Diagram and Dynamics of the Liquid Crystal Isopentylcyanobiphenyl (5*CB). J. Phys. Chem. B 2011, 115, 6437–6444. [Google Scholar] [CrossRef]
- Krawczyk, J.; Massalska-Arodź, M.; Rozwadowski, T. Low-temperature dynamics of (S)-4-(1-methylheptyloxy)-4′-cyanobiphenyl (8*OCB) and (S)-4-(2-methylbutyl)-4′-cyanobiphenyl (5*CB) in disordered crystalline and glassy phases. Liq. Cryst. 2019, 46, 94–101. [Google Scholar] [CrossRef]
- Pawlus, S.; Mierzwa, M.; Paluch, M.; Rzoska, S.J.; Roland, C.M. Dielectric and mechanical relaxation in isooctylcyanobiphenyl (8*OCB). J. Phys. Condens. Matter 2010, 22, 235101. [Google Scholar] [CrossRef] [PubMed]
- Mierzwa, M.; Paluch, M.; Rzoska, S.J.; Zioło, J. Ordering effect on dynamics in glass-forming mixture of liquid. In Soft Matter under Exogenic Impacts; NATO Sci. Series II; Springer: Berlin/Heidelberg, Germany, 2007; Volume 242. [Google Scholar]
- Viciosa, M.T.; Nunes, A.M.; Fernandes, A.; Almeida, P.L.; Godinho, M.H.; Dionísio, M.D. Dielectric studies of the nematic mixture E7 on a hydroxypropylcellulose substrate. Liq. Cryst. 2002, 29, 429–441. [Google Scholar] [CrossRef]
- Thoen, J.; Menu, G. Temperature dependence of the static relative permittivity of octylcyanobiphenyl (8CB). Mol. Cryst. Liq. Cryst. 1983, 97, 163–176. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. Critical behaviour of dielectric permittivity in the isotropic phase of nematogens. Phys. Rev. E 1996, 54, 6452–6456. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. The quasi-critical behaviour of dielectric permittivity in the isotropic phase of smectogenic n-cyanobiphenyls. Phys. Rev. E 2000, 61, 5349–5354. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Czupryński, K. Phase transitions from the isotropic liquid to liquid crystalline mesophases studied by ’linear’ and ’nonlinear’ static dielectric permittivity. Phys. Rev. E 2000, 61, 5355–5360. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Heterogeneity-related dynamics in isotropic n-pentylcyanobiphenyl. Phys. Rev. E 2006, 73, 022501. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A. Quasi-Tricritical’ and Glassy Dielectric Properties of a Nematic Liquid Crystalline Material. Crystals 2020, 10, 297. [Google Scholar] [CrossRef]
- Łoś, J.; Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S.; Czupryński, K. Fluctuations-driven dielectric properties of liquid crystalline octyloxycyanobiphenyl and its nanocolloids. Soft Matter 2022, 18, 4502–4512. [Google Scholar] [CrossRef]
- Koperwas, K.; Adrjanowicz, K.; Wojnarowska, Z.; Jedrzejowska, A.; Knapik, J.; Paluch, M. Glass-forming tendency of molecular liquids and the strength of the intermolecular attractions. Sci. Rep. 2016, 6, 36934. [Google Scholar] [CrossRef]
- Corezzi, S.; Campani, E.; Rolla, P.A. Changes in the dynamics of supercooled systems revealed by dielectric spectroscopy. J. Chem. Phys. 1999, 111, 9343–9351. [Google Scholar] [CrossRef]
- Wojnarowska, Z.; Paluch, M. Dielectric and Mechanical Signature of Anti-Parallel Ordering in Simple Van Der Waals Glass-Formers. J. Phys. Chem. C 2022, 126, 17353–17358. [Google Scholar] [CrossRef]
- Capponi, S.; Napolitano, S.; Wübbenhorst, M. Supercooled liquids with enhanced orientational order. Nat. Commun. 2012, 3, 1233. [Google Scholar] [CrossRef]
- Schönhals, A. Evidence for a universal crossover behaviour of the dynamic glass transition. Europhys. Lett. 2001, 56, 815–821. [Google Scholar] [CrossRef]
- Mistura, L. behaviour of the dielectric constant near a critical point in fluid systems. J. Chem. Phys. 1973, 59, 4563–4565. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Urbanowicz, P.; Drozd-Rzoska, A.; Paluch, M.; Habdas, P. Pressure behaviour of dielectric permittivity on approaching the critical consolute point. Europhys. Lett. 1999, 45, 334–340. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J. High-pressure behaviour of dielectric constant in a binary critical mixture. Phys. Rev. E 2020, 102, 042610. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J. Kerr effect and nonlinear dielectric effect on approaching the critical consolute point. Phys. Rev. E 1993, 48, 1136–1143. [Google Scholar] [CrossRef]
- Guiselin, B.; Berthier, L.; Tarjus, G. Random-field ising model criticality in a glass-forming liquid. Phys. Rev. E 2020, 102, 042129. [Google Scholar] [CrossRef]
- Feio, G.; Figueirinhas, J.L.; Tajbakhsh, A.R.; Terentjev, E.M. Critical fluctuations and random-anisotropy glass transition in nematic elastomers. Phys. Rev. B 2008, 78, 020201. [Google Scholar] [CrossRef]
- Bertr, C.E.; Linegar, K.L.; Kostko, A.F.; Anisimov, M.A. Multiscale dynamics of pretransitional fluctuations in the isotropic phase of a lyotropic liquid crystal. Phys. Rev. E 2009, 79, 041704. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A.; Zhao, Z. Fluctuations, clusters, and phase transitions in liquids, solutions, and glasses: From metastable water to phase change memory materials. Faraday Discuss. 2013, 167, 625–641. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. Roles of bond orientational ordering in glass transition and crystallization. J. Physics Condens. Matter 2011, 23, 284115. [Google Scholar] [CrossRef] [PubMed]
- Sengers, J.V.; Bedeaux, D.; Mazur, P.; Greer, S.C. Behaviour of the dielectric constant of fluids near a critical point. Physica A 1980, 104, 573. [Google Scholar] [CrossRef]
- Bertrand, C.E.; Sengers, J.V.; Anisimov, M.A. Critical behaviour of the dielectric constant in asymmetric fluids. J. Phys. Chem. B 2011, 115, 14000. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starzonek, S.; Łoś, J.; Rzoska, S.J.; Drozd-Rzoska, A.; Iglič, A. Are Critical Fluctuations Responsible for Glass Formation? Materials 2024, 17, 3385. https://doi.org/10.3390/ma17143385
Starzonek S, Łoś J, Rzoska SJ, Drozd-Rzoska A, Iglič A. Are Critical Fluctuations Responsible for Glass Formation? Materials. 2024; 17(14):3385. https://doi.org/10.3390/ma17143385
Chicago/Turabian StyleStarzonek, Szymon, Joanna Łoś, Sylwester J. Rzoska, Aleksandra Drozd-Rzoska, and Aleš Iglič. 2024. "Are Critical Fluctuations Responsible for Glass Formation?" Materials 17, no. 14: 3385. https://doi.org/10.3390/ma17143385
APA StyleStarzonek, S., Łoś, J., Rzoska, S. J., Drozd-Rzoska, A., & Iglič, A. (2024). Are Critical Fluctuations Responsible for Glass Formation? Materials, 17(14), 3385. https://doi.org/10.3390/ma17143385






