Research on the Corrosion Detection of Rebar in Reinforced Concrete Based on SMFL Technology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Preparation
2.1.1. Materials for Concrete Specimens
2.1.2. Corrosive Materials for Specimens
2.2. The Methods for Testing
2.2.1. The Corrosion Method of Specimens
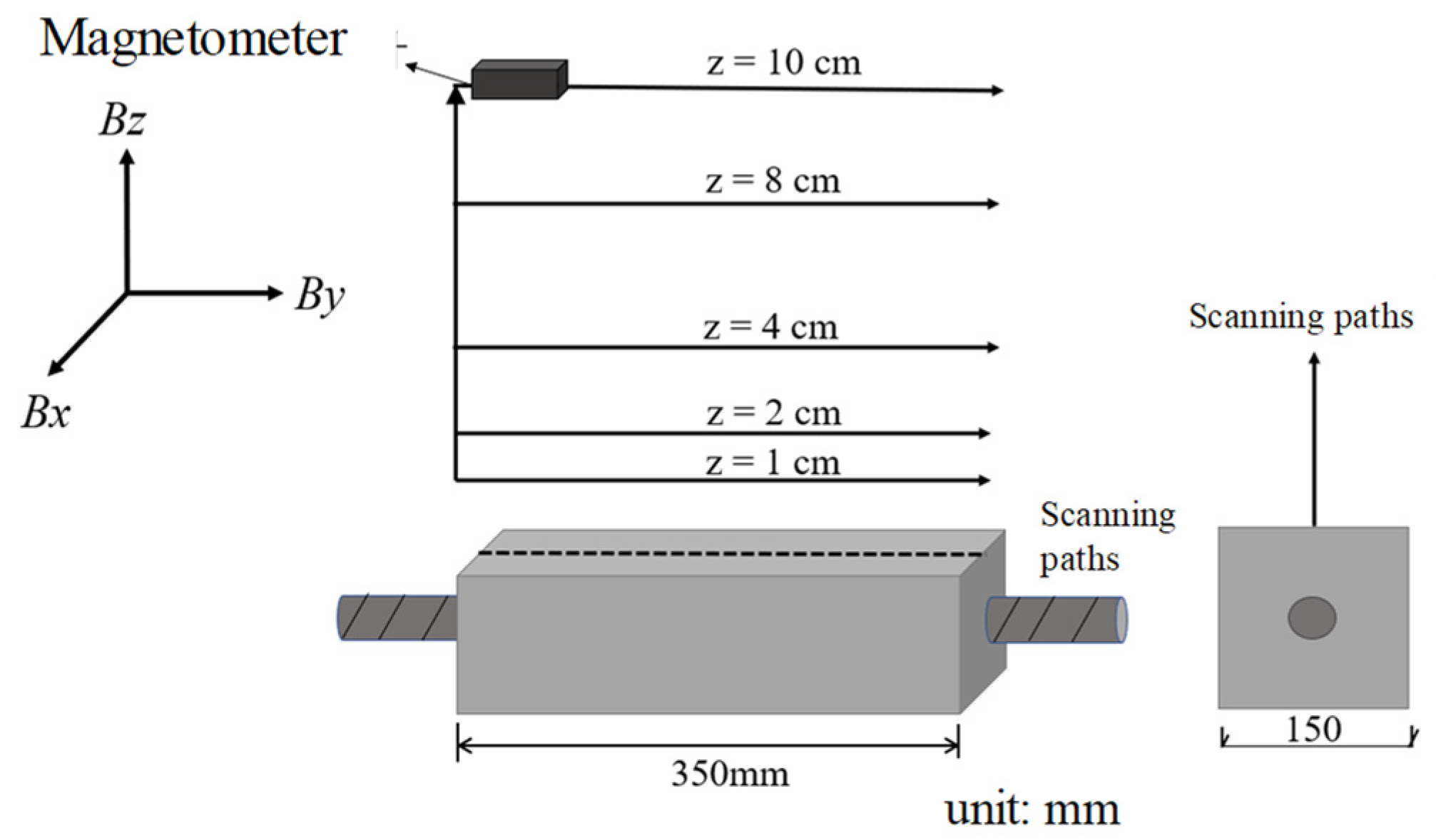
2.2.2. The Collection Method of the SMFL Signal on Corroded Specimens
2.3. Theory Background of Testing
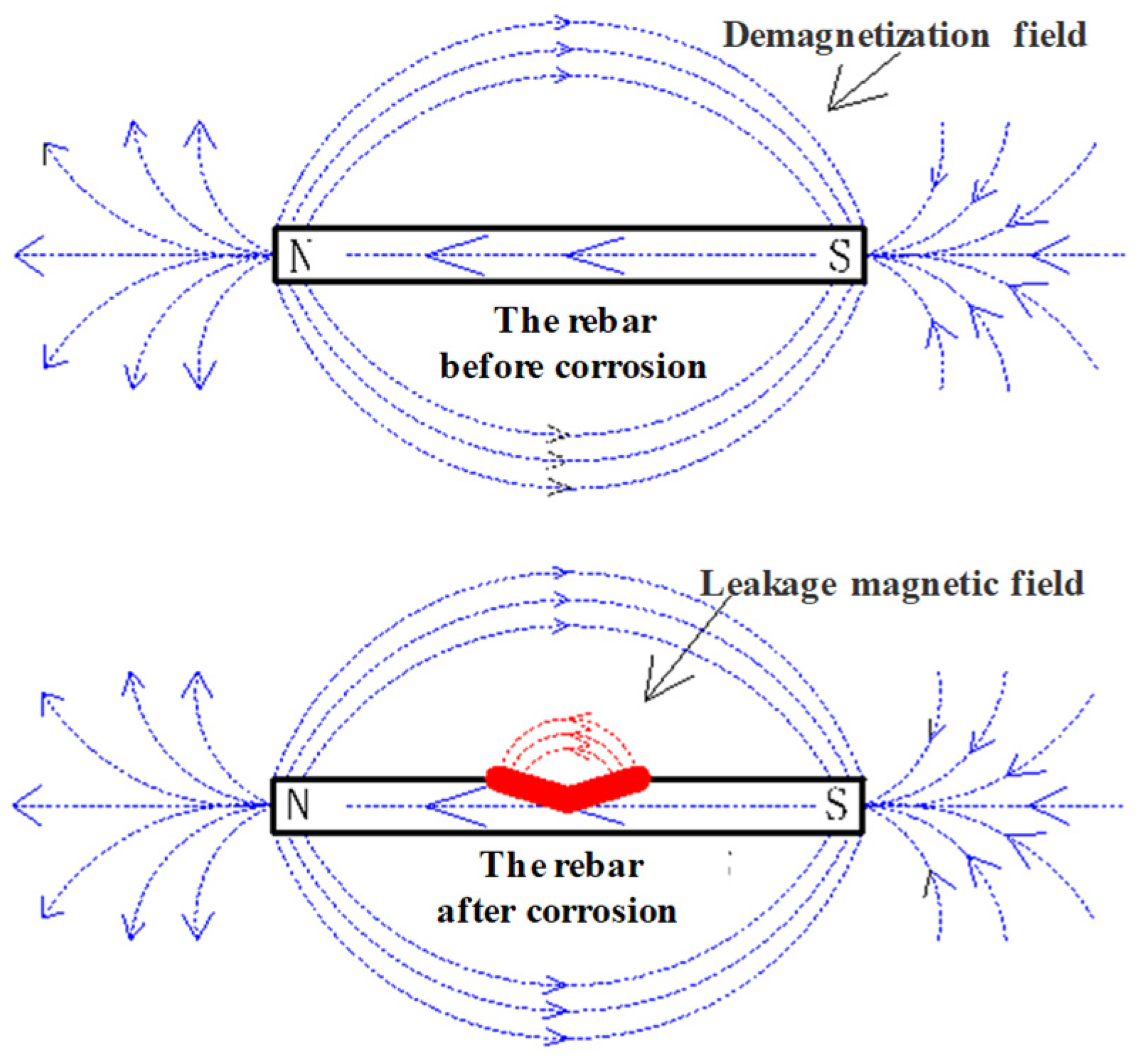
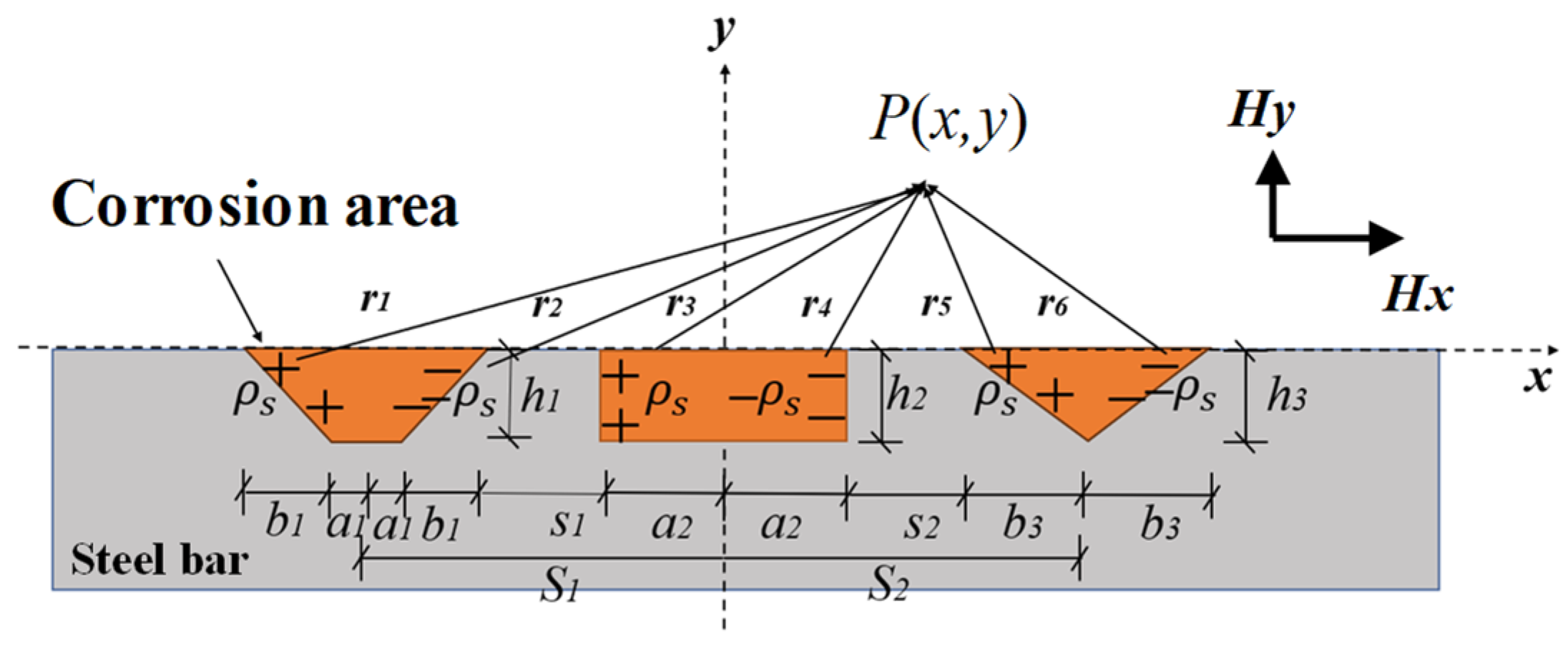
2.3.1. The Magnetic Field Induced by Corrosion
2.3.2. The Magnetic Field Induced by Corrosion Expansion Force
2.3.3. The Magnetic Field Induced by the Coupling Effect of Corrosion and Corrosion Expansion Force
3. Results and Discussion
3.1. Results of Corrosion
3.2. Analysis of SMFL Signals during the Corrosion Process of Specimens
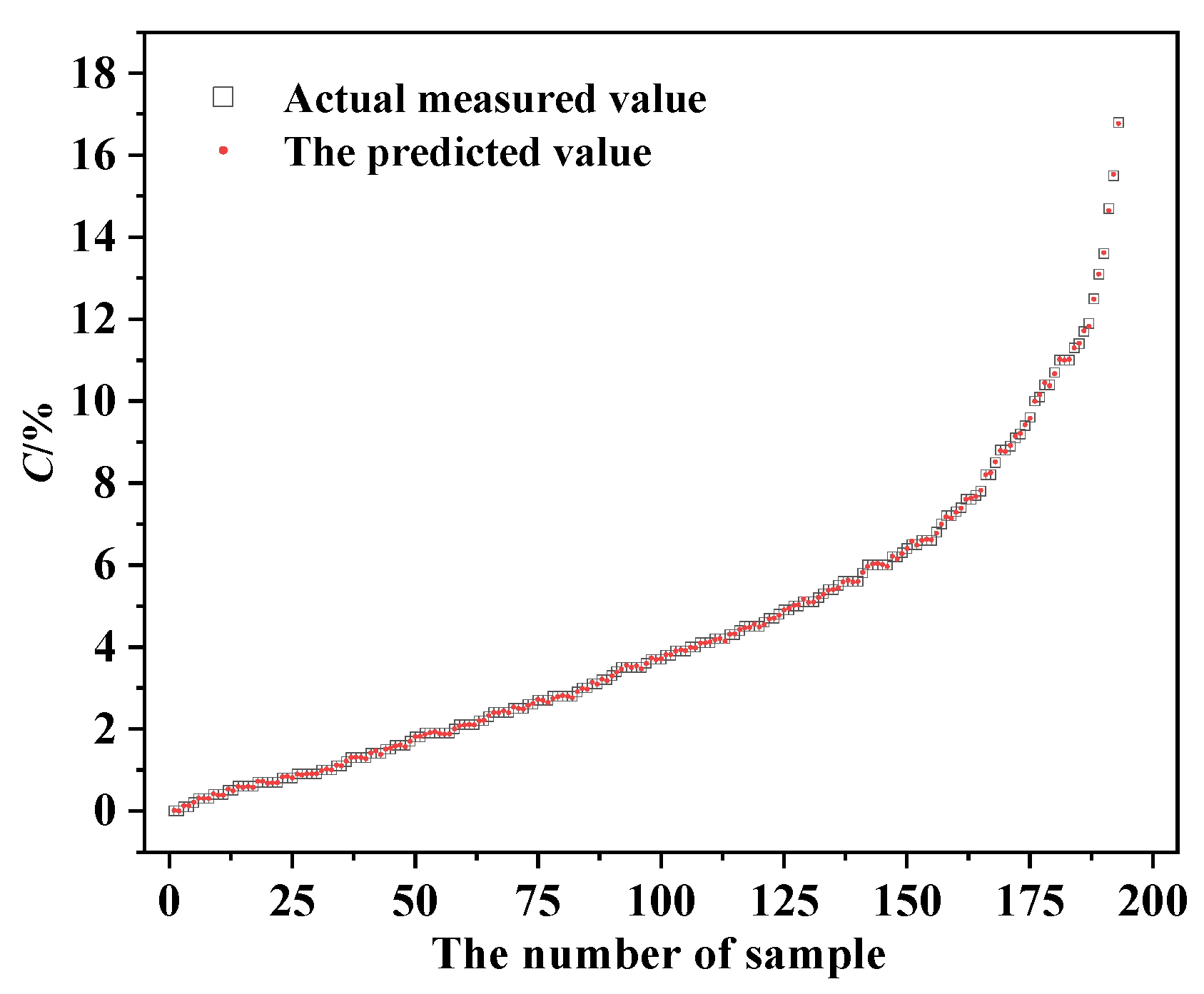
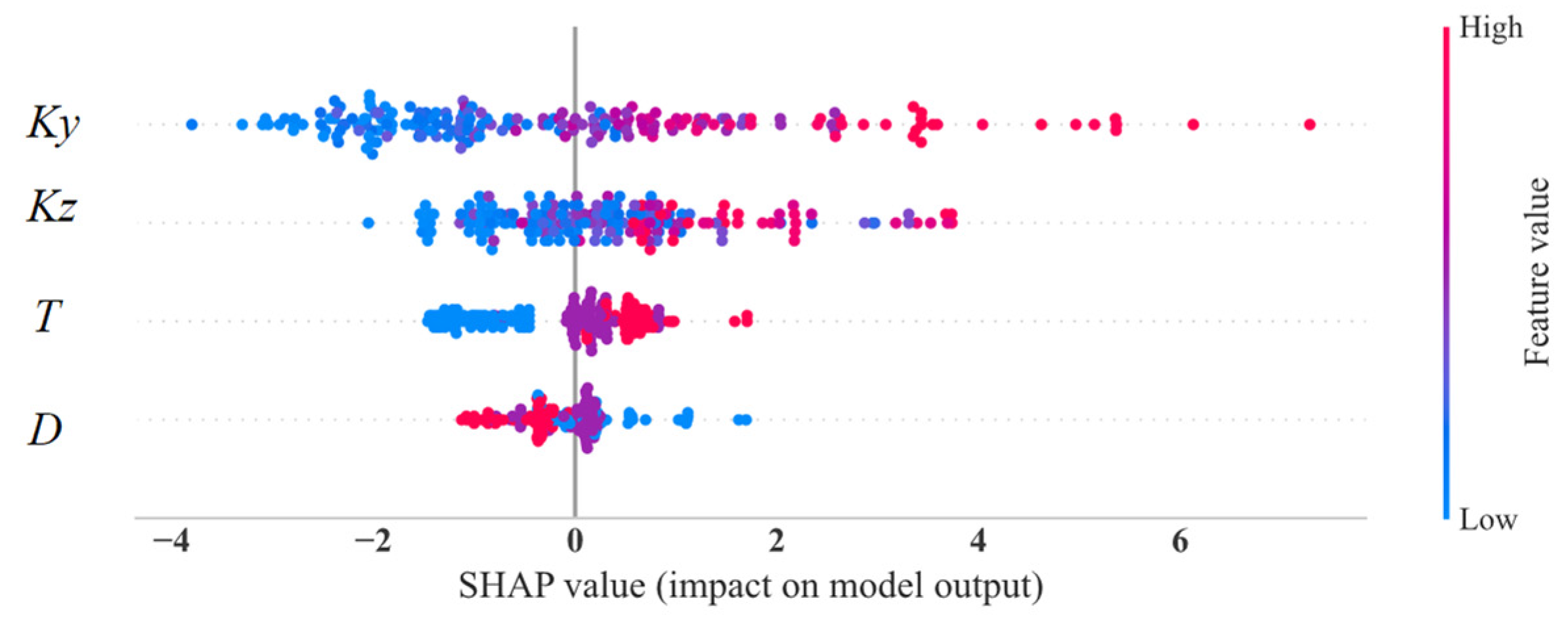
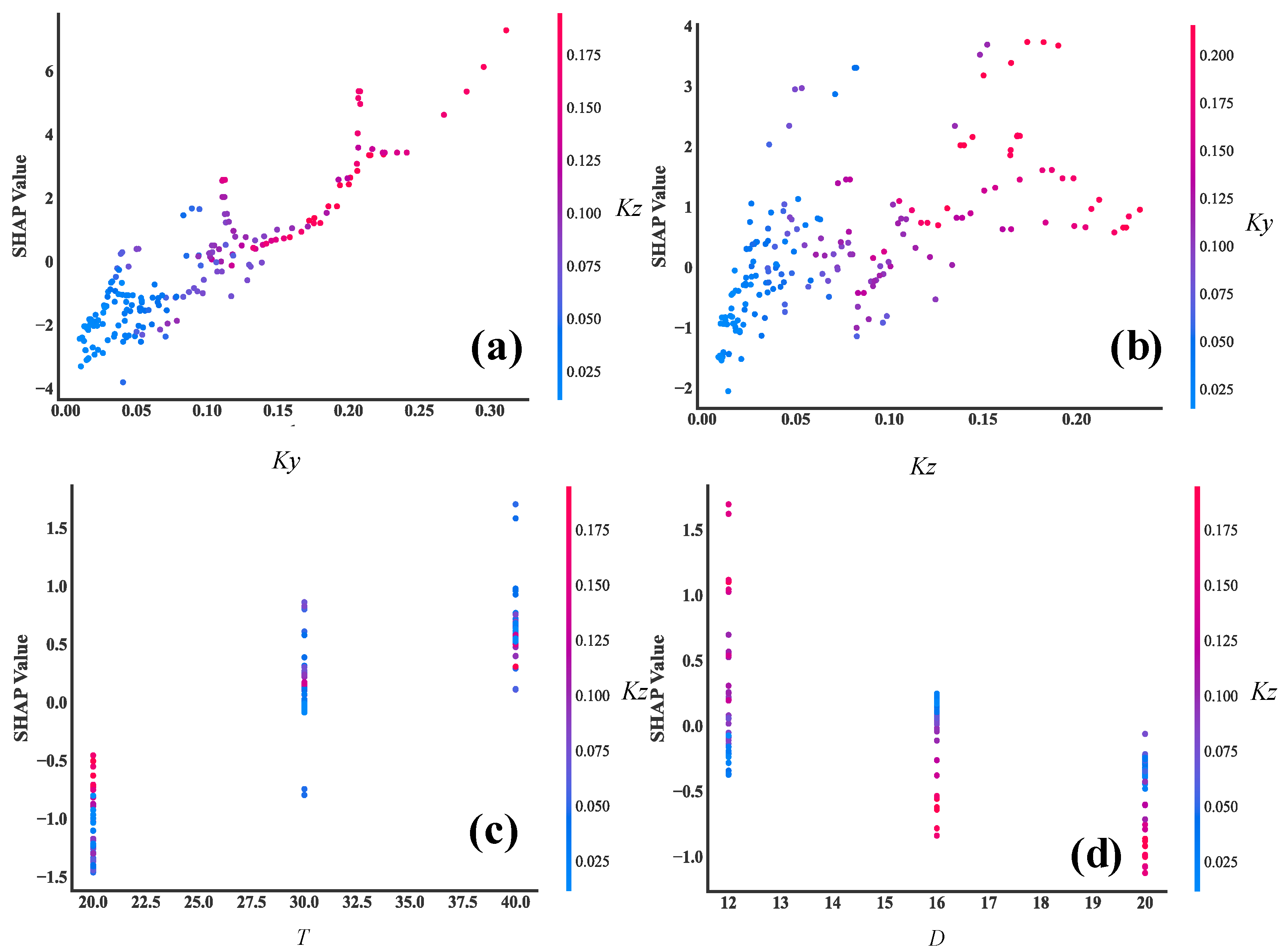
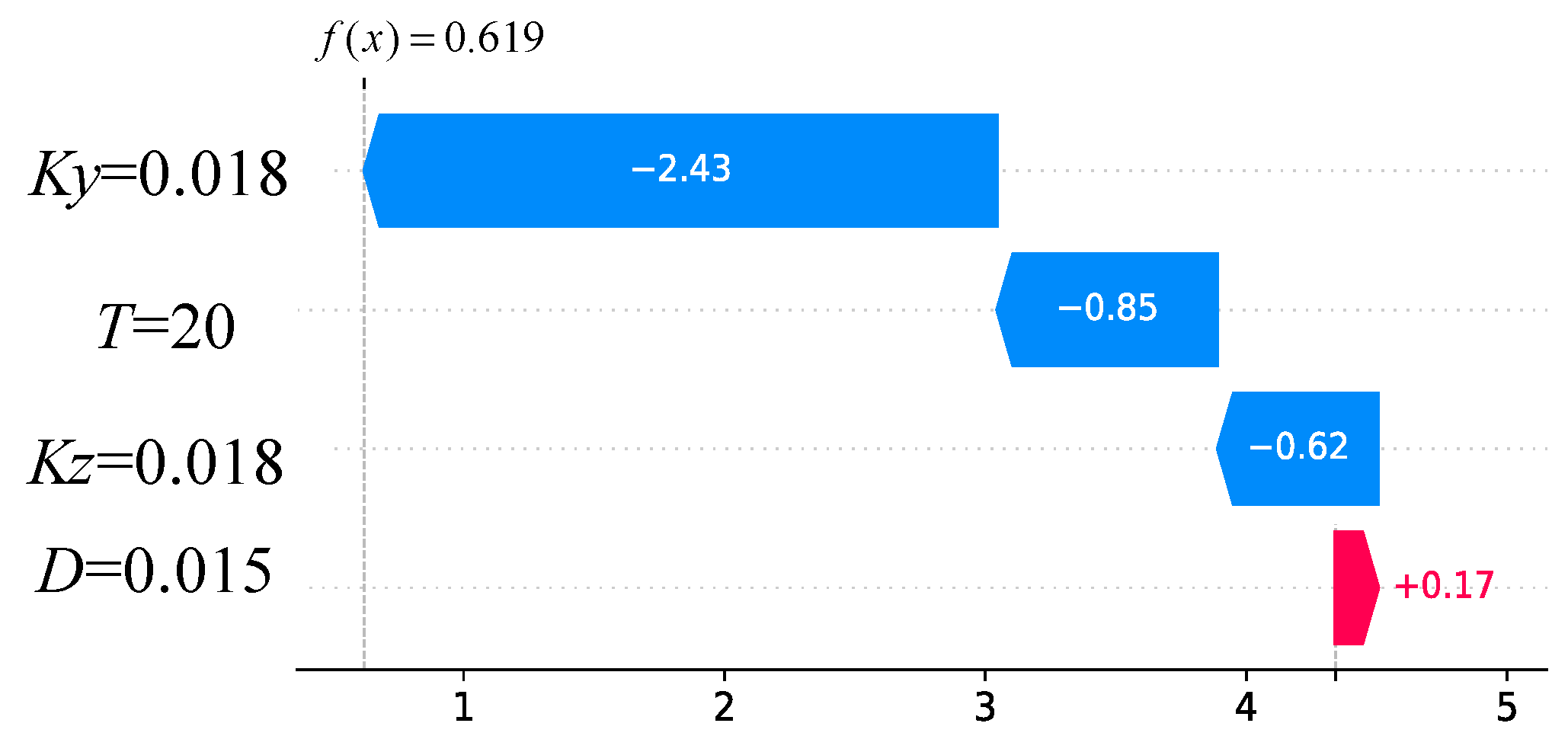
3.3. Corrosion Degree Assessment of the Rebar Based on XGBoost Algorithm
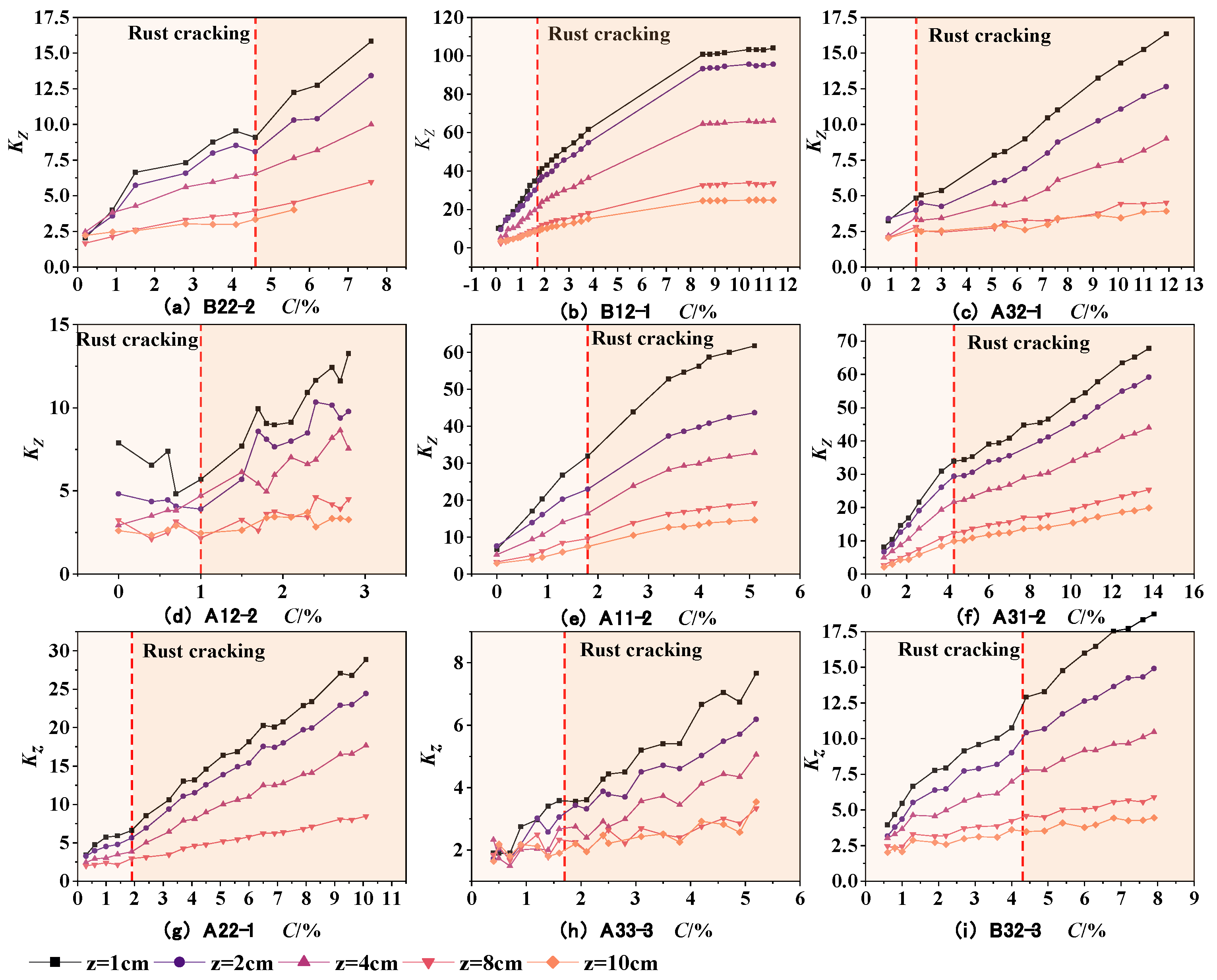
3.3.1. The Magnetic Parameters of the Characterizing Corrosion Degree
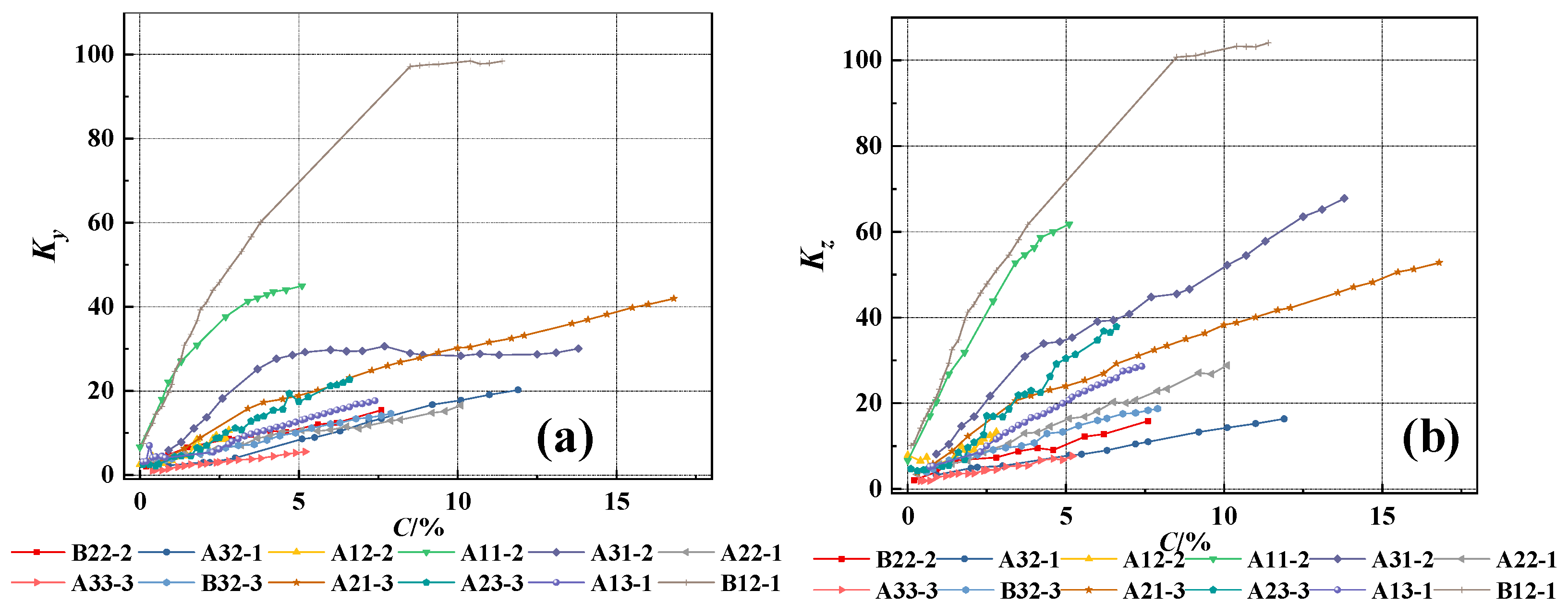
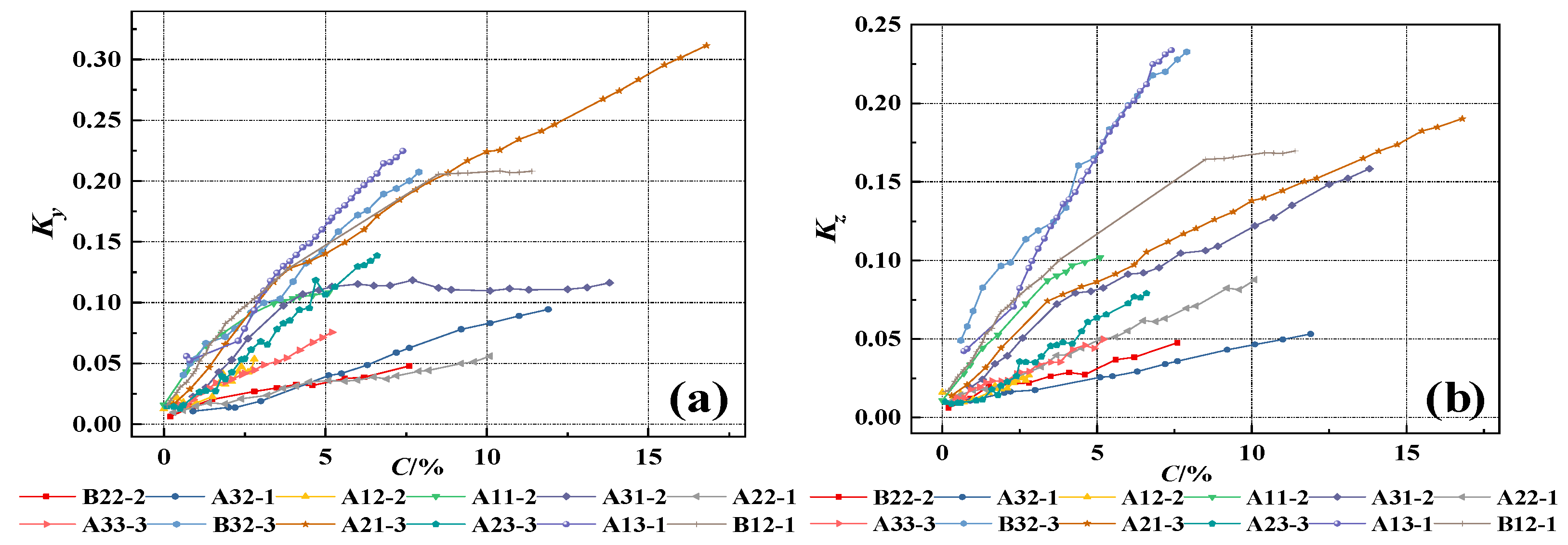
3.3.2. Assessment of the Rebar Corrosion Degree Based on Multiple Parameters
4. Conclusions
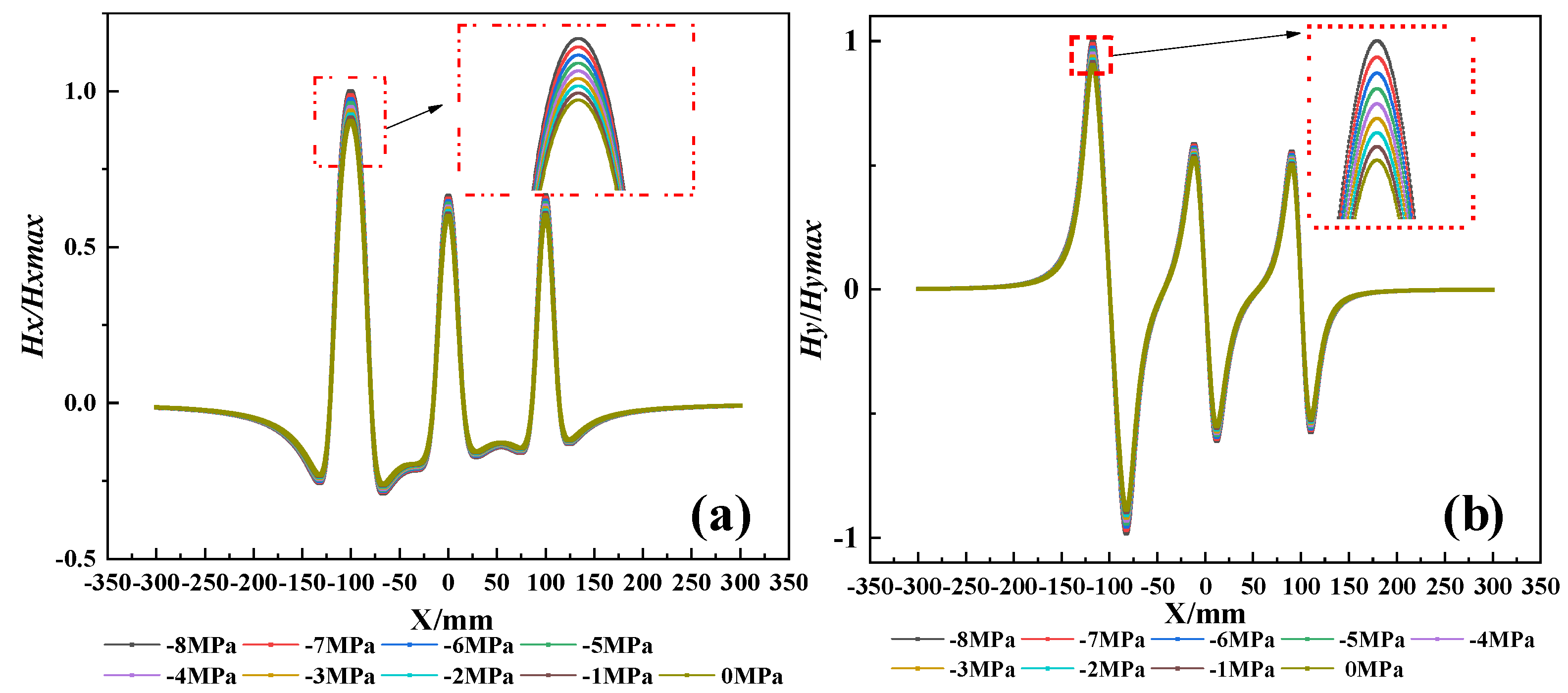
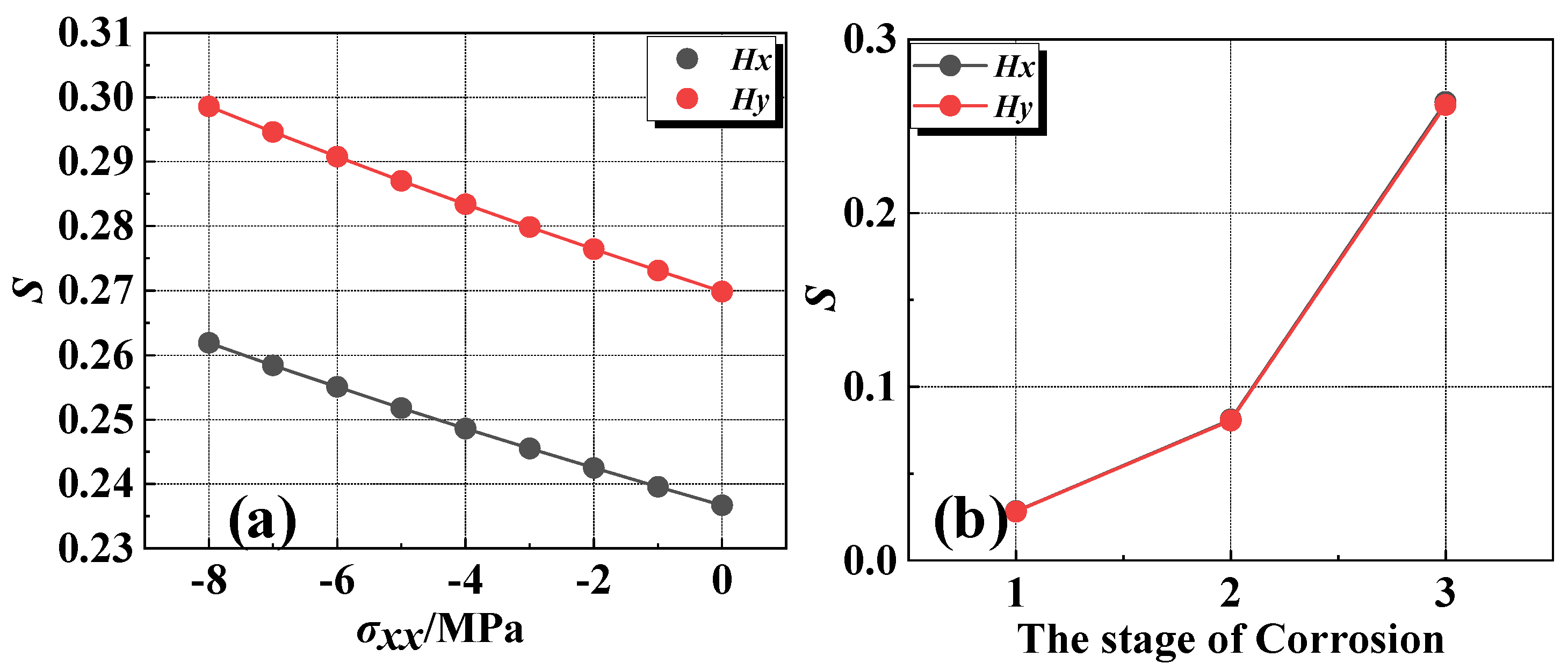
- A magnetic dipole model coupling with a multi-defect is established and the influence of the corrosion expansion force and corrosion degree on the SMFL signal is analyzed. The results show that the standard deviation of the magnetic field intensity caused by corrosion varied by up to 833%, while that caused by corrosion expansion force did not exceed 10%. Therefore, the influence of the corrosion expansion force on the detection of corrosion damage can be ignored;
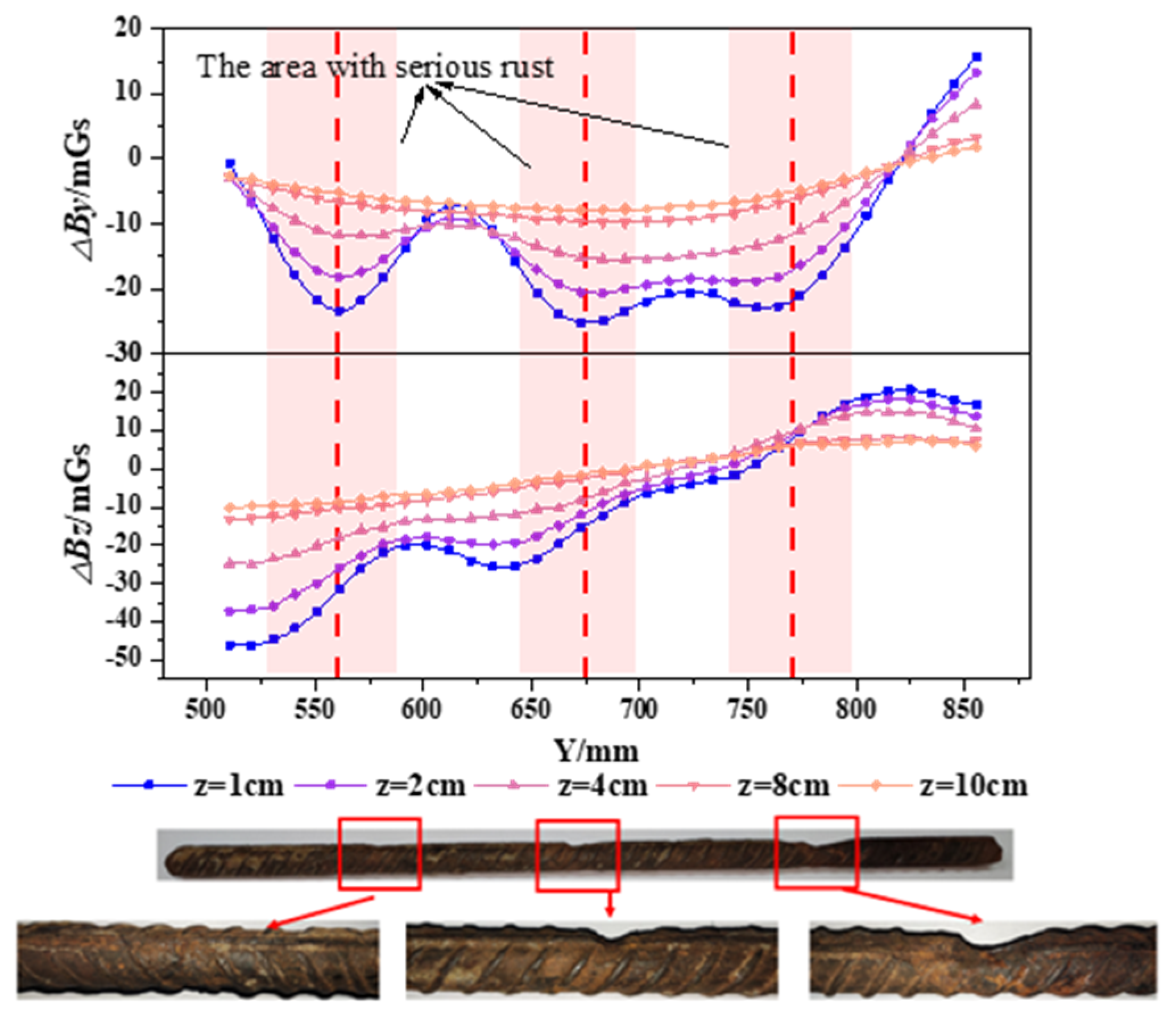
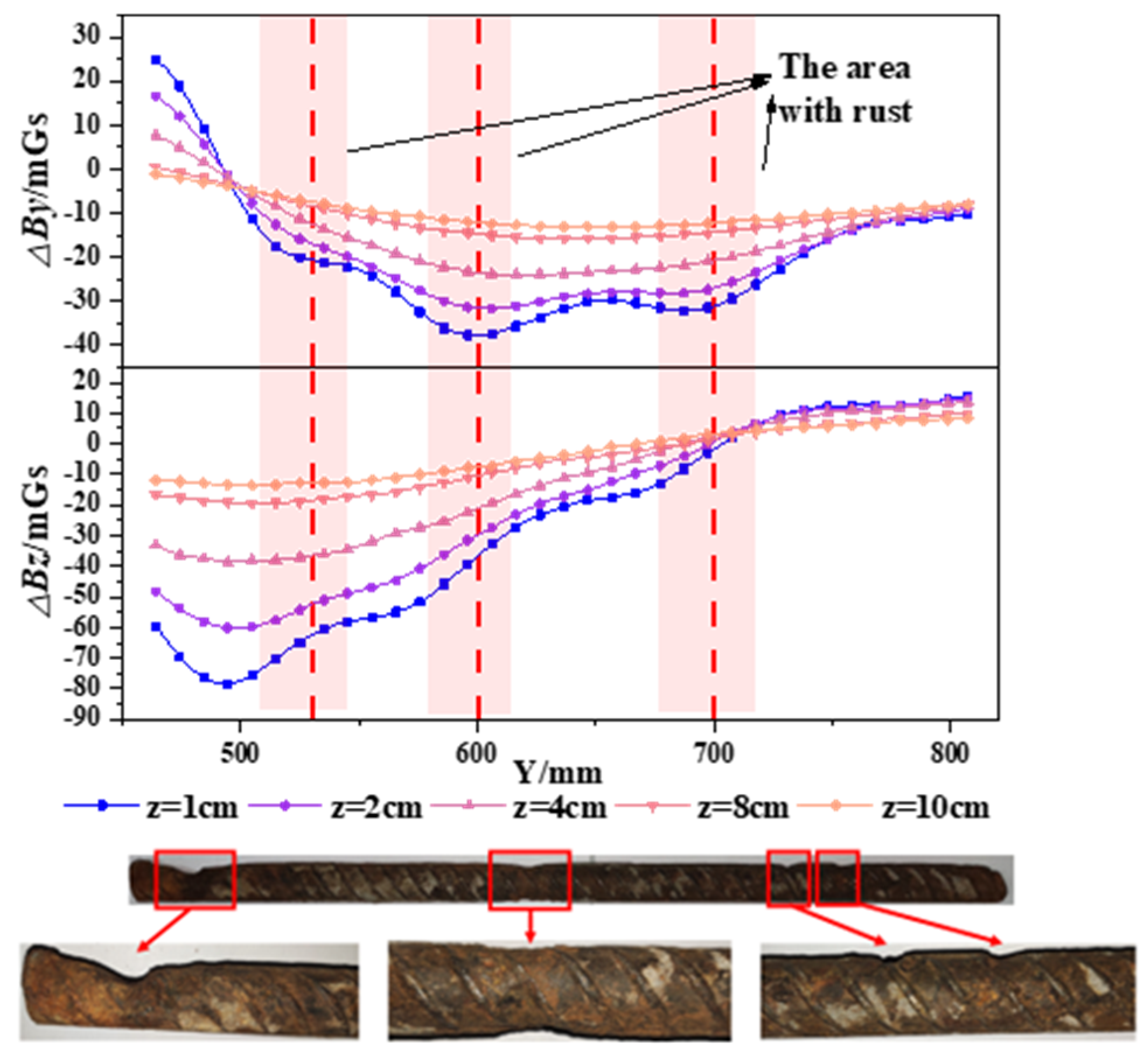
- Experimental results show that the trough positions of the ΔBy curves and the intersection points of the ΔBz curves obtained at different measurement heights are in good agreement with the positions of severe corrosion of the rebars. Compared to the △Bz, the severe corrosion area of rebars could be more accurately identified based on the change in △By curves;
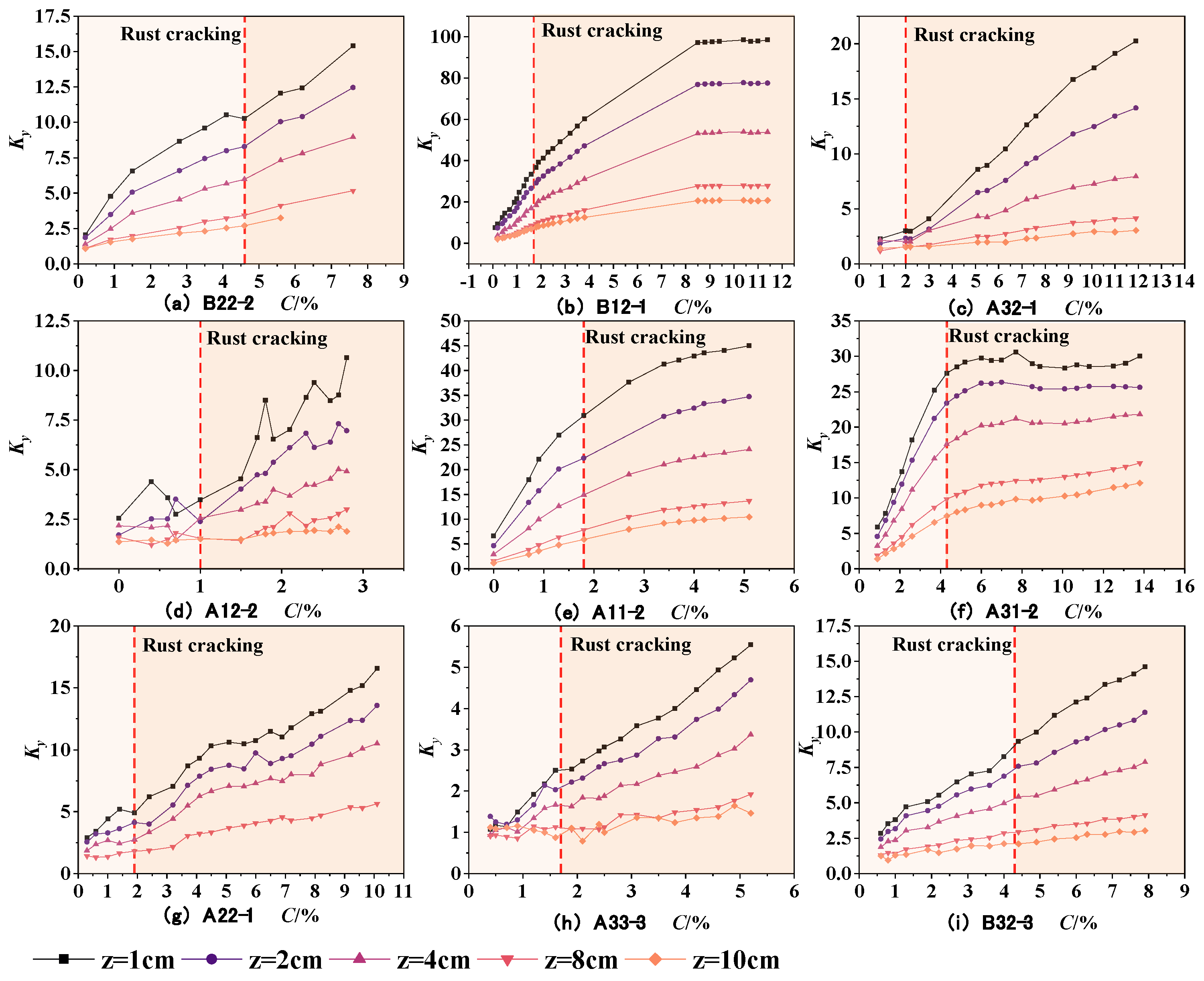
- The experimental results indicate that the SMFL curves of rebars in reinforced concrete change monotonically with the increase in the corrosion degree. Based on this characteristic of change, the proposed quantification parameters Ky and Kz have a good positive correlation with the corrosion degree of the rebars;
- Based on the proposed magnetic parameters and the geometric parameters of the specimens, the corrosion degree of the specimens can be accurately determined according to the prediction model. The average absolute error of the prediction results is 8.33%, which is within 10%. It is a useful prediction for the corrosion degree of rebars in reinforced concrete structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DorMohammadi, H.; Pang, Q.; Murkute, P. Investigation of chloride-induced depassivation of iron in alkaline media by reactive force field molecular dynamics. NPJ Mater. Degrad. 2019, 3, 19. [Google Scholar] [CrossRef]
- Fernandez, I.; Bairán, J.M.; Marí, A.R. Corrosion effects on the mechanical properties of reinforcing steel bars. Fatigue and σ–ε behavior. Constr. Build. Mater. 2015, 101, 772–783. [Google Scholar] [CrossRef]
- Balestra, C.; Lima, M.; Silva, A. Corrosion degree effect on nominal and effective strengths of naturally corroded reinforcement. J. Mater. Civ. Eng. 2016, 28, 04016103. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Ozbolt, J. Bond strength evaluation of corroded steel bars via the surface crack width induced by reinforcement corrosion. Eng. Struct. 2017, 152, 506–522. [Google Scholar] [CrossRef]
- Bezuidenhout, S.; van Zijl, G.P. Corrosion propagation in cracked reinforced concrete, toward determining residual service life. Struct. Concr. 2019, 20, 2183–2193. [Google Scholar] [CrossRef]
- Chen, H.; Nepal, J. Load bearing capacity reduction of concrete structures due to reinforcement corrosion. Struct. Eng. Mech. 2020, 75, 455–464. [Google Scholar]
- Braganca, M.; Portella, K.; Bonato, M. Electrochemical impedance behavior of mortar subjected to a sulfate environment—A comparison with chloride exposure models. Constr. Build. Mater. 2014, 68, 650–658. [Google Scholar] [CrossRef]
- Zheng, Y.; Wen, Y.; Pan, T. Fractal characteristics and damage evaluation of corroded beams under four-point bending tests based on acoustic emission techniques. Measurement 2022, 202, 111792. [Google Scholar] [CrossRef]
- Feng, J.; Li, J.; Gao, K. Portable automatic detection system with infrared imaging for measuring steel wires corrosion damage. Autom. Constr. 2023, 156, 105150. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Ding, F. Detection of early-stage rebar corrosion using a polarimetric ground penetrating radar system. Constr. Build. Mater. 2022, 317, 125768. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, X.; Jiang, H. Grading Evaluation of Overall Corrosion Degree of Corroded RC Beams via SMFL Technique. Struct. Control Health Monit. 2023, 2023, 6672823. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, H.; Zhou, J. An SMFL-based non-destructive quantification method for the localized corrosion cross-sectional area of rebar. Corros. Sci. 2021, 192, 109793. [Google Scholar] [CrossRef]
- Tong, K.; Zhang, H.; Zhao, R. Investigation of SMFL monitoring technique for evaluating the load-bearingcapacity of RC bridges. Eng. Struct. 2023, 293, 116667. [Google Scholar] [CrossRef]
- Shi, P.; Bai, P.; Chen, H. The magneto-elastoplastic coupling effect on the magnetic flux leakage signal. J. Magn. Magn. Mater. 2020, 504, 166669. [Google Scholar] [CrossRef]
- Shi, P.; Jin, K.; Zheng, X. A general nonlinear magnetomechanical model for ferromagnetic materials under a constant weak magnetic field. J. Appl. Phys. 2016, 119, 145103. [Google Scholar] [CrossRef]
- Hao, S.; Shi, P. Theoretical and analytical solutions of force magnetic coupling magnetic dipoles in magnetic memory detection. J. Appl. Phys. 2021, 70, 105–114. [Google Scholar]
- Shi, P.; Jin, K.; Zheng, X. A magnetomechanical model for the magnetic memory method. Int. J. Mech. Sci. 2017, 124, 229–241. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Zhao, R. Experimental study on detection of rebar corrosion in concrete based on metal magnetic memory. Int. J. Robot. Autom. 2017, 32, 530–537. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, L.; Zhao, R. The non-destructive test of steel corrosion in reinforced concrete bridges using a micro-magnetic sensor. Sensors 2016, 16, 1439. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, H.; Zhou, J. Magnetic memory detection of corroded reinforced concrete considering the influence of tensile load. Int. J. Appl. Electrom. 2022, 68, 483–499. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, L.; Zhao, R. A new judging criterion for corrosion testing of reinforced concrete based on self-magnetic flux leakage. Int. J. Appl. Electrom. 2017, 54, 123–130. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Zhou, J. A multi-dimensional evaluation of wire breakage in bridge cable based on self-magnetic flux leakage signals. J. Magn. Magn. Mater. 2023, 566, 170321. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, W.; Jing, Y. Quantitative linear correlation between self-magnetic flux leakage field variation and corrosion unevenness of corroded rebars. Measurement 2023, 218, 113173. [Google Scholar] [CrossRef]
- Chen, L.; Liu, X.; Lin, Y. Quantitative corrosion detection of reinforced concrete based on self-magnetic flux leakage and rust spot area. Eng. Res. Express. 2022, 4, 035063. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, J.; Zhao, Q. Quantitative detection of corroded reinforced concrete of different sizes based on SMFL. KSCE J. Civ. Eng. 2022, 26, 143–154. [Google Scholar] [CrossRef]
- Qiu, J.; Zhou, J.; Zhao, S. Statistical quantitative evaluation of bending strength of corroded RC beams via SMFL technique. Eng. Struct. 2020, 209, 110168. [Google Scholar] [CrossRef]
- Zhang, H.; Qi, J.; Zheng, Y. Characterization and grading assessment of rebar corrosion in loaded RC beams via SMFL technology. Constr. Build. Mater. 2024, 411, 134484. [Google Scholar] [CrossRef]
- MOHURD of the People’s Republic of China. Code for Design of Concrete Structures (GB 50010-2010); China Architecture & Building Press: Beijing, China, 2010.
- Zeng, Y.; Gu, X.; Zhang, W. Exploration of accelerated corrosion methods for steel bars in concrete. Struct. Eng. 2009, 25, 101–105. [Google Scholar]
- Liu, X.; Miao, S. Corrosion of steel bars in concrete structures and its durability calculation. J. Civ. Eng. 1990, 4, 69–78. [Google Scholar]
- Shi, P. Several analytical solutions for the magnetic dipole model of defect leakage magnetic field. China Acad. J. Electron. Publ. House 2015, 3, 1–7. [Google Scholar]
- Shi, P.; Hao, S. Analytical solution of magneto-mechanical magnetic dipole model for metal magnetic memory method. Acta Phys. Sin. 2021, 70, 034101. [Google Scholar] [CrossRef]
- Jin, B.; Sun, N.; Fang, Q. Research on non-uniform rust expansion force of steel bars in concrete components. J. Sol. Mec. 2022, 4, 456–466. [Google Scholar]
- Qiu, J.; Zhang, H.; Zhou, J. Experimental analysis of the correlation between bending strength and SMFL of corroded RC beams. Constr. Build. Mater. 2019, 214, 594–605. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Feng, D.; Wang, W.; Mangalathu, S. Interpretable XGBoost-SHAP machine-learning model for shear strength prediction of squat RC walls. J. Struct. Eng. 2021, 147, 04021173. [Google Scholar] [CrossRef]









| Chemical Component (Mass Fraction)/% | |||||
|---|---|---|---|---|---|
| Brand | C | Si | Mn | S | P |
| HRB400 | ≤0.25 | ≤0.8 | ≤1.6 | ≤0.04 | ≤0.04 |
| Number | I/A | Current Density/µA·cm−2 | Theoretical Corrosion Rate/% | Actual Corrosion Rate/% |
|---|---|---|---|---|
| B22-2 | 0.2 | 1136.82 | 7.6 | 5.5 |
| A32-1 | 0.2 | 1136.82 | 11.9 | 14.9 |
| A12-2 | 0.2 | 1136.82 | 2.8 | 2.7 |
| A11-2 | 0.2 | 1515.76 | 5.0 | 5.5 |
| A31-2 | 0.2 | 1515.76 | 13.8 | 10.6 |
| A22-1 | 0.2 | 1136.82 | 10.1 | 10.7 |
| A33-3 | 0.2 | 909.46 | 5.2 | 6.5 |
| B32-3 | 0.2 | 1136.82 | 7.9 | 5.4 |
| B12-1 | 0.2 | 1136.82 | 11.4 | 9.0 |
| Max Tree Depth | Learning Rate | Number of Base Learners |
|---|---|---|
| 4 | 0.96 | 40 |
| Number | Actual Corrosion Rate % | Predicted Corrosion Rate % | Number | Actual Corrosion Rate % | Predicted Corrosion Rate % |
|---|---|---|---|---|---|
| 1 | 8.8 | 8.8 | 21 | 1.5 | 1.5 |
| 2 | 13.1 | 13.1 | 22 | 2.4 | 2.4 |
| 3 | 4.9 | 4.9 | 23 | 3.7 | 3.7 |
| 4 | 6.6 | 6.6 | 24 | 8.2 | 8.2 |
| 5 | 3.9 | 3.9 | 25 | 2.5 | 2.5 |
| 6 | 0.6 | 0.6 | 26 | 4.5 | 4.5 |
| 7 | 9.4 | 9.4 | 27 | 0.8 | 0.8 |
| 8 | 8.5 | 8.5 | 28 | 2.1 | 2.1 |
| 9 | 4.0 | 4.0 | 29 | 3.9 | 3.9 |
| 10 | 3.8 | 3.8 | 30 | 2.7 | 2.7 |
| 11 | 11.0 | 11.0 | 31 | 1.6 | 1.6 |
| 12 | 2.3 | 2.3 | 32 | 8.8 | 8.8 |
| 13 | 9.1 | 9.1 | 33 | 10.0 | 10.0 |
| 14 | 2.8 | 2.7 | 34 | 0.6 | 0.6 |
| 15 | 2.2 | 2.2 | 35 | 1.7 | 1.7 |
| 16 | 3.2 | 3.2 | 36 | 4.2 | 4.8 |
| 17 | 6.3 | 6.3 | 37 | 4.7 | 4.7 |
| 18 | 4.1 | 4.1 | 38 | 0.3 | 0.3 |
| 19 | 6.8 | 6.8 | 39 | 4.4 | 4.4 |
| 20 | 3.9 | 3.9 | 40 | 5.1 | 5.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Kong, Y.; Liu, B.; Ouyang, B.; He, Z.; Liao, L. Research on the Corrosion Detection of Rebar in Reinforced Concrete Based on SMFL Technology. Materials 2024, 17, 3421. https://doi.org/10.3390/ma17143421
Tian H, Kong Y, Liu B, Ouyang B, He Z, Liao L. Research on the Corrosion Detection of Rebar in Reinforced Concrete Based on SMFL Technology. Materials. 2024; 17(14):3421. https://doi.org/10.3390/ma17143421
Chicago/Turabian StyleTian, Hongsong, Yujiang Kong, Bin Liu, Bin Ouyang, Zhenfeng He, and Leng Liao. 2024. "Research on the Corrosion Detection of Rebar in Reinforced Concrete Based on SMFL Technology" Materials 17, no. 14: 3421. https://doi.org/10.3390/ma17143421
APA StyleTian, H., Kong, Y., Liu, B., Ouyang, B., He, Z., & Liao, L. (2024). Research on the Corrosion Detection of Rebar in Reinforced Concrete Based on SMFL Technology. Materials, 17(14), 3421. https://doi.org/10.3390/ma17143421




