Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions
Abstract
:1. Introduction
2. Experimental Procedure
2.1. The Workpiece Material
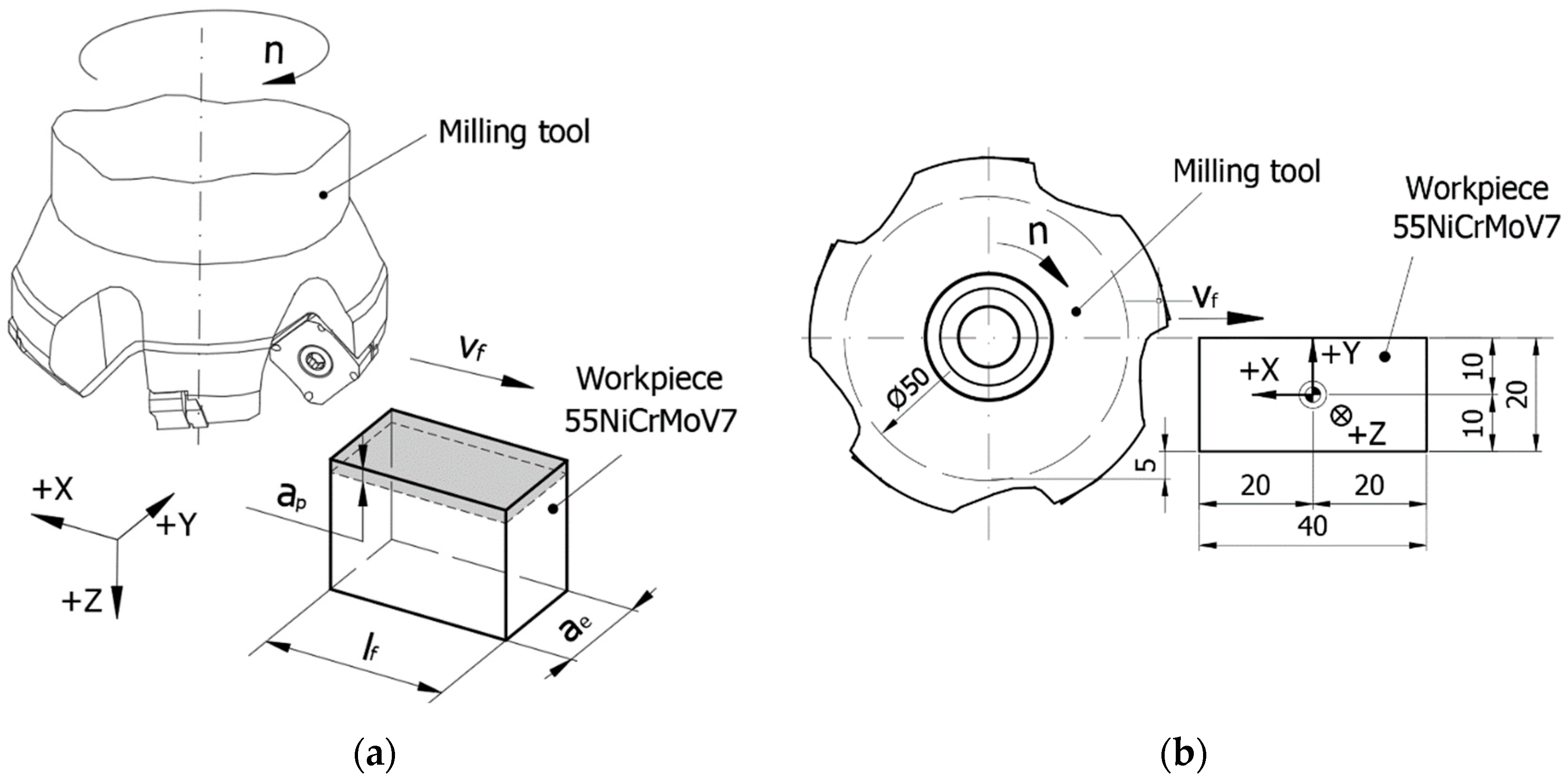
2.2. Work Scheme and Experimental Stand
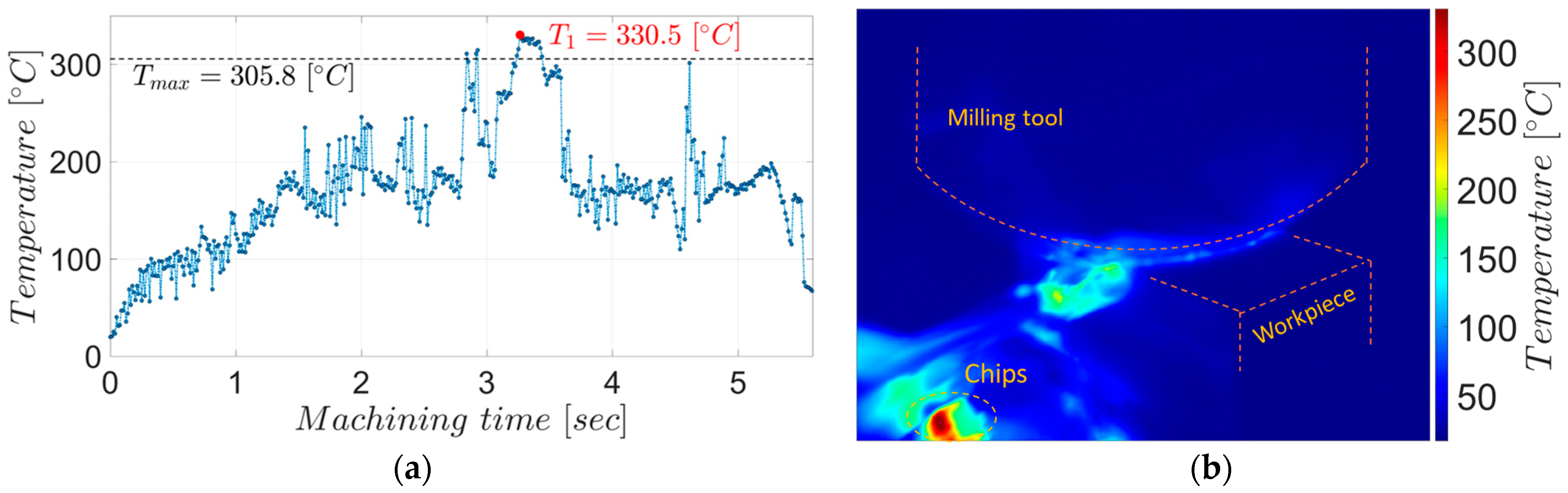
2.3. Measuring Temperatures in the Process
- A steel sample was heated to 500 °C using electric resistance.
- During heating, the following were recorded simultaneously:
- Thermographic images from one surface of the heated sample (40 mm × 20 mm) using an Optris PI400i thermal imaging camera.
- Temperature values of the half surface of the sample using a calibrated K-type thermocouple, the NI9210 acquisition module, the cDAQ-9171 uni-modular platform, and Matlab R2023 software from the Analog Input Recorder.
- The emissivity data recorded by the thermographic camera were correlated with the temperature values measured with the thermocouple.
2.4. Measuring the Cutting Force
2.5. Performed Experiments and Activities
3. Results and Discussions
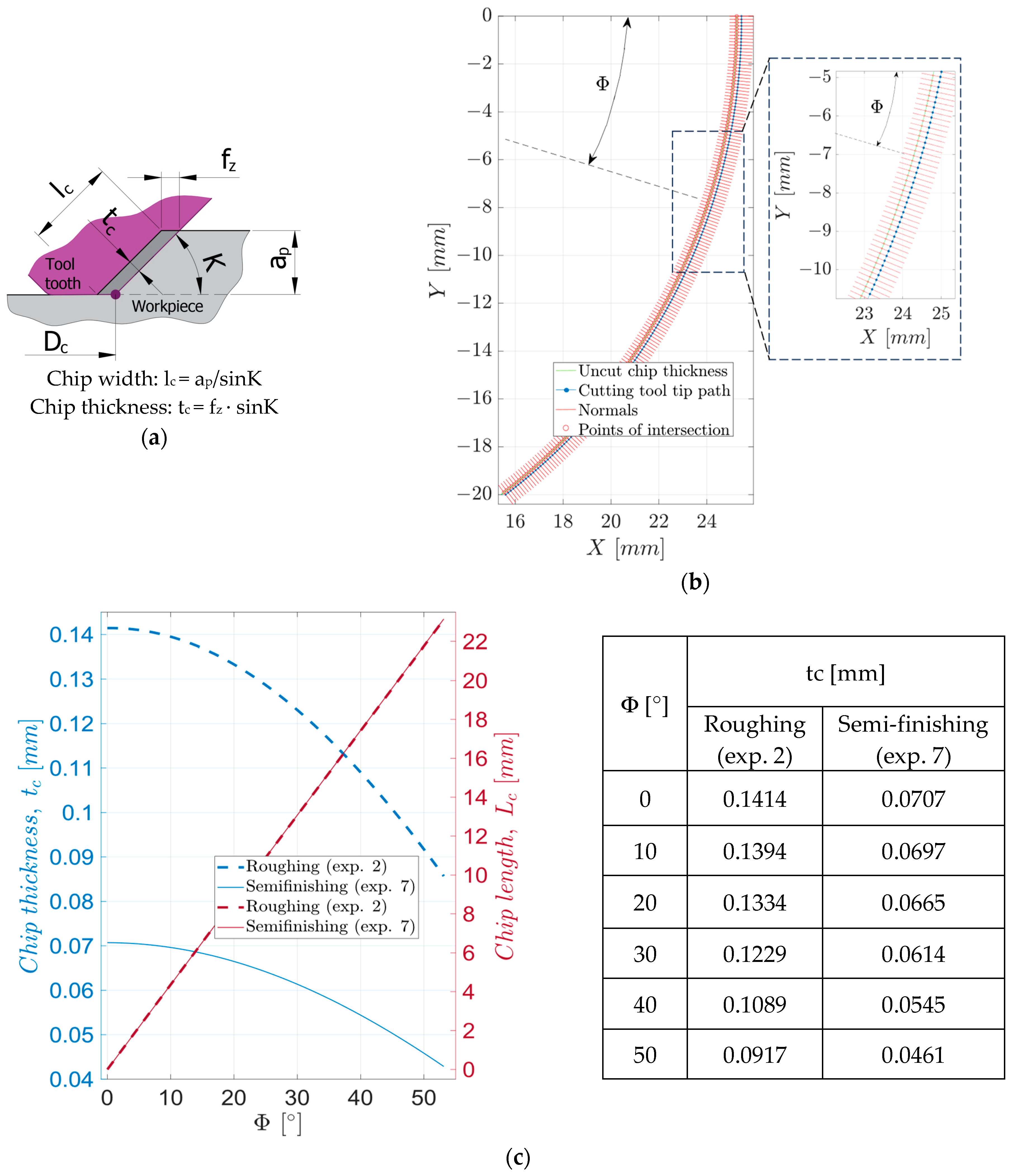
3.1. Analysis of the Geometric Shape of the Chips during Roughing and Semi-Finishing Milling
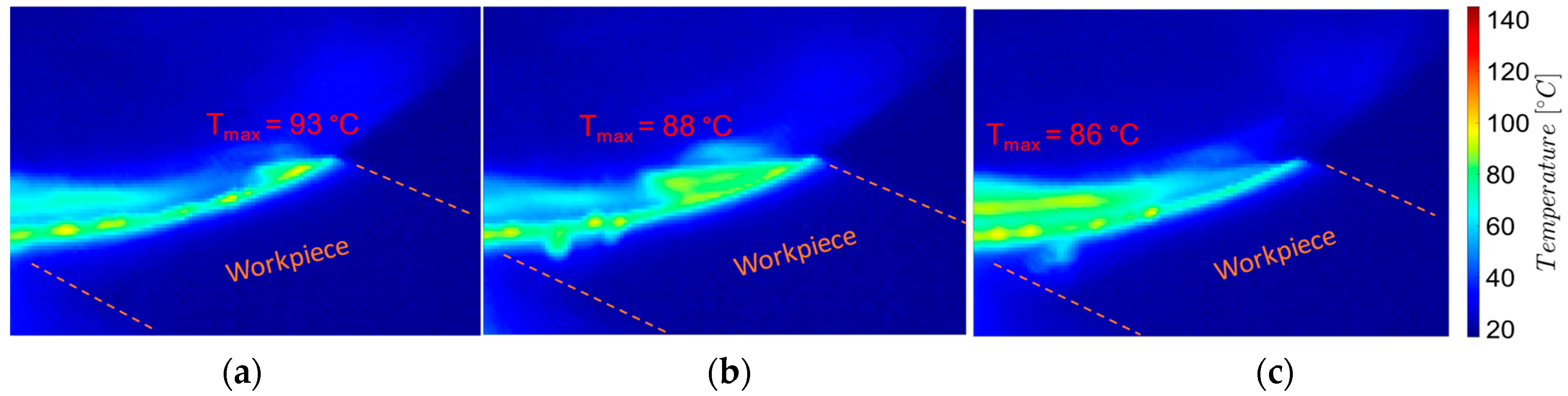
3.2. Process Temperature Analysis during Roughing and Semi-Finishing Milling
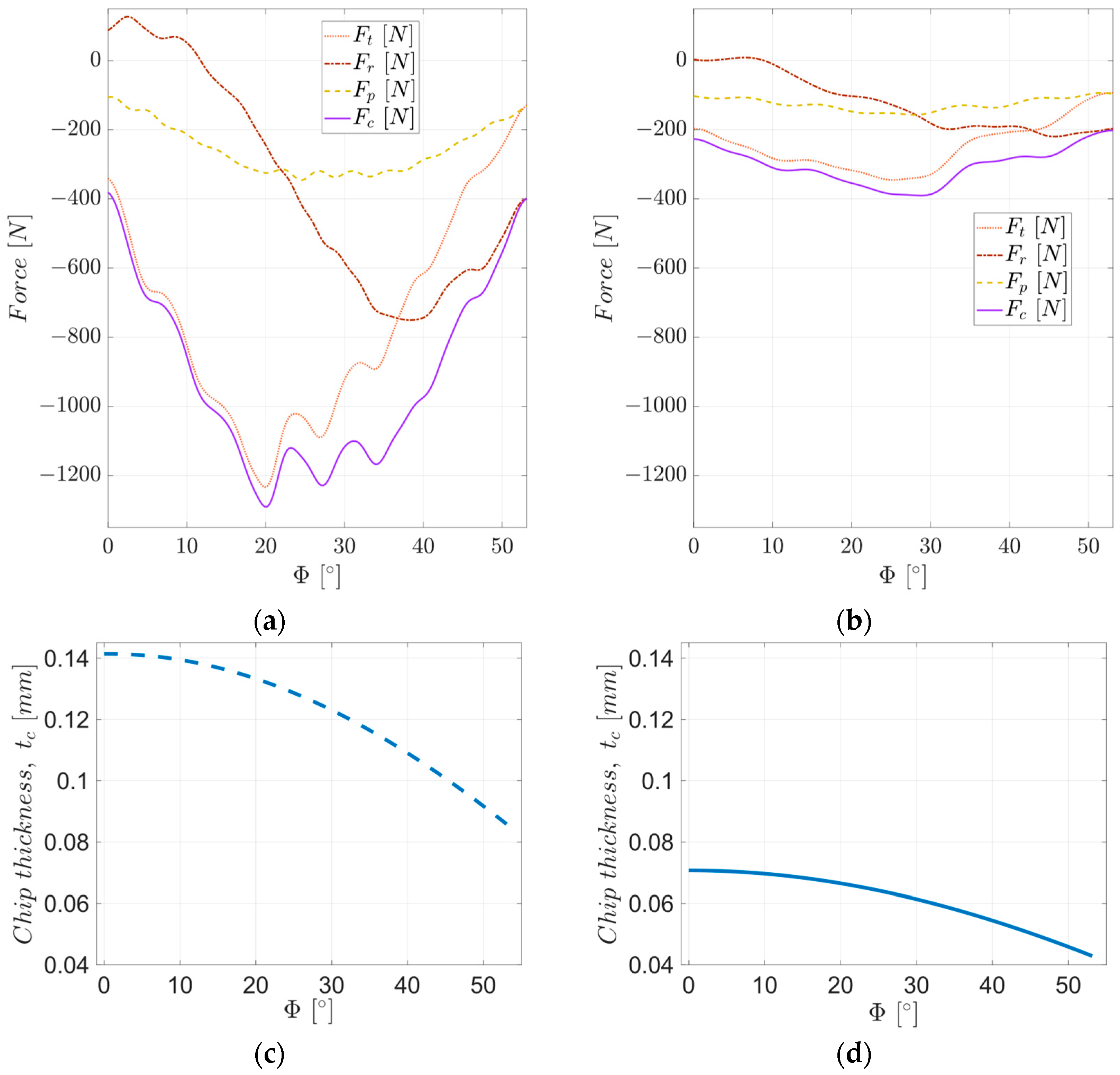
3.3. Analysis of Cutting Force during Roughing and Semi-Finishing Milling
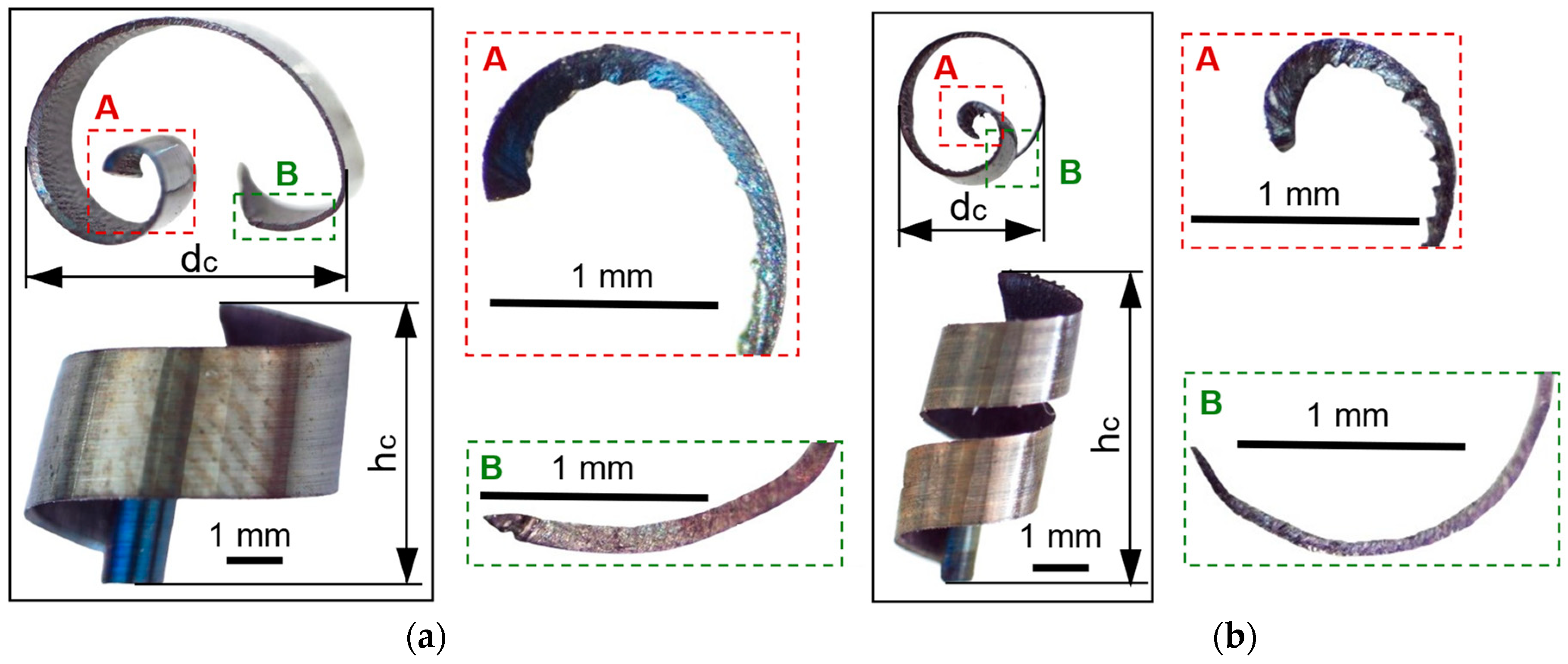
3.4. Analysis of Chip Morphology during Roughing and Semi-Finishing Milling
- -
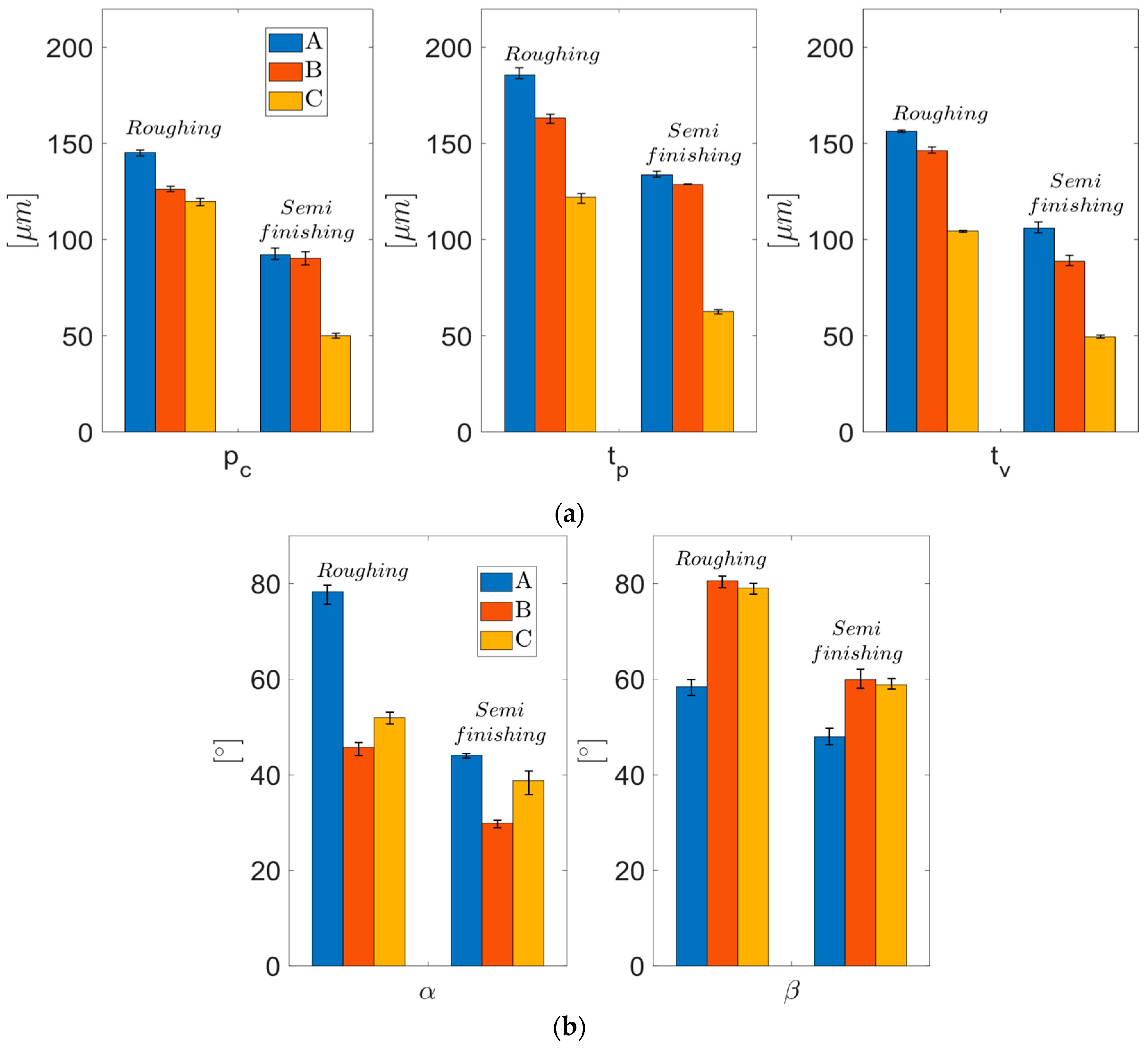
- all the values of the five parameters analyzed are higher for chips detached during roughing than those detached during semi-finishing, a fact explained by the very different intensities of the cutting regimes used in these experiments;
- -
- all the values of the dimensional parameters of chip segmentation have a decreasing evolution, from the starting area of the chip towards the end area of the chip, a fact determined by the decrease in the thickness of the chip, both the uncut and the detached one, as can be seen from Figure 14 and Figure 20;
- -
- the values of the angular parameters of chip segmentation have a different evolution along the chip: while the shear angle α has high values in the starting zone of the chip (A), it decreases in its middle zone (B) and increases again towards the end zone of the chip (C), the bulge angle β has an inverse evolution, with lower values at the beginning of the chip, maximum values in the middle zone, and lower values again in the end zone of the chip. This evolution of the sizes of the two angles is correlated with the evolution of the cutting forces during chip detachment, as presented and analyzed in the previous section: high values of the cutting force during the formation of a chip are associated with a small shear angle and a large camber angle;
- -
- the shear angle α has values below 45 degrees in the case of semi-finishing chips, which means that the chip formation mechanism is shear deformation. In comparison, in the case of roughing, the values of the shear angle α above 45 degrees show that chip deformation is not only a pure shear deformation [11].
- -
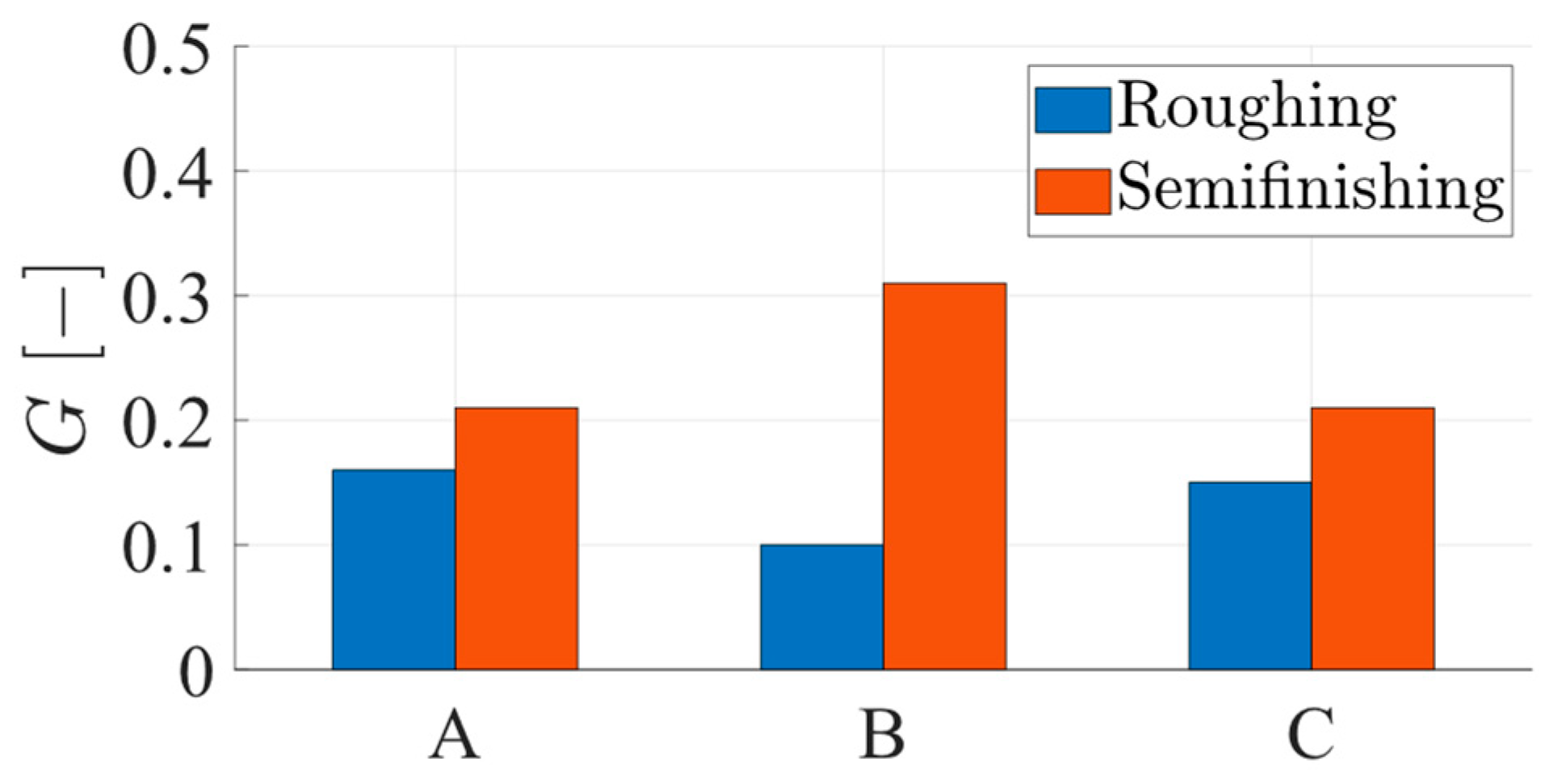
- the values of the degree of chip segmentation, G, are higher in the case of semi-finishing chips, where it was shown that the mechanism of chip formation is shear deformation;
- -
- the degree of segmentation of the chips has relatively close values in the area of the beginning, respectively, of the end of the chip, but the values in the median zone of the chip length are different from these: lower in the case of roughing chips results in a more intense cutting operation, respectively, higher in the case of semi-finishing chips results at a less intense cutting operation.
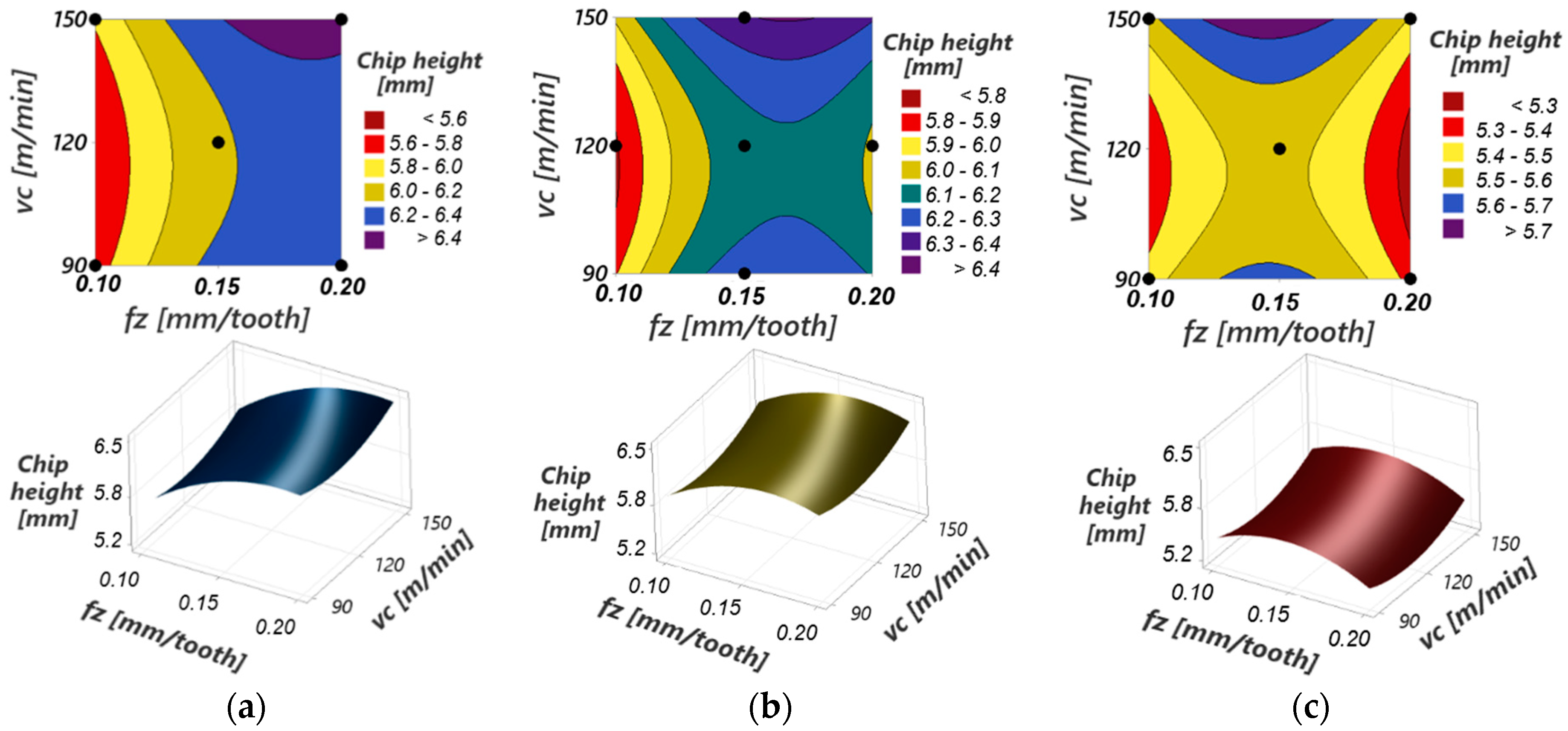
3.5. Influence of the Cutting Parameters on the Microscopic Dimensions of the Chips
- -
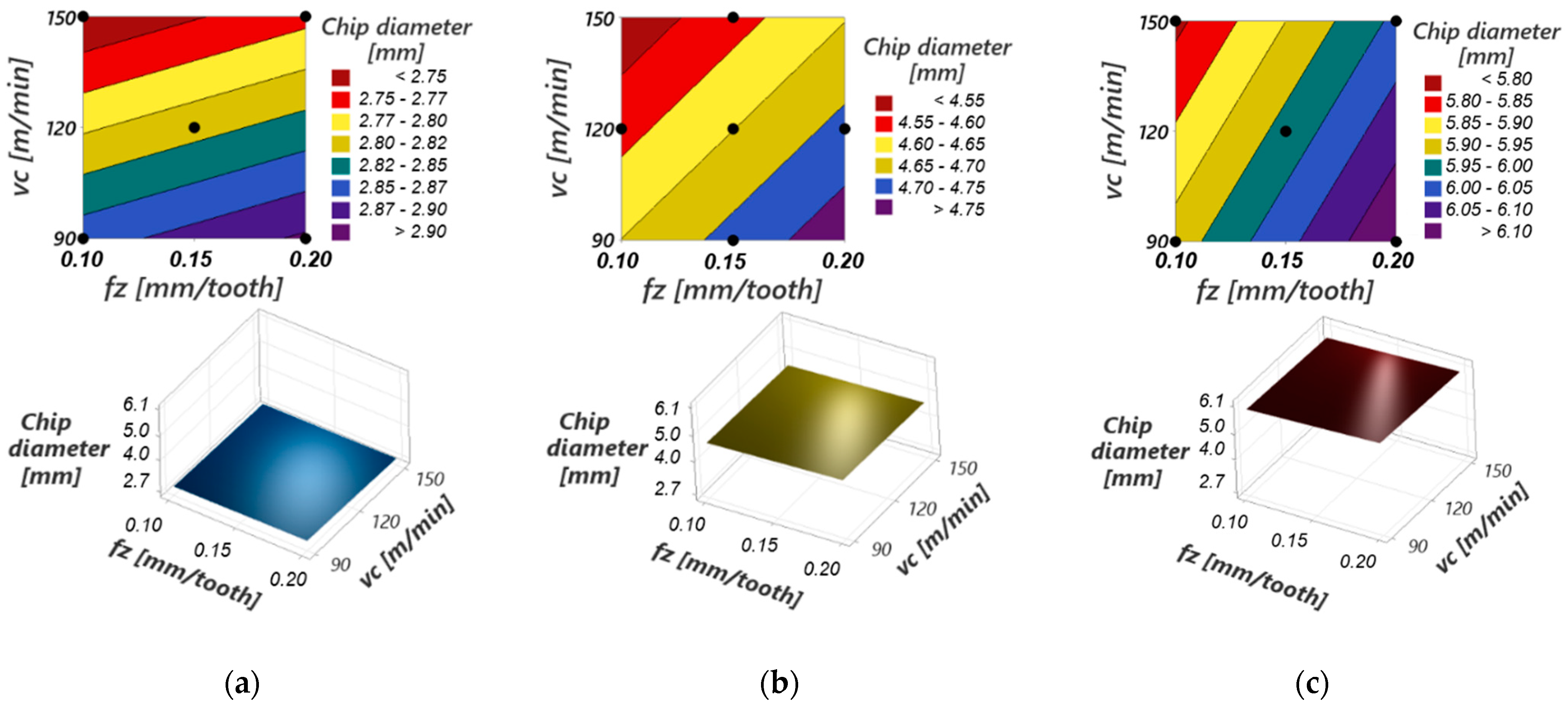
- At constant values of the cutting depth and cutting speed, the maximum height of the detached chip has a maximum value for a feed per tooth fz between the experimental limits (0.1 and 0.2 mm/tooth). The value of this maximum decreases with the increase in the cutting depth.
- -
- At constant values of the cutting depth and feed per tooth, the maximum height of the detached chip has a minimum value for a cutting speed vc between the experimental limits (90 and 150 m/min).
4. Conclusions
- The two machining methods being investigated show similarities in the evolution of temperatures and cutting forces during the machining, as well as in the variation of dimensional and angular parameters of chip segmentation. These similarities are due to the similar mechanisms of chip formation and shear deformation in both processes.
- The two machining methods differ in the levels of temperature, cutting forces, and dimensional and angular parameters of chip segmentation. In roughing machining, these differences are higher due to the larger dimensions of the uncut chip, which significantly impacts the phenomena occurring at the workpiece-tool-chip interfaces. This leads to a sharp increase in both mechanical and thermal processes during material removal.
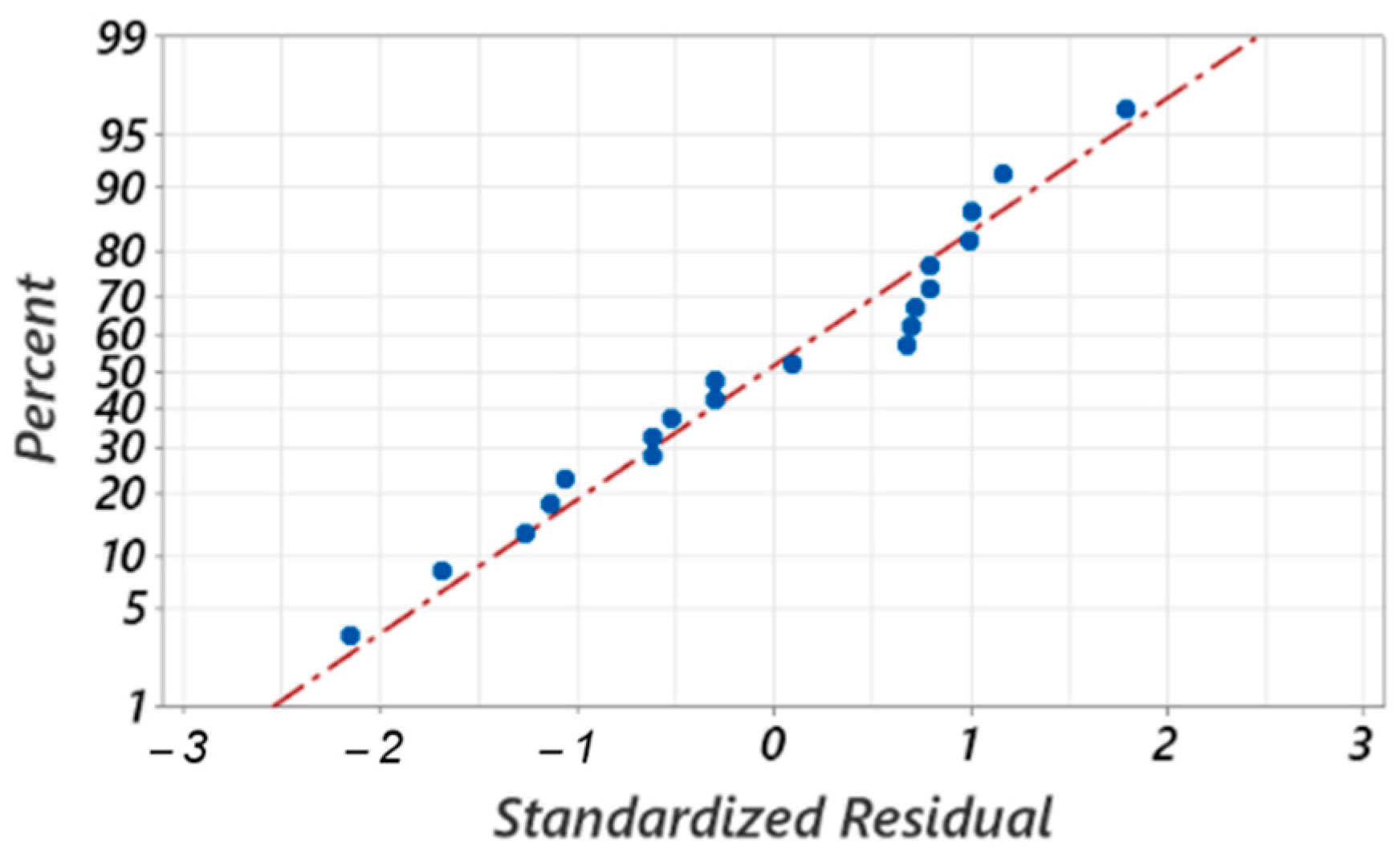
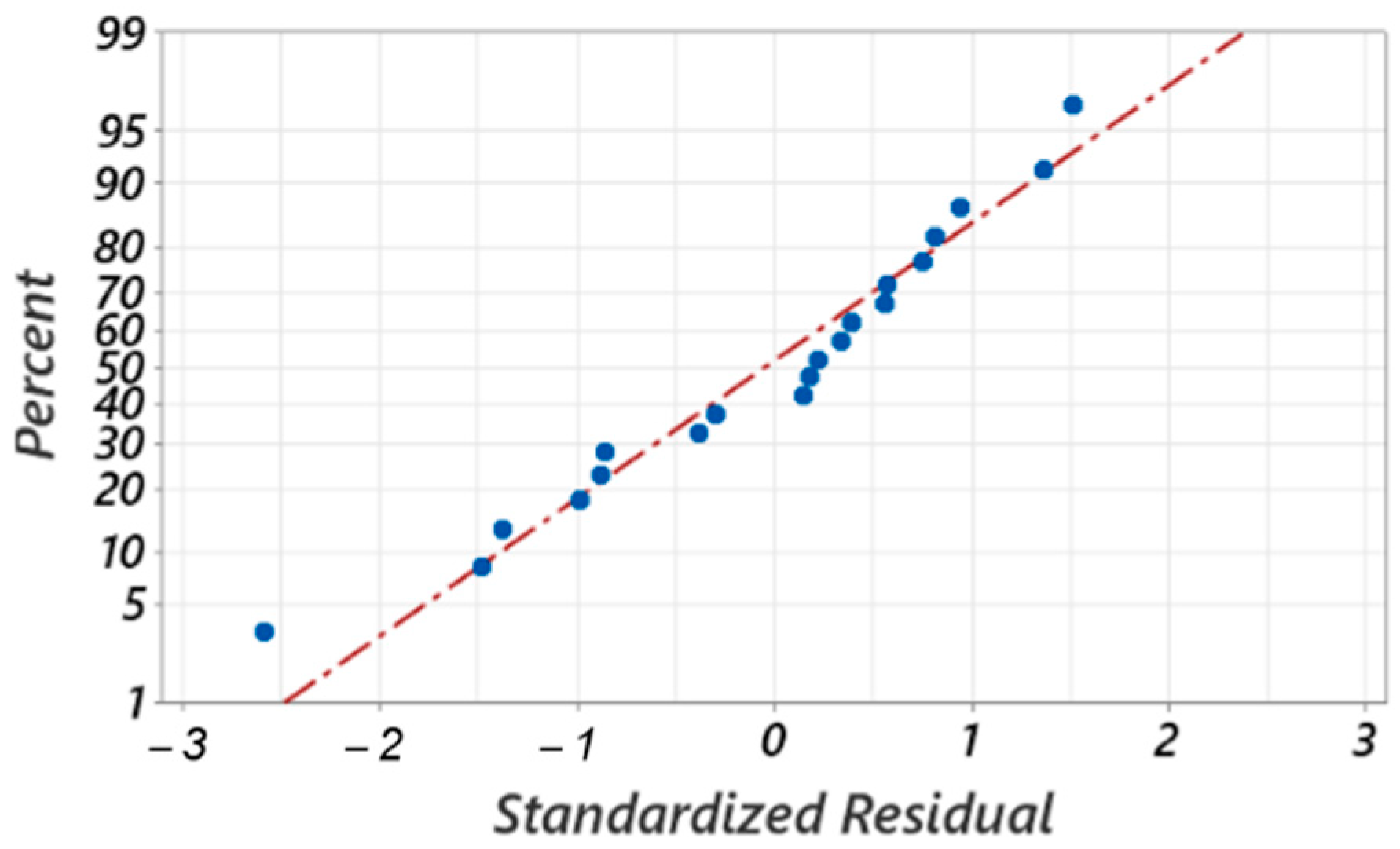
- This study has shown that it is possible to use regression functions to mathematically model the dependence of the separated chips’ size on the cutting process parameters. The functions identified are second-order polynomials and are considered suitable with high coefficients of determination at a confidence level of 95% (alpha = 0.05).
- To achieve small-sized chips, it is important to set the cutting parameters in the following order: cutting depth, feed per tooth, and cutting speed, with the lowest possible values for the first two while maintaining productivity during the machining process.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| FX | Force measured in the X-axis direction | pc | Tooth pitch between shear planes |
| FY | Force measured in the Y-axis direction | tp | Chip peak height |
| FZ | Force measured in the Z-axis direction | tv | Chip valley height |
| Ft | Tangential cutting force | α | Shear angle |
| Fr | Radial cutting force | β | Bulge angle |
| Fp | Inward force | G | Degree of segmentation |
| Fc | Cutting force | ANOVA | Analysis of variance |
| Φ | Positioning angle of the tooltip | RSM | Response surface methodology |
| Φa | Active machining angle | CCD | Central composite design |
| ap | Cutting depth | DOF | Degrees of freedom |
| fz | Feed per tooth | SeqSS | Sequential sum of squares |
| vc | Cutting speed | PCR | Percentage Contribution Ratio |
| ae | Cutting width | AdjSS | Adjusted sum of squares |
| lf | Machining length | AdjMS | Adjusted mean squares |
| Dc | Tool diameter | F-Value | Fisher distribution |
| zc | Number of tool teeth | p-Value | Null-hypothesis significance testing |
| K | Entering angle | SD | Standard deviation |
| dc | Maximum chip curling diameter | R-sq | Coefficient of determination R2 |
| hc | Maximum chip height | R-sq (adj) | Adjusted R2 |
| lc | Uncut chip width | PRESS | Predicted residual error sum of squares |
| tc | Uncut chip thickness | R-sq (pred) | Predicted R2 |
| Lc | Uncut chip length | AICc | Corrected Akaike’s Information Criterion |
| BIC | Bayesian Information Criterion |
References
- Patel, G.C.M.; Chate, G.R.; Parappagoudar, M.B.; Gupta, K. Machining of Hard Materials: A Comprehensive Approach to Experimentation, Modeling and Optimization; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Davim, J.P. (Ed.) Machining of Hard Materials; Springer: London, UK, 2011. [Google Scholar]
- Wang, G.; Zhou, X.; Wu, X.; Ma, J. Failure and Control of PCBN Tools in the Process of Milling Hardened Steel. Metals 2019, 9, 885. [Google Scholar] [CrossRef]
- Singh, B.K.; Roy, H.; Mondal, B.; Roy, S.S.; Mandal, N. Measurement of chip morphology and multi criteria optimization of turning parameters for machining of AISI 4340 steel using Y-ZTA cutting insert. Measurement 2019, 142, 181–194. [Google Scholar] [CrossRef]
- Wang, R.; Wang, X.; Yan, P.; Zhou, T.; Jiao, L.; Teng, L.; Zhao, B. The effects of cryogenic cooling on tool wear and chip morphology in turning of tantalum-tungsten alloys Ta-2.5W. J. Manuf. Process. 2023, 86, 152–162. [Google Scholar] [CrossRef]
- Elbah, M.; Fnides, B.; Laouici, H.; Yallese, A. Modélisation et optimisation des conditions de coupe en tournage dur par la technique de Taguchi en utilisant la MSR. UPB Sci. Bull. Ser. D 2021, 83, 195–210. [Google Scholar]
- Cui, X.; Zhao, J. Effects of cutting parameters on chip morphology and tool wear in high-speed face milling of hardened steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 921–931. [Google Scholar] [CrossRef]
- Li, S.; Zheng, G.; Ding, F.; Zhang, J.; Cheng, X.; Cui, E. Influence of clean cooling medium on the hard drilling performance and machined surface integrity of 42CrMo steel. Mater. Today Commun. 2024, 39, 109049. [Google Scholar] [CrossRef]
- Lazoglu, I.; Boz, Y.; Erdim, H. Five-axis milling mechanics for complex free form surfaces. CIRP Ann. 2011, 60, 117–120. [Google Scholar] [CrossRef]
- Yao, Z.; Shen, J.; Wu, M.; Zhang, D.; Luo, M. Position-dependent milling process monitoring and surface roughness prediction for complex thin-walled blade component. Mech. Syst. Signal Process. 2023, 198, 110439. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.B. An experimental and analytical analysis on chip morphology, phase transformation, oxidation, and their relationships in finish hard milling. Int. J. Mach. Tools Manuf. 2009, 49, 805–813. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Jiang, Y.; He, Y.; Xu, X.; Zhao, W. Investigation on Morphological Evolution of Chips for Ti6Al4V Alloys with the Increasing Milling Speed. Procedia CIRP 2016, 46, 408–411. [Google Scholar] [CrossRef]
- Hariprasad, B.; Selvakumar, S.J.; Samuel, R.D. Effect of cutting edge radius on end milling Ti–6Al–4V under minimum quantity cooling lubrication—Chip morphology and surface integrity study. Wear 2022, 498–499, 204307. [Google Scholar] [CrossRef]
- Chen, X.; Tang, J.; Ding, H.; Liu, A. Experimental study on the evolution of chip morphology, chip formation, and surface topography with cutting parameters, and their relationships in dry milling of cast aluminum alloy with PCD inserter. J. Mech. Sci. Technol. 2021, 35, 1651–1662. [Google Scholar] [CrossRef]
- Alipanahi, A.; Mahboubkhah, M.; Barari, A. Cross-sensitivity control in a novel four-component milling dynamometer for simultaneous measurement of tri-axial forces and torque. Measurement 2022, 191, 110788. [Google Scholar] [CrossRef]
- Gomez, M.F.; Schmitz, T.L. Displacement-based dynamometer for milling force measurement. Procedia Manuf. 2019, 34, 867–875. [Google Scholar] [CrossRef]
- Gomez, M.; Schmitz, T. Low-cost, constrained-motion dynamometer for milling force measurement. Manuf. Lett. 2020, 25, 34–39. [Google Scholar] [CrossRef]
- Uddin, M.S.; Songyi, D. On the design and analysis of an octagonal–ellipse ring based cutting force measuring transducer. Measurement 2016, 90, 168–177. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, K.; Zhao, Y.; Zan, Z.; Sun, J. Development and testing of a wireless rotating triaxial vibration measuring tool holder system for milling process. Measurement 2020, 163, 108034. [Google Scholar] [CrossRef]
- Rizal, M.; Ghani, J.A.; Nuawi, M.Z.; Haron, C.H.C. An embedded multi-sensor system on the rotating dynamometer for real-time condition monitoring in milling. Int. J. Adv. Manuf. Technol. 2018, 95, 811–823. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, Y.; Li, Y.; Zhao, Y.; Wang, P. A novel dynamometer for monitoring milling process. Int. J. Adv. Manuf. Technol. 2017, 92, 2535–2543. [Google Scholar] [CrossRef]
- Xu, J.; Shen, J.; Li, L.; Guo, G.; Zhu, X.; Meng, Y.; Chen, M. Milling machinability analysis of GW63K rare-earth magnesium alloys based on the concept of clean cutting. J. Mater. Res. Technol. 2023, 26, 9380–9391. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, J.; Zhang, G.; Xu, C.; Yi, M. Finite element analysis of Ti1-xAlxN coated tools cutting performance and tool wear during Ti–6Al–4V milling. J. Mater. Res. Technol. 2023, 25, 166–182. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Jiang, R.; Xiong, Y.; Lin, K.; Li, J.; Shan, C. Analytical model of workpiece temperature in axial ultrasonic vibration-assisted milling in situ TiB2/7050Al MMCs. Int. J. Adv. Manuf. Technol. 2022, 119, 1659–1672. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Zhao, W. A new method for cutting force prediction in peripheral milling of complex curved surface. Int. J. Adv. Manuf. Technol. 2016, 86, 117–128. [Google Scholar] [CrossRef]
- Cui, X.; Zhao, J.; Tian, X. Cutting forces, chip formation, and tool wear in high-speed face milling of AISI H13 steel with CBN tools. Int. J. Adv. Manuf. Technol. 2013, 64, 1737–1749. [Google Scholar] [CrossRef]
- Günay, M. Modeling and multiple optimization in face milling of hardfacing welding applied steel: Force, roughness, power. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6652–6664. [Google Scholar] [CrossRef]
- Cui, X.B.; Guo, J.X.; Wang, X.Y. Cutting Force in High-Speed Face Milling AISI H13 Steel. Key Eng. Mater. 2015, 667, 35–40. [Google Scholar] [CrossRef]
- Karaguzel, U.; Bakkal, M.; Budak, E. Modeling and Measurement of Cutting Temperatures in Milling. Procedia CIRP 2016, 46, 173–176. [Google Scholar] [CrossRef]
- Bolar, G.; Adhikari, R.; Nayak, S.N.; Joshi, S.N. Assessment of ignition risk in dry helical hole milling of AZ31 magnesium alloy considering the machining temperature and chip morphology. J. Manuf. Process. 2022, 77, 260–271. [Google Scholar] [CrossRef]
- Varatharajulu, M.; Duraiselvam, M.; Krishna, P.G.V.; Jagadeesh, B. Tool temperature thermographic study on end milling magnesium AZ31 using carbide tool. Mater. Chem. Phys. 2023, 295, 127077. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, G.; Cheng, X.; Yang, X.; Xu, R.; Zhang, H. Cutting Performance Evaluation of the Coated Tools in High-Speed Milling of AISI 4340 Steel. Materials 2019, 12, 3266. [Google Scholar] [CrossRef]
- John, R.; Lin, R.; Jayaraman, K.; Bhattacharyya, D. Investigation on microstructure characteristics of tool wear and machined surface mechanisms while milling: Kenaf vs glass fiber-reinforced composites. J. Mater. Res. Technol. 2023, 23, 4716–4733. [Google Scholar] [CrossRef]
- Zhou, R. Analytical model of workpiece surface temperature prediction in 4-axis milling process. Int. J. Adv. Manuf. Technol. 2020, 111, 2155–2162. [Google Scholar] [CrossRef]
- Cui, X.; Guo, J.; Zhao, J.; Yan, Y. Chip temperature and its effects on chip morphology, cutting forces, and surface roughness in high-speed face milling of hardened steel. Int. J. Adv. Manuf. Technol. 2015, 77, 2209–2219. [Google Scholar] [CrossRef]
- Cheng, Y.; Guan, R.; Lu, Z.; Xu, M.; Liu, Y. A study on the milling temperature and tool wear of difficult-to-machine 508III steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 2478–2487. [Google Scholar] [CrossRef]
- Niu, J.; Huang, C.; Shi, Z.; Liu, H.; Tang, Z.; Su, R.; Chen, Z.; Li, B.; Wang, Z.; Xu, L. A chip formation mechanism taking into account microstructure evolution during the cutting process: Taking compacted graphite iron machining as an example. Int. J. Mach. Tools Manuf. 2024, 198, 104150. [Google Scholar] [CrossRef]
- Nakayama, K.; Arai, M.; Kanda, T. Machining Characteristics of Hard Materials. CIRP Ann. 1988, 37, 89–92. [Google Scholar] [CrossRef]
- Niu, W.; Wang, Y.; Li, X.; Guo, R. A Joint Johnson–Cook-TANH Constitutive Law for Modeling Saw-Tooth Chip Formation of Ti-6AL-4V Based on an Improved Smoothed Particle Hydrodynamics Method. Materials 2023, 16, 4465. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, S.; Horovistiz, A.; Davim, J.P. Morphological characterization of chip segmentation in Ti-6Al-7Nb machining: A novel method based on digital image processing. Measurement 2023, 206, 112330. [Google Scholar] [CrossRef]
- Vipindas, K.; Mathew, J. Analysis of chip morphology to understand the machining mechanism of micro end milling while machining Ti-6Al-4V. Mater. Today Proc. 2021, 46, 7204–7209. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Huo, X.; Zhao, J. Influences of Cutting Speed and Material Mechanical Properties on Chip Deformation and Fracture during High-Speed Cutting of Inconel 718. Materials 2018, 11, 461. [Google Scholar] [CrossRef]
- Zou, Z.; He, L.; Jiang, H.; Yuan, H. Influence of Microgroove Structure on Cutting Performance and Chip Morphology during the Turning of Superalloy Inconel 718. Materials 2021, 14, 4142. [Google Scholar] [CrossRef]
- Wagner, V.; Vissio, A.; Duc, E.; Pijolat, M. Relationship between cutting conditions and chips morphology during milling of aluminium Al-2050. Int. J. Adv. Manuf. Technol. 2016, 82, 1881–1897. [Google Scholar] [CrossRef]
- Khan, M.A.; Imran, J.S.H.; Khan, M.; Alruqi, M. Machinability analysis of Ti-6Al-4V under cryogenic condition. J. Mater. Res. Technol. 2023, 25, 2204–2226. [Google Scholar] [CrossRef]
- Bhandarkar, L.R.; Behera, M.; Mohanty, P.P.; Sarangi, S.K. Experimental investigation and multi-objective optimization of process parameters during machining of AISI 52100 using high performance coated tools. Measurement 2021, 172, 108842. [Google Scholar] [CrossRef]
- Deng, Q.; Li, D.; Wang, H.; Cao, P.; Wu, Y.; Wang, S. Study of the noise reduction by optimizing ultra-high speed milling parameters by DoE method. UPB Sci. Bull. Ser. D 2023, 85, 319–332. [Google Scholar]
- Kumar, S.S.; Bara, A.; Bhaskar, P.; Sai, K.K.; Rajiv, L.S.; Singh, S.L. Optimization of process parameters based on RSM and GRA method for machining of Inconel-600 by electric discharge machining. Mater. Today Proc. 2021, 44, 2551–2555. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mitra, S.; Bose, D. An investigation on dimensional accuracy and surface topography in powder mixed WEDM using RSM and GRA-PCA. Mater. Today Proc. 2021, 44, 1524–1530. [Google Scholar] [CrossRef]
- Koli, Y.; Yuvaraj, N.; Aravindan, S.V. Multi-response mathematical model for optimization of process parameters in CMT welding of dissimilar thickness AA6061-T6 and AA6082-T6 alloys using RSM-GRA coupled with PCA. Adv. Ind. Manuf. Eng. 2021, 2, 100050. [Google Scholar] [CrossRef]
- I.S. EN ISO 6507-01:2018; Metallic Materials- Vickers hardness test—Part 1: Teste Method. NSAI Standards: Dublin, Ireland, 2018.
- I.S. EN ISO 6507-02:2018; Metallic Materials- Vickers hardness test—Part 2: Verification and Calibration of Testing Machines. NSAI Standards: Dublin, Ireland, 2018.
- ISO 6892-1:2009(E); Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2009.
- Smith, G.T. Cutting Tool Technology; Springer: London, UK, 2008. [Google Scholar]
- Wang, D.; Yin, L.; Hänel, A.; Teicher, U.; Penter, L.; Seidel, A.; Harst, S.; Ihlenfeldt, S. Cutting performance of binderless nano-polycrystalline cBN and PcBN milling tools for high-speed milling of hardened steel. Ceram. Int. 2023, 49, 34757–34773. [Google Scholar] [CrossRef]
- Yıldırım, Ç.V.; Kıvak, T.; Sarıkaya, M.; Şirin, Ş. Evaluation of tool wear, surface roughness/topography and chip morphology when machining of Ni-based alloy 625 under MQL, cryogenic cooling and CryoMQL. J. Mater. Res. Technol. 2020, 9, 2079–2092. [Google Scholar] [CrossRef]
- Liu, D.; Ni, C.; Wang, Y.; Zhu, L. Review of serrated chip characteristics and formation mechanism from conventional to additively manufactured titanium alloys. J. Alloys Compd. 2024, 970, 172573. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kasim, M.S.; Che, H.C.H.; Ghani, J.A.; Hadi, M.A.; Izamshah, R.; Anand, T.J.S.; Mohamed, S.B. Cost evaluation on performance of a PVD coated cutting tool during end-milling of Inconel 718 under MQL conditions. Trans. IMF 2016, 94, 175–181. [Google Scholar] [CrossRef]
- Noordin, M.Y.; Venkatesh, V.C.; Sharif, S.; Elting, S.; Abdullah, A. Application of response surface methodology in describing the performance of coated carbide tools when turning AISI 1045 steel. J. Mater. Process. Technol. 2004, 145, 46–58. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, J.; Fan, G.; Xu, C.; Du, J. The effect of chip formation on the cutting force and tool wear in high-speed milling Inconel 718. Int. J. Adv. Manuf. Technol. 2023, 127, 335–348. [Google Scholar] [CrossRef]
- Li, A.; Zhao, J.; Hou, G. Effect of cutting speed on chip formation and wear mechanisms of coated carbide tools when ultra-high-speed face milling titanium alloy Ti-6Al-4V. Adv. Mech. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef]

















| Chemical Element | C | Fe | Si | Ni | Cr | Mn | Mo | V | S | p |
|---|---|---|---|---|---|---|---|---|---|---|
| Effective values (wt%) | 0.56 (ISO) | 93.68 | 1.231 | 1.717 | 1.174 | 0.963 | 0.3 | 0.103 | 0.2 | 0.004 |
| Measurement error (%) | - | 0.07 | 0.01 | 0.008 | 0.004 | 0.005 | 0.001 | 0.002 | - | - |
| Hardness [HV] | Ultimate Tensile Stress [MPa] | Relative Elongation [%] |
|---|---|---|
| 477.4 ± 3 | 1371.7 | 7.1 |
| Exp. nb. | Normalized Independent Variables | Physical Independent Variables | ||||
|---|---|---|---|---|---|---|
| ap [mm] | fz [mm/Tooth] | vc [m/min] | ap [mm] | fz [mm/Tooth] | vc [m/min] | |
| 1. | 1 | 1 | 1 | 2 | 0.2 | 150 |
| 2. | 1 | 1 | −1 | 2 | 0.2 | 90 |
| 3. | 1 | −1 | 1 | 2 | 0.1 | 150 |
| 4. | 1 | −1 | −1 | 2 | 0.1 | 90 |
| 5. | −1 | 1 | 1 | 1 | 0.2 | 150 |
| 6. | −1 | 1 | −1 | 1 | 0.2 | 90 |
| 7. | −1 | −1 | 1 | 1 | 0.1 | 150 |
| 8. | −1 | −1 | −1 | 1 | 0.1 | 90 |
| 9. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| 10. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| 11. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| 12. | −1 | 0 | 0 | 1 | 0.15 | 120 |
| 13. | 1 | 0 | 0 | 2 | 0.15 | 120 |
| 14. | 0 | −1 | 0 | 1.5 | 0.1 | 120 |
| 15. | 0 | 1 | 0 | 1.5 | 0.2 | 120 |
| 16. | 0 | 0 | −1 | 1.5 | 0.15 | 90 |
| 17. | 0 | 0 | 1 | 1.5 | 0.15 | 150 |
| 18. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| 19. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| 20. | 0 | 0 | 0 | 1.5 | 0.15 | 120 |
| Chip Parameter’s | UM | Roughing | Semi-Finishing | |||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |||
| * Φ | positioning angle of the tooltip | ° | 12 | 24 | 46 | 12 | 24 | 46 |
| * Lc | uncut chip length | mm | 5 | 10 | 20 | 5 | 10 | 20 |
| * tc | uncut chip thickness | µm | 167 | 157 | 119 | 83 | 78 | 60 |
| tp | chip peak height | µm | 185.7 | 163.3 | 122.2 | 133.7 | 128.8 | 62.8 |
| tv | chip valley height | µm | 156.5 | 146.4 | 104.4 | 106.2 | 88.9 | 49.6 |
| pc | tooth pitch between shear planes | µm | 145.4 | 126.3 | 119.9 | 92.4 | 90.4 | 50.2 |
| α | shear angle | ° | 78.3 | 45.7 | 51.9 | 44.1 | 29.9 | 38.8 |
| β | bulge angle | ° | 58.4 | 80.6 | 79.1 | 47.9 | 59.9 | 58.8 |
| Source | DOF | Seq SS | PCR | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Model | 9 | 25.2852 | 99.98% | 25.2852 | 2.8095 | 6320.20 | 0.000 |
| Linear | 3 | 24.9276 | 98.57% | 24.9276 | 8.3092 | 18,692.38 | 0.000 |
| ap | 1 | 24.8378 | 98.21% | 24.8378 | 24.8378 | 55,875.12 | 0.000 |
| fz | 1 | 0.0436 | 0.17% | 0.0436 | 0.0436 | 97.99 | 0.000 |
| vc | 1 | 0.0462 | 0.18% | 0.0462 | 0.0462 | 104.02 | 0.000 |
| Square | 3 | 0.3360 | 1.33% | 0.3360 | 0.1120 | 251.92 | 0.000 |
| ap ∙ ap | 1 | 0.3302 | 1.31% | 0.1507 | 0.1507 | 339.01 | 0.000 |
| fz ∙ fz | 1 | 0.0056 | 0.02% | 0.0053 | 0.0053 | 12.03 | 0.006 |
| vc ∙ vc | 1 | 0.0001 | 0.00% | 0.0001 | 0.0001 | 0.22 | 0.652 |
| 2-Way Interaction | 3 | 0.0217 | 0.09% | 0.0217 | 0.0072 | 16.30 | 0.000 |
| ap ∙ fz | 1 | 0.0171 | 0.07% | 0.0171 | 0.0171 | 38.50 | 0.000 |
| ap ∙ vc | 1 | 0.0045 | 0.02% | 0.0045 | 0.0045 | 10.15 | 0.010 |
| fz ∙ vc | 1 | 0.0001 | 0.00% | 0.0001 | 0.0001 | 0.25 | 0.626 |
| Error | 10 | 0.0044 | 0.02% | 0.0044 | 0.0004 | ||
| Lack-of-Fit | 5 | 0.0022 | 0.01% | 0.0022 | 0.0004 | 0.95 | 0.523 |
| Pure Error | 5 | 0.0023 | 0.01% | 0.0023 | 0.0005 | ||
| Total | 19 | 25.2897 | 100.00% |
| Model | SD | R-sq | R-sq(adj) | PRESS | R-sq(pred) | AICc | BIC |
|---|---|---|---|---|---|---|---|
| 9DOF (Iniţial) | 0.021083 | 99.98% | 99.97% | 0.019496 | 99.92% | −56.48 | −78.52 |
| 5DOF (Final) | 0.032489 | 99.94% | 99.92% | 0.039407 | 99.84% | −64.12 | −66.48 |
| Source | DOF | Seq SS | PCR | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Model | 9 | 2.31925 | 98.53% | 2.31925 | 0.25769 | 74.54 | 0.000 |
| Linear | 3 | 1.25649 | 53.38% | 1.25649 | 0.41883 | 121.15 | 0.000 |
| ap | 1 | 1.00489 | 42.69% | 1.00489 | 1.00489 | 290.68 | 0.000 |
| fz | 1 | 0.21316 | 9.06% | 0.21316 | 0.21316 | 61.66 | 0.000 |
| vc | 1 | 0.03844 | 1.63% | 0.03844 | 0.03844 | 11.12 | 0.008 |
| Square | 3 | 0.77861 | 33.08% | 0.77861 | 0.25954 | 75.07 | 0.000 |
| ap ∙ ap | 1 | 0.61952 | 26.32% | 0.27841 | 0.27841 | 80.53 | 0.000 |
| fz ∙ fz | 1 | 0.08256 | 3.51% | 0.13698 | 0.13698 | 39.62 | 0.000 |
| vc ∙ vc | 1 | 0.07653 | 3.25% | 0.07653 | 0.07653 | 22.14 | 0.001 |
| Two-Way Interaction | 3 | 0.28415 | 12.07% | 0.28415 | 0.09472 | 27.40 | 0.000 |
| ap ∙ fz | 1 | 0.28125 | 11.95% | 0.28125 | 0.28125 | 81.35 | 0.000 |
| ap ∙ vc | 1 | 0.00045 | 0.02% | 0.00045 | 0.00045 | 0.13 | 0.726 |
| fz ∙ vc | 1 | 0.00245 | 0.10% | 0.00245 | 0.00245 | 0.71 | 0.420 |
| Error | 10 | 0.03457 | 1.47% | 0.03457 | 0.00346 | ||
| Lack-of-Fit | 5 | 0.02869 | 1.22% | 0.02869 | 0.00574 | 4.88 | 0.053 |
| Pure Error | 5 | 0.00588 | 0.25% | 0.00588 | 0.00118 | ||
| Total | 19 | 2.35382 | 100.00% |
| Model | SD | R-sq | R-sq(adj) | PRESS | R-sq(pred) | AICc | BIC |
|---|---|---|---|---|---|---|---|
| 9DOF (Initial) | 0.058797 | 98.53% | 97.21% | 0.157325 | 93.32% | −15.45 | −37.50 |
| 7DOF (Final) | 0.055880 | 98.41% | 97.48% | 0.119535 | 94.92% | −32.84 | −41.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malea, C.I.; Niţu, E.L.; Iordache, D.M.; Tabacu, Ş.L.; Negrea, A.D.; Bădulescu, C. Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions. Materials 2024, 17, 3434. https://doi.org/10.3390/ma17143434
Malea CI, Niţu EL, Iordache DM, Tabacu ŞL, Negrea AD, Bădulescu C. Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions. Materials. 2024; 17(14):3434. https://doi.org/10.3390/ma17143434
Chicago/Turabian StyleMalea, Claudiu Ionuţ, Eduard Laurenţiu Niţu, Daniela Monica Iordache, Ştefan Lucian Tabacu, Aurelian Denis Negrea, and Claudiu Bădulescu. 2024. "Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions" Materials 17, no. 14: 3434. https://doi.org/10.3390/ma17143434
APA StyleMalea, C. I., Niţu, E. L., Iordache, D. M., Tabacu, Ş. L., Negrea, A. D., & Bădulescu, C. (2024). Analysis of Face Milling of Hard Steel 55NiCrMoV7 by Studying Rough and Semi-Finished Machining and the Influence of Cutting Parameters on Macroscopic Chip Dimensions. Materials, 17(14), 3434. https://doi.org/10.3390/ma17143434







