Bandgap Calculation and Experimental Analysis of Piezoelectric Phononic Crystals Based on Partial Differential Equations
Abstract
:1. Introduction
2. Structural Modeling and Calculation Methods
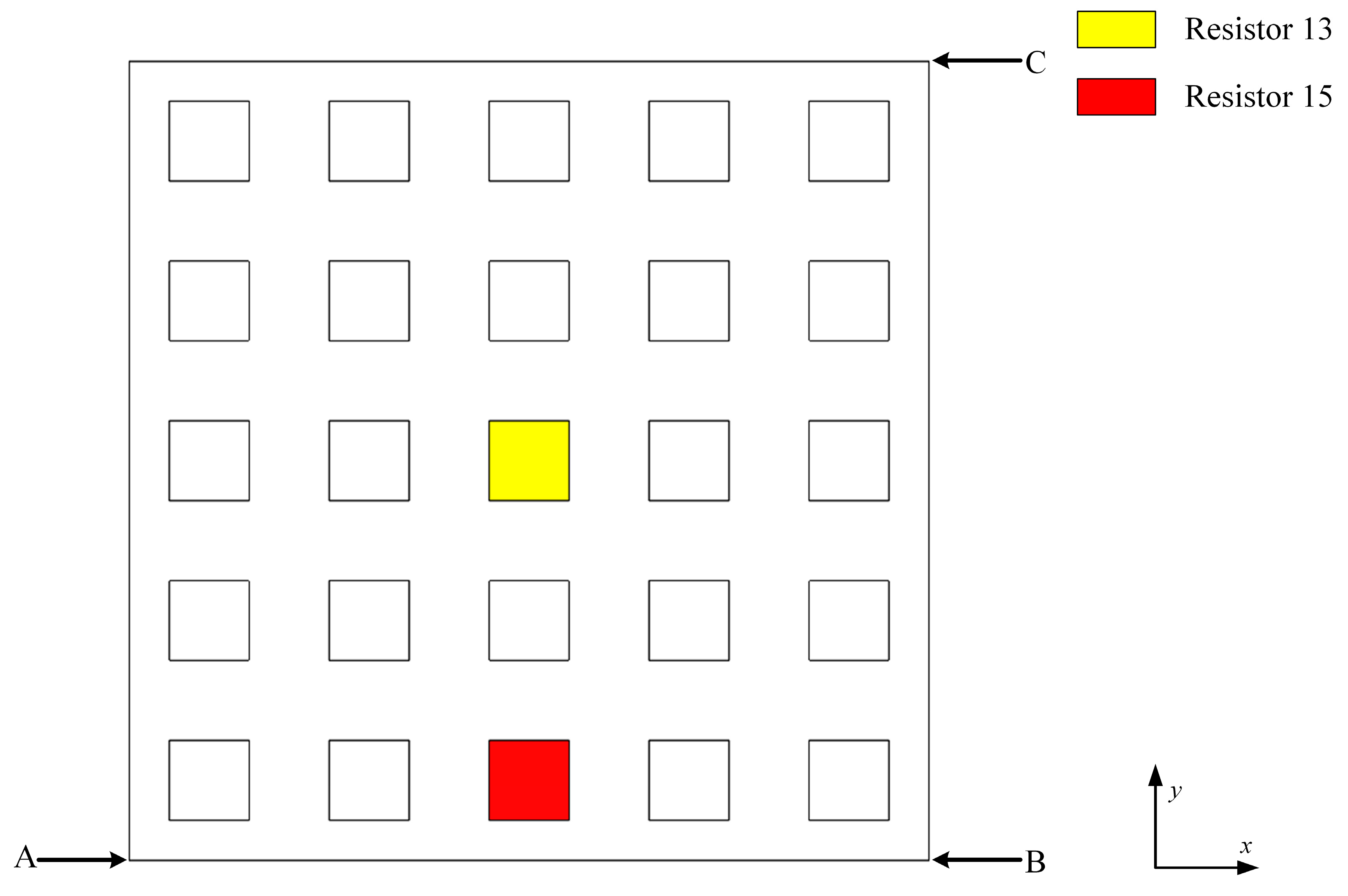
2.1. Calculated Parameters for the Complex Band of Piezoelectric Phononic Crystals
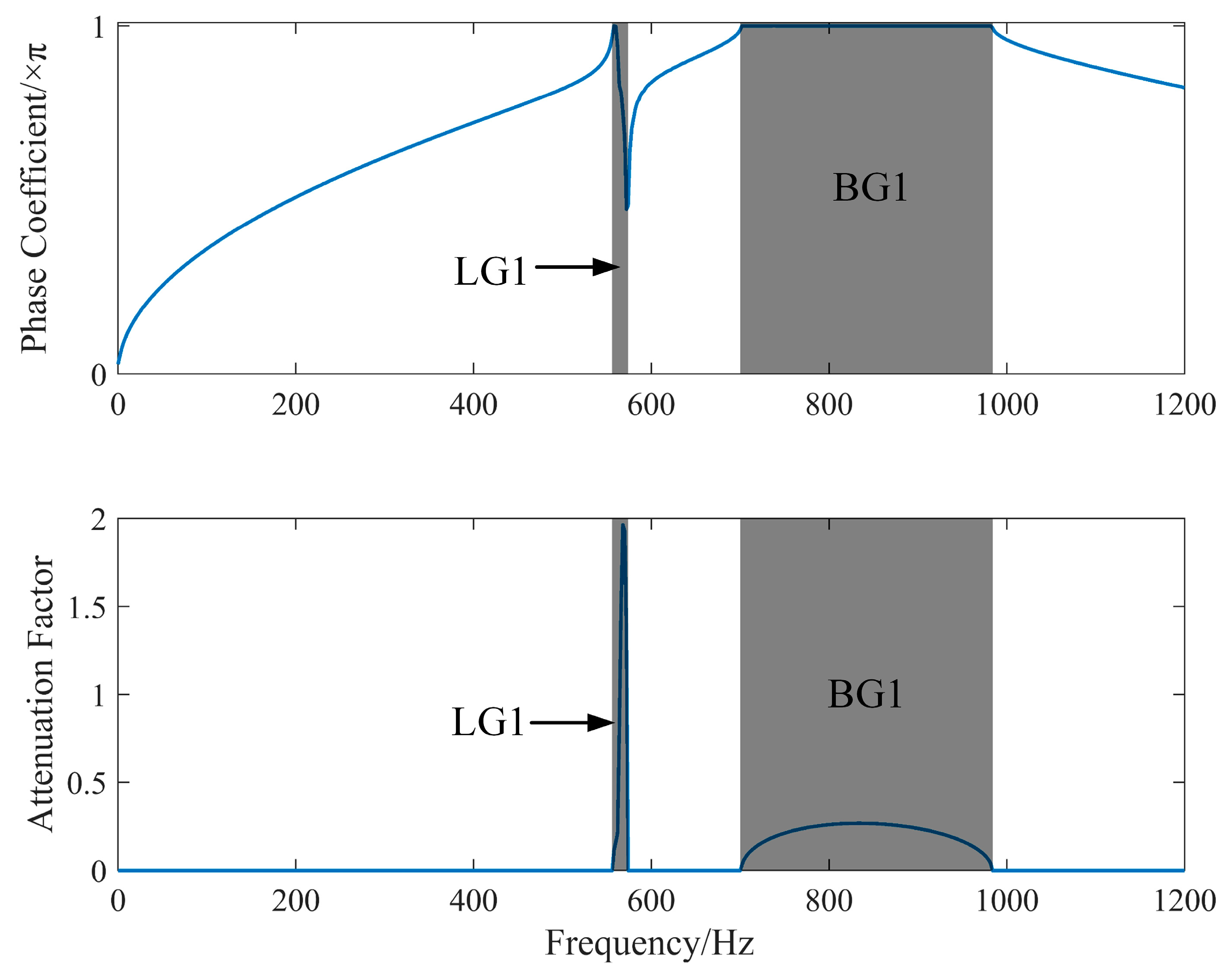
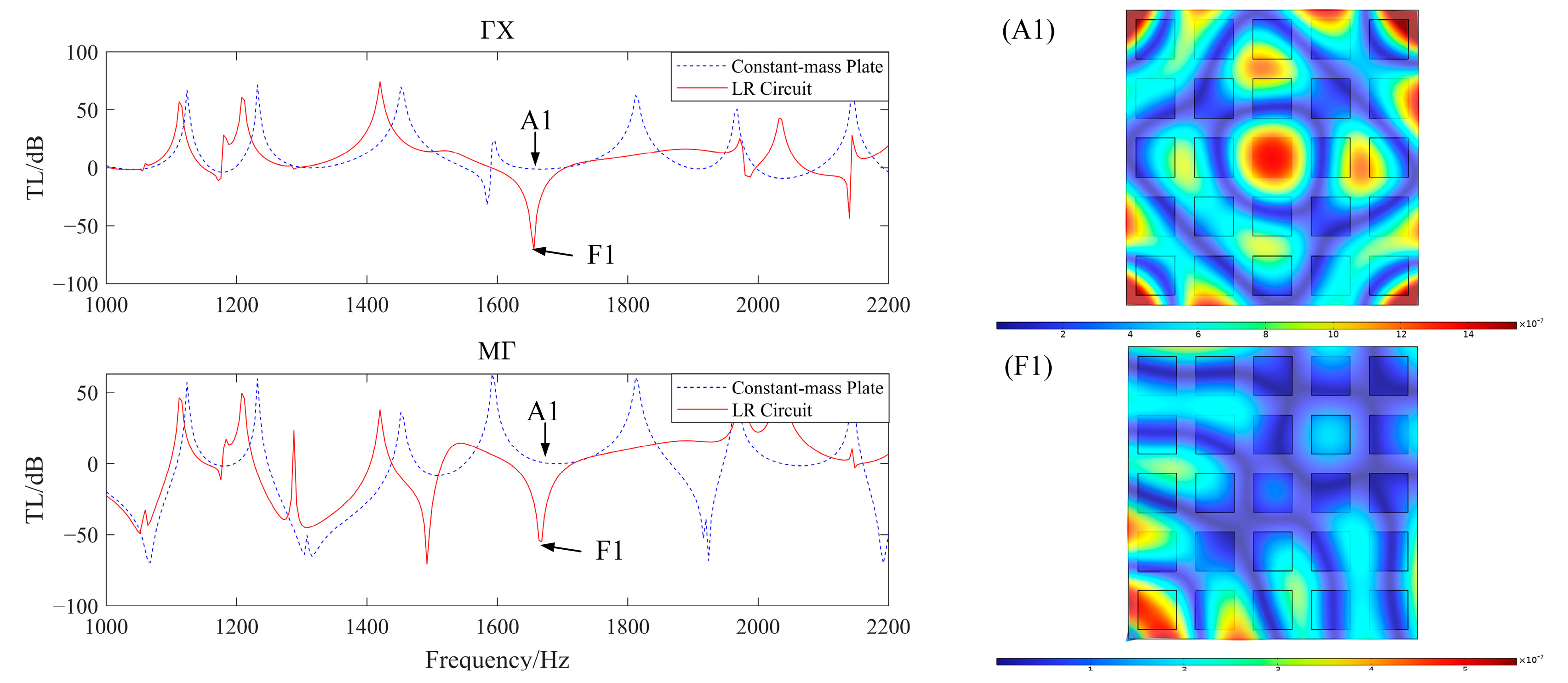
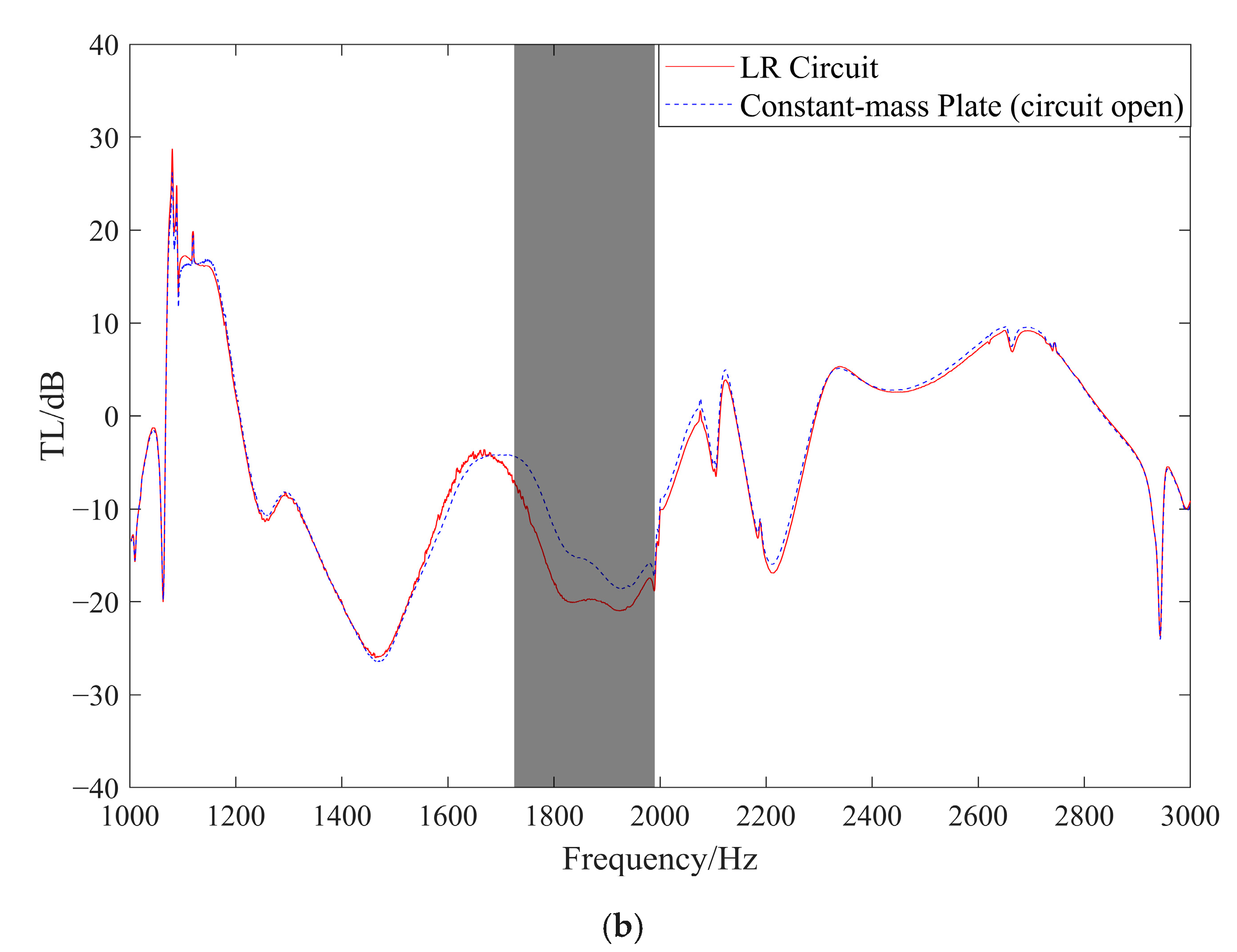
2.2. Model Validation
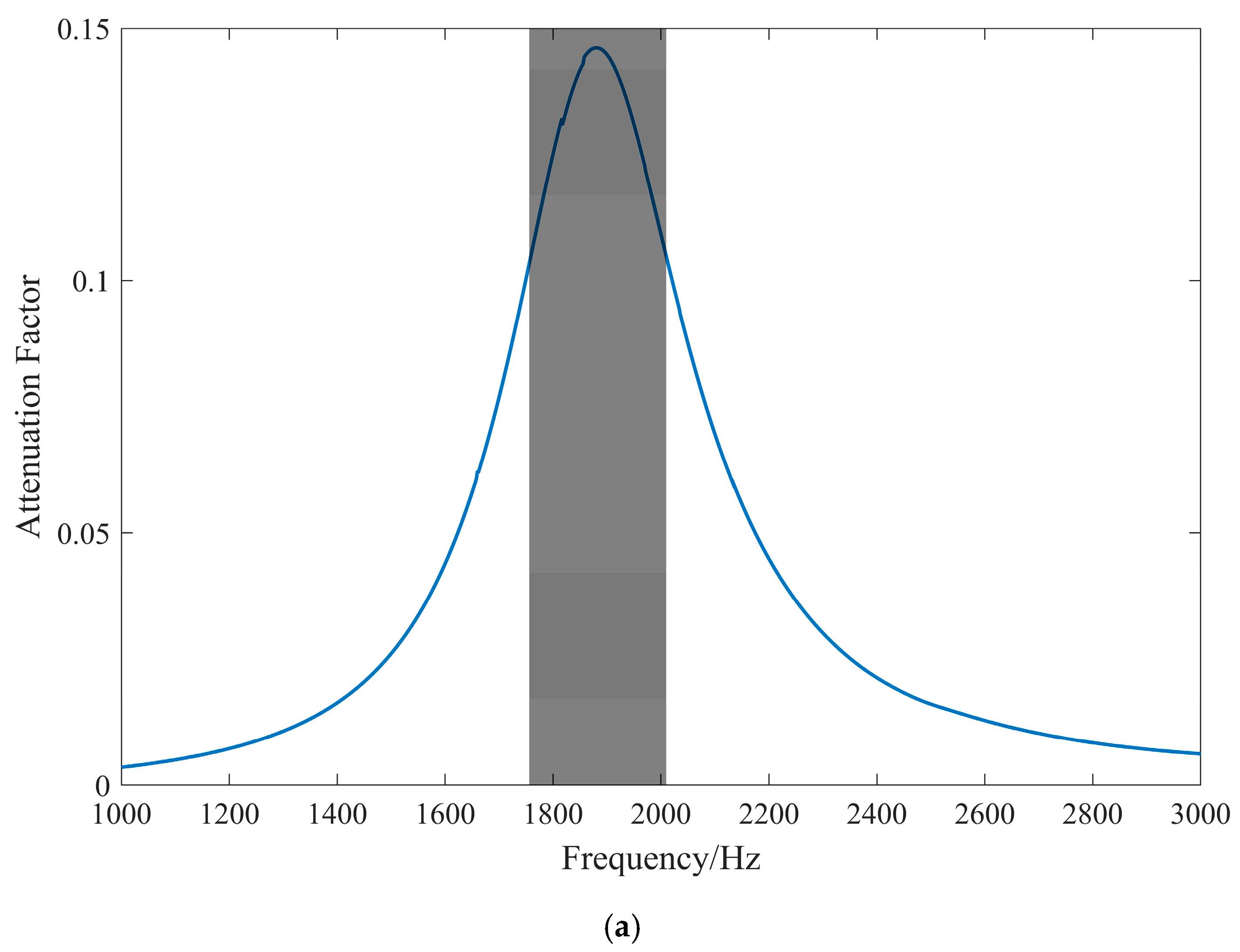
3. Analysis of the Influence Law of Structural/Electrical Parameters Based on Attenuation Coefficients
3.1. Effect of Coverage on Bandgap
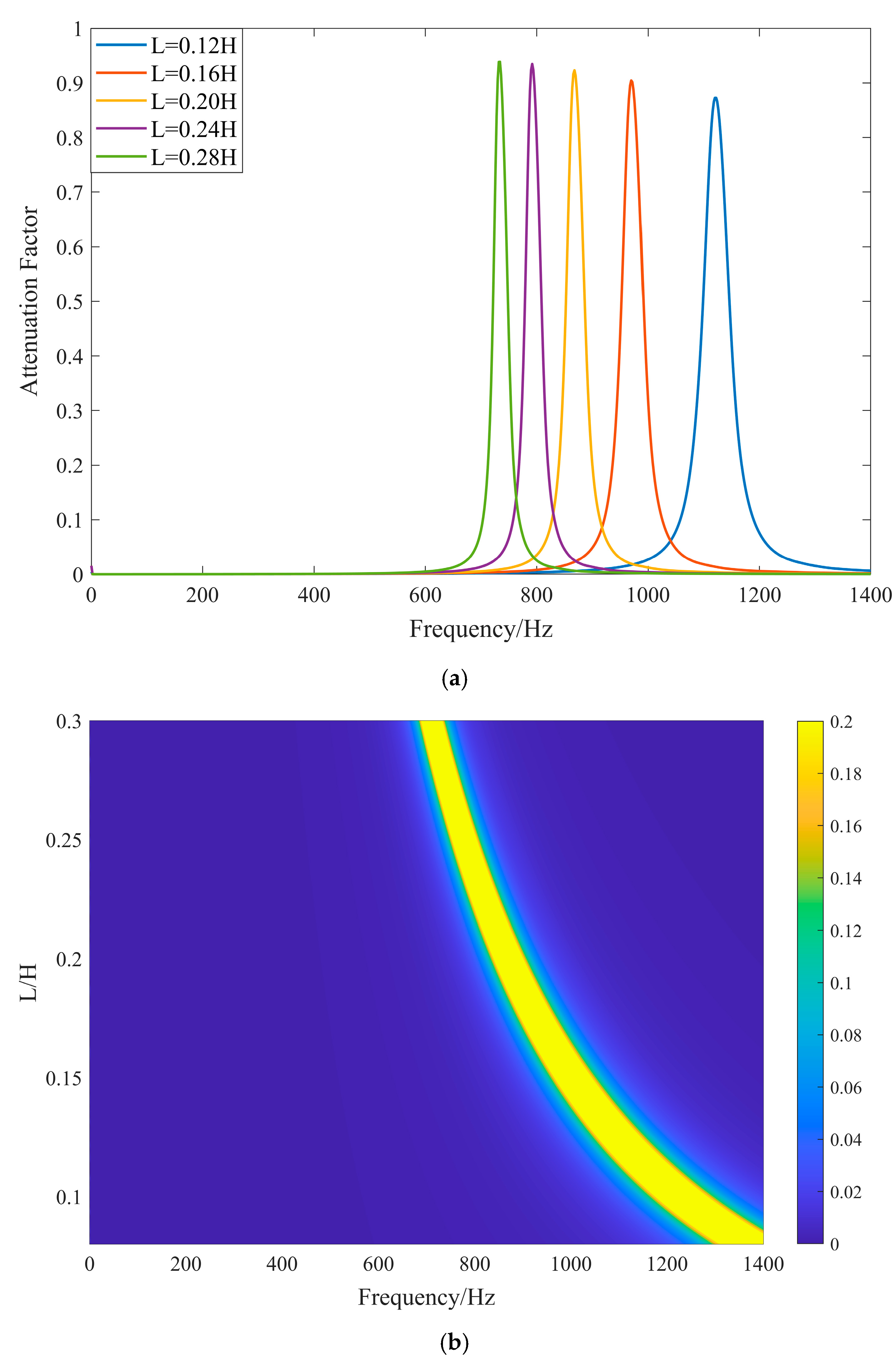
3.2. Effect of Inductance on Bandgap
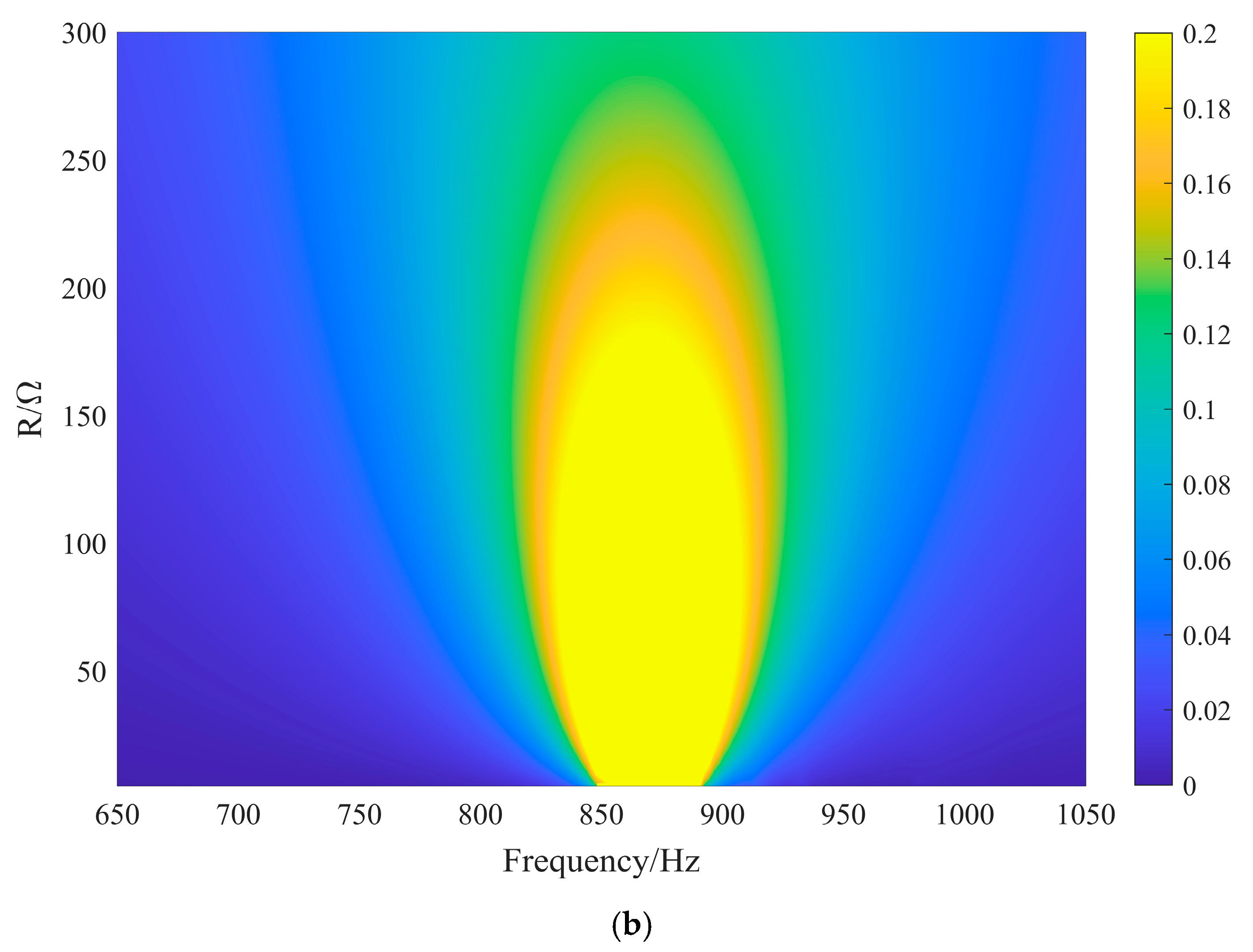
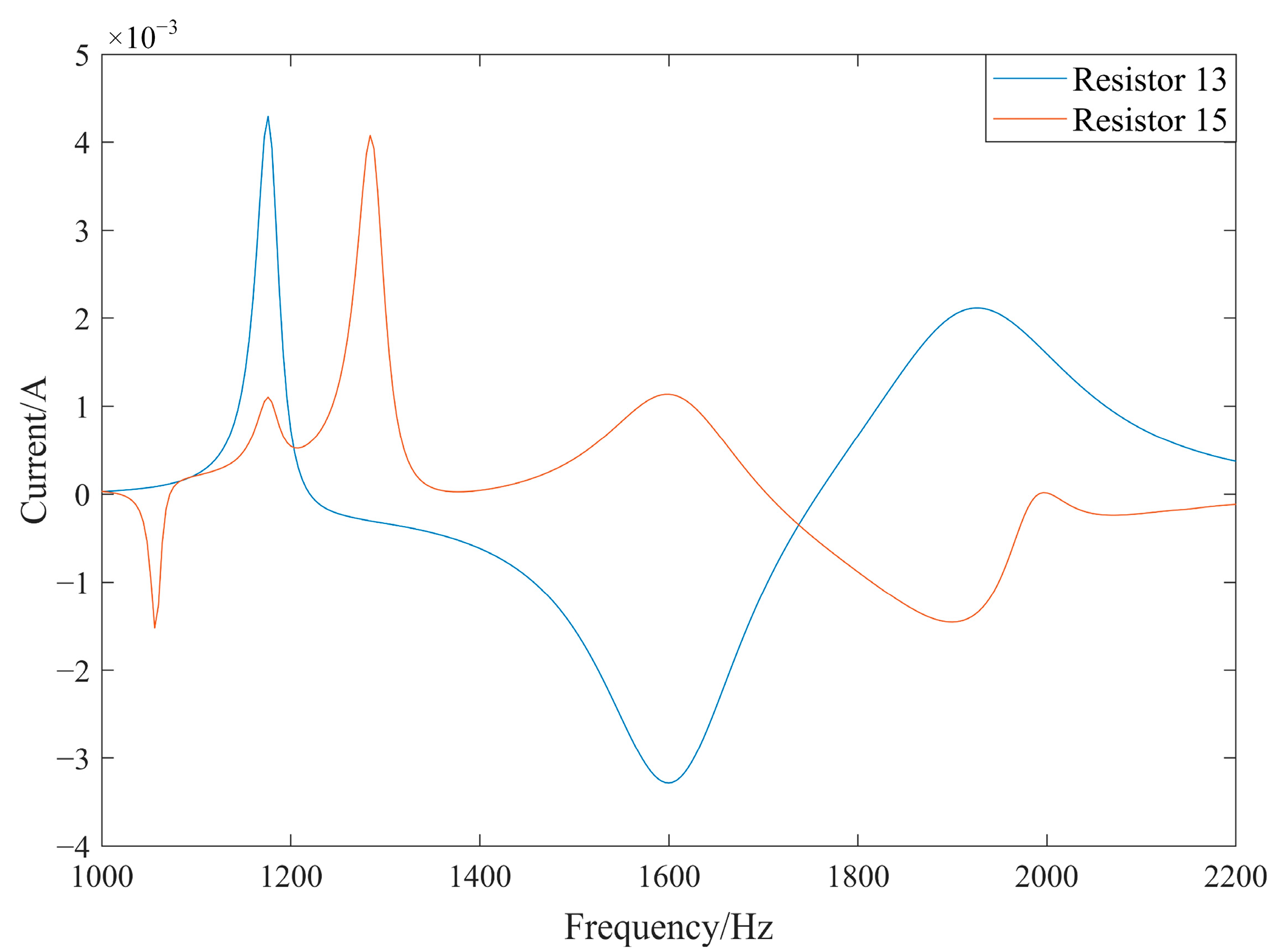
3.3. Effect of Resistance on Bandgap
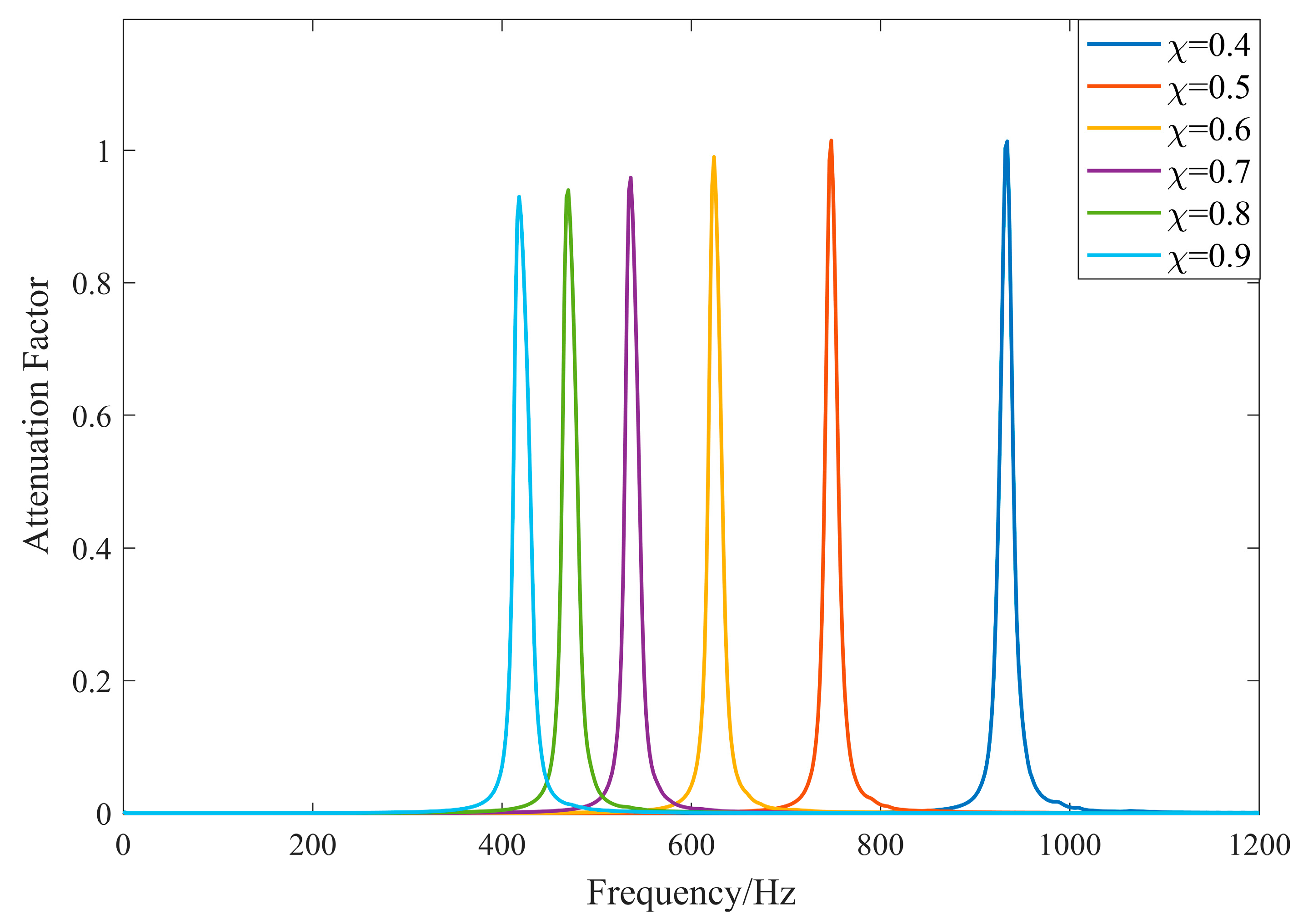
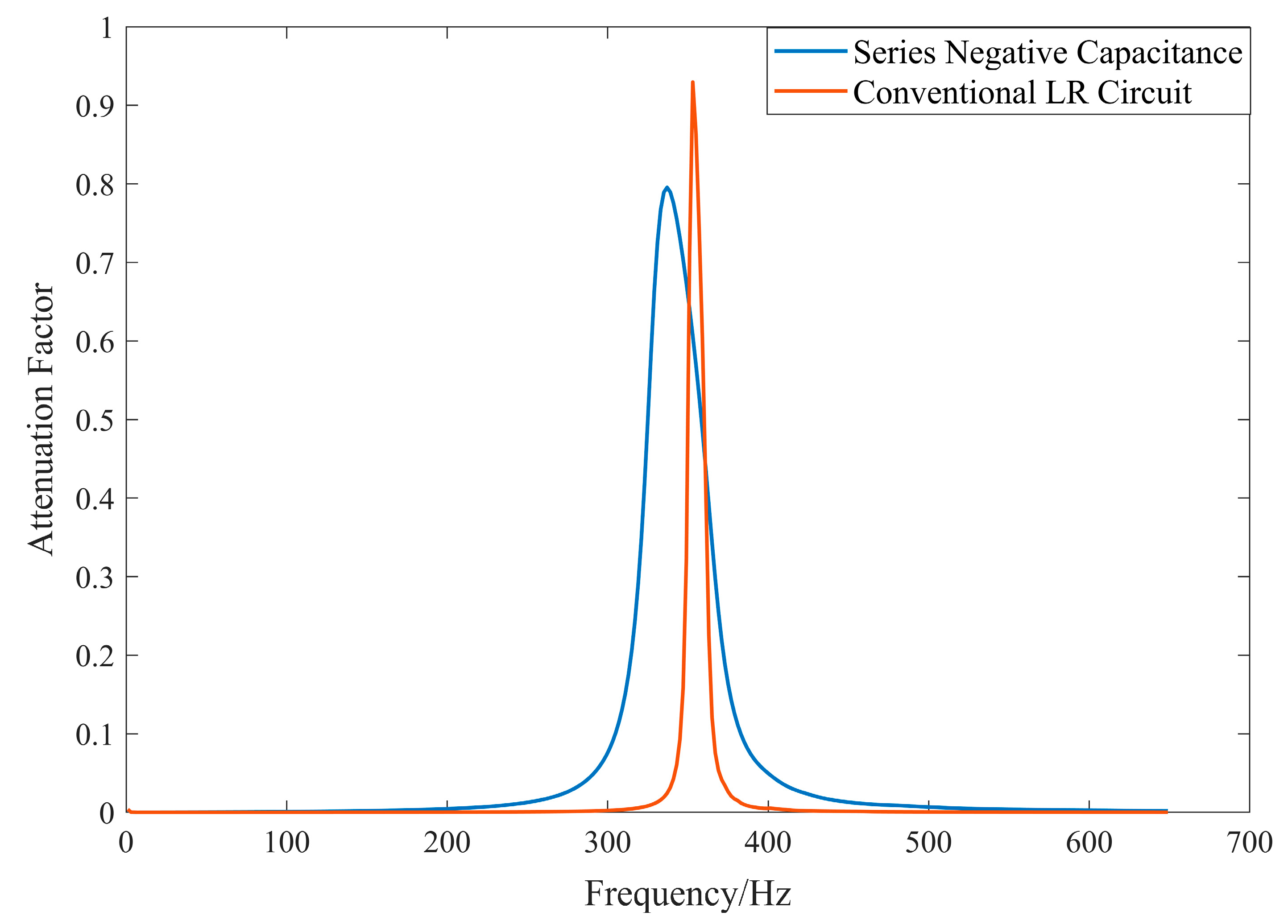
3.4. Effect of Generalized Capacitance on Bandgap
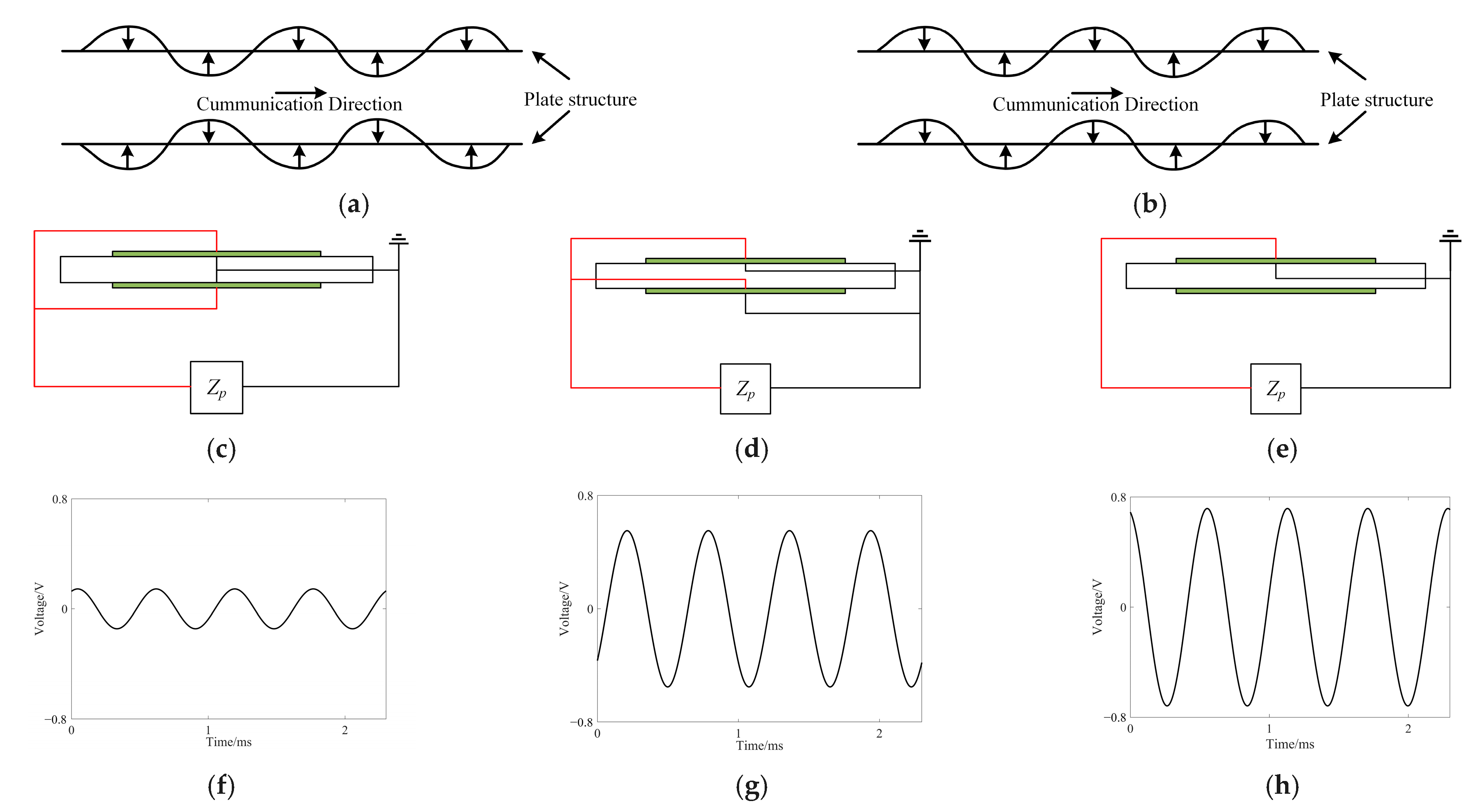
4. Vibration Transfer Simulation Analysis and Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Parameter Substitution Conversion Form (Base Plate)
Appendix B. Parameter Substitution Conversion Form (Piezo-Electric Sheet)
References
- Xiong, F.; Li, Y.; Wang, Y.C. Review on vibration isolation technology. J. Phys. Conf. Ser. 2021, 1820, 012009. [Google Scholar]
- Alujevic, N.; Cakmak, D.; Wolf, H.; Jokić, M. Passive and active vibration isolation systems using inerter. J. Sound Vib. 2018, 418, 163–183. [Google Scholar] [CrossRef]
- Al-Ashmori, M.; Wang, X. A systematic literature review of various control techniques for active seat suspension systems. Appl. Sci. 2020, 10, 1148. [Google Scholar] [CrossRef]
- Jian-Wei, W.; Gang, W.; Sheng-Bing, C.; Ji-Hong, W. Broadband Attenuation in Phononic Beams Induced by Periodic Arrays of Feedback Shunted Piezoelectric Patches. Chin. Phys. Lett. 2012, 29, 064302. [Google Scholar]
- Zuo, S.; Liu, P.; Wu, X.; Zhang, Q.; Kong, Y.; Zhou, D. Study on broad flexural wave bandgaps of piezoelectric phononic crystal plates for the vibration and noise attenuation. Thin Walled Struct. 2022, 178, 109481. [Google Scholar] [CrossRef]
- Kachapi, S.H.H. Nonlinear vibration response of piezoelectric nanosensor: Influences of surface/interface effects. Facta Univ. Ser. Mech. Eng. 2023, 21, 259–272. [Google Scholar]
- Li, G.-H.; Ma, T.-X.; Wang, Y.Z.; Wang, Y.-S. Active control on topological immunity of elastic wave metamaterials. Sci. Rep. 2020, 10, 9376. [Google Scholar] [CrossRef] [PubMed]
- Yi, K.; Matten, G.; Ouisse, M.; Sadoulet-Reboul, E.; Collet, M.; Chevallier, G. Programmable metamaterials with digital synthetic impedance circuits for vibration control. Smart Mater. Struct. 2020, 29, 035005. [Google Scholar] [CrossRef]
- Yi, K.; Collet, M. Broadening low-frequency bandgaps in locally resonant pieoelectric metamaterials by negative capacitance. J. Sound Vib. 2021, 493, 115837. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Ma, T.; Zhang, C. Smart piezoelectric phononic crystals and metamaterials: State-of-the-art review and outlook. Chin. Sci. Bull. 2022, 67, 1305–1325. (In Chinese) [Google Scholar] [CrossRef]
- Kaijun, Y.; Yangyang, C.; Rui, Z. Electromechanical active metamaterials and their applications in controlling elastic wave propagation. Chin. Sci. Bull. 2022, 67, 1290–1304. (In Chinese) [Google Scholar]
- Wang, G.; Cheng, J.Q.; Chen, J.W.; He, Y. Multi-resonant piezoelectric shunting induced by digital controllers for subwavelength elastic wave attenuation in smart metamaterial. Smart Mater. Struct. 2017, 26, 025031. [Google Scholar] [CrossRef]
- Chen, S.B.; Gang, W. Wave propagation in beams with anti-symmetric piezoelectric shunting arrays. Chin. Phys. B 2016, 25, 034301. [Google Scholar] [CrossRef]
- Zou, P.; Ren, L.; Wang, Q.; Qian, D.; Zhang, Z.; Ge, H. Tunability of “spring-mass” resonator on band gaps with surface effects of a piezoelectric phononic crystal double-layer nanobeam. Ferroelectrics 2023, 614, 56–69. [Google Scholar] [CrossRef]
- Lian, Z.; Jiang, S.; Hu, H.; Dai, L.; Chen, X.; Jiang, W. An Enhanced Plane Wave Expansion Method to Solve Piezoelectric Phononic Crystal with Resonant Shunting Circuits. Shock. Vib. 2016, 4, 4015363. [Google Scholar] [CrossRef]
- Hu, L.-Q.; Wang, S.; Lin, S.-Y. Analysis on vibration characteristics of large-size rectangular piezoelectric composite plate based on quasi-periodic phononic crystal structure. Chin. Phys. B 2022, 31, 054302. [Google Scholar] [CrossRef]
- Sugino, C.; Leadenham, S.; Ruzzene, M.; Erturk, A. On the mechanism of bandgap formation in locally resonant finite elastic metamaterials. Appl. Phys. 2016, 120, 134501. [Google Scholar]
- Hu, G.; Xu, J.; Tang, L.; Lan, C.; Das, R. Tunable metamaterial beam using negative capacitor for local resonators coupling. J. Intell. Mater. Syst. Struct. 2020, 31, 389–407. [Google Scholar] [CrossRef]
- Xiao, H.; Li, T.; Zhang, L.; Liao, W.H.; Tan, T.; Yan, Z. Metamaterial based piezoelectric acoustic energy harvesting: Electromechanical coupled modeling and experimental validation. Mech. Syst. Signal Process. 2023, 185, 109808. [Google Scholar] [CrossRef]
- Kargozarfard, M.H.; Sedighi, H.M.; Yaghootian, A.; Valipour, A. Nonreciprocal wave propagation in a time-space modulated metasurface using the modified plane wave expansion method. Thin Walled Struct. 2024, 195, 111335. [Google Scholar] [CrossRef]
- Shen, X.; Yi, K.; Jing, X.; Liu, Z.; Zhu, R. Desian of electromechanical coupled metamaterial plates for low frequency vibration control in aircraft structures. Acta Aeronaut. Astronaut. Sin. 2023, 44, 226959. [Google Scholar]
- Liu, P.; Zuo, S.; Wu, X.; Sun, L.; Zhang, Q. Study on the vibration attenuation property of one finite and hybrid piezoelectric phononic crystal beam. Eur. J. Mech. A Solids 2020, 84, 104017. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, C.; Dong, Y.; Zhu, S.; Pei, W.; Weng, J. Research on bending vibration characteristics of phononic crystal plates based on Mindlin’s piezoelectric plate theory. Smart Mater. Struct. 2023, 32, 105012. [Google Scholar] [CrossRef]
- Sugino, C.; Ruzzene, M.; Erturk, A. An analytical framework for locally resonant piezoelectric metamaterial plates. Int. J. Solids Struct. 2020, 182, 281–294. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, S.; Liu, Z.; Song, Y.; Xiao, Y. Light-weight large-scale tunable metamaterial panel for low-frequency sound insulation. Appl. Phys. Express 2020, 13, 067003. [Google Scholar] [CrossRef]
- Chen, S.B.; Wen, J.-H.; Wang, G.; Wen, X.-S. Tunable band gaps in acoustic metamaterials with periodic arrays of resonant shunted piezos. Chin. Phys. B 2013, 22, 074301. [Google Scholar] [CrossRef]
- Milić, P.; Marinković, D.; Klinge, S.; Ćojbašić, Ž. Reissner-mindlin based isogeometric finite element formulation for piezoelectric active laminated shells. Teh. Vjesn. 2023, 30, 416–425. [Google Scholar]
- Nestorović, T.; Marinković, D.; Shabadi, S.; Trajkov, M. User defined finite element for modeling and analysis of active piezoelectric shell structures. Meccanica 2014, 49, 1763–1774. [Google Scholar] [CrossRef]
- Collet, M.; Ouisse, M.; Ichchou, M.N. Structural energy flow optimization through adaptive shunted piezoelectric metacomposites. J. Intell. Mater. Syst. Struct. 2012, 23, 1661–1677. [Google Scholar] [CrossRef]
- Oudich, M.; Badreddine Assouar, M. Complex band structures and evanescent Bloch waves in two-dimensional finite phononic plate. J. Appl. Phys. 2012, 112, 104509. [Google Scholar] [CrossRef]

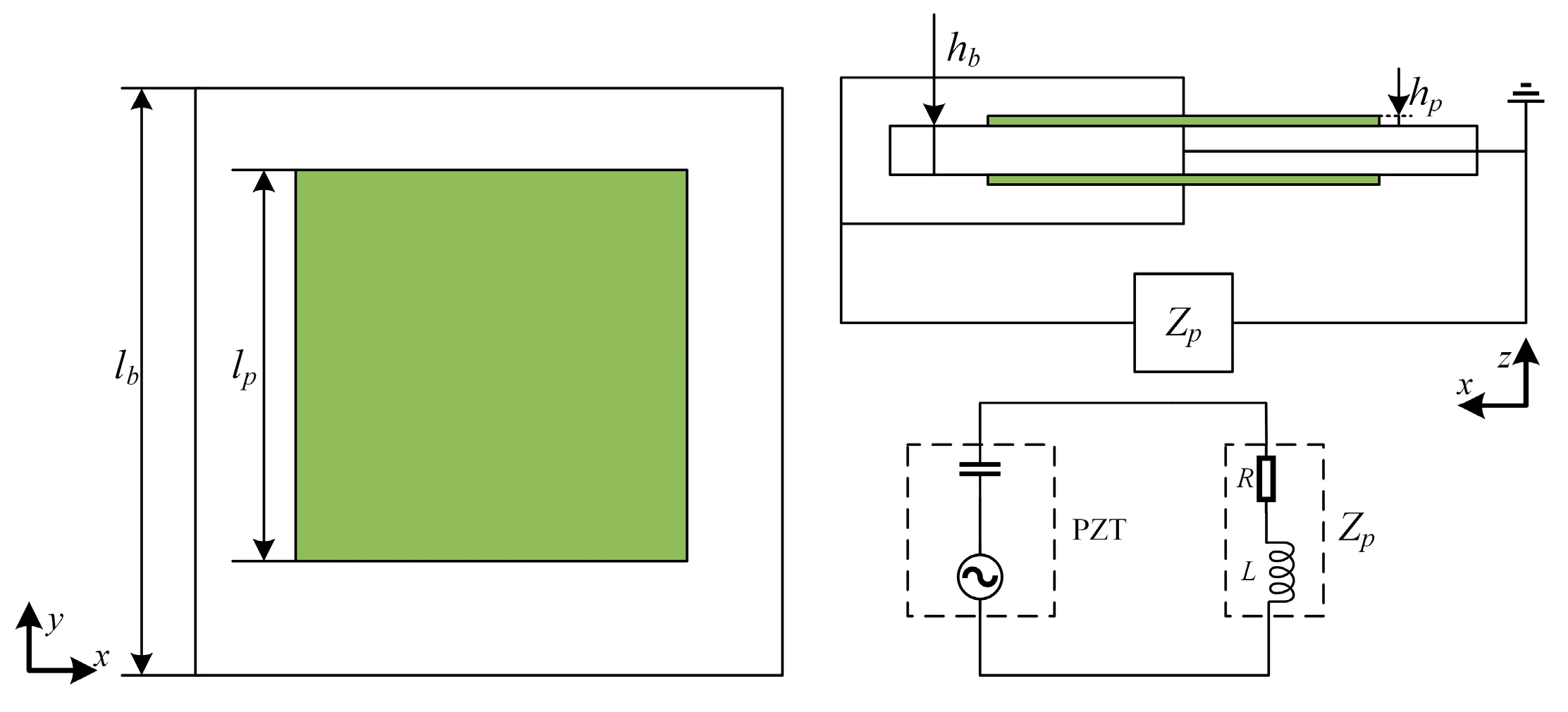
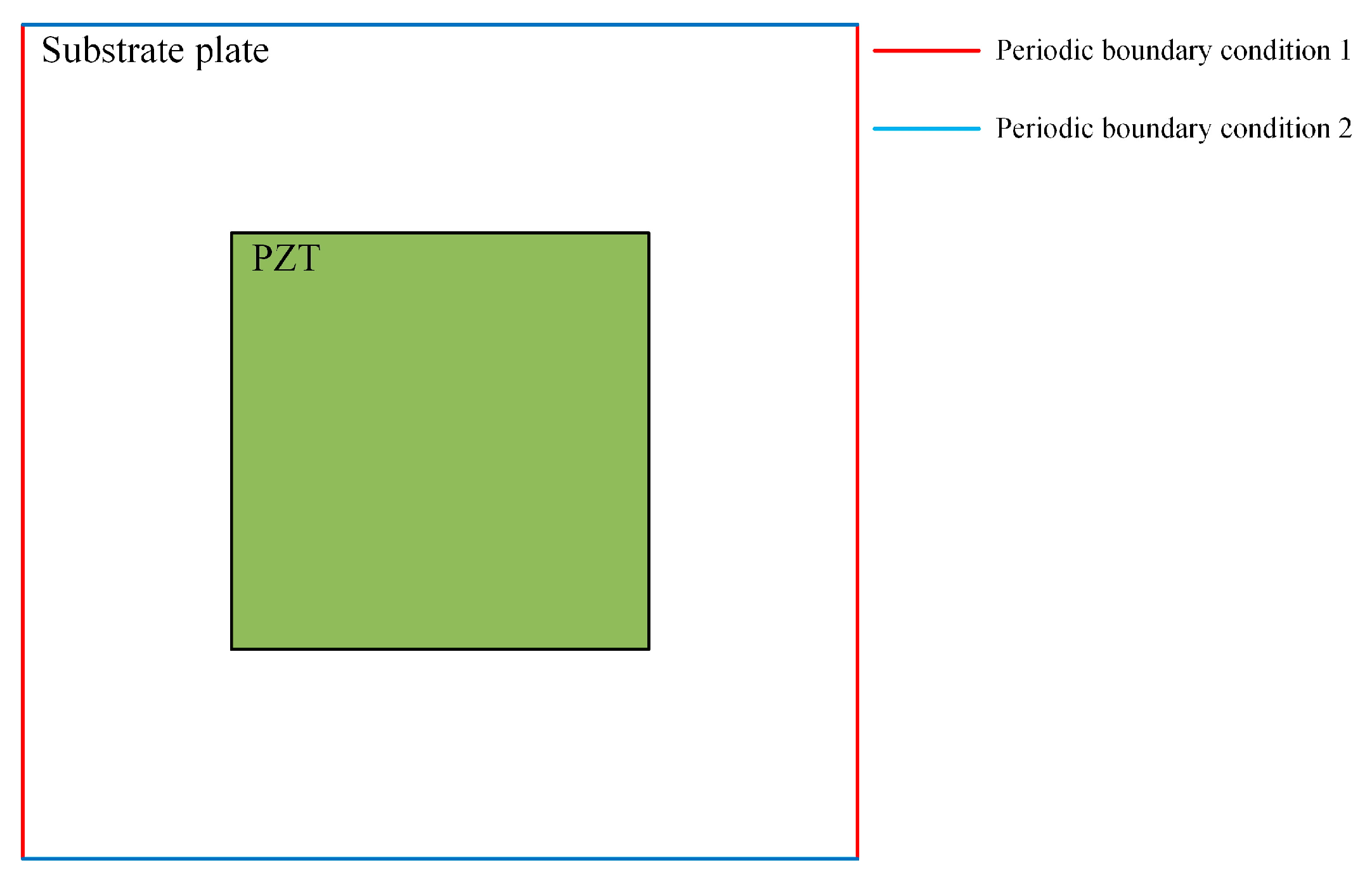




| Name | Parameter |
|---|---|
| Width of a single unit cell lb/mm | 80 |
| Thickness of a single unit cell hb/mm | 5 |
| Density ρ/(kg/m3) | 1180 |
| Young’s modulus Yb/Pa | 4.35 × 109 |
| Poisson’s ratio μb | 0.37 |
| Name | Parameter |
|---|---|
| Width of a single unit cell lp/mm | 40 |
| Thickness of a single unit cell hp/mm | 0.2 |
| Density ρ/(kg/m3) | 7500 |
| Flexibility coefficient /(m2/N) | 1.65 × 10−11 |
| Flexibility coefficient /(m2/N) | −4.78 × 10−12 |
| Flexibility coefficient /(m2/N) | 4.26 × 10−11 |
| Piezoelectric constant d31/(C/N) | −2.74 × 10−10 |
| Dielectric constant /(F/m) | 3.01 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Han, Y.; Jiang, Y.; Xie, M.; Jiang, Y.; Tang, K. Bandgap Calculation and Experimental Analysis of Piezoelectric Phononic Crystals Based on Partial Differential Equations. Materials 2024, 17, 3780. https://doi.org/10.3390/ma17153780
Song C, Han Y, Jiang Y, Xie M, Jiang Y, Tang K. Bandgap Calculation and Experimental Analysis of Piezoelectric Phononic Crystals Based on Partial Differential Equations. Materials. 2024; 17(15):3780. https://doi.org/10.3390/ma17153780
Chicago/Turabian StyleSong, Chunsheng, Yurun Han, Youliang Jiang, Muyan Xie, Yang Jiang, and Kangchao Tang. 2024. "Bandgap Calculation and Experimental Analysis of Piezoelectric Phononic Crystals Based on Partial Differential Equations" Materials 17, no. 15: 3780. https://doi.org/10.3390/ma17153780






