X-IGA Used for Orthotropic Material Crack Growth
Abstract
1. Introduction
2. Methodology
2.1. Overview of IGA and X-IGA
2.2. IGA Concept
2.3. NURBS for Two Dimensions
3. Mathematical Formulation
3.1. Elastic Behaviour Law for Anisotropic Material
3.2. Expression of the Displacement near the Crack
3.3. The SIF Using the Interaction Energy Integral Method
- (1) denotes the integral in the true state over an arbitrary area around the crack.
- (2) denotes the integral in the auxiliary state, chosen to coincide with the crack tip asymptotic field. It satisfies both the equilibrium and the traction-free boundary condition on the crack surface.
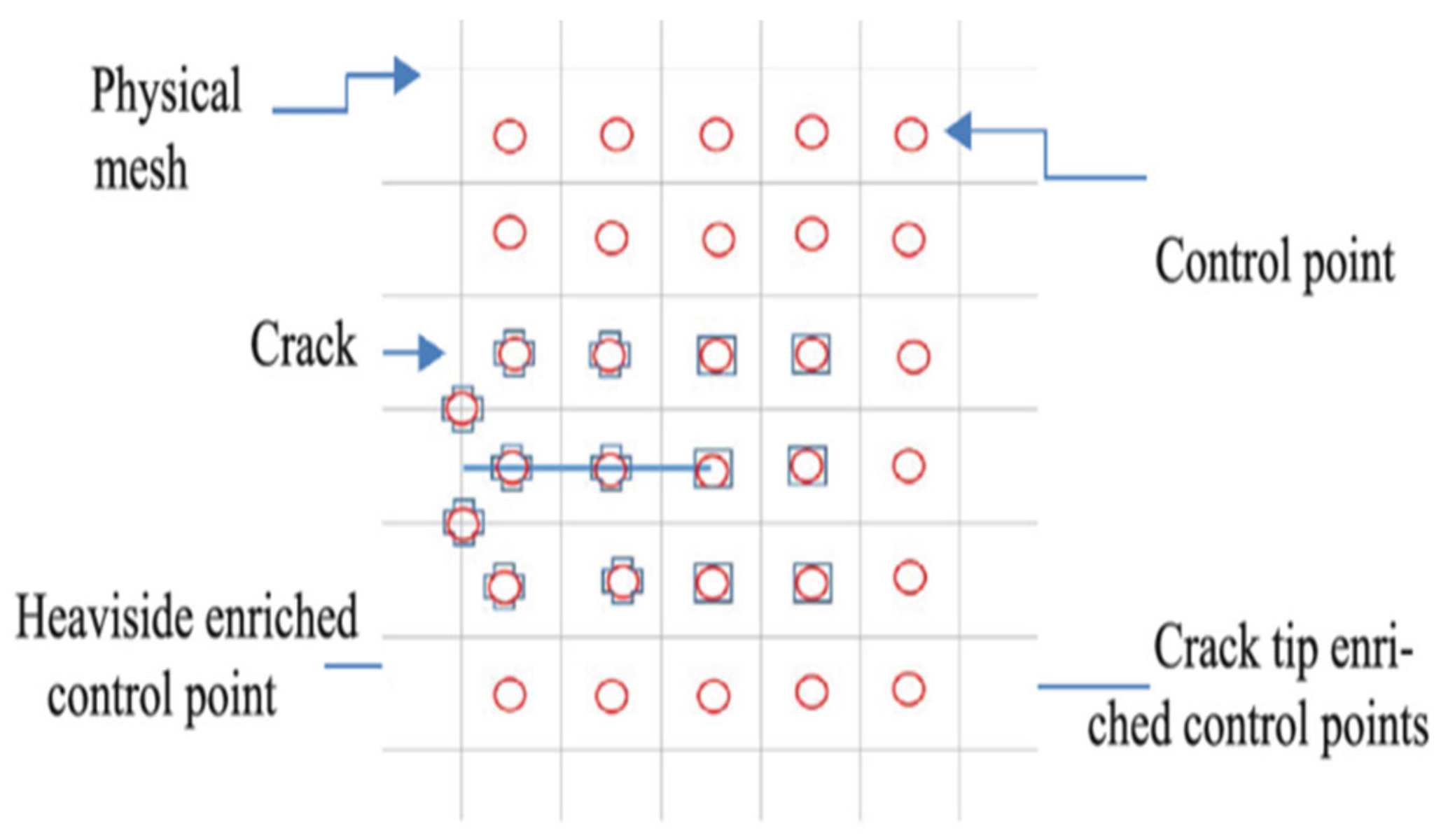
3.4. X-IGA Formulation for Linear Elastic Fracture
- H(x) is the Heaviside function defined as H(x) = .
- N1, N2, and NTIP represent the number of standard IGA elements, the number of elements enriched with the Heaviside function, and the number of knots enriched near the crack front, respectively. F(x) denotes the enrichment function near the crack front. The total displacement is now expressed as follows:
3.5. IGA Stiffness Matrix Construction
4. Simulation and Discussion
4.1. Geometry and Material Inputs Data
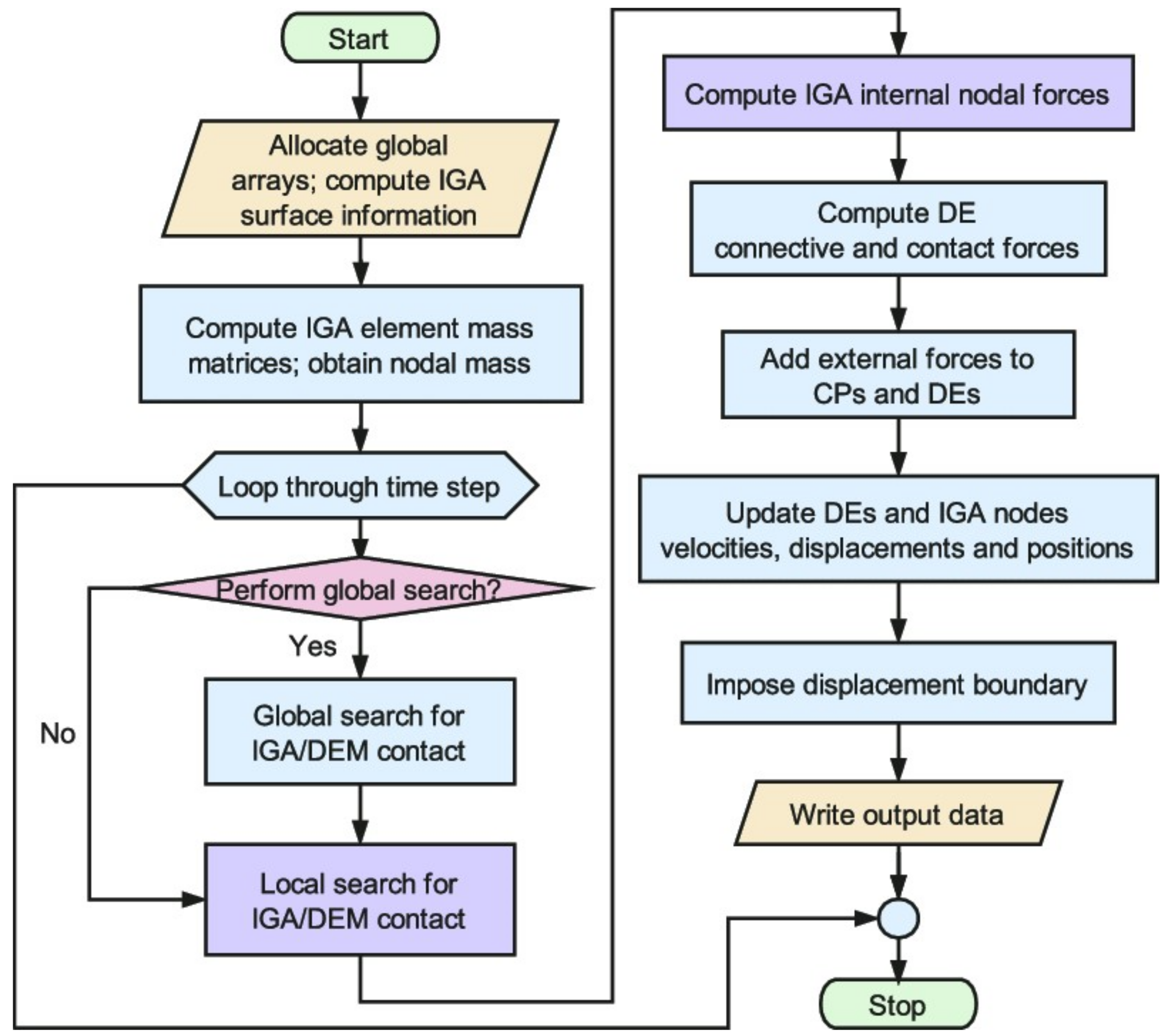
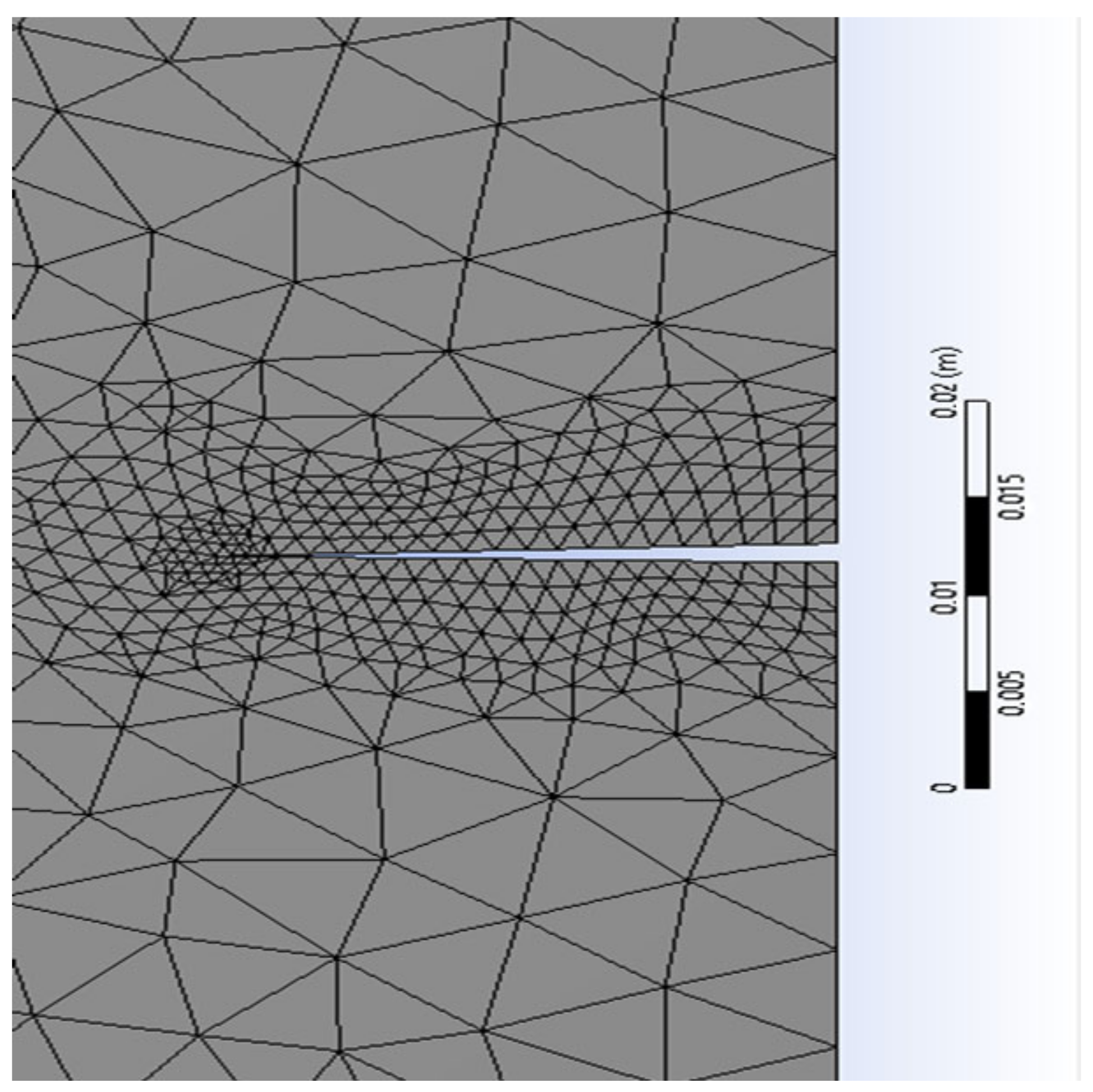
4.2. X-IGA and X-FEM Pre-Processing
| IGA Model with Enriched Control Points Near the Two Cracks | Boundary Conditions |
|---|---|
| Total number of control points = 1296 Uknot = [0 0 0 0.5 1 1 1]; Vknot = [0 0 0 1 1 1]; | 50 MPA stress applied in the upper side. Fixation in the lower side. |
4.3. Results and Discussion
5. Conclusions
- The numerical simulation process used in X-IGA is significantly faster than that of its FEM equivalent. This is mainly because control points are directly used, and the stiffness matrix is constructed using NURBS basis functions.
- The smooth transition from Computer-Aided Design (CAD) to the solution stage is made possible by this seamless integration, which eliminates the need for intermediate preprocessing tools and streamlines the computational workflow.
- The research suggests a new and straightforward design strategy to improve X-IGA’s usability and accessibility for composite anisotropic materials by using just the neutral to simplify the reduction of the three-dimensional (3D) and two-dimensional (2D) representations, which makes it easier to pre-process with X-IGA code and two-dimensional code.
- The convergence of the X-FEM results in the function of refining demonstrates the reliability of the results and can replace the experimental study to test the efficiency of the proposed X-IGA approach.
- NURBS functions are naturally precise and adaptable when it comes to approximating curved geometries; therefore, there is no need for significant modification.
- The Lagrange function’s approximation of curved geometry frequently requires significant refinement, which increases the need for elements and nodes in polygonal approximations and lengthens runtime, particularly when refinement is needed around a crack.
- This query highlights how dynamic and constantly changing numerical simulations are, and, as such, it is worth investigating further in the continuing effort to improve computational techniques in the fields of engineering and materials science.
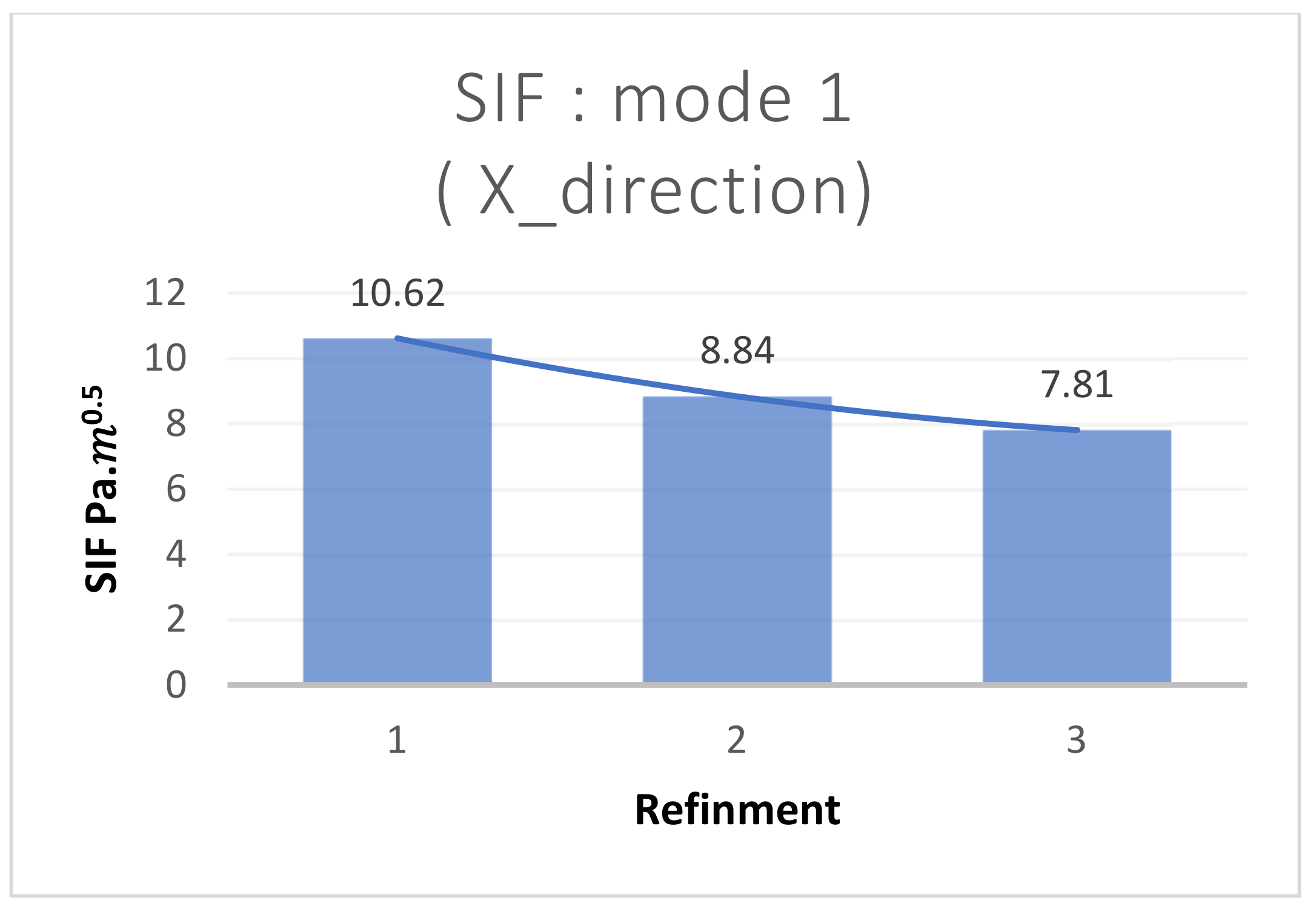
- According to [36,37], X-IGA with few control points shows smaller SIF errors than the X-FEM, which can be attributed to NURBS functions’ accuracy in approximating curved geometries [38]. NURBS are able to accurately represent curved form behaviour in addition to approximating the true geometry. On the other hand, using Lagrange functions to approximate curved geometry necessitates a significant amount of refining [34], which raises the element and node requirements for polygonal approximations [39], which in turn lengthens runtime, particularly when refinement is required around a crack.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alshoaibi, A.; Alsharaa, A.K. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 5953. [Google Scholar] [CrossRef]
- Mark, A. Essential boundary conditions and multi-point constraints in finite element analysis. Comput. Methods Appl. Mech. Eng. 2001, 190, 6323–6339. [Google Scholar]
- Koubaiti, O.; El Khalfi, A. Solving the problem of constraints due to Dirichlet boundary conditions in the context of the mini element method. Int. J. Mech. 2020, 14, 12–22. [Google Scholar]
- Koubaiti, O.; El-Mekkaoui, J.; El Khalfi, A. Complete study for solving Navier-Lamé equation with new boundary condition using mini element method. Int. J. Mech. 2019, 12, 46–58. [Google Scholar]
- Wang, D.; Xuan, J. An improved NURBS-based isogeometric analysis with enhanced treatment of essential boundary conditions. Comput. Methods Appl. Mech. Eng. 2010, 199, 2425–2436. [Google Scholar] [CrossRef]
- Hughes, T.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- El-Mekkaoui, J.; El Khalfi, A. Resolution of stokes equations with the Ca,b boundary condition using mixed finite elements method. Trans. Math. 2013, 2, 586–597. [Google Scholar]
- Templeton, E.L.; Baudet, A.; Bhat, H.S.; Dmowska, R.; Rice, J.R.; Rosakis, A.J.; Rousseau, C.E. Finite element simulations of dynamic shear rupture experiments and dynamic path selection along kinked and branched faults. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Montassir, S.; Moustabchir, H.; El Khalfi, A.; Vlase, S.; Scutaru, M.L. Numerical Study of Crack Prediction and Growth in Automotive Wheel Rims. Materials 2024, 17, 1020. [Google Scholar] [CrossRef] [PubMed]
- Hattori, G.; Rojas-Díaz, R.; Sukumar, A.S.; García-Sánchez, F. New anisotropic crack-tip enrichment functions for the extended finite element method. Comput. Mech. 2012, 50, 591–601. [Google Scholar] [CrossRef]
- Dag, S.; Arman, E.; Yildirim, B. Computation of thermal fracture parameters for orthotropic functionally graded materials using Jk –integral. Int. J. Solids Struct. 2010, 47, 3480–3488. [Google Scholar] [CrossRef]
- Nakano, H.; Sekiguchi, Y.; Toshiyuki, S. FEM stress analysis and strength prediction of scarf adhesive joints under static bending moments. Int. J. Adhes. Adhes. 2013, 44, 166–173. [Google Scholar] [CrossRef]
- Lam, K.Y.; Nguyen-Thoi, T.; Liu, G.R. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J. Sound Vib. 2019, 320, 1100–1130. [Google Scholar]
- Liu, H.; Huang, J.; Zhang, W. Numerical algorithm based on extended barycentric Lagrange interpolant for two dimensional integro-differential equations. Appl. Math. Comput. 2021, 396, 125931. [Google Scholar] [CrossRef]
- Thierry, C.; Hugues, D.; Richard, D. Parallel meshing and remeshing. Appl. Math. Model. 2000, 25, 153–175. [Google Scholar]
- Barros, F.B.; Silva, R. Extended isogeometric analysis: A two-scale coupling FEM/IGA for 2D elastic fracture problems. Comput. Mech. 2023, 73, 639–665. [Google Scholar]
- Seweryn, A. Modeling of singular stress fields using finite element method. Int. J. Solids Struct. 2002, 39, 4787–4804. [Google Scholar] [CrossRef]
- Nie, D.; Zhang, X. Engineering Fracture Mechanics XFEM with partial Heaviside function enrichment for fracture analysis. Eng. Fract. Mech. 2021, 241, 107375. [Google Scholar]
- Geniaut, S.; Galenne, E. A simple method for crack growth in mixed mode with X-FEM. Int. J. Solids Struct. 2012, 49, 2094–2106. [Google Scholar] [CrossRef]
- Montassir, S.; Moustabchir, H.; El Khalfi, A.; Scutaru, M.L.; Vlase, S. Fracture Modelling of a Cracked Pressurized Cylindrical Structure by Using Extended Iso-Geometric Analysis (X-IGA). Mathematics 2021, 194, 2990. [Google Scholar] [CrossRef]
- Abdulnaser, A.; Yahya, F. 3D modelling of fatigue crack growth and life predictions using ANSYS. Ain Shams Eng. J. 2022, 13, 101636. [Google Scholar]
- Sundeep, M.; Harpreet, A.; Medha, V. Performance and Design of Steel Structures Reinforced with FRP Composites: A state-of-the-art review. Eng. Fail. Anal. 2023, 138, 106371. [Google Scholar]
- Bai, B.; Ci, H.; Lei, H.; Cui, Y. A local integral-generalized finite difference method with mesh-meshless duality and its application. Eng. Anal. Bound. Elem. 2022, 139, 14–39. [Google Scholar] [CrossRef]
- McLachlan, R.I. Spatial Discretization of Partial Differential Equations with Integrals. IMA J. Numer. Anal. 2003, 23, 645–664. [Google Scholar] [CrossRef]
- Moes, N.; Belytschko, T. X-FEM, de nouvelles frontières pour les éléments finis. Eur. J. Comput. Mech. 2012, 11, 305–318. [Google Scholar] [CrossRef]
- Yakoubi, K.; Montassir, S.; Moustabchir, H.; El Khalfi, A.; Pruncu, C.I.; Arbaoui, J.; Farooq, M. An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure. Mathematics 2021, 9, 507. [Google Scholar] [CrossRef]
- Wang, Y. Structural Design Optimization Using Isogeometric Analysis. Comput. Model. Eng. Sci. 2021, 117, 455–507. [Google Scholar]
- Thanh, N.; Josef, K. Rotation free isogeometric thin shell analysis using PHT-splines. Comput. Methods Appl. Mech. Eng. 2011, 200, 3410–3424. [Google Scholar] [CrossRef]
- Li, R.; Shao, Q.; Enlai, G.; Liu, Z. Elastic anisotropy measure for two-dimensional crystals. Extrem. Mech. Lett. 2019, 34, 100615. [Google Scholar] [CrossRef]
- Bui, T.Q. Extended isogeometric dynamic and static fracture analysis for cracks in piezoelectric materials using NURBS. Comput. Methods Appl. Mech. Eng. 2015, 295, 470–509. [Google Scholar] [CrossRef]
- Hughes, T.; Engel, G.; Mazzei, L.; Larson, M. The Continuous Galerkin Method Is Locally Conservative. J. Comput. Phys. 2000, 163, 467–488. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Bordas, S.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simul. 2015, 117, 89–116. [Google Scholar] [CrossRef]
- Berezovski, A.; Kolman, R.; Blažek, J.; Kopačka, J.; Dušan, G.; Plešek, J. Comparative study of finite element method, isogeometric analysis, and finite volume method in elastic wave propagation of stress discontinuities. In Proceedings of the 11th European Conference on Non-Destructive Testing (ECNDT 2014), Prague, Czech Republic, 6–10 October 2014. [Google Scholar]
- Ji, Y.; Li, J.-G.; Yu, Y.Y.; Zhu, C.G. h-Refinement method for toric parameterization of planar multi-sided computational domain in isogeometric analysis. Comput. Aided Geom. Des. 2022, 93, 102065. [Google Scholar] [CrossRef]
- Mei, C.; Wang, Q.; Yu, C.; Xia, Z. IGA Based Bi-Layer Fiber Angle Optimization Method for Variable Stiffness Composites. Comput. Model. Eng. Sci. 2020, 124, 179–202. [Google Scholar] [CrossRef]
- Sundeep, M.; Harpreet, S.A.; Medha, V. Crystallization kinetics and fragility of a metallic glass composite. Scr. Mater. 2015, 95, 62–65. [Google Scholar]
- Baharin, M.S.; Shahrum, A.; Salvinder, S.; Khairul, F. Computational fatigue failure analysis of magnesium alloy core structure inside the metal sandwich panels under constant spectrum loadings. Eng. Fail. Anal. 2022, 139, 106194. [Google Scholar] [CrossRef]
- Oesterle, B.; Geiger, F.; Forster, D.; Fröhlich, M.; Bischoff, M. A study on the approximation power of NURBS and the significance of exact geometry in isogeometric pre-buckling analyses of shells. Comput. Methods Appl. Mech. Eng. 2022, 397, 115144. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Alonso, A.; Antelo, L.T.; Arias-Mendez, A.; Quiroga, E.L.; Rivas, D.; Vilas, C. Model Identification and on-line optimal control of food processes. In Proceedings of the V International Conference on Computational Methods for Coupled Problems in Science and Engineering, Santa Eulàlia, Spain, 17–19 June 2013. [Google Scholar]
- Ettaye, G.; El Barkany, A.; Jabri, A.; El Khalfi, A. Optimizing the integrated production and maintenance using generic algorithm. Int. J. Eng. Bus. Manag. 2018, 10, 102018. [Google Scholar] [CrossRef]
- DeDontney, N.; Rice, J.R.; Dmowska, R. Finite Element Modeling of Branched Ruptures Including Off-Fault Plasticity. Bull. Seismol. Soc. Am. 2012, 102, 541–562. [Google Scholar] [CrossRef]
- Mercuri, M.; Pathirage, M.; Gregori, A.; Cusatis, G. Influence of self-weight on size effect of quasi-brittle materials: Generalized analytical formulation and application to the failure of irregular masonry arches. Int. J. Fract. 2023, 246, 117–144. [Google Scholar] [CrossRef]
- Cusatis, G.; Schauffert, E.A. Cohesive crack analysis of size effect. Eng. Fract. Mech. 2009, 76, 2163–2173. [Google Scholar] [CrossRef]
- Dag, S.; Yildirim, B.; Sarikaya, D. Mixed-mode fracture analysis of orthotropic functionally graded materials under mechanical and thermal loads. Int. J. Solids Struct. 2007, 44, 7816–7840. [Google Scholar] [CrossRef][Green Version]
- Gao, W.; Wang, J.; Yin, S.; Feng, Y. A coupled 3D isogeometric and discrete element approach for modeling interactions between structures and granular matters. Computer Methods Appl. Mech. Eng. 2019, 354, 441–463. [Google Scholar] [CrossRef]





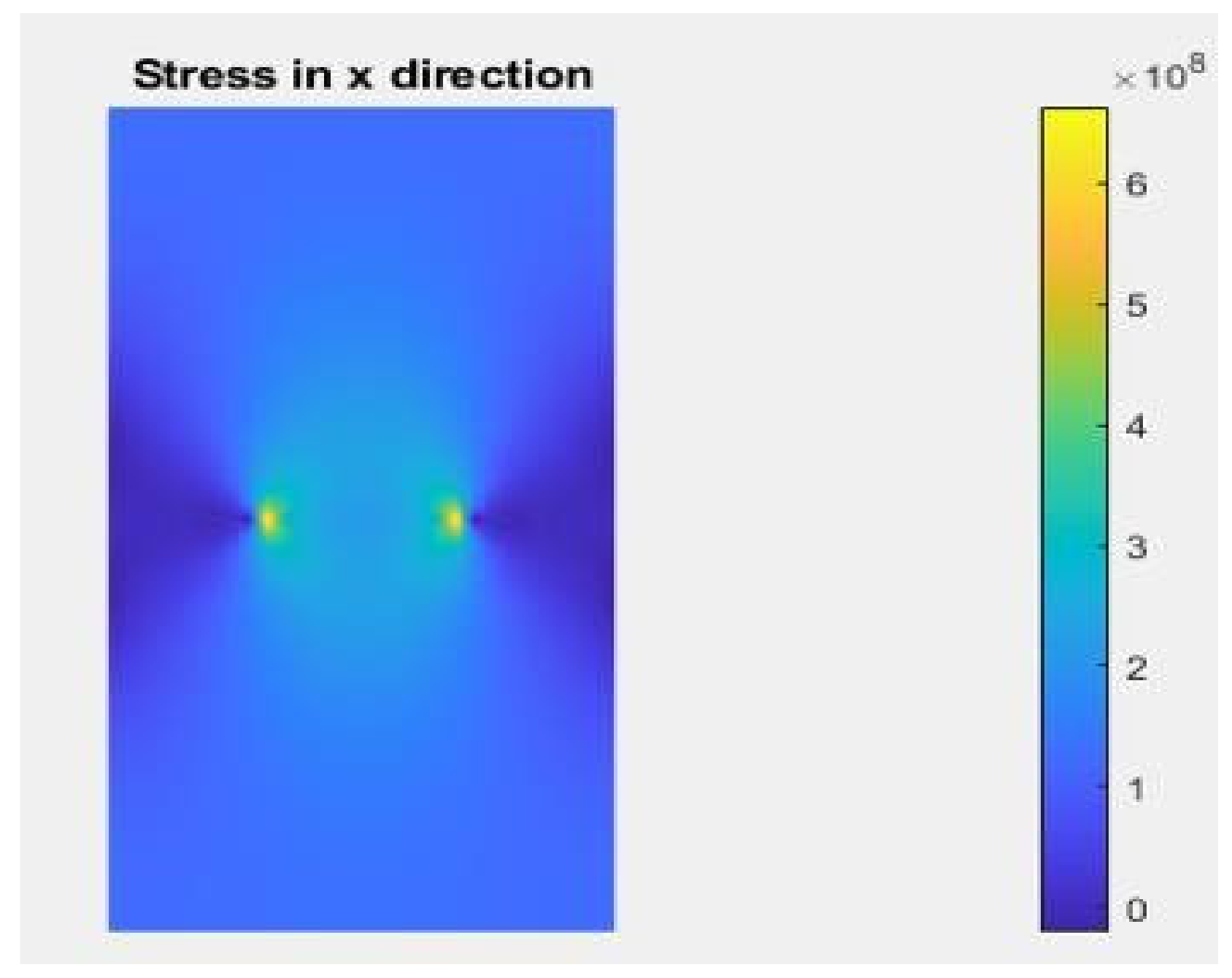
| Length | Thickness | Initial Crack Length: a |
|---|---|---|
| 200 mm | 2 mm | 20 mm (two crack on the middle) |
| Material | Young Modulus in X Direction [GPa] | Young Modulus in Y Direction [GPa] | Poisson Coefficient XY | Coulomb Modulus XY [GPa] |
|---|---|---|---|---|
| Orthotropic composite material | 121 | 8.6 | 0.27 | 4.9 |
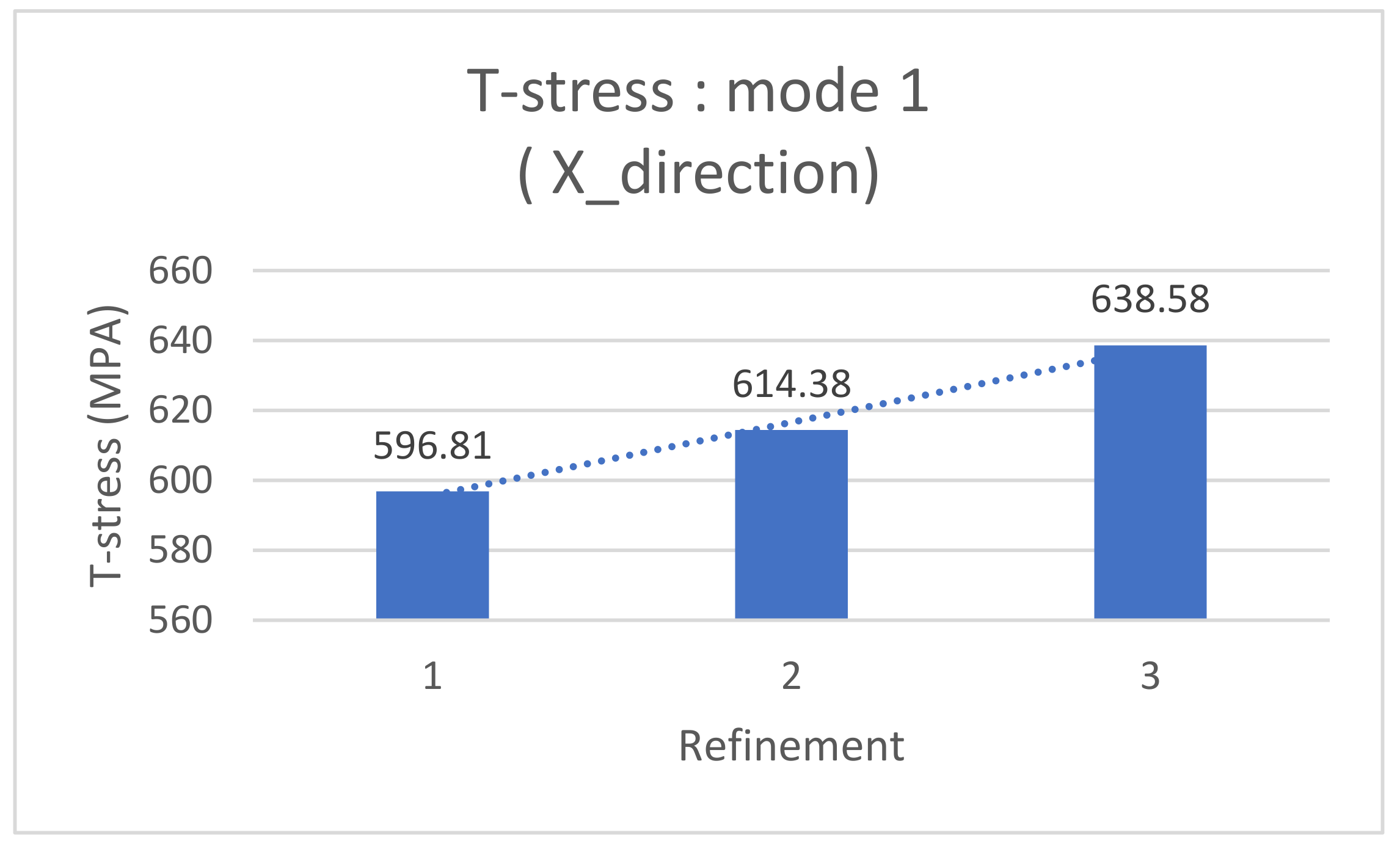
| Number of Refinement around Cracks | SIF in Mode 1 ) | T-Stress (MPa) |
|---|---|---|
| 1 | 10.62 | 596.81 |
| 2 | 8.84 | 614.38 |
| 3 | 7.814 | 638.58 |
| X-IGA Type of Refinement | h-Refinement |
|---|---|
| Maximum value of T-stress | 638.58 MPa |
| Numerical Approach | X-FEM | X-IGA |
|---|---|---|
| Maximum value | 0.0206 | 0.0209 |
| Numerical Approach | X-FEM | X-IGA |
|---|---|---|
| Maximum stress intensity factor | 7.814 × 105 Pa·m0.5. | 7.835 × 105 Pa·m0.5. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrada Gouzi, M.; El Khalfi, A.; Vlase, S.; Scutaru, M.L. X-IGA Used for Orthotropic Material Crack Growth. Materials 2024, 17, 3830. https://doi.org/10.3390/ma17153830
Berrada Gouzi M, El Khalfi A, Vlase S, Scutaru ML. X-IGA Used for Orthotropic Material Crack Growth. Materials. 2024; 17(15):3830. https://doi.org/10.3390/ma17153830
Chicago/Turabian StyleBerrada Gouzi, Mohammed, Ahmed El Khalfi, Sorin Vlase, and Maria Luminita Scutaru. 2024. "X-IGA Used for Orthotropic Material Crack Growth" Materials 17, no. 15: 3830. https://doi.org/10.3390/ma17153830
APA StyleBerrada Gouzi, M., El Khalfi, A., Vlase, S., & Scutaru, M. L. (2024). X-IGA Used for Orthotropic Material Crack Growth. Materials, 17(15), 3830. https://doi.org/10.3390/ma17153830









