Some Unfamiliar Structural Stability Aspects of Unsymmetric Laminated Composite Plates
Abstract
:1. Introduction
2. Finite Element Analysis: Set-Up and Solver
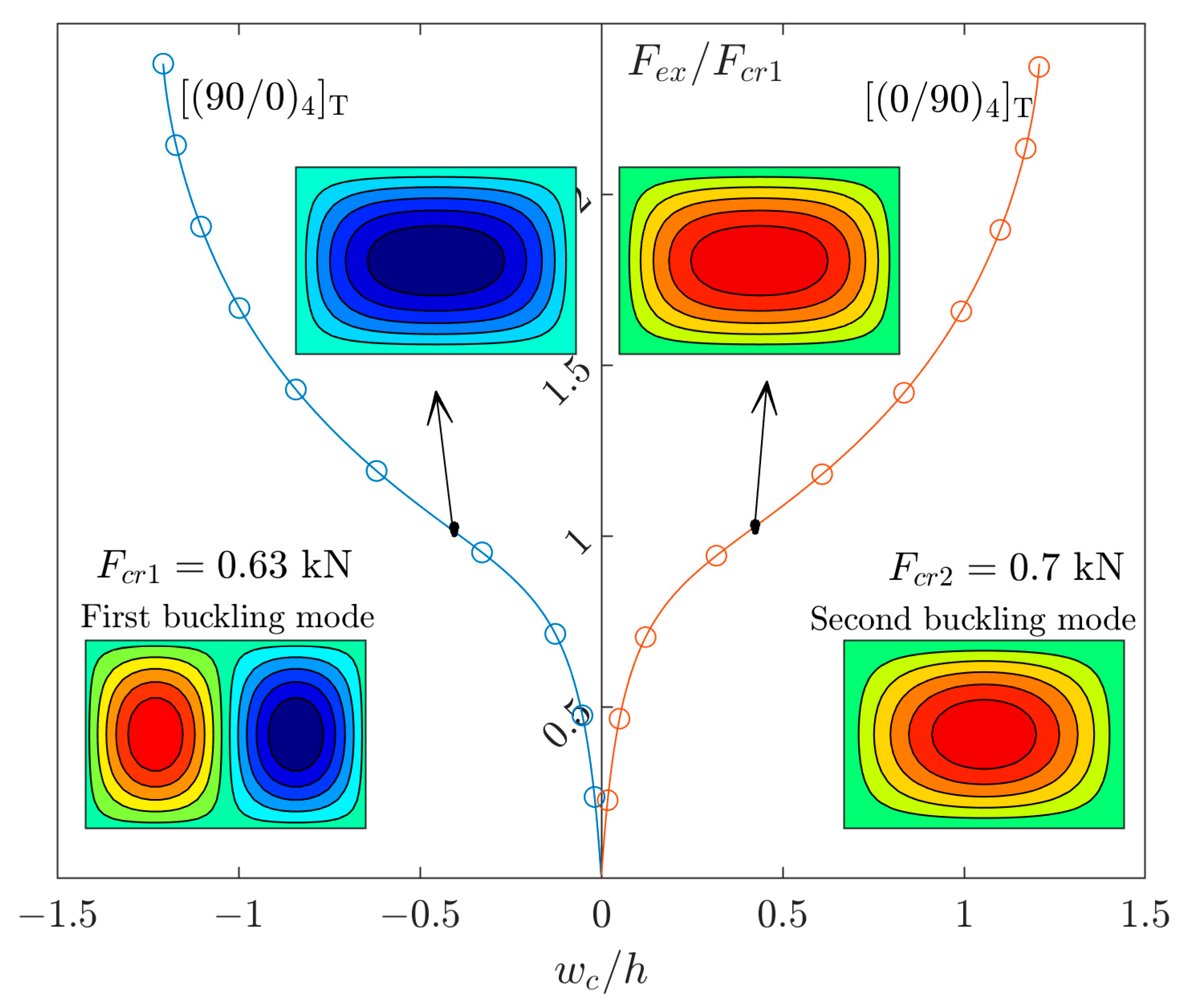
3. Unsymmetric Laminated Composite Plates with Simply Supported Edges
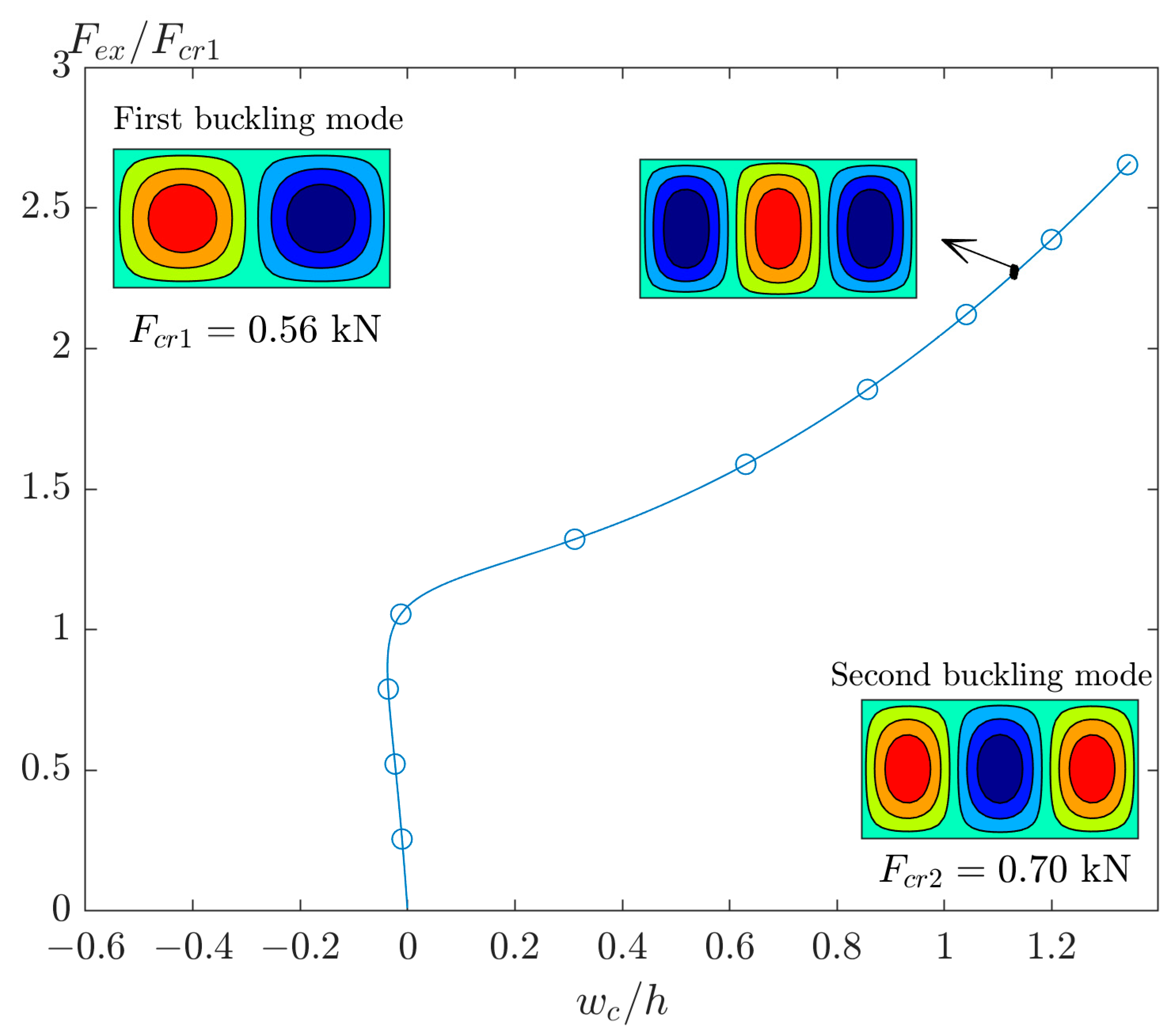
4. Different Modes in Buckling and Post-Buckling of Non-Square Plates
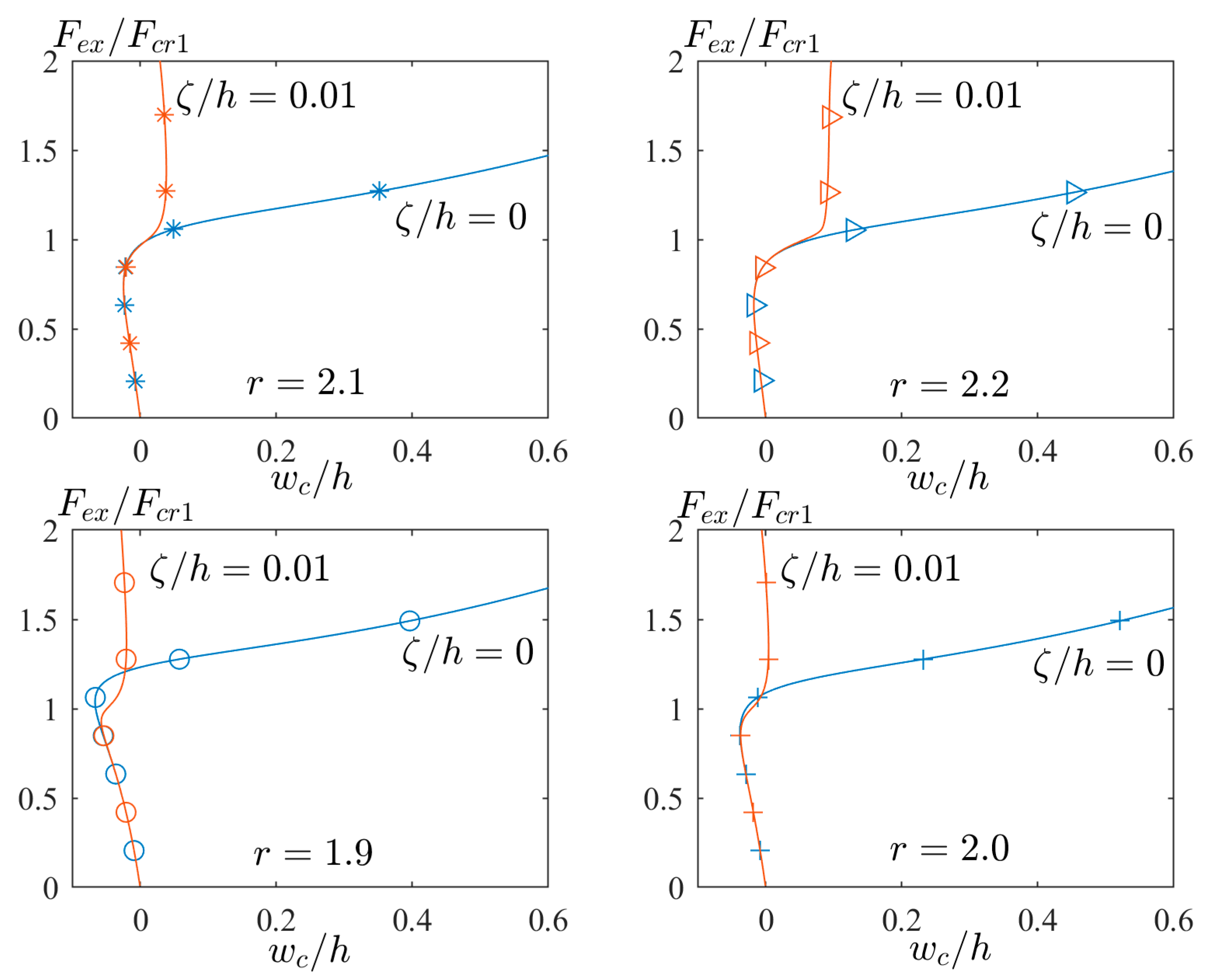
5. Existence of Tertiary Equilibrium Path
6. Conclusions
- (a)
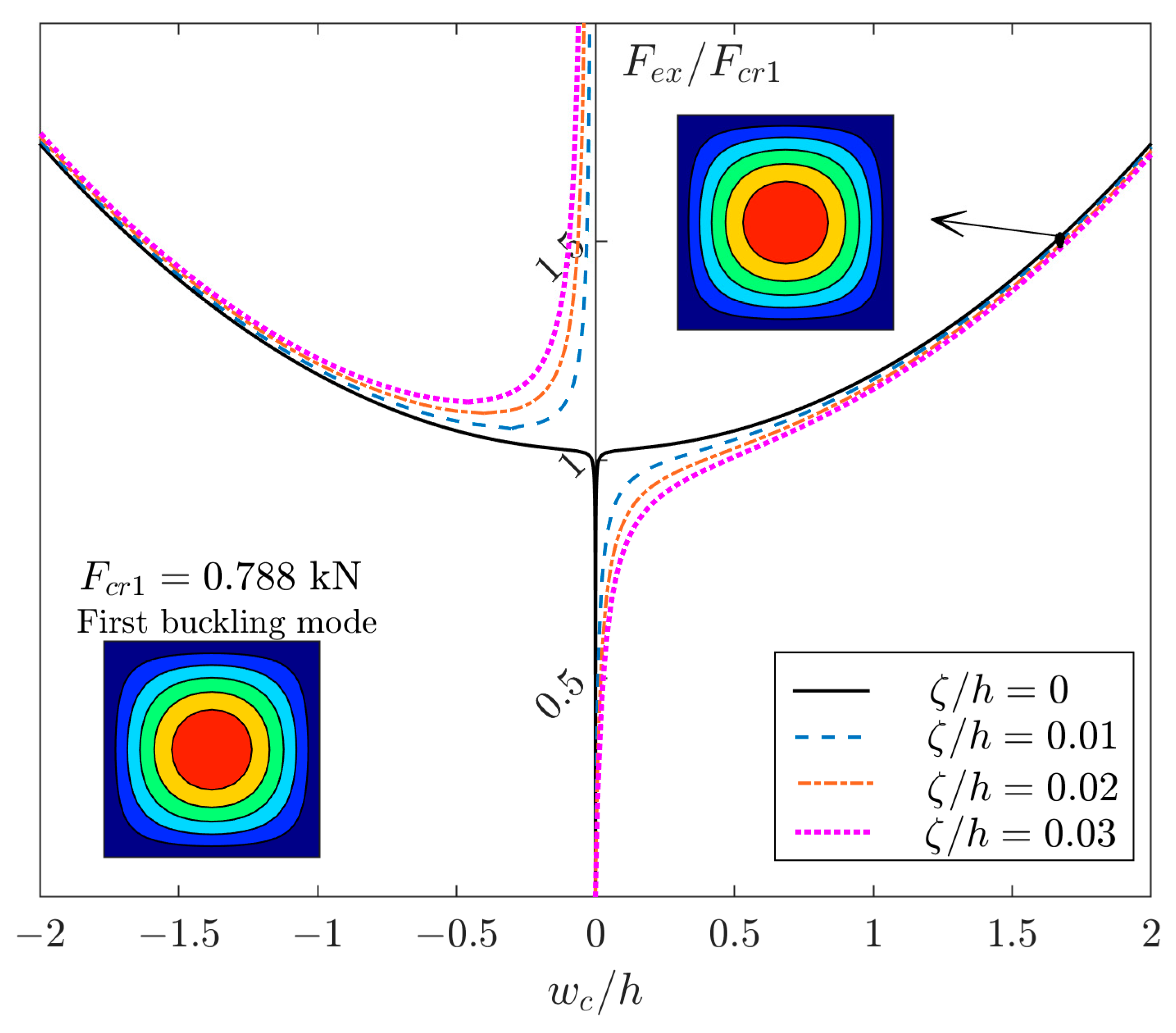
- Nonzero extension–bending coupling: These couplings, i.e., and , are present for some unsymmetric laminated composite plates. The plate with cross ply lamination, i.e., [0/90]n (n = 2, 4, 8, …), is one of the practical examples.
- (b)
- Simply supported boundary conditions: The edges should have no resistance against rotation. It is like a simple pin or free edge without any moment reactions. In the current results, a simple pin or so-called simply supported boundary conditions are investigated.
- (c)
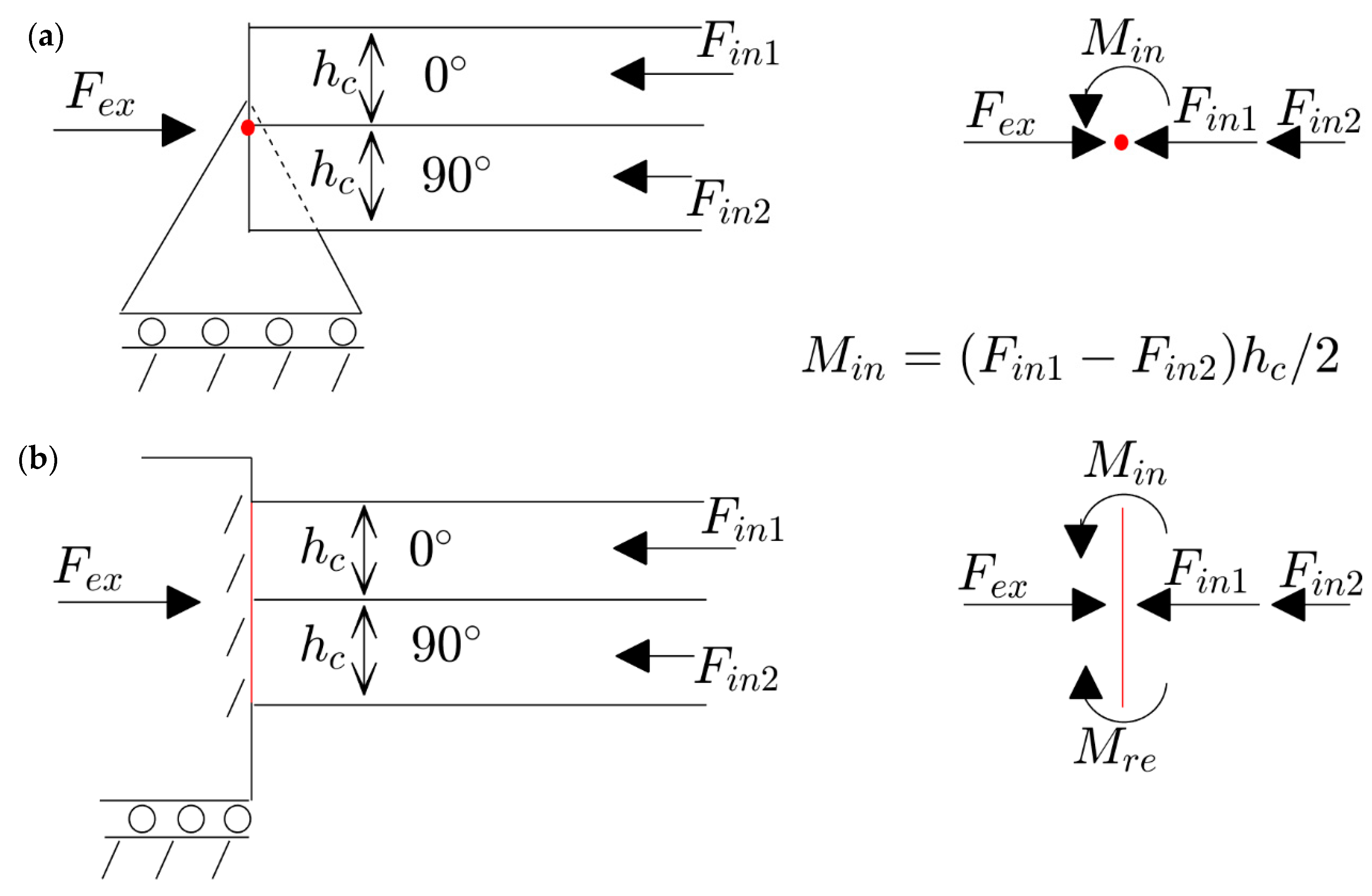
- No eccentricity of load and boundary conditions: The resultant of in-plane compressions (through the thickness) and locations of pins should coincide in the middle plane. One of the practical cases is the uniform distribution of compression with which the resultant will coincide in the middle plane.
- (d)
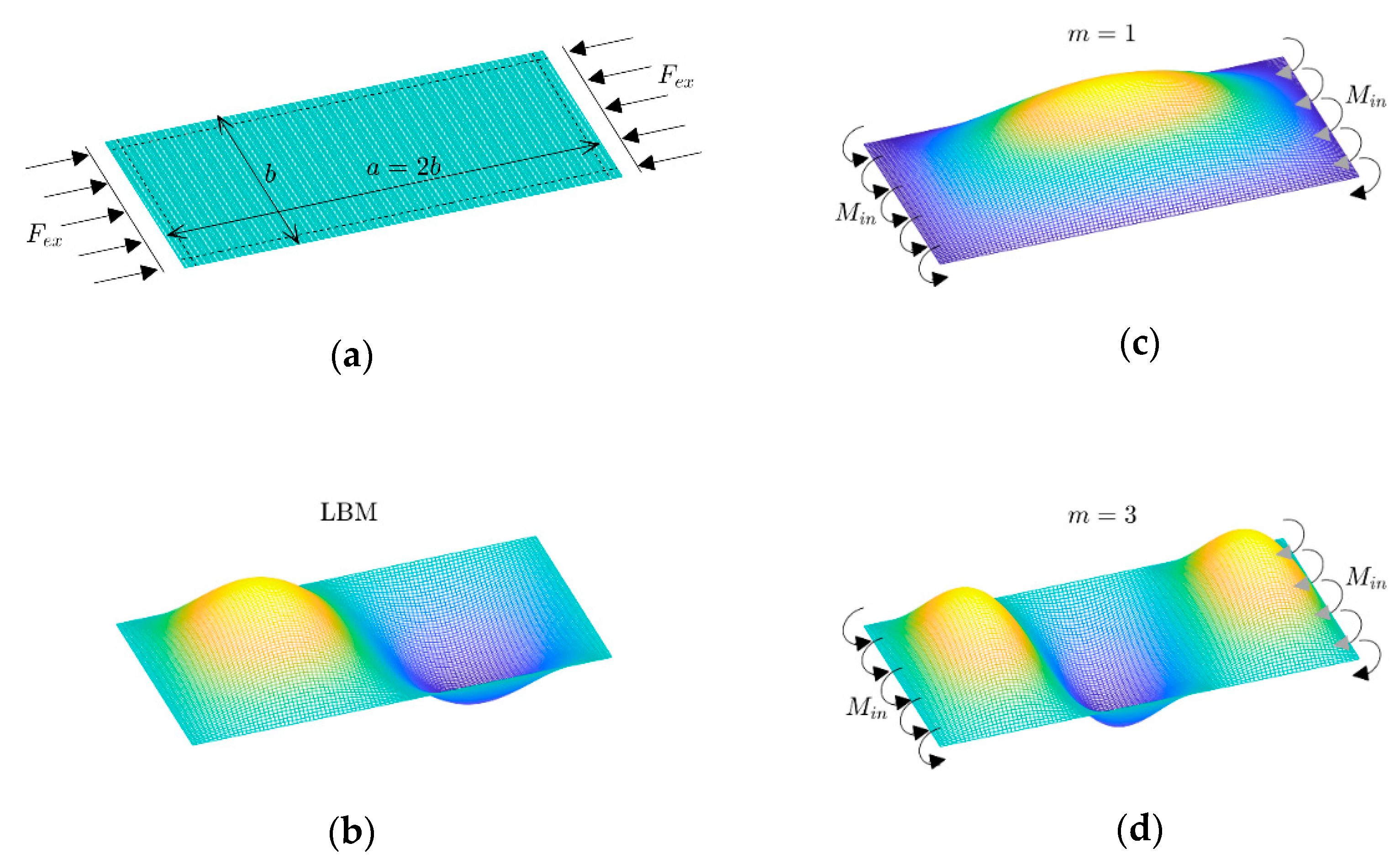
- Aspect ratio: The length of the plate should be larger than the width to have an even number of half-waves in the first linear buckling mode. For GFRP material and a layer arrangement of [(0/90)4], the aspect ratio should be higher than 1.4.
- (a)
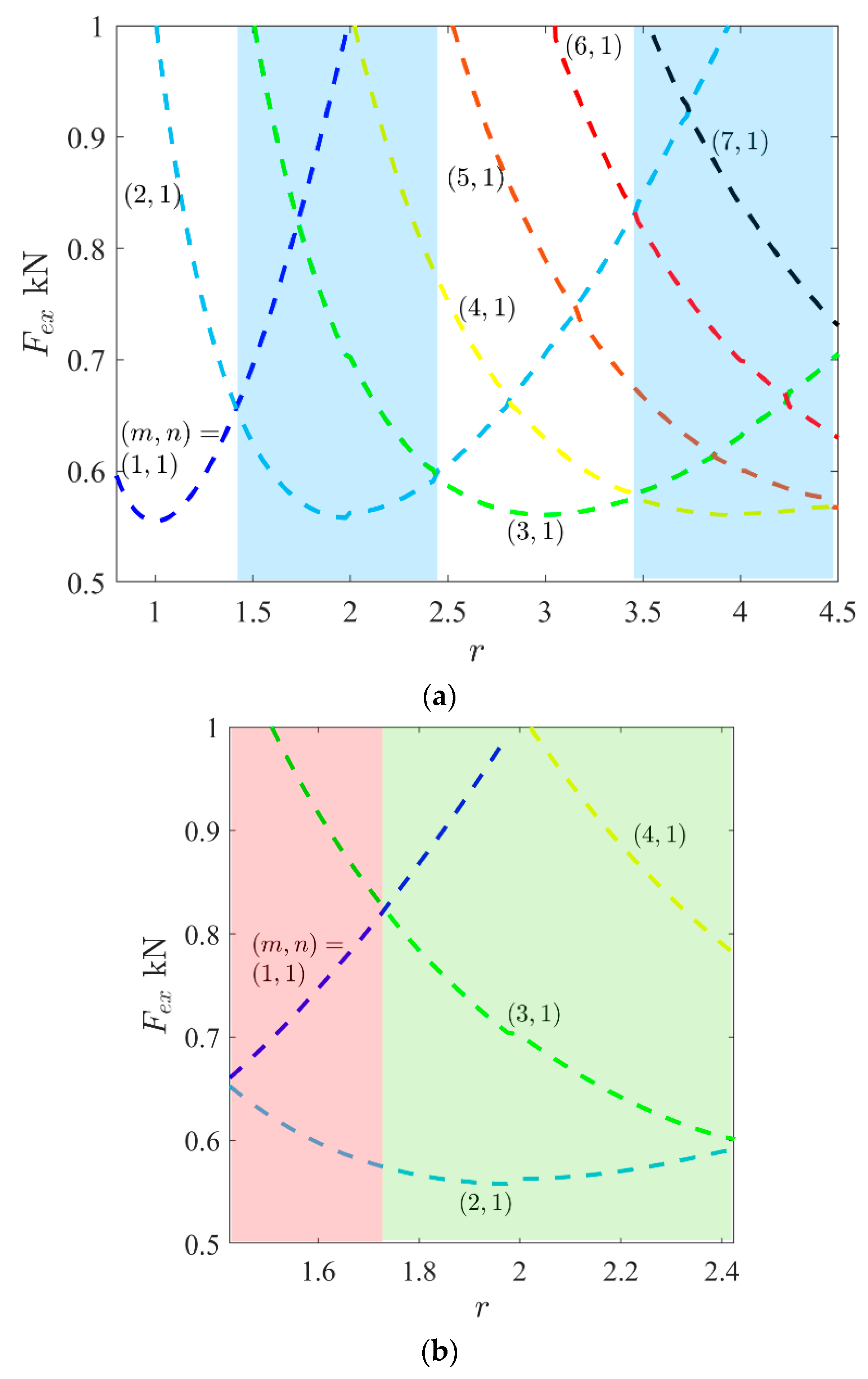
- Unstable second buckling mode: The number of half-waves in the second linear buckling mode should be higher than those in the first linear buckling mode. For example, a GFRP plate with [(0/90)4] and an aspect ratio of 2.1 has first and second buckling mode shapes as (2,1) and (3,1), respectively. So, such a plate has potential to have mode jumping in the post-buckling response.
- (b)
- Imperfection: An amplitude of the imperfection of the first buckling mode should be applied as an initial deflection of the plate. However, it should be a bit larger to overcome the effects of the extension–bending coupling.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kubiak, T.; Bohlooly Fotovat, M. Dynamic response and dynamic buckling of general laminated plates: A semi-inverse method. Compos. Struct. 2023, 324, 117548. [Google Scholar] [CrossRef]
- Cox, B.S.; Groh, R.M.J.; Avitabile, D.; Pirrera, A. Modal nudging in nonlinear elasticity: Tailoring the elastic post-buckling behaviour of engineering structures. J. Mech. Phys. Solids 2018, 116, 135–149. [Google Scholar] [CrossRef]
- Shen, J.; Pirrera, A.; Groh, R.M. Building blocks that govern spontaneous and programmed pattern formation in pre-compressed bilayers. Proc. R. Soc. A 2022, 478, 20220173. [Google Scholar] [CrossRef]
- Shen, J.; Garrad, M.; Zhang, Q.; Leao, O.; Pirrera, A.; Groh, R.M. Active reconfiguration of multistable metamaterials for linear locomotion. Phys. Rev. B 2023, 107, 214103. [Google Scholar] [CrossRef]
- Abramovich, H. Stability and Vibrations of Thin Walled Composite Structures; Woodhead Publishing: Thorston, UK, 2017. [Google Scholar]
- Wadee, M.A.; Hadjipantelis, N.; Bazzano, J.B.; Gardner, L.; Lozano-Galant, J.A. Stability of steel struts with externally anchored prestressed cables. J. Constr. Steel Res. 2020, 164, 105790. [Google Scholar] [CrossRef]
- Champneys, A.R.; Dodwell, T.J.; Groh, R.M.; Hunt, G.W.; Neville, R.M.; Pirrera, A.; Sakhaei, A.H.; Schenk, M.; Wadee, M.A. Happy catastrophe: Recent progress in analysis and exploitation of elastic instability. Front. Appl. Math. Stat. 2019, 5, 34. [Google Scholar] [CrossRef]
- Ungureanu, V.; Dubina, D.; Crisan, A.; Madeo, A.; Zagari, G.; Zucco, G.; Zinno, R. Koiter asymptotic analysis of thin-walled cold-formed steel members. Acta Mech. Et Autom. 2015, 9, 245–251. [Google Scholar] [CrossRef]
- Zhang, Y.; Murphy, K.D. Secondary buckling and tertiary states of a beam on a non-linear elastic foundation. Int. J. Non-Linear Mech. 2005, 40, 795–805. [Google Scholar] [CrossRef]
- Zhang, Y.; Murphy, K.D. Jumping instabilities in the post-buckling of a beam on a partial nonlinear foundation. Acta Mech. Solida Sin. 2013, 26, 500–513. [Google Scholar] [CrossRef]
- Kołakowski, Z. Static and dynamic interactive buckling of composite columns. J. Theor. Appl. Mech. 2009, 47, 177–192. [Google Scholar]
- Kolakowski, Z.; Jankowski, J. Interactive buckling of steel LC-beams under bending. Materials 2019, 12, 1440. [Google Scholar] [CrossRef] [PubMed]
- Becque, J.; Rasmussen, K.J. Experimental investigation of the interaction of local and overall buckling of stainless steel I-columns. J. Struct. Eng. 2009, 135, 1340–1348. [Google Scholar] [CrossRef]
- Wadee, M.A.; Gardner, L. Cellular buckling from mode interaction in I-beams under uniform bending. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 245–268. [Google Scholar] [CrossRef]
- Wadee, M.A.; Bai, L. Cellular buckling in I-section struts. Thin-Walled Struct. 2014, 81, 89–100. [Google Scholar] [CrossRef]
- Shen, J.; Wadee, M.A. Length effects on interactive buckling in thin-walled rectangular hollow section struts. Thin-Walled Struct. 2018, 128, 152–170. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Pirrera, A. On the role of localizations in buckling of axially compressed cylinders. Proc. R. Soc. A 2019, 475, 20190006. [Google Scholar] [CrossRef] [PubMed]
- Pirrera, A.; Avitabile, D.; Weaver, P.M. On the thermally induced bistability of composite cylindrical shells for morphing structures. Int. J. Solids Struct. 2012, 49, 685–700. [Google Scholar] [CrossRef]
- Coburn, B.H.; Pirrera, A.; Weaver, P.M.; Vidoli, S. Tristability of an orthotropic doubly curved shell. Compos. Struct. 2013, 96, 446–454. [Google Scholar] [CrossRef]
- Carrera, E.; Azzara, R.; Daneshkhah, E.; Pagani, A.; Wu, B. Buckling and post-buckling of anisotropic flat panels subjected to axial and shear in-plane loadings accounting for classical and refined structural and nonlinear theories. Int. J. Non-Linear Mech. 2021, 133, 103716. [Google Scholar] [CrossRef]
- Bohlooly Fotovat, M.; Kubiak, T. Non-bifurcation behavior of laminated composite plates under in-plane compression. Bull. Pol. Acad. Sci. Tech. Sci. 2024, 72, e148874. [Google Scholar] [CrossRef]
- Groh, R.M.; Avitabile, D.; Pirrera, A. Generalised path-following for well-behaved nonlinear structures. Comput. Methods Appl. Mech. Eng. 2018, 331, 394–426. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bohlooly Fotovat, M.; Kubiak, T.; Perlikowski, P. Mixed mode nonlinear response of rectangular plates under static and dynamic compression. Thin-Walled Struct. 2023, 184, 110542. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohlooly Fotovat, M. Some Unfamiliar Structural Stability Aspects of Unsymmetric Laminated Composite Plates. Materials 2024, 17, 3856. https://doi.org/10.3390/ma17153856
Bohlooly Fotovat M. Some Unfamiliar Structural Stability Aspects of Unsymmetric Laminated Composite Plates. Materials. 2024; 17(15):3856. https://doi.org/10.3390/ma17153856
Chicago/Turabian StyleBohlooly Fotovat, Mehdi. 2024. "Some Unfamiliar Structural Stability Aspects of Unsymmetric Laminated Composite Plates" Materials 17, no. 15: 3856. https://doi.org/10.3390/ma17153856
APA StyleBohlooly Fotovat, M. (2024). Some Unfamiliar Structural Stability Aspects of Unsymmetric Laminated Composite Plates. Materials, 17(15), 3856. https://doi.org/10.3390/ma17153856





