High Electron Mobility in Si-Doped Two-Dimensional β-Ga2O3 Tuned Using Biaxial Strain
Abstract
1. Introduction
2. Calculation Methods
2.1. Computational Details
2.2. Formation Energies and Carrier Mobility Calculations
3. Results and Discussion
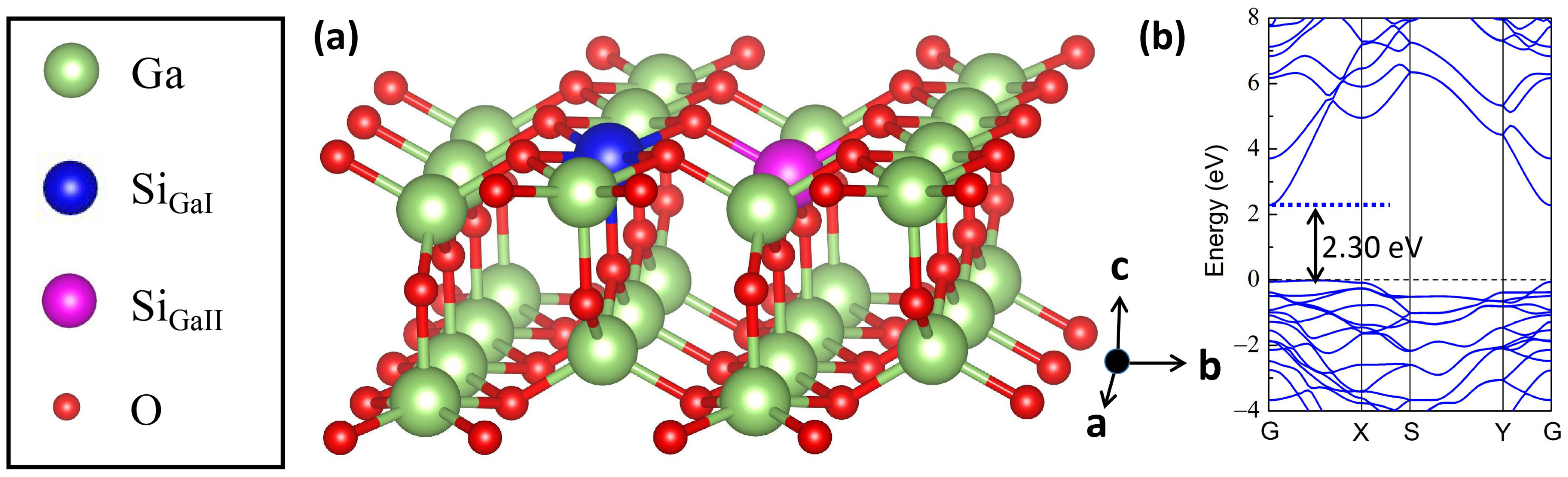
3.1. Structural Stability
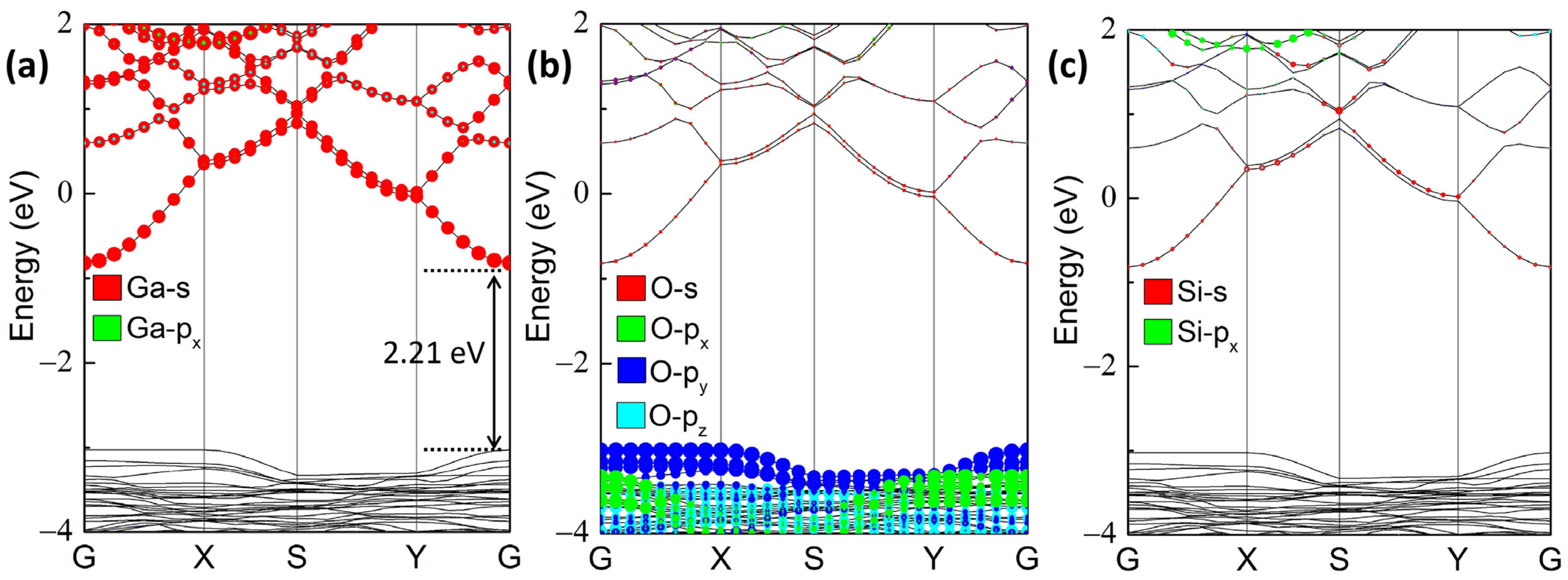
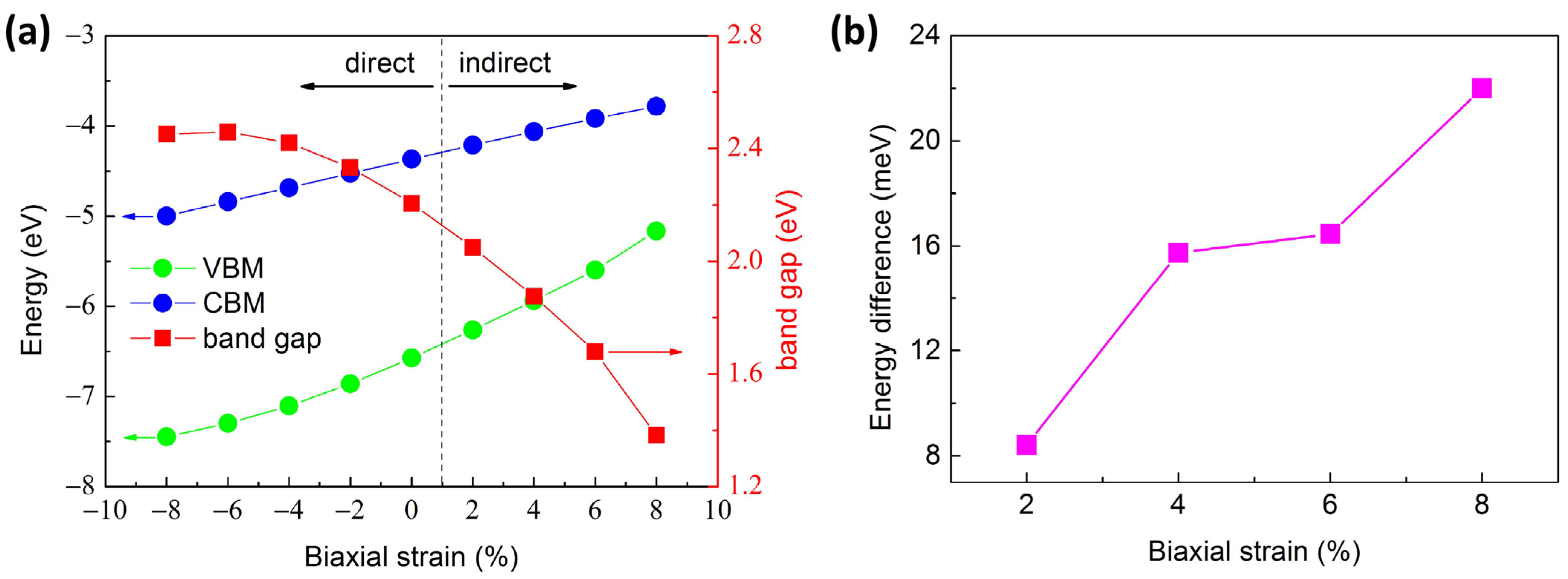
3.2. Strain-Engineered Band Structures
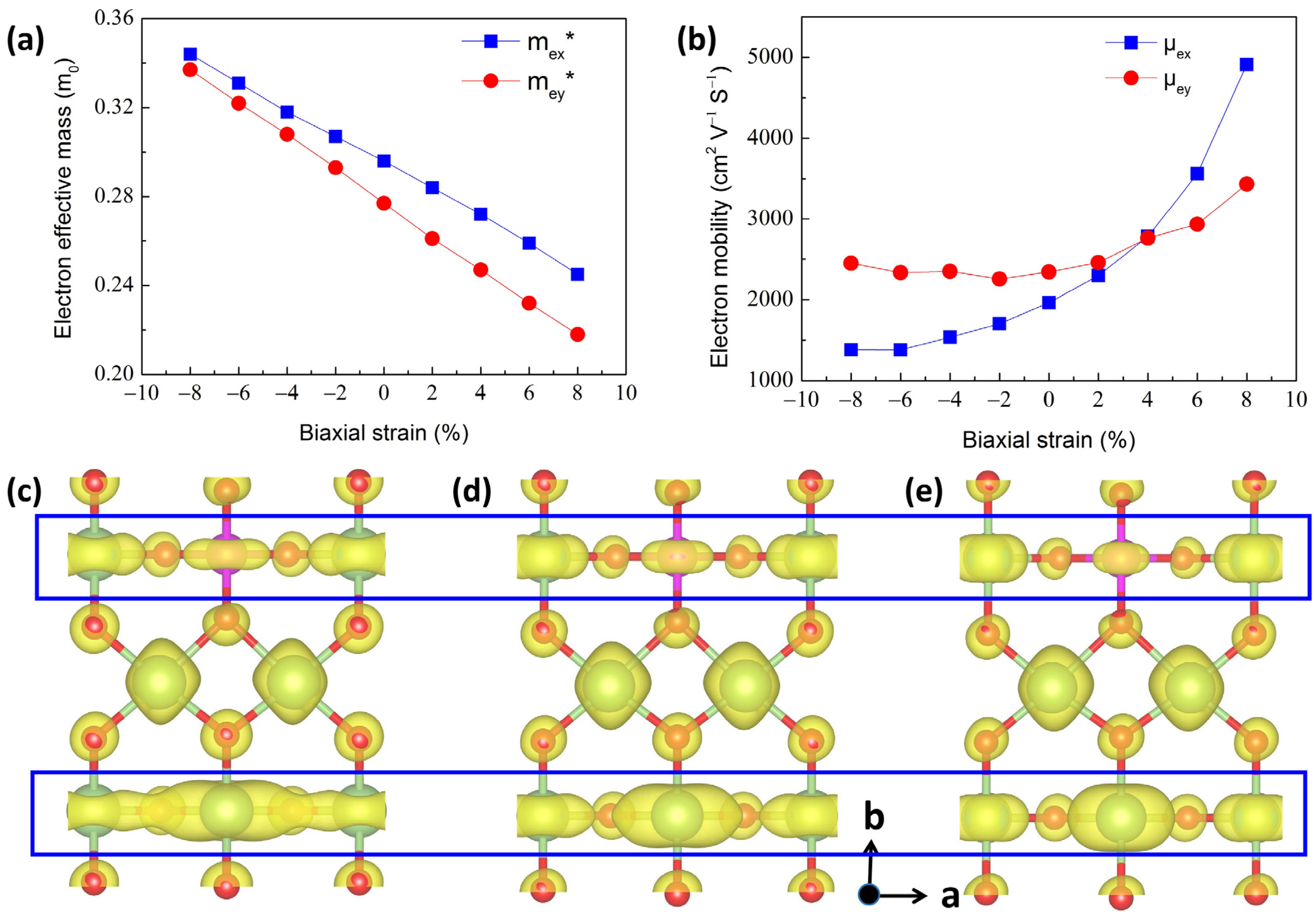
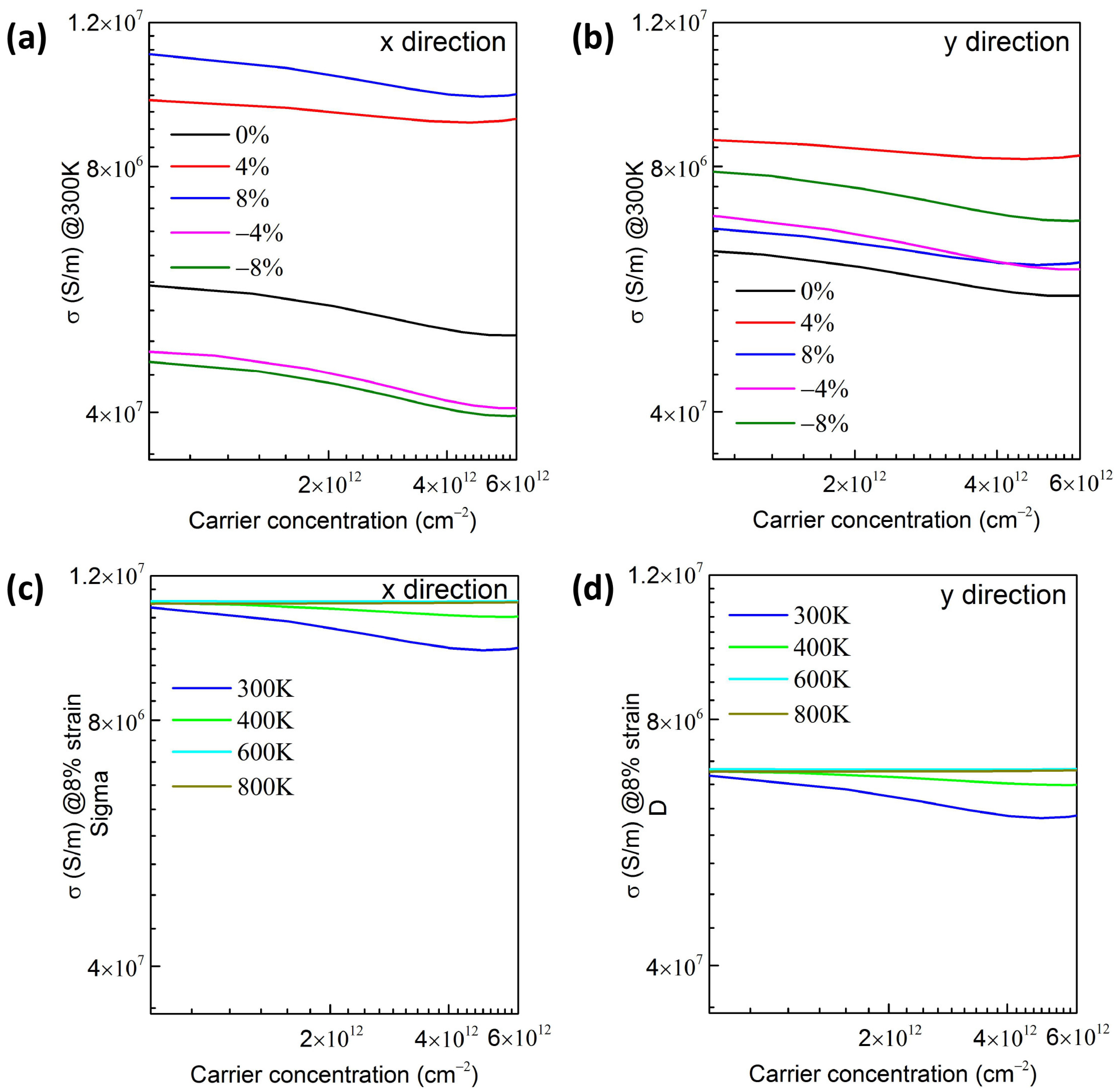
3.3. Strain-Engineered Transport Properties
3.4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jewel, M.U.; Hasan, S.; Crittenden, S.R.; Avrutin, V.; Özgür, Ü.; Morkoç, H.; Ahmad, I. Phase Stabilized MOCVD Growth of β-Ga2O3 Using SiOx on c-Plane Sapphire and AlN/Sapphire Template. Phys. Status Solidi A 2023, 220, 2300036. [Google Scholar] [CrossRef]
- Egyenes-Pörsök, F.; Gucmann, F.; Hušeková, K.; Dobročka, E.; Sobota, M.; Mikolášek, M.; Fröhlich, K.; Ťapajna, M. Growth of α- and β-Ga2O3 epitaxial layers on sapphire substrates using liquid-injection MOCVD. Semicond. Sci. Technol. 2020, 35, 115002. [Google Scholar] [CrossRef]
- Tarntair, F.-G.; Huang, C.-Y.; Rana, S.; Lin, K.-L.; Hsu, S.-H.; Kao, Y.-C.; Pratap, S.J.; Chen, Y.-C.; Tumilty, N.; Liu, P.-L.; et al. Material Properties of n-Type β-Ga2O3 Epilayers with In Situ Doping Grown on Sapphire by Metalorganic Chemical Vapor Deposition. Adv. Electron. Mater. 2023, 2300679. [Google Scholar] [CrossRef]
- Simon, J.; Protasenko, V.; Lian, C.; Xing, H.; Jena, D. Polarization-Induced Hole Doping in Wide-Band-Gap Uniaxial Semiconductor Heterostructures. Science 2010, 327, 60–64. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Ma, C.; Wu, M. Exploring the effective P-type dopants in two-dimensional Ga2O3 by first-principles calculations. AIP Adv. 2024, 14, 055221. [Google Scholar] [CrossRef]
- Werner, P.; Casula, M.; Miyake, T.; Aryasetiawan, F.; Millis, A.J.; Biermann, S. Satellites and large doping and temperature dependence of electronic properties in hole-doped BaFe2As2. Nat. Phys. 2012, 8, 331–337. [Google Scholar] [CrossRef]
- Bhuiyan, A.; Meng, L.; Huang, H.-L.; Hwang, J.; Zhao, H. In situ MOCVD growth and band offsets of Al2O3 dielectric on β-Ga2O3 and β-(AlxGa1−x)2O3 thin films. J. Appl. Phys. 2022, 132, 165301. [Google Scholar] [CrossRef]
- Bhuiyan, A.; Meng, L.; Huang, H.-L.; Sarker, J.; Chae, C.; Mazumder, B.; Hwang, J.; Zhao, H. Metalorganic chemical vapor deposition of β-(AlxGa1−x)2O3 thin films on (001) β-Ga2O3 substrates. APL Mater. 2023, 11, 041112. [Google Scholar] [CrossRef]
- Víllora, E.G.; Shimamura, K.; Yoshikawa, Y.; Ujiie, T.; Aoki, K. Electrical conductivity and carrier concentration control in Ga2O3 by Si doping. Appl. Phys. Lett. 2008, 92, 202120. [Google Scholar] [CrossRef]
- Baldini, M.; Albrecht, M.; Fiedler, A.; Irmscher, K.; Schewski, R.; Wagner, G. Si- and Sn-Doped Homoepitaxial β-Ga2O3 Layers Grown by MOVPE on (010)-Oriented Substrates. ECS J. Solid State Sci. Technol. 2017, 6, Q3040. [Google Scholar] [CrossRef]
- Hernandez, A.; Islam, M.M.; Saddatkia, P.; Codding, C.; Dulal, P.; Agarwal, S.; Janover, A.; Novak, S.; Huang, M.; Dang, T.; et al. A MOCVD growth and characterization of conductive homoepitaxial Si-doped Ga2O3. Results Phys. 2021, 25, 104167. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Peterson, C.; Itoh, T.; Roy, S.; Cooke, J.; Rebollo, S.; Ranga, P.; Sensale-Rodriguez, B.; Krishnamoorthy, S. Enhancing the electron mobility in Si-doped (010) β-Ga2O3 films with low-temperature buffer layers. APL Mater. 2023, 11, 021110. [Google Scholar] [CrossRef]
- Zhang, F.; Saito, K.; Tanaka, T.; Nishio, M.; Guo, Q. Electrical properties of Si doped Ga2O3 films grown by pulsed laser deposition. J. Mater. Sci. Mater. Electron. 2015, 26, 9624–9629. [Google Scholar] [CrossRef]
- Khartsev, S.; Nordell, N.; Hammar, M.; Purans, J.; Hallén, A. High-Quality Si-Doped β-Ga2O3 Films on Sapphire Fabricated by Pulsed Laser Deposition. Phys. Status Solidi B 2021, 258, 2000362. [Google Scholar] [CrossRef]
- Wong, M.H.; Sasaki, K.; Kuramata, A.; Yamakoshi, S.; Higashiwaki, M. Electron channel mobility in silicon-doped Ga2O3 MOSFETs with a resistive buffer layer. Jpn. J. Appl. Phys. 2016, 55, 1202B9. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, C.; Liu, Y. Why Two-Dimensional semiconductors generally have low electron mobility. Phys. Rev. Lett. 2020, 125, 177701. [Google Scholar] [CrossRef]
- Jindal, A.; Saha, A.; Li, Z.; Taniguchi, T.; Watanabe, K.; Hone, J.C.; Birol, T.; Fernandes, R.M.; Dean, C.R.; Pasupathy, A.N.; et al. Coupled ferroelectricity and superconductivity in bilayer Td-MoTe2. Nature 2023, 613, 48. [Google Scholar] [CrossRef] [PubMed]
- Mitra, A.; Corticelli, A.; Ribeiro, P.; McClarty, P.A. Magnon Interference tunneling spectroscopy as a probe of 2D magnetism. Phys. Rev. Lett. 2023, 130, 066701. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Pazos, S.; Aguirre, F.; Shen, Y.; Yuan, Y.; Zheng, W.; Alharbi, O.; Villena, M.A.; Fang, B.; Li, X.; et al. Hybrid 2D–CMOS microchips for memristive applications. Nature 2023, 618, 57. [Google Scholar] [CrossRef]
- Xu, X.; Pan, Y.; Liu, S.; Han, B.; Gu, P.; Li, S.; Xu, W.; Peng, Y.; Han, Z.; Chen, J.; et al. Seeded 2D epitaxy of large-area single-crystal films of the van der Waals semiconductor 2H MoTe2. Science 2021, 372, 195–200. [Google Scholar] [CrossRef]
- Azmi, R.; Ugur, E.; Seitkhan, A.; Aljamaan, F.; Subbiah, A.S.; Liu, J.; Harrison, G.T.; Nugraha, M.I.; Eswaran, M.K.; Babics, M.; et al. Damp heat–stable perovskite solar cells with tailored-dimensionality 2D/3D heterojunctions. Science 2022, 376, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Sidhik, S.; Wang, Y.; De Siena, M.; Asadpour, R.; Torma, A.J.; Terlier, T.; Ho, K.; Li, W.; Puthirath, A.B.; Shuai, X.; et al. Deterministic fabrication of 3D/2D perovskite bilayer stacks for durable and efficient solar cells. Science 2022, 377, 1425–1430. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.S.; Verma, A.; Peelaers, H.; Protasenko, V.; Rouvimov, S.; Xing, H.; Seabaugh, A.; Haensch, W.; de Walle, C.V.; Galazka, Z.; et al. High-voltage field effect transistors with wide-bandgap β-Ga2O3 nanomembranes. Appl. Phys. Lett. 2014, 104, 203111. [Google Scholar] [CrossRef]
- Kwon, Y.; Lee, G.; Oh, S.; Kim, J.; Pearton, S.J.; Ren, F. Tuning the thickness of exfoliated quasi-two-dimensional β-Ga2O3 flakes by plasma etching. Appl. Phys. Lett. 2017, 110, 131901. [Google Scholar] [CrossRef]
- Su, J.; Guo, R.; Lin, Z.; Zhang, S.; Zhang, J.; Chang, J.; Hao, Y. Unusual Electronic and Optical Properties of Two-Dimensional Ga2O3 Predicted by Density Functional Theory. J. Phys. Chem. C 2018, 122, 24592–24599. [Google Scholar] [CrossRef]
- Peng, L.; Hu, L.; Fang, X. Low-dimensional nanostructure ultraviolet photodetectors. Adv. Mater. 2013, 25, 5321–5328. [Google Scholar] [CrossRef] [PubMed]
- Zou, R.; Zhang, Z.; Liu, Q.; Hu, J.; Sang, L.; Liao, M.; Zhang, W. High detectivity solar-blind high-temperature deep-ultraviolet photodetector based on multi-layered (l00) facet-oriented β-Ga2O3 nanobelts. Small 2014, 10, 1848–1856. [Google Scholar] [CrossRef]
- Oh, S.; Kim, J.; Ren, F.; Pearton, S.J.; Kim, J. Quasi-two-dimensional β-gallium oxide solar-blind photodetectors with ultrahigh responsivity. J. Mater. Chem. C 2016, 4, 9245–9250. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, K.; Li, R.; Jia, Y.; Lu, Q.; Wang, S.; Chen, H.; Ma, F. Doping induced indirect-to-direct bandgap transition of two-dimensional Ga2O3. Appl. Surf. Sci. 2021, 553, 149458. [Google Scholar] [CrossRef]
- Guo, R.; Su, J.; Lin, Z.; Zhang, J.; Qin, Y.; Zhang, J.; Chang, J.; Hao, Y. Understanding the potential of 2D Ga2O3 in flexible optoelectronic devices: Impact of uniaxial strain and electric field. Adv. Theory Simul. 2019, 2, 1900106. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 169–186. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Anam, B.; Gaston, N. Structural, Thermal, and Electronic Properties of Two-Dimensional Gallium Oxide (β-Ga2O3) from First-Principles Design. ChemPhysChem 2021, 22, 2362–2370. [Google Scholar] [CrossRef]
- Yu, M.; Peng, B.; Sun, K.; Yu, J.; Yuan, L.; Hu, J.; Zhang, Y.; Jia, R. First principles investigation of photoelectric properties of Ga2O3 Doped with group IV elements (Si, Ge, Sn). Mater. Today Commun. 2023, 34, 105127. [Google Scholar] [CrossRef]
- Dong, L.; Yu, J.; Zhang, Y.; Jia, R. Elements (Si, Sn, and Mg) doped α-Ga2O3: First-principles investigations and predictions. Comp. Mater. Sci. 2019, 156, 273–279. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comp. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]
- Zeng, H.; Wu, M.; Ma, C.; Fu, X.; Gao, H. Tunable electronic, transport, and optical properties of fluorine- and hydrogen-passivated two-dimensional Ga2O3 by uniaxial strain. J. Phys. D Appl. Phys. 2024, 57, 315105. [Google Scholar] [CrossRef]
- Dong, L.; Jia, R.; Li, C.; Xin, B.; Zhang, Y. Ab initio study of N-doped β-Ga2O3 with intrinsic defects: The structural, electronic and optical properties. J. Alloys Compd. 2017, 712, 379–385. [Google Scholar] [CrossRef]
- Dong, L.; Zhou, S.; Gong, L.; Wang, W.; Zhang, L.; Yang, C.; Yu, J.; Liu, W. Modulation in structural and electronic properties of 2D Ga2O3 by chemical passivation. J. Mater. Chem. C 2020, 8, 12551–12559. [Google Scholar] [CrossRef]
- Su, J.; Zhang, J.; Guo, R.; Lin, Z.; Liu, M.; Zhang, J.; Chang, J.; Hao, Y. Mechanical and thermodynamic properties of two-dimensional monoclinic Ga2O3. Mater. Des. 2019, 184, 108197. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, C.; Zhang, Y.; Qi, C.; Li, H.; Wang, T.; Ma, G.; Liu, Y.; Dong, S.; Huo, M. Modulation of electronic and optical properties by surface vacancies in low-dimensional β-Ga2O3. Phys. Chem. Chem. Phys. 2019, 21, 14745–14752. [Google Scholar] [CrossRef]
- Sasaki, K.; Kuramata, A.; Masui, T.; Víllora, E.G.; Shimamura, K.; Yamakoshi, S. Device-Quality β-Ga2O3 Epitaxial Films Fabricated by Ozone Molecular Beam Epitaxy. Appl. Phys. Express 2012, 5, 035502. [Google Scholar] [CrossRef]
- Alema, F.; Hertog, B.; Osinsky, A.; Mukhopadhyay, P.; Toporkov, M.; Schoenfeld, W.V. Fast growth rate of epitaxial β–Ga2O3 by close coupled showerhead MOCVD. J. Cryst. Growth 2017, 475, 77–82. [Google Scholar] [CrossRef]
- Li, Y.; Yang, S.; Li, J. Modulation of the Electronic Properties of Ultrathin Black Phosphorus by Strain and Electrical Field. J. Phys. Chem. C 2014, 118, 23970–23976. [Google Scholar] [CrossRef]
- Peelaers, H.; Van de Walle, C. Lack of quantum confinement in Ga2O3 nanolayers. Phys. Rev. B 2017, 96, 081409(R). [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, Z.; Gao, Z.; Qian, Q.; Hua, M. Tunable properties of novel Ga2O3 monolayer for electronic and optoelectronic applications. ACS Appl. Mater. Interfaces 2020, 12, 30659–30669. [Google Scholar] [CrossRef]
- Luan, S.; Dong, L.; Jia, R. Analysis of the structural, anisotropic elastic and electronic properties of β-Ga2O3 with various pressures. J. Cryst. Growth 2019, 505, 74–81. [Google Scholar] [CrossRef]
- Furthmüller, J.; Bechstedt, F. Quasiparticle bands and spectra of Ga2O3 polymorphs. Phys. Rev. B 2016, 93, 115204. [Google Scholar] [CrossRef]
- Adachi, K.; Ogi, H.; Takeuchi, N.; Nakamura, N.; Watanabe, H.; Ito, T.; Ozaki, Y. Unusual elasticity of monoclinic β-Ga2O3. J. Appl. Phys. 2018, 124, 085102. [Google Scholar] [CrossRef]
- Guo, R.; Su, J.; Yuan, H.; Zhang, P.; Lin, Z.; Zhang, J.; Chang, J.; Hao, Y. Surface functionalization modulates the structural and optoelectronic properties of two-dimensional Ga2O3. Mater. Today Phys. 2020, 12, 100192. [Google Scholar] [CrossRef]
- Li, X.; Zuo, X.; Li, H.; Han, L.; Gao, Q.; Li, D.; Cui, B.; Liu, D.; Qu, F. Exotic magnetism in As-doped α/β-In2Se3 monolayers with tunable anisotropic carrier mobility. Phys. Chem. Chem. Phys. 2019, 21, 19234–19241. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Zhang, G.; Zhang, Y.-W. Polarity-reversed robust carrier mobility in monolayer MoS2 nanoribbons. J. Am. Chem. Soc. 2014, 136, 6269–6275. [Google Scholar] [CrossRef]
- Tong, L.; He, J.; Yang, M.; Chen, Z.; Zhang, J.; Lu, Y.; Zhao, Z. Anisotropic carrier mobility in buckled two-dimensional GaN. Phys. Chem. Chem. Phys. 2017, 19, 23492–23496. [Google Scholar] [CrossRef]
- Ng, T.K.; Holguin-Lerma, J.; Kang, C.H.; Ashry, I.; Zhang, H.; Bucci, G.; Ooi, B. Group-III-nitride and halide-perovskite semiconductor gain media for amplified spontaneous emission and lasing applications. J. Phys. D Appl. Phys. 2021, 54, 143001. [Google Scholar] [CrossRef]
- Wang, N.; Li, M.; Xiao, H.; Gong, H.; Liu, Z.; Zu, X.; Qiao, L. Optimizing the thermoelectric transport properties of Bi2O2Se monolayer via biaxial strain. Phys. Chem. Chem. Phys. 2019, 21, 15097–15105. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.; Ma, C.; Wu, M. High Electron Mobility in Si-Doped Two-Dimensional β-Ga2O3 Tuned Using Biaxial Strain. Materials 2024, 17, 4008. https://doi.org/10.3390/ma17164008
Zeng H, Ma C, Wu M. High Electron Mobility in Si-Doped Two-Dimensional β-Ga2O3 Tuned Using Biaxial Strain. Materials. 2024; 17(16):4008. https://doi.org/10.3390/ma17164008
Chicago/Turabian StyleZeng, Hui, Chao Ma, and Meng Wu. 2024. "High Electron Mobility in Si-Doped Two-Dimensional β-Ga2O3 Tuned Using Biaxial Strain" Materials 17, no. 16: 4008. https://doi.org/10.3390/ma17164008
APA StyleZeng, H., Ma, C., & Wu, M. (2024). High Electron Mobility in Si-Doped Two-Dimensional β-Ga2O3 Tuned Using Biaxial Strain. Materials, 17(16), 4008. https://doi.org/10.3390/ma17164008





