Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Microstructural Characterization
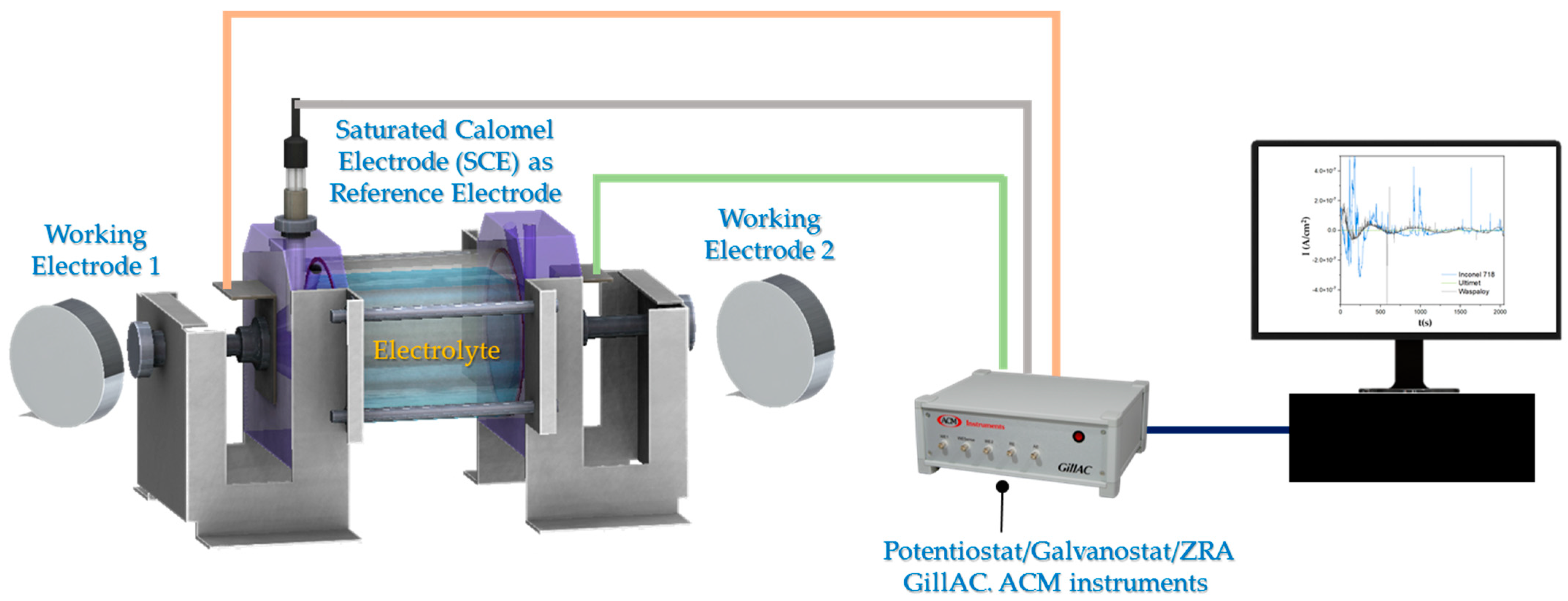
2.3. Electrochemical Testing
3. Results and Discussion
3.1. Electrochemical Noise (EN)
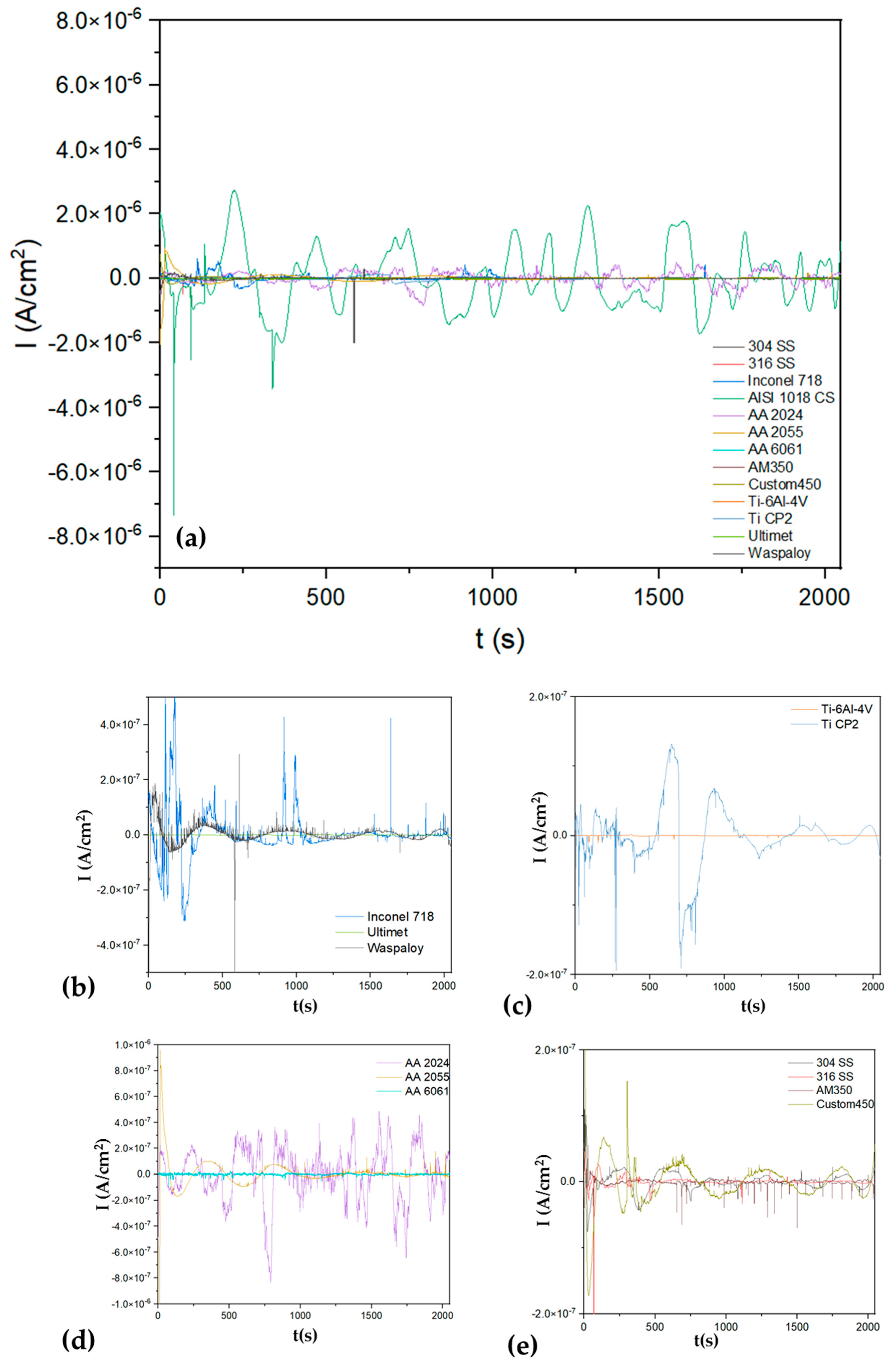
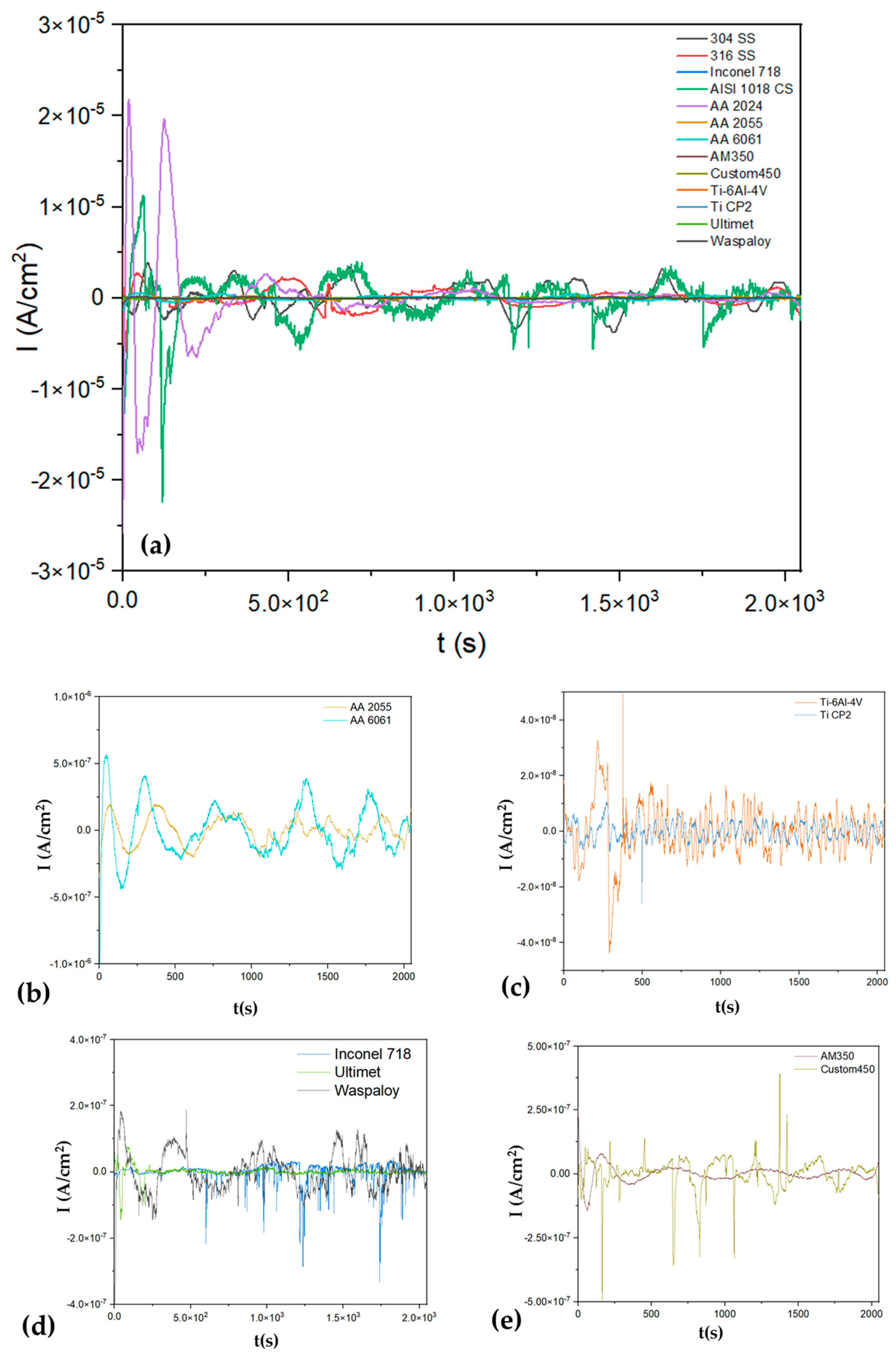
3.1.1. Time-Domain Analysis
3.1.2. Frequency-Domain Analysis
Power Spectral Density and Noise Impedance (Zn)
3.1.3. Time-Frequency Domain Analysis
Wavelets Analysis
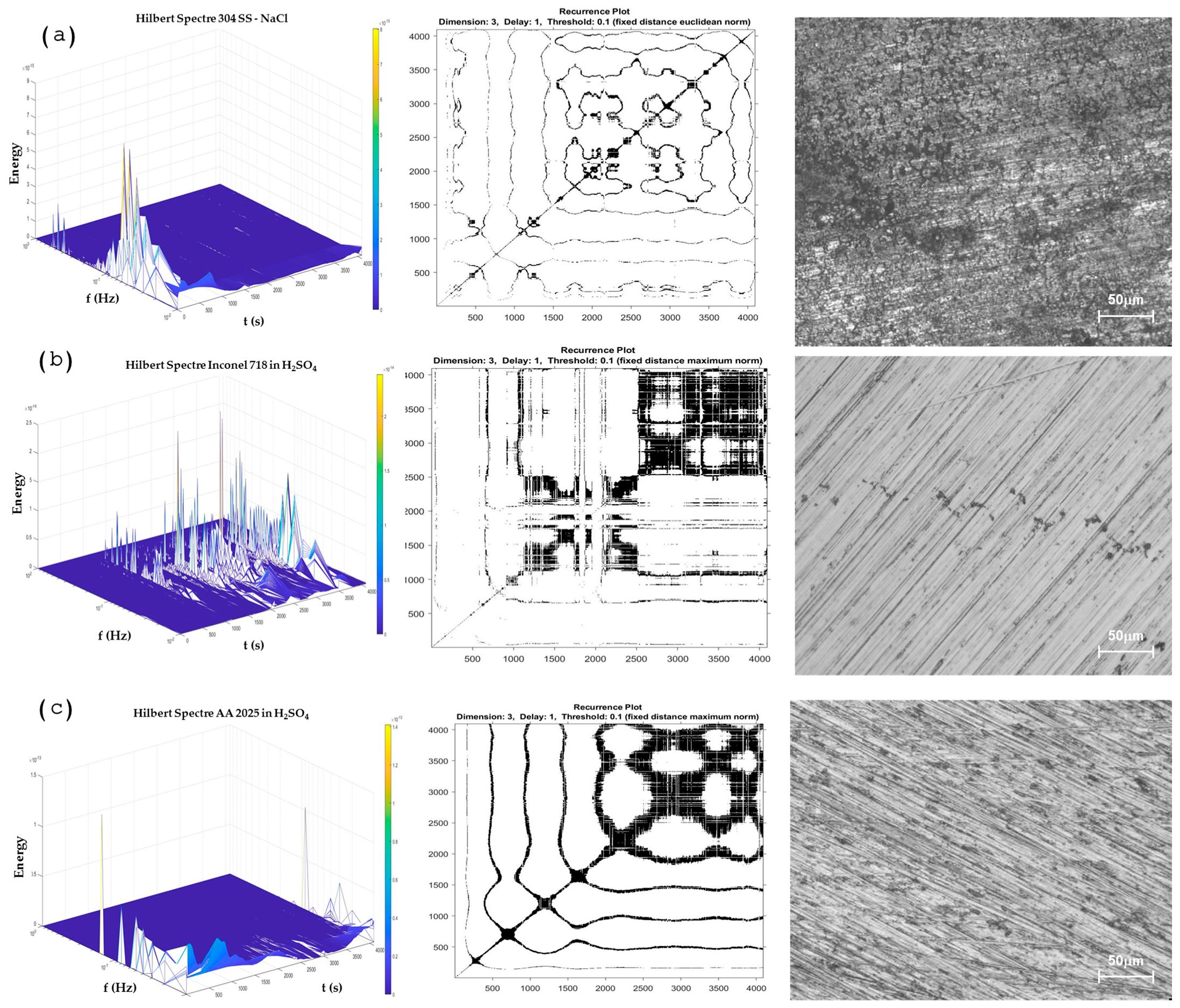
Hilbert–Huang Transform Analysis and Recurrence Plots
4. Discussion
5. Conclusions
- This study concludes that statistical and slope (PSD) analysis present limitations in determining the corrosion type and some corrosion processes. This can be attributed to the complexity of the EN signal. It is the divergences that determine the type of corrosion that occurs in alloys.
- Statistical analysis presented limitations in all the analyses; localization index, kurtosis, and skewness showed different results in all the analyses. Some authors attribute this to the presence of different corrosion processes in the system; however, it can be confusing and speculative. For that reason, it is important to use a different method to determine the corrosion process in a material.
- The analysis of wavelets presented better results in determining corrosion type compared with statistical and PSD (slope) methods; however, the limitation of analyzing different types of signals limits this method.
- The analysis by HHT and RP presented the best results for determining the corrosion process and type. This is because methods present several advantages to analyzing chaotic signals. Hence, HHT and RP are recommended for analyzing EN signals more than statistical, wavelet, or slope methods. That is because of the nature of the corrosion signal; it is a complex signal, and the EN should be analyzed with the correct tools. The results converged with the results presented by the different authors mentioned in the discussion.
- It is important to complement the results of determinism and RR with the RPs as a visual reference. This is due to the results of DET and RR when a passive and a pitting system are presented. The pitting process presents DET values from 0.5 to 0.8 as well as a passivation system, but the graphic system is different. In passivation, a dot system is present, while in the pitting system, there are horizontal and vertical lines.
- In the HHT and RPs methods, the transition of corrosion processes as the break and regeneration of the passive layer, as well as the pitting generation of the predominance of a uniform process, can be observed. At HHT, the breaking of the passive layer is shown with energy at high frequencies and energy accumulation at low frequencies at subsequent seconds of energy presented at high frequencies.
- The use of Rn and Zn to determine corrosion resistance can be accepted, and they presented similar results. The higher values were obtained by Ti C2 and Ti-6Al-4V exposed in H2SO4 with 271,851 and 325,751 Ω·cm2 by Rn and 742,824 and 939,575 Ω·cm2 by Zn. Although the values are not the same, Rn and Zn can be considered homologues.
- It is important to define a method for correct EN analysis. If one analysis is correct, it can easily be applied to study neuronal networks or machine learning.
- EN is a powerful technique that can be employed in situ due to its non-destructive properties. Also, using this technique to detect different corrosion systems and some galvanic couples in the alloy phase is helpful for a correct alloy design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stern, M.; Geary, A.L. Electrochemical polarization. I. A theoretical analysis of the shape of the polarization curves. J. Electrochem. Soc. 1957, 104, 56–63. [Google Scholar] [CrossRef]
- Pellegrini-Cervantes, M.J.; Almeraya-Calderon, F.; Borunda-Terrazas, A.; Bautista-Margulis, R.G.; Chacón-Nava, J.G.; Fajardo-San-Miguel, G.; Almaral-Sanchez, J.L.; Barrios-Durstewitz, C.; Martinez-Villafañe, A. Corrosion Resistance, Porosity and Strength of lended Portland Cement Mortar Containing Rice Husk Ash and Nano-SiO2. Int. J. Electrochem. Sci. 2013, 8, 10697–10710. [Google Scholar] [CrossRef]
- Volmer, M.; Weber, A. Keimbildung in nbersättigten Gebilden. Z. Phys. Chem. 1959, 119, 277–3013. [Google Scholar] [CrossRef]
- Butler, J.A.V. Studies in heterogeneous equilibria, II. The kinetic interpretation of the Nernst theory of electromotive force. Trans. Faraday Soc. 1924, 19, 729–733. [Google Scholar] [CrossRef]
- Butler, J.A.V. Studies in heterogeneous equilibria, I. Conditions at the boundary surface of crystalline solids and liquids, and the application of statistical mechanics. Trans. Faraday Soc. 1924, 19, 659–665. [Google Scholar] [CrossRef]
- Macdonald, D.D. Review of mechanistic analysis by electrochemical impedance spectroscopy. Electrochim. Acta 1990, 35, 1509–1525. [Google Scholar] [CrossRef]
- Silverman, D.C. Tutorial on Cyclic Potentiodynamic Polarization Technique. In Proceedings of the CORROSION 98, San Diego, CA, USA, 22–27 March 1998. [Google Scholar]
- Silverman, D.C. Practical Corrosion Prediction Using Electrochemical Techniques. In Uhlig’s Corrosion Handbook, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1129–1166. [Google Scholar] [CrossRef]
- Kearns, J.R.; Scully, J.R.; Roberge, P.R.; Reichert, D.L.; Dawson, J.L. Electrochemical Noise Measurement for Corrosion Applications; ASTM International: West Conshohocken, PA, USA, 2015; ISBN 080312032X. [Google Scholar]
- Sanchez-Amaya, J.M.; Cottis, R.A.; Botana, F.J. Shot Noise and Statistical Parameters for the Estimation of Corrosion Mechanisms. Corros. Sci. 2005, 47, 3280–3299. [Google Scholar] [CrossRef]
- Cottis, R.A. Interpretation of Electrochemical Noise Data. Corrosion 2001, 57, 265–285. [Google Scholar] [CrossRef]
- Bertocci, U.; Huet, F. Noise Analysis Applied to Electrochemical Systems. Corrosion 1995, 51, 131–144. [Google Scholar] [CrossRef]
- Bertocci, U.; Kruger, J. Studies of Passive Film Breakdown by Detection and Analysis of Electrochemical Noise. Surf. Sci. 1980, 101, 608–618. [Google Scholar] [CrossRef]
- Al-Zanki, I.A.; Gill, J.S.; Dawson, J.L. Electrochemical Noise Measurements on Mild Steel in 0.5 M Sulphuric Acid. Mater. Sci. Forum 1986, 8, 463–476. [Google Scholar] [CrossRef]
- Eden, D.A.; Rothwell, A.N. Electrochemical Noise Data: Analysis, Interpretation and Presentation; NACE International: Houston, TX, USA, 1992; pp. 1–12. [Google Scholar]
- Bertocci, U.; Gabrielli, C.; Huet, F.; Keddam, M.; Rousseau, P. Noise Resistance Applied to Corrosion Measurements: II. Experimental Tests. J. Electrochem. Soc. 1997, 144, 37–43. [Google Scholar] [CrossRef]
- Eden, D.A.; John, D.G.; Dawson, J.L. Corrosion Monitoring. International Patent Wo 87/0722, 19 November 1997. [Google Scholar]
- Mansfeld, F.; Sun, Z.; Hsu, C.H.; Nagiub, A. Concerning Trend Removal in Electrochemical Noise Measurements. Corros. Sci. 2001, 43, 341–352. [Google Scholar] [CrossRef]
- Lee, C.C.; Mansfeld, F. Analysis of Electrochemical Noise Data for a Passive System in the Frequency Domain. Corros. Sci. 1998, 40, 959–962. [Google Scholar] [CrossRef]
- Homborg, A.M.; Tinga, T.; Van Westing, E.P.M.; Zhang, X.; Ferrari, G.M.; De Wit, J.H.W.; Mol, J.M.C. A Critical Appraisal of the Interpretation of Electrochemical Noise for Corrosion Studies. Corrosion 2014, 70, 971–987. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Cao, F.; Liao, X.; Liu, W.; Zheng, L.; Zhang, J.; Cao, C. Study of Pitting Corrosion on Mild Steel during Wet–Dry Cycles by Electrochemical Noise Analysis Based on Chaos Theory. Corros. Sci. 2013, 66, 183–195. [Google Scholar] [CrossRef]
- Mansfeld, F.; Sun, Z. Technical Note: Localization Index Obtained from Electrochemical Noise Analysis. Corrosion 1999, 55, 915–918. [Google Scholar] [CrossRef]
- Reid, S.A.; Eden, D.A. Assessment of Corrosion. U.S. Patent US9264824B1, 24 July 2001. [Google Scholar]
- Eden, D.A. Electrochemical Noise—The First Two Octaves. In Proceedings of the CORROSION 98, San Diego, CA, USA, 22–27 March 1998; Volume 1998. [Google Scholar]
- Villegas-Tovar, J.; Gaona-Tiburcio, C.; Lara-Banda, M.; Maldonado-Bandala, E.; Baltazar-Zamora, M.A.; Cabral-Miramontes, J.; Nieves-Mendoza, D.; Olguin-Coca, J.; Estupiñan-Lopez, F.; Almeraya-Calderón, F. Electrochemical Corrosion Behavior of Passivated Precipitation Hardening Stainless Steels for Aerospace Applications. Metals 2023, 13, 835. [Google Scholar] [CrossRef]
- Almeraya-Calderón, F.; Jáquez-Muñoz, J.M.; Maldonado-Bandala, E.; Cabral-Miramontes, J.; Nieves-Mendoza, D.; Olgui-Coca, J.; Lopez-Leon, L.D.; Estupiñán-López, F.; Lira-Martínez, A.; Gaona Tiburcio, C. Corrosion Resistance of Titanium Alloys Anodized in Alkaline Solutions. Metals 2023, 13, 1510. [Google Scholar] [CrossRef]
- Coakley, J.; Vorontsov, V.A.; Littrell, K.C.; Heenan, R.K.; Ohnuma, M.; Jones, N.G.; Dye, D. Nanoprecipitation in a Beta-Titanium Alloy. J. Alloys Compd. 2015, 623, 146–156. [Google Scholar] [CrossRef]
- Legat, A.; Doleček, V. Corrosion Monitoring System Based on Measurement and Analysis of Electrochemical Noise. Corrosion 1995, 51, 295–300. [Google Scholar] [CrossRef]
- Uruchurtu, J.C.; Dawson, J.L. Noise Analysis of Pure Aluminum under Different Pitting Conditions. Corrosion 1987, 43, 19–26. [Google Scholar] [CrossRef]
- Bertocci, U.; Huet, F.; Nogueira, R.P.; Rousseau, P. Drift Removal Procedures in the Analysis of Electrochemical Noise. Corrosion 2002, 58, 337–347. [Google Scholar] [CrossRef]
- Botona Pedemonte, F.J.; Aballe Villero, A.; Marcos Bárcena, M. Ruido Electroquímico. Métodos de Análisis; Septem Ediciones, S.L.: Oviedo, Spain, 2002; ISBN 84-95687-33-X. [Google Scholar]
- Mehdipour, M.; Naderi, R.; Markhali, B.P. Electrochemical Study of Effect of the Concentration of Azole Derivatives on Corrosion Behavior of Stainless Steel in H2SO4. Prog. Org. Coatings 2014, 77, 1761–1767. [Google Scholar] [CrossRef]
- Cappeln, F.; Bjerrum, N.J.; Petrushina, I.M. Electrochemical Noise Measurements of Steel Corrosion in the Molten NaCl-K2SO4 System. J. Electrochem. Soc. 2005, 152, B228. [Google Scholar] [CrossRef]
- Calabrese, L.; Galeano, M.; Proverbio, E. Identifying Corrosion Forms on Synthetic Electrochemical Noise Signals by the Hilbert–Huang Transform Method. Corros. Eng. Sci. Technol. 2018, 53, 492–501. [Google Scholar] [CrossRef]
- Mansfeld, F.; Han, L.T.; Lee, C.C.; Zhang, G. Evaluation of Corrosion Protection by Polymer Coatings Using Electrochemical Impedance Spectroscopy and Noise Analysis. Electrochim. Acta 1998, 43, 2933–2945. [Google Scholar] [CrossRef]
- Legat, A.; Doleček, V. Chaotic Analysis of Electrochemical Noise Measured on Stainless Steel. J. Electrochem. Soc. 1995, 142, 1851–1858. [Google Scholar] [CrossRef]
- Martínez-Aparicio, B.; Martínez-Bastidas, D.; Gaona-Tiburcio, C.; Martin, U.; Cabral-Miramontes, J.; Almeraya-Calderón, F. Localized corrosion of 15–5 PH and 17–4 PH stainless steel in NaCl solution. J. Solid State Electrochem. 2023, 27, 2993–3001. [Google Scholar] [CrossRef]
- Lentka, Ł.; Smulko, J. Methods of Trend Removal in Electrochemical Noise Data—Overview. Measurement 2019, 131, 569–581. [Google Scholar] [CrossRef]
- Homborg, A.M.; Cottis, R.A.; Mol, J.M.C. An Integrated Approach in the Time, Frequency and Time-Frequency Domain for the Identification of Corrosion Using Electrochemical Noise. Electrochim. Acta 2016, 222, 627–640. [Google Scholar] [CrossRef]
- Homborg, A.M.; Oonincx, P.J.; Mol, J.M.C. Wavelet Transform Modulus Maxima and Holder Exponents Combined with Transient Detection for the Differentiation of Pitting Corrosion Using Electrochemical Noise. Corrosion 2018, 74, 1001–1010. [Google Scholar] [CrossRef] [PubMed]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Cai, C.; Zhang, Z.; Cao, F.; Gao, Z.; Zhang, J.; Cao, C. Analysis of Pitting Corrosion Behavior of Pure Al in Sodium Chloride Solution with the Wavelet Technique. J. Electroanal. Chem. 2005, 578, 143–150. [Google Scholar] [CrossRef]
- Homborg, A.M.; van Westing, E.P.M.; Tinga, T.; Zhang, X.; Oonincx, P.J.; Ferrari, G.M.; de Wit, J.H.W.; Mol, J.M.C. Novel Time–Frequency Characterization of Electrochemical Noise Data in Corrosion Studies Using Hilbert Spectra. Corros. Sci. 2013, 66, 97–110. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Yen, N.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Non-linear and Non-Stationary Time Series Analysis. Proc. R. Soc. A 1996, 454, 903–995. [Google Scholar] [CrossRef]
- Lafront, A.M.; Safizadeh, F.; Ghali, E.; Houlachi, G. Study of the Copper Anode Passivation by Electrochemical Noise Analysis Using Spectral and Wavelet Transforms. Electrochim. Acta 2010, 55, 2505–2512. [Google Scholar] [CrossRef]
- Hai, L.; Guo-qiang, X.; Pan, Z.; Hua-sen, Z.; Khan, M.Y. The Hilbert–Huang Transform-Based Denoising Method for the TEM Response of a PRBS Source Signal. Pure Appl. Geophys. 2016, 173, 2777–2789. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L. Recurrence Quantification Analysis: Introduction and Historical Context. Int. J. Bifurcat. Chaos 2007, 17, 3477–3481. [Google Scholar] [CrossRef]
- Garcia-Ochoa, E. Recurrence Plots: A New Methodology for Electrochemical Noise Signal Analysis. J. Electroanal. Chem. 2020, 864, 114092. [Google Scholar] [CrossRef]
- Marwan, N.; Kraemer, K.H. Trends in Recurrence Analysis of Dynamical Systems. Eur. Phys. J. Spec. Top. 2023, 232, 5–27. [Google Scholar] [CrossRef]
- Montoya-Rangel, M.; de Oca, N.G.M.; Gaona-Tiburcio, C.; Colás, R.; Cabral-Miramontes, J.; Nieves-Mendoza, D.; Maldonado-Bandala, E.; Chacón-Nava, J.; Almeraya-Calderón, F. Electrochemical Noise Measurements of Advanced High-Strength Steels in Different Solutions. Metals 2020, 10, 1232. [Google Scholar] [CrossRef]
- Arellano-Pérez, J.H.; Escobar-Jiménez, R.F.; Granados-Lieberman, D.; Gómez-Aguilar, J.F.; Uruchurtu-Chavarín, J.; Alvarado-Martínez, V.M. Electrochemical Noise Signals Evaluation to Classify the Type of Corrosion Using Synchrosqueezing Transform. J. Electroanal. Chem. 2019, 848, 113249. [Google Scholar] [CrossRef]
- Ren, Z.; Li, Q.; Yang, X.; Wang, J. A Novel Method for Identifying Corrosion Types and Transitions Based on Adaboost and Electrochemical Noise. Anti-Corros. Methods Mater. 2023, 70, 78–85. [Google Scholar] [CrossRef]
- Montoya-Rangel, M.; Garza-Montes-de-Oca, N.F.; Gaona-Tiburcio, C.; Almeraya-Calderón, F. Corrosion Mechanism of Advanced High Strength Dual-Phase Steels by Electrochemical Noise Analysis in Chloride Solutions. Mater. Today Commun. 2023, 35, 105663. [Google Scholar] [CrossRef]
- Ye, Z.; Guan, L.; Li, Y.; Zhong, J.; Liao, L.; Xia, D.; Huang, J. Understanding the Galvanic Corrosion of Cu-Ni Alloy/2205 DSS Couple Using Electrochemical Noise and Microelectrochemical Studies. Corros. Sci. 2023, 224, 111512. [Google Scholar] [CrossRef]
- Shahri, Z.; Allahkaram, S.R.; Soltani, R.; Jafari, H. Electrochemical Analysis on Localized Corrosion of PEO/Magnesium Oxide Coating. J. Alloys Compd. 2024, 1003, 175572. [Google Scholar] [CrossRef]
- Homborg, A.; Mol, A.; Tinga, T. Corrosion Classification through Deep Learning of Electrochemical Noise Time-Frequency Transient Information. Eng. Appl. Artif. Intell. 2024, 133, 108044. [Google Scholar] [CrossRef]
- Salunkhe, V.G.; Khot, S.M.; Desavale, R.G.; Yelve, N.P. Unbalance Bearing Fault Identification Using Highly Accurate Hilbert–Huang Transform Approach. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2023, 6, 031005. [Google Scholar] [CrossRef]
- Jamali, S.S.; Wu, Y.; Homborg, A.M.; Lemay, S.G.; Gooding, J.J. Interpretation of Stochastic Electrochemical Data. Curr. Opin. Electrochem. 2024, 46, 101505. [Google Scholar] [CrossRef]
- Lee, Y.N.; Jung, M.J.; Jo, S.W.; Rahim, G.; Lee, S.G.; Choi, K.S. Fast-Settling Onboard Electrochemical Impedance Spectroscopy System Adopting Two-Stage Hilbert Transform. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023. [Google Scholar] [CrossRef]
- Ortíz-Corona, J.; Uruchurtu-Chavarin, J.; García-Ochoa, E.M.; González-Sánchez, J.A.; Larios-Duran, E.R.; Rodríguez-Gómez, F.J. Monitoring of Silver Alloy Tarnishing in Sulphides by Electrochemical Noise Measurements: Application of Statistical and Recurrence Plot Analysis. Electrochim. Acta 2024, 495, 144388. [Google Scholar] [CrossRef]
- Luo, B.; Wei, Q.; Hu, S.; Manoach, E.; Deng, T.; Cao, M. A Novel Cross-Domain Identification Method for Bridge Damage Based on Recurrence Plot and Convolutional Neural Networks. J. Vibroeng. 2024, 26, 1–22. [Google Scholar] [CrossRef]
- Lin, R.L.; Li, W.Y.; Li, L.; Liao, C.J. High-Dissolution Mechanism of Ti–48Al–2Cr–2Nb Alloy in Electrochemical Machining from a Non-linear Dynamic Perspective. Adv. Eng. Mater. 2024, 26, 2302083. [Google Scholar] [CrossRef]
- Martínez-Villafañe, A.; Almeraya-Calderón, M.F.; Gaona-Tiburcio, C.; Gonzalez-Rodriguez, J.G.; Porcayo-Calderón, J. High-Temperature Degradation and Protection of Ferritic and Austenitic Steels in Steam Generators. J. Mater. Eng. Perform. 1997, 7, 108–113. [Google Scholar] [CrossRef]
- ASTM E3-95; Standard Practice for Preparation of Metallographic Specimens. ASTM International: West Conshohocken, PA, USA, 2007.
- ASTM G199; Standard Guide for Electrochemical Noise Measurement. ASTM International: West Conshohocken, PA, USA, 2020.
- Jaquez-Muñoz, J.; Gaona-Tiburcio, C.; Lira-Martinez, A.; Zambrano-Robledo, P.; Maldonado-Bandala, E.; Samaniego-Gamez, O.; Nieves-Mendoza, D.; Olguin-Coca, J.; Estupiñan-Lopez, F.; Almeraya-Calderon, F. Susceptibility to Pitting Corrosion of Ti CP2, Ti-6Al-2Sn-4Zr-2Mo, and Ti-6Al-4V Alloys for Aeronautical Applications. Metals 2021, 11, 1002. [Google Scholar] [CrossRef]
- Jáquez-Muñoz, J.M.; Gaona-Tiburcio, C.; Méndez-Ramírez, C.T.; Baltazar-Zamora, M.Á.; Estupinán-López, F.; Bautista-Margulis, R.G.; Cuevas-Rodríguez, J.; Flores-De los Rios, J.P.; Almeraya-Calderón, F. Corrosion of Titanium Alloys Anodized Using Electrochemical Techniques. Metals 2023, 13, 476. [Google Scholar] [CrossRef]
- Almeraya-Calderon, F.; Villegas-Tovar, M.; Maldonado-Bandala, E.; Lara-Banda, M.; Baltazar-Zamora, M.A.; Santiago-Hurtado, G.; Nieves-Mendoza, D.; Lopez-Leon, L.D.; Jaquez-Muñoz, J.M.; Estupiñán-López, F.; et al. Use of Electrochemical Noise for the Study of Corrosion by Passivated CUSTOM 450 and AM 350 Stainless Steels. Metals 2024, 14, 341. [Google Scholar] [CrossRef]
- Coakley, J.; Isheim, D.; Radecka, A.; Dye, D.; Stone, H.J.; Seidman, D.N. Microstructural Evolution in a Superelastic Metastable Beta-Ti Alloy. Scr. Mater. 2017, 128, 87–90. [Google Scholar] [CrossRef]
- Nazarnezhad-Bajestani, M.; Neshati, J.; Siadati, M.H. Determination of SS321 Pitting Stage in FeCl3 Solution Based on Electrochemical Noise Measurement Data Using Artificial Neural Network. J. Electroanal. Chem. 2019, 845, 31–38. [Google Scholar] [CrossRef]
- Aballe, A.; Bethencourt, M.; Botana, F.J.; Marcos, M.; Sánchez-Amaya, J.M. Use of Wavelets to Study Electrochemical Noise Transients. Electrochim. Acta 2001, 46, 2353–2361. [Google Scholar] [CrossRef]
- Cottis, R.A.; Homborg, A.M.; Mol, J.M.C. The Relationship between Spectral and Wavelet Techniques for Noise Analysis. Electrochim. Acta 2016, 202, 277–287. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, X.; Hu, X.; Hu, J. The Multi-Disturbance Complex Power Quality Signal HHT Detection Technique. In Proceedings of the 2012 IEEE Innovative Smart Grid Technologies—ISGT Asia, Tianjin, China, 21–24 May 2012. [Google Scholar] [CrossRef]
- Jáquez-Muñoz, J.M.; Gaona-Tiburcio, C.; Chacón-Nava, J.; Cabral-Miramontes, J.; Nieves-Mendoza, D.; Maldonado-Bandala, E.M.; Delgado, A.D.; Flores-De Los Rios, J.P.; Bocchetta, P.; Almeraya-Calderón, F. Electrochemical Corrosion of Titanium and Titanium Alloys Anodized in H2SO4 and H3PO4 Solutions. Coatings 2022, 12, 325. [Google Scholar] [CrossRef]
- Lara-Banda, M.; Gaona-Tiburcio, C.; Zambrano-Robledo, P.; Delgado, E.M.; Cabral-Miramontes, J.A.; Nieves-Mendoza, D.; Maldonado-Bandala, E.; Estupiñan-López, F.; Chacón-Nava, J.G.; Almeraya-Calderón, F. Alternative to Nitric Acid Passivation of 15-5 and 17-4PH Stainless Steel Using Electrochemical Techniques. Materials 2020, 13, 2836. [Google Scholar] [CrossRef] [PubMed]
- Bocchetta, P.; Chen, L.Y.; Tardelli, J.D.C.; Dos Reis, A.C.; Almeraya-Calderón, F.; Leo, P. Passive Layers and Corrosion Resistance of Biomedical Ti-6Al-4V and β-Ti Alloys. Coatings 2021, 11, 487. [Google Scholar] [CrossRef]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–446. [Google Scholar] [CrossRef]
- Liu, W.; Wang, D.; Chen, X.; Wang, C.; Liu, H. Recurrence Plot-Based Dynamic Analysis on Electrochemical Noise of the Evolutive Corrosion Process. Corros. Sci. 2017, 124, 93–102. [Google Scholar] [CrossRef]
- Acuña-González, N.; García-Ochoa, E.; González-Sánchez, J. Assessment of the Dynamics of Corrosion Fatigue Crack Initiation Applying Recurrence Plots to the Analysis of Electrochemical Noise Data. Int. J. Fatigue 2008, 30, 1211–1219. [Google Scholar] [CrossRef]
- Li, J.; Du, C.W.; Liu, Z.Y.; Li, X.G.; Liu, M. Effect of Microstructure on the Corrosion Resistance of 2205 Duplex Stainless Steel. Part 2: Electrochemical Noise Analysis of Corrosion Behaviors of Different Microstructures Based on Wavelet Transform. Constr. Build. Mater. 2018, 189, 1294–1302. [Google Scholar] [CrossRef]
- Cui, J.; Yu, D.; Long, Z.; Xi, B.; He, X.; Pei, Y. Application of Electrochemical Noise (EN) Technology to Evaluate the Passivation Performances of Adsorption and Film-Forming Type Corrosion Inhibitors. J. Electroanal. Chem. 2019, 855, 113584. [Google Scholar] [CrossRef]
- Gaona-Tiburcio, C.; Montoya, R.M.; Cabral, M.J.A.; Estupiñan, L.F.; Zambrano, R.P.; Orozco, C.R.; Chacon-Nava, J.G.; Baltazar, Z.M.A.; Almeraya-Caldero, F. Corrosion Resistance of Multilayer Coatings Deposited by PVD on Inconel 718 Using Electrochemical Impedance Spectroscopy Technique. Coatings 2020, 10, 521. [Google Scholar] [CrossRef]
- Abdulmutaali, A.; Hou, Y.; Aldrich, C.; Lepkova, K. An Online Monitoring Approach of Carbon Steel Corrosion via the Use of Electrochemical Noise and Wavelet Analysis. Metals 2024, 14, 66. [Google Scholar] [CrossRef]
- Hou, Y.; Aldrich, C.; Lepkova, K.; Machuca, L.L.; Kinsella, B. Monitoring of Carbon Steel Corrosion by Use of Electrochemical Noise and Recurrence Quantification Analysis. Corros. Sci. 2016, 112, 63–72. [Google Scholar] [CrossRef]
- Valavanis, D.; Spanoudaki, D.; Gkili, C.; Sazou, D. Using Recurrence Plots for the Analysis of the Nonlinear Dynamical Response of Iron Passivation-Corrosion Processes. Chaos 2018, 28, 085708. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Ochoa, E.; Maldonado, P.; Corvo, F. Non-linear Dynamics of Potassium Iodide Adsorption on the Interface of Carbon Steel in Acidic Medium. Mater. Corros. 2020, 71, 1152–1159. [Google Scholar] [CrossRef]
- Marwan, N.; Webber, C.L.; Macau, E.E.N.; Viana, R.L. Introduction to Focus Issue: Recurrence Quantification Analysis for Understanding Complex Systems. Chaos 2018, 28, 85601. [Google Scholar] [CrossRef]
- Martínez-Ramos, C.; Olguin-Coca, J.; Lopez-Leon, L.D.; Gaona-Tiburcio, C.; Lara-Banda, M.; Maldonado-Bandala, E.; Castañeda-Robles, I.; Jaquez-Muñoz, J.M.; Cabral-Miramontes, J.; Nieves-Mendoza, D.; et al. Electrochemical Noise Analysis Using Experimental Chaos Theory, Power Spectral Density and Hilbert–Huang Transform in Anodized Aluminum Alloys in Tartaric–Phosphoric–Sulfuric Acid Solutions. Metals 2023, 13, 1850. [Google Scholar] [CrossRef]
- Gaona-Tiburcio, C.; Almeraya-Calderón, F.; Chacon-Nava, J.G.; Matutes-Aquino, J.A.; Martinez-Villafañe, A. Electrochemical response of permanent magnets in different solutions. J. Alloys Compd. 2004, 369, 78–80. [Google Scholar] [CrossRef]
- Gaona-Tiburcio, C.; Jáquez-Muñoz, J.M.; Nieves-Mendoza, D.; Maldonado-Bandala, E.; Lara-Banda, M.; Lira-Martinez, M.A.; Reyes-Blas, H.; Baltazar-Zamora, M.Á.; Landa-Ruiz, L.; Lopez-Leon, L.D.; et al. Corrosion Behavior of Titanium Alloys (Ti CP2, Ti-6Al-2Sn-4Zr-2Mo, Ti-6Al-4V and Ti Beta-C) with Anodized and Exposed in NaCl and H2SO4 Solutions. Metals 2024, 14, 160. [Google Scholar] [CrossRef]
- Cerezo, H.R.; Tiburcio, C.G.; Miramontes, J.A.C.; Almeraya-Calderón, F. Electrochemical characterization of Al–Li alloys AA2099 and AA2055 for aeronautical applications: Effect of thermomechanical treatments. J. Solid State Electrochem. 2023, 27, 3101–3117. [Google Scholar] [CrossRef]






| Alloys | Rn (Ω·cm2) | LI | Corrosion Type | Kurtosis | Corrosion Type | Skewness | Corrosion Type |
|---|---|---|---|---|---|---|---|
| 304 SS | 54,772 ± 11 | 0.07 ± 0.02 | Mix | 4.5 ± 0.8 | Loc | −1 ± 0.2 | Uni |
| 316 SS | 66,621 ± 10 | 0.2 ± 0.03 | Loc | 26 ± 2 | Loc | −29 ± 0.8 | Loc |
| Inconel 718 | 57,745 ± 8 | 0.12 ± 0.08 | Loc | 12 ± 1.2 | Loc | 1 ± 0.5 | Loc |
| 1018 CS | 2817 ± 14 | 0.03 ± 0.01 | Mix | 4 ± 1.0 | Loc | 0 ± 0.7 | Uni |
| AA 2024 | 43,856 ± 9 | 0.28 ± 0.1 | Loc | 4 ± 0.6 | Loc | −1 ± 0.3 | Uni |
| AA 2055 | 15,212 ± 20 | 0.18 ± 0.07 | Loc | 72 ± 3 | Loc | −4 ± 0.8 | Loc |
| AA 6061 | 170,057 ± 24 | 0.06 ± 0.02 | Mix | 22 ± 2.6 | Loc | −2 ± 0.9 | Loc |
| AM350 | 76,329 ± 13 | 0.02 ± 0.02 | Mix | 69 ± 4 | Loc | −4 ± 1.2 | Loc |
| Custom450 | 17,038 ± 24 | 0.16 ± 0.12 | Loc | 87 ± 6 | Loc | 5 ± 0.9 | Loc |
| Ti-6Al-4V | 175,051 ± 29 | 0.01 ± 0.01 | Mixt | 188 ± 5 | Loc | −0 ± 0.3 | Uni |
| Ti CP2 | 204,605 ± 24 | 0.36 ± 0.08 | Loc | 6 ± 1.5 | Loc | −0 ± 0.6 | Uni |
| Ultimet | 75,342 ± 26 | 0.13 ± 0.03 | Loc | 538 ± 7 | Loc | 13 ± 1.1 | Loc |
| Waspaloy | 14,451 ± 14 | 0.05 ± 0.02 | Mix | 10 ± 1.3 | Loc | −17 ± 1.4 | Loc |
| Alloys | Rn (Ω·cm2) | LI | Corrosion Type | Kurtosis | Corrosion Type | Skewness | Corrosion Type |
|---|---|---|---|---|---|---|---|
| 304 SS | 326 ± 5 | 0.01 ± 0.02 | Mix | 3 ± 0.8 | Uni | 0 ± 0.2 | Uni |
| 316 SS | 1208 ± 15 | 0.06 ± 0.02 | Mix | 6 ± 0.2 | Loc | −0 ± 0.7 | Uni |
| Inconel 718 | 90,112 ± 20 | 0.4 ± 0.1 | Loc | 32 ± 1.5 | Loc | −4 ± 0.3 | Loc |
| 1018 CS | 130 ± 8 | 0.06 ± 0.02 | Mix | 14 ± 1.1 | Loc | −2 ± 0.1 | Loc |
| AA 2024 | 249 ± 12 | 0.01 ± 0.01 | Mix | 15 ± 1.7 | Loc | 1 ± 0.1 | Uni |
| AA 2055 | 3564 ± 29 | 0.009 ± 0.001 | Uni | 3 ± 1.3 | Uni | −0 ± 0.3 | Uni |
| AA 6061 | 2384 ± 20 | 0.4 ± 0.1 | Loc | 6 ± 0.8 | Loc | −0 ± 0.3 | Loc |
| AM350 | 12,563 ± 24 | 0.02 ± 0.004 | Mix | 14 ± 0.7 | Loc | 0 ± 0.6 | Uni |
| Custom450 | 4484 ± 33 | 0.03 ± 0.02 | Mix | 15 ± 0.5 | Loc | −2 ± 0.2 | Loc |
| Ti-6Al-4V | 325,751 ± 16 | 0.4 ± 0.02 | Loc | 6 ± 0.3 | Loc | −0 ± 0.5 | Uni |
| Ti CP2 | 271,851 ± 123 | 0.04 ± 0.005 | Mix | 4 ± 1.2 | Loc | 0 ± 0.2 | Uni |
| Ultimet | 25,560 ± 37 | 0.5 ± 0.04 | Loc | 28 ± 2.5 | Loc | −3 ± 0.7 | Loc |
| Waspaloy | 6356 ± 57 | 0.01 ± | Mix | 16 ± 1.1 | Loc | −1 ± 0.6 | Loc |
| NaCl Solution | H2SO4 Solution | ||||||
|---|---|---|---|---|---|---|---|
| Alloys | Slope (dBi) | Limit Frequency | Zn (Ω·cm2) | Alloys | Slope (dBi) | Limit Frequency | Zn (Ω·cm2) |
| 304 SS | −14 ± 1 | −130 ± 12 | 63,123 ± 70 | 304 SS | −15 ± 1.2 | −109 ± 5 | 612 ± 12 |
| 316 SS | −12 ± 0.8 | −140 ± 15 | 183,756 ± 122 | 316 SS | −17 ± 1 | −100 ± 3 | 1129 ± 67 |
| Inconel 718 | −13 ± 1.1 | −130 ± 9 | 85,956 ± 130 | Inconel 718 | −10 ± 1.1 | −133 ± 8 | 268,894 ± 50 |
| 1018 CS | −17 ± 1.2 | −106 ± 14 | 1342 ± 27 | 1018 CS | −9 ± 0.5 | −106 ± 4 | 136 ± 8 |
| AA 2024 | −15 ± 0.7 | −122 ± 11 | 109,304 ± 159 | AA 2024 | −11 ± 0.4 | −107 ± 8 | 2493 ± 36 |
| AA 2055 | −2 ± 0.5 | −119 ± 8 | 36,459 ± 98 | AA 2055 | −15 ± 0.3 | −121 ± 2 | 2567 ± 38 |
| AA 6061 | −6 ± 0.9 | −145 ± 10 | 162,779 ± 211 | AA 6061 | −10 ± 0.7 | −115 ± 9 | 5983 ± 69 |
| AM350 | −5 ± 0.3 | −138 ± 14 | 46,864 ± 136 | AM350 | −7 ± 0.4 | −123 ± 10 | 11,072 ± 96 |
| Custom450 | −2 ± 0.2 | −123 ± 13 | 3242 ± 67 | Custom450 | −19 ± 1.3 | −122 ± 9 | 1793 ± 82 |
| Ti-6Al-4V | −12 ± 0.4 | −155 ± 13 | 223,794 ± 177 | Ti-6Al-4V | −12 ± 0.9 | −140 ± 11 | 939,575 ± 241 |
| Ti CP2 | −13 ± 0.8 | −128 ± 10 | 222,411 ± 389 | Ti CP2 | −9 ± 0.4 | −154 ± 13 | 742,824 ± 265 |
| Ultimet | −4 ± 0.5 | −151 ± 17 | 59,992 ± 450 | Ultimet | −4 ± 0.2 | −135 ± 7 | 34,595 ± 76 |
| Waspaloy | −5 ± 0.8 | −123 ± 15 | 9656 ± 87 | Waspaloy | −11 ± 0.3 | −119 ± 9 | 2328 ± 53 |
| NaCl Solution | H2SO4 Solution | ||||||
|---|---|---|---|---|---|---|---|
| Alloys | RR | Det | RR/Det | Alloy | RR | Det | RR/Det |
| 304 SS | 0.067 ± 0.002 | 0.985 ± 0.002 | 0.067 ± 0.002 | 304 SS | 0.028 ± 0.002 | 0.953 ± 0.001 | 0.029 ± 0.002 |
| 316 SS | 0.155 ± 0.03 | 0.989 ± 0.03 | 0.156 ± 0.03 | 316 SS | 0.042 ± 0.004 | 0.970 ± 0.003 | 0.042 ± 0.003 |
| Inconel 718 | 0.101 ± 0.07 | 0.975 ± 0.06 | 0.103 ± 0.07 | Inconel 718 | 0.056 ± 0.003 | 0.802 ± 0.004 | 0.062 ± 0.004 |
| 1018 CS | 0.042 ± 0.09 | 0.963 ± 0.07 | 0.044 ± 0.08 | 1018 CS | 0.011 ± 0.003 | 0.642 ± 0.002 | 0.017 ± 0.003 |
| AA 2024 | 0.017 ± 0.008 | 0.809 ± 0.007 | 0.021 ± 0.008 | AA 2024 | 0.172 ± 0.004 | 0.990 ± 0.004 | 0.171 ± 0.004 |
| AA 2055 | 0.171 ± 0.08 | 0.992 ± 0.06 | 0.173 ± 0.07 | AA 2055 | 0.026 ± 0.004 | 0.800 ± 0.003 | 0.028 ± 0.003 |
| AA 6061 | 0.001 ± 0.0002 | 0.269 ± 0.0001 | 0.004 ± 0.0002 | AA 6061 | 0.025 ± 0.003 | 0.932 ± 0.003 | 0.030 ± 0.003 |
| AM350 | 0.029 ± 0.005 | 0.802 ± 0.005 | 0.036 ± 0.005 | AM350 | 0.058 ± 0.003 | 0.956 ± 0.001 | 0.060 ± 0.002 |
| CUSTOM450 | 0.095 ± 0.002 | 0.990 ± 0.003 | 0.096 0.003 | CUSTOM450 | 0.048 ± 0.007 | 0.958 ± 0.008 | 0.051 ± 0.008 |
| Ti-6Al-4V | 0.076 ± 0.001 | 0.960 ± 0.002 | 0.079 ± 0.002 | Ti-6Al-4V | 0.017 ± 0.004 | 0.759 ± 0.005 | 0.022 ± 0.005 |
| Ti CP2 | 0.085 ± 0.007 | 0.986 ± 0.009 | 0.086 ± 0.008 | Ti CP2 | 0.002 ± 0.003 | 0.393 ± 0.002 | 0.006 ± 0.003 |
| Ultimet | 0.039 ± 0.004 | 0.907 ± 0.003 | 0.043 ± 0.003 | Ultimet | 0.013 ± 0.007 | 0.544 ± 0.008 | 0.025 ± 0.008 |
| Waspaloy | 0.099 ± 0.002 | 0.967 ± 0.001 | 0.102 ± 0.001 | Waspaloy | 0.008 ± 0.001 | 0.064 ± 0.001 | 0.123 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jáquez-Muñoz, J.M.; Gaona-Tiburcio, C.; Méndez-Ramírez, C.T.; Martínez-Ramos, C.; Baltazar-Zamora, M.A.; Santiago-Hurtado, G.; Estupinan-Lopez, F.; Landa-Ruiz, L.; Nieves-Mendoza, D.; Almeraya-Calderon, F. Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials. Materials 2024, 17, 4013. https://doi.org/10.3390/ma17164013
Jáquez-Muñoz JM, Gaona-Tiburcio C, Méndez-Ramírez CT, Martínez-Ramos C, Baltazar-Zamora MA, Santiago-Hurtado G, Estupinan-Lopez F, Landa-Ruiz L, Nieves-Mendoza D, Almeraya-Calderon F. Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials. Materials. 2024; 17(16):4013. https://doi.org/10.3390/ma17164013
Chicago/Turabian StyleJáquez-Muñoz, Jesús Manuel, Citlalli Gaona-Tiburcio, Ce Tochtli Méndez-Ramírez, Cynthia Martínez-Ramos, Miguel Angel Baltazar-Zamora, Griselda Santiago-Hurtado, Francisco Estupinan-Lopez, Laura Landa-Ruiz, Demetrio Nieves-Mendoza, and Facundo Almeraya-Calderon. 2024. "Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials" Materials 17, no. 16: 4013. https://doi.org/10.3390/ma17164013
APA StyleJáquez-Muñoz, J. M., Gaona-Tiburcio, C., Méndez-Ramírez, C. T., Martínez-Ramos, C., Baltazar-Zamora, M. A., Santiago-Hurtado, G., Estupinan-Lopez, F., Landa-Ruiz, L., Nieves-Mendoza, D., & Almeraya-Calderon, F. (2024). Electrochemical Noise Analysis: An Approach to the Effectivity of Each Method in Different Materials. Materials, 17(16), 4013. https://doi.org/10.3390/ma17164013










