The Overload Effect on the Crack Tip Damage Mechanism in a 7075 Aluminum Alloy
Abstract
:1. Introduction
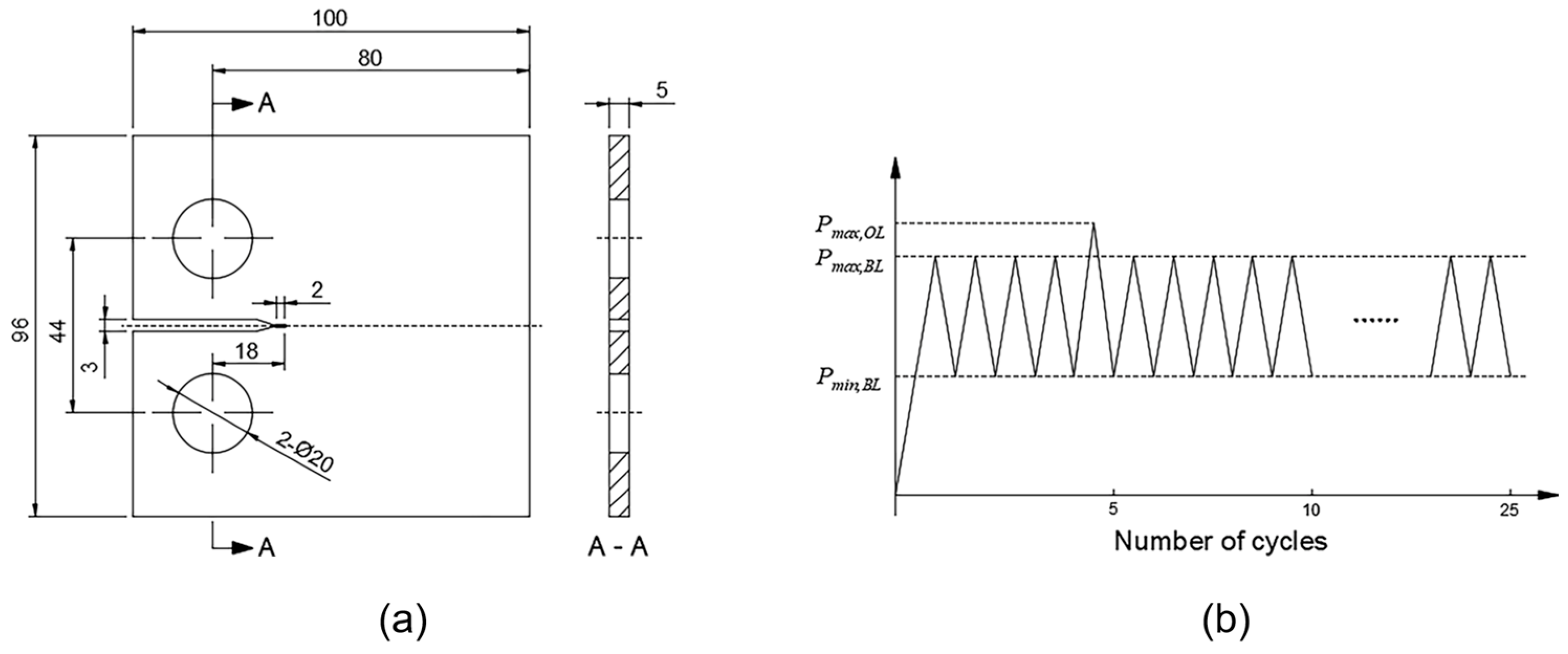
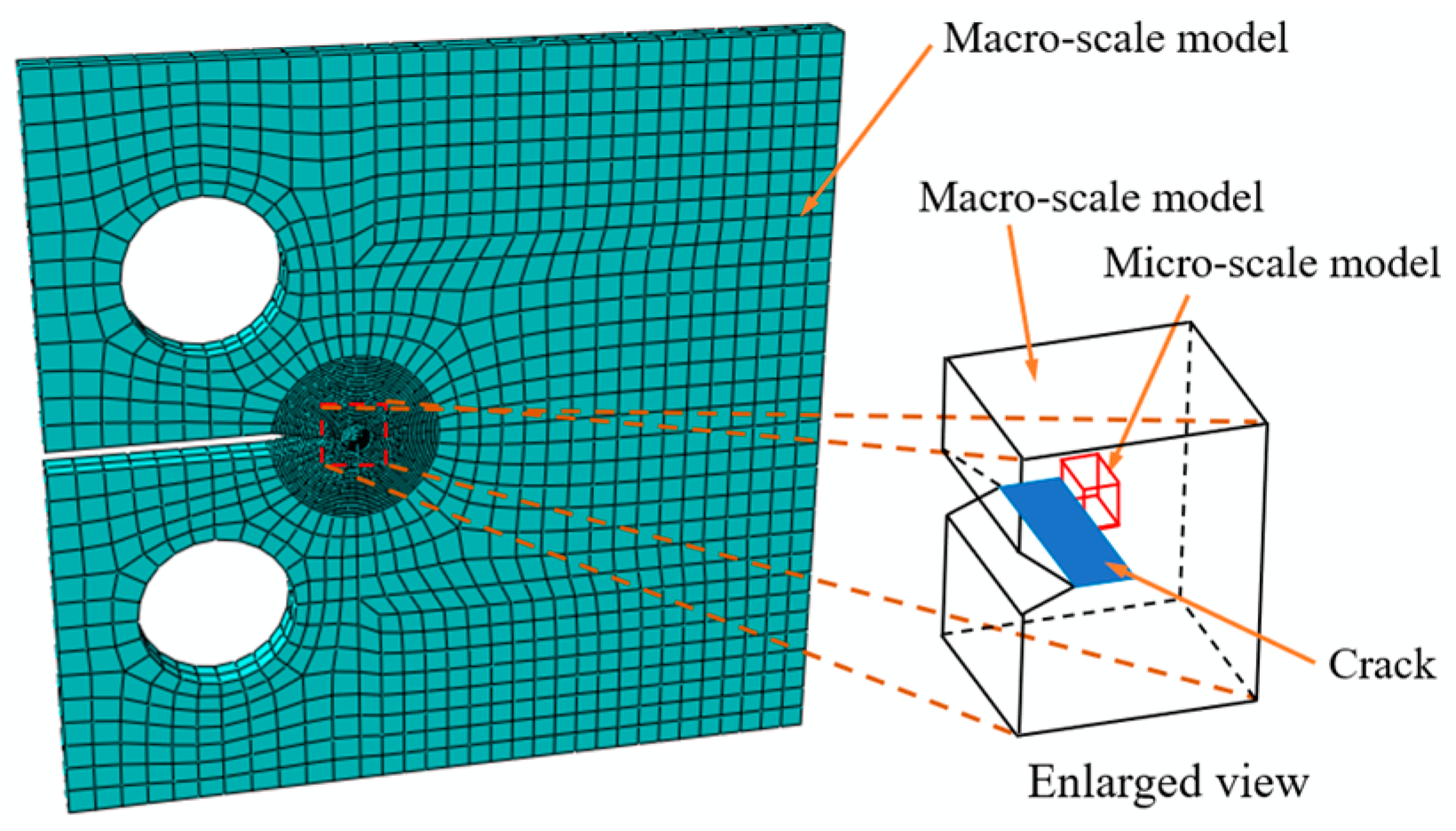
2. Dual-Scale Modeling
3. Constitutive Models and Parameter Calibration
3.1. Brief Introduction to the Chaboche–LCFD Model
3.2. Brief Introduction to the CPFEM–LCFD Model
3.3. Damage Evolution Model
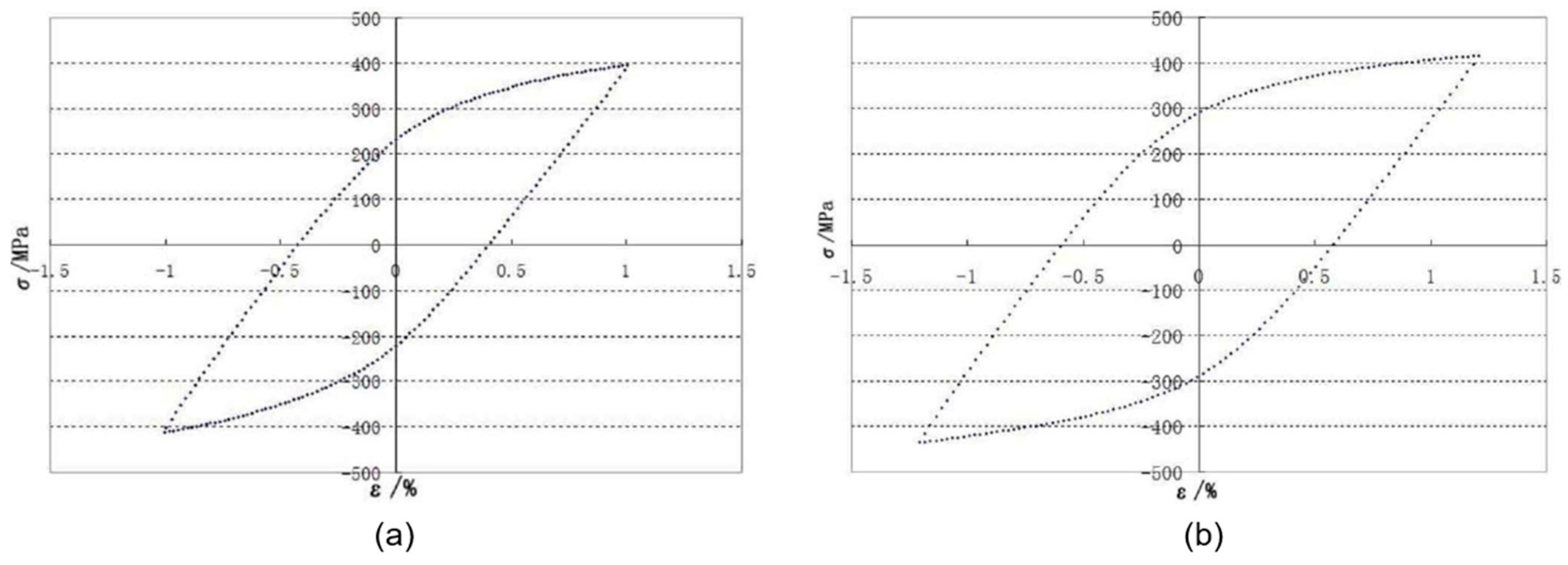
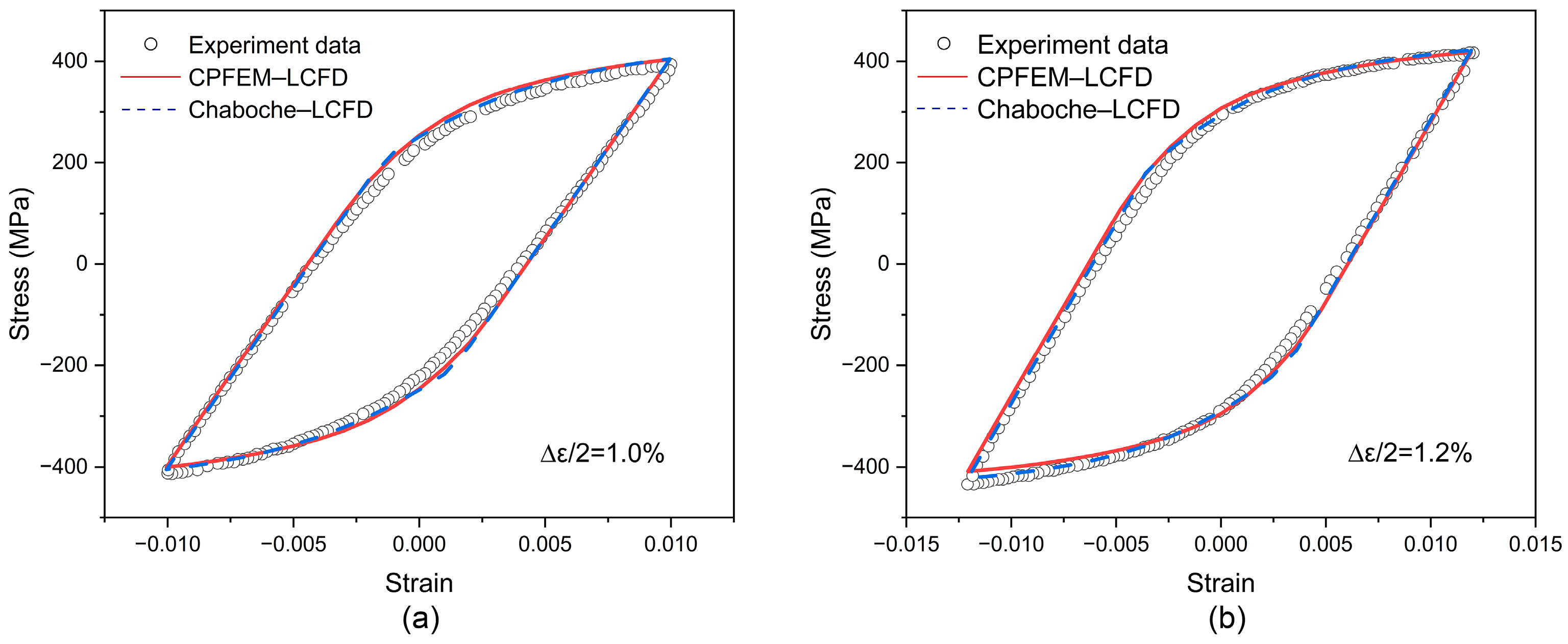
3.4. Parameter Calibration
4. Discussion
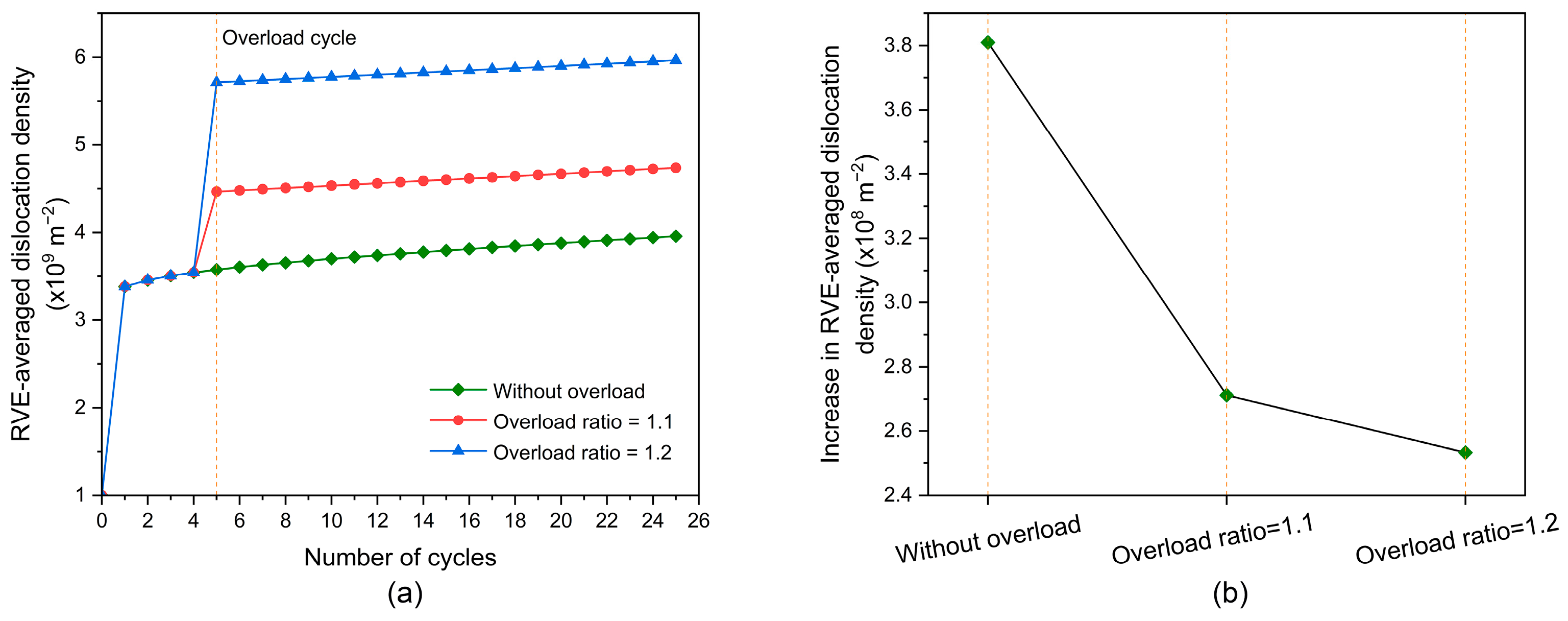
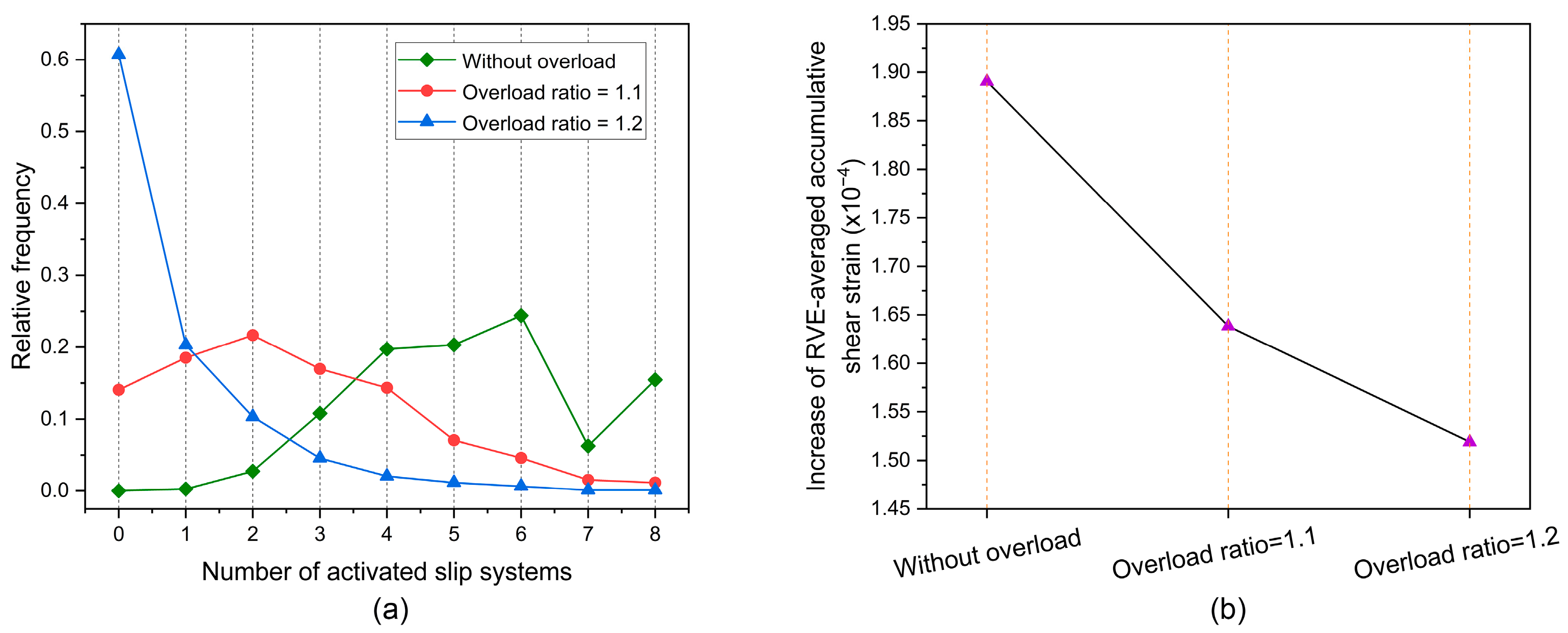
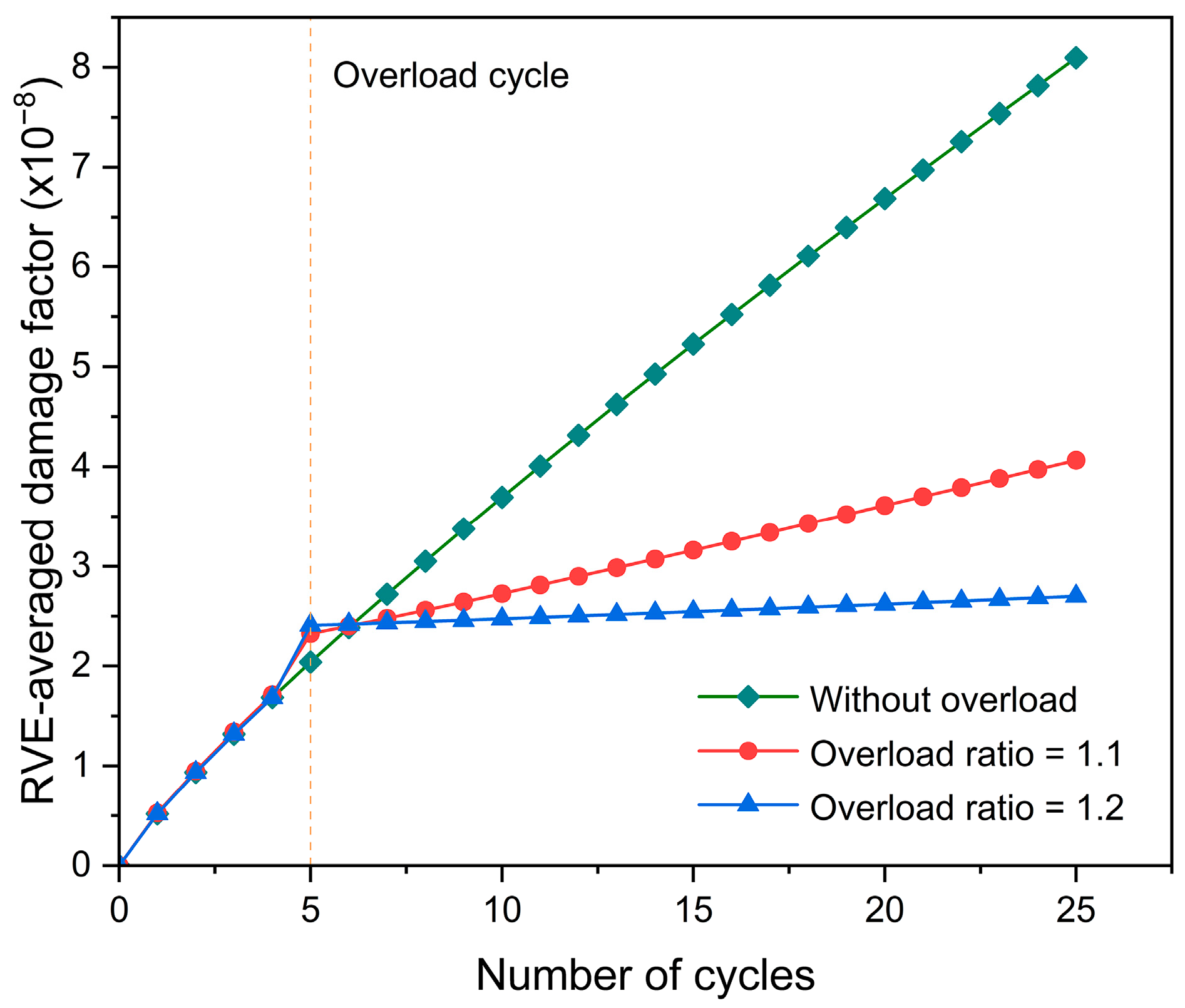
4.1. Evolution of Dislocation Density and Fatigue Damage Ahead of Crack Tip
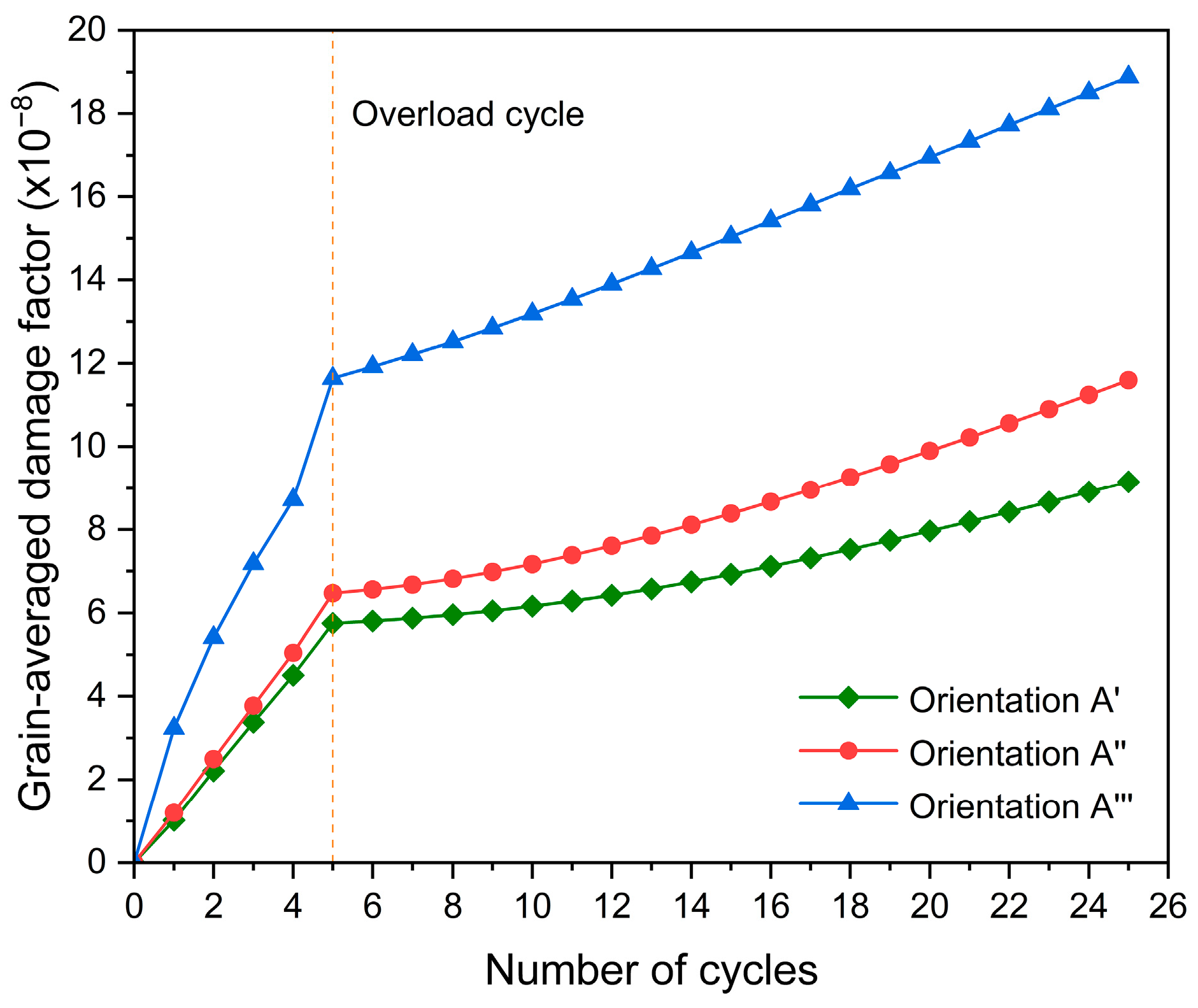
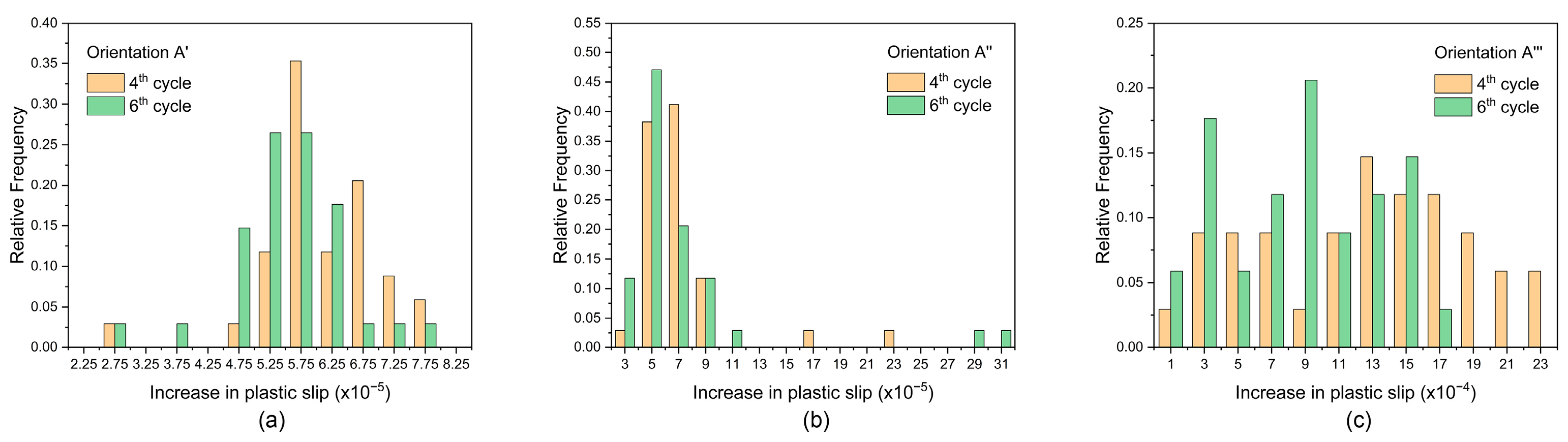
4.2. Effect of Crystallographic Orientation on Damage Accumulation Ahead of Crack Tip
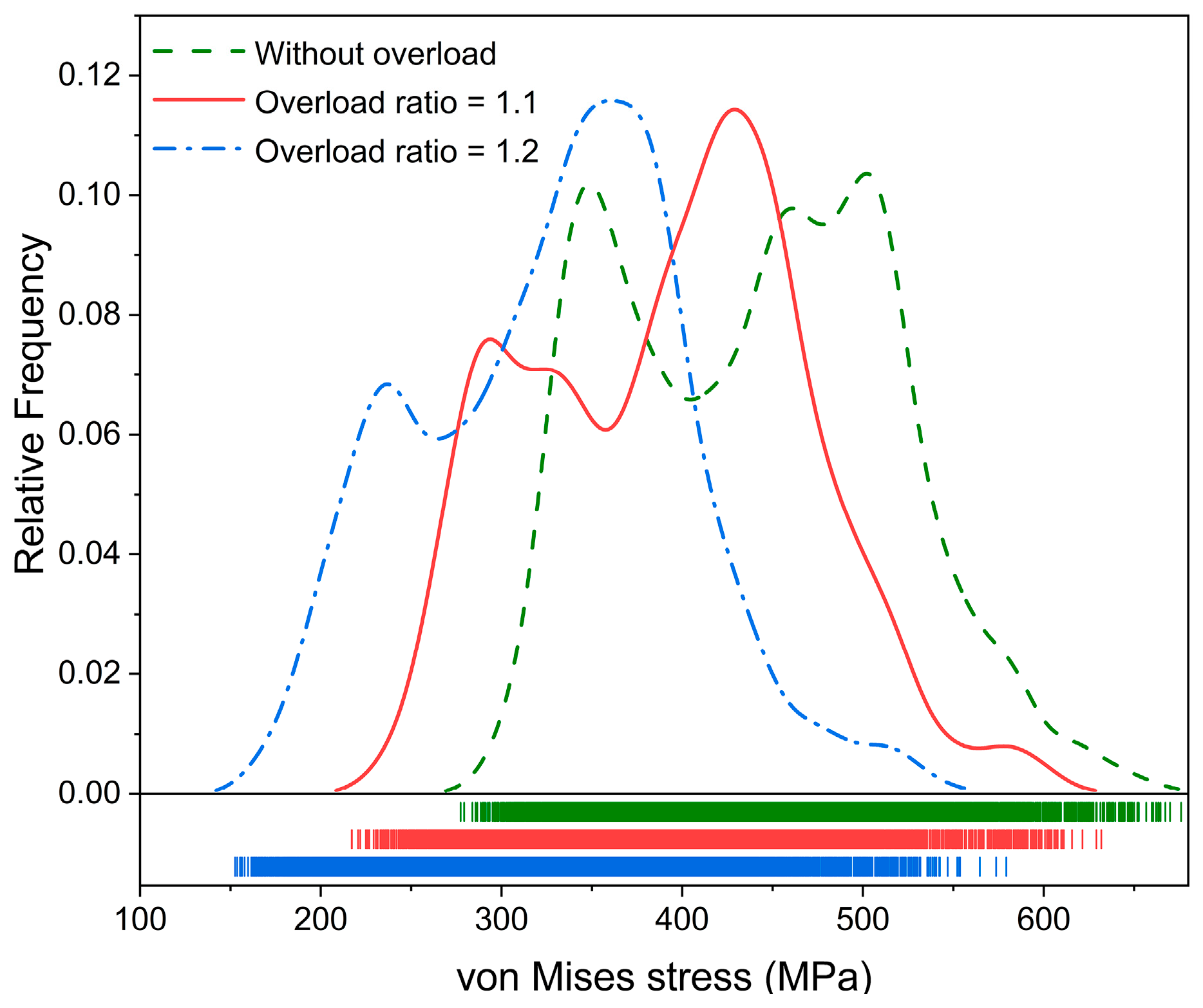
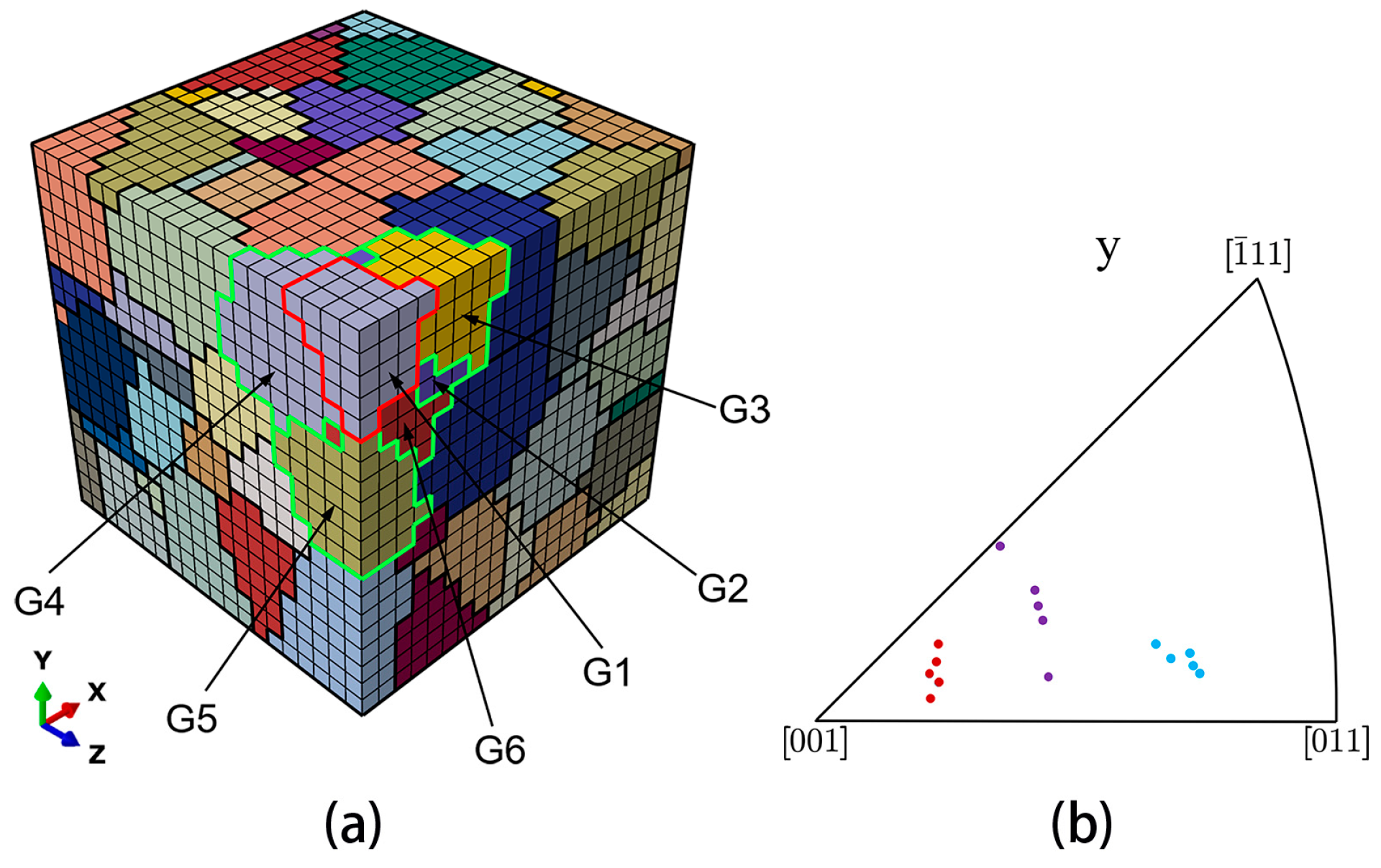
4.3. Effect of the Nearest Neighbor Grains on Damage Evolution Ahead of Crack Tip
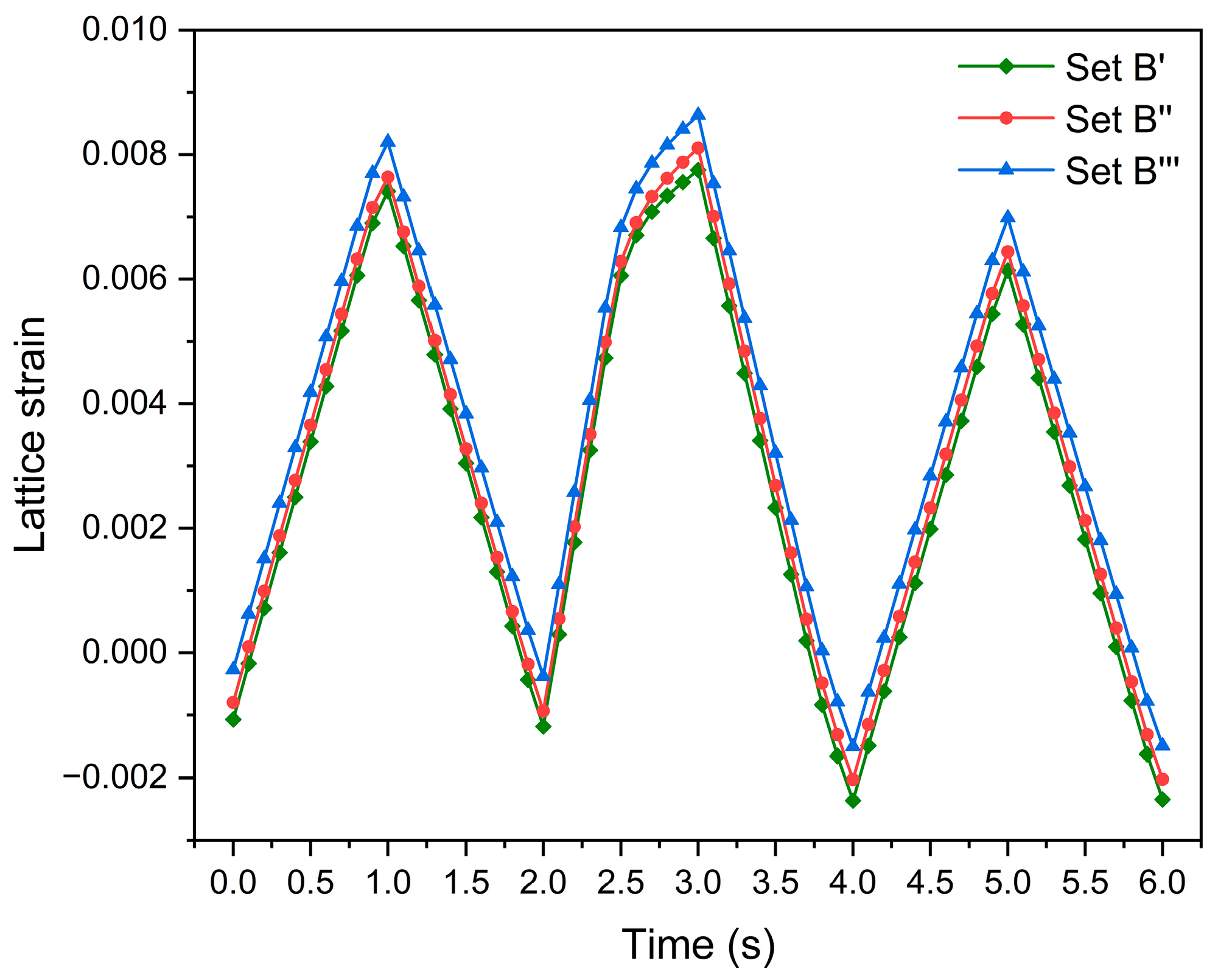
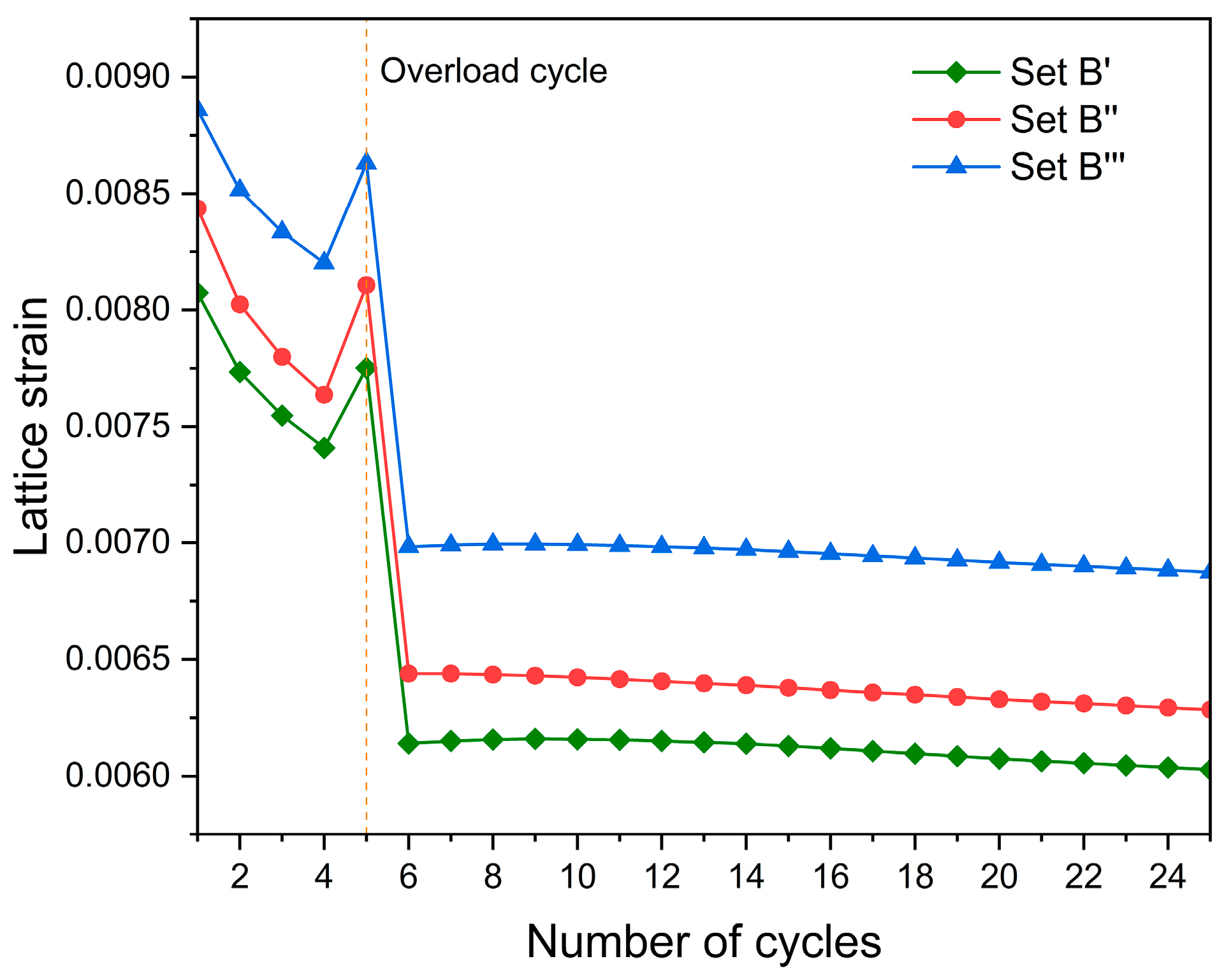
4.4. Effect of the Nearest Neighbor Grains on Lattice Strain Evolution Ahead of Crack Tip
5. Conclusions
- (1)
- The number of activated slip systems is reduced because of the overload effect, causing the rate of increase in dislocation density and damage to decrease before the dislocation density is saturated.
- (2)
- The overload effect changes the crystallographic-orientation-dependent activities of the slip systems, which contributes to the fact that the rate of increase in damage lowers after overload.
- (3)
- The stress and elastic strain of the grain are affected by the crystallographic orientations of its nearest neighbor grains, which eventually affects the rate of increase in damage.
- (4)
- The lattice strain of the grain decreases and is significantly affected by the crystallographic orientations of its nearest neighbor grains.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Liang, H.; Zhan, R.; Wang, D.; Deng, C.; Xu, X.; Guo, B. Effect of crack-tip deformation on fatigue crack growth: A comparative study under overload/underload conditions. Theor. Appl. Fract. Mech. 2022, 118, 103268. [Google Scholar] [CrossRef]
- Tu, W.; Yue, J.; Xie, H.; Tang, W. Fatigue crack propagation behavior of high-strength steel under variable amplitude loading. Eng. Fract. Mech. 2021, 247, 107642. [Google Scholar] [CrossRef]
- Liang, H.; Zhan, R.; Wang, D.; Deng, C.; Guo, B.; Xu, X. Fatigue crack growth under overload/underload in different strength structural steels. J. Constr. Steel Res. 2022, 192, 107213. [Google Scholar] [CrossRef]
- Saarimäki, J.; Moverare, J.; Eriksson, R.; Johansson, S. Influence of overloads on dwell time fatigue crack growth in Inconel 718. Mater. Sci. Eng. A 2014, 612, 398–405. [Google Scholar] [CrossRef]
- Lee, E.U.; Glinka, G.; Vasudevan, A.K.; Iyyer, N.; Phan, N.D. Fatigue of 7075-T651 aluminum alloy under constant and variable amplitude loadings. Int. J. Fatigue 2009, 31, 1858–1864. [Google Scholar] [CrossRef]
- Lee, S.Y.; Liaw, P.K.; Choo, H.; Rogge, R.B. A study on fatigue crack growth behavior subjected to a single tensile overload: Part I. An overload-induced transient crack growth micromechanism. Acta Mater. 2011, 59, 485–494. [Google Scholar] [CrossRef]
- Daneshpour, S.; Dyck, J.; Ventzke, V.; Huber, N. Crack retardation mechanism due to overload in base material and laser welds of Al alloys. Int. J. Fatigue 2012, 42, 95–103. [Google Scholar] [CrossRef]
- He, W.; Wang, C.; Deng, J.; Xie, D.; Zhang, Z. Effect of single tensile overload on fatigue crack growth behavior based on plastically dissipated energy and critical distance theory. Eng. Fract. Mech. 2020, 223, 106744. [Google Scholar] [CrossRef]
- Li, Y.; Aubin, V.; Rey, C.; Bompard, P. Polycrystalline numerical simulation of variable amplitude loading effects on cyclic plasticity and microcrack initiation in austenitic steel 304L. Int. J. Fatigue 2012, 42, 71–81. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, J.; Jiang, Y. A study of fatigue crack growth of 7075–T651 aluminum alloy. Int. J. Fatigue 2008, 30, 1169–1180. [Google Scholar] [CrossRef]
- Celik, C.E.; Vardar, O.; Kalenderoglu, V. Comparison of retardation behaviour of 2024-T3 and 7075-T6 Al alloys. J. Mater. Process. Technol. 2004, 153–154, 945–951. [Google Scholar] [CrossRef]
- Noroozi, A.H.; Glinka, G.; Lambert, S. Prediction of fatigue crack growth under constant amplitude loading and a single overload based on elasto-plastic crack tip stresses and strains. Eng. Fract. Mech. 2008, 75, 188–206. [Google Scholar] [CrossRef]
- Louat, N.; Sadananda, K.; Duesbery, M.; Vasudevan, A.K. A theoretical evaluation of crack closure. Metall. Trans. A 1993, 24, 2225–2232. [Google Scholar] [CrossRef]
- Antunes, F.V.; Sousa, T.; Branco, R.; Correia, L. Effect of crack closure on non-linear crack tip parameters. Int. J. Fatigue 2015, 71, 53–63. [Google Scholar] [CrossRef]
- Chen, R.; Zhu, M.L.; Xuan, F.Z.; Wu, S.C.; Fu, Y.N. Near-tip strain evolution and crack closure of growing fatigue crack under a single tensile overload. Int. J. Fatigue 2020, 134, 105478. [Google Scholar] [CrossRef]
- Seo, S.; Huang, E.W.; Woo, W.; Lee, S.Y. Neutron diffraction residual stress analysis during fatigue crack growth retardation of stainless steel. Int. J. Fatigue 2017, 104, 408–415. [Google Scholar] [CrossRef]
- Salvati, E.; Zhang, H.; Fong, K.S.; Song, X.; Korsunsky, A.M. Separating plasticity-induced closure and residual stress contributions to fatigue crack retardation following an overload. J. Mech. Phys. Solids 2017, 98, 222–235. [Google Scholar] [CrossRef]
- Wahab, M.A.; Rohrsheim, G.R.; Park, J.H. Experimental study on the influence of overload induced residual stress field on fatigue crack growth in aluminium alloy. J. Mater. Process. Technol. 2004, 153–154, 945–951. [Google Scholar] [CrossRef]
- Suresh, S. Micromechanisms of fatigue crack growth retardation following overloads. Eng. Fract. Mech. 1983, 18, 577–593. [Google Scholar] [CrossRef]
- Tvergaard, V. Effect of underloads or overloads in fatigue crack growth by crack-tip blunting. Eng. Fract. Mech. 2006, 73, 869–879. [Google Scholar] [CrossRef]
- Tvergaard, V. Overload effects in fatigue crack growth by crack-tip blunting. Int. J. Fatigue 2005, 27, 1389–1397. [Google Scholar] [CrossRef]
- Kermanidis, A.T.; Pantelakis, S.G. Prediction of crack growth following a single overload in aluminum alloy with sheet and plate microstructure. Eng. Fract. Mech. 2011, 78, 2325–2337. [Google Scholar] [CrossRef]
- Xu, G.; Dong, Q.; Yang, P.; Deng, J. Effect of overload on low cycle fatigue crack growth behavior considering accumulative plastic damage. J. Fail. Anal. Prev. 2022, 22, 346–355. [Google Scholar]
- Jiang, W.; Yu, Y.; Zhang, W.; Xiao, C.; Woo, W. Residual stress and stress fields change around fatigue crack tip: Neutron diffraction measurement and finite element modeling. Int. J. Pres. Ves. Pip. 2020, 179, 104024. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V. Crack-tip stress-strain fields during cyclic loading and effect of overload. Int. J. Fract. 2006, 139, 333–340. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V. Finite-deformation analysis of the crack-tip fields under cyclic loading. Int. J. Solids Struct. 2009, 46, 1937–1952. [Google Scholar] [CrossRef]
- Bahloul, A.; Bouraoui, C. The overload effect on the crack-tip cyclic plastic deformation response in SA333 Gr 6 C-Mn steel. Theor. Appl. Fract. Mech. 2019, 99, 27–35. [Google Scholar] [CrossRef]
- Alvarez, J.E.; Ramos, C.C.R.; Galvis, A.F.; Sollero, P. A fully dynamic bridging approach for modeling the intergranular failure mechanisms in 2D polycrystalline materials. Mech. Mater. 2021, 159, 103920. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Zeng, T.; Yao, Y. Crystal plasticity model to predict fatigue crack nucleation based on the phase transformation theory. Acta Mech. Sin. 2019, 35, 1033–1043. [Google Scholar] [CrossRef]
- Carroll, J.D.; Abuzaid, W.; Lambros, J.; Sehitoglu, H. High resolution digital image correlation measurements of strain accumulation in fatigue crack growth. Int. J. Fatigue 2013, 57, 140–150. [Google Scholar] [CrossRef]
- Lam, T.-N.; Chin, H.-H.; Zhang, X.; Feng, R.; Wang, H.; Chiang, C.-Y.; Lee, S.Y.; Kawasaki, T.; Harjo, S.; Liaw, P.K.; et al. Tensile overload-induced texture effects on the fatigue resistance of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2023, 245, 118585. [Google Scholar] [CrossRef]
- Lee, S.Y.; Huang, E.W.; Wu, W.; Liaw, P.K.; Paradowska, A.M. Development of crystallographic-orientation-dependent internal strains around a fatigue-crack tip during overloading and underloading. Mater. Charact. 2013, 79, 7–14. [Google Scholar] [CrossRef]
- Salvati, E.; O’Connor, S.; Sui, T.; Nowell, D.; Korsunsky, A.M. A study of overload effect on fatigue crack propagation using EBSD, FIB-DIC and FEM methods. Eng. Fract. Mech. 2016, 167, 210–223. [Google Scholar] [CrossRef]
- Zhang, W.; Simpson, C.A.; Lopez-Crespo, P.; Mokhtarishirazabad, M.; Buslaps, T.; Pippan, R.; Withers, P.J. The effect of grain size on the fatigue overload behaviour of nickel. Mater. Des. 2020, 189, 108526. [Google Scholar] [CrossRef]
- Zhang, W.; Simpson, C.A.; Leitner, T.; Zhang, X.; Pippan, R.; Withers, P.J. The effect of anisotropic microstructure on the crack growth and fatigue overload behaviour of ultrafine-grained nickel. Acta Mater. 2020, 184, 225–240. [Google Scholar] [CrossRef]
- Vasco-Olmo, J.M.; James, M.N.; Christopher, C.J.; Patterson, E.A.; Díaz, F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 969–981. [Google Scholar] [CrossRef]
- Luo, C.; Yuan, H. Anisotropic thermomechanical fatigue of a nickel-base single-crystal superalloy Part I: Effects of crystal orientations and damage mechanisms. Int. J. Fatigue 2023, 168, 107438. [Google Scholar] [CrossRef]
- Yuan, G.-J.; Zhang, X.-C.; Chen, B.; Tu, S.-T.; Zhang, C.-C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Ihara, C.; Tanaka, T. A stochastic damage accumulation model for crack initiation in high-cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2001, 23, 375–380. [Google Scholar] [CrossRef]
- Sagar, S.P.; Das, S.; Parida, N.; Bhattacharya, D.K. Non-linear ultrasonic technique to assess fatigue damage in structural steel. Scr. Mater. 2006, 55, 199–202. [Google Scholar]
- Stopka, K.S.; Yaghoobi, M.; Allison, J.E.; McDowell, D.L. Simulated effects of sample size and grain neighborhood on the modeling of extreme value fatigue response. Acta Mater. 2022, 224, 117524. [Google Scholar] [CrossRef]
- Zheng, L.L.; Gao, Y.F.; Wang, Y.D.; Stoica, A.D.; An, K.; Wang, X.L. Grain orientation dependence of lattice strains and intergranular damage rates in polycrystals under cyclic loading. Scr. Mater. 2013, 68, 265–268. [Google Scholar] [CrossRef]
- Ekh, M.; Lillbacka, R.; Runesson, K. A model framework for anisotropic damage coupled to crystal (visco)plasticity. Int. J. Plast. 2004, 20, 2143–2159. [Google Scholar] [CrossRef]
- Farukh, F.; Zhao, L.G.; Jiang, R.; Reed, P.; Proprentner, D.; Shollock, B.A. Realistic microstructure-based modelling of cyclic deformation and crack growth using crystal plasticity. Comput. Mater. Sci. 2016, 111, 395–405. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, F.; Chen, T. Effect of single overload on fatigue crack growth in QSTE340TM steel and retardation model modification. Eng. Fract. Mech. 2019, 212, 81–94. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Shi, G.; Gao, Y.; Wang, X.; Zhang, Y. Mechanical properties and constitutive models of low yield point steels. Constr. Build. Mater. 2018, 175, 570–587. [Google Scholar] [CrossRef]
- Basan, R.; Franulović, M.; Prebil, I.; Kunc, R. Study on Ramberg-Osgood and Chaboche models for 42CrMo4 steel and some approximations. J. Constr. Steel Res. 2017, 136, 65–74. [Google Scholar] [CrossRef]
- Koo, G.H.; Lee, J.H. Investigation of ratcheting characteristics of modified 9Cr-1Mo steel by using the Chaboche constitutive model. Int. J. Pres. Ves. Pip. 2007, 84, 284–292. [Google Scholar] [CrossRef]
- Trinh, T.D.; Iwamoto, T. A Crystal Plasticity Simulation on Strain-induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata. Metals 2021, 11, 1316. [Google Scholar] [CrossRef]
- Rehrl, C.; Völker, B.; Kleber, S.; Antretter, T.; Pippan, R. Crystal orientation changes: A comparison between a crystal plasticity finite element study and experimental results. Acta Mater. 2012, 60, 2379–2386. [Google Scholar] [CrossRef]
- Zhang, W.T.; Jiang, R.; Zhao, Y.; Zhang, L.C.; Zhang, L.; Zhao, L.G.; Song, Y.D. Effects of temperature and microstructure on low cycle fatigue behaviour of a PM Ni-based superalloy: EBSD assessment and crystal plasticity simulation. Int. J. Fatigue 2022, 159, 106818. [Google Scholar] [CrossRef]
- Sharma, R.; Sargeant, D.; Daroju, S.; Knezevic, M.; Miles, M.P.; Fullwood, D.T. Multi-strain path deformation behavior of AA6016-T4: Experiments and crystal plasticity modeling. Int. J. Solids Struct. 2022, 244–245, 111536. [Google Scholar] [CrossRef]
- Pesin, A.; Korchunov, A.; Pustovoytov, D. Numerical study of grain evolution and dislocation density during asymmetric rolling of aluminum alloy 7075. Key Eng. Mater. 2015, 685, 162–166. [Google Scholar] [CrossRef]
- Khadyko, M.; Dumoulin, S.; Cailletaud, G.; Hopperstad, O.S. Latent hardening and plastic anisotropy evolution in AA6060 aluminium alloy. Int. J. Plast. 2016, 76, 51–74. [Google Scholar] [CrossRef]
- Kitayama, K.; Tomé, C.N.; Rauch, E.F.; Gracio, J.J.; Barlat, F. A crystallographic dislocation model for describing hardening of polycrystals during strain path changes. Application to low carbon steels. Int. J. Plast. 2013, 46, 54–69. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Oskay, C.; Hu, P.; Ying, L.; Wang, D. Experimental and computational study of microstructural effect on ductile fracture of hot-forming materials. Mater. Sci. Eng. A 2018, 724, 298–323. [Google Scholar] [CrossRef]
- Bathias, C. Retrospective view on the role of the plastic zone at a fatigue crack tip. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 1301–1306. [Google Scholar] [CrossRef]
- Paul, S.K. Numerical models of plastic zones and associated deformations for elliptical inclusions in remote elastic loading-unloading with different R-ratios. Eng. Fract. Mech. 2016, 152, 72–80. [Google Scholar] [CrossRef]
- Paul, S.K. Numerical models of plastic zones and associated deformations for a stationary crack in a C(T) specimen loaded at different R-ratios. Theor. Appl. Fract. Mech. 2016, 84, 183–191. [Google Scholar] [CrossRef]
- Lemaitre, J. Coupled elasto-plasticity and damage constitutive equations. Comput. Meth. Appl. Mech. Eng. 1985, 51, 31–49. [Google Scholar] [CrossRef]
- Brünig, M.; Gerke, S.; Hagenbrock, V. Micro-mechanical studies on the effect of the stress triaxiality and the Lode parameter on ductile damage. Int. J. Plast. 2013, 50, 49–65. [Google Scholar] [CrossRef]
- Yu, F.; Jar, P.Y.B.; Hendry, M.T. Constitutive analysis of pressure-insensitive metals under axisymmetric tensile loading: A stress triaxiality-dependent plasticity damage model. Int. J. Mech. Sci. 2018, 142–143, 21–32. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, C.; Chen, J.; Huang, Z. A crystal plasticity model of low cycle fatigue damage considering dislocation density, stress triaxiality and Lode parameter. Int. J. Fatigue 2023, 175, 107823. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, M.L.; Zhang, C.J.; He, P.F.; Dai, Y. Experimental investigation and crystal plasticity modeling of combined high and low cycle loading on AISI 4140 steel. Int. J. Fatigue 2023, 168, 107465. [Google Scholar] [CrossRef]
- Xu, C. Research on Low Cycle Fatigue Behavior and Damage Mechanism of 7075 Aluminum Alloy. Master’ Thesis, Shanghai University of Engineering Science, Shanghai, China, 2012. [Google Scholar]
- Bong, H.J.; Lee, J.; Hu, X.; Sun, X.; Lee, M. Predicting forming limit diagrams for magnesium alloys using crystal plasticity finite elements. Int. J. Plast. 2020, 126, 102630. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Jia, Y.-F.; Li, D.-F.; Yuan, G.-J.; Zhang, X.-C.; Tu, S.-T. A modified kinematic hardening model considering hetero-deformation induced hardening for bimodal structure based on crystal plasticity. Int. J. Mech. Sci. 2021, 191, 106068. [Google Scholar] [CrossRef]
- Bacca, M.; Hayhurst, D.R.; McMeeking, R.M. Continuous dynamic recrystallization during severe plastic deformation. Mech. Mater. 2018, 90, 148–156. [Google Scholar] [CrossRef]
- Messerschmidt, U.; Bartsch, M. Generation of dislocations during plastic deformation. Mater. Chem. Phys. 2003, 81, 518–523. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tome, C.N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metal. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Kirchlechner, C.; Imrich, P.J.; Liegl, W.; Pörnbacher, J.; Micha, J.S.; Ulrich, O.; Motz, C. On the reversibility of dislocation slip during small scale low cycle fatigue. Acta Mater. 2015, 94, 69–77. [Google Scholar] [CrossRef]
- Zhang, J.; Joshi, S.P. Phenomenological crystal plasticity modeling and detailed micromechanical investigations of pure magnesium. J. Mech. Phys. Solids 2012, 60, 945–972. [Google Scholar] [CrossRef]
- Kanjarla, A.K.; Lebensohn, R.A.; Balogh, L.; Tomé, C.N. Study of internal lattice strain distributions in stainless steel using a full-field elasto-viscoplastic formulation based on fast Fourier transforms. Acta Mater. 2012, 60, 3094–3106. [Google Scholar] [CrossRef]







| AA2 | AA3 | AA6 | BB2 | BB4 | BB5 | CC1 | CC3 | CC5 | DD1 | DD4 | DD6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AA2 | M0 | M1 | M1 | M3 | M4 | M4 | M2 | M4 | M5 | M2 | M5 | M4 |
| AA3 | M0 | M1 | M4 | M2 | M5 | M4 | M3 | M4 | M5 | M2 | M4 | |
| AA6 | M0 | M5 | M5 | M2 | M5 | M4 | M2 | M4 | M4 | M3 | ||
| BB2 | M0 | M1 | M1 | M2 | M5 | M4 | M2 | M4 | M5 | |||
| BB4 | M0 | M1 | M5 | M2 | M4 | M4 | M3 | M4 | ||||
| BB5 | M0 | M4 | M4 | M3 | M5 | M4 | M2 | |||||
| CC1 | M0 | M1 | M1 | M3 | M4 | M4 | ||||||
| CC3 | M0 | M1 | M4 | M2 | M5 | |||||||
| CC5 | M0 | M4 | M5 | M2 | ||||||||
| DD1 | M0 | M1 | M1 | |||||||||
| DD4 | M0 | M1 | ||||||||||
| DD6 | M0 |
| M1 | M2 | M3 | M4 | M5 | M6 |
|---|---|---|---|---|---|
| 0.068 | 0.068 | 0.0454 | 0.625 | 0.137 | 0.122 |
| C1 | λ1 | C2 | λ2 | C3 |
|---|---|---|---|---|
| 30,000 MPa | 350 | 3000 MPa | 70 | 265 MPa |
| λ3 | σ0 | Qsat | ||
| 50 | 255 MPa | 55 MPa | 15 |
| C11 | C12 | C44 | K | n | r1 |
|---|---|---|---|---|---|
| 98,413 MPa | 44,214 MPa | 27,099 MPa | 35 MPa | 50 | 25,000 MPa |
| r2 | τ0 | μ | b | G | kdeb |
| 650 | 95 MPa | 0.9 | 2.86 × 10−10 m | 27,862 MPa | 0.086 |
| k1 | ψ | q | p | ||
| 5 × 106 m−1 | 0.55 | 75.61 MPa | 107 | 685 MPa | 0.8 |
| σY | ϑ | υ | M | ||
| 405 MPa | 35.5 | 3.5 × 10−13 | 2.2 |
| Misorientation | Schmid Factor | |||
|---|---|---|---|---|
| Grain G1 | Set B′ | Set B″ | Set B‴ | |
| 35° | 0.33 | 0.36 | 0.39 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, C.; Zheng, Z.; Li, L.; Sun, T. The Overload Effect on the Crack Tip Damage Mechanism in a 7075 Aluminum Alloy. Materials 2024, 17, 4088. https://doi.org/10.3390/ma17164088
Xie C, Zheng Z, Li L, Sun T. The Overload Effect on the Crack Tip Damage Mechanism in a 7075 Aluminum Alloy. Materials. 2024; 17(16):4088. https://doi.org/10.3390/ma17164088
Chicago/Turabian StyleXie, Changji, Zhanguang Zheng, Li Li, and Teng Sun. 2024. "The Overload Effect on the Crack Tip Damage Mechanism in a 7075 Aluminum Alloy" Materials 17, no. 16: 4088. https://doi.org/10.3390/ma17164088





