Study of Ultra-High Performance Concrete Mechanical Behavior under High Temperatures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Composition of UHPC
2.2. Factorial Design
2.3. Combination of Study Factors
2.4. Mixing and Casting Procedure
- (1)
- Add 50% of the cement + 100% of the silica + 100% of the water, and mix for 5 min at low speed;
- (2)
- Add 25% of the cement + 100% of the additive, and mix for 5 min at medium speed;
- (3)
- Add 25% of the cement and mix for 5 min at high speed;
- (4)
- Add 100% of the sand + 100% of the quartz powder, and mix for 5 min at high speed;
- (5)
- Add fibers evenly and mix for 5 min, with the speed being low during fiber insertion and high soon after.
2.5. Description of the Drying Process and Application of High Temperatures
2.6. Tests Performed
3. Results and Discussion
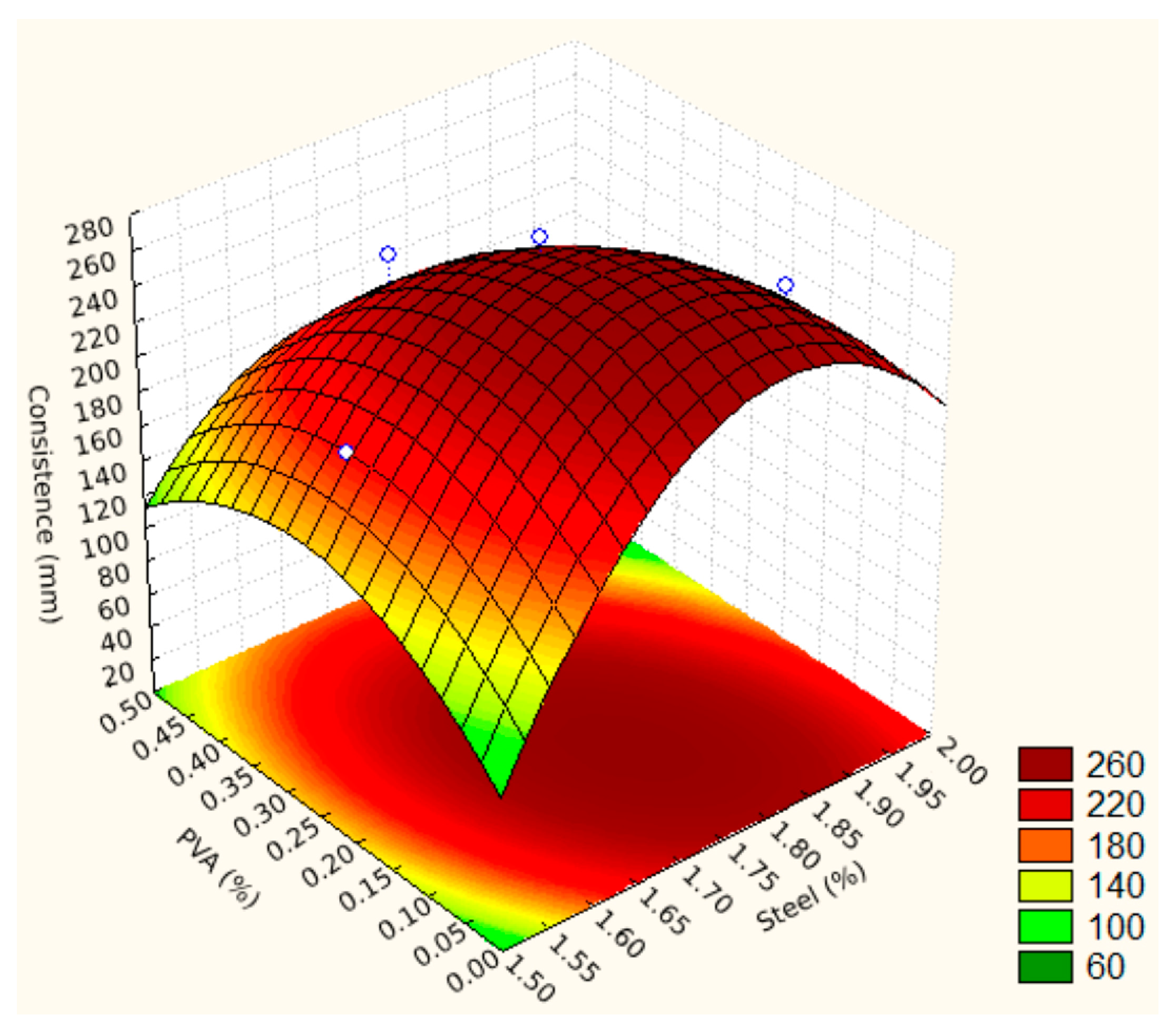
3.1. Consistence Index
- Ca: UHPC, which may be self-compacting (diameter 270 mm). Generally able to be placed without vibration or use of a mechanical flow aid;
- Cv: viscous UHPC (230 mm diameter < 270 mm). Generally able to be placed without vibration but which requires the use of a mechanical flow aid;
- Ct: UHPC exhibiting a flow threshold (diameter < 230 mm). Generally able to flow under the effect of dynamic shearing but whose free surface at rest may keep sloping.
1611.1337948474 × P − 883.33333333313 × P2 − 751.11111111085 × A × P
3.2. Compressive Strength and Elasticity Modulus
- A factorial 23 design was used to determine an initial response surface;
- The response surface equation from the previous step was used to determine the fc values of the missing cells to carry out two 22 factorial designs, wherein the PVA fiber was set at 0.25% and the steel fiber was set at 1.75%. In this way, the fc values were determined for a temperature equal to 310 °C;
- Once the fc values for a temperature equal to 310 °C were obtained, a 23 factorial design was carried out in order to determine the remaining fc values (for temperatures equal to 482 °C and 600 °C);
- Finally, a final 23 factorial design was performed using all tests and estimated values to construct the response surface to be analyzed.
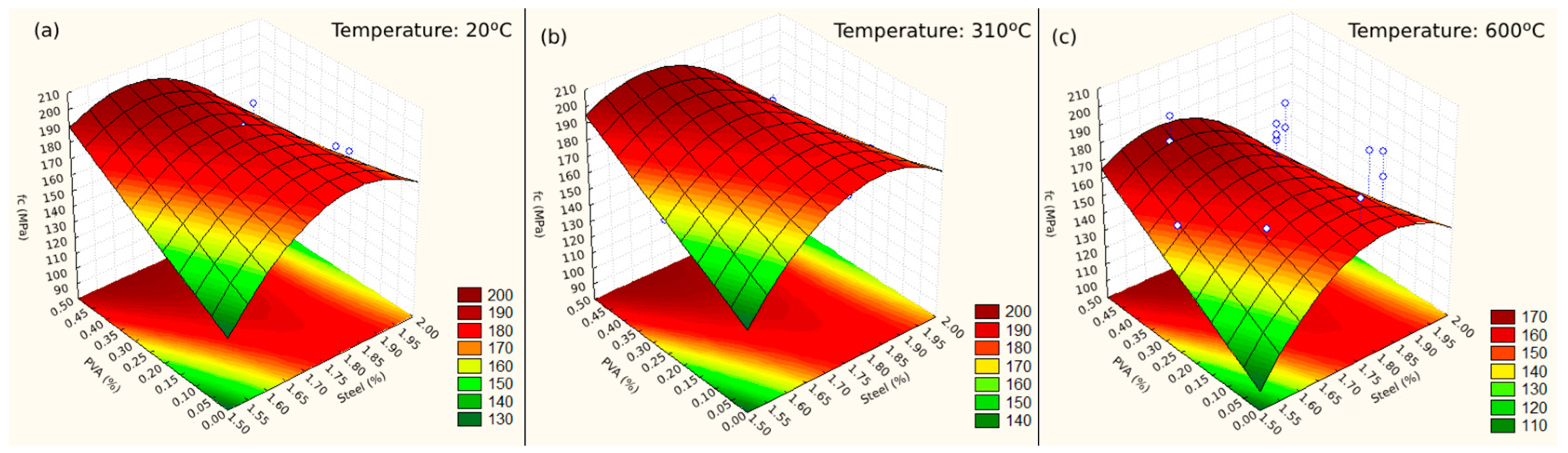
3.2.1. Compressive Strength
1849.9247355629 × A − 505.4942376002 × A2 + 678.7990434340 × P + 0.0017623997 × P2 −
0.0000006460 × T × P − 367.5148148148 × A × P
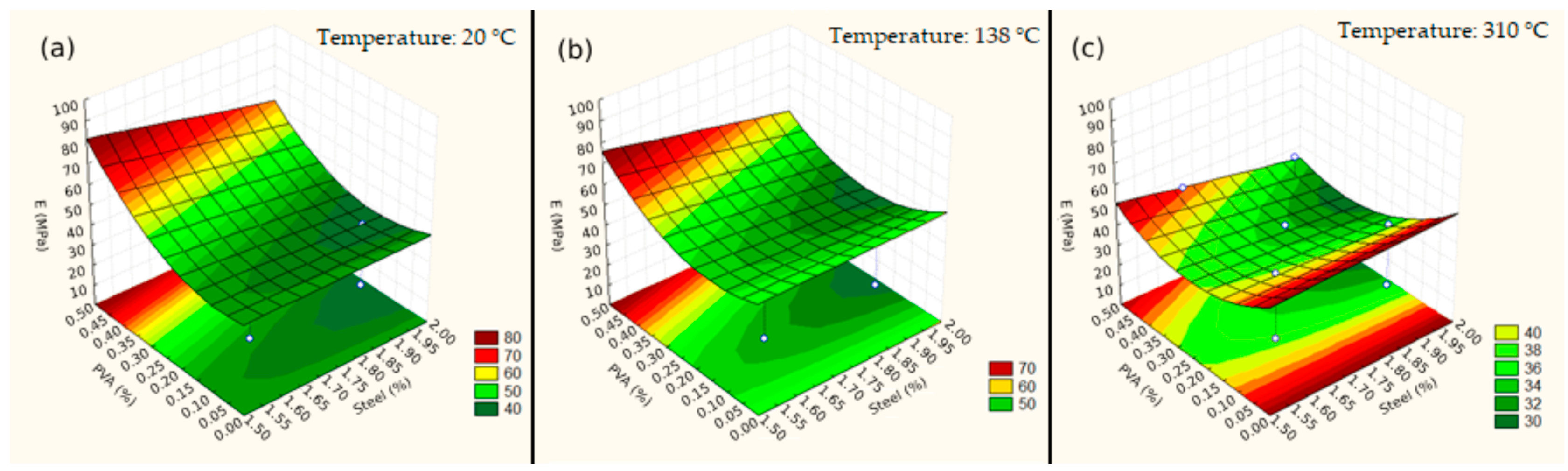
3.2.2. Elasticity Modulus
A − 0.0003231396 × A2 + 84.7319703553 × P + 220,5596768604 × P2 −
0.0000000311 × T × A − 0.2717441860 × T × P − 75.77777778 × A × P
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christ, R.; Pacheco, F.; Tutikian, B.; Helene, P. Aplicação do concreto de ultra-alto desempenho (UHPC) em sistema construtivo habitacional no brasil. Concreto Construções 2019, 4, 52–55. [Google Scholar]
- Sohail, M.G.; Wang, B.; Jain, A.; Kahraman, R.; Ozerkan, N.G.; Gencturk, B.; Dawood, M.; Belarbi, A. Advancements in concrete mix designs: High-performance and ultrahigh-performance concretes from 1970 to 2016. J. Mater. Civ. Eng. 2018, 30, 04017310. [Google Scholar] [CrossRef]
- François, T.; Sébastien, B.; Yves, B.; Alain, S. Twenty years-long French experience in UHPFRC application and paths opened from the completion of the standards for UHPFRC. In Proceedings of the UHPC 2018, 2nd International Conference on UHPC Materials and Structures, Fuzhou, China, 7–10 November 2018; p. 24, bibliogr. ffhal-01955204v2. [Google Scholar]
- Costa, A.C.S.d.S.; Cabral, A.E.B. Estudo comparativo entre o concreto autoadensável e o concreto convencional vibrado em obra vertical. Ambiente Construído 2019, 19, 289–301. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Q.; Shang, H.; Wang, J.; Song, N. Development of sustainable ultra-high-performance concrete (UHPC) by synergistic utilization of red mud and limestone powder. J. Build. Eng. 2024, 90, 109372. [Google Scholar] [CrossRef]
- Mohamed, A.; Abdullah, Z.; Ibrahim, A.; Mostafa, R. Effect of industrial wastes on the properties of sustainable ultra-high-performance concrete: Ganite, ceramic, and glass. Constr. Build. Mater. 2024, 428, 136292. [Google Scholar]
- Chu, H.; Wang, Q.; Zhang, W. Optimizing ecological ultra-high performance concrete prepared with incineration bottom ash: Utilization of Al2O3 micro powder for improved mechanical properties and durability. Constr. Build. Mater. 2024, 426, 136152. [Google Scholar] [CrossRef]
- Cunha, V.; Al-Rikabi, T.; Barros, J. Betão de alta resistência reforçado com fibras exposto a elevadas temperaturas. In Proceedings of the HAC2018|V Congreso Iberoamericano de Hormigón Autocompactante y Hormigones Especiales, València, Spain, 6 May 2018; pp. 455–464. [Google Scholar]
- Britez, C.; Carvalho, M.; Helene, P. Fire impacts on concrete structures. a brief review. Alconpat 2020, 10, 1–21. [Google Scholar]
- Wu, H.; Lin, X.; Zhou, A. A review of mechanical properties of fibre reinforced concrete at elevated temperatures. Cem. Concr. Res. 2020, 135, 106–117. [Google Scholar] [CrossRef]
- Zhu, Y.; Hussein, H.; Kumar, A.; Chen, G. A review: Material and structural Properties of UHPC at elevated temperatures or fire conditions. Cem. Concr. Compos. 2021, 123, 104212. [Google Scholar] [CrossRef]
- Park, J.-J.; Yoo, D.-Y.; Kim, S.; Kim, S.-W. Benefits of synthetic fibers on the residual mechanical performance of UHPFRC after exposure to iso standard fire. Cem. Concr. Compos. 2019, 104, 103401. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Abushanab, A.; Alam, M.S. Hybrid machine learning model and predictive equations for compressive stress-strain constitutive modelling of confined ultra-high-performance concrete (UHPC) with normal-strength steel and high-strength steel spirals. Eng. Struct. 2024, 304, 117633. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Alam, M.S. Peak and ultimate stress-strain model of confined ultra-high-performance concrete (UHPC) using hybrid machine learning model with conditional tabular generative adversarial network. Appl. Soft Comput. 2024, 154, 111353. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Alam, M.S. Performance-based seismic design of Ultra-High-Performance Concrete (UHPC) bridge columns with design example—Powered by explainable machine learning model. Eng. Struct. 2024, 314, 118346. [Google Scholar] [CrossRef]
- Vigneshwari, M.; Arunachalam, K.; Angayarkanni, A. Replacement of silica fume with thermally treated rice husk ash in reactive powder concrete. J. Clean. Prod. 2018, 188, 264–277. [Google Scholar] [CrossRef]
- NF P18-470; Concrete—Ultra-High Performance Fibre-Reinforced Concrete—Specifications, Performance, Production and Conformity. Association Française de Normalisation: Saint-Denis, France, 2016; p. 94.
- NBR 16697; Cimento Portland—Requisitos. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2018.
- Fan, D.; Zhu, J.; Fan, M.; Lu, J.-X.; Chu, S.; Dong, E.; Yu, R. Intelligent design and manufacturing of ultra-high performance concrete (UHPC)—A review. Constr. Build. Mater. 2023, 385, 131495. [Google Scholar] [CrossRef]
- Ferdosian, I.; Camoes, A. Eco-efficient ultra-high performance concrete development by means of response surface methodology. Cem. Concr. Compos. 2017, 84, 146–156. [Google Scholar] [CrossRef]
- Ghafari, E.; Costa, H.; Julio, E. Rsm-based model to predict the performance of self-compacting UHPC reinforced with hybrid steel micro-fibers. Constr. Build. Mater. 2014, 66, 375–383. [Google Scholar] [CrossRef]
- Santos, R.L.B. Análise de Dados e Superfície de Resposta: Um Estudo de Caso para Melhorar o Desempenho de um Serviço. Ph.D. Thesis, Universidade Federal Fluminense, Niterói, RJ, Brazil, 2017. [Google Scholar]
- Wang, X.; Wu, D.; Zhang, J.; Yu, R.; Hou, D.; Shui, Z. Design of sustainable ultra-high performance concrete: A review. Constr. Build. Mater. 2021, 307, 124643. [Google Scholar] [CrossRef]
- Dey, A.; Rumman, R.; Wakjira, T.G.; Jindal, A.; Bediwy, A.G.; Islam, M.S.; Alam, M.S.; Al Martini, S.; Sabouni, R. Towards net-zero emission: A case study investigating sustainability potential of geopolymer concrete with recycled glass powder and gold mine tailings. J. Build. Eng. 2024, 86, 108683. [Google Scholar] [CrossRef]
- Nassif, N.; Zeiada, W.; Al-Khateeb, G.; Haridy, S.; Altoubat, S. Assessment of Punching Shear Strength of Fiber-reinforced Concrete Flat Slabs Using Factorial Design of Experiments. Jordan J. Civ. Eng. 2022, 16, 139–154. [Google Scholar]
- Sumitomo, G.S. Study of the Mechanical Behavior of UHPFRC Produced with Steel and PVA Fibers Subjected to High Temperatures. Master’s Thesis, Pontifical Catholic University of Campinas, Campinas, Brazil, 2022. [Google Scholar]
- Sanchayan, S.; Foster, S.J. High temperature behaviour of hybrid steel–pva fibre reinforced reactive powder concrete. Mater. Struct. 2016, 49, 769–782. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K. Effect of hybrid fibers on fresh, mechanical properties, and autogenous shrinkage of cost effective UHPC. J. Mater. Civ. Eng. 2018, 30, 04018030. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Kim, S.; Park, G.-J.; Park, J.-J. Residual performance of hpfrcc exposed to fire—Effects of matrix strength, synthetic fiber, and fire duration. Constr. Build. Mater. 2020, 241, 118038. [Google Scholar] [CrossRef]
- Amran, M. Fire-induced spalling of ultra-high performance concrete: A systematic critical review. Constr. Build. Mater. 2023, 373, 130869. [Google Scholar] [CrossRef]
- Iffat, S.; Bose, B. A review on concrete structures in fire. Int. J. Civ. Environ. Struct. Constr. Archit. Eng. 2016, 10, 109–114. [Google Scholar]
- NBR 7215; Cimento Portland—Determinação da Resistência à Compressão de Corpos de Prova Cilíndricos. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2019.
- NBR 5739; Concreto—Ensaio de Compressão de Corpos de Prova Cilíndricos. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2018.
- NBR 8522-1; Concreto Endurecido—Determinação dos Módulos de Elasticidade e de Deformação—Parte 1: Módulos Estáticos à Compressão. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2021.
- Mayhoub, O.; Nasr, E.-S.; Ali, Y.; Kohail, M. The influence of ingredients on the properties of reactive powder concrete: A review. Ain Shams Eng. J. 2020, 12, 145–158. [Google Scholar] [CrossRef]
- Rasul, M.; Ahmad, S.; Adekunle, S.K.; Al-Dulaijan, S.U.; Maslehuddin, M.; Ali, S.I. Evaluation of the Effect of Exposure Duration and Fiber Content on the Mechanical Properties of Polypropylene Fiber-Reinforced UHPC Exposed to Sustained Elevated Temperature. J. Test. Eval. 2020, 48, 4355–4369. [Google Scholar] [CrossRef]



| Cement | Silica Fume | Quartz Sand | Quartz Powder | Superplasticizer | Water |
|---|---|---|---|---|---|
| 922.880 | 179.160 | 1015.168 | 92.288 | 36.915 | 179.160 |
| Variable | Symbol | Type | Value Range | |
|---|---|---|---|---|
| Minimum | Maximum | |||
| Temperature (°C) | T | Independent | 20 | 600 |
| Steel fiber (%) | FA | Independent | 1.5 | 2.0 |
| PVA fiber (%) | FPVA | Independent | 0 | 0.5 |
| Fluidity (mm) | Vr1 | Dependent | - | - |
| Compressive strength (MPa) | Vr2 | Dependent | - | - |
| Elasticity modulus (GPa) | Vr3 | Dependent | - | - |
| Variable | Coded Variable | ||||
|---|---|---|---|---|---|
| −α | −1 | 0 | 1 | α | |
| T | 20 | 138 | 310 | 482 | 600 |
| FA | 1.50 | 1.60 | 1.75 | 1.90 | 2.00 |
| FPVA | 0.00 | 0.10 | 0.25 | 0.40 | 0.50 |
| Mix | Coded Variable | Experimental Values | |||||
|---|---|---|---|---|---|---|---|
| T | FA | FPVA | T (°C) | FA (%) | FPVA (%) | ||
| Factorial points | T1 | −1 | −1 | −1 | 138 | 1.60 | 0.10 |
| T2 | −1 | −1 | 1 | 138 | 1.60 | 0.40 | |
| T3 | −1 | 1 | −1 | 138 | 1.90 | 0.10 | |
| T4 | −1 | 1 | 1 | 138 | 1.90 | 0.40 | |
| T5 | 1 | −1 | −1 | 482 | 1.60 | 0.10 | |
| T6 | 1 | −1 | 1 | 482 | 1.60 | 0.40 | |
| T7 | 1 | 1 | −1 | 482 | 1.90 | 0.10 | |
| T8 | 1 | 1 | 1 | 482 | 1.90 | 0.40 | |
| Axial points | T9 | −1.682 | 0 | 0 | 20 | 1.75 | 0.25 |
| T10 | 1.682 | 0 | 0 | 600 | 1.75 | 0.25 | |
| T11 | 0 | −1.682 | 0 | 310 | 1.50 | 0.25 | |
| T12 | 0 | 1.682 | 0 | 310 | 2.00 | 0.25 | |
| T13 | 0 | 0 | −1.682 | 310 | 1.75 | 0.00 | |
| T14 | 0 | 0 | 1.682 | 310 | 1.75 | 0.50 | |
| Center points | T15 | 0 | 0 | 0 | 310 | 1.75 | 0.25 |
| T16 | 0 | 0 | 0 | 310 | 1.75 | 0.25 | |
| Mix | Consistence Index (Flow Table) | |
|---|---|---|
| Diameter (mm) | Classes (NF P-18 470 [17]) | |
| 1 and 5 | 203.33 | Ct |
| 2 and 6 | 175.40 | Ct |
| 3 and 7 | 257.93 | Cv |
| 4 and 8 | 162.40 | Ct |
| 9 | 278.05 | Ca |
| 10 | 251.70 | Cv |
| 11 | 204.45 | Ct |
| 12 | 191.23 | Ct |
| 13 | 250.80 | Cv |
| 14 | 215.08 | Ct |
| 15 and 16 | 328.53 | Ca |
| Mix | Temp. (°C) | Steel (%) | PVA (%) | Resp. Surface fc* (MPa) | Experimental fc (MPa) |
|---|---|---|---|---|---|
| 1 | 138 | 1.60 | 0.10 | 169.86 | 169.47 |
| 2 | 138 | 1.60 | 0.40 | 196.70 | 196.71 |
| 3 | 138 | 1.90 | 0.10 | 182.78 | 182.66 |
| 4 | 138 | 1.90 | 0.40 | 177.13 | 176.81 |
| 5 # | 482 | 1.60 | 0.10 | 156.15 | 155.76 |
| 6 # | 482 | 1.60 | 0.40 | 182.99 | 183.00 |
| 7 # | 482 | 1.90 | 0.10 | 169.07 | 168.95 |
| 8 # | 482 | 1.90 | 0.40 | 163.42 | 163.10 |
| 9 | 20 | 1.75 | 0.25 | 186.22 | 186.22 |
| 10 | 600 | 1.75 | 0.25 | 163.10 | 163.10 |
| 11 # | 310 | 1.50 | 0.25 | 163.25 | 163.25 |
| 12 # | 310 | 2.00 | 0.25 | 157.66 | 157.66 |
| 13 # | 310 | 1.75 | 0.00 | 183.14 | 229.29 |
| 14 # | 310 | 1.75 | 0.50 | 200.96 | 249.91 |
| 15 | 310 | 1.75 | 0.25 | 192.05 | 195.00 |
| 16 | 310 | 1.75 | 0.25 | 192.05 | 189.10 |
| Factors | Sum of Squares (SS) | Degree of Freedom (df) | Mean Square (MS) | Fcalculated | p |
|---|---|---|---|---|---|
| (1) Temperature (°C) (L) | 643.130 | 1 | 643.130 | 221.45 | 0.000 |
| Temperature (°C) (Q) | 315.872 | 1 | 315.872 | 121.16 | 0.000 |
| (2) Steel (%) (L) | 38.150 | 1 | 38.150 | 13.14 | 0.011 |
| Steel (%) (Q) | 1168.896 | 1 | 1168.896 | 402.50 | 0.000 |
| (3) PVA (%) (L) | 387.631 | 1 | 387.631 | 133.48 | 0.000 |
| PVA (%) (Q) | 0.000 | 1 | 0.000 | 0.00 | 1.000 |
| 1 L by 2 L | 0.000 | 1 | 0.000 | 0.00 | 1.000 |
| 1 L by 3 L | 0.000 | 1 | 0.000 | 0.00 | 1.000 |
| 2 L by 3 L | 547.022 | 1 | 547.022 | 188.36 | 0.000 |
| Error | 17.425 | 6 | 2.904 | - | - |
| Total SS | 3144.827 | 15 | - | - | - |
| SS | df | MS | Fcalculated | Ftable | |
|---|---|---|---|---|---|
| Regression (SSR) | 3190.222 | 9 | 354.469 | 122.06 | 4.10 |
| Residual | 17.425 | 6 | 2.904 | - | - |
| Total (SST) | 3207.646 | 15 | - | - | - |
| Author | Steel Fiber (%) | PVA Fiber (%) | 20 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 700 °C | 1049 °C |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sanchayan and Foster (2016) [27] | 2.00 | 0.00 | 170.00 | 176.15 | 188.68 | 172.87 | - | - | - | - | - |
| 1.50 | 0.50 | 150.00 | 158.88 | 183.06 | 187.50 | 143.59 | 87.34 | 80.92 | 41.94 | - | |
| 1.00 | 1.00 | 158.00 | 163.20 | 170.46 | 161.12 | 141.89 | 50.93 | 48.51 | 30.14 | - | |
| 0.50 | 1.50 | 145.00 | 143.57 | 163.60 | 150.72 | 117.81 | 87.29 | 59.62 | 31.00 | - | |
| 0.00 | 2.00 | 134.00 | 146.34 | 152.07 | 134.88 | 92.57 | 72.29 | - | - | - | |
| Park et al. (2019) [15] | 1.50 | 0.20 | 192.00 | - | - | - | - | - | - | - | 11.80 |
| 1.50 | 0.30 | 194.00 | - | - | - | - | - | - | - | 17.40 | |
| Equation (3) | 2.00 | 0.00 | 165.88 | 170.97 | 173.60 | 172.09 | - | - | - | - | - |
| 1.50 | 0.50 | 189.30 | 194.38 | 197.02 | 195.51 | 189.87 | 180.10 | 166.19 | 148.14 | - | |
| 1.00 | 1.00 | 143.73 | 148.81 | 151.44 | 149.94 | 144.30 | 134.52 | 120.61 | 102.57 | - | |
| 0.50 | 1.50 | 29.17 | 34.25 | 36.88 | 35.38 | 29.74 | 19.96 | 6.05 | −11.99 | - | |
| 0.00 | 2.00 | −154.38 | −149.30 | −146.67 | −148.17 | −153.81 | −163.58 | - | - | - | |
| 1.50 | 0.20 | 151.04 | - | - | - | - | - | - | - | 14.50 | |
| 1.50 | 0.30 | 163.80 | - | - | - | - | - | - | - | 27.25 |
| Mix | Temp. (°C) | Steel (%) | PVA (%) | Resp. Surface E* (GPa) | Experimental E (GPa) |
|---|---|---|---|---|---|
| 1 | 138 | 1.60 | 0.10 | 48.78 | 48.83 |
| 2 | 138 | 1.60 | 0.40 | 59.53 | 59.71 |
| 3 | 138 | 1.90 | 0.10 | 46.92 | 46.98 |
| 4 | 138 | 1.90 | 0.40 | 50.97 | 51.04 |
| 5 # | 482 | 1.60 | 0.10 | 17.76 | 17.93 |
| 6 # | 482 | 1.60 | 0.40 | 0.72 | - |
| 7 # | 482 | 1.90 | 0.10 | 15.89 | 16.08 |
| 8 # | 482 | 1.90 | 0.40 | −7.85 | - |
| 9 | 20 | 1.75 | 0.25 | 44.27 | 44.27 |
| 10 # | 600 | 1.75 | 0.25 | −31.47 | - |
| 11 # | 310 | 1.50 | 0.25 | 38.27 | 38.27 |
| 12 # | 310 | 2.00 | 0.25 | 29.50 | 29.50 |
| 13 | 310 | 1.75 | 0.00 | 53.13 | 53.13 |
| 14 | 310 | 1.75 | 0.50 | 42.21 | 42.21 |
| 15 | 310 | 1.75 | 0.25 | 33.89 | 36.91 |
| 16 | 310 | 1.75 | 0.25 | 33.89 | 30.86 |
| Factors | Sum of Squares (SS) | Degree of freedom (df) | Mean Square (MS) | Fcalculated | p |
|---|---|---|---|---|---|
| (1) Temperature (°C) (L) | 6904.215 | 1 | 6904.215 | 2263.52 | 0.000 |
| Temperature (°C) (Q) | 878.985 | 1 | 878.985 | 288.17 | 0.000 |
| (2) Steel (%) (L) | 93.762 | 1 | 93.762 | 30.74 | 0.001 |
| Steel (%) (Q) | 0.000 | 1 | 0.000 | 0.00 | 1.000 |
| (3) PVA (%) (L) | 145.481 | 1 | 145.481 | 47.70 | 0.000 |
| PVA (%) (Q) | 222.534 | 1 | 222.534 | 72.96 | 0.000 |
| 1 L by 2 L | 0.000 | 1 | 0.000 | 0.00 | 1.000 |
| 1 L by 3 L | 393.233 | 1 | 393.233 | 128.92 | 0.000 |
| 2 L by 3 L | 23.256 | 1 | 23.256 | 7.62 | 0.033 |
| Error | 18.301 | 6 | 3.050 | - | - |
| Total SS | 9381.874 | 15 | - | - | - |
| SS | df | MS | Fcalculated | Ftable | |
|---|---|---|---|---|---|
| Regression (SSR) | 9363.572 | 9 | 1040.397 | 341.09 | 4.10 |
| Residual | 18.301 | 6 | 3.050 | - | - |
| Total (SST) | 9381.874 | 15 | - | - | - |
| Author | Steel Fiber (%) | Polymeric Fiber (%) | Elasticity Modulus, in GPa (Exposure Temperature in °C) | |||
|---|---|---|---|---|---|---|
| Room Temperature | 20 °C~200 °C | 200 °C~400 °C | 400 °C~600 °C | |||
| Sanchayan and Foster (2016) [27] | 2.00 | - | 46.30 | 45.92 (200 °C) | 43.09 (300 °C) | - |
| 1.00 | 1.00 (PVA) | 42.10 | 42.27 (200 °C) | 36.94 (300 °C) | 6.53 (600 °C) | |
| - | 2.00 (PVA) | 40.80 | 37.30 (200 °C) | 33.64 (300 °C) | - | |
| Rasul, M.; Ahmad, S.; Adekunle, S.K.; Al-Dulaijan, S.U.; Maslehuddin, M.; Ali, S.I. [36] | - | 0.26 (PP) | 47.81 | - | 45.00 (300 °C) | - |
| - | 0.52 (PP) | 47.25 | - | 43.13 (300 °C) | - | |
| - | 0.78 (PP) | 43.50 | - | 43.88 (300 °C) | - | |
| - | 1.04 (PP) | 46.13 | - | 39.38 (300 °C) | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sumitomo, G.S.; Pimentel, L.L.; Jacintho, A.E.P.G.A.; Forti, N.C.S. Study of Ultra-High Performance Concrete Mechanical Behavior under High Temperatures. Materials 2024, 17, 4212. https://doi.org/10.3390/ma17174212
Sumitomo GS, Pimentel LL, Jacintho AEPGA, Forti NCS. Study of Ultra-High Performance Concrete Mechanical Behavior under High Temperatures. Materials. 2024; 17(17):4212. https://doi.org/10.3390/ma17174212
Chicago/Turabian StyleSumitomo, Guilherme S., Lia L. Pimentel, Ana Elisabete P. G. A. Jacintho, and Nadia C. S. Forti. 2024. "Study of Ultra-High Performance Concrete Mechanical Behavior under High Temperatures" Materials 17, no. 17: 4212. https://doi.org/10.3390/ma17174212
APA StyleSumitomo, G. S., Pimentel, L. L., Jacintho, A. E. P. G. A., & Forti, N. C. S. (2024). Study of Ultra-High Performance Concrete Mechanical Behavior under High Temperatures. Materials, 17(17), 4212. https://doi.org/10.3390/ma17174212






