Microwave Plasma Pencil for Surface Treatment: Numerical Study of Electromagnetic Radiation and Experimental Verification
Abstract
1. Introduction
2. Design and Properties of MPP
3. Model Description
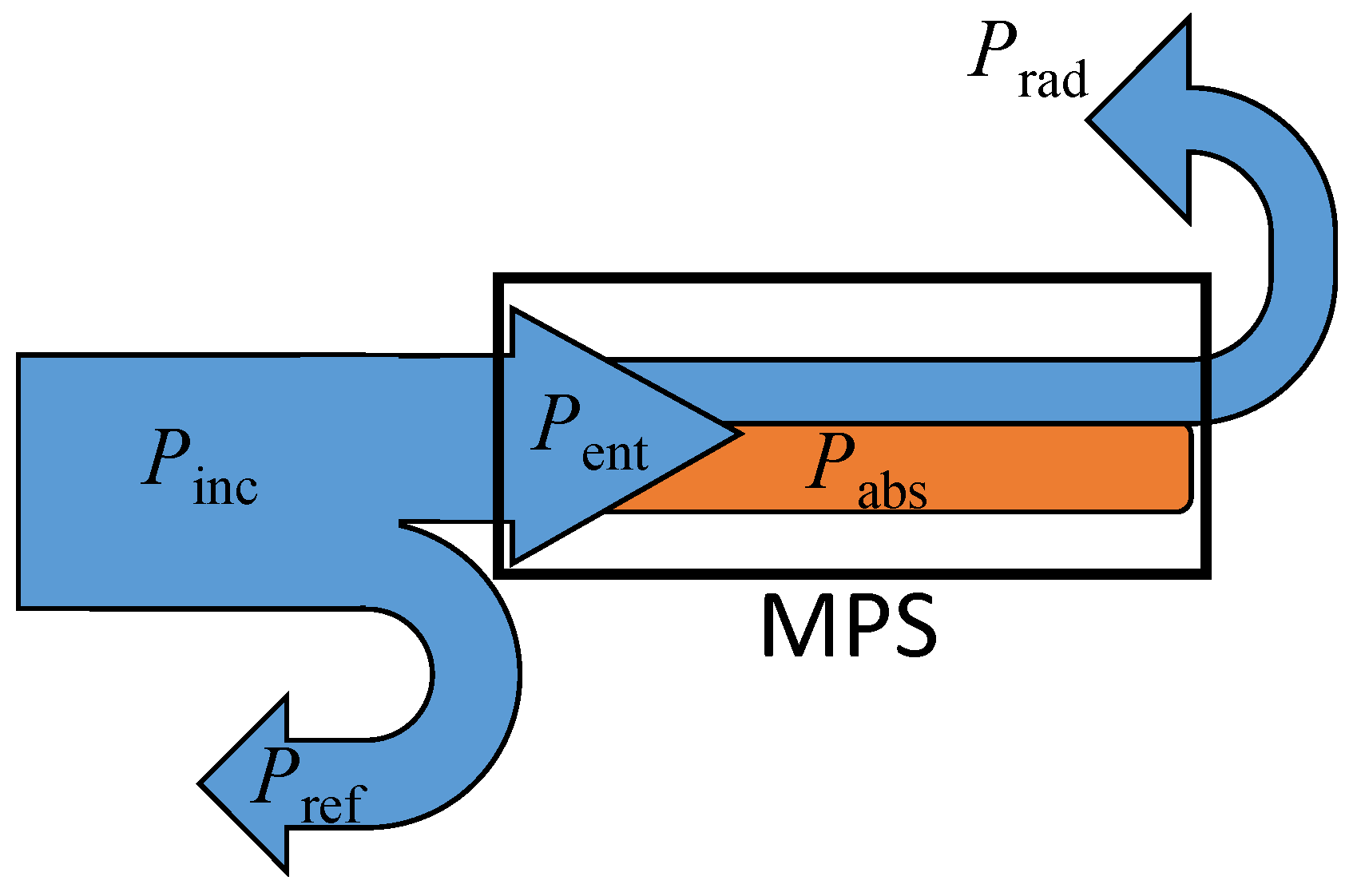
3.1. Power Flow Analysis
3.2. Calculation Domain
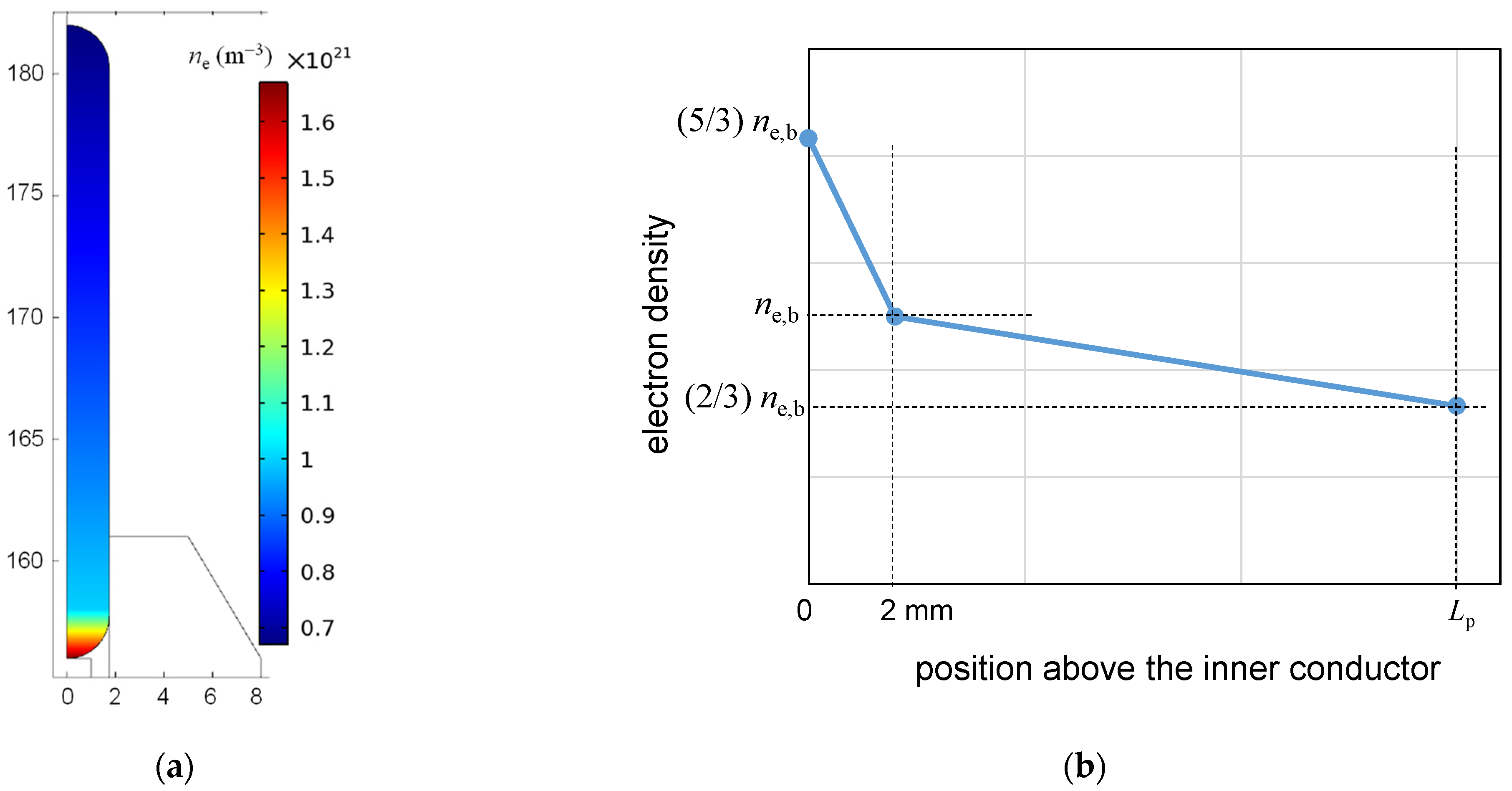
3.3. Governing Equations and Calculation Parameters
4. Calculation Results
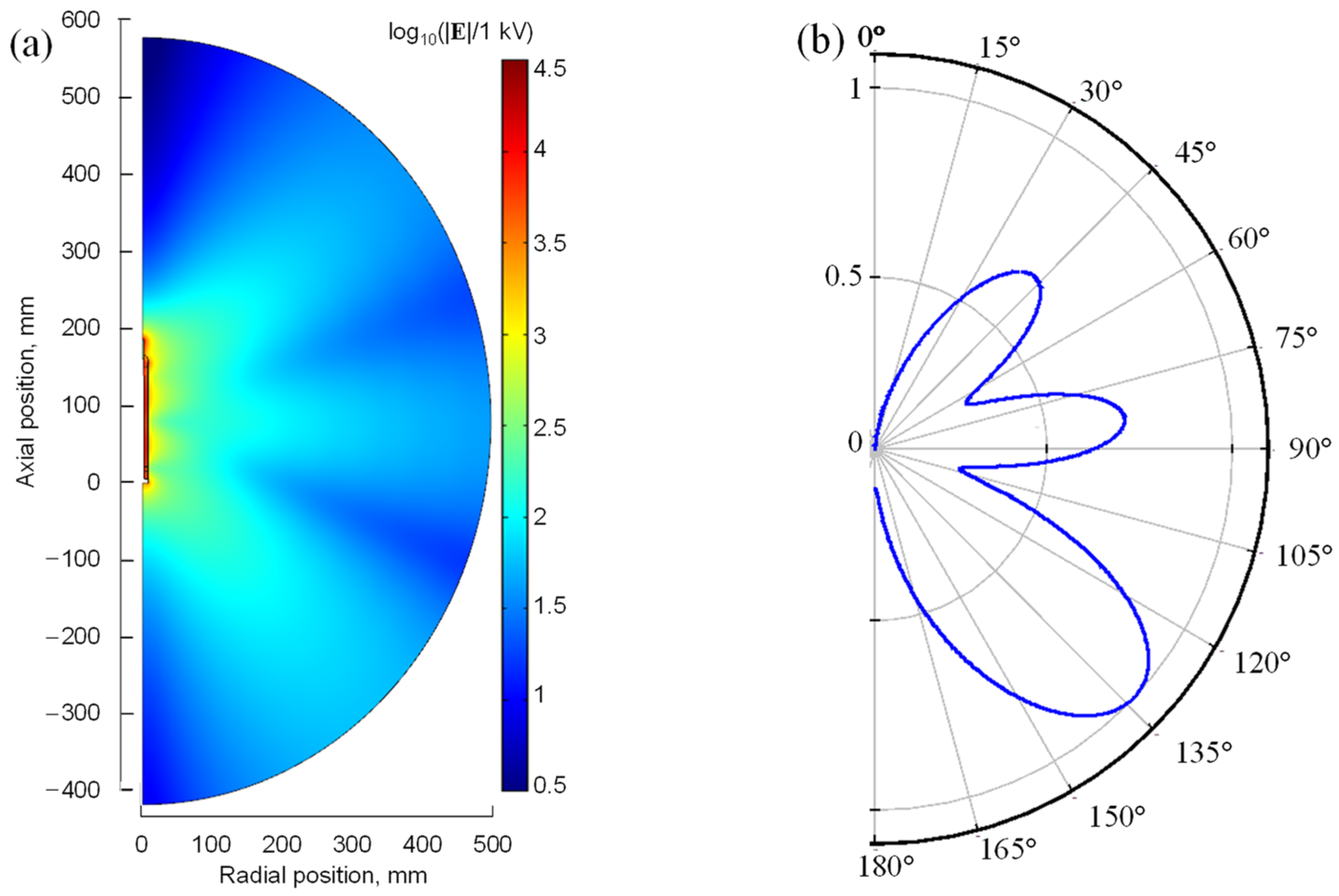
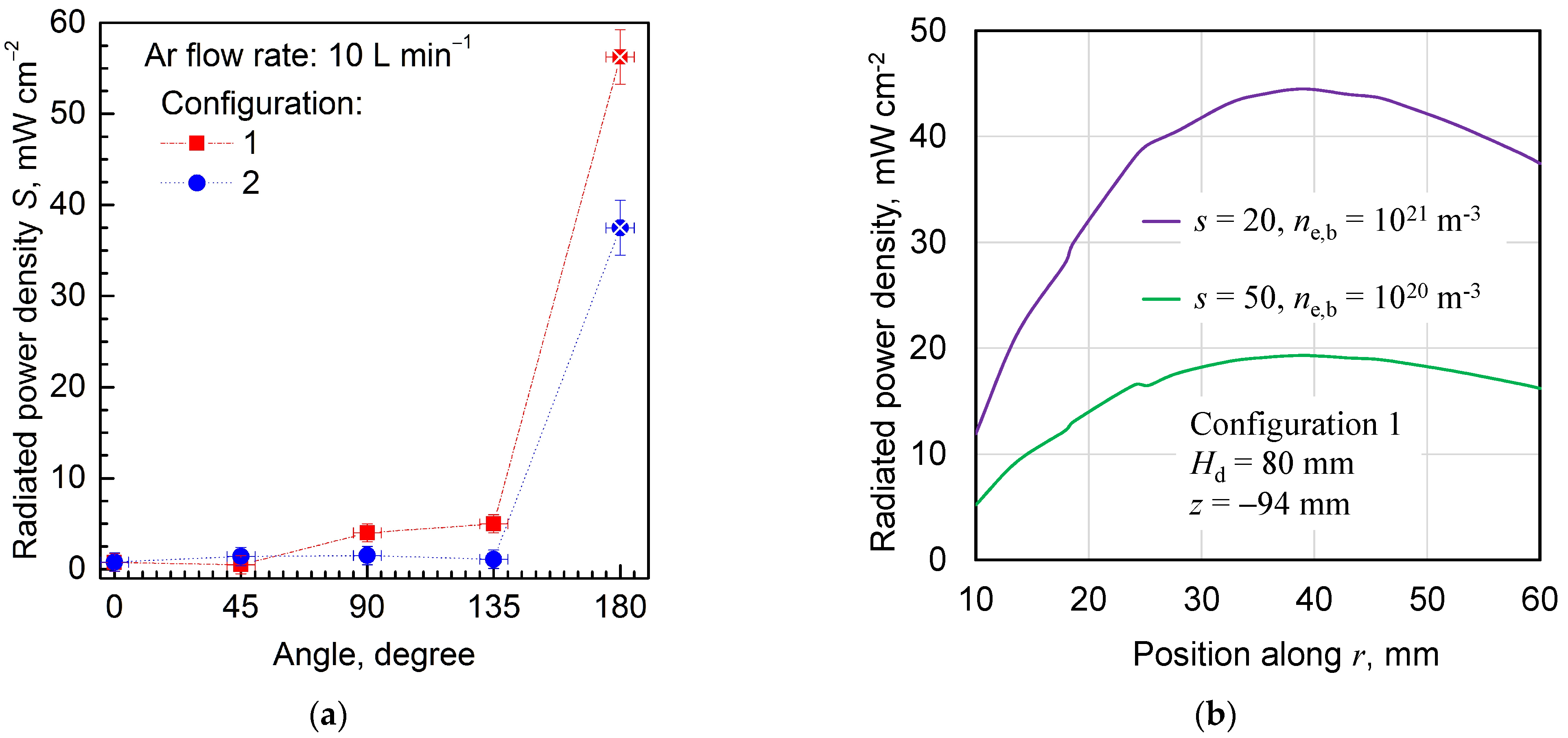
4.1. Spatial Distribution of the Electric Field and Radiation Pattern
4.2. The Effect of the Radiation Sphere Radius and Electron Density on Power Ratios
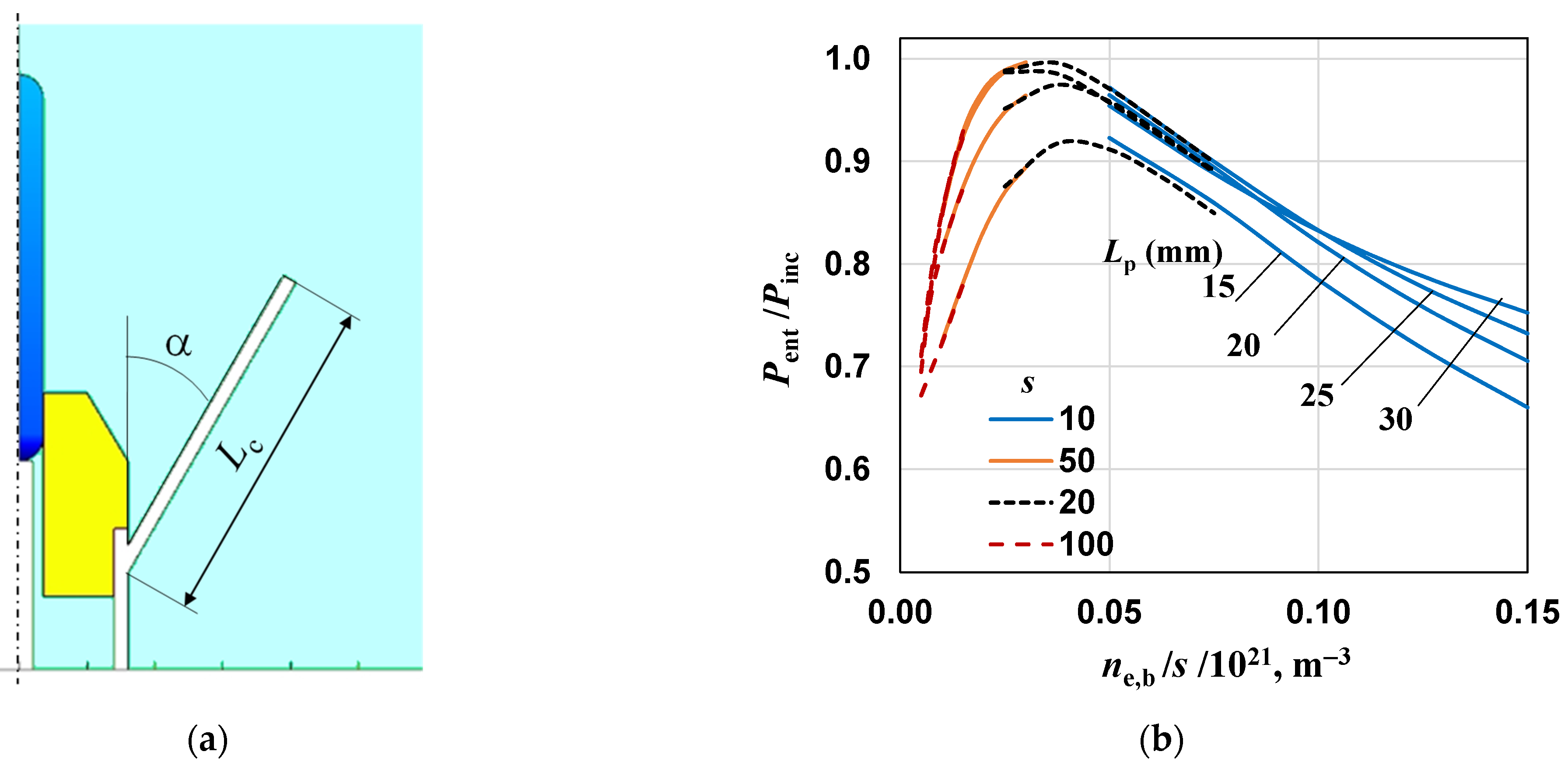
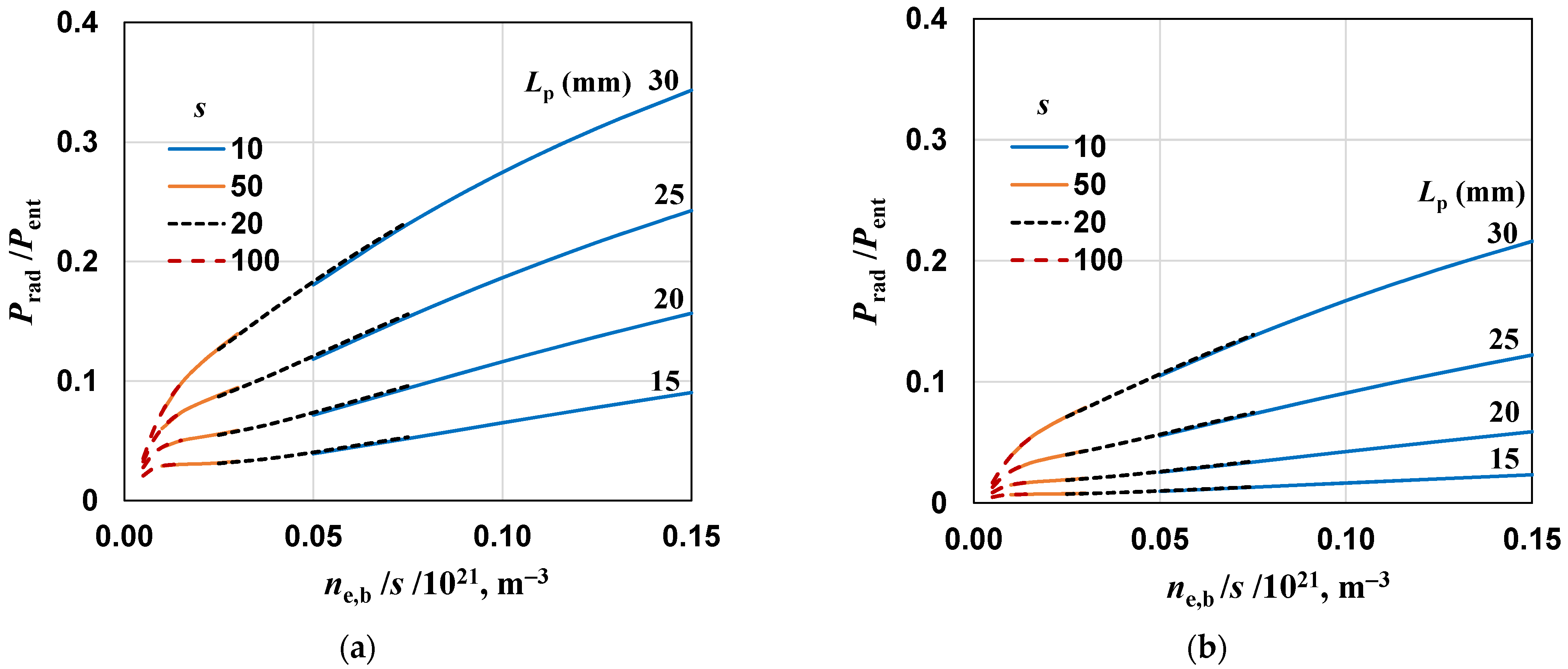
4.3. The Effect of the Plasma Column Length Lp on Power Ratios
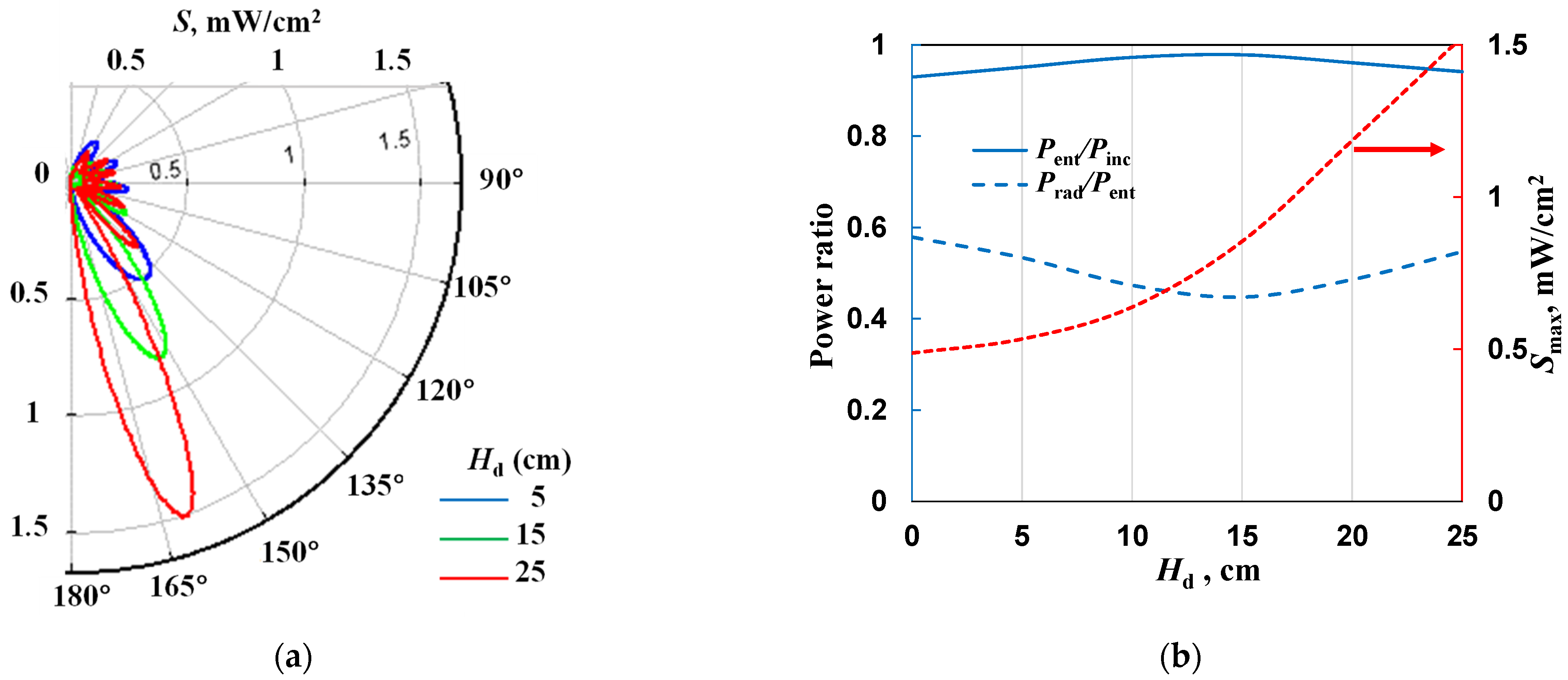
4.4. The Effect of the MPP Length on Power Ratios and Radiation Patterns
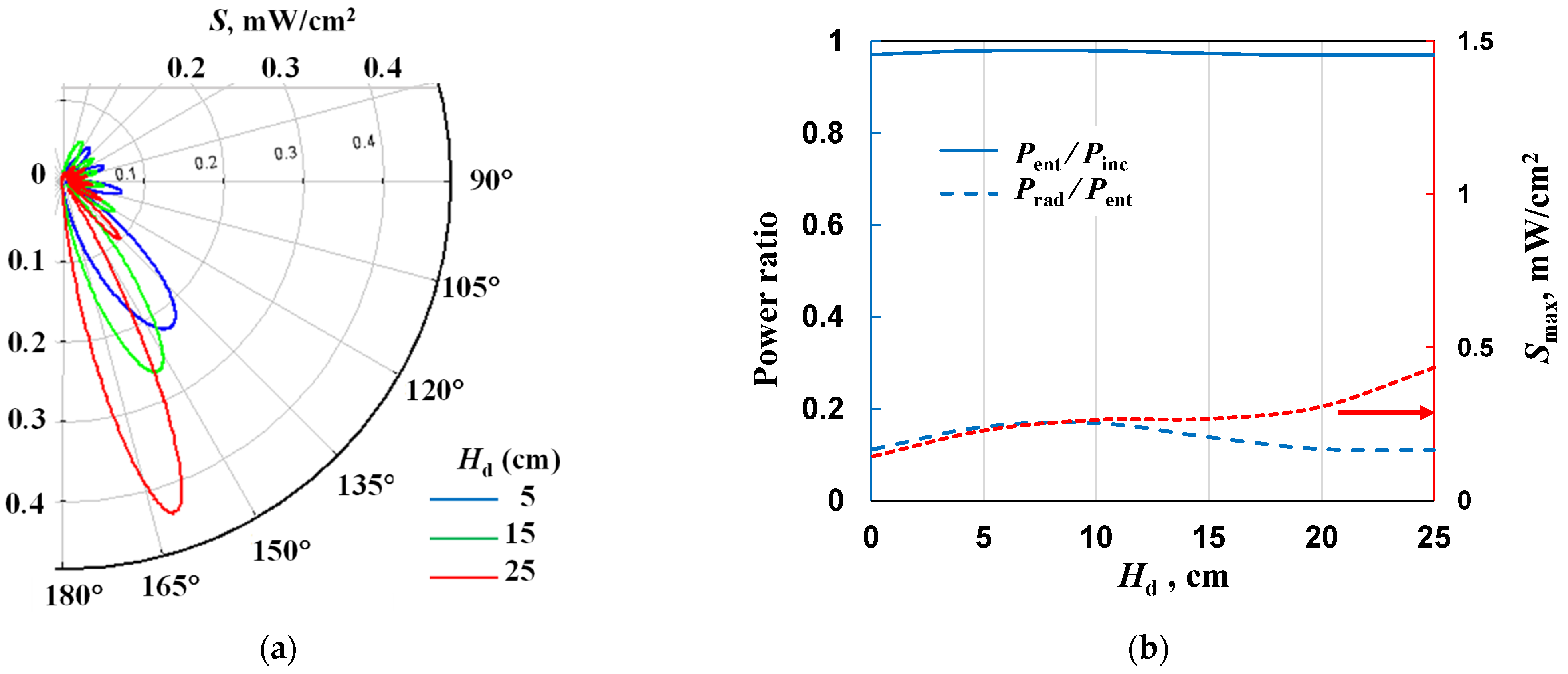
4.5. The Effect of the Shielding Cone on Power Ratios and Radiation Patterns
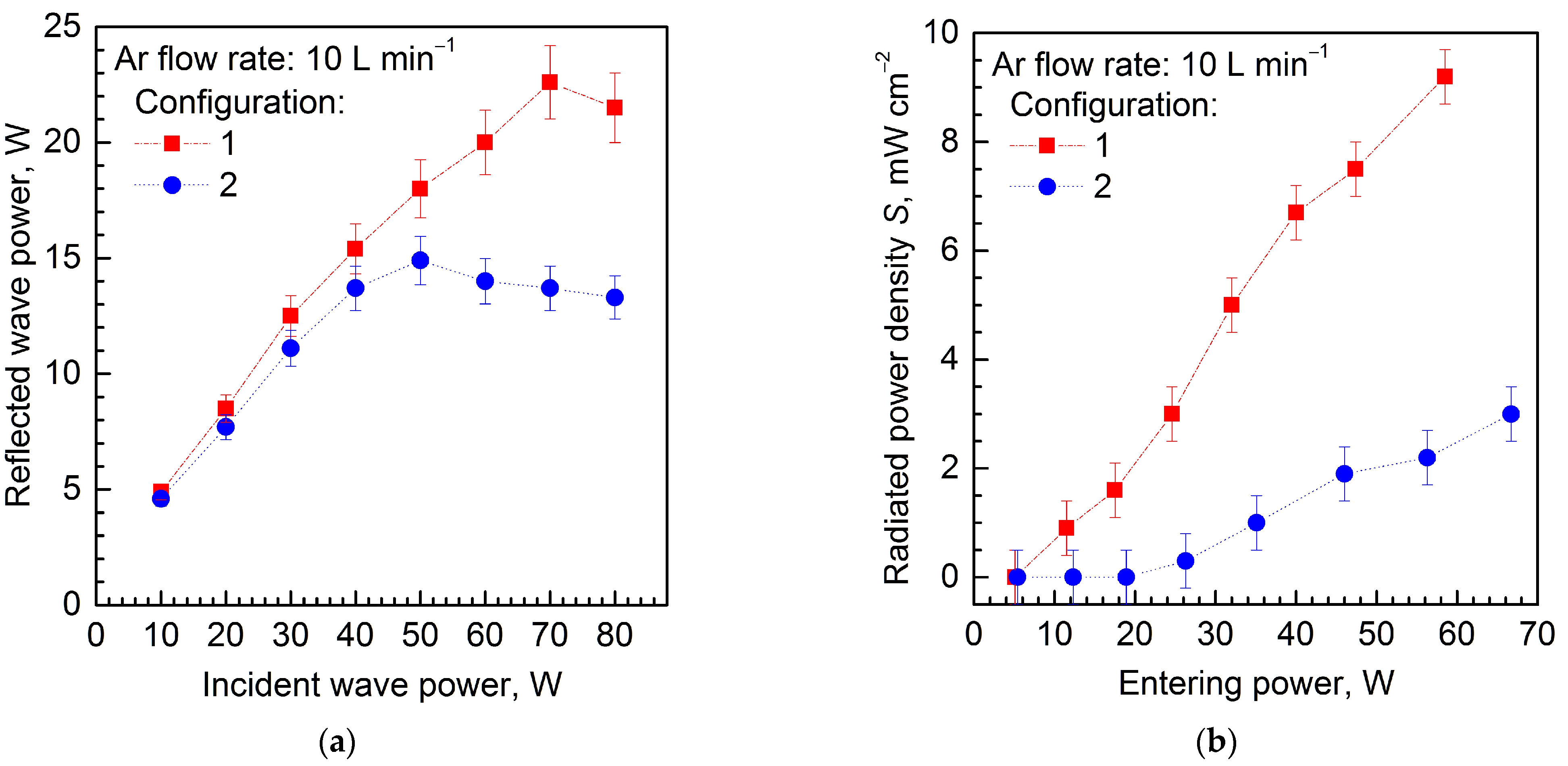
5. Experimental Results and Discussion
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hegemann, D.; Gaiser, S. Plasma Surface Engineering for Manmade Soft Materials: A Review. J. Phys. D Appl. Phys. 2021, 55, 173002. [Google Scholar] [CrossRef]
- Bertin, M.; Leitao, E.M.; Bickerton, S.; Verbeek, C.J.R. A Review of Polymer Surface Modification by Cold Plasmas toward Bulk Functionalization. Plasma Process. Polym. 2024, 21, 2300208. [Google Scholar] [CrossRef]
- Elashry, S.; ELsaeed, H.; El-Siragy, N.M. Microwave Plasma Discharge-Assisted Surface Modification of PVA Films: Coatings and Food Packaging. Eur. Phys. J. Plus 2022, 137, 1252. [Google Scholar] [CrossRef]
- Hnilica, J.; Potočňáková, L.; Stupavská, M.; Kudrle, V. Rapid Surface Treatment of Polyamide 12 by Microwave Plasma Jet. Appl. Surf. Sci. 2014, 288, 251–257. [Google Scholar] [CrossRef]
- Storr, B.; Kodali, D.; Chakrabarty, K.; Baker, P.A.; Rangari, V.; Catledge, S.A. Single-Step Synthesis Process for High-Entropy Transition Metal Boride Powders Using Microwave Plasma. Ceramics 2021, 4, 257–264. [Google Scholar] [CrossRef]
- Munir, M.A.; Naz, M.Y.; Shukrullah, S.; Naz, A.; Irfan, M.; Rahman, S.; Mursal, S.N.F. Tailoring Properties of Ni0.50Co0.50DyxFe2−xO4 Ceramics Using Microwave Non-Thermal Plasma for High-Frequency Devices. Appl. Phys. A 2024, 130, 563. [Google Scholar] [CrossRef]
- Jašek, O.; Toman, J.; Jurmanová, J.; Šnírer, M.; Kudrle, V.; Buršíková, V. Study of Graphene Layer Growth on Dielectric Substrate in Microwave Plasma Torch at Atmospheric Pressure. Diam. Relat. Mater. 2020, 105, 107798. [Google Scholar] [CrossRef]
- Bundaleska, N.; Tsyganov, D.; Dias, A.; Felizardo, E.; Henriques, J.; Dias, F.M.; Abrashev, M.; Kissovski, J.; Tatarova, E. Microwave Plasma Enabled Synthesis of Free Standing Carbon Nanostructures at Atmospheric Pressure Conditions. Phys. Chem. Chem. Phys. 2018, 20, 13810–13824. [Google Scholar] [CrossRef]
- Lee, B.-J.; Jo, S.-I.; Jeong, G.-H. Synthesis and in Situ Nitrogen Doping of ZnO Nanomaterials Using a Microwave Plasma System at Atmospheric Pressure. Appl. Phys. A 2019, 125, 723. [Google Scholar] [CrossRef]
- Li, D.; Tong, L.; Gao, B. Synthesis of Multiwalled Carbon Nanotubes on Stainless Steel by Atmospheric Pressure Microwave Plasma Chemical Vapor Deposition. Appl. Sci. 2020, 10, 4468. [Google Scholar] [CrossRef]
- Melero, C.; Rincón, R.; Muñoz, J.; Zhang, G.; Sun, S.; Perez, A.; Royuela, O.; González-Gago, C.; Calzada, M.D. Scalable Graphene Production from Ethanol Decomposition by Microwave Argon Plasma Torch. Plasma Phys. Control Fusion 2018, 60, 014009. [Google Scholar] [CrossRef]
- Heo, S.; Lim, T.; Kim, B.S.; Suk, J.W.; Bak, M.S. Impact of N2 Admixture on the Synthesis of Graphitic Carbon Nanoparticles Using Atmospheric-Pressure Microwave Plasma. J. Phys. D Appl. Phys. 2022, 55, 275201. [Google Scholar] [CrossRef]
- Ouaras, K.; Lombardi, G.; Hassouni, K. Nanoparticles Synthesis in Microwave Plasmas: Peculiarities and Comprehensive Insight. Sci. Rep. 2024, 14, 4653. [Google Scholar] [CrossRef] [PubMed]
- Dytrych, P.; Kluson, P.; Solcova, O.; Kment, S.; Stranak, V.; Cada, M.; Hubicka, Z. Shape Selective Photoinduced Electrochemical Behavior of Thin ZnO Layers Prepared by Surfatron. Thin Solid Film. 2015, 597, 131–139. [Google Scholar] [CrossRef]
- Kment, S.; Kluson, P.; Stranak, V.; Virostko, P.; Krysa, J.; Cada, M.; Pracharova, J.; Kohout, M.; Morozova, M.; Adamek, P.; et al. Photo-Induced Electrochemical Functionality of the TiO2 Nanoscale Films. Electrochim. Acta 2009, 54, 3352–3359. [Google Scholar] [CrossRef]
- Narimisa, M.; Krčma, F.; Onyshchenko, Y.; Kozáková, Z.; Morent, R.; De Geyter, N. Atmospheric Pressure Microwave Plasma Jet for Organic Thin Film Deposition. Polymers 2020, 12, 354. [Google Scholar] [CrossRef]
- Gazal, Y.; Dublanche-Tixier, C.; Chazelas, C.; Colas, M.; Carles, P.; Tristant, P. Multi-Structural TiO2 Film Synthesised by an Atmospheric Pressure Plasma-Enhanced Chemical Vapour Deposition Microwave Torch. Thin Solid Film. 2016, 600, 43–52. [Google Scholar] [CrossRef]
- Perraudeau, A.; Dublanche-Tixier, C.; Tristant, P.; Chazelas, C. Dynamic Mode Optimization for the Deposition of Homogeneous TiO2 Thin Film by Atmospheric Pressure PECVD Using a Microwave Plasma Torch. Appl. Surf. Sci. 2019, 493, 703–709. [Google Scholar] [CrossRef]
- Bónová, L.; Zhu, W.; Patel, D.K.; Krogstad, D.V.; Ruzic, D.N. Atmospheric Pressure Microwave Plasma for Aluminum Surface Cleaning. J. Vac. Sci. Technol. A 2020, 38, 023002. [Google Scholar] [CrossRef]
- Matsubayashi, T.; Hidaka, H.; Muguruma, H. Microwave-Assisted Atmospheric Pressure Plasma Polymerization of Hexamethyldisiloxane. Jpn. J. Appl. Phys. 2016, 55, 076201. [Google Scholar] [CrossRef]
- Durocher-Jean, A.; Durán, I.R.; Asadollahi, S.; Laroche, G.; Stafford, L. Deposition of Anti-Fog Coatings on Glass Substrates Using the Jet of an Open-to-Air Microwave Argon Plasma at Atmospheric Pressure. Plasma Process. Polym. 2020, 17, 1900229. [Google Scholar] [CrossRef]
- Tudoran, C.; Roşu, M.-C.; Coroş, M. A Concise Overview on Plasma Treatment for Application on Textile and Leather Materials. Plasma Process. Polym. 2020, 17, 2000046. [Google Scholar] [CrossRef]
- Schnabel, U.; Andrasch, M.; Weltmann, K.-D.; Ehlbeck, J.; Schnabel, U.; Andrasch, M. Inactivation of Microorganisms in Tyvek® Packaging by Microwave Plasma Processed Air. Glob. J. Biol. Agric. Health Sci. 2015, 4, 185–192. [Google Scholar]
- Dong, Y.; Zhang, J.; Zhang, P.; Tian, H.; Yu, D. Jet Morphology Analysis of Microwave-Generated Plasma for Microfabrication of Optics. Plasma Process. Polym. 2022, 19, 2200084. [Google Scholar] [CrossRef]
- Li, Y.; Bai, Y.; Yu, D.; Wang, R.; Mu, Y.; Jin, W.; Yu, B. Investigation of a Novel Atmospheric Pressure Microwave Cold Plasma Torch and Its Characteristics. Chem. Res. Chin. Univ. 2024. [Google Scholar] [CrossRef]
- Ogata, K.; Terashima, K. Characterizations of Strip-Line Microwave Micro Atmospheric Plasma and Its Application to Neutralization. J. Appl. Phys. 2009, 106, 023301. [Google Scholar] [CrossRef]
- Rincón, R.; Muñoz, J.; Morales-Calero, F.J.; Orejas, J.; Calzada, M.D. Assessment of Two Atmospheric-Pressure Microwave Plasma Sources for H2 Production from Ethanol Decomposition. Appl. Energy 2021, 294, 116948. [Google Scholar] [CrossRef]
- Gines, A.R.B.; Wada, M. Sheet Plasma Excitation by a 2.45 GHz Microwave Power Introduced through a Local Gas Injection Type Dielectric Window. Plasma Fusion Res. 2020, 15, 1401005. [Google Scholar] [CrossRef]
- Hamdan, A.; Liu, J.-L.; Cha, M.S. Microwave Plasma Jet in Water: Characterization and Feasibility to Wastewater Treatment. Plasma Chem. Plasma Process. 2018, 38, 1003–1020. [Google Scholar] [CrossRef]
- Lebedev, Y.A. Microwave Discharges: Generation and Diagnostics. J. Phys. Conf. Ser. 2010, 257, 012016. [Google Scholar] [CrossRef]
- Ferreira, C.M.; Moisan, M. Microwave Discharges: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-1-4899-1130-8. [Google Scholar]
- Conrads, H.; Schmidt, M. Plasma Generation and Plasma Sources. Plasma Sources Sci. Technol. 2000, 9, 441–454. [Google Scholar] [CrossRef]
- Jin, Q.; Zhu, C.; Border, M.W.; Hieftje, G.M. A Microwave Plasma Torch Assembly for Atomic Emission Spectrometry. Spectrochim. Acta Part B At. Spectrosc. 1991, 46, 417–430. [Google Scholar] [CrossRef]
- Bilgic, A.M.; Prokisch, C.; Broekaert, J.A.C.; Voges, E. Design and Modelling of a Modified 2.45 GHz Coaxial Plasma Torch for Atomic Spectrometry. Spectrochim. Acta Part B At. Spectrosc. 1998, 53, 773–777. [Google Scholar] [CrossRef]
- Czylkowski, D.; Hrycak, B.; Jasiński, M.; Dors, M.; Mizeraczyk, J. Atmospheric Pressure Microwave Microplasma Microorganism Deactivation. Surf. Coat. Technol. 2013, 234, 114–119. [Google Scholar] [CrossRef]
- Hrycak, B.; Jasiński, M.; Mizeraczyk, J. Spectroscopic Investigations of Microwave Microplasmas in Various Gases at Atmospheric Pressure. Eur. Phys. J. D 2010, 60, 609–619. [Google Scholar] [CrossRef]
- Janča, J.; Klíma, M.; Slaviček, P.; Zajíčková, L. HF Plasma Pencil—New Source for Plasma Surface Processing. Surf. Coat. Technol. 1999, 116, 547–551. [Google Scholar] [CrossRef]
- Barekzi, N.; Laroussi, M. Dose-Dependent Killing of Leukemia Cells by Low-Temperature Plasma. J. Phys. D Appl. Phys. 2012, 45, 422002. [Google Scholar] [CrossRef]
- Winter, J.; Brandenburg, R.; Weltmann, K.-D. Atmospheric Pressure Plasma Jets: An Overview of Devices and New Directions. Plasma Sources Sci. Technol. 2015, 24, 064001. [Google Scholar] [CrossRef]
- Mizeraczyk, J.; Dors, M.; Jasiński, M.; Hrycak, B.; Czylkowski, D. Atmospheric Pressure Low-Power Microwave Microplasma Source for Deactivation of Microorganisms. Eur. Phys. J. Appl. Phys. 2013, 61, 24309. [Google Scholar] [CrossRef]
- Haryński, Ł.; Czylkowski, D.; Hrycak, B.; Karczewski, J.; Gumieniak, J.; Kramek, A.; Ryl, J.; Grochowska, K.; Dors, M.; Siuzdak, K. Nitrogen Plasma-Induced Crystallization of Anodic TiO2 Nanotubes for Solar Photoelectrochemistry. Appl. Surf. Sci. 2023, 615, 156472. [Google Scholar] [CrossRef]
- Moisan, M.; Levif, P.; Nowakowska, H. Space-Wave (Antenna) Radiation from the Wave Launcher (Surfatron) before the Development of the Plasma Column Sustained by the EM Surface Wave: A Source of Microwave Power Loss. AMPERE Newsl. 2019, 98, 9–19. [Google Scholar]
- Nowakowska, H.; Czylkowski, D.; Hrycak, B.; Jasinski, M. Numerical and Experimental Analysis of Radiation from a Microwave Plasma Source of the TIAGO Type. Plasma Sources Sci. Technol. 2021, 30, 095011. [Google Scholar] [CrossRef]
- Sadeghikia, F.; Talafi Noghani, M.; Simard, M.R. Experimental Study on the Surface Wave Driven Plasma Antenna. AEU-Int. J. Electron. Commun. 2016, 70, 652–656. [Google Scholar] [CrossRef]
- Djourelova, M.; Petrova, T.; Ghanashev, I.; Zhelyazkov, I. Axial Structure of a Shielded Plasma Column Sustained by a Dipolar Electromagnetic Wave. J. Phys. D Appl. Phys. 1993, 26, 1601–1610. [Google Scholar] [CrossRef]
- The COMSOL® Software Product Suite. Available online: https://www.comsol.com/products (accessed on 20 August 2024).
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark Profile Calculations for the Hβ Line of Hydrogen. Astrophys. J. 1962, 135, 272. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardeñoso, V. New Plasma Diagnosis Tables of Hydrogen Stark Broadening Including Ion Dynamics. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- Aliev, Y.M.; Schlüter, H.; Shivarova, A. Guided-Wave-Produced Plasmas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; ISBN 978-3-540-65273-1. [Google Scholar]
- Bogachev, N.N.; Gusein-zade, N.G.; Nefedov, V.I. Radiation Pattern and Radiation Spectrum of the Plasma Asymmetrical Dipole Antenna. Plasma Phys. Rep. 2019, 45, 372–375. [Google Scholar] [CrossRef]
- Belyaev, B.A.; Leksikov, A.A.; Leksikov, A.A.; Serzhantov, A.M.; Bal’va, Y.F. Nonlinear Behavior of Plasma Antenna Vibrator. IEEE Trans. Plasma Sci. 2014, 42, 1552–1559. [Google Scholar] [CrossRef]
- Shivarova, A.; Stoychev, T. Harmonic Surface Wave Propagation in Plasma. I. Second Order Harmonic Waves Generated by One Fundamental Wave. Plasma Phys. 1980, 22, 517–518. [Google Scholar] [CrossRef]
- Georgieva, V.; Berthelot, A.; Silva, T.; Kolev, S.; Graef, W.; Britun, N.; Chen, G.; van der Mullen, J.; Godfroid, T.; Mihailova, D.; et al. Understanding Microwave Surface-Wave Sustained Plasmas at Intermediate Pressure by 2D Modeling and Experiments. Plasma Process. Polym. 2017, 14, 1600185. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-471-66782-7. [Google Scholar]
- COMSOL RF Module User’s Guide (Ver. 4.1); COMSOL AB: Stockholm, Sweden, 2010.
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann Equation to Obtain Electron Transport Coefficients and Rate Coefficients for Fluid Models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Phelps, A.V. PHELPS Database. 1997. Available online: www.lxcat.net/Phelps (accessed on 4 June 2013).
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications with MATLAB®, MAPLE, and COMSOL, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-39510-4. [Google Scholar]
- Chen, C.; Fu, W.; Zhang, C.; Lu, D.; Han, M.; Yan, Y. Dual-Frequency Microwave Plasma Source Based on Microwave Coaxial Transmission Line. Appl. Sci. 2021, 11, 9873. [Google Scholar] [CrossRef]
- Guan, C.; Zhan, L.; Yao, S. Finite Element Simulation and Experimental Research on Uniformity Regulation of Microwave Heating of Composite Materials. Polymers 2022, 14, 3484. [Google Scholar] [CrossRef] [PubMed]


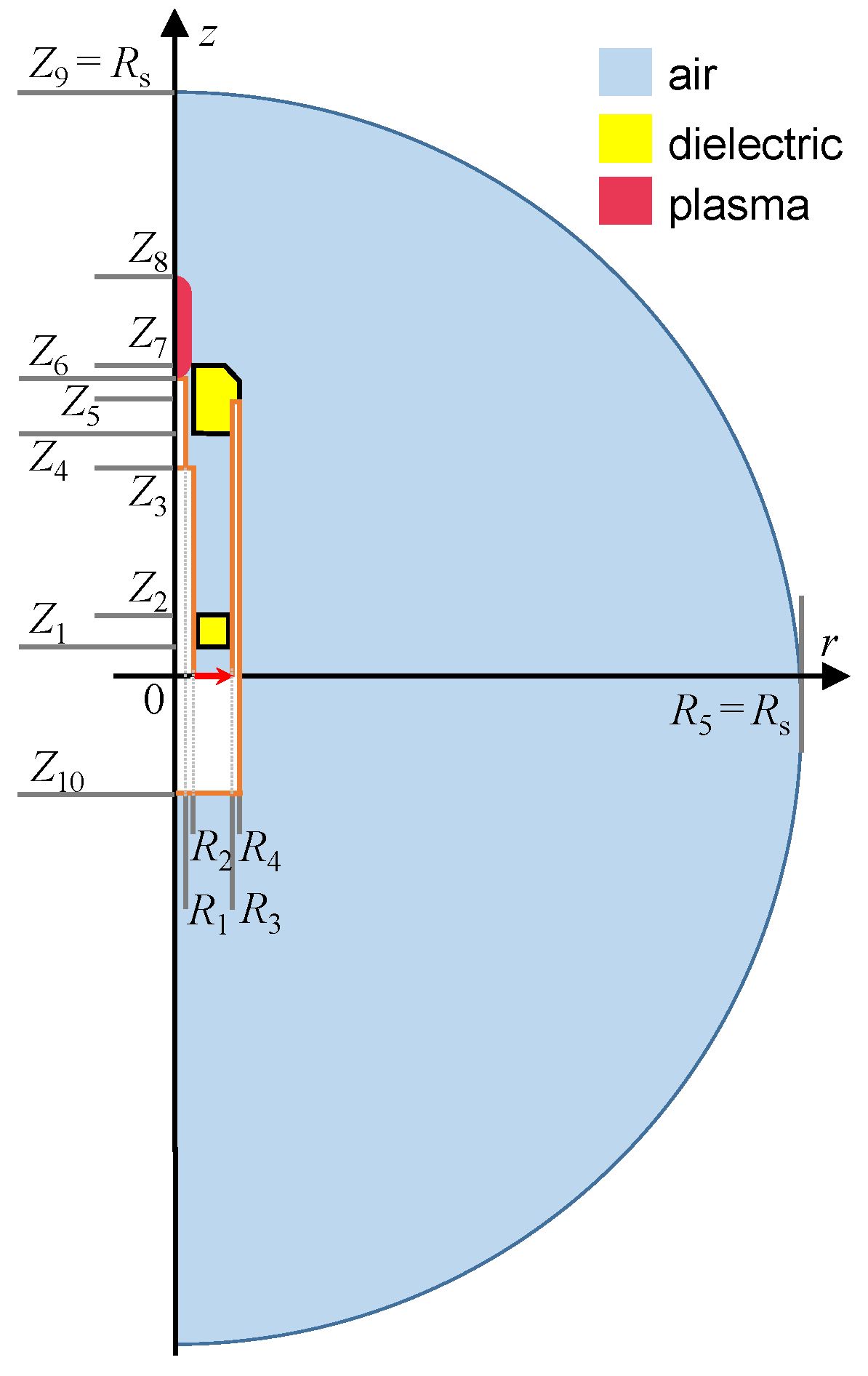




| Parameter | Description | Value, mm |
|---|---|---|
| Z1 | Dielectric disk bottom edge | 10 |
| Z2 | Dielectric disk upper edge | 16 |
| Z3 | Top rod beginning | 135 |
| Z4 | Ceramic tip bottom edge | 146 |
| Z5 | Outer conductor end | 151 |
| Z6 | Top rod end | 156 |
| Z7 | Ceramic tip upper edge | 161 |
| Z8 | Plasma column end | 151 + Lp |
| Z9 | Radiation sphere radius | Rs |
| Z10 | MPP’s bottom edge | Hd |
| R1 | Top rod radius | 1.1 |
| R2 | Inner conductor radius | 1.75 |
| R3 | Outer conductor inner radius | 7 |
| R4 | Outer conductor outer radius | 8 |
| R5 | Radiation sphere radius | Rs |
| Boundary | Type | Formula |
|---|---|---|
| Metal surface | Perfect electric conductor | n × E = 0 1 |
| Axis | Axial symmetry | n × E = 0 |
| Radiation sphere | Scattering boundary condition | n × (∇ × E) – j k0 n × (E × n) = 0 |
| Excitation plane | Coaxial port with power ON | see [46,55] |
| Configuration | Shielding | Argon Flow Rate, L min−1 | Incident Wave Power, W |
|---|---|---|---|
| 1 | No shielding | 10 | 10–80 |
| 2 | Cone-shaped screen: Lc = 20 mm, opening angle of 20° | 10 | 10–80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowakowska, H.; Czylkowski, D.; Hrycak, B.; Jasiński, M. Microwave Plasma Pencil for Surface Treatment: Numerical Study of Electromagnetic Radiation and Experimental Verification. Materials 2024, 17, 4369. https://doi.org/10.3390/ma17174369
Nowakowska H, Czylkowski D, Hrycak B, Jasiński M. Microwave Plasma Pencil for Surface Treatment: Numerical Study of Electromagnetic Radiation and Experimental Verification. Materials. 2024; 17(17):4369. https://doi.org/10.3390/ma17174369
Chicago/Turabian StyleNowakowska, Helena, Dariusz Czylkowski, Bartosz Hrycak, and Mariusz Jasiński. 2024. "Microwave Plasma Pencil for Surface Treatment: Numerical Study of Electromagnetic Radiation and Experimental Verification" Materials 17, no. 17: 4369. https://doi.org/10.3390/ma17174369
APA StyleNowakowska, H., Czylkowski, D., Hrycak, B., & Jasiński, M. (2024). Microwave Plasma Pencil for Surface Treatment: Numerical Study of Electromagnetic Radiation and Experimental Verification. Materials, 17(17), 4369. https://doi.org/10.3390/ma17174369







