Low-Frequency Sound-Insulation Performance of Labyrinth-Type Helmholtz and Thin-Film Compound Acoustic Metamaterial
Abstract
:1. Introduction
2. Structure Design and Calculation Method
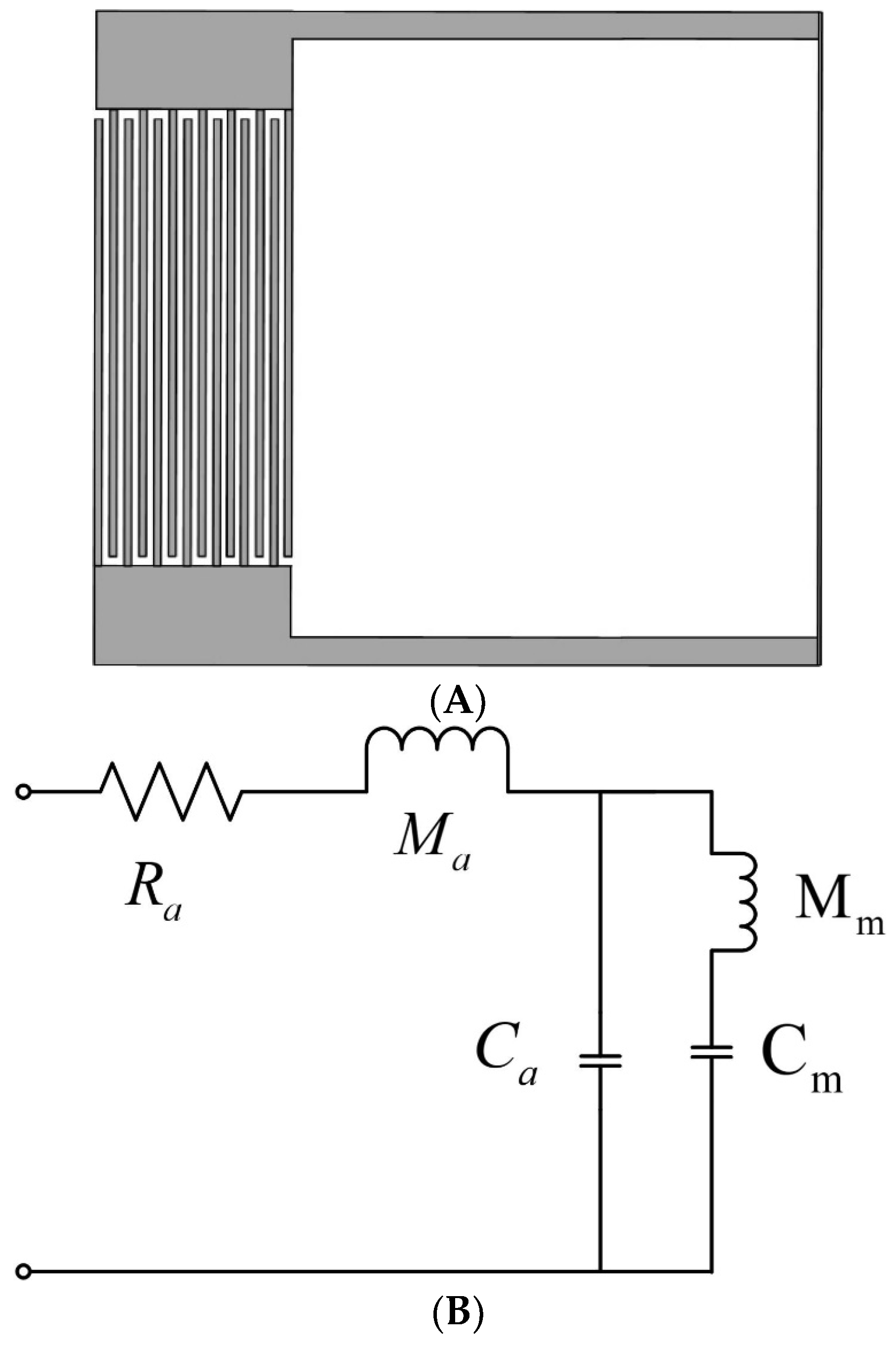
2.1. Structural Design
2.2. Numerical Model
3. Analysis of Sound-Insulation Mechanism and Establishment of Equivalent Model
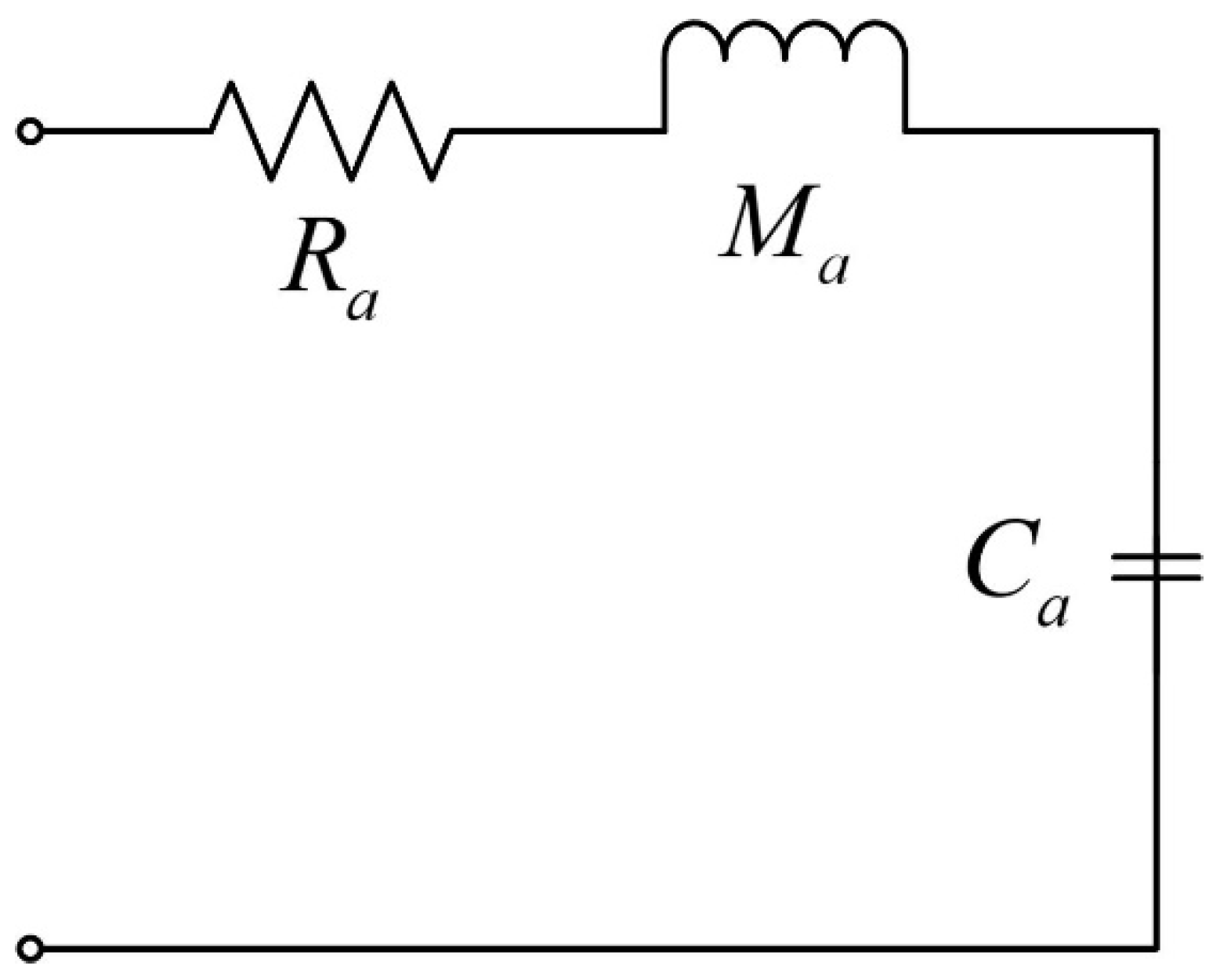
3.1. Analysis of Sound-Insulation Mechanism
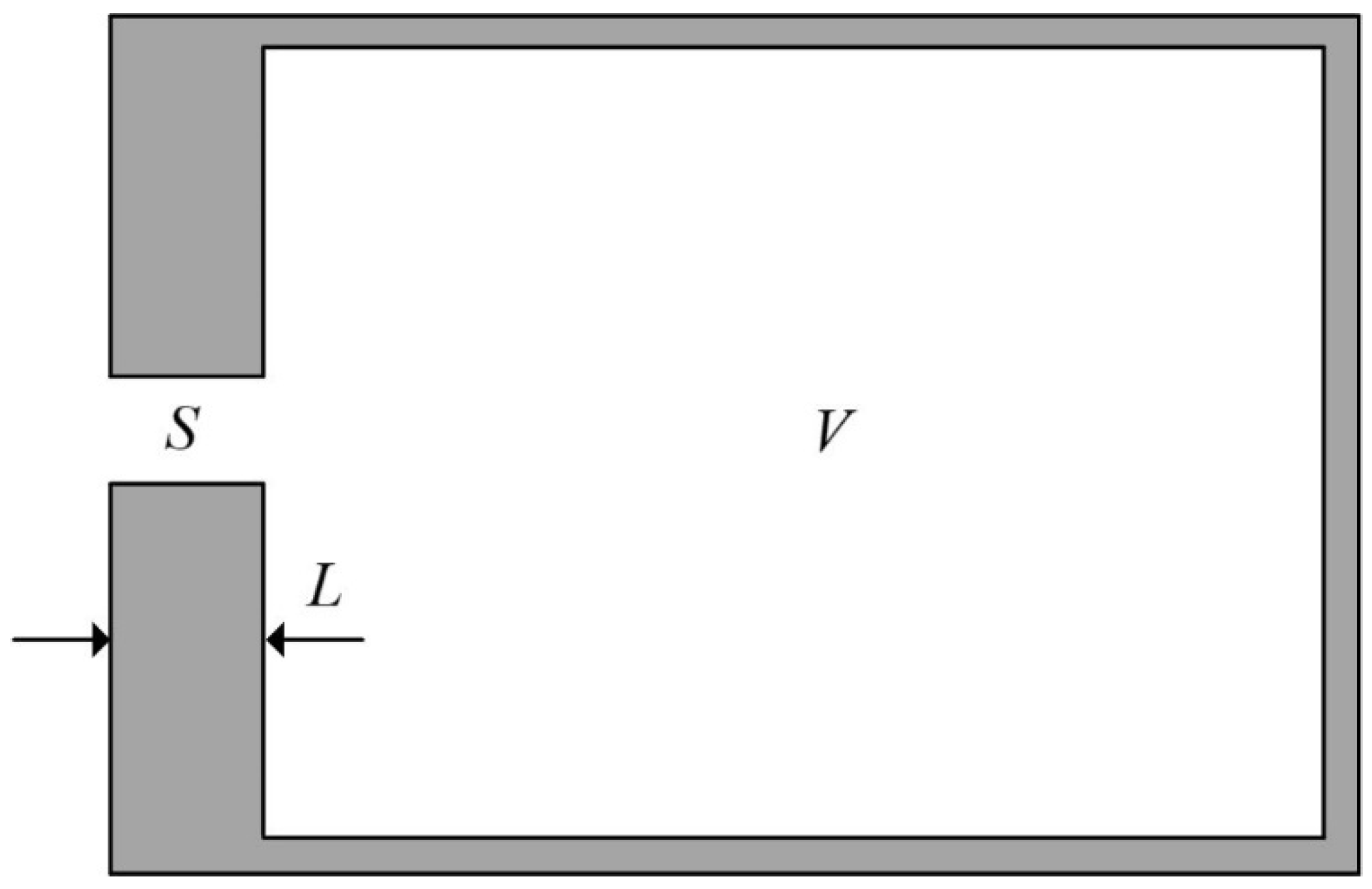
3.2. Equivalent Modeling
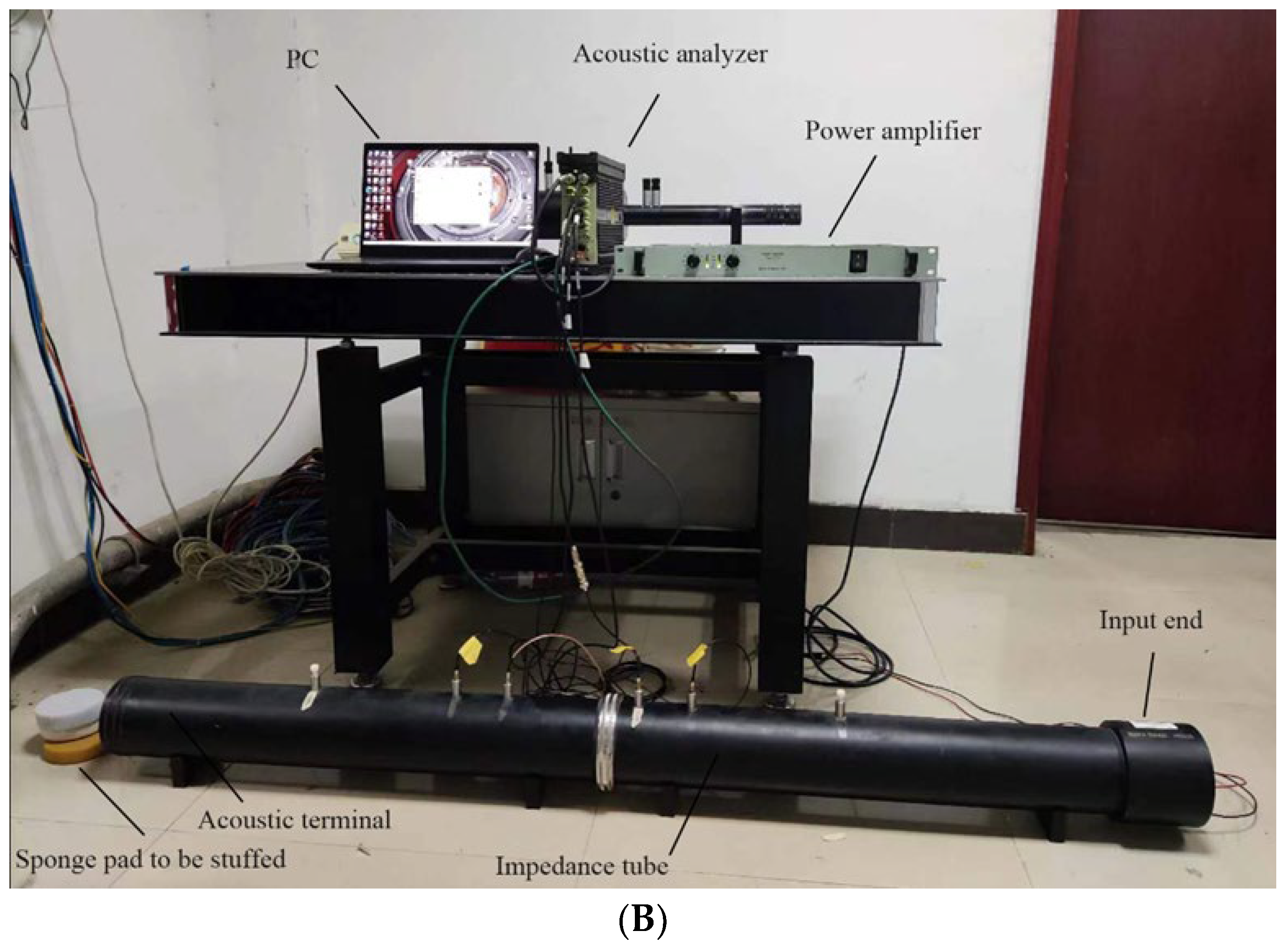
4. Experimental Verification
5. Exploring the Determinants of Performance Evaluation of Low-Frequency Sound Insulation
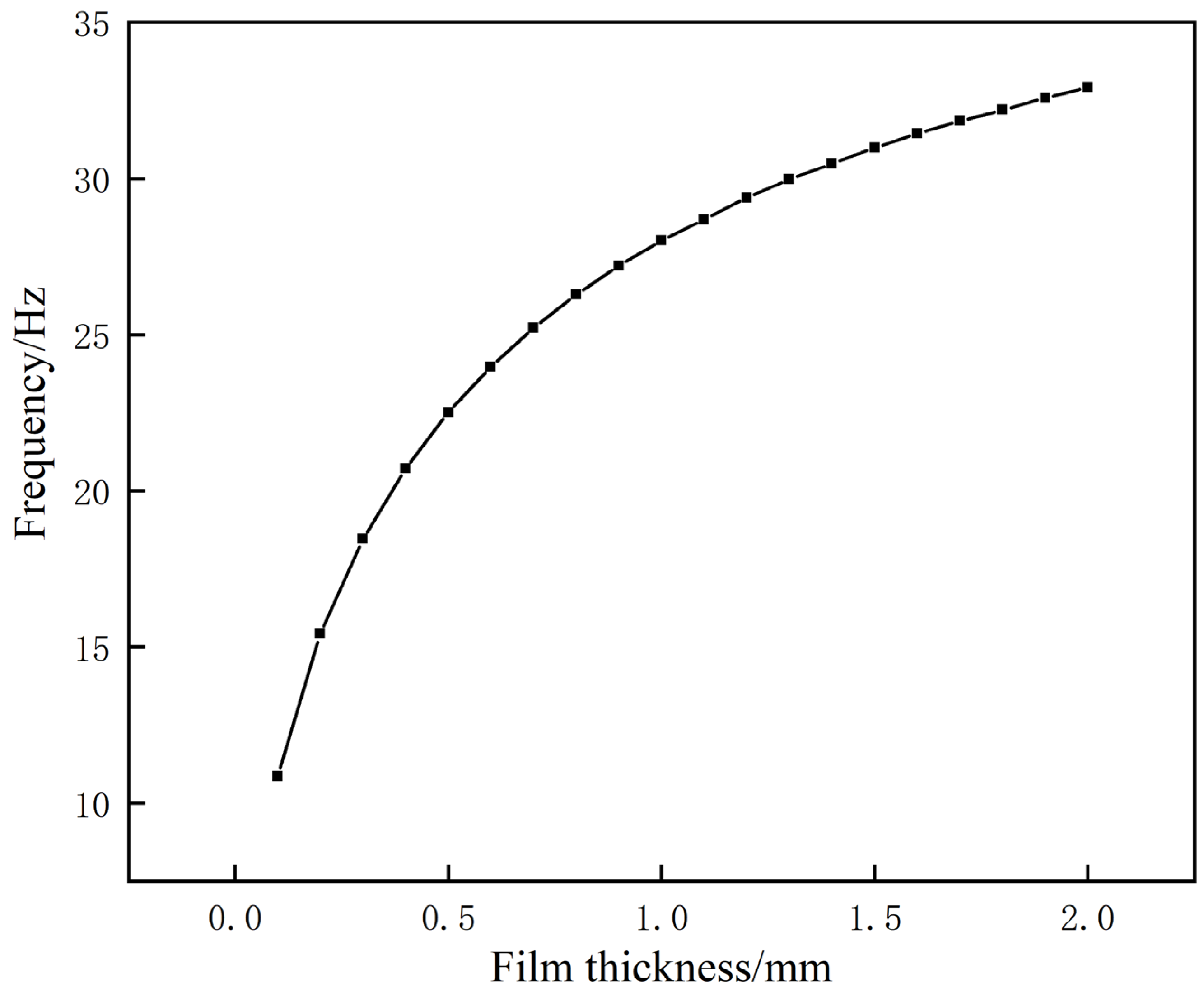
5.1. Effect of Film Thickness on the Frequency of the First Sound-Insulation Peak
5.2. Effect of Film Tension on the Frequency of the First Sound-Insulation Peak
5.3. The Influence of the Initial Orientation on the Amplitude of the Initial Sound-Insulation Peak
5.4. Effect of Cavity Volume on the Frequency of the First Sound-Insulation Peak
6. Conclusions
- (1)
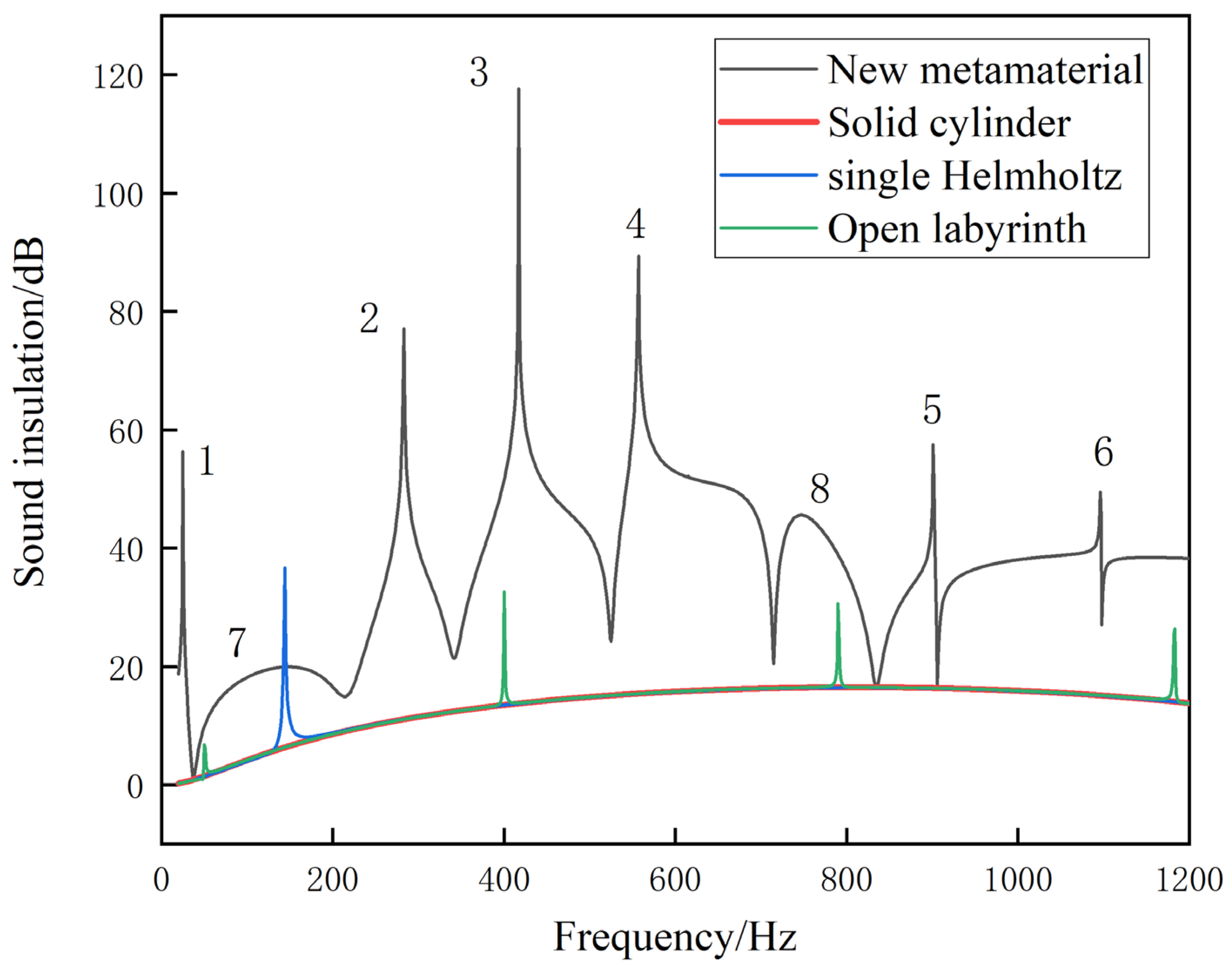
- Through the use of finite element analysis, the sound-insulation performance of metamaterials over a frequency range of 20–1200 Hz was comprehensively evaluated. This analysis identified several notable peaks in sound-insulation performance, reflecting the overall high efficiency of sound insulation. A particularly notable feature was the presence of a sound-insulation peak at a minimum frequency of 26.3 Hz, indicative of the material’s robust sound-insulation capability. These experimental results were fully consistent with the theoretical calculations, providing validation of the theoretical model’s accuracy and further supporting the use of metamaterials as potential sound-insulation materials.
- (2)
- In order to better understand the sound-insulation mechanism of metamaterials, a comprehensive analysis of sound pressure and vibration patterns at the frequency of the first sound-insulation peak was carried out. The equivalent model method was used to construct the corresponding model. The consistency between the results of the equivalent model method and those of the finite element method was used to verify the accuracy of the equivalent model and gain further insights into the sound-insulation mechanism.
- (3)
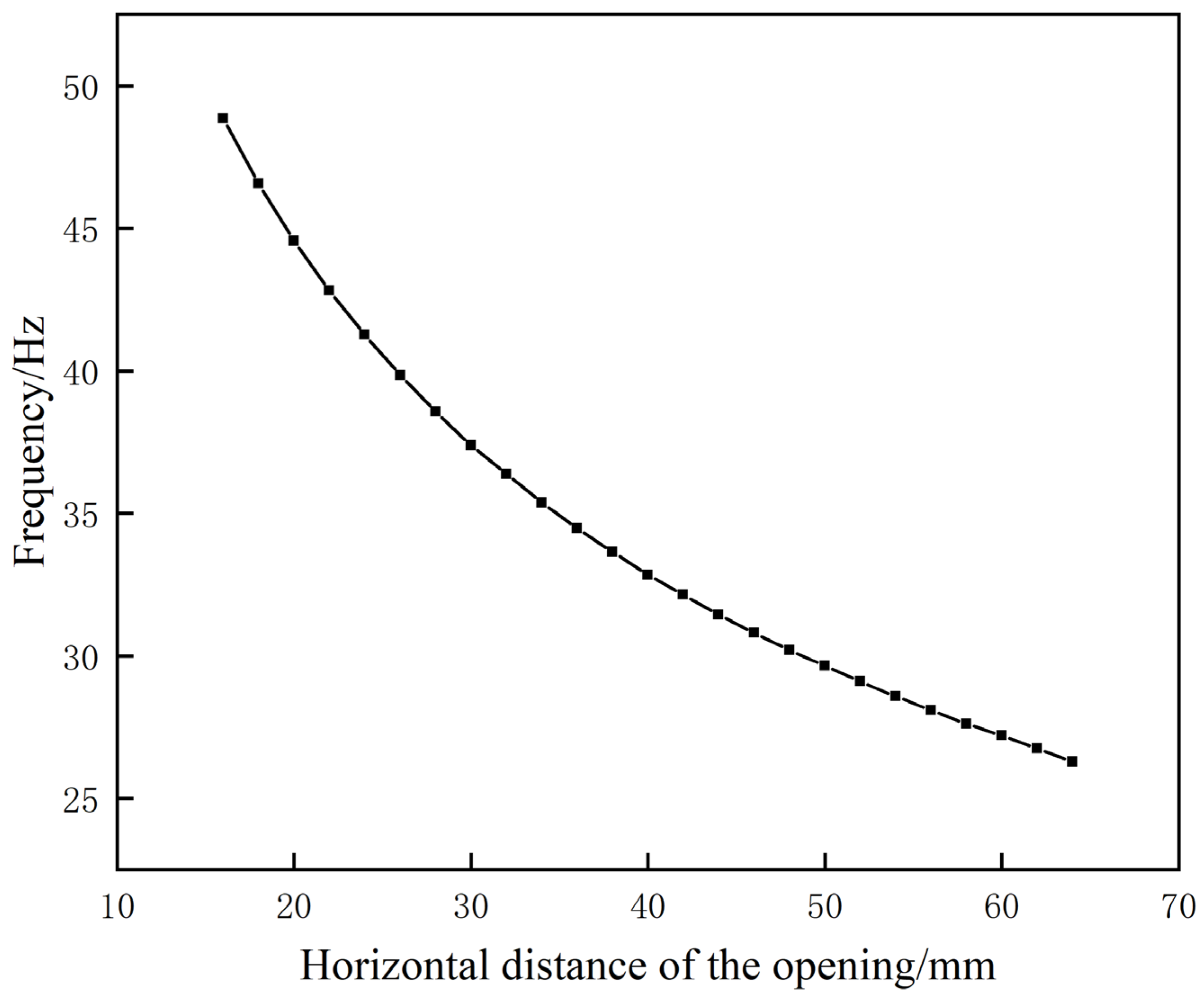
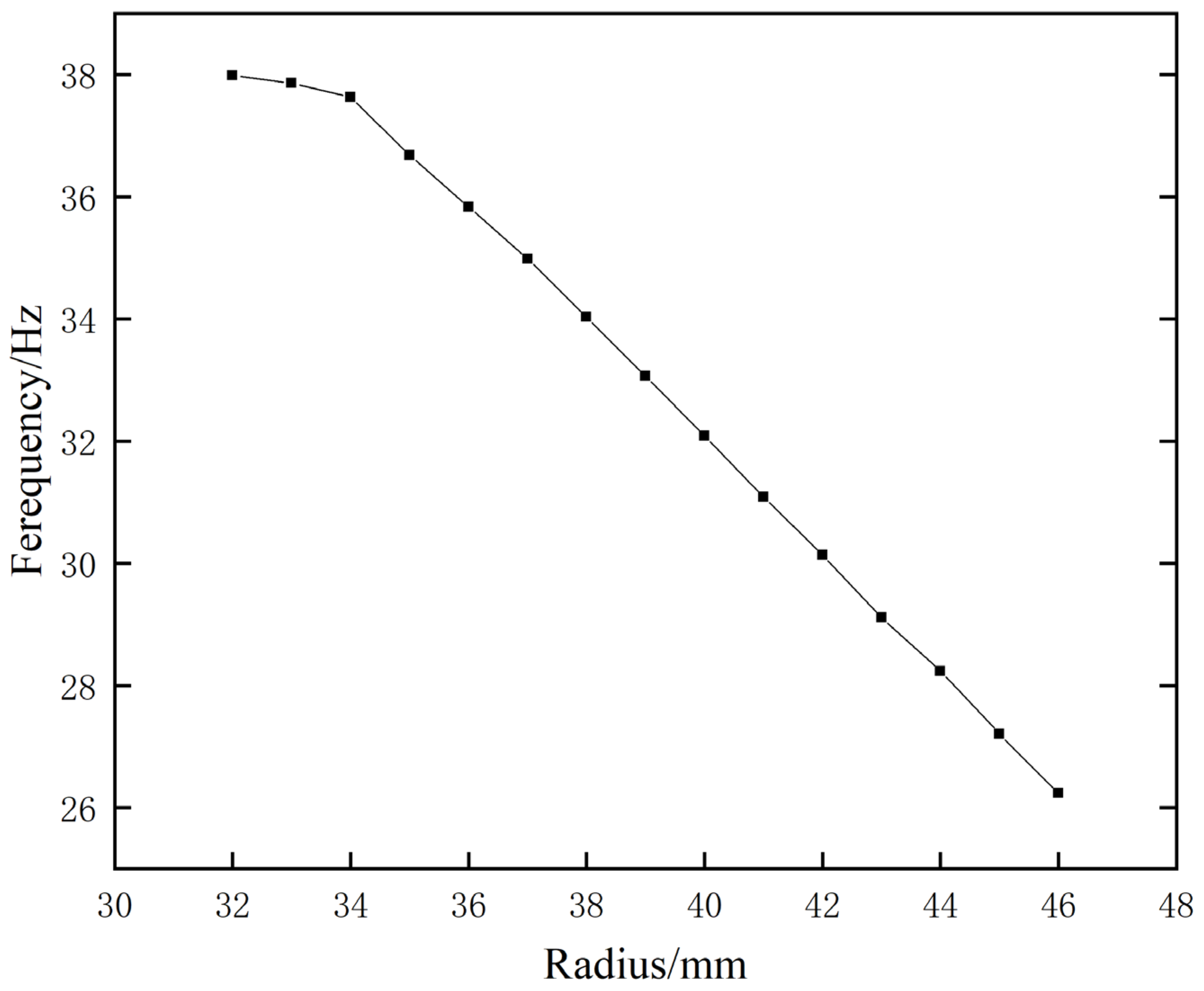
- The equivalent model established in (2) was used to investigate the factors that influence the sound insulation of metamaterials. The results of the analysis revealed that increasing the horizontal distance between two openings and the volume of the inner cavity can substantially reduce the first resonance frequency, thereby enhancing the sound-insulation performance of metamaterials. In addition, it should be noted that the larger the aperture width and the farther the aperture position is from the central plane, the higher the first resonant frequency will be. Therefore, specific parameter settings should be determined based on the specific application scenario.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cantuaria, M.L.; Pedersen, E.R.; Poulsen, A.H.; Raaschou-Nielsen, O.; Hvidtfeldt, U.A.; Levin, G.; Jensen, S.S.; Schmidt, J.H.; Sørensen, M. Transportation Noise and Risk of Tinnitus: A Nationwide Cohort Study from Denmark. Environ. Health Perspect. 2023, 131, 27001. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, M.; Zuo, L.; Wu, X.; Chen, M.; Li, X.; An, T.; Chen, L.; Xu, W.; Peng, S.; et al. Environmental noise exposure and health outcomes: An umbrella review of systematic reviews and meta-analysis. Eur. J. Public Health 2023, 33, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.-W.; Zhao, S.-D.; Wang, Y.-S.; Zhang, C. Topology optimization of anisotropic broadband double-negative elastic metamaterials. J. Mech. Phys. Solids 2017, 105, 54–80. [Google Scholar] [CrossRef]
- Naify, C.J.; Haberman, M.R.; Titovich, A. What is an acoustic metamaterial? J. Acoust. Soc. Am. 2023, 153, A118. [Google Scholar] [CrossRef]
- Gao, N.; Liu, J.; Deng, J.; Chen, D.; Huang, Q.; Pan, G. Design and performance of ultra-broadband composite meta-absorber in the 200 Hz-20 kHz range. J. Sound Vib. 2023, 574, 118229. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic Metamaterials for Noise Reduction: A Review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Dong, H.-W.; Shen, C.; Zhao, S.-D.; Qiu, W.; Zheng, H.; Zhang, C.; Cummer, S.A.; Wang, Y.; Fang, D.; Cheng, L. Achromatic metasurfaces by dispersion customization for ultra-broadband acoustic beam engineering. Natl. Sci. Rev. 2022, 9, nwac030. [Google Scholar] [CrossRef] [PubMed]
- Peri, V.; Song, Z.-D.; Serra-Garcia, M.; Engeler, P.; Queiroz, R.; Huang, X.; Deng, W.; Liu, Z.; Bernevig, B.A.; Huber, S.D. Experimental characterization of fragile topology in an acoustic metamaterial. Science 2020, 367, 797–800. [Google Scholar] [CrossRef] [PubMed]
- Darabi, A.; Ni, X.; Leamy, M.; Alù, A. Reconfigurable Floquet elastodynamic topological insulator based on synthetic angular momentum bias. Sci. Adv. 2020, 6, eaba8656. [Google Scholar] [CrossRef] [PubMed]
- Dandsena, J. Estimating effective acoustic properties of various configuration of perforated panels. Noise Control. Eng. J. 2023, 71, 208–223. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. Statics, vibration, and buckling of sandwich plates with metamaterial cores characterized by negative thermal expansion and negative Poisson’s ratio. Appl. Math. Mech. 2023, 44, 1457–1486. [Google Scholar] [CrossRef]
- Li, F.; Chen, Y.; Zhu, D. Revealing the Sound Transmission Loss Capacities of Sandwich Metamaterials with Re-Entrant Negative Poisson’s Ratio Configuration. Materials 2023, 16, 5928. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Huang, G. Some topics on elastic metamaterials. Acta Mech. Sin. 2023, 39, 1–2. [Google Scholar] [CrossRef]
- Hao, L.; Li, Y.; Yan, X.; Yang, X.; Guo, X.-D.; Xie, Y.; Pang, S.; Chen, Z.; Zhu, W. Tri-Band Negative Modulus Acoustic Metamaterial with Nested Split Hollow Spheres. Front. Mater. 2022, 9, 909671. [Google Scholar] [CrossRef]
- Chen, M.; Meng, D.; Jiang, H.; Wang, Y. Investigation on the Band Gap and Negative Properties of Concentric Ring Acoustic Metamaterial. Shock. Vib. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Kong, D. A thin-film acoustic metamaterial absorber with tunable sound absorption characteristics. J. Acoust. Soc. Am. 2023, 153, 3493–3500. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Xu, Y.G.; Cui, H. Research on Low Frequency Sound Insulation Properties of Membrane-Type Acoustic Metamaterials. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sanya, China, 12–14 November 2021; Volume 1210. [Google Scholar]
- Cui, H.; Liu, C.; Hu, H. Research on Low-Frequency Noise Control Based on Fractal Coiled Acoustic Metamaterials. Shock. Vib. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Liu, Z.; Fan, Q.; Lin, T.R. A study of low frequency sound insulation mechanism of a perforated plate-type acoustic metamaterial. J. Sound Vib. 2023, 558, 117775. [Google Scholar] [CrossRef]
- Dogra, S.; Gupta, A. Design, Manufacturing, and Acoustical Analysis of a Helmholtz Resonator-Based Metamaterial Plate. Acoustics 2021, 3, 630–641. [Google Scholar] [CrossRef]
- Bucciarelli, F.; Fierro, G.P.M.; Meo, M. A multilayer microperforated panel prototype for broadband sound absorption at low frequencies. Appl. Acoust. 2019, 146, 134–144. [Google Scholar] [CrossRef]
- Lu, K.; Wu, J.; Guan, D.; Gao, N.; Jing, L. A lightweight low-frequency sound insulation membrane-type acoustic metamaterial. AIP Adv. 2016, 6, 025116. [Google Scholar] [CrossRef]
- Benhala, B.; Lemkalli, B.; Idrissi, M.; Mir, A.; Achaoui, Y.; Raihani, A.; Boukili, B.; Sallem, A.; Qbadou, M. Lightweight panels based on Helmholtz resonators for low-frequency acoustic insulation. In Proceedings of the E3S Web of Conferences, Tamilnadu, India, 22–23 November 2023; Volume 469. [Google Scholar] [CrossRef]
- Yang, X.; Yang, F.; Shen, X.-m.; Wang, E.; Zhang, X.; Shen, C.; Peng, W. Development of Adjustable Parallel Helmholtz Acoustic Metamaterial for Broad Low-Frequency Sound Absorption Band. Materials 2022, 15, 5938. [Google Scholar] [CrossRef] [PubMed]
- Li, H.Z.; Liu, X.; Liu, Q.; Li, S.; Yang, J.-S.; Tong, L.-l.; Shi, S.; Schmidt, R.; Schröder, K.-U. Sound insulation performance of double membrane-type acoustic metamaterials combined with a Helmholtz resonator. Appl. Acoust. 2023, 205, 109297. [Google Scholar] [CrossRef]
- He, Z.-H.; Zhao, J.-B.; Yao, H.; Chen, X. Sound insulation performance of Helmholtz cavity with thin film bottom. Acta Phys. Sin. 2019, 68. [Google Scholar] [CrossRef]
- Hu, G.; Tang, L.; Yang, Y. Acoustic metamaterial containing an array of Helmholtz resonators coupled with mass-loaded membranes. In Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; SPIE: Cergy-Pontoise, France, 2020. [Google Scholar]
- Kennedy, J.; Flanagan, L.; Dowling, L.; Bennett, G.J.; Rice, H.J.; Trimble, D. The Influence of Additive Manufacturing Processes on the Performance of a Periodic Acoustic Metamaterial. Int. J. Polym. Sci. 2019, 2019, 7029143. [Google Scholar] [CrossRef]
- Fusaro, G.; Barbaresi, L.; Cingolani, M.; Garai, M.; Ida, E.; Prato, A.; Schiavi, A. Investigation of the impact of additive manufacturing techniques on the acoustic performance of a coiled-up resonator. J. Acoust. Soc. Am. 2023, 153, 2921. [Google Scholar] [CrossRef] [PubMed]
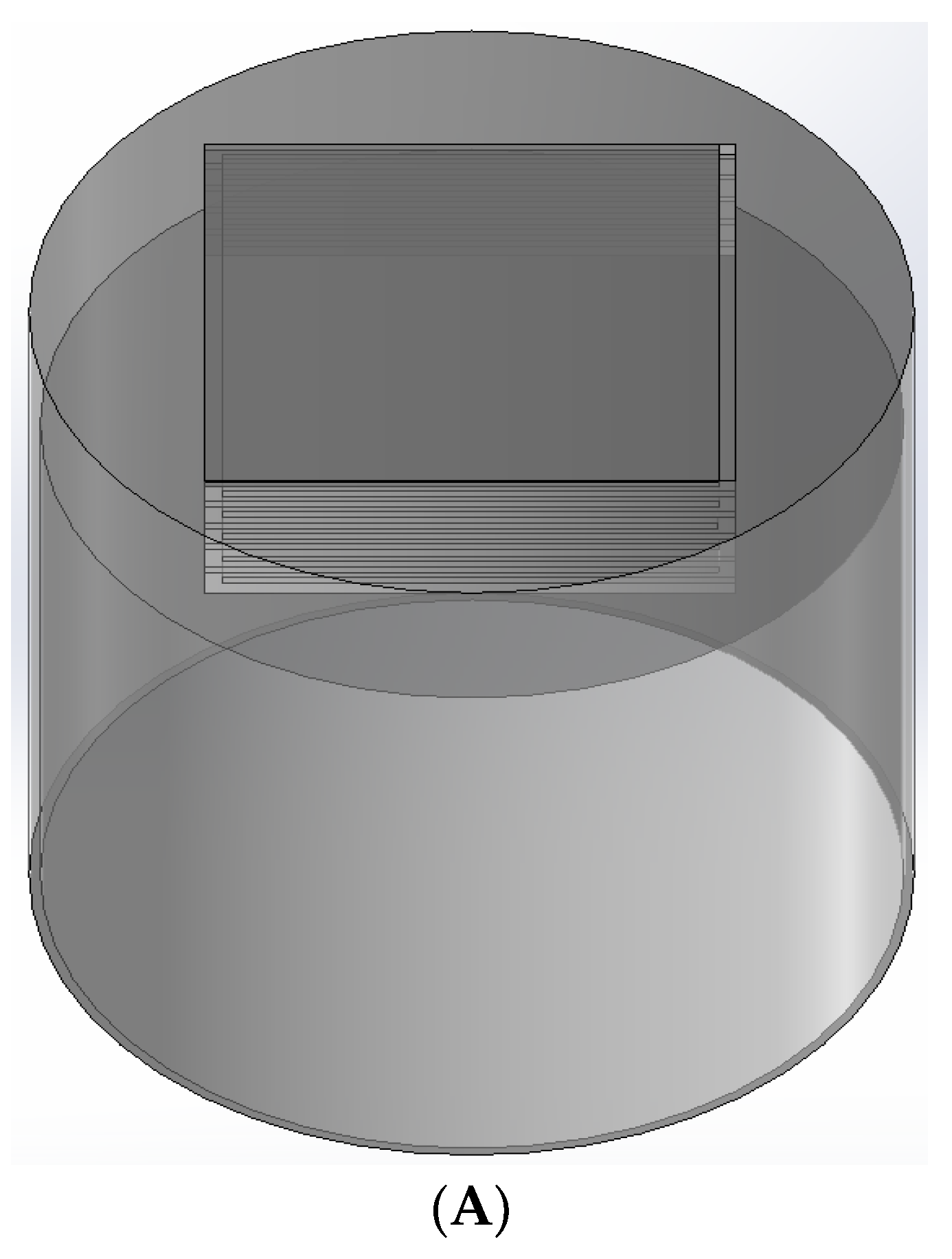
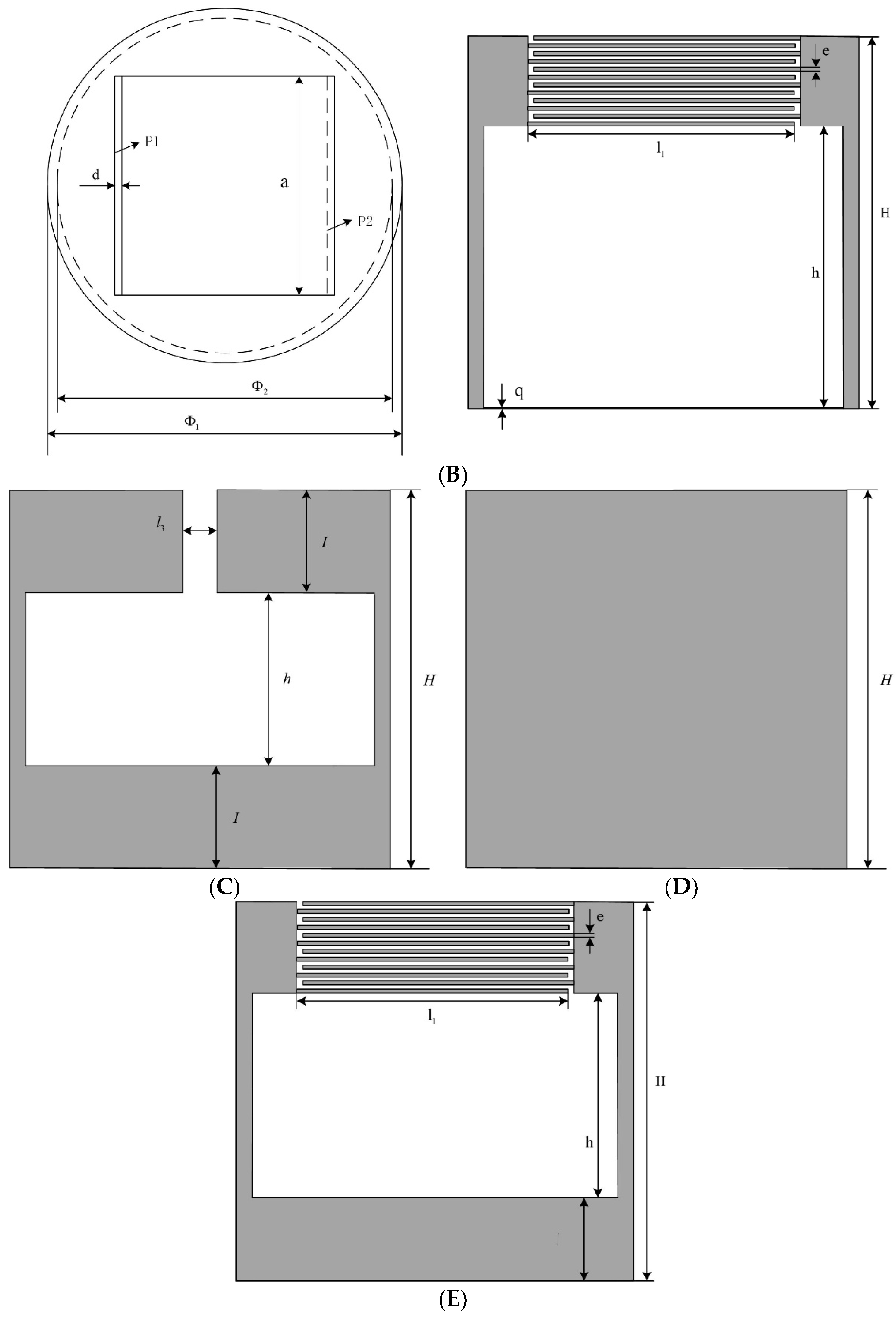





| Materials | Poisson’s Ratio | Density (kg/m3) | Young’s Modulus (Pa) |
|---|---|---|---|
| Rubber | 0.469 | 1300 | |
| Resin | 0.340 | 1100 |
| Method | First Peak Frequency of Sound Insulation |
|---|---|
| Equivalence modeling approach | 25.9 (Hz) |
| Finite element method | 26.3 (Hz) |
| Inaccuracies | 1.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Zhao, J.; Liu, H.; Zhang, X.; Zhang, G.; Yao, H. Low-Frequency Sound-Insulation Performance of Labyrinth-Type Helmholtz and Thin-Film Compound Acoustic Metamaterial. Materials 2024, 17, 4475. https://doi.org/10.3390/ma17184475
Hu P, Zhao J, Liu H, Zhang X, Zhang G, Yao H. Low-Frequency Sound-Insulation Performance of Labyrinth-Type Helmholtz and Thin-Film Compound Acoustic Metamaterial. Materials. 2024; 17(18):4475. https://doi.org/10.3390/ma17184475
Chicago/Turabian StyleHu, Peizhou, Jingbo Zhao, Hong Liu, Xiaosheng Zhang, Guangjun Zhang, and Hong Yao. 2024. "Low-Frequency Sound-Insulation Performance of Labyrinth-Type Helmholtz and Thin-Film Compound Acoustic Metamaterial" Materials 17, no. 18: 4475. https://doi.org/10.3390/ma17184475
APA StyleHu, P., Zhao, J., Liu, H., Zhang, X., Zhang, G., & Yao, H. (2024). Low-Frequency Sound-Insulation Performance of Labyrinth-Type Helmholtz and Thin-Film Compound Acoustic Metamaterial. Materials, 17(18), 4475. https://doi.org/10.3390/ma17184475





