Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load
Abstract
:1. Introduction
2. Materials and Methods
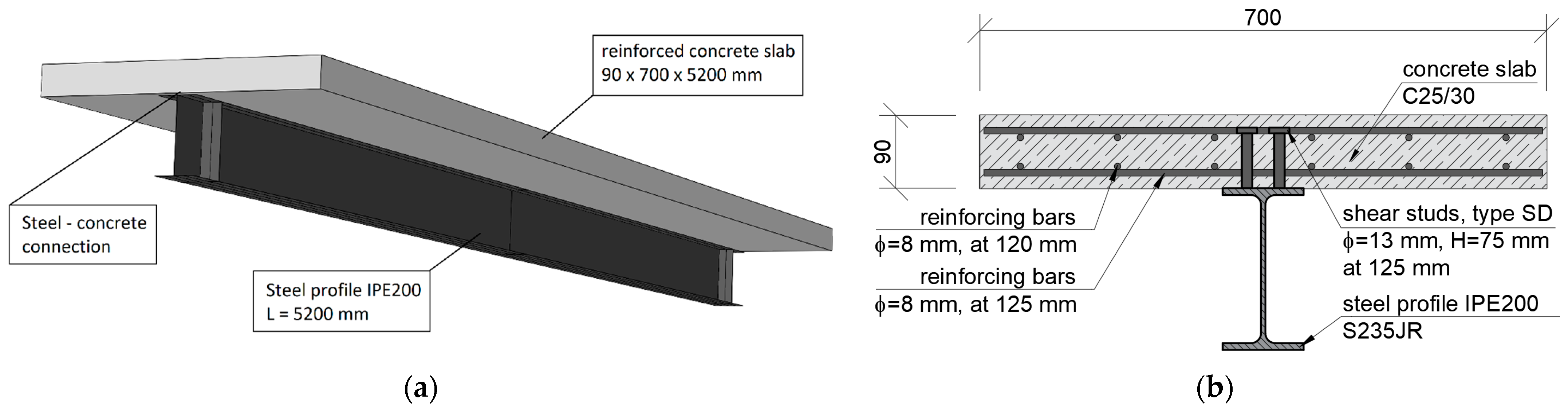
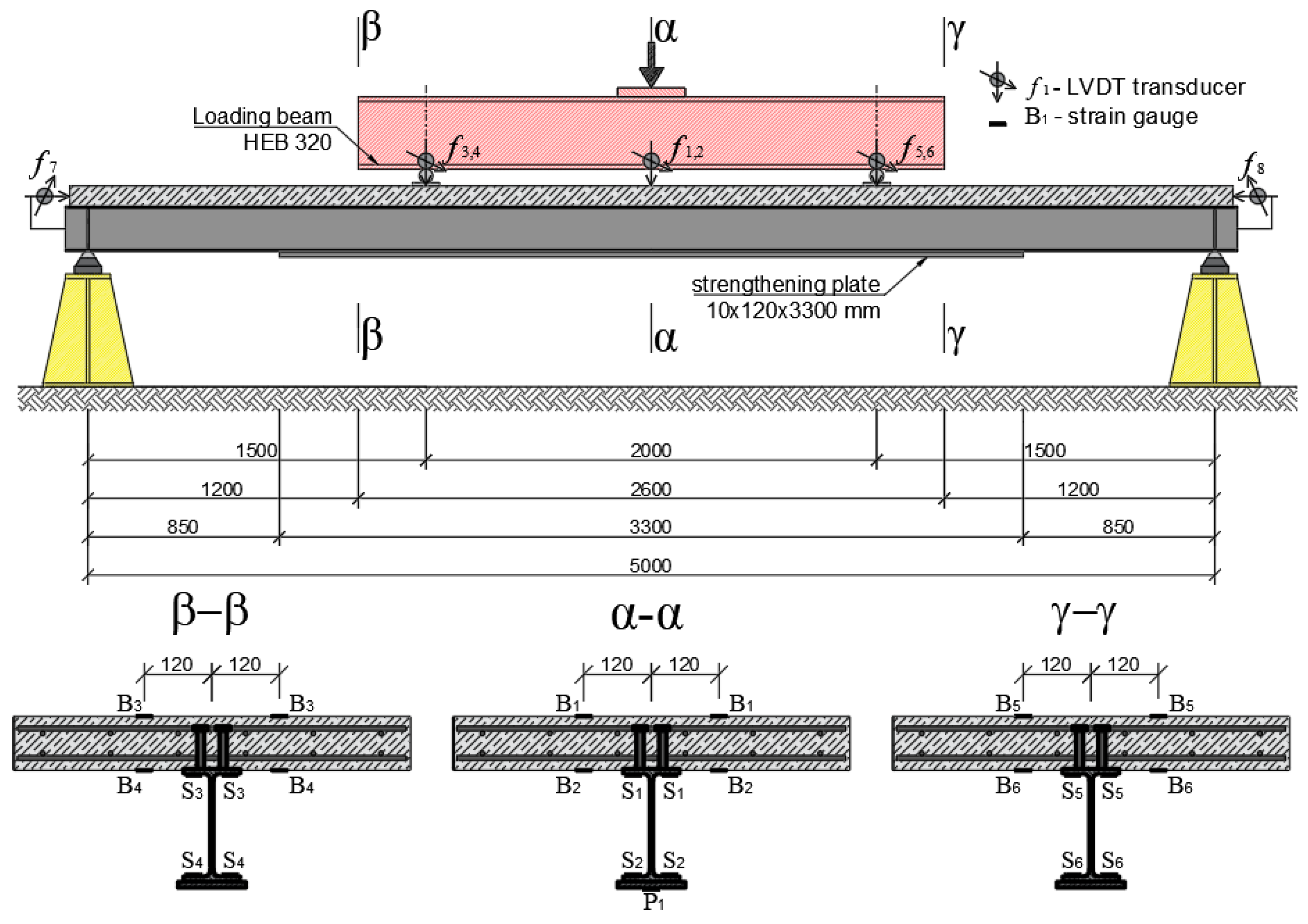
2.1. Test Element Design
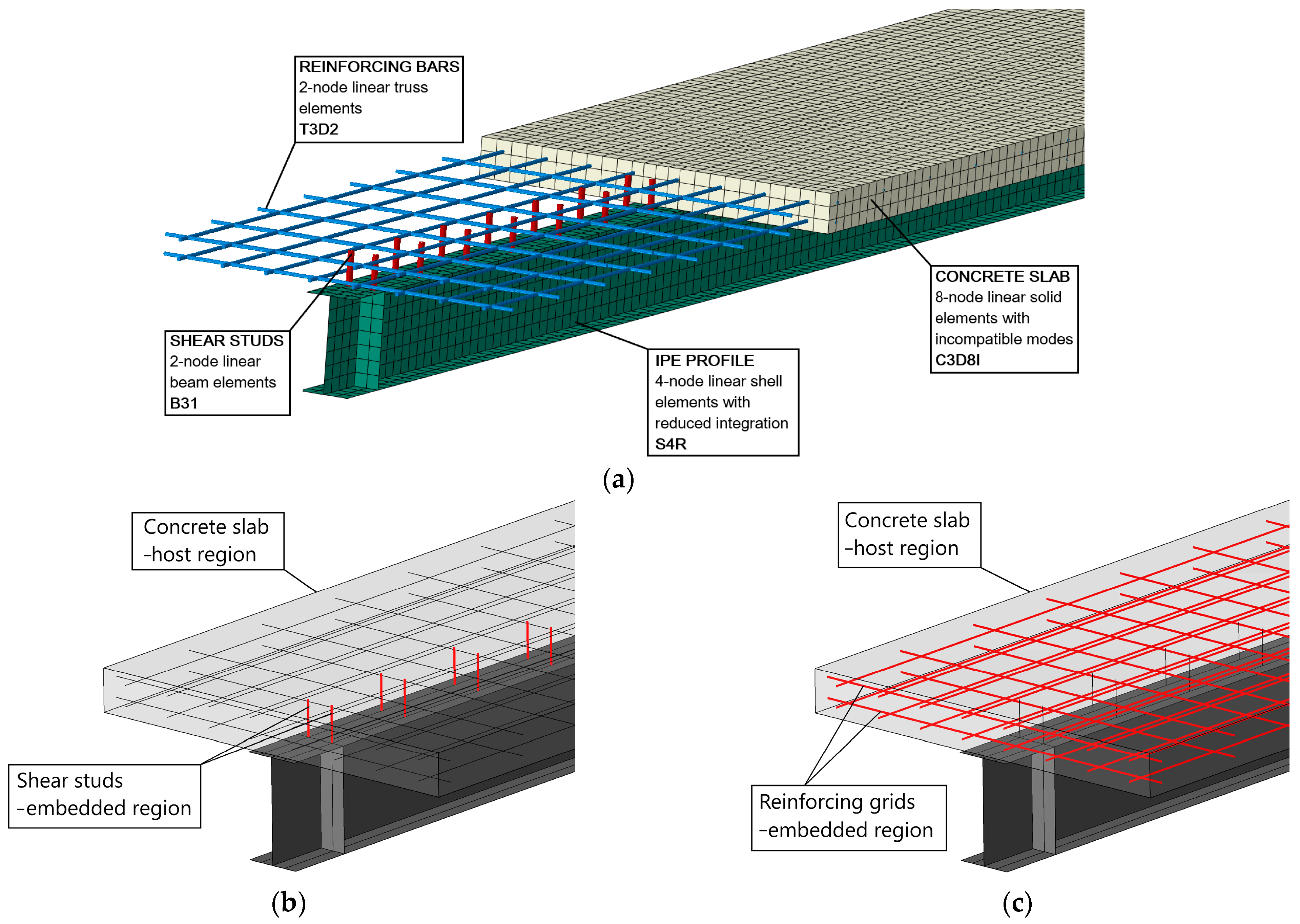
2.2. Numerical Model
2.3. Experimental Specimens
2.4. Steel
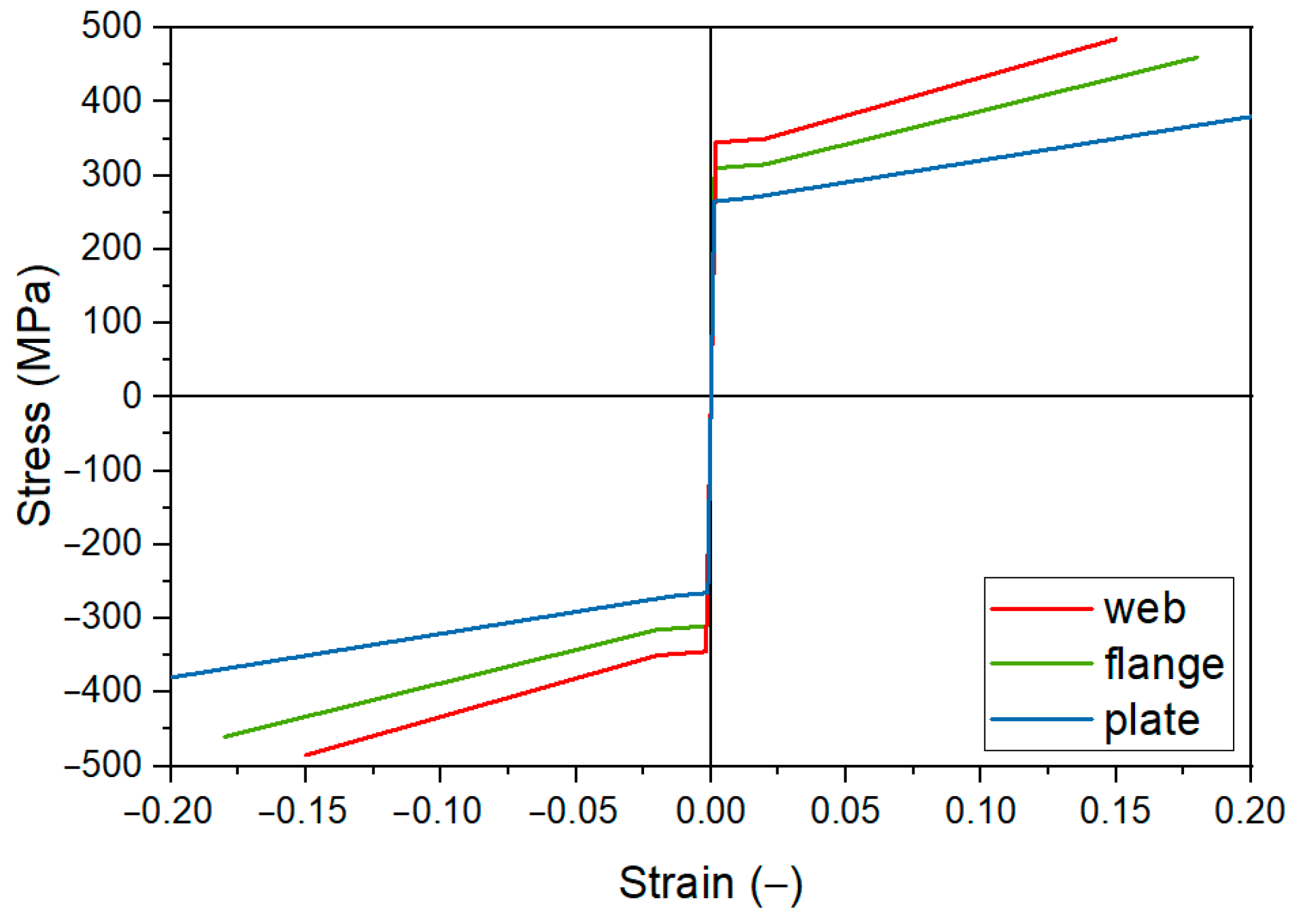
2.4.1. Material Tests
2.4.2. Material Model
2.5. Concrete
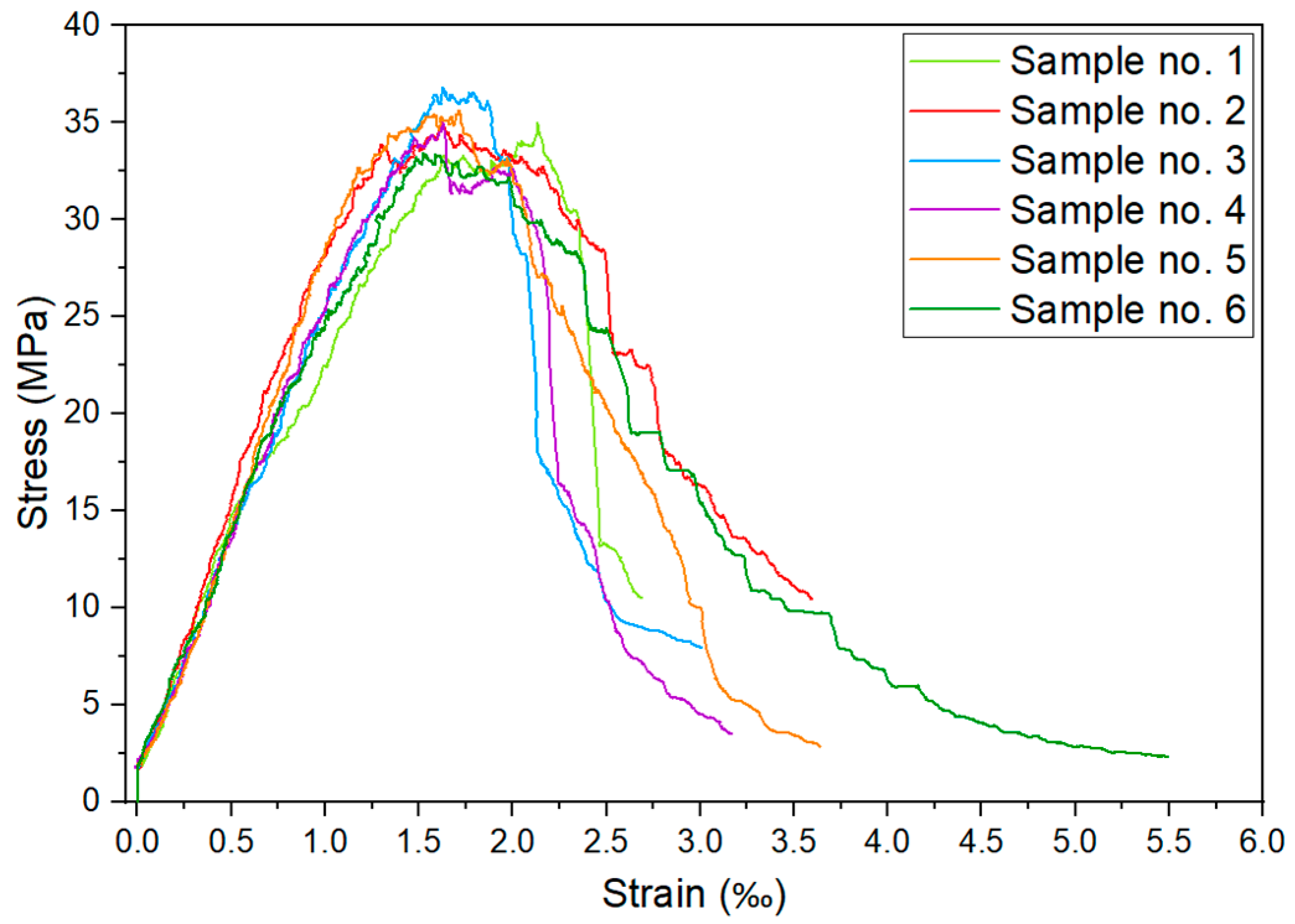
2.5.1. Material Tests
2.5.2. Material Model
2.6. Initial Assumptions
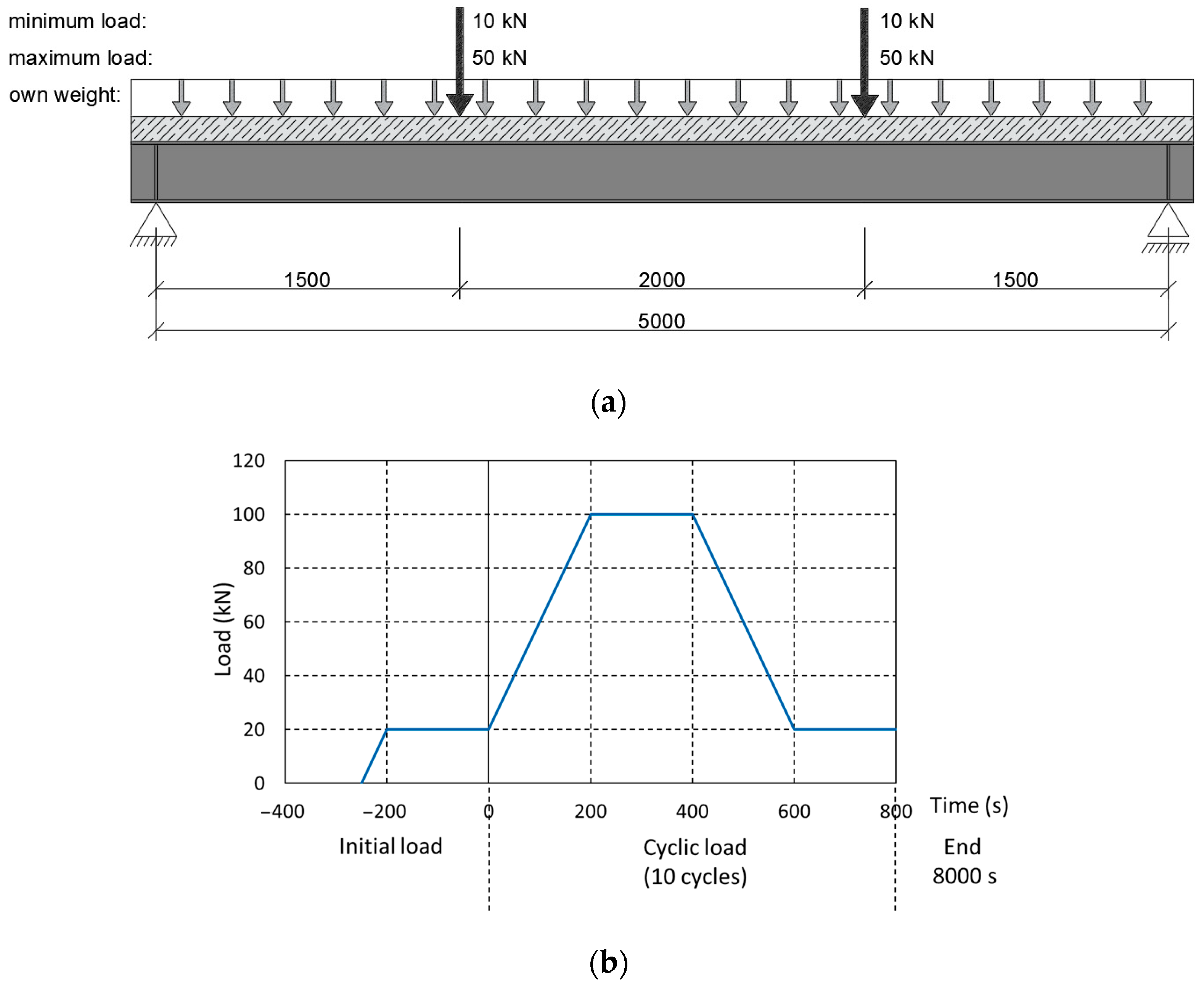
2.6.1. Cyclic Preload
- Ramp up to 100 kN in 200 s (speed—0.4 kN/s);
- Maintain the load for 200 s;
- Ramp down to 20 kN in 200 s (speed—0.4 kN/s);
- Maintain the load for 200 s.
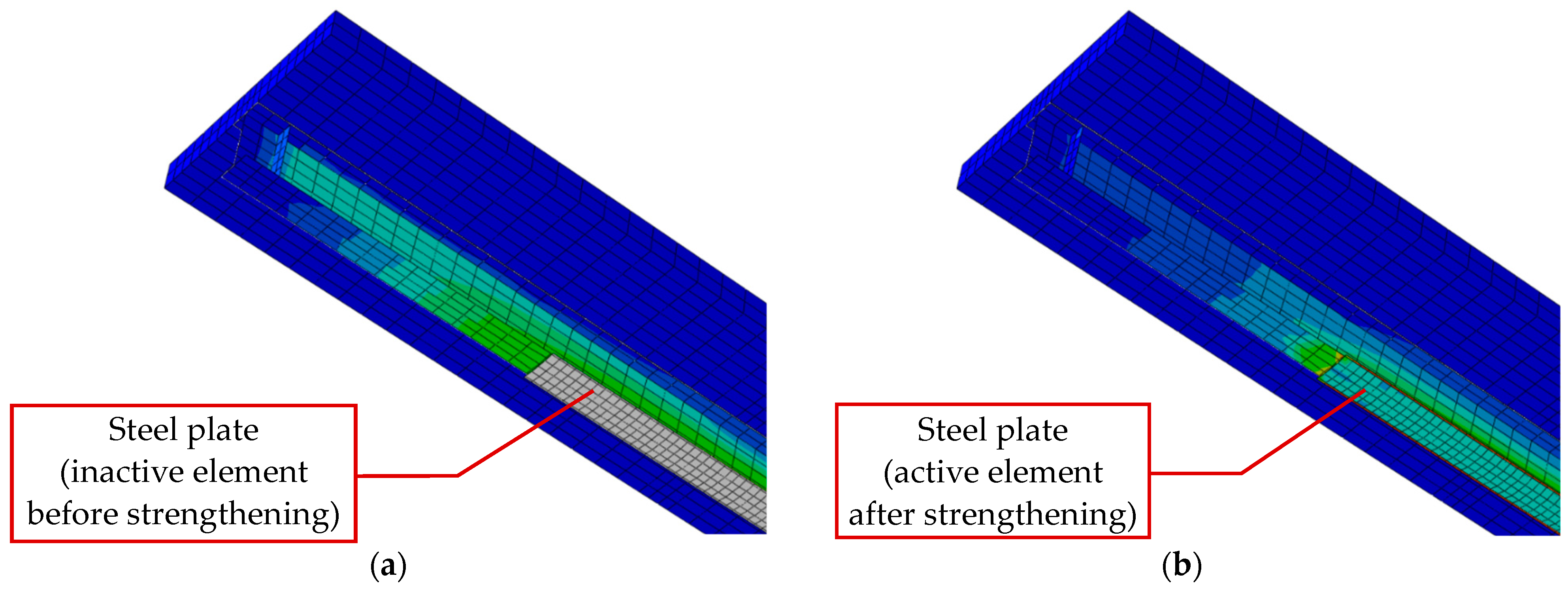
2.6.2. Strengthening under Load
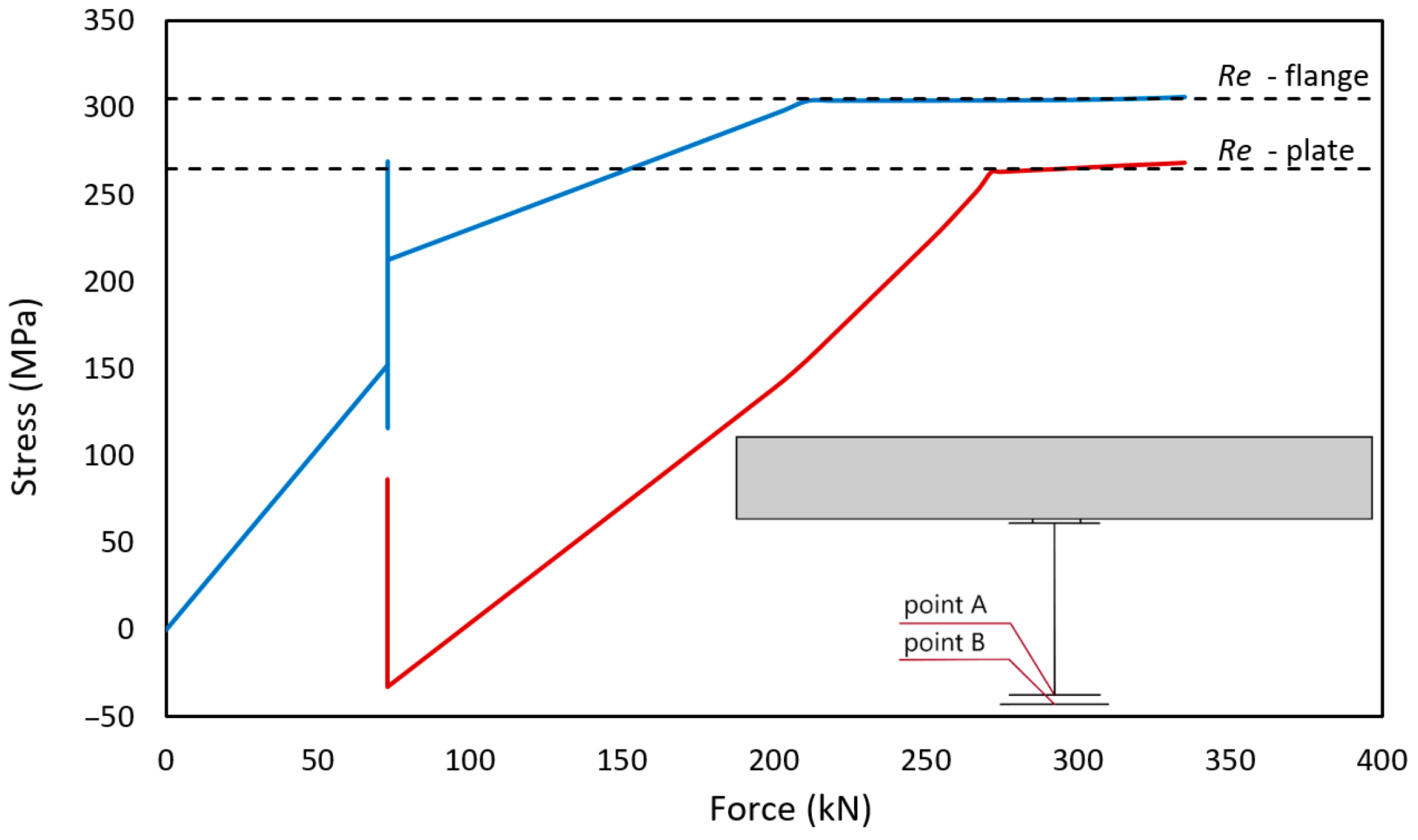
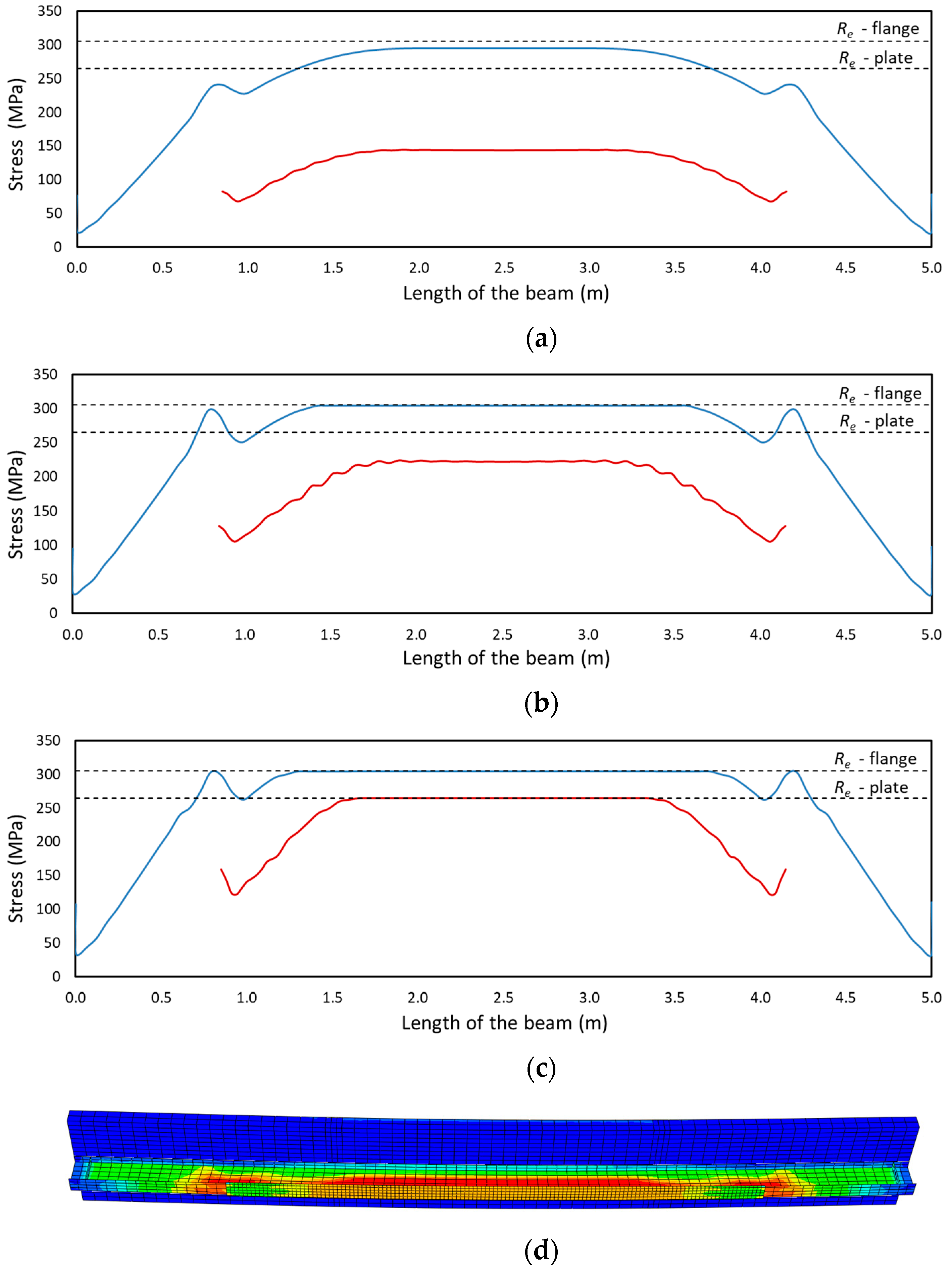
- The first step was the introduction of a preload, simulating the stress state of the structure before strengthening. This load was set in such a way that the ultimate limit state condition was maintained during each strengthening step. The welding of the structure, through rapid heating to significant temperatures, caused local weakening of the section. This can be taken into account in the calculation by assuming a reduced cross-sectional area. A force of 60 kN was taken as the preload. Together with the dead load, the assumed level of the preload results in 163 MPa of stress in the bottom flange of the steel beam (welding point) (Figure 11). After taking into account the reduction in stiffness during welding, the stresses increase to 228 MPa, which constitutes 97% of the allowable stress.
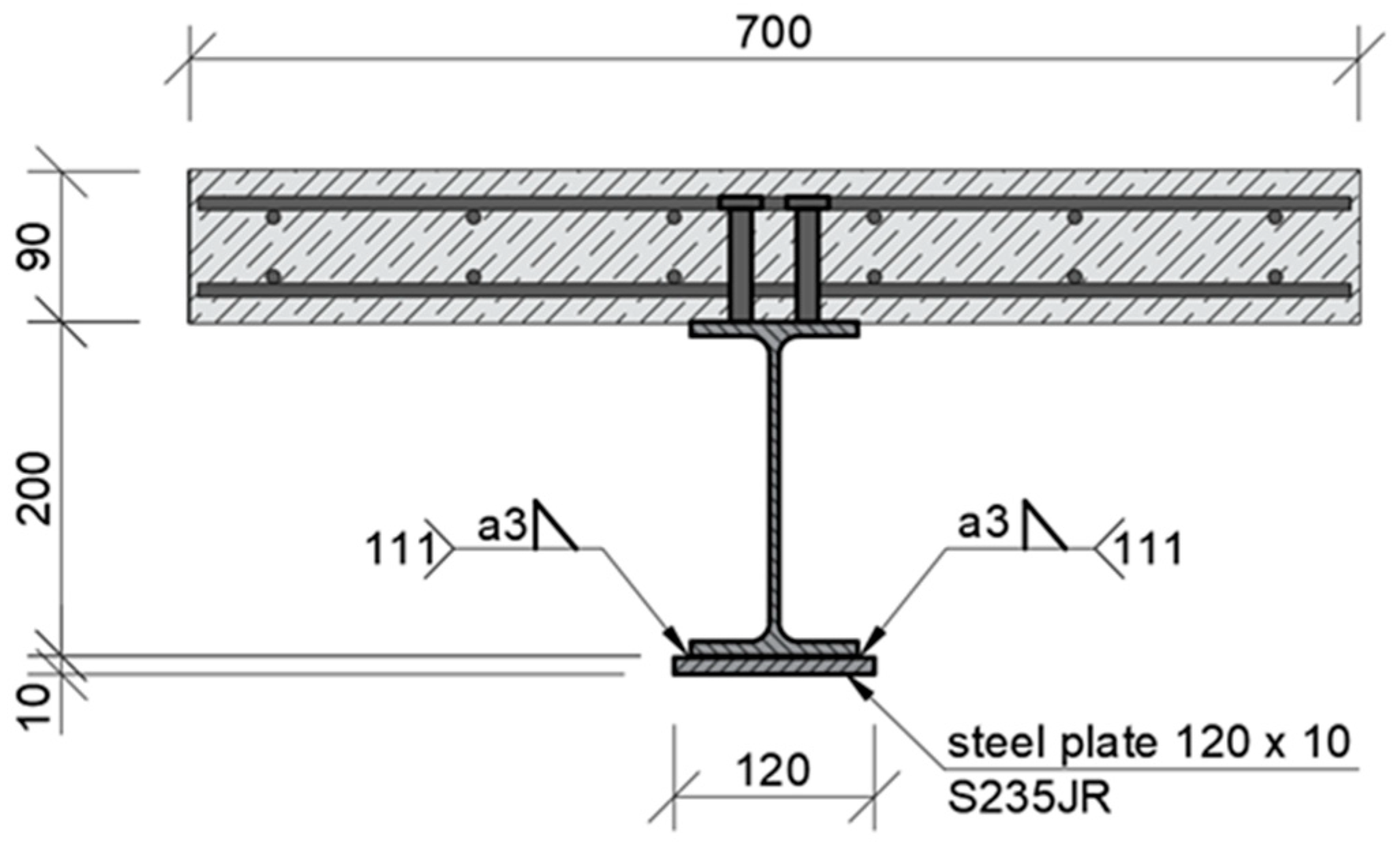
- The second stage was the strengthening process, which consisted of welding an additional plate to the bottom flange of the steel beam. The dimensions of the plate were optimised based on the energy parameters [50]. A plate with a section of 10 mm × 120 mm and a length of 3300 mm was adopted. Its location in the beam cross-section is shown in Figure 11. The strengthening plate was 20 mm wider than the bottom flange of the IPE200 beam to improve the quality of the fillet weld at the PB position.
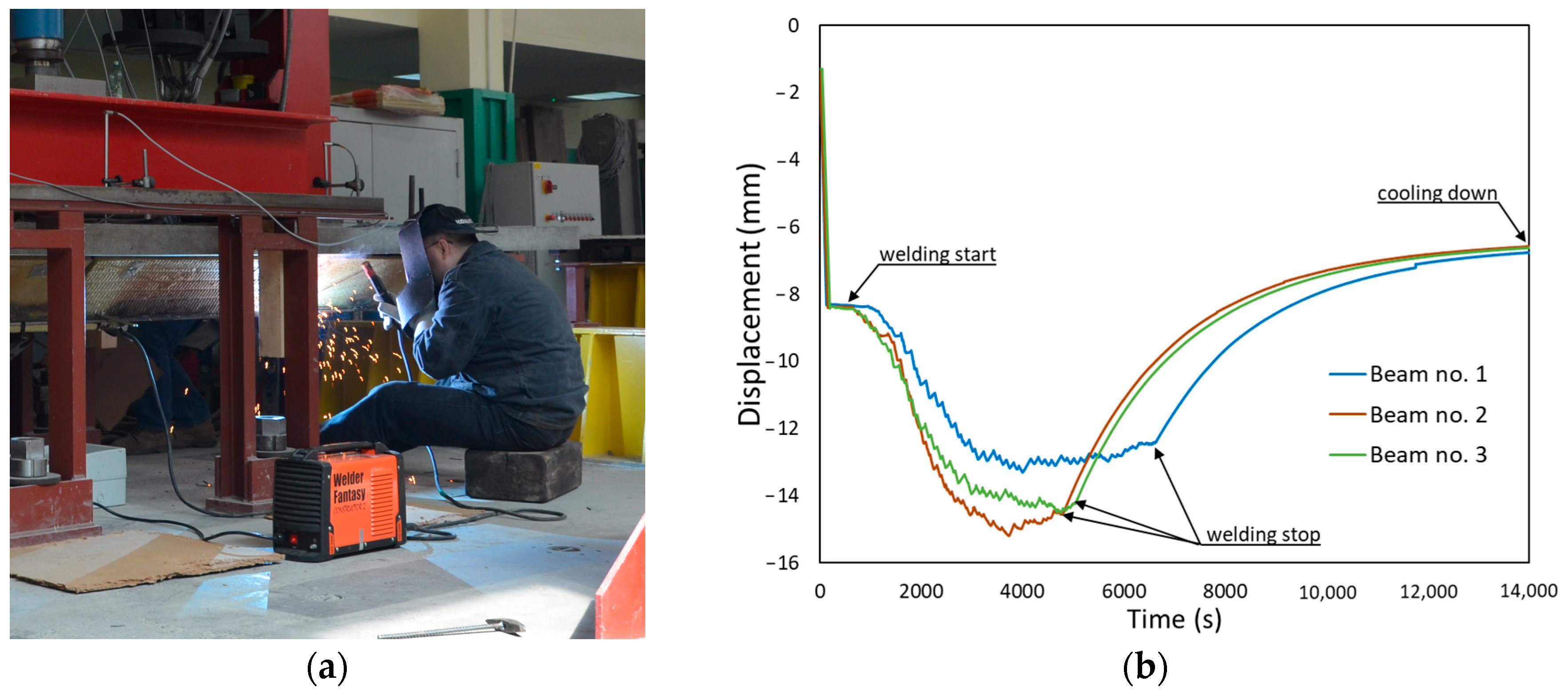
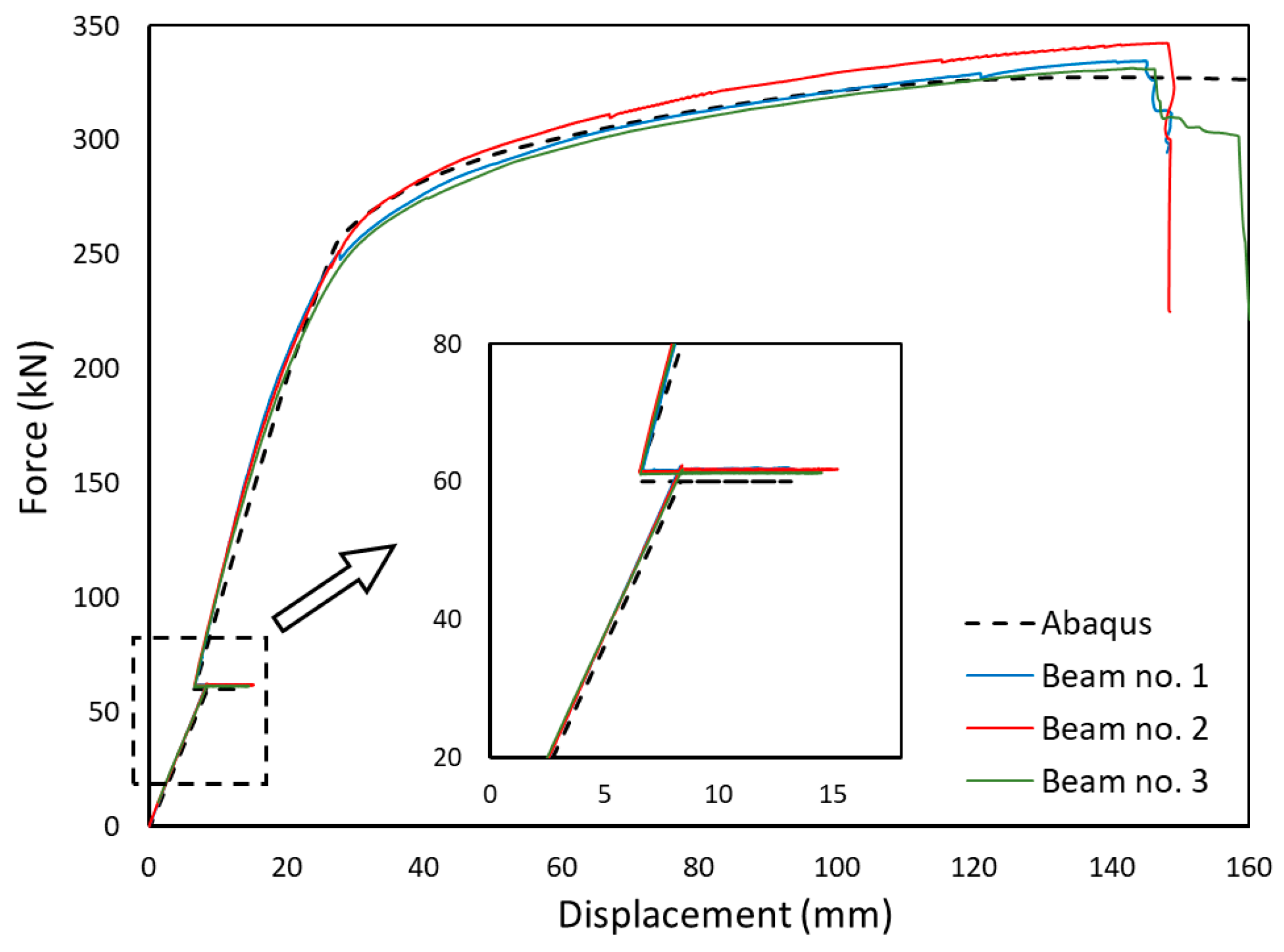
- Once the strengthening process was complete and the structure had cooled completely, the load was increased until the yielding and failure of the models. This approach allowed the recording of the plastic load-bearing capacity of the beam resulting from the full redistribution of stresses between the reinforced element and the strengthening. The failure mechanism of the beam was also determined.
2.7. Numerical Analysis
2.8. Experimental Tests
3. Results
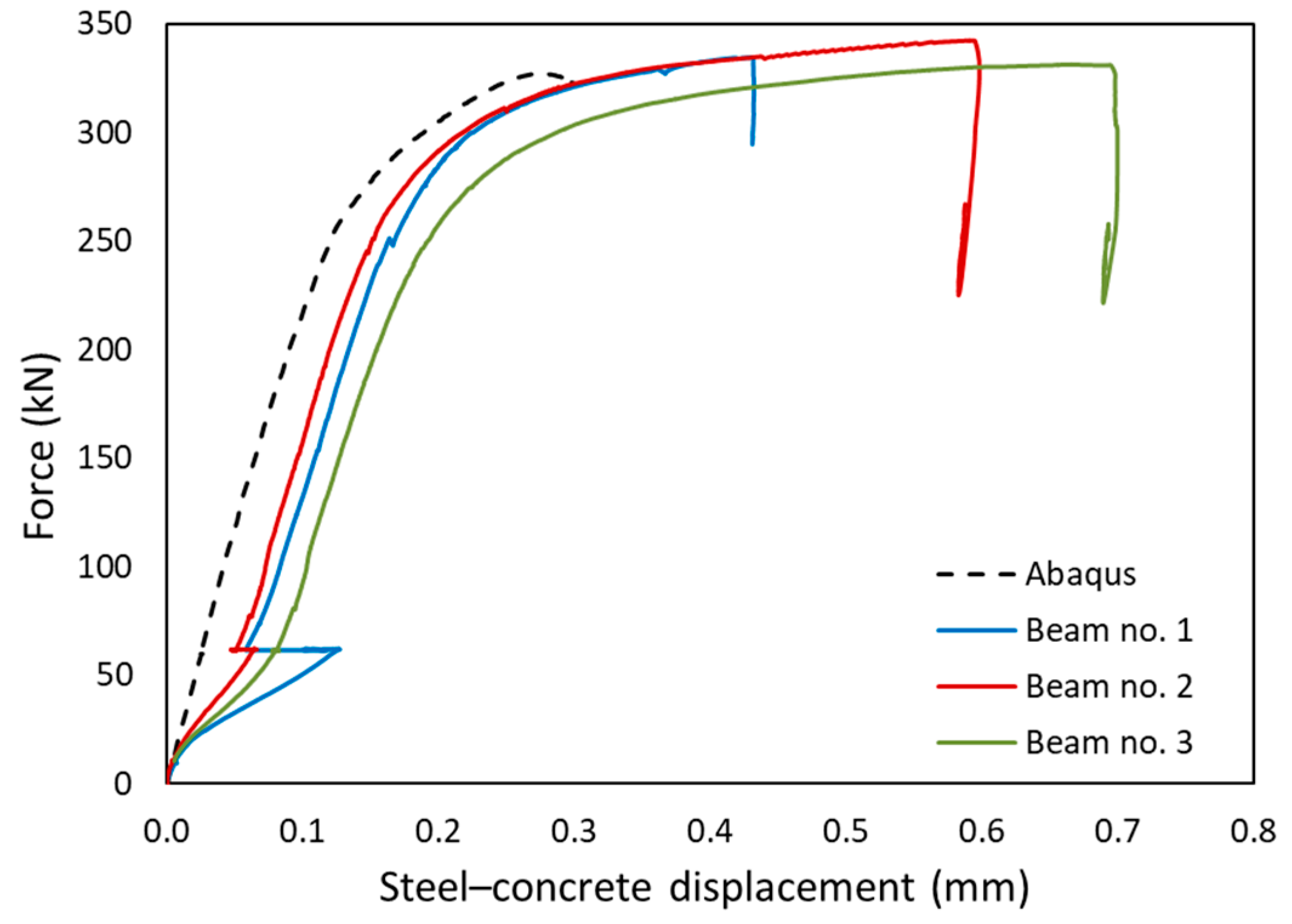
3.1. Displacement
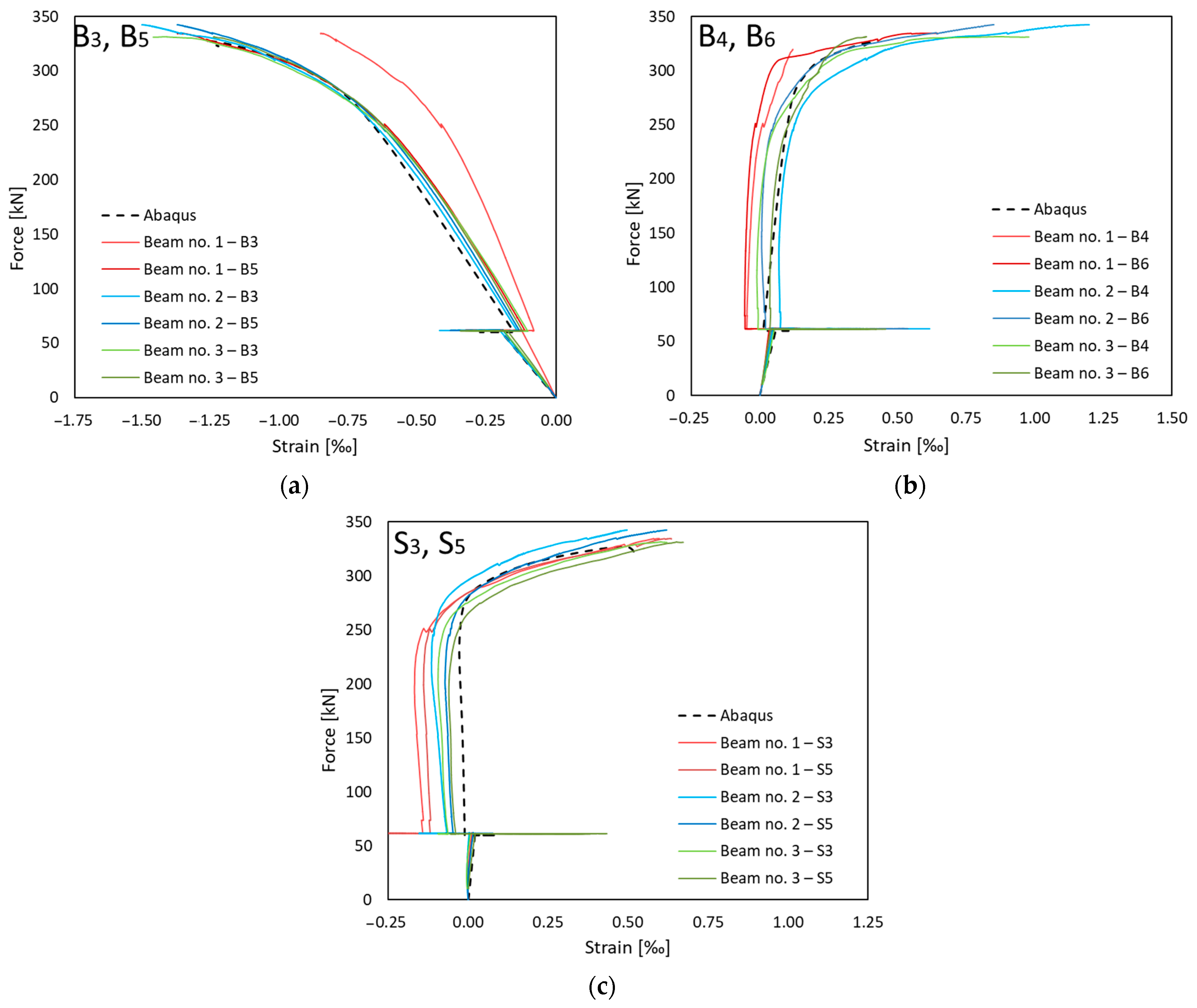
3.2. Strains
3.3. Discussion
4. Summary and Conclusions
- The use of the Abaqus software package allowed the precise simulation of the behaviour of the composite element, with a clear division into the brittle concrete part and the plastic steel part. Particularly, the Concrete Damage Plasticity Model was useful. The model allows for a non-linear description of the properties of concrete, independently in the analysis of compression and tension. In addition, it provides the possibility to model the stiffness degradation of concrete in the critical range and the cracking of the material.
- Owing to the functions available in Abaqus, the process of strengthening the structure under load was modelled. From a numerical analysis point of view, this is a non-standard task, as it requires a change in the model geometry (addition of a strengthening plate) during calculation.
- The numerical model allows the reinforced member to be tested over the full load range, including its yielding and stress redistribution between the element and the strengthening plate.
- The properly experimentally verified numerical model allows for many subsequent numerical analyses to be conducted, without generating further research costs.
- The research presented in this paper confirms the effectiveness of strengthening structures under load. Of course, this requires a number of technological conditions for the safe conduct of the process. However, it allows for much faster and cheaper performance of the strengthening of an existing object, without the need to remove all the equipment located on the modernised floor.
- When a structure is strengthened under load, it is extremely important to correctly estimate welding deformations. This issue requires extended analysis in future studies.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Polus, Ł.; Szumigała, M. An experimental and numerical study of aluminium–concrete joints and composite beams. Arch. Civ. Mech. Eng. 2019, 19, 375–390. [Google Scholar] [CrossRef]
- Szumigała, M.; Polus, Ł. An numerical simulation of an aluminium-concrete beam. Procedia Eng. 2017, 172, 1086–1092. [Google Scholar] [CrossRef]
- Georgantzia, E.; Gkantou, M.; Kamaris, G.S. Aluminium alloys as structural material: A review of research. Eng. Struct. 2021, 227, 111372. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Concrete-filled double-skin aluminum circular hollow section stub columns. Thin-Walled Struct. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Experimental and numerical investigations of aluminium-timber composite beams with bolted connections. Structures 2021, 34, 1942–1960. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Experimental Study of Aluminium-Timber Composite Bolted Connections Strengthened with Toothed Plates. Materials 2022, 15, 5271. [Google Scholar] [CrossRef] [PubMed]
- Saleh, S.M.; Jasim, N.A. Structural Behavior of Timber Aluminum Composite Beams under Static Loads. IJERT-Int. J. Eng. Res. Technol. 2014, 3, 1166–1173. [Google Scholar]
- Chybiński, M.; Polus, Ł. Structural Behaviour of Aluminium–Timber Composite Beams with Partial Shear Connections. Appl. Sci. 2023, 13, 1603. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and numerical study of steel-timber composite (STC) beams. J. Constr. Steel Res. 2016, 122, 367–378. [Google Scholar] [CrossRef]
- Loss, C.; Davison, B. Innovative composite steel-timber floors with prefabricated modular components. Eng. Struct. 2017, 132, 695–713. [Google Scholar] [CrossRef]
- Aspila, A.; Heinisuo, M.; Mela, K.; Malaska, M.; Pajunen, S. Elastic design of steel-timber composite beams. Wood Mater. Sci. Eng. 2022, 17, 243–252. [Google Scholar] [CrossRef]
- Strzelecka, J.; Polus, Ł.; Chybiński, M. Theoretical and Numerical Analyses of Steel-timber Composite Beams with LVL Slabs. Civ. Environ. Eng. Rep. 2023, 33, 64–84. [Google Scholar] [CrossRef]
- Szumigała, M.; Szumigała, E.; Polus, Ł. Laboratory tests of new connectors for timber-concrete composite structures. Eng. Trans. 2018, 66, 161–173. [Google Scholar]
- Auclair, S.C.; Sorelli, L.; Salenikovich, A. A new composite connector for timber-concrete composite structures. Constr. Build. Mater. 2016, 112, 84–92. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Gregori, A.; Xue, J.; Demartino, C.; Toso, M. Timber-concrete composite bridges: Three case studies. J. Traffic Transp. Eng. 2018, 5, 429–438. [Google Scholar] [CrossRef]
- Dias, A.; Skinner, J.; Crews, K.; Tannert, T. Timber-concrete-composites increasing the use of timber in construction. Eur. J. Wood Wood Prod. 2016, 74, 443–451. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Valipour, H.R.; Ataei, A. Timber-timber composite (TTC) connections and beams: An experimental and numerical study. Constr. Build. Mater. 2021, 303, 124493. [Google Scholar] [CrossRef]
- Hoffmeister, B.; Di Biase, P.; Richter, C.; Feldmann, M. Innovative steel-glass components for high-performance building skins: Testing of full-scale prototypes. Glas. Struct. Eng. 2017, 2, 57–78. [Google Scholar] [CrossRef]
- Vild, M.; Bajer, M. Strengthening under Load: The Effect of Preload Magnitudes. Procedia Eng. 2016, 161, 343–348. [Google Scholar] [CrossRef]
- Subhani, M.; Al-Ameri, R.; Kabir, M.I. Hybrid strengthening of steel-concrete composite beam, part 1: Experimental investigation. J. Constr. Steel Res. 2018, 141, 23–35. [Google Scholar] [CrossRef]
- Wang, S.; Su, Q.; Jiang, X.; Ghafoori, E. Stability of steel columns strengthened under preload: Numerical study with experimental validation. J. Constr. Steel Res. 2022, 197, 107440. [Google Scholar] [CrossRef]
- Pathirana, S.W.; Uy, B.; Mirza, O.; Zhu, X. Strengthening of existing composite steel-concrete beams utilising bolted shear connectors and welded studs. J. Constr. Steel Res. 2015, 114, 417–430. [Google Scholar] [CrossRef]
- Wierzbicki, K. Influence of Bimoment Restraints on the Load-Bearing Capacity of a Steel I-Beam. Civ. Environ. Eng. Rep. 2020, 30, 33–47. [Google Scholar] [CrossRef]
- Liu, Y.; Gannon, L. Finite element study of steel beams reinforced while under load. Eng. Struct. 2009, 31, 2630–2642. [Google Scholar] [CrossRef]
- Liu, Y.; Gannon, L. Experimental behavior and strength of steel beams strengthened while under load. J. Constr. Steel Res. 2009, 65, 1346–1354. [Google Scholar] [CrossRef]
- Ibrahim, S.A.; Dessouki, A.K.; El-Sa’Eed, S.A. Lateral buckling behavior and strengthening techniques of coped steel I-beams. J. Constr. Steel Res. 2015, 108, 11–22. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, Y.; Chen, Z.; Dong, X. Axial-compression mechanical properties of square steel columns strengthened by welding under high load. J. Constr. Steel Res. 2021, 176, 106390. [Google Scholar] [CrossRef]
- Vild, M.; Bajer, M. Strengthening of steel columns under load: Torsional-flexural buckling. Adv. Mater. Sci. Eng. 2016, 2016, 2765821. [Google Scholar] [CrossRef]
- Mimoto, T.; Sakaki, T.; Mihara, T.; Yoshitake, I. Strengthening system using post-tension tendon with an internal anchorage of concrete members. Eng. Struct. 2016, 124, 29–35. [Google Scholar] [CrossRef]
- Seręga, S.; Faustmann, D.H. Flexural strengthening of reinforced concrete beams using external tendons. Eng. Struct. 2022, 252, 113277. [Google Scholar] [CrossRef]
- Elbelbisi, A.H.; El-Sisi, A.A.; Hassan, H.A.; Salim, H.A.; Shabaan, H.F. Parametric Study on Steel–Concrete Composite Beams Strengthened with Post-Tensioned CFRP Tendons. Sustainability 2022, 14, 15792. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zong, L.; Zhu, R.X.; Liu, X.Y.; Shi, Y.J. Behavior of I-section steel beam welding reinforced while under load. J. Constr. Steel Res. 2015, 106, 278–288. [Google Scholar] [CrossRef]
- Liu, H.; Hu, J.; Yang, Y.; Chen, Z.; Wang, L. Circular steel tubes strengthened by welding angle steel under preloading condition. J. Constr. Steel Res. 2021, 184, 106816. [Google Scholar] [CrossRef]
- Park, J.; An, G. Prediction of the welding distortion of large steel structure with mechanical restraint using equivalent load methods. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 315–325. [Google Scholar] [CrossRef]
- Vild, M.; Bajer, M.; Barnat, J. Column Stability during Welding. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052019. [Google Scholar] [CrossRef]
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019.
- Kmiecik, P.; Kamiński, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Jason, L.; Huerta, A.; Pijaudier-Cabot, G.; Ghavamian, S. An elastic plastic damage formulation for concrete: Application to elementary tests and comparison with an isotropic damage model. Comput. Methods Appl. Mech. Eng. 2006, 195, 7077–7092. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. 2005, No. 6, 53–69. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Voyiadjis, G.; Taqieddin, Z. Elastic Plastic and Damage Model for Concrete Materials: Part I-Theoretical Formulation. Int. J. Struct. Chang. Solids 2009, 1, 31–59. [Google Scholar]
- Vital, W.; Silva, R.; de Morais, M.V.G.; Emidio Sobrinho, B.; Pereira, R.; Evangelista, F. Application of bridge information modelling using laser scanning for static and dynamic analysis with concrete damage plasticity. Alex. Eng. J. 2023, 79, 608–628. [Google Scholar] [CrossRef]
- Xue, L.; Ren, X.; Ballarini, R. Damage-plasticity modeling of shear failure in reinforced concrete structures. Eng. Fract. Mech. 2023, 290, 109536. [Google Scholar] [CrossRef]
- Ayhan, B.; Lale, E. Modeling strain rate effect on tensile strength of concrete using damage plasticity model. Int. J. Impact Eng. 2022, 162, 104132. [Google Scholar] [CrossRef]
- Seok, S.; Haikal, G.; Ramirez, J.A.; Lowes, L.N.; Lim, J. Finite element simulation of bond-zone behavior of pullout test of reinforcement embedded in concrete using concrete damage-plasticity model 2 (CDPM2). Eng. Struct. 2020, 221, 110984. [Google Scholar] [CrossRef]
- Saleh, M.; AlHamaydeh, M.; Zakaria, M. Finite element analysis of reinforced concrete deep beams with square web openings using damage plasticity model. Eng. Struct. 2023, 278, 115496. [Google Scholar] [CrossRef]
- Le Minh, H.; Khatir, S.; Abdel Wahab, M.; Cuong-Le, T. A concrete damage plasticity model for predicting the effects of compressive high-strength concrete under static and dynamic loads. J. Build. Eng. 2021, 44, 103239. [Google Scholar] [CrossRef]
- Szewczyk, P.; Szumigała, M. Static Equilibrium Paths of Steel-Concrete Composite Beam Strengthened Under Load. Civ. Environ. Eng. Rep. 2019, 28, 101–111. [Google Scholar] [CrossRef]
- Szewczyk, P.; Szumigała, M. Numerical Modelling Of The Strengthening Process Of Steel-Concrete Composite Beams. Civ. Environ. Eng. Rep. 2016, 19, 99–110. [Google Scholar] [CrossRef]
- Szewczyk, P.; Szumigała, M. Optimal design of steel–concrete composite beams strengthened under load. Materials 2021, 14, 4715. [Google Scholar] [CrossRef] [PubMed]










| Reh [MPa] | Rel [MPa] | Rm [MPa] | E [GPa] | A [%] | ||
|---|---|---|---|---|---|---|
| web | 368 | 343 | 482 | 205 | 26 | |
| s | 7.58 | 7.5 | 4.84 | 2.31 | 2.03 | |
| flange | 328 | 307 | 460 | 204 | 31 | |
| s | 9.02 | 7.65 | 5.07 | 2.29 | 0.71 | |
| plate | 271 | 264 | 383 | 204 | 36 | |
| s | 11.26 | 10.84 | 5.78 | 1.12 | 1.94 |
| Parameter | Average Strength f [MPa] | Standard Deviation s [MPa] | Minimum Strength fmin [MPa] | |
|---|---|---|---|---|
| compression test | cubes | 52.79 | 2.60 | 50.18 |
| cylinders | 36.52 | 1.62 | 34.80 | |
| tensile test | cubes | 3.41 | 0.22 | 3.14 |
| beams | 6.43 | 0.43 | 5.99 | |
| Load [kN] | Concrete | Steel | ||
|---|---|---|---|---|
[MPa] | [MPa] | |||
| 33 (2 × 10 + DL) | 4.06 | 0.24 | 73.02 | 0.31 |
| 113 (2 × 50 + DL) | 13.90 | 0.84 | 250.02 | 1.06 |
| Measuring Point | Type | Location |
|---|---|---|
| P | Force transducer, HBM C6A 500 kN | α-α |
| f1, f2 | LVDT transducer, HBM WA/200 mm | α-α |
| f3, f4 | LVDT transducer, HBM WA/50 mm | Concentrated force (between α-α and β-β) |
| f5, f6 | LVDT transducer, HBM WA/50 mm | Concentrated force (between α-α and γ-γ) |
| f7, f8 | LVDT transducer, HBM WA/20 mm | Left and right ends of the beam |
| B1, B2 | Half-bridge strain gauge measuring point | α-α |
| S1, S2 | ||
| B3, B4 | Half-bridge strain gauge measuring point | β-β |
| S3, S4 | ||
| B5, B6 | Half-bridge strain gauge measuring point | γ-γ |
| S5, S6 | ||
| P1 | Half-bridge strain gauge measuring point | α-α |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szewczyk, P. Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load. Materials 2024, 17, 4510. https://doi.org/10.3390/ma17184510
Szewczyk P. Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load. Materials. 2024; 17(18):4510. https://doi.org/10.3390/ma17184510
Chicago/Turabian StyleSzewczyk, Piotr. 2024. "Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load" Materials 17, no. 18: 4510. https://doi.org/10.3390/ma17184510
APA StyleSzewczyk, P. (2024). Experimental and Numerical Study of Steel–Concrete Composite Beams Strengthened under Load. Materials, 17(18), 4510. https://doi.org/10.3390/ma17184510







