Vibrational Analysis of Composite Conical-Cylindrical Shells with Functionally Graded Coatings in Thermal Environments
Abstract
1. Introduction
2. Theoretical Formulation
2.1. Establishment of the Model
2.2. Equivalent Material Parameters of Composite Material Matrix
2.3. Equivalent Material Parameters of Functionally Graded Coating
2.4. Energy Analysis of CCSs with FGCs
2.5. Displacement Function Assumptions and Solutions
3. Experimental Test
3.1. Specimen Preparation
3.2. Test System and Experimental Method
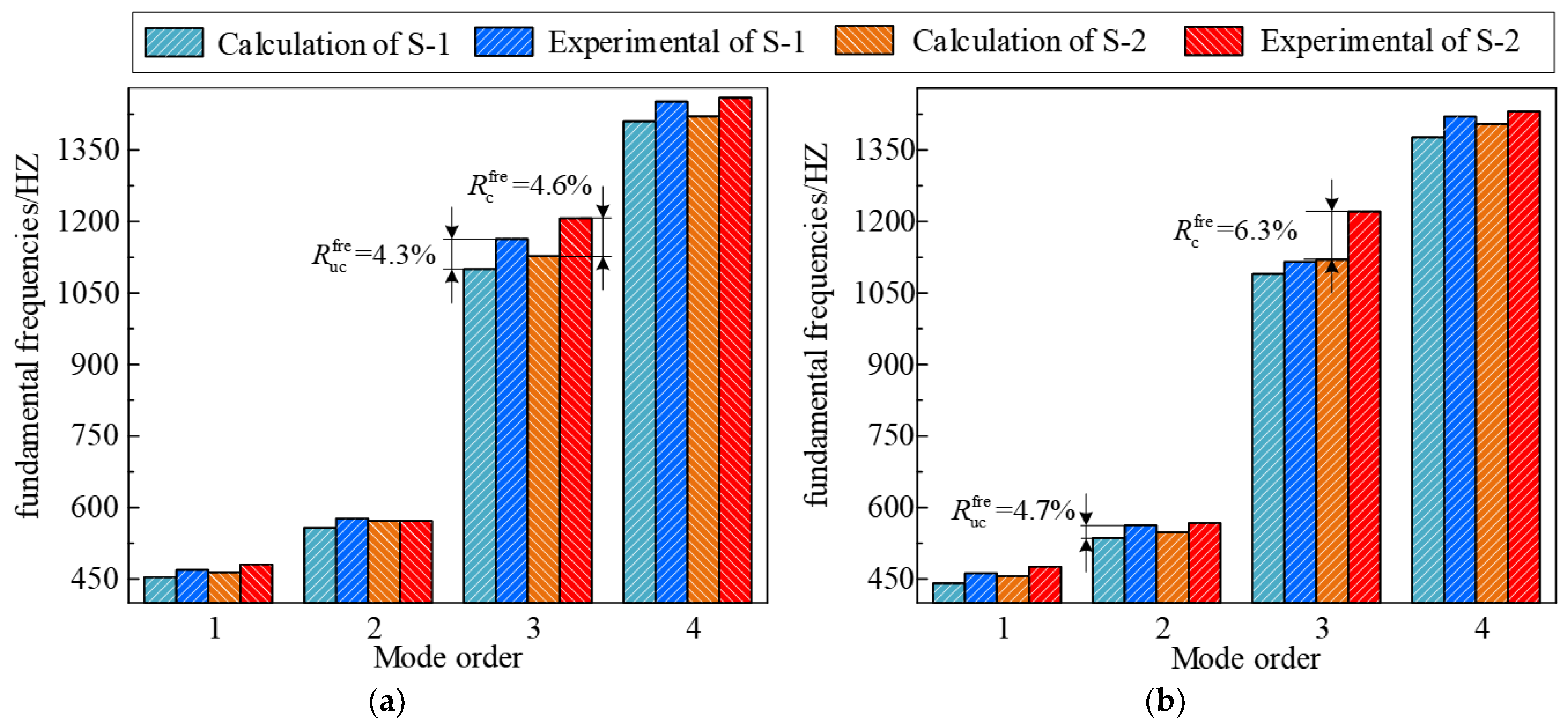
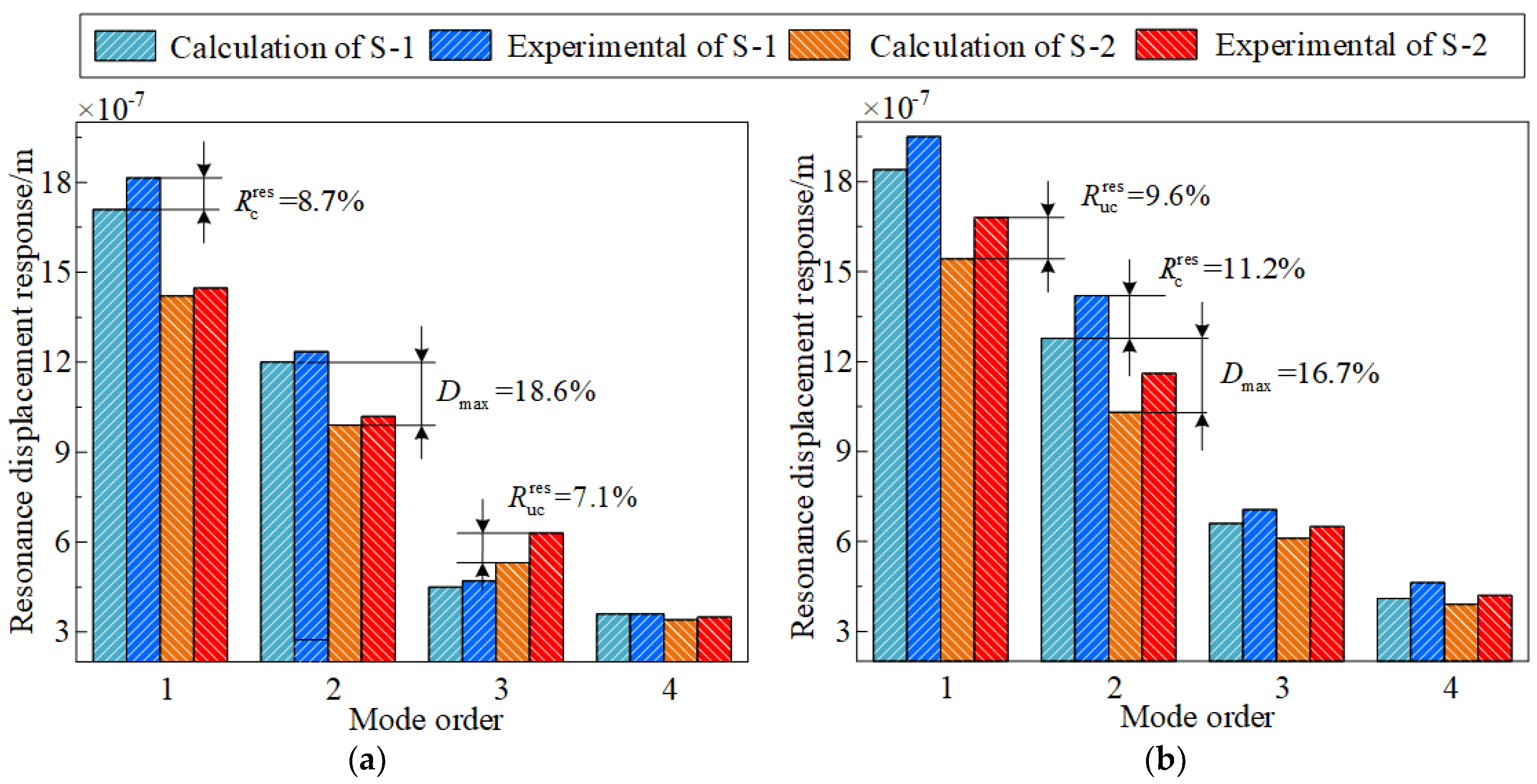
3.3. Numerical Verification and Analysis
4. Parametric Analysis
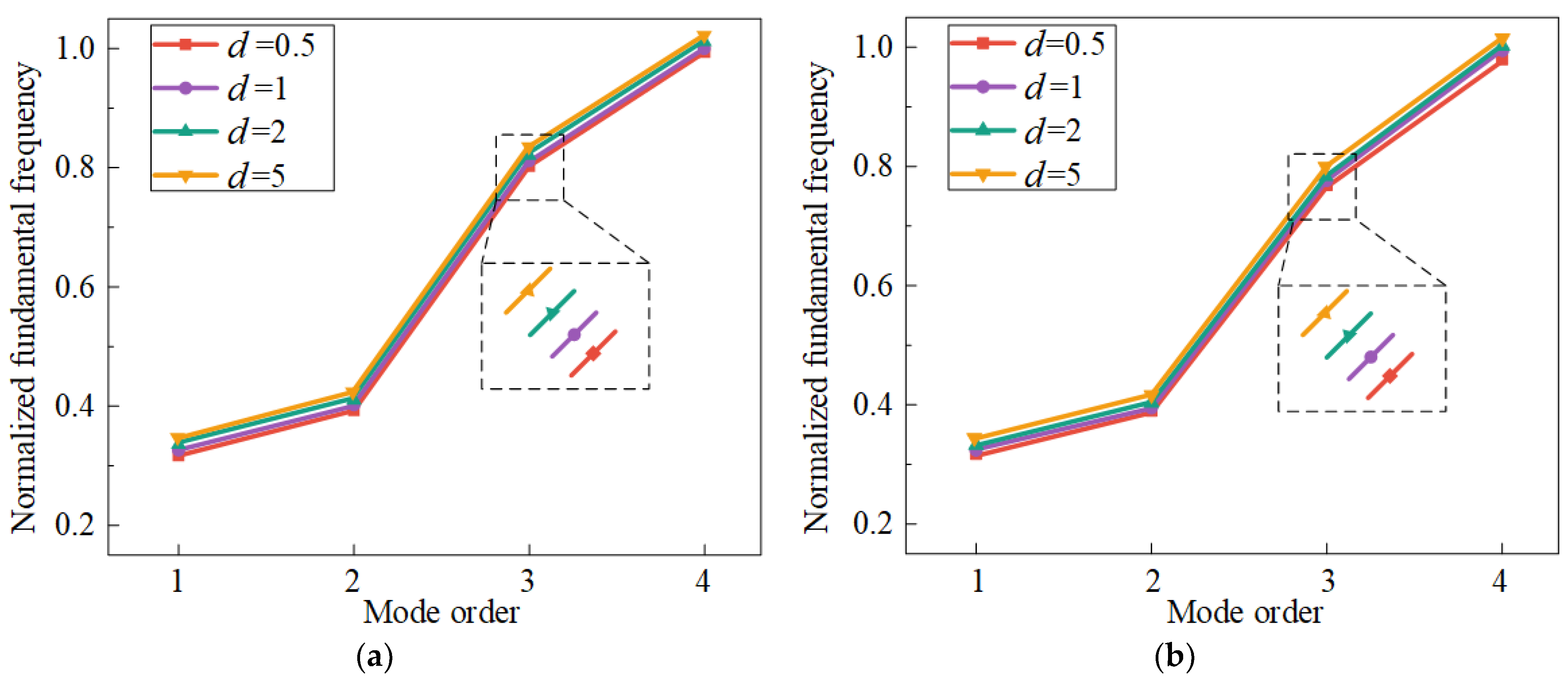
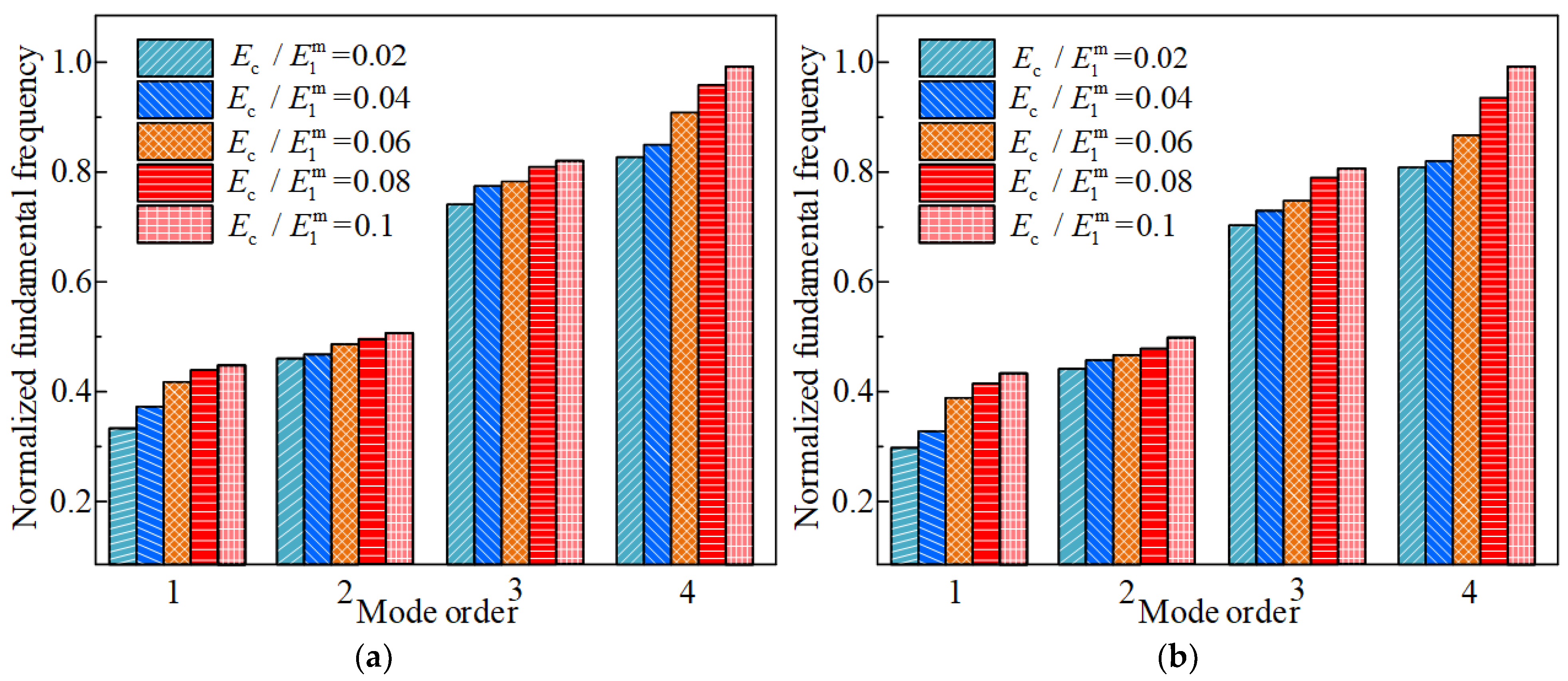
4.1. Effect of Coating Gradient Index on Vibration Property
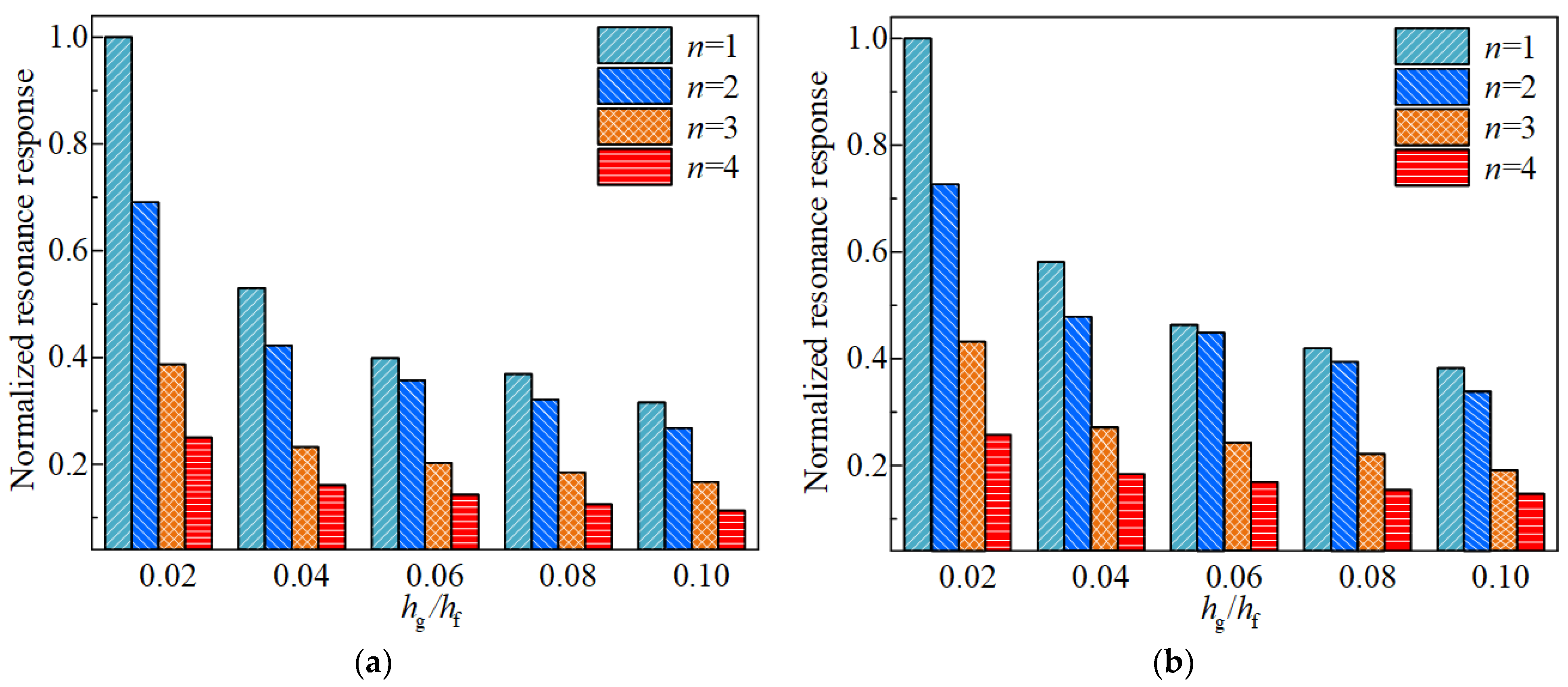
4.2. Effect of FGC Thickness Proportion on Vibration Property
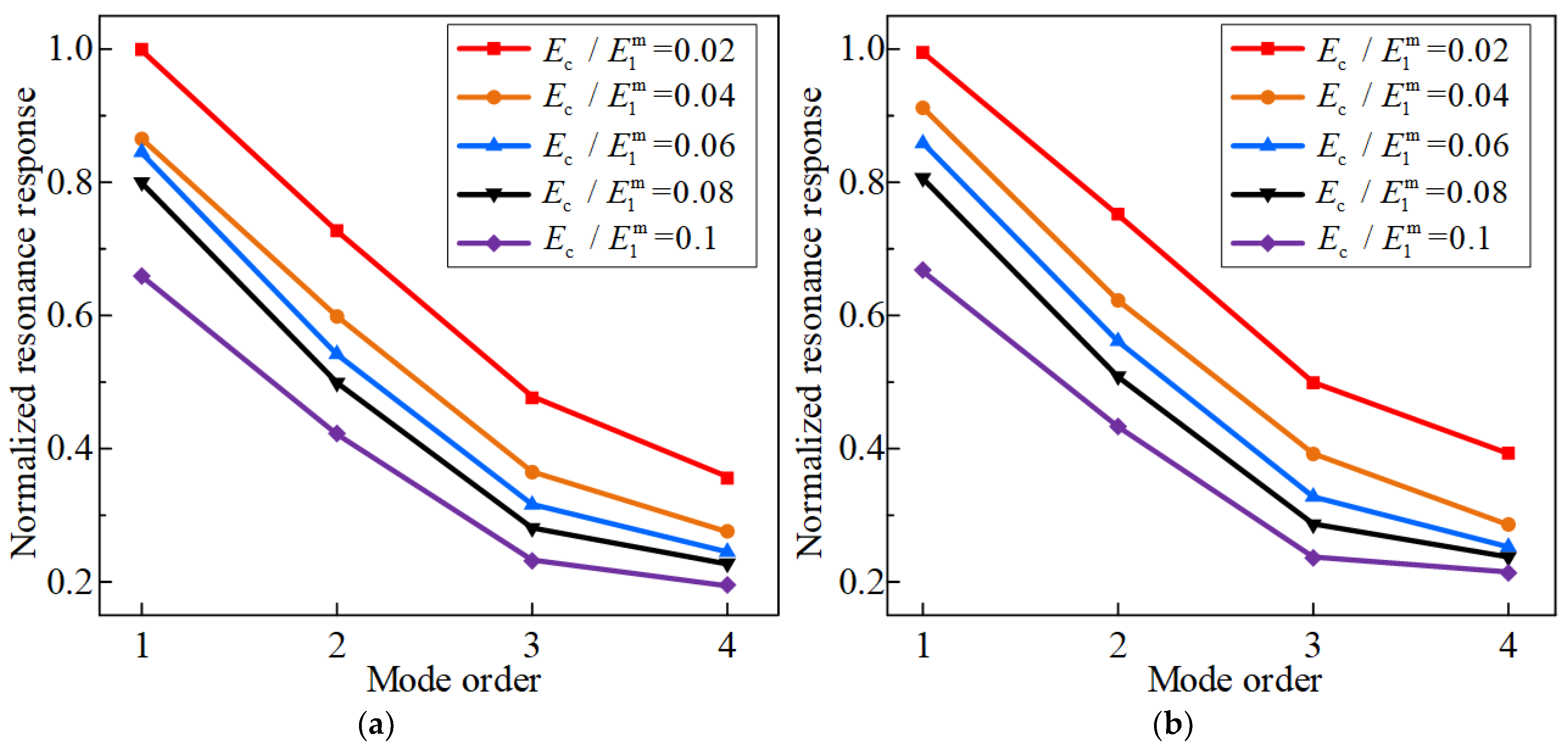
4.3. Effect of Young’s Modulus Ratio between FGC and CCSs
5. Conclusions
- (1)
- The current model can reliably predict the vibration behavior of coated and uncoated specimens in thermal environments, and the vibration features of the structure are affected by the temperature. As the temperature rises, the fundamental frequency of the CCS with FGC tends to decrease, but the resonant response steadily increases.
- (2)
- Experimental and theoretical studies show that the specimens with functionally graded coatings have a smaller resonant response than those without coatings. Therefore, it can be concluded that FGC contributes to the ability of the structure to suppress vibration.
- (3)
- The dynamic behavior of the CCS with FGC is significantly impacted by the material parameters of the functionally graded coating, such as the functionally graded index, thickness, and Young’s modulus. Therefore, reasonably selecting the above parameters to enhance the anti-vibration capabilities of the structure is recommended.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ansari, R.; Torabi, J.; Faghih Shojaei, M. Free vibration analysis of embedded functionally graded carbon nanotube-reinforced composite conical/cylindrical shells and annular plates using a numerical approach. J. Vib. Control 2018, 24, 1123–1144. [Google Scholar] [CrossRef]
- Bulut, M. A numerical investigation on vibration analysis of fiber reinforced and truncated conical hollow shells with different fiber orientations. J. Inst. Sci. Technol. 2018, 8, 259–269. [Google Scholar] [CrossRef][Green Version]
- Haghgoo, M.; Ansari, R.; Hassanzadeh-Aghdam, M.K. A multiscale analysis for free vibration of fuzzy fiber-reinforced nanocomposite conical shells. Thin Walled Struct. 2020, 153, 106845. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, G. Nonlinear vibration and stability of sandwich functionally graded porous plates reinforced with graphene platelets in subsonic flow on elastic foundation. Thin Walled Struct. 2024, 194, 111327. [Google Scholar] [CrossRef]
- Zarei, M.; Rahimi, G.H.; Hemmatnezhad, M. On the free vibrations of joined grid-stiffened composite conical-cylindrical shells. Thin Walled Struct. 2021, 161, 107465. [Google Scholar] [CrossRef]
- Shi, X.; Zuo, P.; Zhong, R.; Guo, C.; Wang, Q. Thermal vibration analysis of functionally graded conical-cylindrical coupled shell based on spectro-geometric method. Thin Walled Struct. 2022, 175, 109138. [Google Scholar] [CrossRef]
- Sobhani, E.; Moradi-Dastjerdi, R.; Behdinan, K.; Masoodi, A.R.; Ahmadi-Pari, A.R. Multifunctional trace of various reinforcements on vibrations of three-phase nanocomposite combined hemispherical-cylindrical shells. Compos. Struct. 2022, 279, 114798. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Fantuzzi, N. Analytical solution of stability and vibration problem of clamped cylindrical shells containing functionally graded layers within shear deformation theory. Alex. Eng. J. 2023, 64, 141–154. [Google Scholar] [CrossRef]
- Wang, C.; Song, X.; Zang, J.; Zhang, Y. Experimental and theoretical investigation on vibration of laminated composite conical-cylindrical-combining shells with elastic foundation in hygrothermal environment. Compos. Struct. 2023, 323, 117470. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, X.C.; Li, H.; Xu, P.Y.; Sun, X.C.; Zhang, Y.F.; Gu, D.W.; Han, Q.K.; Wen, B.C. The vibration characteristics analysis of fiber-reinforced thin-walled conical-cylindrical composite shells with artificial spring technique. Int. J. Struct. Stab. Dyn. 2024, 2550200. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, L.; Hua, F.; You, Q.; He, W.; Zhou, H.; Gao, J.; Wu, W.; Zhou, X. Random and harmonic responses of plain woven carbon fiber reinforced conical-conical shell based on machine learning multiscale modelling. Thin Walled Struct. 2024, 203, 112220. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Yang, Y.; Fang, Y.; Wang, H.; Wang, X.; Zhang, H.; Wang, H.; Cao, H.; Hou, J.; et al. Vibration behaviours of composite conical–cylindrical shells with damping coating: Theory and experiment. Thin Walled Struct. 2024, 203, 112218. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, X.C.; Li, H.; Xu, P.Y.; Sun, X.C.; Zhang, Y.F.; Gu, D.W.; Han, Q.K.; Wen, B.C. A mathematical model for analyzing the vibration characteristics of fiber-reinforced thin-walled conical-cylinder composite shells with local bolt missing by the artificial spring method. Appl. Math. Model. 2024, 136, 115609. [Google Scholar] [CrossRef]
- Mohammadi, F.; Sedaghati, R. Vibration analysis and design optimization of viscoelastic sandwich cylindrical shell. J. Sound Vib. 2012, 331, 2729–2752. [Google Scholar] [CrossRef]
- Yang, C.; Jin, G.; Liu, Z.; Wang, X.; Miao, X. Vibration and damping analysis of thick sandwich cylindrical shells with a viscoelastic core under arbitrary boundary conditions. Int. J. Mech. Sci. 2015, 92, 162–177. [Google Scholar] [CrossRef]
- Biswal, D.K.; Mohanty, S.C. Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers. Compos. Part B Eng. 2019, 159, 72–85. [Google Scholar] [CrossRef]
- Jin, Y.; Shi, Y.; Yu, G.-C.; Wei, G.-T.; Hu, B.; Wu, L.-Z. A multifunctional honeycomb metastructure for vibration suppression. Int. J. Mech. Sci. 2020, 188, 105964. [Google Scholar] [CrossRef]
- Jin, Y.; Jia, X.Y.; Wu, Q.Q.; Yu, G.C.; Zhang, X.L.; Chen, S.; Wu, L.Z. Design of cylindrical honeycomb sandwich meta-structures for vibration suppression. Mech. Syst. Signal Process. 2022, 163, 108075. [Google Scholar] [CrossRef]
- Song, X.; Cao, T.; Gao, P.; Han, Q. Vibration and damping analysis of cylindrical shell treated with viscoelastic damping materials under elastic boundary conditions via a unified Rayleigh-Ritz method. Int. J. Mech. Sci. 2020, 165, 105158. [Google Scholar] [CrossRef]
- Safarov, I.; Teshaev, M.; Marasulov, A.; Jurayev, T.; Raxmonov, B. Vibrations of Cylindrical Shell Structures Filled with Layered Viscoelastic Material. In Proceedings of the E3S Web of Conferences, Hyderabad, India, 24–26 September 2021; EDP Sciences: Les Ulis, France, 2021; Volume 264, p. 01027. [Google Scholar]
- Madeira, J.F.A.; Araújo, A.L.; Soares, C.M.; Soares, C.M. Multiobjective optimization for vibration reduction in composite plate structures using constrained layer damping. Comput. Struct. 2020, 232, 105810. [Google Scholar] [CrossRef]
- Sahoo, S.R.; Ray, M.C. Active control of doubly curved laminated composite shells using elliptical smart constrained layer damping treatment. Thin Walled Struct. 2019, 140, 373–386. [Google Scholar] [CrossRef]
- Jackstadt, A.; Liebig, W.V.; Kärger, L. Analytical modeling and investigation of constrained layer damping in hybrid laminates based on a unified plate formulation. Int. J. Mech. Sci. 2022, 216, 106964. [Google Scholar] [CrossRef]
- Vinyas, M. Vibration control of skew magneto-electro-elastic plates using active constrained layer damping. Compos. Struct. 2019, 208, 600–617. [Google Scholar] [CrossRef]
- Li, J.; Xue, Y.; Li, F.; Narita, Y. Active vibration control of functionally graded piezoelectric material plate. Compos. Struct. 2019, 207, 509–518. [Google Scholar] [CrossRef]
- Dong, Z.; Faria, C.; Pluymers, B.; Hromčík, M.; Šebek, M.; Desmet, W. Structure-preserving low-order modeling approach of laminated composite plates integrated with macro-fiber composite transducers for dynamic applications. Compos. Struct. 2019, 208, 287–297. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Li, X.; Yang, J. Active control of dynamic behaviors of graded graphene reinforced cylindrical shells with piezoelectric actuator/sensor layers. Appl. Math. Model. 2020, 82, 252–270. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, W.; Luo, H.; Zhang, R. Modeling and active control of geometrically nonlinear vibration of composite laminates with macro fiber composite. Compos. Struct. 2023, 321, 117292. [Google Scholar] [CrossRef]
- Shahverdi, H.; Barati, M.R. Vibration analysis of porous functionally graded nanoplates. Int. J. Eng. Sci. 2017, 120, 82–99. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, K.; Fu, T.; Shi, C. Bending and elastic vibration of a novel functionally graded polymer nanocomposite beam reinforced by graphene nanoplatelets. Nanomaterials 2019, 9, 1690. [Google Scholar] [CrossRef]
- Shafiei, N.; She, G.L. On vibration of functionally graded nano-tubes in the thermal environment. Int. J. Eng. Sci. 2018, 133, 84–98. [Google Scholar] [CrossRef]
- Esfahani, S.; Khadem, S.E.; Mamaghani, A.E. Nonlinear vibration analysis of an electrostatic functionally graded nano-resonator with surface effects based on nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 151, 508–522. [Google Scholar] [CrossRef]
- Fathi, R.; Wei, H.; Saleh, B.; Radhika, N.; Jiang, J.; Ma, A.; Ahmed, M.H.; Li, Q.; Ostrikov, K.K. Past and present of functionally graded coatings: Advancements and future challenges. Appl. Mater. Today 2022, 26, 101373. [Google Scholar] [CrossRef]
- Sathish, M.; Radhika, N.; Saleh, B. A critical review on functionally graded coatings: Methods, properties, and challenges. Compos. Part B Eng. 2021, 225, 109278. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W.; Yang, J.; Han, Q. Analytical analysis of forced vibration of the hard-coating cylindrical shell with material nonlinearity and elastic constraint. Compos. Struct. 2018, 187, 281–293. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, H.; Yu, X.; Yang, J. Modeling and analysis of forced vibration of the thin-walled cylindrical shell with arbitrary multi-ring hard coating under elastic constraint. Thin Walled Struct. 2022, 173, 109037. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, H.; Zhai, J.; Chen, H.; Zhu, Q.; Han, Q. Vibration reduction of the blisk by damping hard coating and its intentional mistuning design. Aerosp. Sci. Technol. 2019, 84, 1049–1058. [Google Scholar] [CrossRef]
- Zhang, W.; Niu, Y.; Behdinan, K. Vibration characteristics of rotating pretwisted composite tapered blade with graphene coating layers. Aerosp. Sci. Technol. 2020, 98, 105644. [Google Scholar] [CrossRef]
- Du, D.; Sun, W.; Yan, X.; Xu, K. Nonlinear vibration analysis of the rotating hard-coating cylindrical shell based on the domain decomposition method. Thin Walled Struct. 2021, 159, 107236. [Google Scholar] [CrossRef]
- Liew, K.M.; Yang, J.; Wu, Y.F. Nonlinear vibration of a coating-FGM-substrate cylindrical panel subjected to a temperature gradient. Comput. Methods Appl. Mech. Eng. 2006, 195, 1007–1026. [Google Scholar] [CrossRef]
- Cao, D.; Liu, B.; Yao, M.; Zhang, W. Free vibration analysis of a pre-twisted sandwich blade with thermal barrier coatings layers. Sci. China Technol. Sci. 2017, 60, 1747–1761. [Google Scholar] [CrossRef]
- Reghu, V.R.; Shankar, V.; Ramaswamy, P. Challenges in plasma spraying of 8% y2o3-zro2 thermal barrier coatings on al alloy automotive piston and influence of vibration and thermal fatigue on coating characteristics. Mater. Today Proc. 2018, 5, 23927–23936. [Google Scholar] [CrossRef]
- Sankar, V.; Ramkumar, P.; Sebastian, D.; Joseph, D.; Jose, J.; Kurian, A. Optimized thermal barrier coating for gas turbine blades. Mater. Today Proc. 2019, 11, 912–919. [Google Scholar] [CrossRef]
- Li, H.; Deng, Y.; Zhao, S.; Qin, Z.; Wang, L.; Xiang, Y.; Du, D.; Wu, H. Thermal-vibration ageing characteristics of three thin-walled cylindrical shells covered with a functionally graded protective coating: Modeling, analysis and test. Eur. J. Mech. A Solids 2023, 102, 105112. [Google Scholar] [CrossRef]
- Sun, C.; Yang, Y.; Li, H.; Xu, H.; Zhao, F.; Xu, Z.; Sun, G.; Hou, J.; Li, H. Prediction of vibration fatigue life of fiber reinforced composite thin plates with functionally graded coating under base random excitation. Thin Walled Struct. 2024, 200, 111891. [Google Scholar] [CrossRef]
- Feo, L.; Lovisi, G.; Penna, R. Free vibration analysis of functionally graded nanobeams based on surface stress-driven nonlocal model. Mech. Adv. Mater. Struct. 2023, 1–9. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M. On boundary conditions for thermally loaded FG beams. Int. J. Eng. Sci. 2017, 119, 109–127. [Google Scholar] [CrossRef]
- Shen, H.S.; Yang, D.Q. Nonlinear vibration of functionally graded fiber-reinforced composite laminated cylindrical shells in hygrothermal environments. Appl. Math. Model. 2015, 39, 1480–1499. [Google Scholar] [CrossRef]
- Prakash, T.; Ganapathi, M. Supersonic flutter characteristics of functionally graded flat panels including thermal effects. Compos. Struct. 2006, 72, 10–18. [Google Scholar] [CrossRef]
- Li, H.; Cao, J.; Han, J.; Li, J.; Yang, Y. Dynamic modeling and vibration suppression evaluation of composite honeycomb hemispherical shell with functional gradient protective coating. Thin Walled Struct. 2024, 202, 112066. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.Q.; Chai, Q. Free vibration analysis of a spinning functionally graded spherical–cylindrical–conical shell with general boundary conditions in a thermal environment. Thin Walled Struct. 2022, 180, 109768. [Google Scholar] [CrossRef]
- Bonneux, N. Exceptional Jacobi polynomials. J. Approx. Theory 2019, 239, 72–112. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Cigeroglu, E.; Özgüven, H.N. A new modal superposition method for nonlinear vibration analysis of structures using hybrid mode shapes. Mech. Syst. Signal Process. 2018, 107, 317–342. [Google Scholar] [CrossRef]
- Li, H.; Dong, B.; Cao, J.; Zhao, J.; Xiong, J.; Yang, Y.; Du, D.; Sun, W.; Wang, X.; Wu, H. Vibration behaviours of foam-filled grille composite sandwich cylindrical shells. Int. J. Mech. Sci. 2023, 256, 108533. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Zhang, H.; Qin, Z.; Wang, Z.; Deng, Y.; Xiong, J.; Wang, X.; Ha, S.K. Amplitude-dependent damping characteristics of all-composite sandwich plates with a foam-filled hexagon honeycomb core. Mech. Syst. Signal Process. 2023, 186, 109845. [Google Scholar] [CrossRef]
- Wu, B. A correction of the half-power bandwidth method for estimating damping. Arch. Appl. Mech. 2015, 85, 315–320. [Google Scholar] [CrossRef]




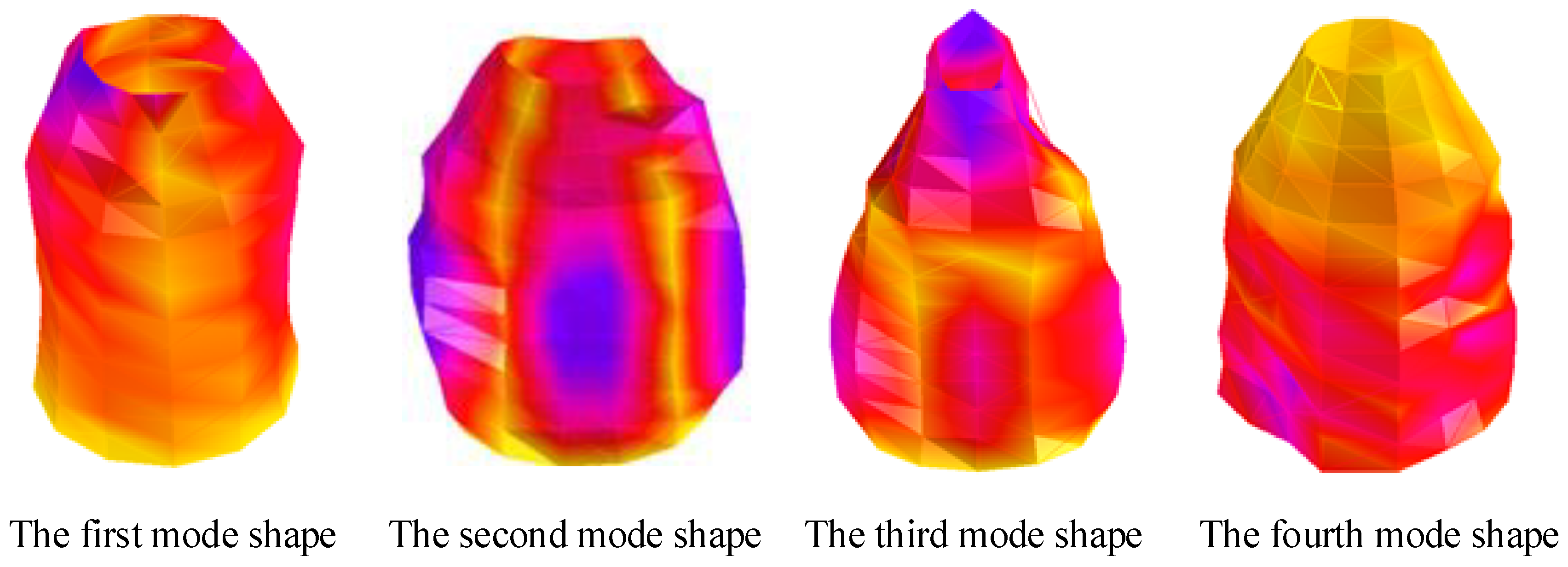


| Type | Young’s Modulus | Shear Modulus | Poisson’s Ratio | Density |
|---|---|---|---|---|
| The fiber-reinforced materials | ||||
| The polymer matrix | ||||
| Coating component A | ||||
| Coating component B |
| Type | Geometry and Material Parameters |
|---|---|
| CCSs FGC | , , , , , , , , , , , , , , , , , , , , , , , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, Y.; Hou, J.; Wang, X.; Zhang, H.; Wang, H.; Li, H. Vibrational Analysis of Composite Conical-Cylindrical Shells with Functionally Graded Coatings in Thermal Environments. Materials 2024, 17, 4576. https://doi.org/10.3390/ma17184576
Li J, Yang Y, Hou J, Wang X, Zhang H, Wang H, Li H. Vibrational Analysis of Composite Conical-Cylindrical Shells with Functionally Graded Coatings in Thermal Environments. Materials. 2024; 17(18):4576. https://doi.org/10.3390/ma17184576
Chicago/Turabian StyleLi, Jinan, Yao Yang, Junxue Hou, Xiangping Wang, Haiyang Zhang, Haizhou Wang, and Hui Li. 2024. "Vibrational Analysis of Composite Conical-Cylindrical Shells with Functionally Graded Coatings in Thermal Environments" Materials 17, no. 18: 4576. https://doi.org/10.3390/ma17184576
APA StyleLi, J., Yang, Y., Hou, J., Wang, X., Zhang, H., Wang, H., & Li, H. (2024). Vibrational Analysis of Composite Conical-Cylindrical Shells with Functionally Graded Coatings in Thermal Environments. Materials, 17(18), 4576. https://doi.org/10.3390/ma17184576






