Enhanced Cyclically Stable Plasticity Model for Multiaxial Behaviour of Magnesium Alloy AZ31 under Low-Cycle Fatigue Conditions
Abstract
:1. Introduction
2. Material and Methods
3. Calculation
3.1. Input Data Definition
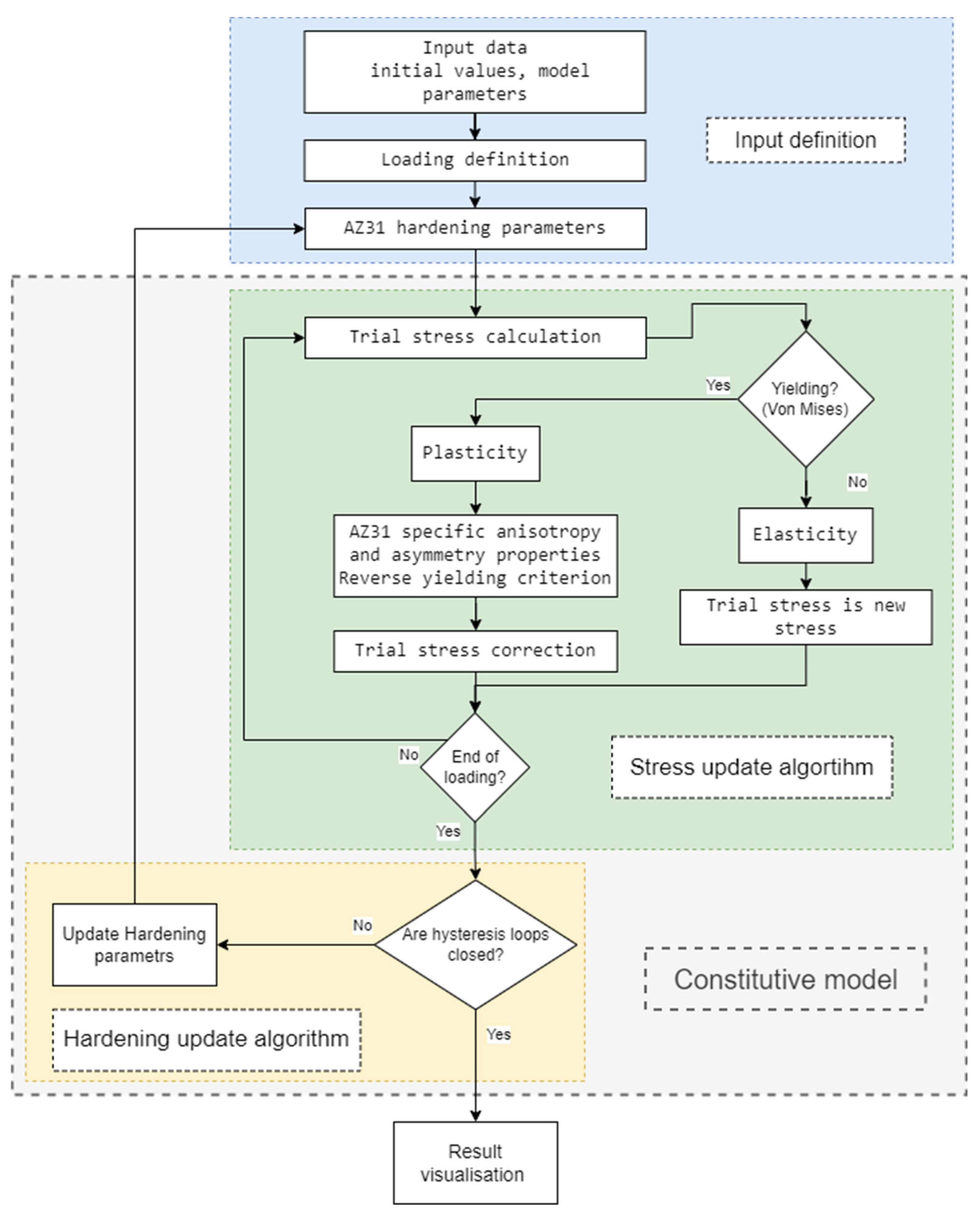
3.2. Stress Update Algorithm
3.3. Hardening Update Algorithm
4. Results and Discussion
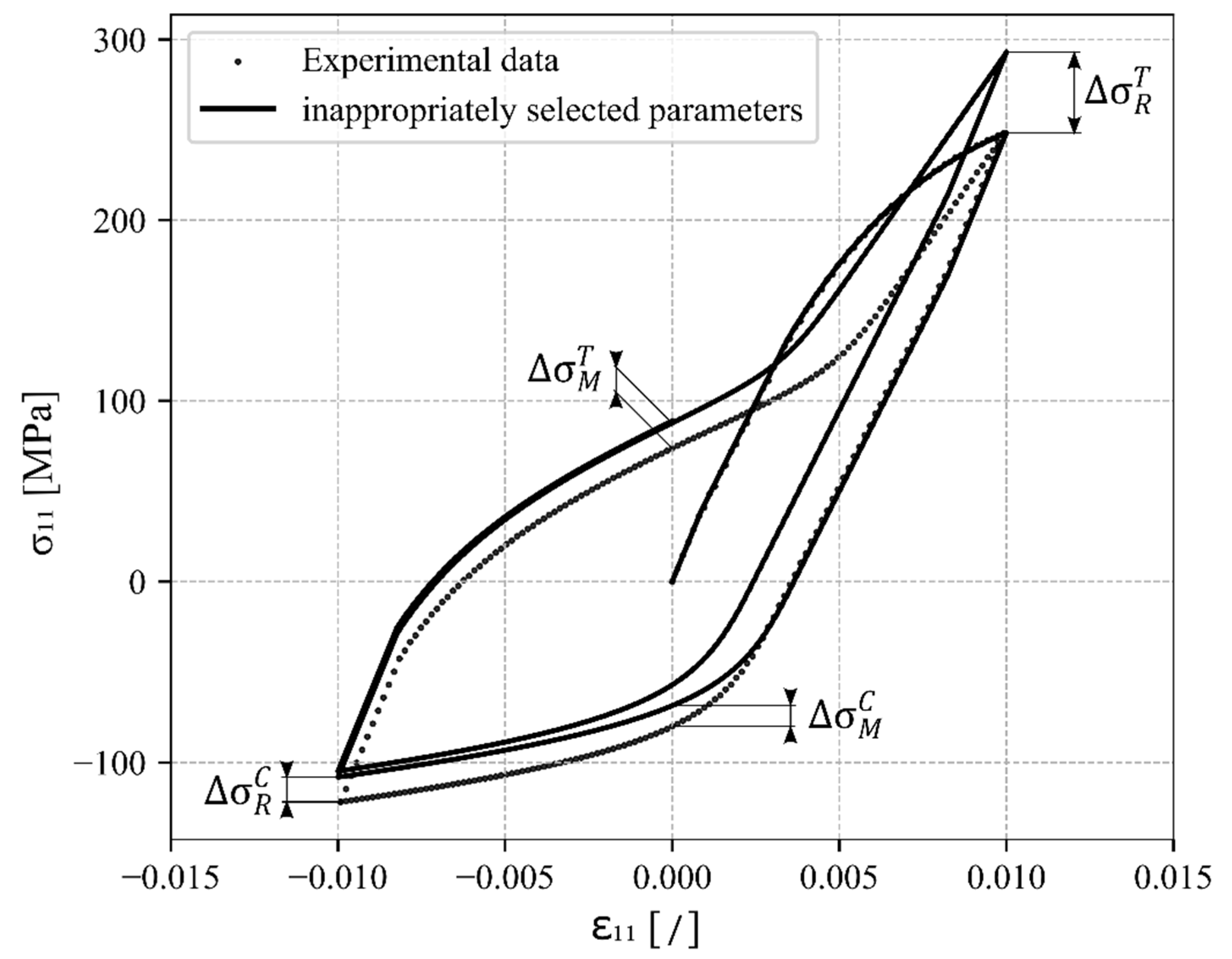
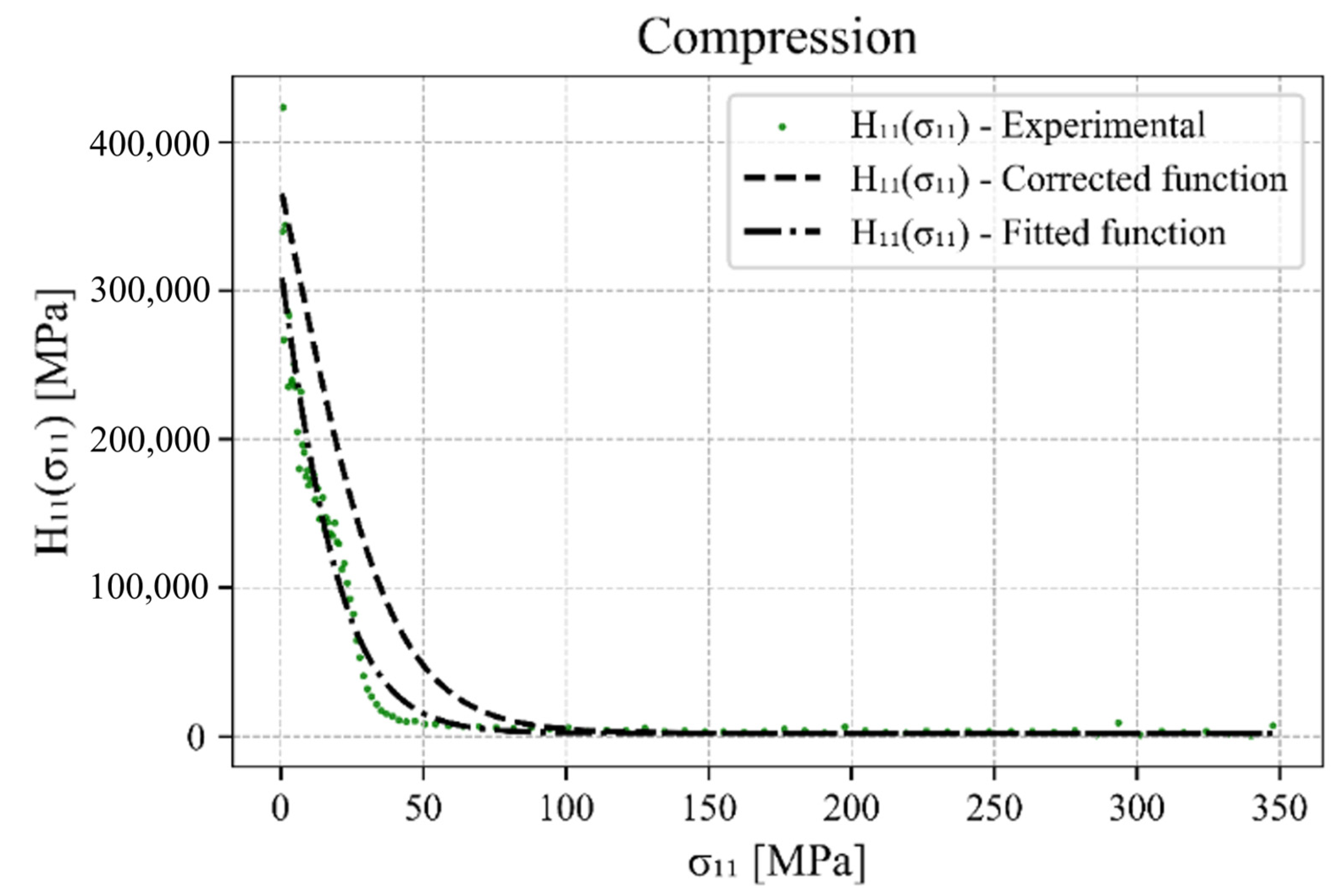
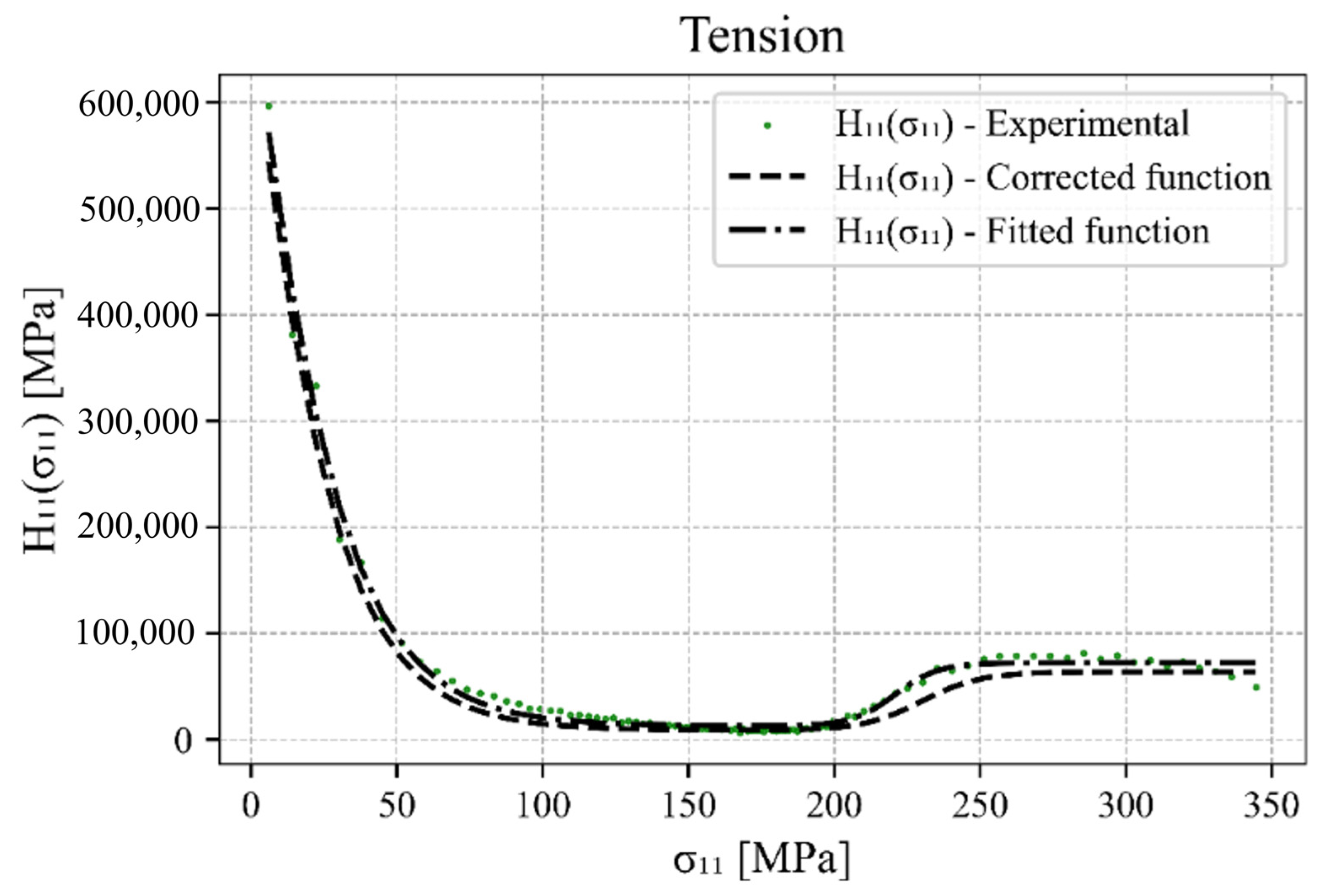
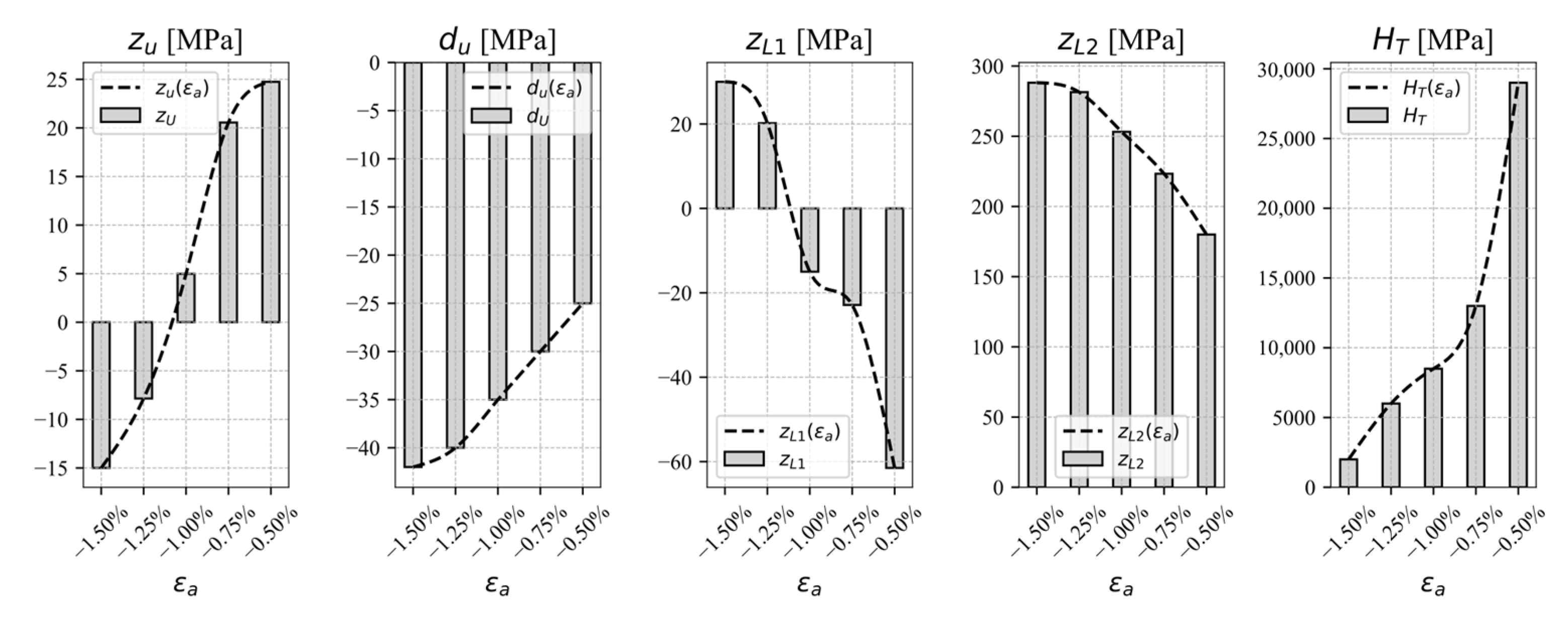
4.1. Hardening Parameters Definition
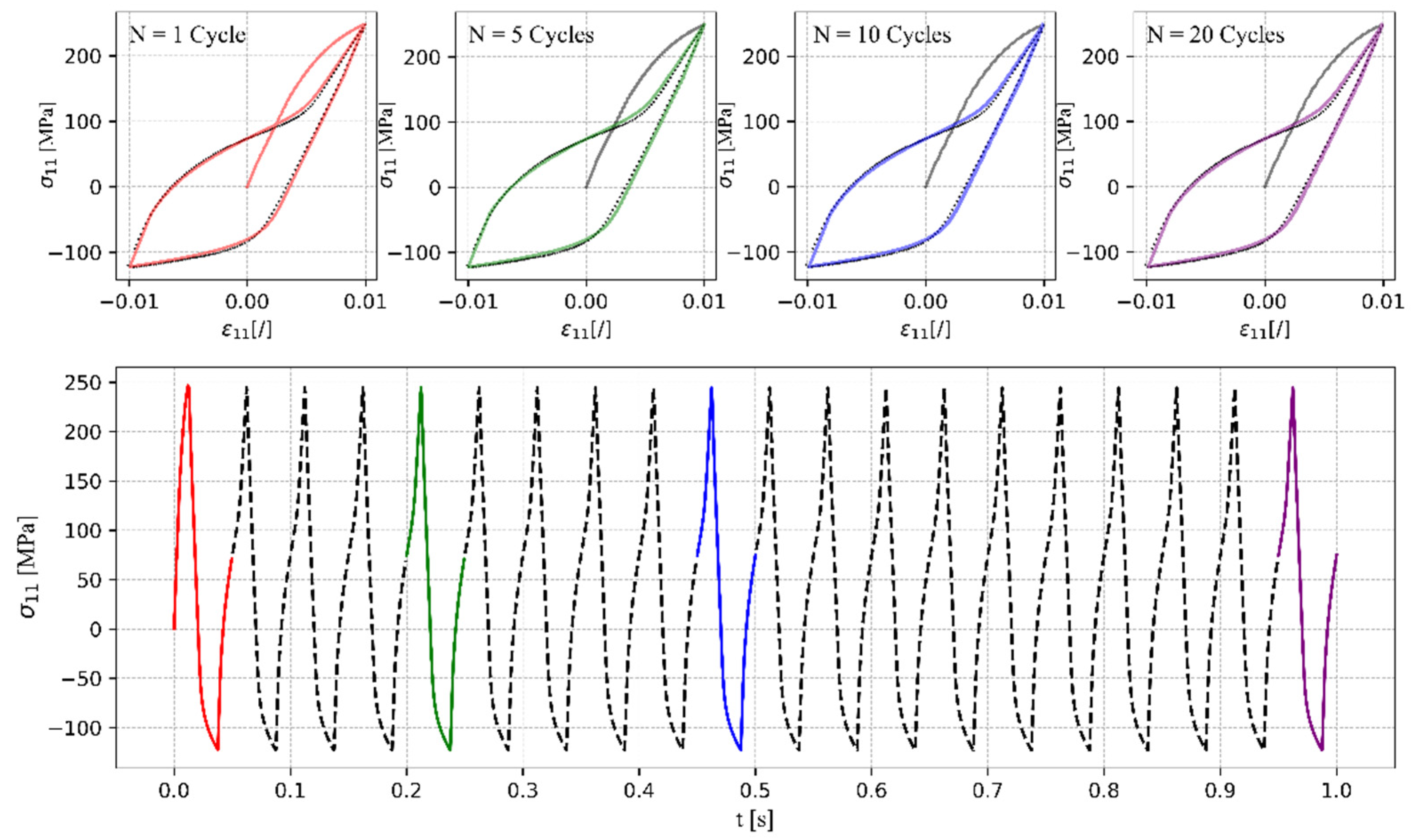
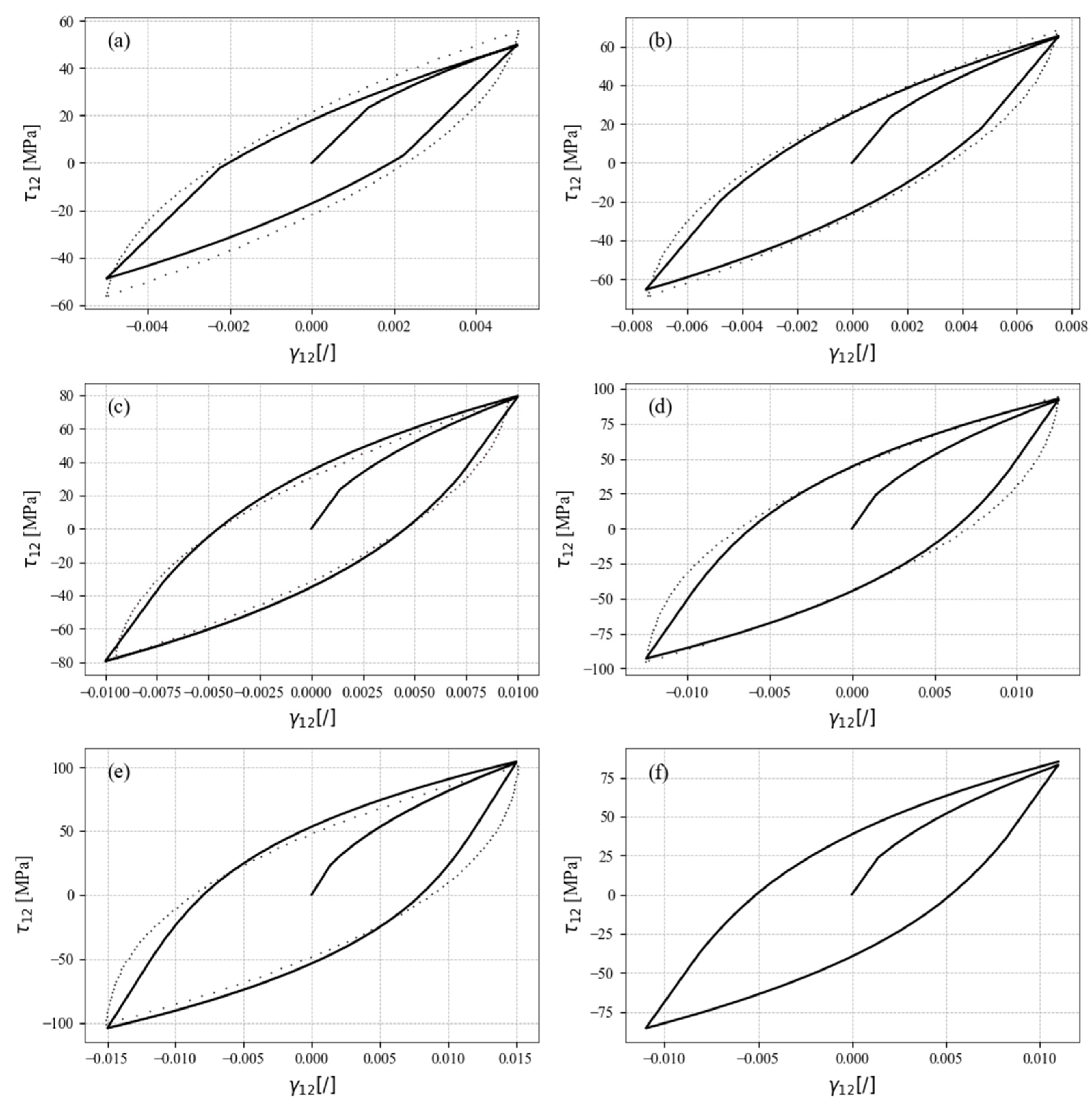
4.2. Uniaxial Tensile–Compressive and Pure Shear Loading
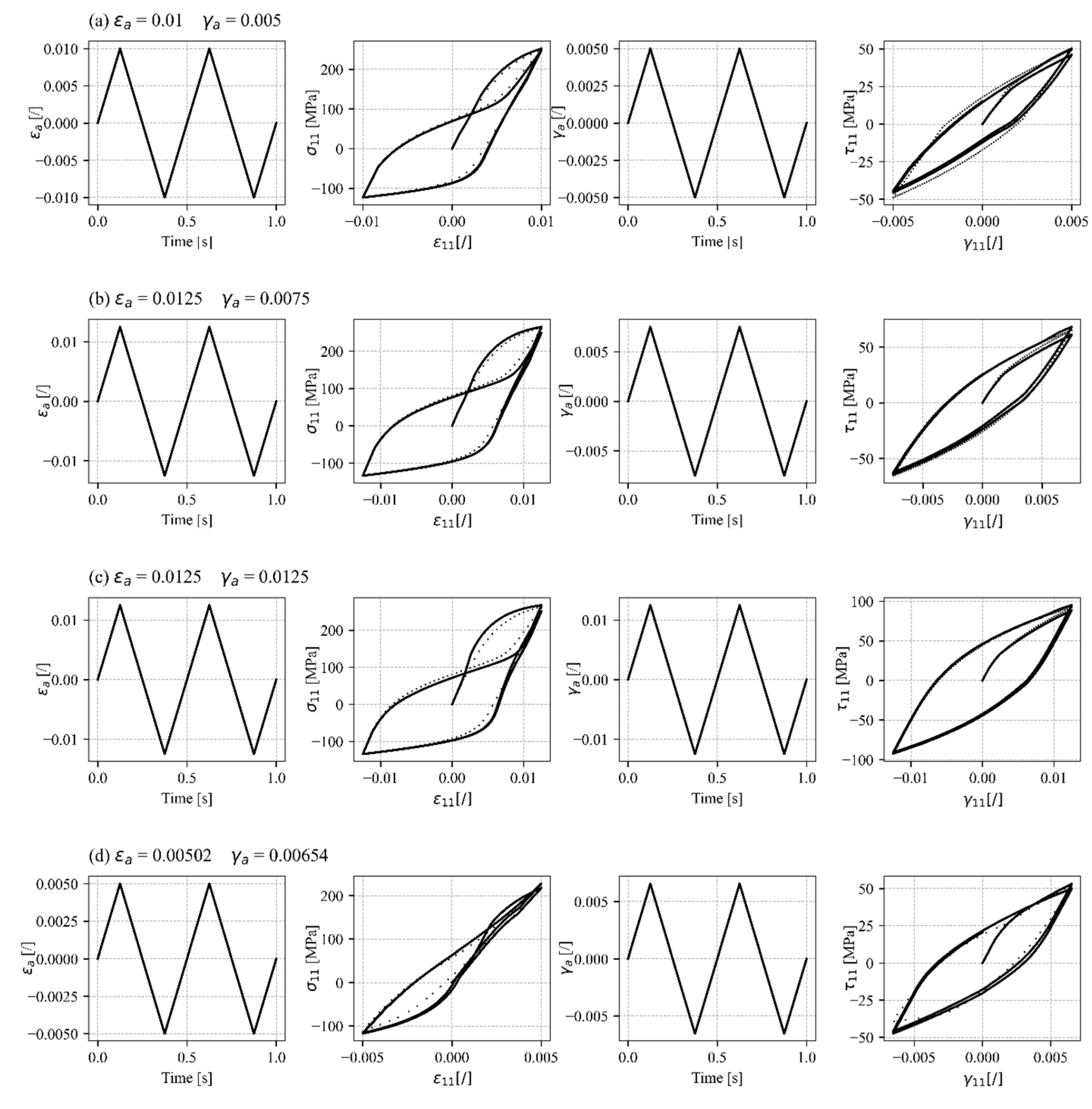
4.3. Multiaxial Proportional and Non-Proportional Loading
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, B.; Yang, J.; Zhang, X.; Yang, Q.; Zhang, J.; Li, X. Development and application of magnesium alloy parts for automotive OEMs: A review. J. Magnes. Alloy. 2023, 11, 15–47. [Google Scholar] [CrossRef]
- Zhang, J.; Miao, J.; Balasubramani, N.; Cho, D.H.; Avey, T.; Chang, C.-Y.; Luo, A.A. Magnesium research and applications: Past, present and future. J. Magnes. Alloy. 2023, 11, 3867–3895. [Google Scholar] [CrossRef]
- Joost, W.J.; Krajewski, P.E. Towards magnesium alloys for high-volume automotive applications. Scr. Mater. 2017, 128, 107–112. [Google Scholar] [CrossRef]
- Golroudbary, S.R.; Makarava, I.; Repo, E.; Kraslawski, A.; Luukka, P. Magnesium Life Cycle in Automotive Industry. Procedia CIRP 2022, 105, 589–594. [Google Scholar] [CrossRef]
- Kiani, M.; Gandikota, I.; Rais-Rohani, M.; Motoyama, K. Design of lightweight magnesium car body structure under crash and vibration constraints. J. Magnes. Alloy. 2014, 2, 99–108. [Google Scholar] [CrossRef]
- Luo, A.A. Magnesium casting technology for structural applications. J. Magnes. Alloy. 2013, 1, 2–22. [Google Scholar] [CrossRef]
- Li, Y.Q.; Li, F.; Kang, F.W.; Du, H.Q.; Chen, Z.Y. Recent research and advances in extrusion forming of magnesium alloys: A review. J. Alloy. Compd. 2023, 953, 170080. [Google Scholar] [CrossRef]
- Li, T.; Song, J.; Zhang, A.; You, G.; Yang, Y.; Jiang, B.; Qin, X.; Xu, C.; Pan, F. Progress and prospects in Mg-alloy super-sized high pressure die casting for automotive structural components. J. Magnes. Alloy. 2023, 11, 4166–4180. [Google Scholar] [CrossRef]
- Masuda, K.; Ishihara, S.; Oguma, N.; Ishiguro, M.; Sakamoto, Y. Elasto-Plastic Fatigue Crack Growth Behavior of Extruded Mg Alloy with Deformation Anisotropy Due to Stress Ratio Fluctuation. Materials 2022, 15, 755. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H.; Wang, Q.; He, J. A Fatigue Life Prediction Method Based on Strain Intensity Factor. Materials 2017, 10, 689. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Okotete, E.A. Enhancing plastic deformability of Mg and its alloys—A review of traditional and nascent developments. J. Magnes. Alloy. 2017, 5, 460–475. [Google Scholar] [CrossRef]
- Suh, B.-C.; Shim, M.-S.; Shin, K.; Kim, N.J. Current issues in magnesium sheet alloys: Where do we go from here? Scr. Mater. 2014, 84–85, 1–6. [Google Scholar] [CrossRef]
- Catorceno, L.L.C.; de Abreu, H.F.G.; Padilha, A.F. Effects of cold and warm cross-rolling on microstructure and texture evolution of AZ31B magnesium alloy sheet. J. Magnes. Alloy. 2018, 6, 121–133. [Google Scholar] [CrossRef]
- Gryguc, A.; Shaha, S.K.; Behravesh, S.B.; Jahed, H.; Wells, M.; Williams, B. Improvement of Fatigue Properties of AZ31B Extruded Magnesium Alloy through Forging. Frat. Ed Integrita Strutt. Struct. Integr. 2020, 14, 152–165. [Google Scholar] [CrossRef]
- Wang, F.; Agnew, S.R. Dislocation transmutation by tension twinning in magnesium alloy AZ31. Int. J. Plast. 2016, 81, 63–86. [Google Scholar] [CrossRef]
- Frydrych, K.; Libura, T.; Kowalewski, Z.; Maj, M.; Kowalczyk-Gajewska, K. On the role of slip, twinning and detwinning in magnesium alloy AZ31B sheet. Mater. Sci. Eng. A 2021, 813, 141152. [Google Scholar] [CrossRef]
- Mackenzie, L.; Pekguleryuz, M. The influences of alloying additions and processing parameters on the rolling microstructures and textures of magnesium alloys. Mater. Sci. Eng. A 2008, 480, 189–197. [Google Scholar] [CrossRef]
- Nakata, T.; Kamado, S. Towards tailoring basal texture of rolled Mg alloy sheet by recrystallization for high room-temperature formability: A review. J. Magnes. Alloy. 2023, 11, 3992–4010. [Google Scholar] [CrossRef]
- Nguyen, N.-T.; Seo, O.S.; Lee, C.A.; Lee, M.-G.; Kim, J.-H.; Kim, H.Y. Mechanical Behavior of AZ31B Mg Alloy Sheets under Monotonic and Cyclic Loadings at Room and Moderately Elevated Temperatures. Materials 2014, 7, 1271–1295. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, B.; Song, B.; Yu, Z.; He, D.; Chai, Y.; Zhang, J.; Pan, F. The effects of orientation control via tension-compression on microstructural evolution and mechanical behavior of AZ31 Mg alloy sheet. J. Magnes. Alloy. 2020, 10, 411–422. [Google Scholar] [CrossRef]
- Dai, H.; Sun, M.; Cheng, Y. Deformation Behavior of AZ31 Magnesium Alloy with Pre-Twins under Biaxial Tension. Materials 2024, 17, 3377. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Yang, C.; Peng, Y.; Zhang, F.; Pan, F. Anisotropy of wrought magnesium alloys: A focused overview. J. Magnes. Alloy. 2022, 10, 1476–1510. [Google Scholar] [CrossRef]
- Sadeghi, A.; Mortezapour, H.; Samei, J.; Pekguleryuz, M.; Wilkinson, D. Anisotropy of mechanical properties and crystallographic texture in hot rolled AZ31+XSr sheets. J. Magnes. Alloy. 2019, 7, 466–473. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.-G.; Bang, W.; Lee, C.S. Effect of anisotropy on the low-cycle fatigue behavior of rolled AZ31 magnesium alloy. Mater. Sci. Eng. A 2009, 527, 417–423. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Y.; Carneiro, L.; Wang, H.; Jiang, Y. Evaluation of elastic-viscoplastic self-consistent models for a rolled AZ31B magnesium alloy under monotonic loading along five different material orientations and free-end torsion. J. Magnes. Alloy. 2023, 11, 1264–1275. [Google Scholar] [CrossRef]
- Guo, X.; Chapuis, A.; Wu, P.; Liu, Q.; Mao, X. Experimental and numerical investigation of anisotropic and twinning behavior in Mg alloy under uniaxial tension. Mater. Des. 2016, 98, 333–343. [Google Scholar] [CrossRef]
- Liu, T.; Yang, Q.; Guo, N.; Lu, Y.; Song, B. Stability of twins in Mg alloys—A short review. J. Magnes. Alloy. 2020, 8, 66–77. [Google Scholar] [CrossRef]
- Peng, P.; Yu, D.; Guo, X.; Zhang, P.; Chai, S.; Dai, Q.; Lu, J. Significantly improvement in formability and ductility of AZ31 Mg alloy by differential temperature rolling. J. Mater. Res. Technol. 2023, 26, 1293–1305. [Google Scholar] [CrossRef]
- Dallmeier, J.; Huber, O.; Saage, H.; Eigenfeld, K. Uniaxial cyclic deformation and fatigue behavior of AM50 magnesium alloy sheet metals under symmetric and asymmetric loadings. Mater. Des. 2015, 70, 10–30. [Google Scholar] [CrossRef]
- Gong, W.; Zheng, R.; Harjo, S.; Kawasaki, T.; Aizawa, K.; Tsuji, N. In-situ observation of twinning and detwinning in AZ31 alloy. J. Magnes. Alloy. 2022, 10, 3418–3432. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, Z.; Kang, G. Experimental investigation on uniaxial cyclic plasticity of cast AZ91 magnesium alloy. J. Magnes. Alloy. 2023, 11, 3255–3271. [Google Scholar] [CrossRef]
- Hama, T.; Nakata, T.; Higuchi, K.; Yoshida, H.; Jono, Y. Plastic deformation behavior of a Mg-1.5Zn-0.1Ca (mass%) alloy sheet under different strain paths. Mater. Sci. Eng. A 2023, 869, 144772. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, Z.; Hu, B.; Yu, C.; Kang, G. Experimental study on temperature-dependent ratchetting-fatigue interaction of extruded AZ31 magnesium alloy. Int. J. Fatigue 2024, 180, 108106. [Google Scholar] [CrossRef]
- Lv, L.; Shao, L.; Lin, H.; Jin, T. Deformation and mechanical responses of AZ31B magnesium alloy under combined shear-compression loading conditions. Mater. Today Commun. 2022, 31, 103551. [Google Scholar] [CrossRef]
- Li, H.; Kang, G.; Liu, Y.; Jiang, H. Non-proportionally multiaxial cyclic deformation of AZ31 magnesium alloy: Experimental observations. Mater. Sci. Eng. A 2016, 671, 70–81. [Google Scholar] [CrossRef]
- Gryguć, A.; Karparvarfard, S.M.H.; Roostaei, A.; Toscano, D.; Shaha, S.; Behravesh, B.; Jahed, H. On the Load Multiaxiality Effect on the Cyclic Behaviour of Magnesium Alloys. In Minerals, Metals and Materials Series; Springer: Cham, Switzerland, 2020; pp. 151–159. [Google Scholar] [CrossRef]
- Iftikhar, C.M.A.; Khan, A.S. The evolution of yield loci with finite plastic deformation along proportional and non-proportional loading paths in an annealed extruded AZ31 magnesium alloy. Int. J. Plast. 2021, 143, 103007. [Google Scholar] [CrossRef]
- Iftikhar, C.M.A.; Brahme, A.; Inal, K.; Khan, A.S. An evolution of subsequent yield loci under proportional and non-proportional loading path of ‘as-received’ extruded AZ31 magnesium alloy: Experiments and CPFEM modeling. Int. J. Plast. 2022, 151, 103216. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.; Wang, J. Modelling the role of slips and twins in magnesium alloys under cyclic shear. Comput. Mater. Sci. 2015, 96, 214–218. [Google Scholar] [CrossRef]
- Pandey, A.; Kabirian, F.; Hwang, J.-H.; Choi, S.-H.; Khan, A.S. Mechanical responses and deformation mechanisms of an AZ31 Mg alloy sheet under dynamic and simple shear deformations. Int. J. Plast. 2015, 68, 111–131. [Google Scholar] [CrossRef]
- Whitmore, L.; Nischler, A.; Saage, H.; Huber, O. In Situ Pure Shear Tests on Textured Magnesium AZ31B Sheets. Metals 2024, 14, 404. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, K.; Wang, H.; Jiang, Y.; Sun, X.; Liu, C.; Yu, Q.; Jiang, Y.; Wu, P.; Wang, H. On the cyclic torsion behavior of extruded AZ61A magnesium alloy tube. Int. J. Fatigue 2023, 174, 107704. [Google Scholar] [CrossRef]
- Wang, F.; Feng, M.; Jiang, Y.; Dong, J.; Zhang, Z. Cyclic shear deformation and fatigue of extruded Mg-Gd-Y magnesium alloy. J. Mater. Sci. Technol. 2019, 39, 74–81. [Google Scholar] [CrossRef]
- Litrop, A.; Klemenc, J.; Nagode, M.; Šeruga, D. Design of a Shear Test Fixture System and Optimization of a Metal Shear Specimen for Cyclic Loading. J. Test. Eval. 2022, 50, 20210681. [Google Scholar] [CrossRef]
- Litrop, A.; Klemenc, J.; Nagode, M.; Šeruga, D. Recent advances in the in-plane shear testing of Mg alloy sheets. J. Magnes. Alloy. 2023, 11, 405–424. [Google Scholar] [CrossRef]
- Xiong, Y.; Yu, Q.; Jiang, Y. Multiaxial fatigue of extruded AZ31B magnesium alloy. Mater. Sci. Eng. A 2012, 546, 119–128. [Google Scholar] [CrossRef]
- Albinmousa, J.; Jahed, H. Multiaxial effects on LCF behaviour and fatigue failure of AZ31B magnesium extrusion. Int. J. Fatigue 2014, 67, 103–116. [Google Scholar] [CrossRef]
- Anes, V.; Bumba, F.; Reis, L.; Freitas, M. Determination of the Relationship between Proportional and Non-Proportional Fatigue Damage in Magnesium Alloy AZ31 BF. Crystals 2023, 13, 688. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Y.; Guo, D.; Yang, C.; Zhang, X.; Peng, Y.; Wu, L.; Shi, B. Anisotropic mechanical behavior and corresponding microstructure evolution of extruded AZ31 under combined normal/shear stress states. Mater. Sci. Eng. A 2019, 760, 415–425. [Google Scholar] [CrossRef]
- Kang, G.-Z.; Li, H. Review on cyclic plasticity of magnesium alloys: Experiments and constitutive models. Int. J. Miner. Met. Mater. 2021, 28, 567–589. [Google Scholar] [CrossRef]
- Li, F.-F.; Fang, G. Modeling of 3D plastic anisotropy and asymmetry of extruded magnesium alloy and its applications in three-point bending. Int. J. Plast. 2020, 130, 102704. [Google Scholar] [CrossRef]
- Pahlevanpour, A.; Karparvarfard, S.; Shaha, S.; Behravesh, S.; Adibnazari, S.; Jahed, H. Anisotropy in the quasi-static and cyclic behavior of ZK60 extrusion: Characterization and fatigue modeling. Mater. Des. 2018, 160, 936–948. [Google Scholar] [CrossRef]
- Tong, L.; Zheng, M.; Kamado, S.; Zhang, D.; Meng, J.; Cheng, L.; Zhang, H. Reducing the tension–compression yield asymmetry of extruded Mg–Zn–Ca alloy via equal channel angular pressing. J. Magnes. Alloy. 2015, 3, 302–308. [Google Scholar] [CrossRef]
- Plunkett, B.; Cazacu, O.; Barlat, F. Orthotropic yield criteria for description of the anisotropy in tension and compression of sheet metals. Int. J. Plast. 2007, 24, 847–866. [Google Scholar] [CrossRef]
- Liu, F.; Tang, X.; Jin, J.; Deng, L.; Wang, X.; Long, J.; Chai, F. A constitutive model incorporating the interplay of dynamic recrystallization and twinning during hot deformation of AZ31 magnesium alloy. J. Mater. Res. Technol. 2024, 28, 1990–2007. [Google Scholar] [CrossRef]
- Li, H.; Larsson, F.; Colliander, M.H.; Ekh, M. Elastic-viscoplastic self-consistent modeling for finite deformation of polycrystalline materials. Mater. Sci. Eng. A 2021, 799, 140325. [Google Scholar] [CrossRef]
- Toth, L.S.; Sahoo, S.K.; Molinari, A. Analysis of the energy balance of plastically deformed polycrystals in viscoplastic self-consistent modelling. Eur. J. Mech.–A/Solids 2023, 100, 105019. [Google Scholar] [CrossRef]
- Li, L.; Muránsky, O.; Flores-Johnson, E.; Kabra, S.; Shen, L.; Proust, G. Effects of strain rate on the microstructure evolution and mechanical response of magnesium alloy AZ31. Mater. Sci. Eng. A 2017, 684, 37–46. [Google Scholar] [CrossRef]
- Ardeljan, M.; Beyerlein, I.J.; McWilliams, B.A.; Knezevic, M. Strain rate and temperature sensitive multi-level crystal plasticity model for large plastic deformation behavior: Application to AZ31 magnesium alloy. Int. J. Plast. 2016, 83, 90–109. [Google Scholar] [CrossRef]
- Hama, T.; Suzuki, T.; Hatakeyama, S.; Fujimoto, H.; Takuda, H. Role of twinning on the stress and strain behaviors during reverse loading in rolled magnesium alloy sheets. Mater. Sci. Eng. A 2018, 725, 8–18. [Google Scholar] [CrossRef]
- Li, H.; Yu, C.; Kang, G. Crystal plasticity modeling of the multiaxial ratchetting of extruded AZ31 Mg alloy. Int. J. Plast. 2022, 152, 103242. [Google Scholar] [CrossRef]
- Bong, H.J.; Hu, X.; Sun, X.; Ren, Y. Temperature-dependent constitutive modeling of a magnesium alloy ZEK100 sheet using crystal plasticity models combined with in situ high-energy X-ray diffraction experiment. J. Magnes. Alloy. 2022, 10, 2801–2816. [Google Scholar] [CrossRef]
- Ottosen, N.S.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, The Netherlands; London, UK, 2005. [Google Scholar]
- Lou, Y.; Zhang, C.; Zhang, S.; Yoon, J.W. A general yield function with differential and anisotropic hardening for strength modelling under various stress states with non-associated flow rule. Int. J. Plast. 2022, 158, 103414. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield criterion for hexagonal closed packed metals. Int. J. Plast. 2005, 22, 1171–1194. [Google Scholar] [CrossRef]
- Nguyen, N.-T.; Lee, M.-G.; Kim, J.H.; Kim, H.Y. A practical constitutive model for AZ31B Mg alloy sheets with unusual stress–strain response. Finite Elem. Anal. Des. 2013, 76, 39–49. [Google Scholar] [CrossRef]
- Lee, C.A.; Lee, M.-G.; Seo, O.S.; Nguyen, N.-T.; Kim, J.H.; Kim, H.Y. Cyclic behavior of AZ31B Mg: Experiments and non-isothermal forming simulations. Int. J. Plast. 2015, 75, 39–62. [Google Scholar] [CrossRef]
- Vigneshwaran, R.; Benzerga, A.A. Assessment of a two-surface plasticity model for hexagonal materials. J. Magnes. Alloys 2023, 11, 4431–4444. [Google Scholar] [CrossRef]
- Noban, M.; Albinmousa, J.; Jahed, H.; Lambert, S. A Continuum-Based Cyclic Plasticity Model for AZ31B Magnesium Alloy under Proportional loading. Procedia Eng. 2011, 10, 1366–1371. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Jahed, H. A cyclic small-strain plasticity model for wrought Mg alloys under multiaxial loading: Numerical implementation and validation. Int. J. Mech. Sci. 2018, 145, 318–329. [Google Scholar] [CrossRef]
- Yoon, J.W.; Lou, Y.; Yoon, J.; Glazoff, M.V. Asymmetric yield function based on the stress invariants for pressure sensitive metals. Int. J. Plast. 2014, 56, 184–202. [Google Scholar] [CrossRef]
- Muhammad, W.; Mohammadi, M.; Kang, J.; Mishra, R.K.; Inal, K. An elasto-plastic constitutive model for evolving asymmetric/anisotropic hardening behavior of AZ31B and ZEK100 magnesium alloy sheets considering monotonic and reverse loading paths. Int. J. Plast. 2015, 70, 30–59. [Google Scholar] [CrossRef]
- Lei, Y.; Yu, C.; Wang, Z.; Xu, X.; Li, H.; Kang, G. Multi-mechanism constitutive model for uniaxial ratchetting of extruded AZ31 magnesium alloy at room temperature. Mech. Mater. 2023, 179, 104607. [Google Scholar] [CrossRef]
- Lee, J.; Bong, H.J.; Kim, S.-J.; Lee, M.-G.; Kim, D. An enhanced distortional-hardening-based constitutive model for hexagonal close-packed metals: Application to AZ31B magnesium alloy sheets at elevated temperatures. Int. J. Plast. 2020, 126, 102618. [Google Scholar] [CrossRef]
- Kim, S.-J.; Lee, Y.-S.; Lee, J.-Y.; Kim, D.; Lee, M.-G. Distortional hardening concept for modeling anisotropic/asymmetric plastic behavior of AZ31B magnesium alloy sheets. Int. J. Plast. 2017, 94, 74–97. [Google Scholar] [CrossRef]
- Murugesan, M.; Yu, J.-H.; Chung, W.; Lee, C.-W. Hybrid Artificial Neural Network-Based Models to Investigate Deformation Behavior of AZ31B Magnesium Alloy at Warm Tensile Deformation. Materials 2023, 16, 5308. [Google Scholar] [CrossRef]
- Šolinc, U.; Klemenc, J.; Nagode, M.; Šeruga, D. A direct approach to modelling the complex response of magnesium AZ31 alloy sheets to variable strain amplitude loading using Prandtl-Ishlinskii operators. Int. J. Fatigue 2019, 127, 291–304. [Google Scholar] [CrossRef]
- Šolinc, U.; Klemenc, J.; Nagode, M.; Šeruga, D. A fast and increment independent technique for continuous calculation of the strain energy dissipated during cyclic loading applied to magnesium alloy AZ31. Int. J. Fatigue 2020, 139, 105779. [Google Scholar] [CrossRef]
- Klemenc, J.; Šeruga, D.; Nagode, A.; Nagode, M. Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy. Materials 2019, 12, 3692. [Google Scholar] [CrossRef]
- Dallmeier, J.; Denk, J.; Huber, O.; Saage, H.; Eigenfeld, K. A phenomenological stress–strain model for wrought magnesium alloys under elastoplastic strain-controlled variable amplitude loading. Int. J. Fatigue 2015, 80, 306–323. [Google Scholar] [CrossRef]
- Pandey, V.; Arora, P.; Gupta, S.K.; Khutia, N.; Dey, P.P. Validating cyclic plasticity material model for three materials subjected to asynchronous axial-torsion conditions. Int. J. Fatigue 2024, 181, 108124. [Google Scholar] [CrossRef]
- Anes, V.; Moreira, R.; Reis, L.; Freitas, M. Simulation of the Cyclic Stress–Strain Behavior of the Magnesium Alloy AZ31B-F under Multiaxial Loading. Crystals 2023, 13, 969. [Google Scholar] [CrossRef]
- Anes, V.; Reis, L.; de Freitas, M. Evaluation of a phenomenological elastic-plastic approach for magnesium alloys under multiaxial loading conditions. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2468–2486. [Google Scholar] [CrossRef]
- Šeruga, D.; Nagode, M. A new approach to finite element modelling of cyclic thermomechanical stress-strain responses. Int. J. Mech. Sci. 2019, 164, 105139. [Google Scholar] [CrossRef]
- Litrop, A.; Zobec, P.; Šeruga, D.; Nagode, M.; Klemenc, J. Experimental Crack Path Analysis of Aluminum Alloy Specimen under Dynamic Shear Loading using Digital Image Correlation Method. Procedia Struct. Integr. 2022, 39, 41–46. [Google Scholar] [CrossRef]
- Albinmousa, J. Multiaxial Fatigue Characterization and Modeling of AZ31B Magnesium Extrusion. Ph.D. Thesis, University Waterloo, Waterloo, Belgium, 2012. Available online: https://uwspace.uwaterloo.ca/handle/10012/6431?show=full (accessed on 28 August 2024).
- Simo, J.C.; Hughes, T.J.R. Computational inelasticity. In Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Lee, M.-G.; Wagoner, R.; Lee, J.; Chung, K.; Kim, H. Constitutive modeling for anisotropic/asymmetric hardening behavior of magnesium alloy sheets. Int. J. Plast. 2007, 24, 545–582. [Google Scholar] [CrossRef]


| Dynamic Parameters | Value | Static Parameters | Value |
|---|---|---|---|
| MPa | |||
| MPa | MPa | ||
| MPa | |||
| MPa | MPa | ||
| MPa | |||
| MPa | MPa | ||
| MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litrop, A.; Klemenc, J.; Nagode, M.; Šeruga, D. Enhanced Cyclically Stable Plasticity Model for Multiaxial Behaviour of Magnesium Alloy AZ31 under Low-Cycle Fatigue Conditions. Materials 2024, 17, 4659. https://doi.org/10.3390/ma17184659
Litrop A, Klemenc J, Nagode M, Šeruga D. Enhanced Cyclically Stable Plasticity Model for Multiaxial Behaviour of Magnesium Alloy AZ31 under Low-Cycle Fatigue Conditions. Materials. 2024; 17(18):4659. https://doi.org/10.3390/ma17184659
Chicago/Turabian StyleLitrop, Aljaž, Jernej Klemenc, Marko Nagode, and Domen Šeruga. 2024. "Enhanced Cyclically Stable Plasticity Model for Multiaxial Behaviour of Magnesium Alloy AZ31 under Low-Cycle Fatigue Conditions" Materials 17, no. 18: 4659. https://doi.org/10.3390/ma17184659
APA StyleLitrop, A., Klemenc, J., Nagode, M., & Šeruga, D. (2024). Enhanced Cyclically Stable Plasticity Model for Multiaxial Behaviour of Magnesium Alloy AZ31 under Low-Cycle Fatigue Conditions. Materials, 17(18), 4659. https://doi.org/10.3390/ma17184659









