Tensile Constitutive Model of Engineered Cementitious Composites Reinforced by High-Strength Steel Wire Mesh
Abstract
1. Introduction
2. Materials and Methods
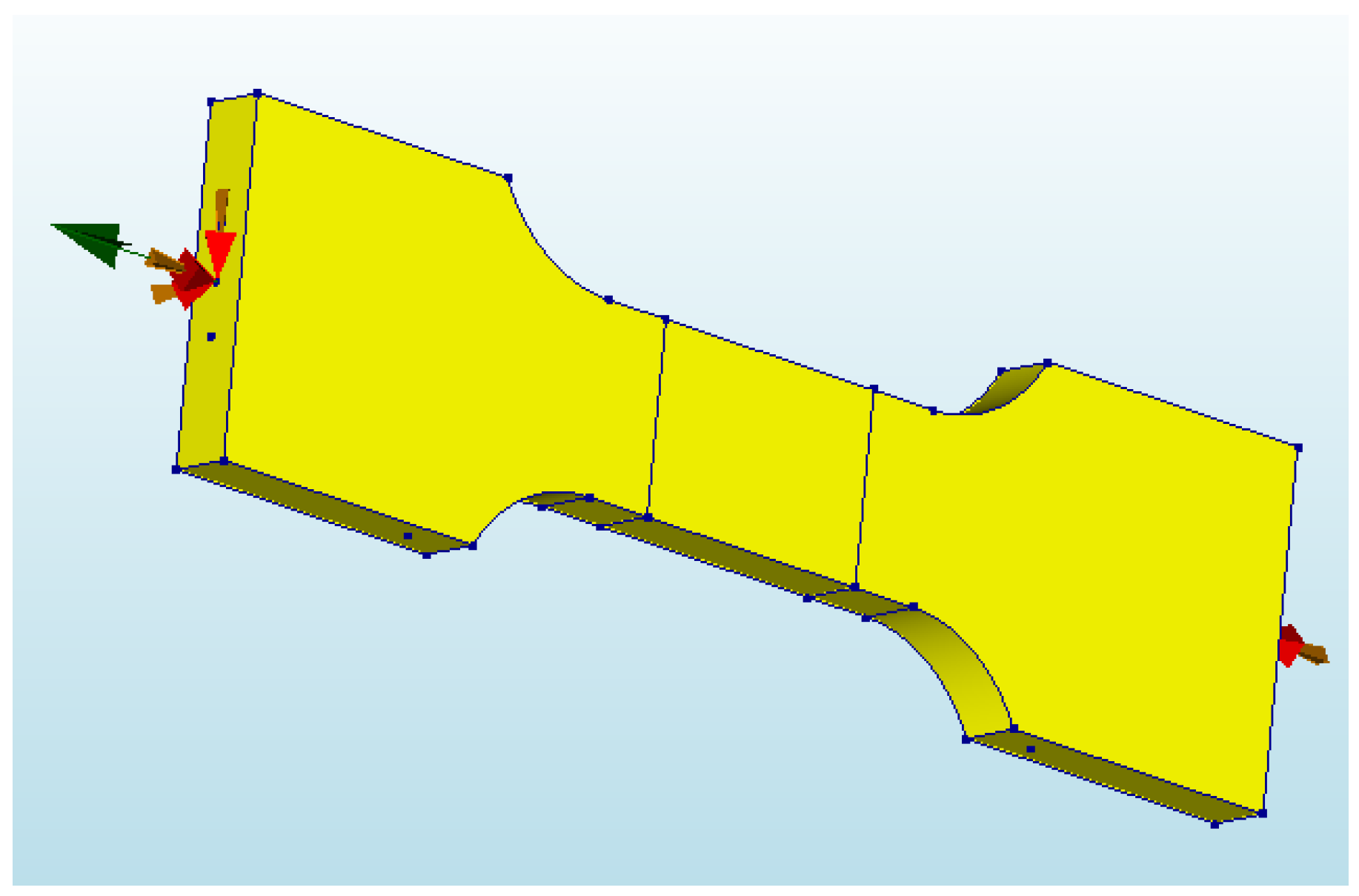
2.1. Geometric Modeling and Material Properties
2.2. Unit Type and Mesh Size
2.3. Interactions between Different Components
2.4. Boundary Conditions and Loading Procedure
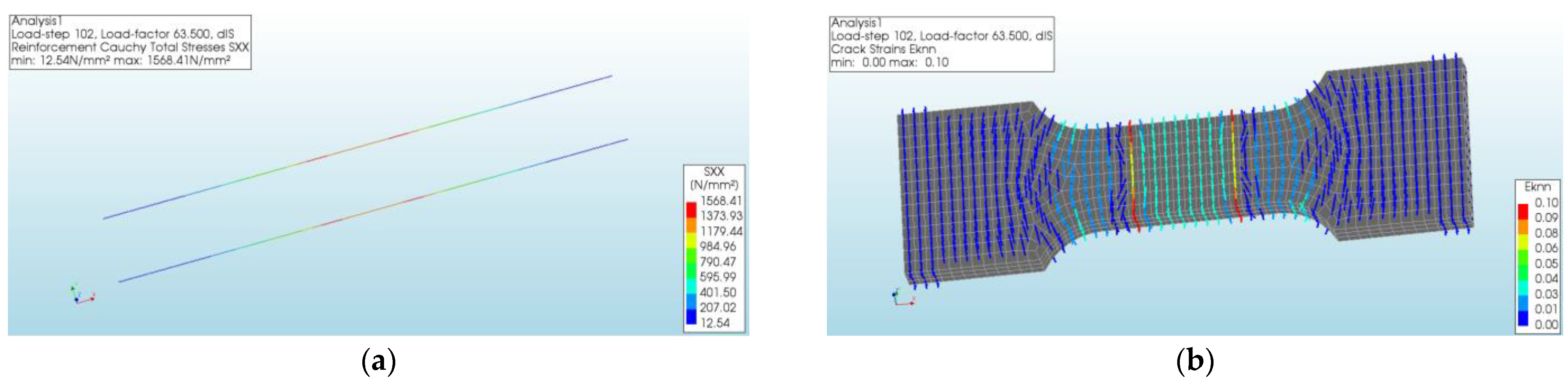
2.5. Validation of the Numerical Model
2.6. Validation of the Constitutive Model
3. Results
3.1. Simulation and Experimental Results
3.2. Derivation of the Tensile Constitutive Model
- (1)
- Elasticity Stage
- (2)
- Plasticity Stage
- (3)
- Fitting Results of the Constitutive Model
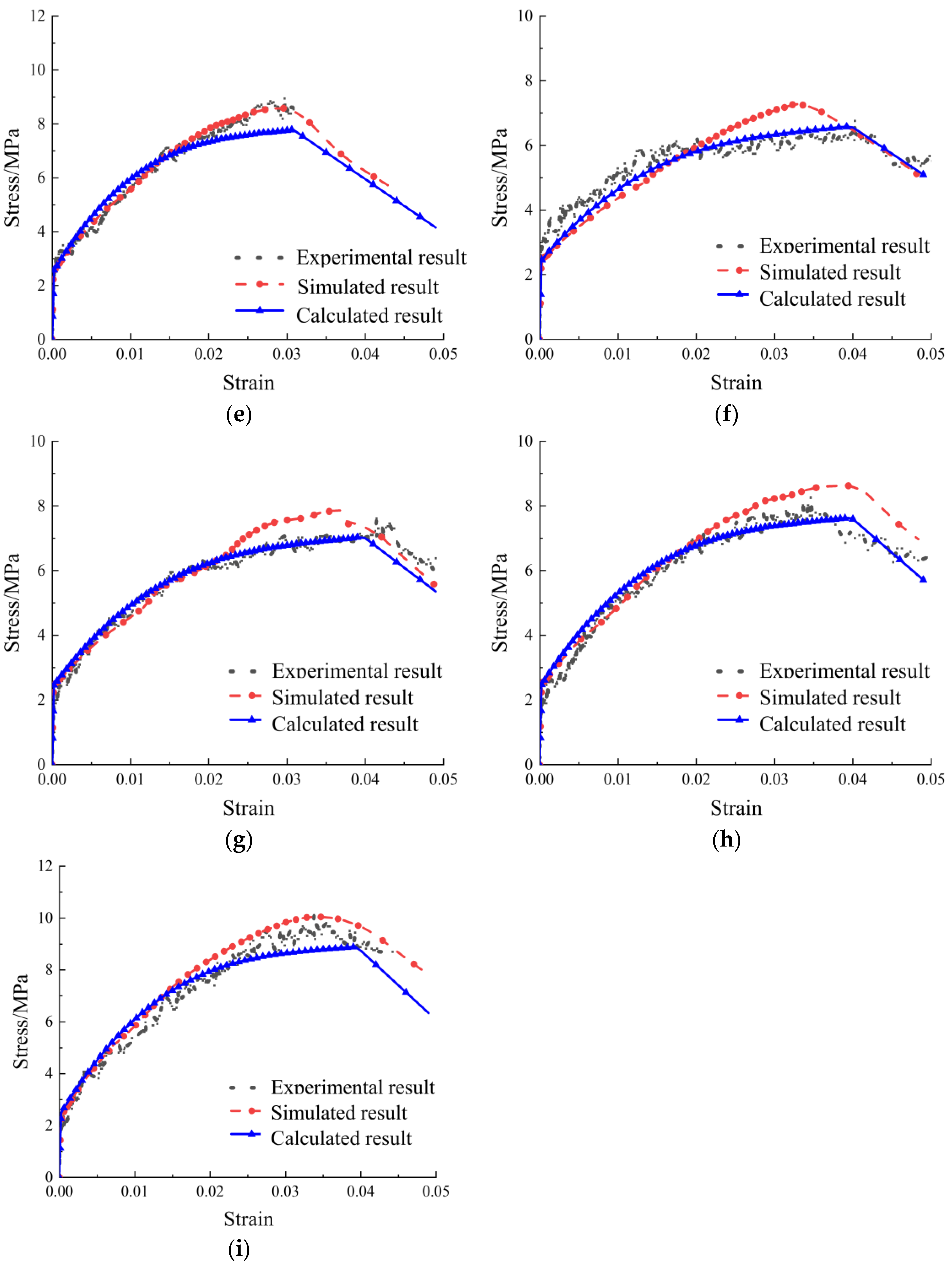
3.3. Validation of the Tensile Constitutive Model
4. Discussion
4.1. Reinforcement of ECCs
4.2. Acquisition and Validation of Constitutive Models
5. Conclusions
- (1)
- High-strength steel wire mesh could greatly increase the tensile strength of the specimens while retaining the high toughness and excellent crack control ability of ECCs.
- (2)
- The combination of experiments and numerical simulations is an effective method to obtain complete stress–strain curves for the derivation of the tensile constitutive model of a new material.
- (3)
- Clarifying the contribution of each component at each stress stage is the key to further derive the constitutive model of high-strength-steel-wire-mesh-reinforced ECCs.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Z.; Zhu, Z.; Accornero, F. Tensile-to-Shear Crack Transition in the Compression Failure of Steel-Fibre-Reinforced Concrete: Insights from Acoustic Emission Monitoring. Buildings 2024, 14, 2039. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, B.; Dai, L.; Yao, M.; Pang, X. Factors Influencing Chloride Ion Diffusion in Reinforced Concrete Structures. Materials 2024, 17, 3296. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Wang, J.; Cui, J.; Yuan, Y.; Song, Y. Experimental Study on the Effects of Carbonated Steel Slag Fine Aggregate on the Expansion Rate, Mechanical Properties and Carbonation Depth of Mortar. Materials 2024, 17, 3279. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Ma, Z. The Effect of Volcanic Stone and Metakaolin on the Compressive Properties of Ultrahigh-Performance Concrete Cubes. Buildings 2024, 14, 2024. [Google Scholar] [CrossRef]
- Shah, A.H.; Wani, E.; Khan, A.S.; Faridi, A.F.; Najiulah, S.M.; Shah, A.A.; Soharwardi, T.K. Engineered Cementitious Composites: An Analysis of the Composition and Behaviour at Ambient and Elevated Temperatures. Iran J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 2549–2569. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Li, Z.P.; He, J.L.; Shi, X.M. High-strength engineered cementitious composites with nanosilica incorporated: Mechanical performance and autogenous self-healing behavior. Cem. Concr. Compos. 2023, 135, 104837. [Google Scholar] [CrossRef]
- Dehghani, A.; Nateghi-Alahi, F.; Fischer, G. Engineered cementitious composites for strengthening masonry infilled reinforced concrete frames. Eng. Struct. 2015, 105, 197–208. [Google Scholar] [CrossRef]
- Li, V.; Wang, S.X. Flexural behaviors of glass fiber-reinforced polymer (GFRP) reinforced engineered cementitious composite beams. Aci. Mater. J. 2001, 98, 483–492. [Google Scholar] [CrossRef]
- Yu, K.Q.; Lu, Z.D.; Dai, J.G. Direct Tensile Properties and Stress–Strain Model of UHP-ECC. J. Mater. Civ. Eng. 2020, 32, 04019334. [Google Scholar] [CrossRef]
- Shi, L.; Lin, S.T.K.; Lu, Y.; Ye, L.; Zhang, Y.X. Artificial neural network based mechanical and electrical property prediction of engineered cementitious composites. Constr. Build. Mater. 2018, 174, 667–674. [Google Scholar] [CrossRef]
- Li, K.; Yu, P.; Liu, W.K.; Wang, X.L. Research on mechanical properties and stress-strain relationship of ECC under compression. Ind. Constr. 2020, 3, 172–177. [Google Scholar] [CrossRef]
- Wang, D.; Che, J.; Liu, H.; Chin, S.C. Enhanced Ductility and Toughness of Desert Sand Engineered Cementitious Composites. Buildings 2023, 13, 1538. [Google Scholar] [CrossRef]
- Mazzuca, P.; Pisani, B.; Firmo, J.P.; Ombres, L. Tensile and bond properties at elevated temperatures of a PBO-FRCM composite system for strengthening concrete elements: Experimental and analytical investigations. Constr. Build. Mater. 2024, 432, 136519. [Google Scholar] [CrossRef]
- Xia, P.Q.; Brownjohn, J.M.W. Residual Stiffness Assessment of Structurally Failed Reinforced Concrete Structure by Dynamic Testing and Finite Element Model Updating. Exp. Mech. 2003, 43, 372–378. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of Residual Flexural Stiffness of Steel Fiber-Reinforced Concrete Beams with Steel Reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef]
- Fischer, G.; Li, V.C. Influence of matrix ductility on tension-stiffening behavior of steel reinforced engineering cementitious composites (ECC). Aci. Struct. J. 2002, 99, 104–114. [Google Scholar] [CrossRef]
- Mihashi, H.; Otsuka, K.; Akita, H.; Kikuchi, T.; Suzuki, S. Bond behavior of a deformed bar in high-performance fiber-reinforced cement composites (HPFRCC). In Proceedings of the 11th International Conference on Fracture, Turin, Italy, 20–25 March 2005. [Google Scholar]
- Zhu, J.T.; Zhao, Y.L.; Li, Y.; Wang, X.L. Experiment on bonding and anchoring performance between high-strength stainless steel wire mesh and engineered cementitious composites. Acta Mater. Compos. Sin. 2020, 7, 1731–1742. [Google Scholar] [CrossRef]
- Li, K.; Zhao, J.L.; Li, Z.Q.; Zhu, J.T. Experiment on non-damaged RC beams strengthened by high-strength steel wire strand meshes reinforced ECC in bending. Acta Mater. Compos. Sin. 2022, 39, 3428–3440. [Google Scholar] [CrossRef]
- Zhu, J.T.; Zhang, K.; Wang, X.L.; Li, K. Study on interfacial bond-slip relationship between HSSWM-ECC and concrete. Eng. Mech. 2022, 39, 204–214. [Google Scholar] [CrossRef]
- Xia, Y.; Ding, C.; Li, Z.J.; Benjamin, W.S.; Hannah, B.B. Numerical modeling of stress-strain relationships for advanced high strength steels. J. Constr. Steel. Res. 2021, 182, 106687. [Google Scholar] [CrossRef]
- Rong, C.; Duan, Z.; Tang, J. Multi-Dimensional Iterative Constitutive Model of Concrete under Complex Stress Conditions in Composite Structures. Buildings 2024, 14, 1837. [Google Scholar] [CrossRef]
- Negar, N.; Mohamed, A.M. Compressive behavior and stress–strain relationships of confined and unconfined UHPC. Constr. Build. Mater. 2021, 272, 121844. [Google Scholar] [CrossRef]
- Mohammad, A.G.; Jürgen, W. Experiments, constitutive modeling, and simulations on the creep behavior of the AgSn transient liquid phase metallic bonds. Microelectron. Reliab. 2024, 154, 115327. [Google Scholar] [CrossRef]
- Tasdemir, B.; Pellegrino, A.; Tagarielli, V. A strategy to formulate data-driven constitutive models from random multiaxial experiments. Sci. Rep. 2022, 12, 22248. [Google Scholar] [CrossRef]
- Xie, Q.; Su, L.; Zhu, Z. Dynamic constitutive model of frozen soil that considers the evolution of volume fraction of ice. Sci. Rep. 2020, 10, 20941. [Google Scholar] [CrossRef]
- Huang, W.; Kang, G.; Ma, P. Uniaxial Electro-Mechanically Coupled Cyclic Deformation of VHB 4905 Dielectric Elastomer: Experiment and Constitutive Model. J. Mater. Eng. Perform. 2024, 33, 2952–2967. [Google Scholar] [CrossRef]
- Zhu, B.; Xiong, L.; Chen, Y. Evaluation of constitutive models used in orthogonal cutting simulation based on coupled Eulerian–Lagrangian formulation. Int. J. Adv. Manuf. Technol. 2024, 131, 183–199. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, C.; Huang, Y.; Zhang, R.; Zhang, J.; Luo, G.; Shen, Q. Accurate Finite Element Simulations of Dynamic Behaviour: Constitutive Models and Analysis with Deep Learning. Materials 2024, 17, 643. [Google Scholar] [CrossRef]
- Ling, C.; Ren, X.; Wang, X.; Li, Y.; Liu, Z.; Wang, B.; Zhao, J. Dynamic Mechanical Properties and Modified Johnson-Cook Model Considering Recrystallization Softening for Nickel-Based Powder Metallurgy Superalloys. Materials 2024, 17, 670. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Kanvinde, A.; Li, G.Q.; Wang, Y.B. A new constitutive model for high strength structural steels. J. Constr. Steel. Res. 2021, 182, 106646. [Google Scholar] [CrossRef]
- Li, F.F.; Chen, W.Z.; Yu, H.D.; Ma, Y.S.; Lei, J. Constitutive model of claystone based on plastic damage and its numerical implementation. J. China. Coal. Soc. 2020, 45, 633–642. [Google Scholar] [CrossRef]
- Wang, X.L.; Yang, G.H.; Qian, W.W.; Li, K.; Zhu, J.T. Tensile Behavior of High-Strength Stainless Steel Wire Rope (HSSSWR)-Reinforced ECC. Int. J. Concr. Struct. Mater. 2021, 15, 43. [Google Scholar] [CrossRef]
- Liu, W.K. Study on the Compression and Tensile Properties and the Tensile Properties and the Constitutive Model of ECC. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 30 May 2018. [Google Scholar]
- Wang, X.L.; Yang, G.H.; Qian, W.W.; Li, K.; Zhu, J.T. Tensile stress-strain relationship of engineered cementitious composites reinforced by high-strength stainless steel wire mesh. Acta Mater. Compos. Sin. 2020, 12, 3220–3228. [Google Scholar] [CrossRef]
- Chou, S.M.; Chai, G.B.; Ling, L. Finite element technique for design of stub columns. Thin. Wall. Struct. 2000, 37, 97–112. [Google Scholar] [CrossRef]
- Singh, S.B.; Munjal, P. Engineered cementitious composite and its applications. Mater. Today Proc. 2020, 32, 797–802. [Google Scholar] [CrossRef]
- Cai, J.M.; Pan, J.L.; Tan, J.W.; Li, X.P. Bond behaviours of deformed steel rebars in engineered cementitious composites (ECC) and concrete. Constr. Build. Mater. 2020, 252, 119082. [Google Scholar] [CrossRef]
- Xu, S.L.; Li, Q.H.; Li, H.D. An experimental study on the flexural properties of carbon textile reinforced ECC. China Civ. Eng. J. 2007, 12, 69–76. [Google Scholar] [CrossRef]
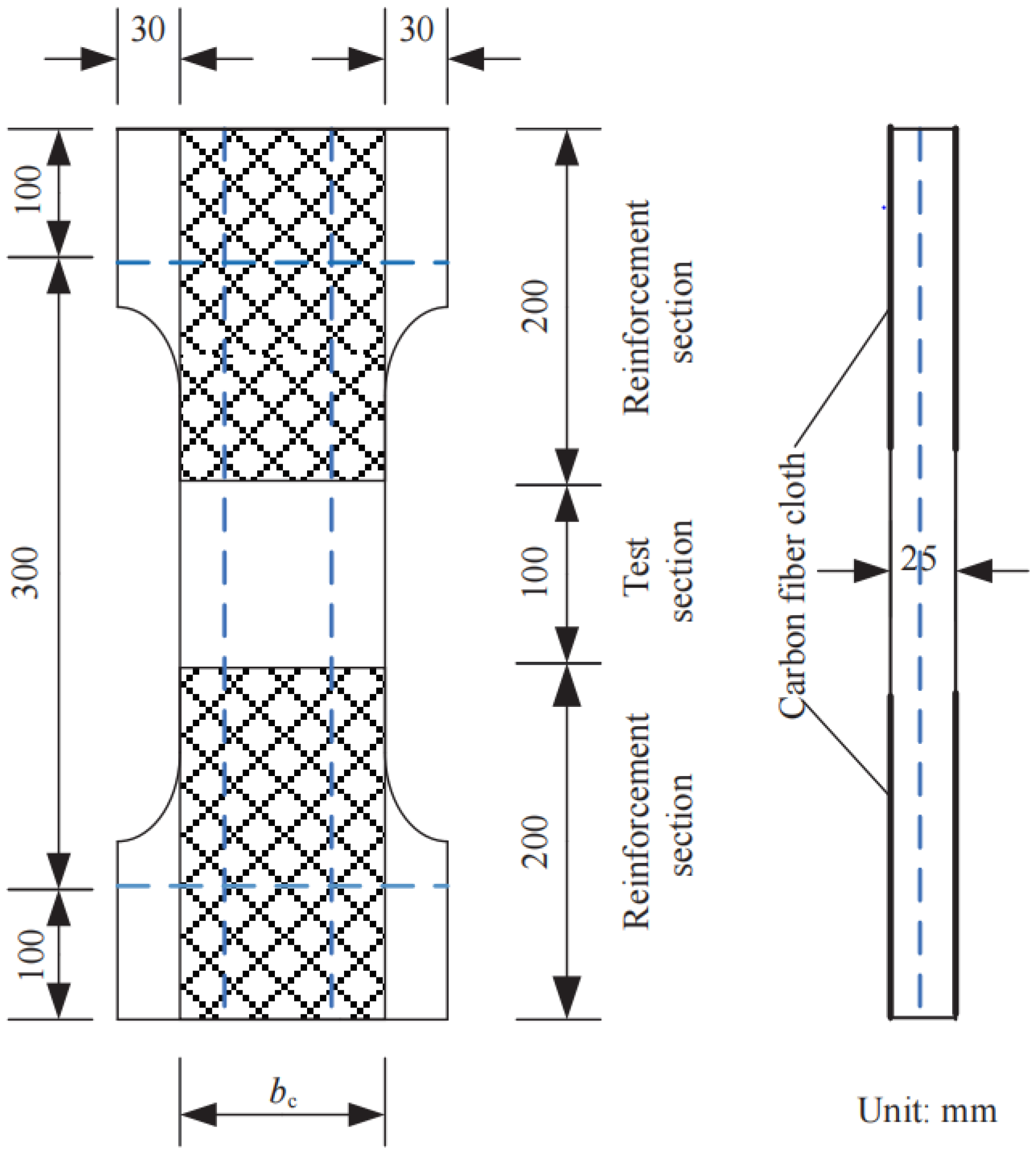






| Number | Test Section Width bc/mm | Distance between Steel Wires | Number of Steel Wires | Reinforcement Ratio | ECCs’ Tensile Strength |
|---|---|---|---|---|---|
| TC12 | 80 | 50 | 2 | 0.0028 | 3.53 |
| TC22 | 70 | 40 | 2 | 0.0032 | 3.53 |
| TC32 | 60 | 30 | 2 | 0.0037 | 3.53 |
| TC42 | 47 | 20 | 2 | 0.0048 | 3.53 |
| TC52 | 90 | 30 | 3 | 0.0037 | 3.53 |
| TD12 | 80 | 50 | 2 | 0.0028 | 3.46 |
| TD22 | 70 | 40 | 2 | 0.0032 | 3.46 |
| TD32 | 60 | 30 | 2 | 0.0037 | 3.46 |
| TD42 | 47 | 20 | 2 | 0.0048 | 3.46 |
| Group | Cement | Sand | Fly Ash | Silica Fume | Water | PVA Fiber | Superplasticizer | Thickener |
|---|---|---|---|---|---|---|---|---|
| TC | 1 | 0.3 | 4 | 0.08 | 1 | 0.02 | 0.06 | 0 |
| TD | 1 | 0.3 | 4 | 0.08 | 1 | 0.02 | 0.06 | 0.006 |
| Type of ECCs | Cracking Stress/MPa | Cracking Strain | Tensile Strength/MPa | Strain Corresponding to Tensile Strength |
|---|---|---|---|---|
| Type 1 | 2.45 | 0.000204 | 3.53 | 0.0279 |
| Type 2 | 2.13 | 0.000189 | 3.46 | 0.0297 |
| Number | Diameter of Steel Wires | Number of Steel Wires | Distance between Steel Wires (mm) | ECCs’ Tensile Strength |
|---|---|---|---|---|
| LA11 | 2.4 | 3 | 25 | 3.53 |
| LA12 | 2.4 | 2 | 50 | 3.86 |
| LA13 | 3.2 | 2 | 50 | 3.53 |
| LA21 | 2.4 | 3 | 20 | 3.53 |
| LA22 | 2.4 | 2 | 40 | 3.86 |
| LA23 | 3.2 | 2 | 40 | 3.53 |
| LA31 | 2.4 | 3 | 15 | 3.53 |
| LA32 | 2.4 | 2 | 30 | 3.86 |
| LA33 | 3.2 | 2 | 30 | 3.53 |
| LA41 | 2.4 | 2 | 20 | 3.86 |
| LA42 | 3.2 | 2 | 20 | 3.53 |
| LA51 | 2.4 | 4 | 20 | 3.53 |
| LA52 | 2.4 | 3 | 30 | 3.86 |
| LA53 | 3.2 | 3 | 30 | 3.53 |
| Number | Diameter of Steel Wires | Number of Steel Wires | Distance between Steel Wires (mm) | ECCs’ Tensile Strength |
|---|---|---|---|---|
| LB11 | 2.4 | 3 | 25 | 3.46 |
| LB12 | 3.2 | 2 | 50 | 3.46 |
| LB21 | 2.4 | 3 | 20 | 3.46 |
| LB22 | 3.2 | 2 | 40 | 3.46 |
| LB31 | 2.4 | 3 | 15 | 3.46 |
| LB32 | 3.2 | 2 | 30 | 3.46 |
| LB41 | 2.4 | 4 | 20 | 3.46 |
| LB42 | 3.2 | 2 | 30 | 3.46 |
| Specimen | Simulated Cracking Stress/MPa | Experimental Cracking Stress/MPa | Cracking Stress Error | Simulated Ultimate Stress/MPa | Experimental Ultimate Stress/MPa | Ultimate Stress Error |
|---|---|---|---|---|---|---|
| TC 12 | 2.21 | 2.20 | 0.45% | 7.44 | 7.09 | 4.94% |
| TC 22 | 2.32 | 2.25 | 3.11% | 8.13 | 7.94 | 2.39% |
| TC 32 | 2.40 | 2.41 | −0.41% | 8.86 | 8.77 | 1.03% |
| TC 42 | 2.49 | 2.56 | −2.73% | 10.18 | 10.65 | −4.41% |
| TC 52 | 2.59 | 2.54 | 1.97% | 8.57 | 8.82 | −2.83% |
| TD 12 | 2.09 | 1.97 | 6.09% | 7.11 | 6.41 | 10.92% |
| TD 22 | 2.13 | 1.99 | 7.04% | 7.87 | 7.81 | 0.77% |
| TD 32 | 2.15 | 2.07 | 3.86% | 8.62 | 8.62 | 0.00% |
| TD 42 | 2.21 | 2.19 | 0.91% | 10.04 | 10.30 | −2.52% |
| Specimen | TC12 | TC22 | TC32 | TC42 | TC52 | TD12 | TD22 | TD32 | TD42 |
|---|---|---|---|---|---|---|---|---|---|
| k | −155 | −198 | −208 | −249 | −228 | −141 | −181 | −195 | −260 |
| R2 | 0.9702 | 0.9979 | 0.9974 | 0.9952 | 0.9910 | 0.9857 | 0.9757 | 0.9794 | 0.9816 |
| ρ | 0.0028 | 0.0032 | 0.0037 | 0.0048 | 0.0037 | 0.0028 | 0.0032 | 0.0037 | 0.0048 |
| α | 0.692 | 0.883 | 0.930 | 1.110 | 1.020 | 0.629 | 0.808 | 0.870 | 1.160 |
| Specimen | Simulated Cracking Stress/MPa | Calculated Cracking Stress/MPa | Cracking Stress Error | Simulated Ultimate Stress/MPa | Calculated Ultimate Stress/MPa | Ultimate Stress Error |
|---|---|---|---|---|---|---|
| LA11 | 2.58 | 2.55 | −1.16% | 9.15 | 8.35 | −8.74% |
| LA12 | 2.13 | 2.23 | 4.69% | 7.57 | 7.08 | −6.47% |
| LA13 | 2.62 | 2.54 | −3.05% | 9.34 | 9.24 | −1.07% |
| LA21 | 2.52 | 2.56 | 1.59% | 10.08 | 9.04 | −10.32% |
| LA22 | 2.32 | 2.14 | −7.76% | 8.23 | 7.54 | −8.38% |
| LA23 | 2.39 | 2.56 | 7.11% | 9.85 | 10.06 | 2.13% |
| LA31 | 2.76 | 2.58 | −6.52% | 11.63 | 9.96 | −14.36% |
| LA32 | 2.28 | 2.13 | −6.58% | 8.97 | 8.15 | −9.14% |
| LA33 | 2.66 | 2.58 | −3.01% | 11.25 | 10.14 | −9.87% |
| LA41 | 2.53 | 2.78 | 9.88% | 10.35 | 9.34 | −9.76% |
| LA42 | 2.63 | 2.61 | −0.76% | 12.85 | 13.25 | 3.11% |
| LA51 | 2.23 | 2.31 | 3.59% | 10.03 | 9.24 | −7.88% |
| LA52 | 2.22 | 2.15 | −3.15% | 8.79 | 8.15 | −7.28% |
| LA53 | 2.24 | 2.29 | 2.23% | 11.14 | 11.14 | 0.00% |
| LB11 | 2.27 | 2.21 | −2.64% | 8.60 | 8.28 | −3.72% |
| LB12 | 2.22 | 2.26 | 1.80% | 8.93 | 9.22 | 3.25% |
| LB21 | 2.16 | 2.22 | 2.78% | 9.77 | 8.97 | −8.19% |
| LB22 | 2.27 | 2.28 | 0.44% | 10.32 | 9.97 | −3.39% |
| LB31 | 2.12 | 2.24 | 5.66% | 10.24 | 9.89 | −3.42% |
| LB32 | 2.32 | 2.29 | −1.29% | 11.37 | 11.05 | −2.81% |
| LB41 | 2.22 | 2.26 | 1.80% | 9.73 | 9.17 | −5.76% |
| LB42 | 2.22 | 2.29 | 3.15% | 11.53 | 11.05 | −4.16% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Gao, R.; Wang, A.; Li, K.; Wu, D.; Li, H.; Li, Y. Tensile Constitutive Model of Engineered Cementitious Composites Reinforced by High-Strength Steel Wire Mesh. Materials 2024, 17, 4709. https://doi.org/10.3390/ma17194709
Li J, Gao R, Wang A, Li K, Wu D, Li H, Li Y. Tensile Constitutive Model of Engineered Cementitious Composites Reinforced by High-Strength Steel Wire Mesh. Materials. 2024; 17(19):4709. https://doi.org/10.3390/ma17194709
Chicago/Turabian StyleLi, Jing, Ruiyuan Gao, Ang Wang, Ke Li, Di Wu, Hao Li, and Yuxuan Li. 2024. "Tensile Constitutive Model of Engineered Cementitious Composites Reinforced by High-Strength Steel Wire Mesh" Materials 17, no. 19: 4709. https://doi.org/10.3390/ma17194709
APA StyleLi, J., Gao, R., Wang, A., Li, K., Wu, D., Li, H., & Li, Y. (2024). Tensile Constitutive Model of Engineered Cementitious Composites Reinforced by High-Strength Steel Wire Mesh. Materials, 17(19), 4709. https://doi.org/10.3390/ma17194709






