Experimental Research on Dynamic Mechanical Properties of High-Density Foamed Concrete
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
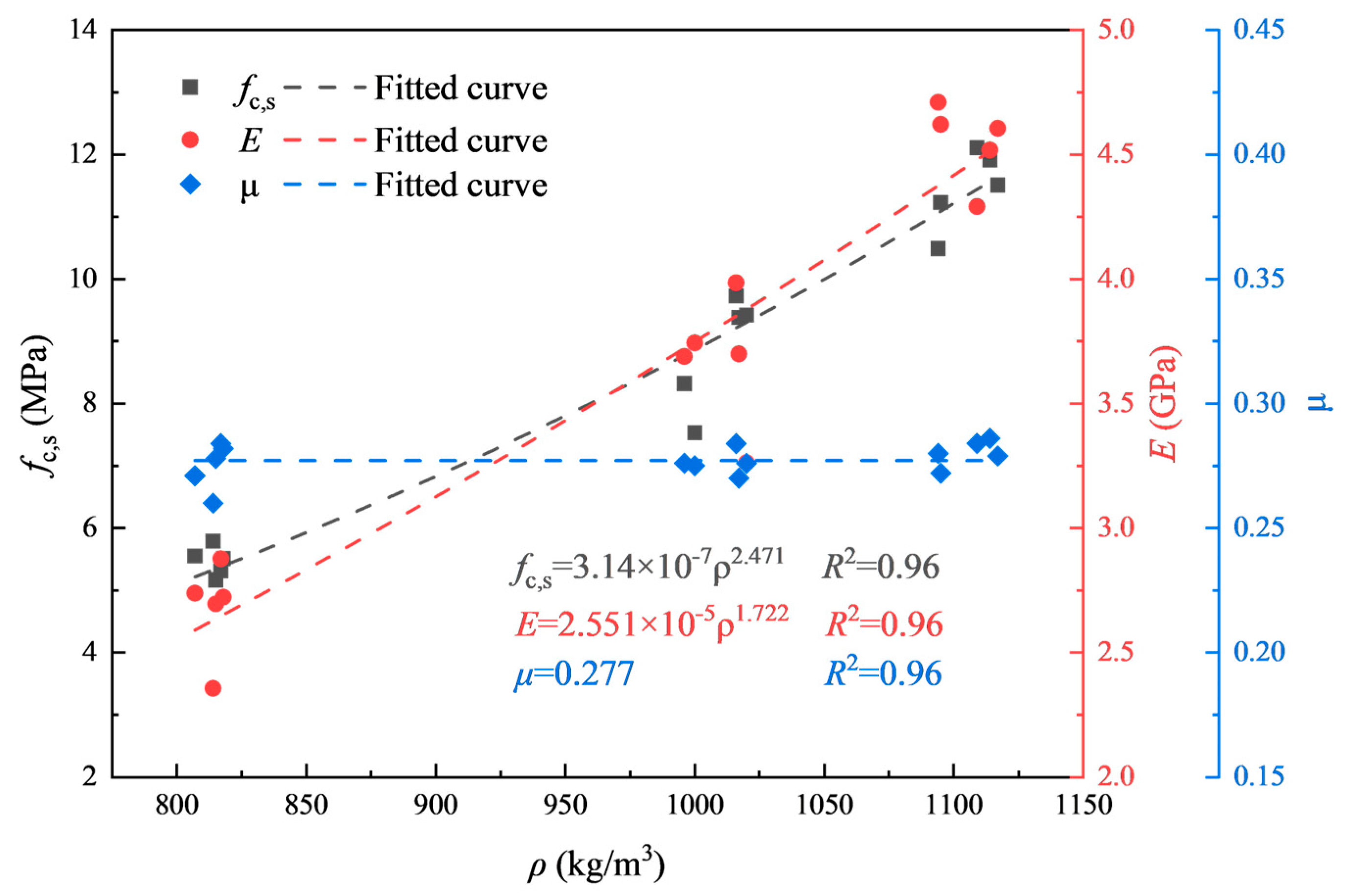
2.2. Quasi-Static Properties of Foamed Concrete
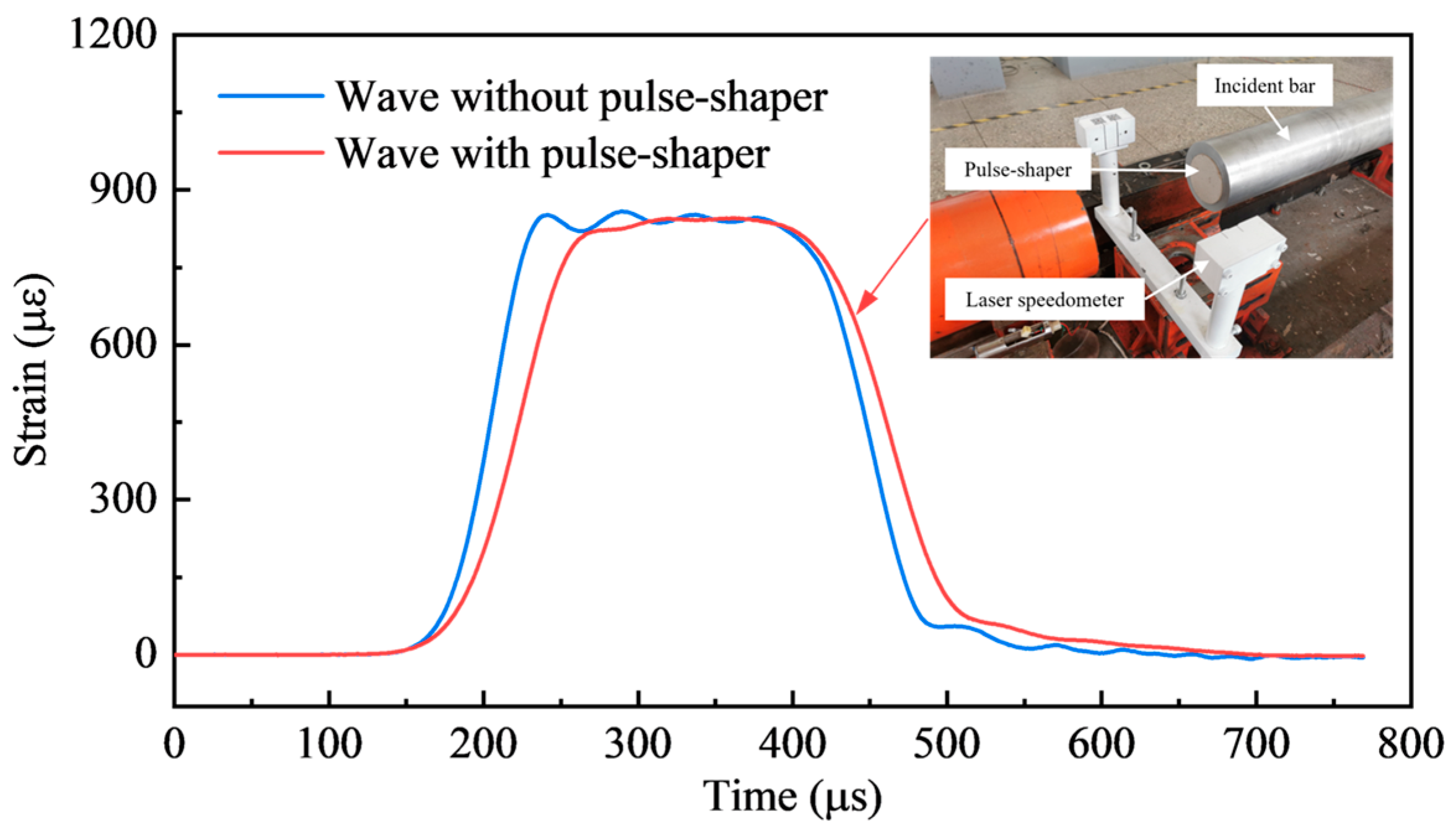
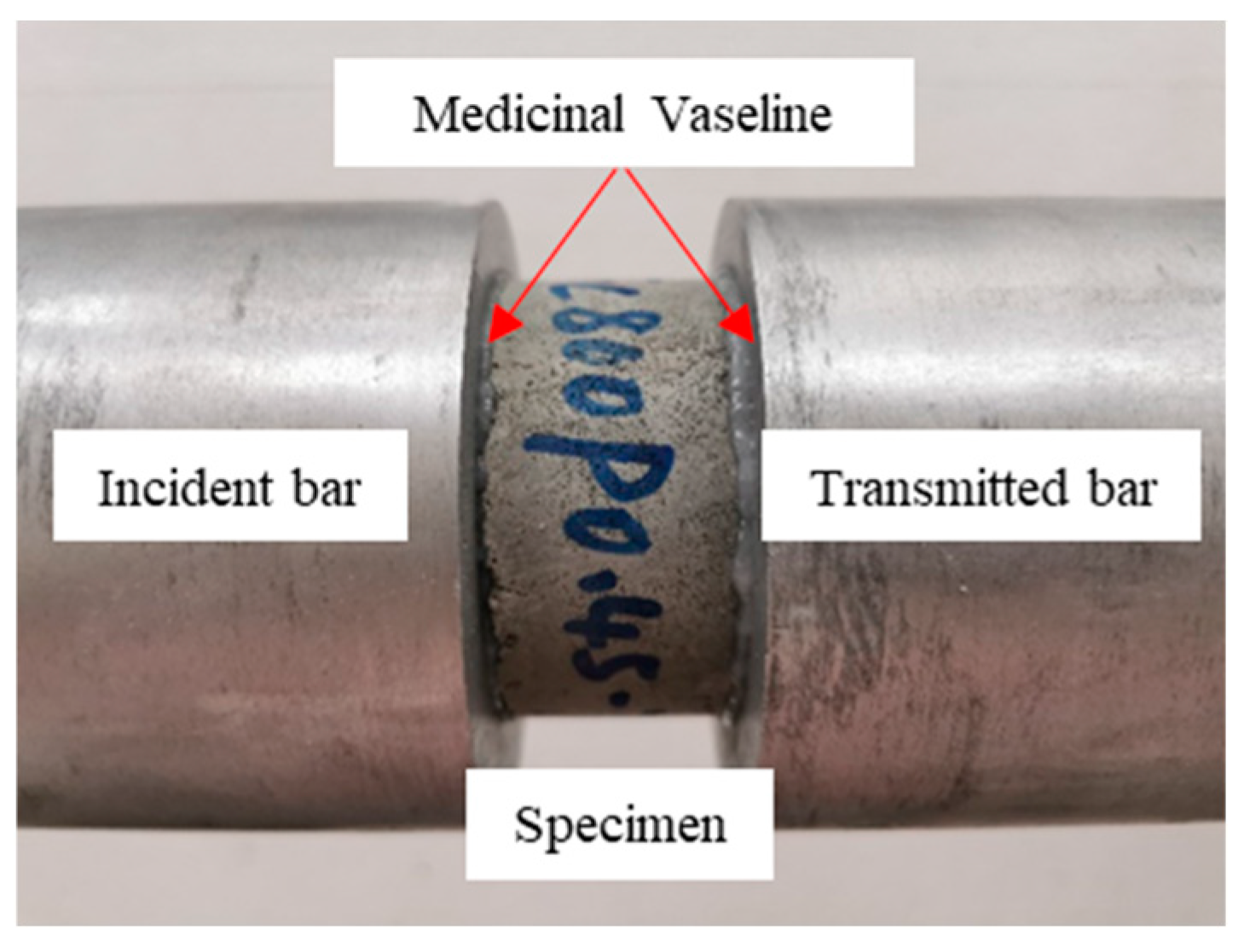
2.3. Experimental Apparatus and Methods for Dynamic Tests
2.4. Data Processing
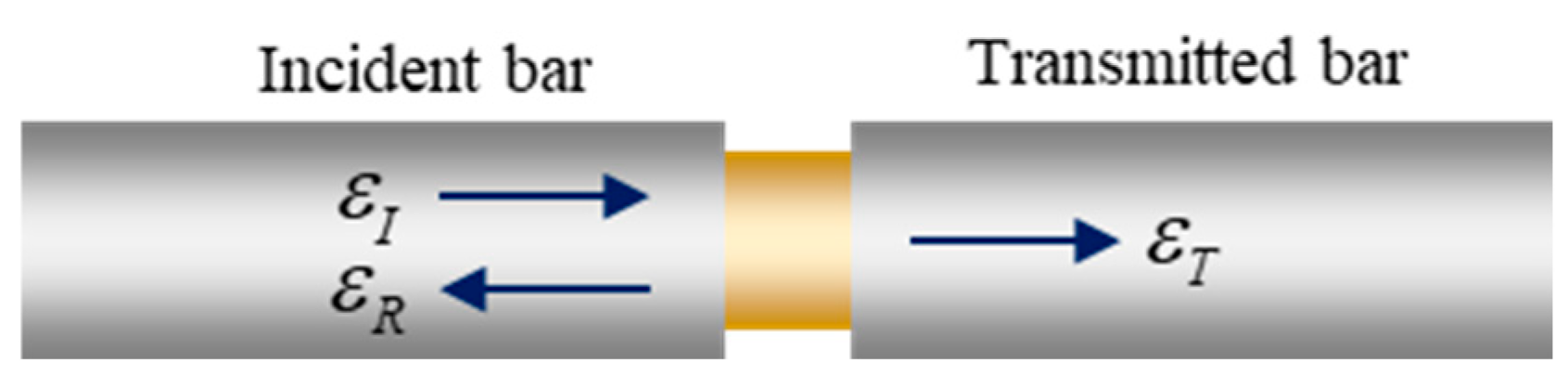
2.4.1. Three-Wave Analysis Method
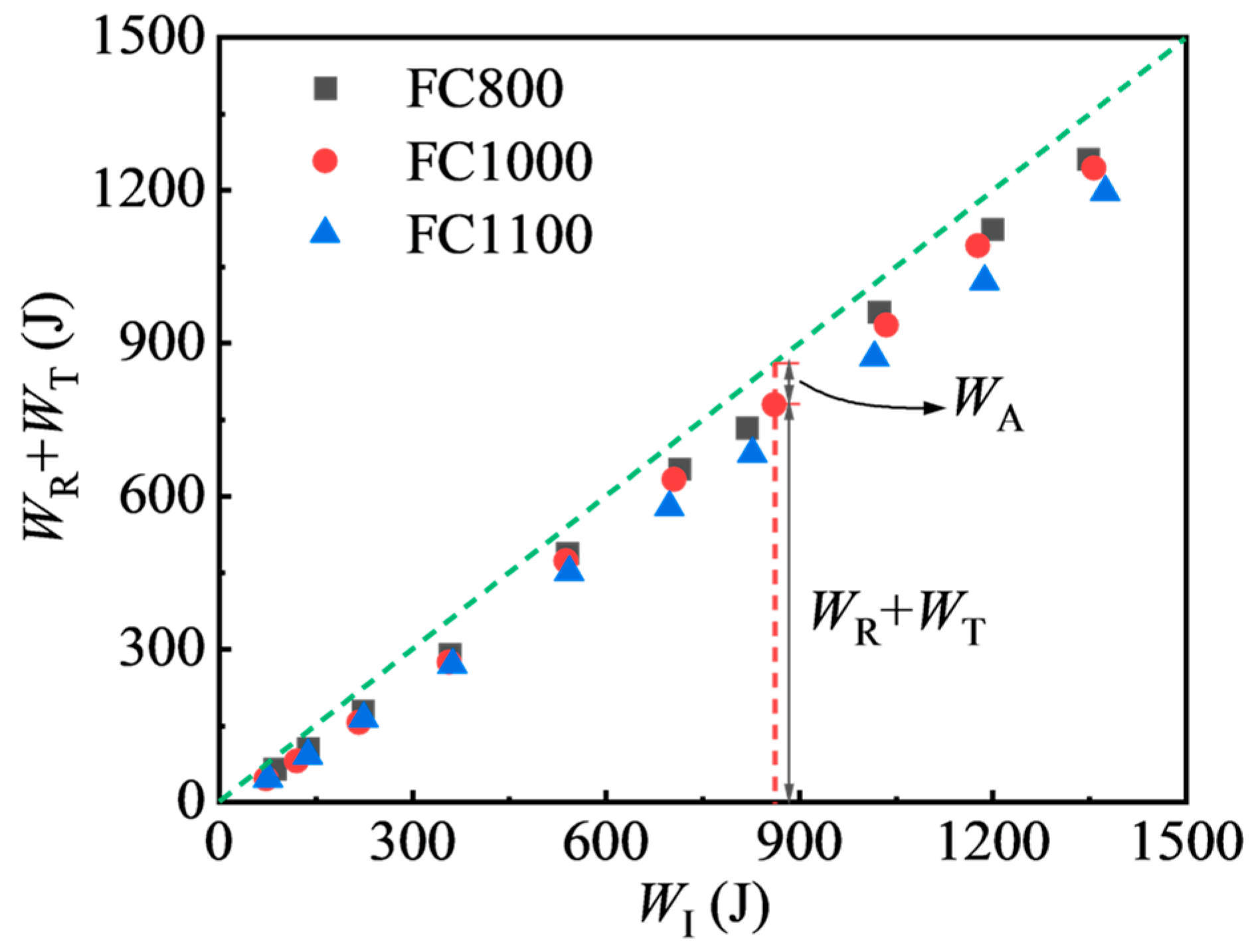
2.4.2. Determination of the Energy Parameters
2.5. Experimental Scheme
3. Results and Discussion
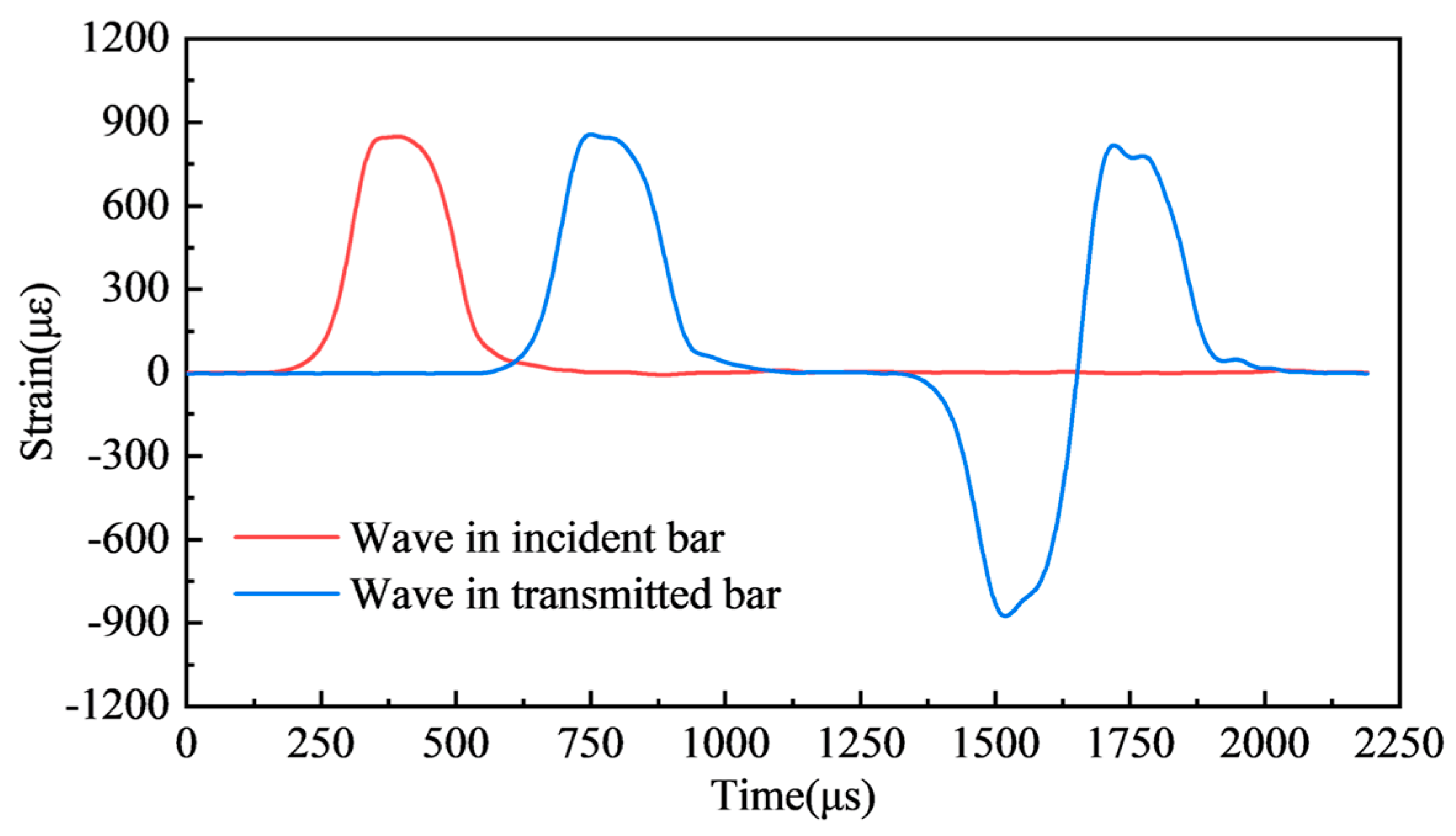
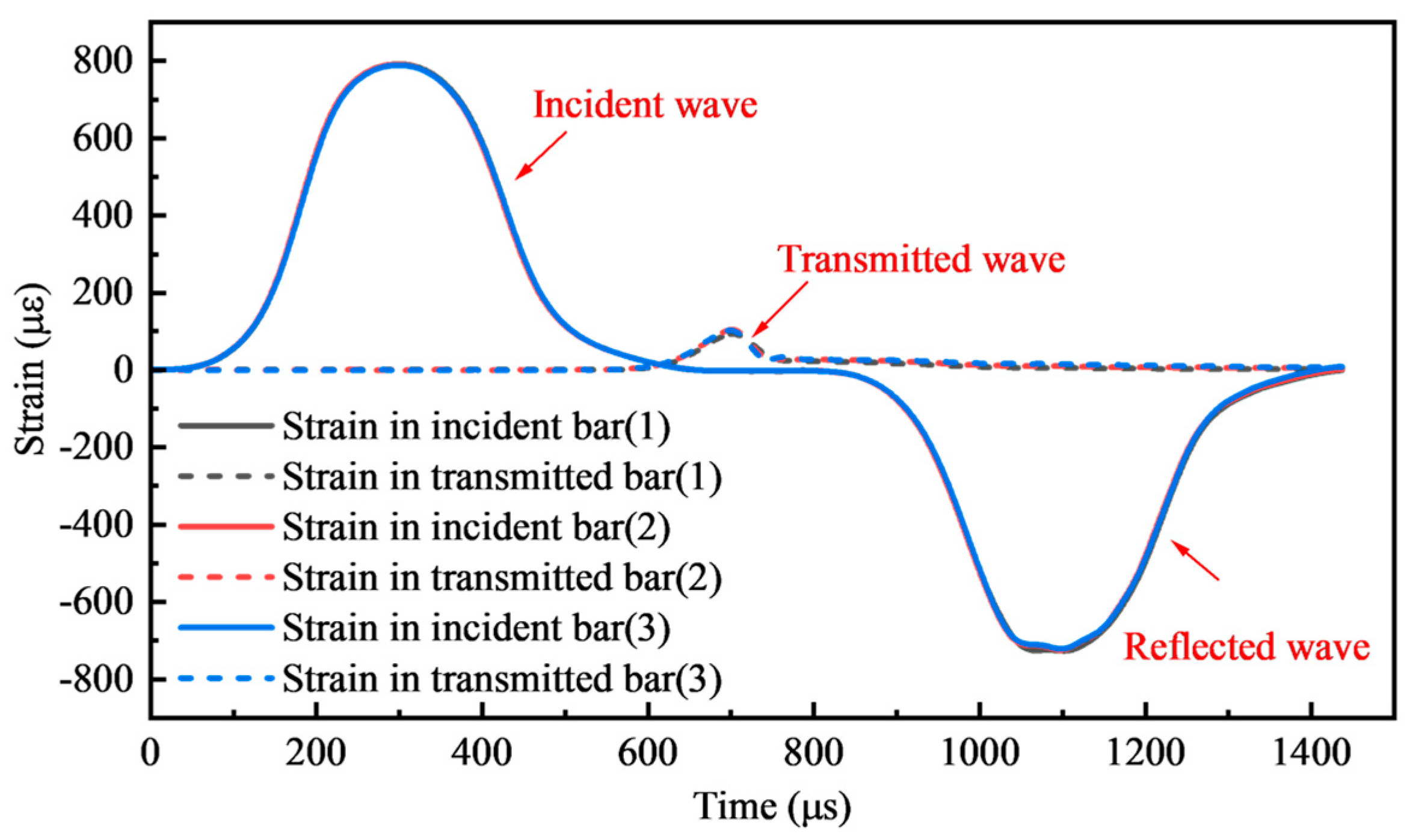
3.1. Validity and Strain Rate Determination of the Test
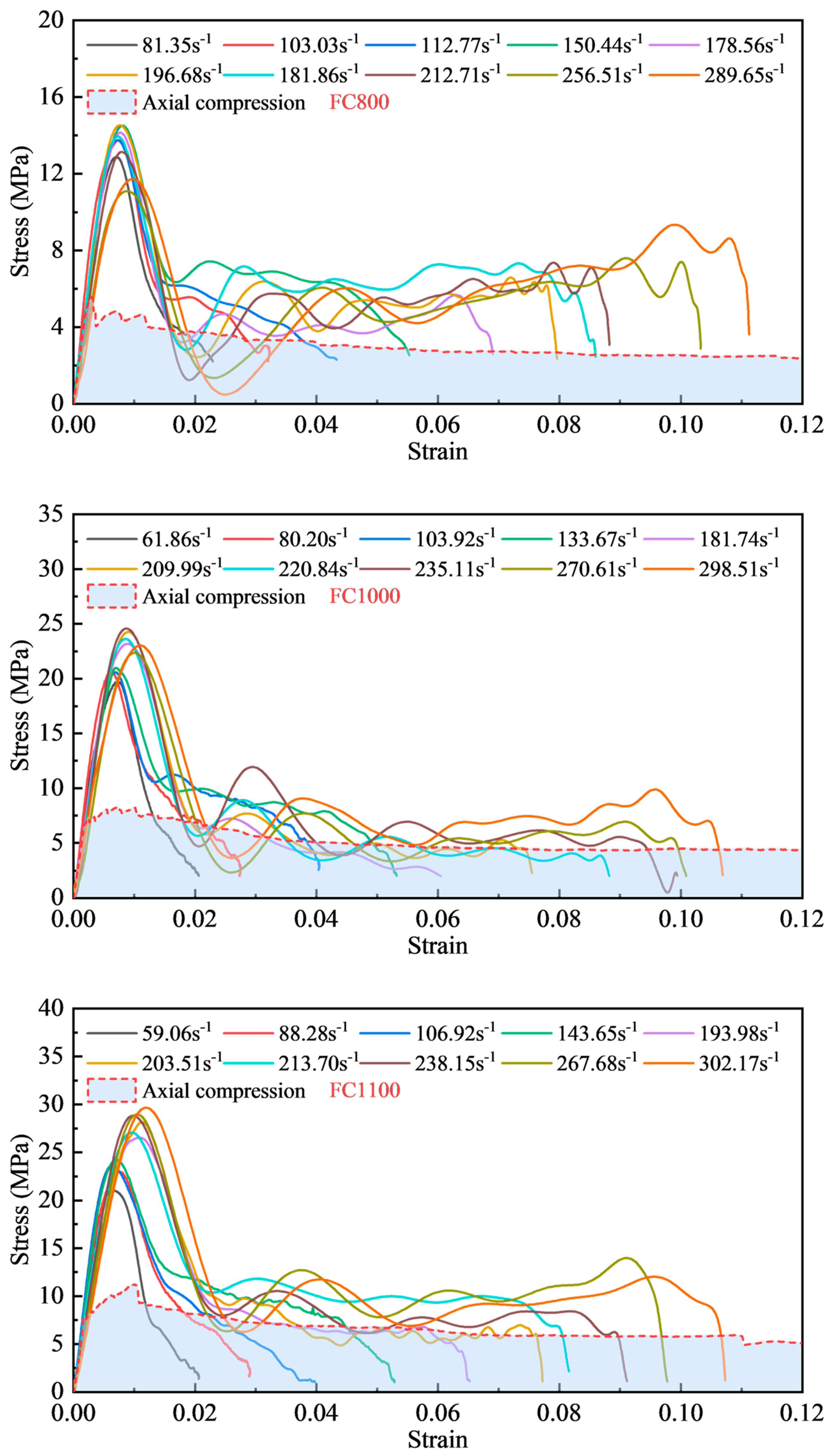
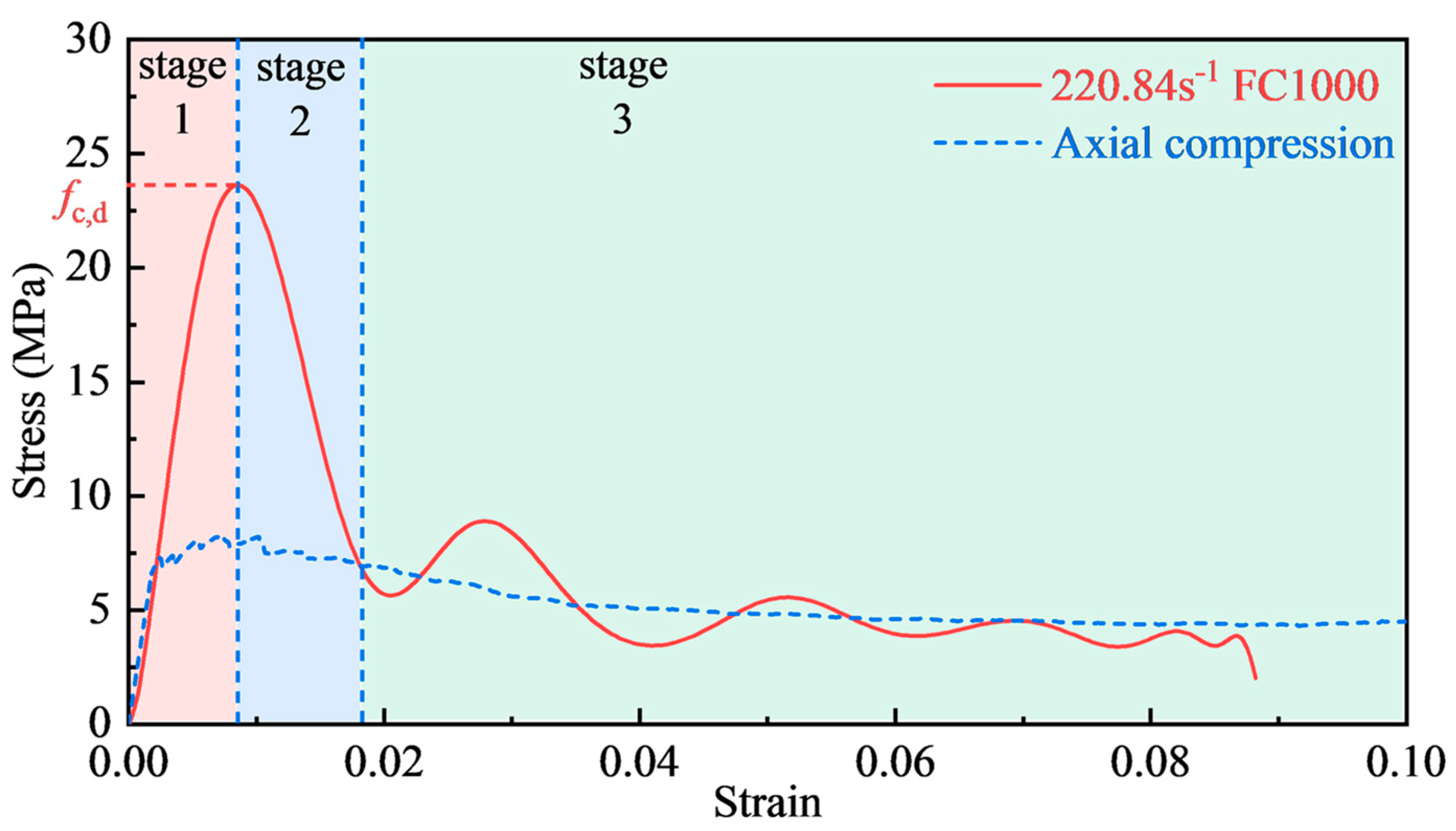
3.2. Dynamic Stress–Strain Curves
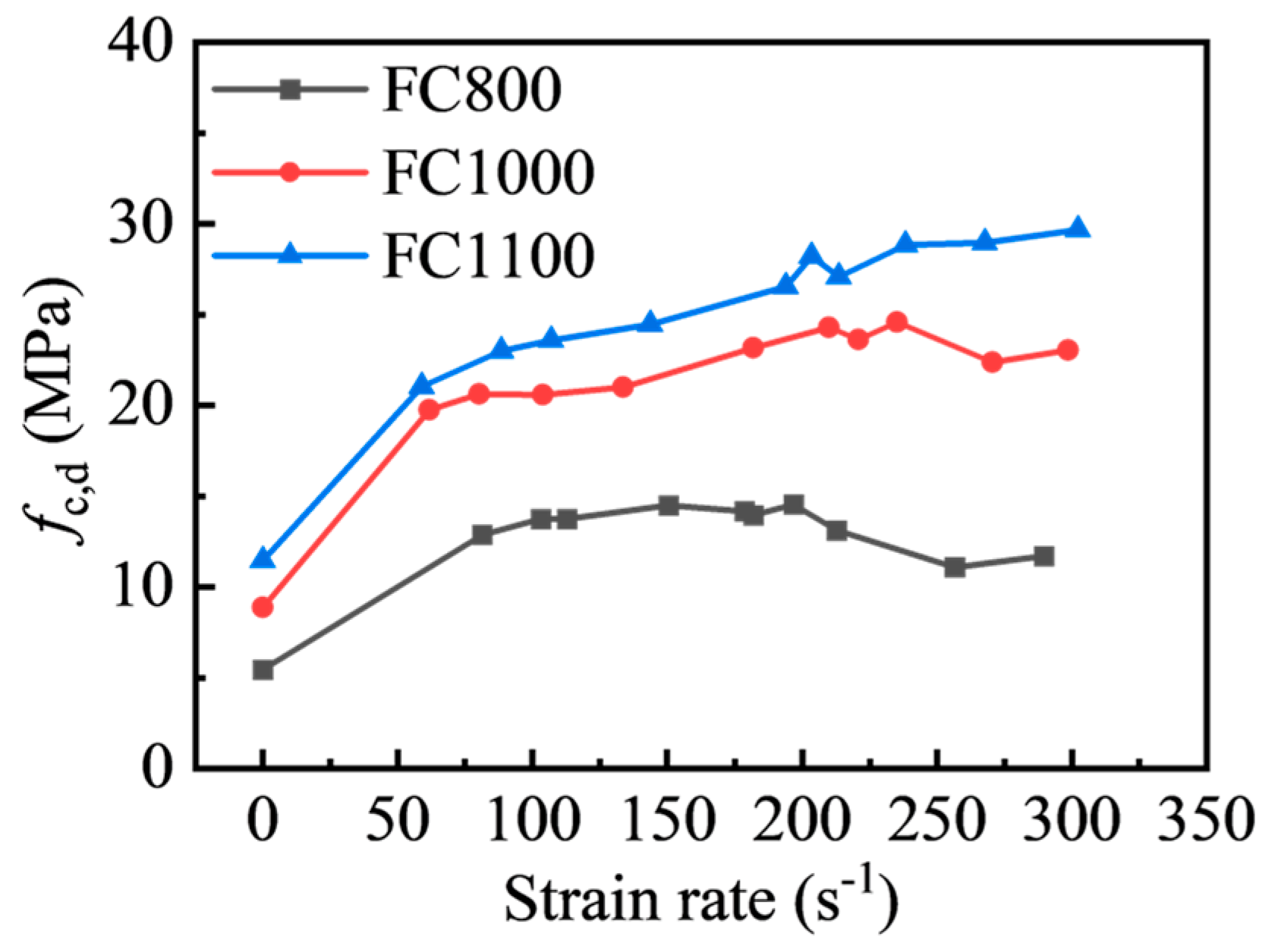
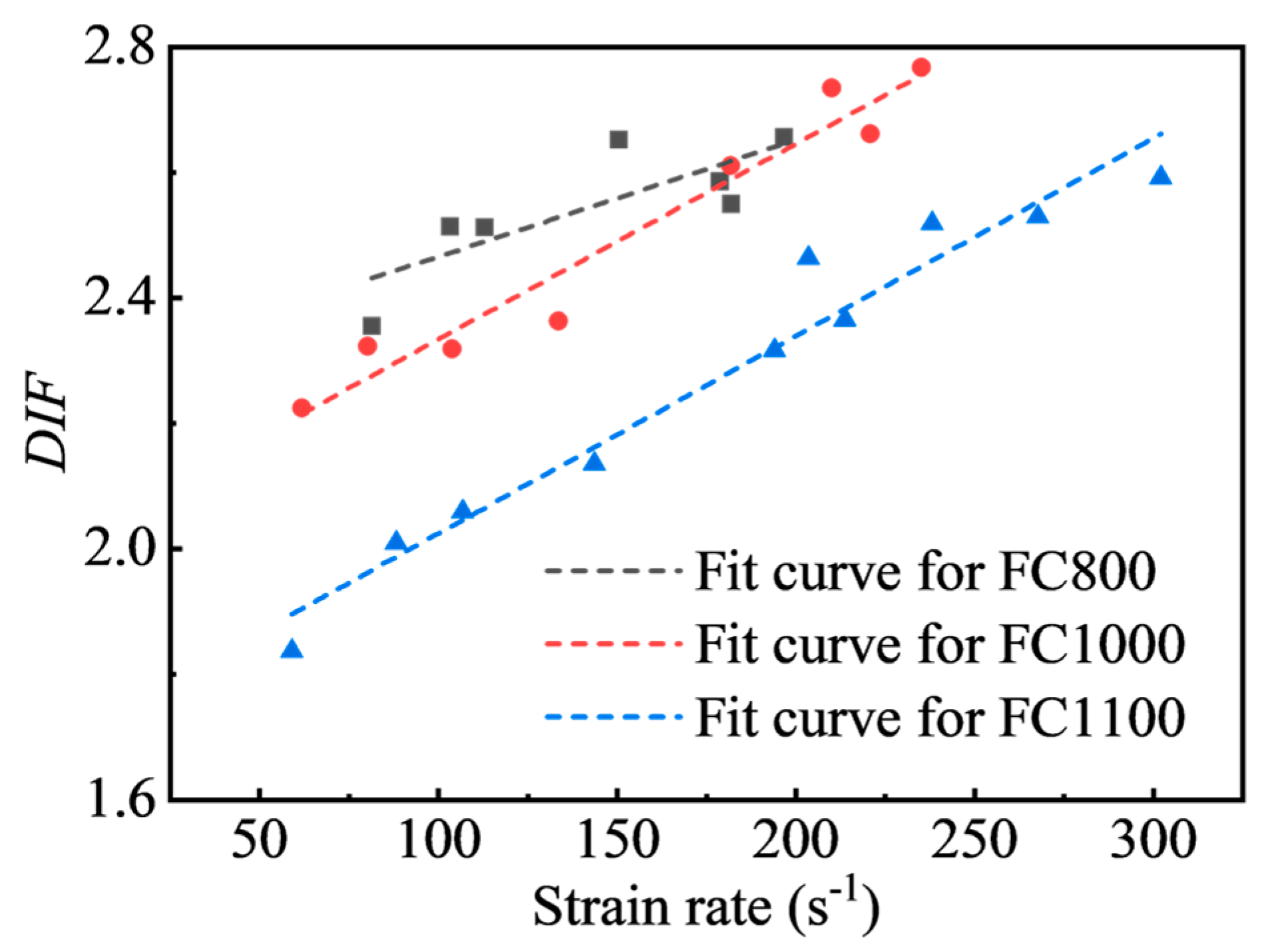
3.3. Dynamic Properties of Foamed Concrete
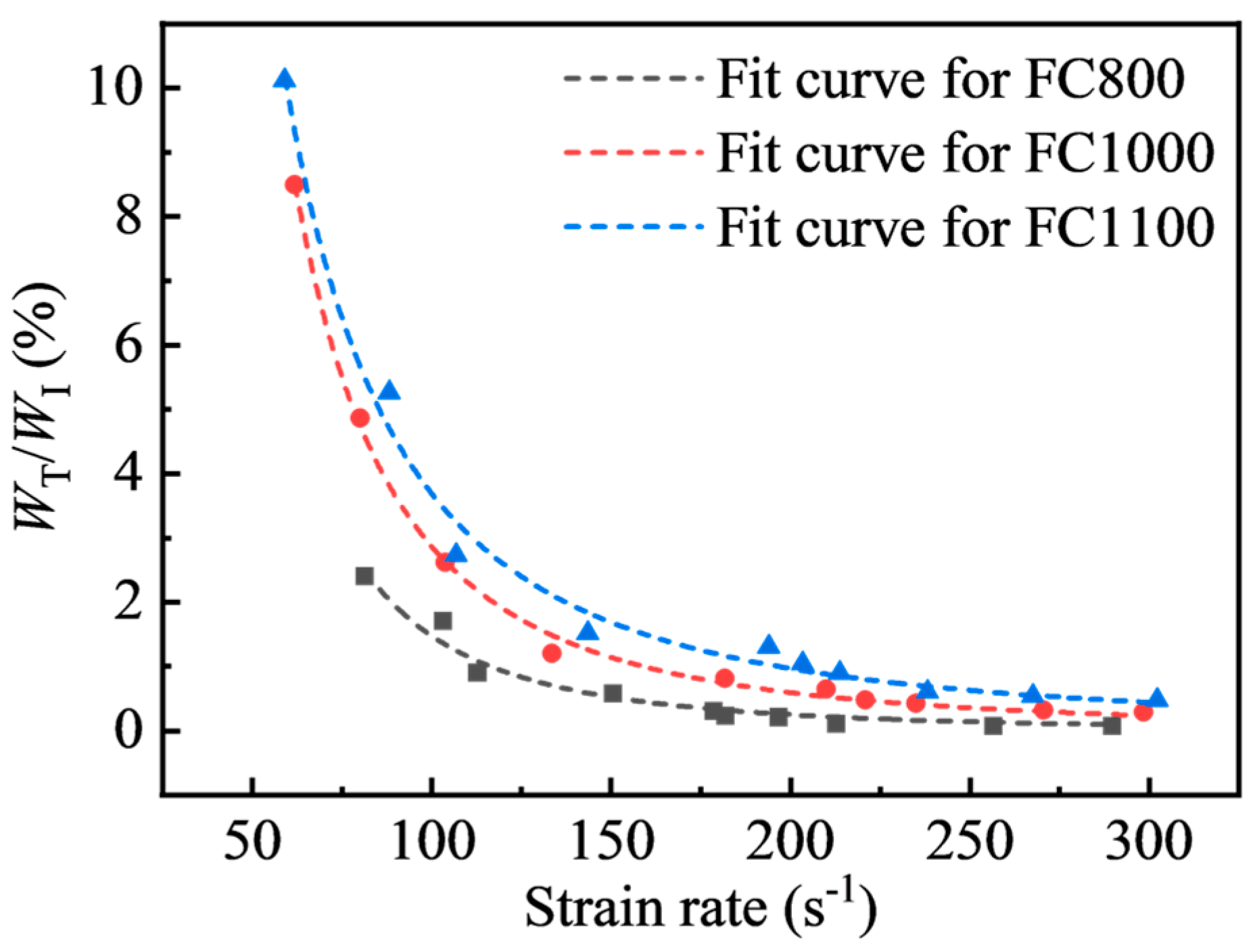
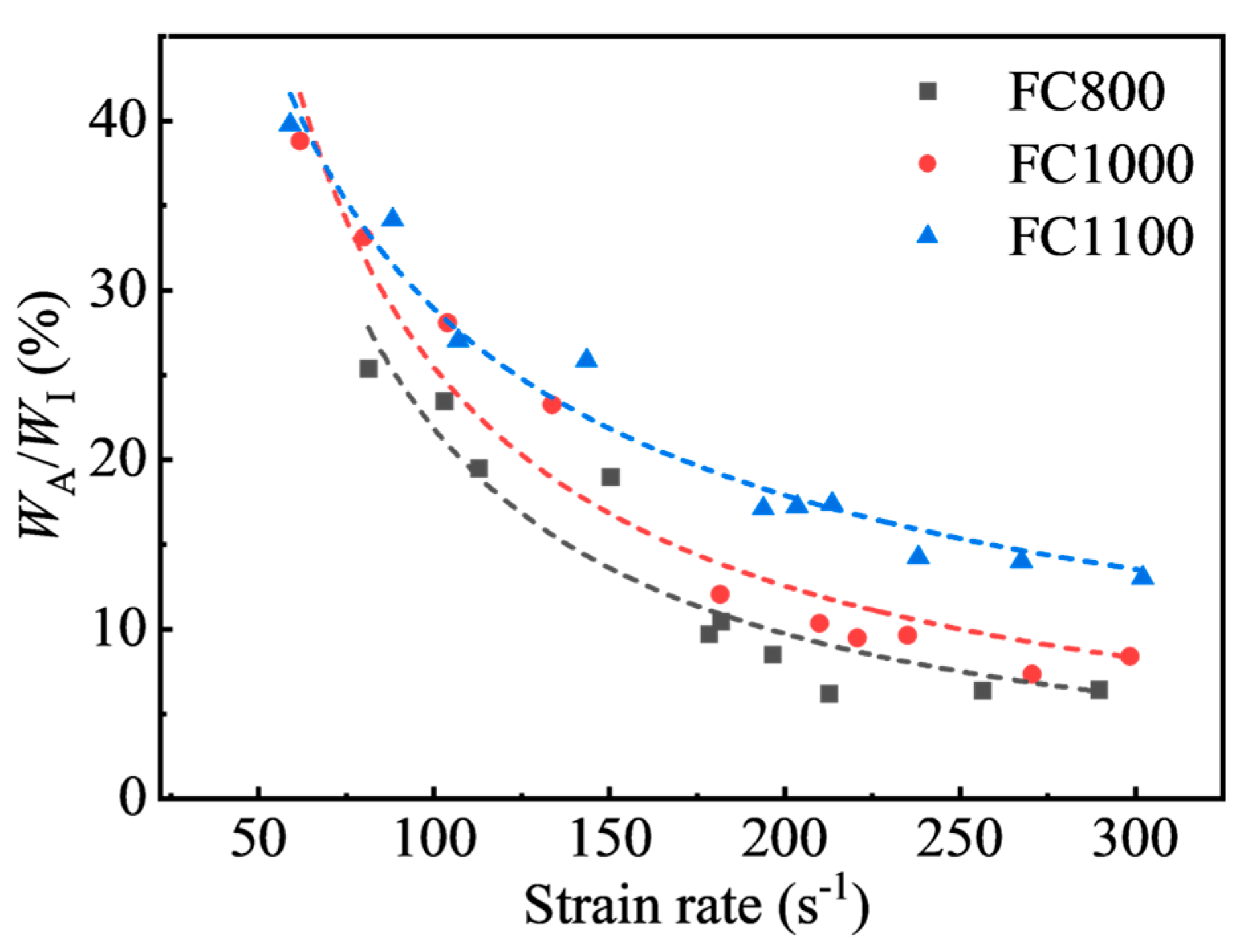
3.4. Energy Absorption Characteristic
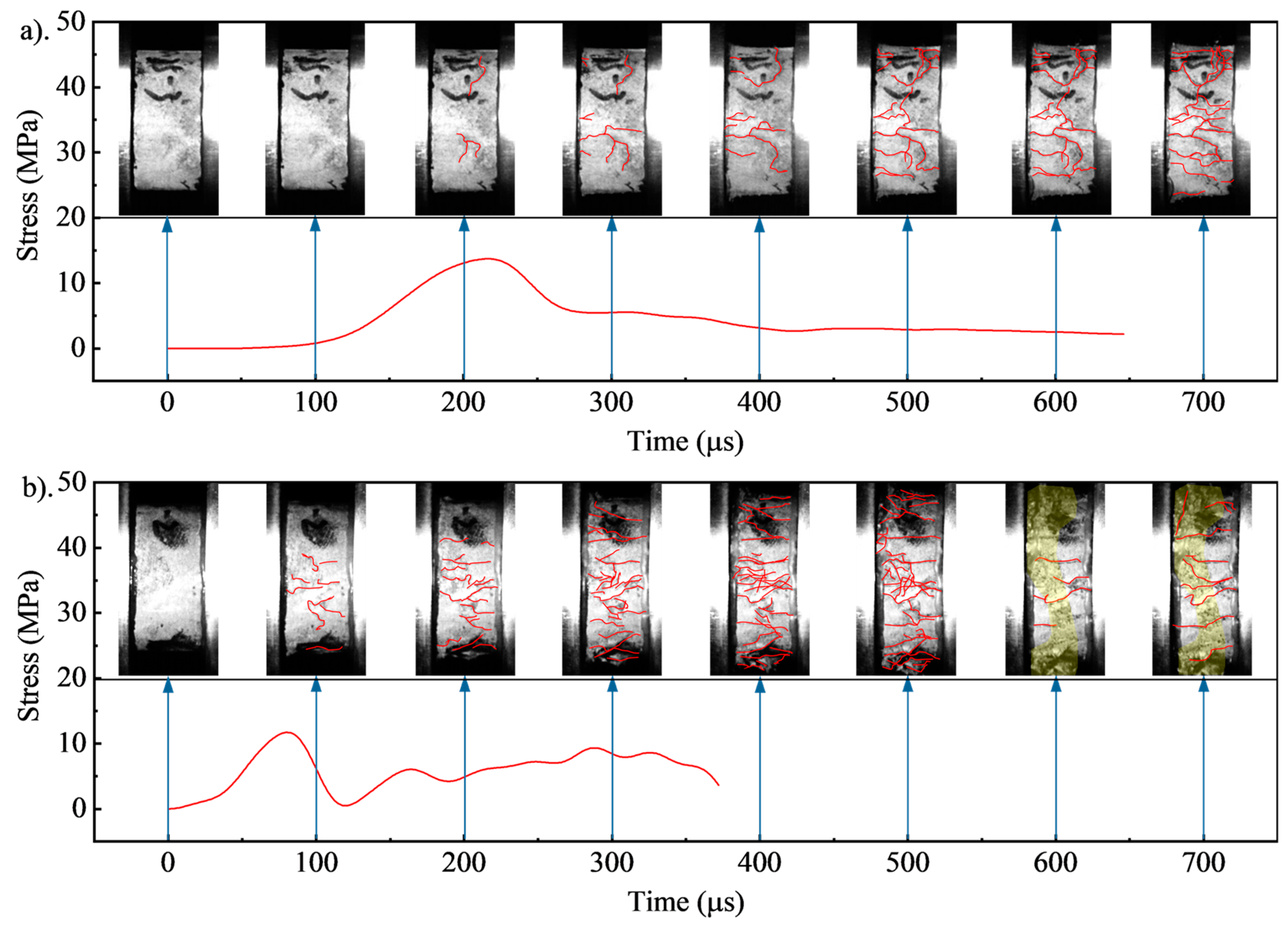
3.5. Failure Process and Patterns
4. Conclusions
- (1)
- The dynamic stress–strain curves of foamed concrete include elastic deformation, decreasing stress, and residual stress stages.
- (2)
- The dynamic compressive strength of foam concrete shows a substantial strain rate correlation, which is much higher than the static compressive strength in the test strain rate range of 59.05 s−1~302.17 s−1. Within the tested strain rate range, the dynamic increase factor of foamed concrete can be expressed by a linear function of the strain rate.
- (3)
- Foamed concrete can effectively prevent energy transmission with a maximum energy transmission coefficient of 10.12%, and the transmission coefficient shows exponential decay as the strain rate rises. Meanwhile, the transmission coefficient declines with increasing dry density. Moreover, the energy absorption efficiency of foamed concrete reduces steadily with increasing strain rate, and the maximum energy absorption rate of foamed concrete is 25.37%, 38.79%, and 39.75% for FC800, FC1000, and FC1100, respectively.
- (4)
- The strain rate considerably affects the failure process and failure modes of foamed concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Amran, Y.H.M.; Farzadnia, N.; Abang Ali, A.A. Properties and Applications of Foamed Concrete; A Review. Constr. Build. Mater. 2015, 101, 990–1005. [Google Scholar] [CrossRef]
- Jones, M.R.; McCarthy, A. Preliminary Views on the Potential of Foamed Concrete as a Structural Material. Mag. Concr. Res. 2005, 57, 21–31. [Google Scholar] [CrossRef]
- Shang, X.; Qu, N.; Li, J. Development and Functional Characteristics of Novel Foam Concrete. Constr. Build. Mater. 2022, 324, 126666. [Google Scholar] [CrossRef]
- Nambiar, E.K.K.; Ramamurthy, K. Air-Void Characterisation of Foam Concrete. Cem. Concr. Res. 2007, 37, 221–230. [Google Scholar] [CrossRef]
- Wee, T.; Daneti, S.B.; Tamilselvan, T. Effect of W/C Ratio on Air-Void System of Foamed Concrete and their Influence on Mechanical Properties. Mag. Concr. Res. 2011, 63, 583–595. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, H.; Lv, B.; Du, C.; Wang, J. Investigation on the Yield and Failure Criterion of Foamed Concrete. J. Build. Eng. 2024, 84, 108604. [Google Scholar] [CrossRef]
- Guo, H.; Guo, W.; Shi, Y. Computational Modeling of the Mechanical Response of Lightweight Foamed Concrete over a Wide Range of Temperatures and Strain Rates. Constr. Build. Mater. 2015, 96, 622–631. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Wang, Y.B.; Wang, X.J.; Shi, N.N. Size Effect of Foam Concrete Subjected to Quasi-static Compression. Mater. Rev. 2021, 35, 18076–18082. [Google Scholar]
- Zhang, Z.; Rao, F.; Ye, G.; Liu, J. Mechanical Performance and Void Structure Change of Foamed Cement Paste Subjected to Static and Cyclic Loading Under Plane Strain Conditions. Materials 2022, 15, 1711. [Google Scholar] [CrossRef]
- Song, Y.; Lange, D. Influence of Fine Inclusions on the Morphology and Mechanical Performance of Lightweight Foam Concrete. Cem. Concr. Compos. 2021, 124, 104264. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Li, Q.M. Structural Behaviour of Composite Sandwich Panels with Plain and Fibre-Reinforced Foamed Concrete Cores and Corrugated Steel Faces. Compos. Struct. 2012, 94, 1555–1563. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, T.; Qu, B.; Fang, C.; Li, L.; Feng, Y.; Jiang, G.; Yu, Y. Experimental Investigation On the Effect of Nano Silica Fume On Physical Properties and Microstructural Characteristics of Lightweight Cement Slurry. Constr. Build. Mater. 2022, 329, 127172. [Google Scholar] [CrossRef]
- Su, Y.; Choi, C.E.; Ng, C.W.W.; Lam, H.W.K.; Wong, L.A.; Lee, C. New Light-Weight Concrete Foam to Absorb Debris-Flow-Entrained Boulder Impact: Large-Scale Pendulum Modelling. Eng. Geol. 2020, 275, 105724. [Google Scholar] [CrossRef]
- Guo, Q.; Gou, Y.; Chen, J.; Zhang, Y.; Zhou, Y. Dynamic Response of Foam Concrete Under Low-Velocity Impact: Experiments and Numerical Simulation. Int. J. Impact Eng. 2020, 146, 103693. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Yang, J.L. Improving Safety of Runway Overrun through Foamed Concrete Aircraft Arresting System: An Experimental Study. Int. J. Crashworthiness 2015, 20, 448–463. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Yang, J.L.; Li, Q.M. An Analytical Model of Foamed Concrete Aircraft Arresting System. Int. J. Impact Eng. 2013, 61, 1–12. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Yu, F.; Yang, Y.; Huang, Z.; Ding, Y. Evaluation of in-Plane Crushing Performance of Printed Randomly Polymeric Honeycombs Filled with Foamed Concrete. Constr. Build. Mater. 2021, 310, 125291. [Google Scholar] [CrossRef]
- Baziar, M.H.; Shahnazari, H.; Kazemi, M. Mitigation of Surface Impact Loading Effects on the Underground Structures with Geofoam Barrier: Centrifuge Modeling. Tunn. Undergr. Space Technol. 2018, 80, 128–142. [Google Scholar] [CrossRef]
- Hongyuan, Z.; Yongsheng, L.I.; Xiaojuan, W.; Jianguo, D.U.; Shangjiang, Y.U.; Ronghua, C. Flexible Protection of Underground Structures with Foam Concrete Subjected to Ground Shocks. J. Beijing Univ. Technol. 2020, 46, 533–539. [Google Scholar]
- Jones, M.R.; Zheng, L. Energy Absorption of Foamed Concrete From Low-Velocity Impacts. Mag. Concr. Res. 2013, 65, 209–219. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Y.; Fan, H.; Jin, F. Investigation of Low-Velocity Impact Behaviors of Foamed Concrete Material. Compos. Part B Eng. 2019, 162, 491–499. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, Y.; Li, Q.M. Damage Behavior and Energy Absorption Characteristics of Foamed Concrete Under Dynamic Load. Constr. Build. Mater. 2022, 357, 129340. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, Y.; Wang, Y.; Lei, M. Experimental Research On the Dynamic Mechanical Properties and Damage Characteristics of Lightweight Foamed Concrete Under Impact Loading. Int. J. Impact Eng. 2020, 140, 103558. [Google Scholar] [CrossRef]
- Ma, K.; Ren, F.; Huang, H.; Yang, X.; Zhang, F. Experimental Investigation on the Dynamic Mechanical Properties and Energy Absorption Mechanism of Foam Concrete. Constr. Build. Mater. 2022, 342, 127927. [Google Scholar] [CrossRef]
- Haijian, H.; Nengping, G.; Chaomin, M.U.; Hui, Z.; Wei, L. Dynamic Mechanical Properties and Constitutive Relation of Foam Concrete. J. Build. Mater. 2020, 23, 466–472. [Google Scholar]
- Yuan, P.; Ma, Q.Y.; Zhang, H.D. SHPB tests for light weight foam concrete. J. Vib. Shock. 2014, 33, 116–119. [Google Scholar]
- Liu, H.Y.; Li, R. Experimental Study on Endergonic Mechanism of Foam Concrete. J. Chengdu Univ. 2010, 29, 166–167. [Google Scholar]
- ASTM D1621-16; Standard Test Method for Compressive Properties of Rigid Cellular Plastics. ASTM: West Conshohocken, PA, USA, 2004.
- Bai, E.L.; Xu, J.Y.; Lu, S.; Lin, K.X.; Zhang, Y.M. Comparative Study On the Dynamic Properties of Lightweight Porous Concrete. RSC Adv. 2018, 8, 14454–14461. [Google Scholar] [CrossRef]
- Chen, W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hassan, M.; Wille, K. Experimental Impact Analysis On Ultra-High Performance Concrete (UHPC) for Achieving Stress Equilibrium (SE) and Constant Strain Rate (CSR) in Split Hopkinson Pressure Bar (SHPB) Using Pulse Shaping Technique. Constr. Build. Mater. 2017, 144, 747–757. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Wang, J.; Wang, Z.; Zhao, Q.; Zhu, L.; Wei, W.; Gao, Z. Study On Dynamic Compressive Mechanical Properties of Freeze-Thaw Concrete. Constr. Build. Mater. 2022, 322, 126499. [Google Scholar] [CrossRef]
- Zilong, Z.; Xin, C.; Xibing, L.; Cao, W.; Xueming, D. Dynamic Response and Energy Evolution of Sandstone Under Coupled Static-Dynamic Compression; Insights From Experimental Study Into Deep Rock Engineering Applications. Rock Mech. Rock Eng. 2020, 53, 1305–1331. [Google Scholar]
- Guo, J.; Chen, Q.; Chen, W.; Cai, J. Tests and Numerical Studies On Strain-Rate Effect On Compressive Strength of Recycled Aggregate Concrete. J. Mater. Civ. Eng. 2019, 31, 4019281. [Google Scholar] [CrossRef]
- Grote, D.L.; Park, S.W.; Zhou, M. Dynamic Behavior of Concrete at High Strain Rates and Pressures: I. Experimental Characterization. Int. J. Impact Eng. 2001, 25, 869–886. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H.; Khan, M.Z.N.; Pham, T.M. Dynamic Compressive Properties of Novel Lightweight Ambient-Cured EPS Geopolymer Composite. Constr. Build. Mater. 2021, 273, 122044. [Google Scholar] [CrossRef]

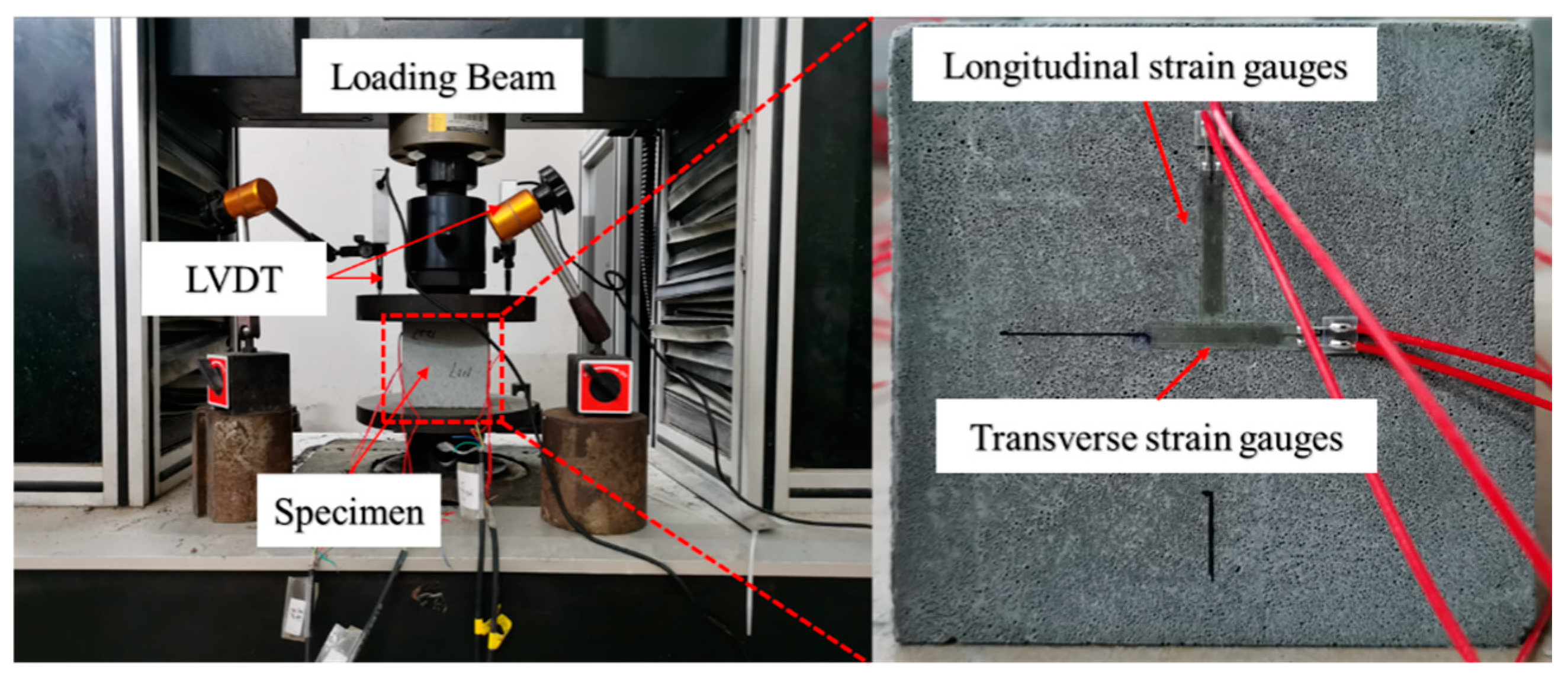
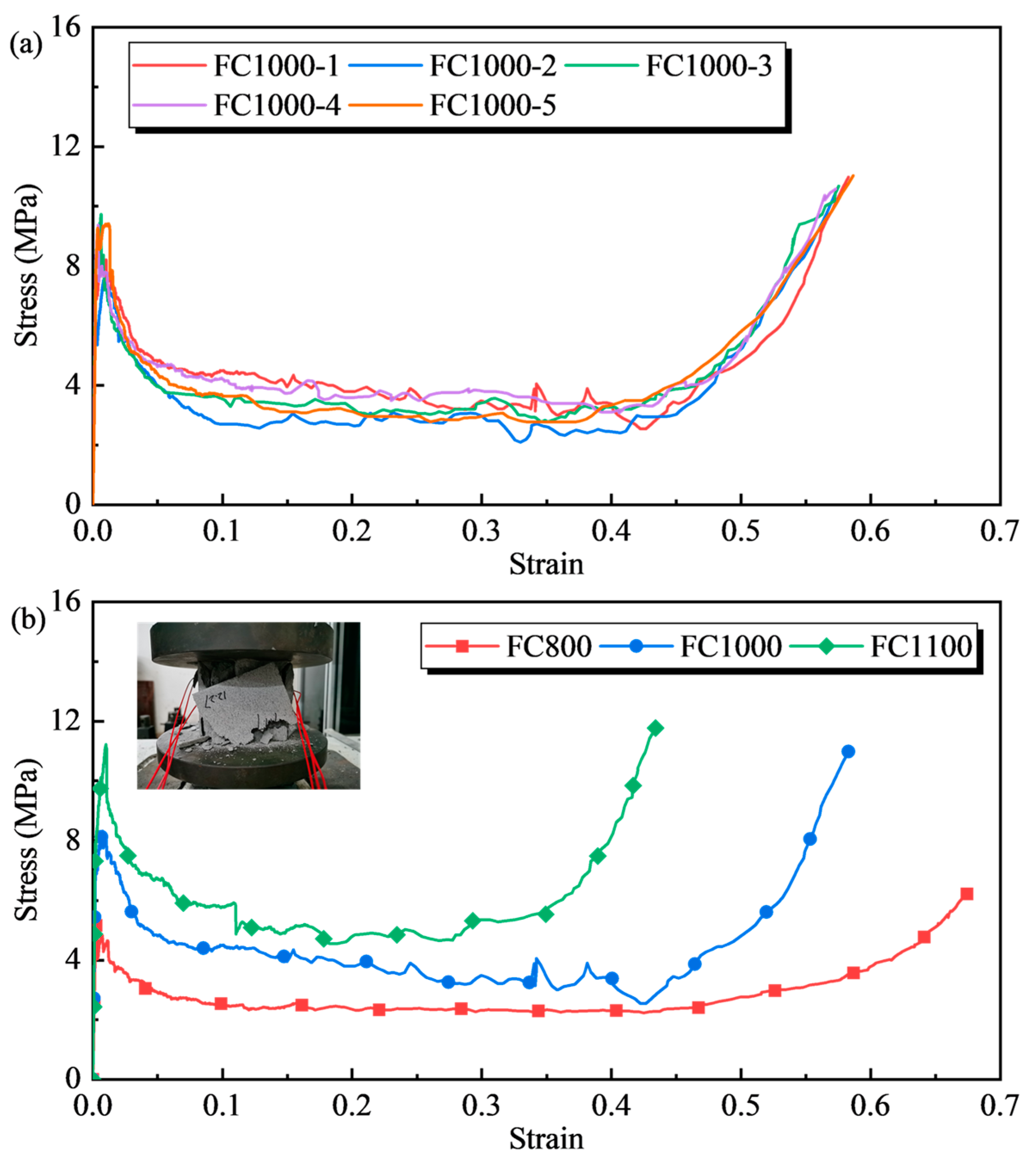
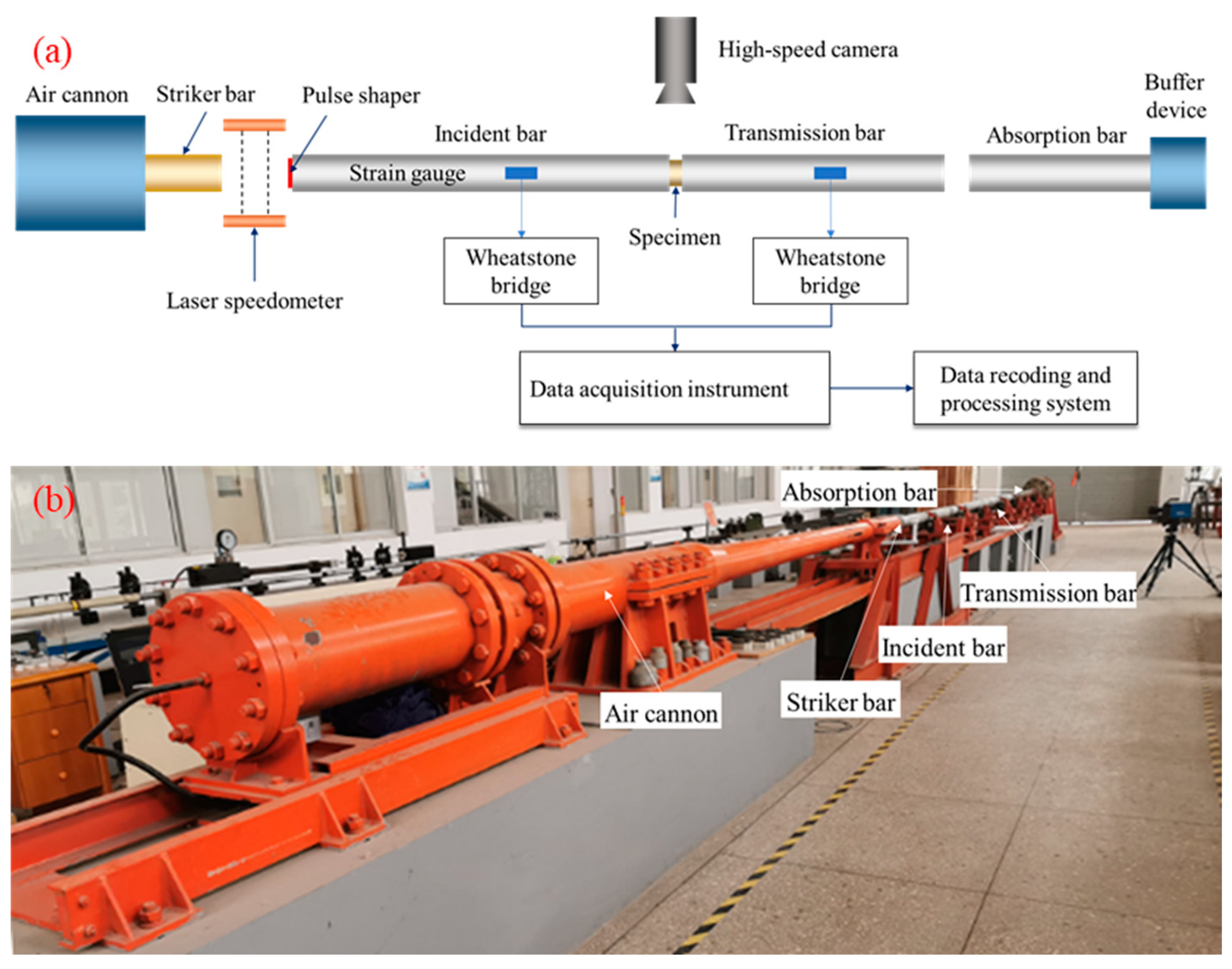



| Group 1 | Component (kg/m3) | ||||
|---|---|---|---|---|---|
| Cement | Fly Ash | Water-Reducing Agent | Foaming Agent | Water | |
| FC800 | 436.0 | 218.0 | 2.6 | 0.389 | 179.7 |
| FC1000 | 560.0 | 240.0 | 4.5 | 0.360 | 201.8 |
| FC1100 | 600.0 | 300.0 | 3.6 | 0.341 | 245.1 |
| Materials | Physical Properties | Manufacturer |
|---|---|---|
| Cement | P.O 42.5R (GB 175-2007) Density = 3100 kg/m3 | Guangzhou Zhujiang Cement Co., Ltd., Guangzhou, China |
| Fly ash | Class II (GB/T 50146-2014) Density = 2.28 kg/m3 Fineness = 1.5% | Guangzhou Pearl River Power Plant, Guangzhou, China |
| Foaming agent | HTL-I Expansion ratio = 26 Defoaming time = 6.5 h | Huatai Building Materials Co., Ltd., Henan, China |
| Water-reducing agent | QL-PC2 Concentration = 16% Water-reducing rate = 25% | Qiangli Construction Materials Co., Ltd., Guangzhou, China |
| Group | ρ /kg·m3 | SD-ρ | fc,s /MPa | SD-fc,s | E /GPa | SD-E | μ | SD-μ |
|---|---|---|---|---|---|---|---|---|
| FC800 | 814 | 4.32 | 5.47 | 0.24 | 2.678 | 0.193 | 0.28 | 0.009 |
| FC1000 | 1009 | 10.96 | 8.88 | 0.92 | 3.676 | 0.261 | 0.28 | 0.005 |
| FC1100 | 1105 | 10.71 | 11.45 | 0.64 | 4.549 | 0.159 | 0.28 | 0.005 |
| Group | ρ (kg/m3) | P (MPa) | v (m/s) | (s−1) | fc,d (MPa) | DIF | WI (J) | WR (J) | WT (J) | WA (J) |
|---|---|---|---|---|---|---|---|---|---|---|
| FC800-0.08 | 775.33 | 0.08 | 4.27 | 81.35 | 12.886 | 2.356 | 86.58 | 62.53 | 2.08 | 21.97 |
| FC800-0.10 | 771.44 | 0.1 | 5.34 | 103.03 | 13.752 | 2.514 | 137.44 | 102.79 | 2.36 | 32.29 |
| FC800-0.15 | 778.79 | 0.15 | 6.99 | 112.77 | 13.747 | 2.513 | 223.11 | 177.55 | 2.04 | 43.52 |
| FC800-0.20 | 766.21 | 0.2 | 8.44 | 150.44 | 14.511 | 2.653 | 357.68 | 287.71 | 2.10 | 67.87 |
| FC800-0.25 | 777.46 | 0.25 | 9.61 | 178.56 | 14.149 | 2.587 | 540.53 | 486.33 | 1.68 | 52.51 |
| FC800-0.30 | 776.58 | 0.3 | 11.54 | 196.68 | 14.533 | 2.657 | 713.77 | 651.56 | 1.57 | 60.65 |
| FC800-0.35 | 781.31 | 0.35 | 11.89 | 181.86 | 13.950 | 2.550 | 819.36 | 731.91 | 1.92 | 85.53 |
| FC800-0.40 | 788.79 | 0.4 | 14.08 | 212.71 | 13.139 | 2.402 | 1024.13 | 959.46 | 1.13 | 63.54 |
| FC800-0.45 | 765.24 | 0.45 | 15.00 | 256.51 | 11.096 | 2.029 | 1200.09 | 1122.51 | 0.97 | 76.61 |
| FC800-0.50 | 772.11 | 0.5 | 16.63 | 289.65 | 11.719 | 2.142 | 1347.35 | 1259.58 | 1.07 | 86.69 |
| FC1000-0.08 | 1037.89 | 0.08 | 4.02 | 61.86 | 19.751 | 2.224 | 73.30 | 38.64 | 6.22 | 28.44 |
| FC1000-0.10 | 984.75 | 0.1 | 5.00 | 80.2 | 20.625 | 2.323 | 120.18 | 74.51 | 5.84 | 39.82 |
| FC1000-0.15 | 983.57 | 0.15 | 7.07 | 103.92 | 20.593 | 2.319 | 217.48 | 150.73 | 5.70 | 61.05 |
| FC1000-0.20 | 975.15 | 0.2 | 8.49 | 133.67 | 20.981 | 2.363 | 357.06 | 269.81 | 4.31 | 82.94 |
| FC1000-0.25 | 1038.64 | 0.25 | 9.64 | 181.74 | 23.179 | 2.610 | 538.21 | 468.92 | 4.40 | 64.90 |
| FC1000-0.30 | 1028.55 | 0.3 | 10.63 | 209.99 | 24.279 | 2.734 | 705.50 | 628.03 | 4.57 | 72.90 |
| FC1000-0.35 | 1031.96 | 0.35 | 11.89 | 220.84 | 23.630 | 2.661 | 860.95 | 775.45 | 4.08 | 81.41 |
| FC1000-0.40 | 1038.64 | 0.4 | 13.83 | 235.11 | 24.577 | 2.768 | 1034.55 | 930.62 | 4.39 | 99.55 |
| FC1000-0.45 | 982.14 | 0.45 | 15.26 | 270.61 | 22.357 | 2.518 | 1176.70 | 1086.83 | 3.77 | 86.09 |
| FC1000-0.50 | 989.3 | 0.5 | 16.64 | 298.51 | 23.038 | 2.594 | 1356.79 | 1239.42 | 3.88 | 113.49 |
| FC1100-0.08 | 1097.7 | 0.08 | 4.17 | 59.06 | 21.034 | 1.837 | 75.68 | 37.93 | 7.66 | 30.09 |
| FC1100-0.10 | 1081.95 | 0.1 | 5.32 | 88.28 | 23.004 | 2.009 | 138.23 | 83.71 | 7.27 | 47.25 |
| FC1100-0.15 | 1095.47 | 0.15 | 6.71 | 106.92 | 23.579 | 2.059 | 224.26 | 157.56 | 6.13 | 60.57 |
| FC1100-0.20 | 1101.19 | 0.2 | 8.40 | 143.65 | 24.449 | 2.135 | 362.52 | 263.35 | 5.50 | 93.66 |
| FC1100-0.25 | 1112.37 | 0.25 | 9.60 | 193.98 | 26.527 | 2.317 | 543.60 | 443.37 | 7.09 | 93.14 |
| FC1100-0.30 | 1099.4 | 0.3 | 10.46 | 203.51 | 28.201 | 2.463 | 698.26 | 570.59 | 7.33 | 120.34 |
| FC1100-0.35 | 1078.39 | 0.35 | 11.94 | 213.7 | 27.076 | 2.365 | 827.17 | 675.98 | 7.41 | 143.79 |
| FC1100-0.40 | 1097.54 | 0.4 | 14.06 | 238.15 | 28.834 | 2.518 | 1016.76 | 865.85 | 6.20 | 144.71 |
| FC1100-0.45 | 1075.87 | 0.45 | 15.21 | 267.68 | 28.958 | 2.529 | 1186.95 | 1014.19 | 6.43 | 166.33 |
| FC1100-0.50 | 1105.74 | 0.5 | 16.58 | 302.17 | 29.671 | 2.591 | 1374.99 | 1189.18 | 6.54 | 179.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; He, Y.; Zhi, X. Experimental Research on Dynamic Mechanical Properties of High-Density Foamed Concrete. Materials 2024, 17, 4781. https://doi.org/10.3390/ma17194781
Guo M, He Y, Zhi X. Experimental Research on Dynamic Mechanical Properties of High-Density Foamed Concrete. Materials. 2024; 17(19):4781. https://doi.org/10.3390/ma17194781
Chicago/Turabian StyleGuo, Menghui, Yongsheng He, and Xudong Zhi. 2024. "Experimental Research on Dynamic Mechanical Properties of High-Density Foamed Concrete" Materials 17, no. 19: 4781. https://doi.org/10.3390/ma17194781
APA StyleGuo, M., He, Y., & Zhi, X. (2024). Experimental Research on Dynamic Mechanical Properties of High-Density Foamed Concrete. Materials, 17(19), 4781. https://doi.org/10.3390/ma17194781






