Next Article in Journal
Single-Atom Underpotential Deposition at Specific Sites of N-Doped Graphene for Hydrogen Evolution Reaction Electrocatalysis
Previous Article in Journal
Overlooked Ionic Contribution of a Chiral Dopant in Cholesteric Liquid Crystals
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 17
Issue 20
10.3390/ma17205081
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Accuracy of Point Load Index and Brazilian Tensile Strength in Predicting the Uniaxial Compressive Strength of the Rocks: A Comparative Study

by
Amin Jamshidi
1 and
Luís Sousa
2,*
1
Department of Geology, Faculty of Basic Sciences, Lorestan University, Khorramabad 681151-44316, Iran
2
Department of Geology and Pole of Geosciences Center, University of Trás-os-Montes e Alto Douro, 5000-801 Vila Real, Portugal
*
Author to whom correspondence should be addressed.
Materials 2024, 17(20), 5081; https://doi.org/10.3390/ma17205081
Submission received: 10 September 2024 / Revised: 5 October 2024 / Accepted: 9 October 2024 / Published: 18 October 2024
(This article belongs to the Section Construction and Building Materials)
Browse Figures
Versions Notes

Abstract

:
Uniaxial compressive strength (UCS) of rocks is one of the main parameters required in the design of geotechnical projects such as tunnels, dams, or rock slopes. According to the literature, there are a large number of predictive regression equations to evaluate the UCS from the point load index (PLI) and Brazilian tensile strength (BTS). However, the equations developed in previous studies have different accuracies in UCS prediction. A more accurate prediction of the UCS will result in a more appropriate design of the geotechnical project, and thus ensure its success during operation. In the present paper, a comparative study was conducted between the accuracy of PLI and BTS in predicting the UCS of the limestone and sandstone. Moreover, the role of porosity (n) on the accuracy of predicting the UCS from PLI and BTS was investigated. Some statistical indices were used to investigating the accuracy of predictive regression equations of UCS. The results revealed that the UCS of rocks can be predicted with a higher accuracy using BTS compared with PLI. Also, the findings showed that the n had a significant role in increasing the accuracy of PLI- and BTS-based regression equations of the UCS predictive. The predictive equations established in the present study can be used in practical applications for indirect evaluation of limestone and sandstone UCS in the site of a geotechnical project.

1. Introduction

In many geotechnical projects such as tunnels, concrete dams, or rock slopes, rocks act as foundations or surrounding materials. The strength characteristics of the rocks are among the key parameters in designing geotechnical projects. Ignoring or not paying enough attention to these characteristics can lead to design errors, and consequently the failure of the project. Any failure in the geotechnical project will result in financial loss or even loss of life. Therefore, an accurate evaluation of the rock strength characteristics and their incorporation as design parameters will increase the success of the geotechnical project during its serviceability.
The uniaxial compressive strength (UCS) is one of the most important and common of the strength characteristics of the rocks, which is used among the input parameters in the design of many geotechnical projects [1,2,3]. The well-known method of measuring the rock UCS is through the laboratory test in accordance with the guidelines provided in the international standards of the International Society for Rock Mechanics (ISRM) [4] and American Society for Testing and Materials (ASTM) [5]. In order to meet the requirements of the aforementioned standards, the specimens required to perform the UCS test must have specific dimensions in the geometric shapes of cylindrical cores or cubes. For some sedimentary rocks containing lamination (such as sandstone and shale), foliated metamorphic rocks (such as slate and schist) and highly weathered rocks such as granite, it is not possible to prepare specimens with the desired dimensions to perform the UCS testing.
A rough assessment of rock UCS is usually required in the preliminary stages of site investigation for a geotechnical project. Therefore, even if it is possible to prepare test specimens, in these steps it will not be necessary to carry out the UCS test. In this situation, indirect tools can be very valuable for a rapid evaluation of rock UCS without performing UCS laboratory tests. Regression equations are among the most common of the practical tools used in previous studies for the indirect evaluation of rock UCS. In regression equations, UCS can be predicted from other inherent characteristics of rocks such as mineralogical composition [6,7,8,9], density (ρ) [10,11], porosity (n) [2,12], water absorption (Wa) [13], point load index (PLI) [14,15], Brazilian tensile strength (BTS) [16,17], P-wave velocity (Vp) [18], Schmidt hammer hardness (SH) [19,20], Block Punch Index (BPI) [21,22], and slake durability index (SDI) [23,24]. Considering the similar nature of PLI and BTS parameters to UCS, which all represent the rock resistance to failure when exposed to external stresses, these strength parameters have been widely used in previous studies to predict the UCS through regression equations. Some predictive equations of UCS from PLI and BTS developed in the previous studies are presented in Table 1 and Table 2.
According to the ISRM [4], the dimension requirements of the rock specimen (i.e., size) for the PLI and BTS tests are almost the same. For example, both tests can be performed on cylindrical cores with a diameter and thickness of 54 and 27 mm, respectively (diameter to thickness ratio of 2). It is obvious that when it is possible to prepare rock specimens for PLI testing, these conditions also exist for BTS testing. Therefore, any PLI or BTS can be used to develop the correlation equations when the objective is to predict rock UCS. Table 1 and Table 2 indicate that there are correlation equations with various forms (i.e., linear, power, logarithmic) and different R2 values ranging from 0.45 to 0.98 between UCS with PLI and BTS. As a result, the PLI and BTS have different accuracies in predicting the UCS of the rocks. A more accurate prediction of the UCS will lead to a more appropriate design of rock-related geotechnical projects, including tunnels, concrete dams and rock slopes. There is a gap in previous research regarding the investigation of the accuracy of PLI and BTS in predicting the UCS of rock. Therefore, the aim of this paper is to conduct a comparative study on the accuracy of PLI and BTS in predicting the UCS of limestone and sandstone. The effect of porosity (n) on the accuracy of the correlation equations between UCS with PLI and BTS was also investigated.

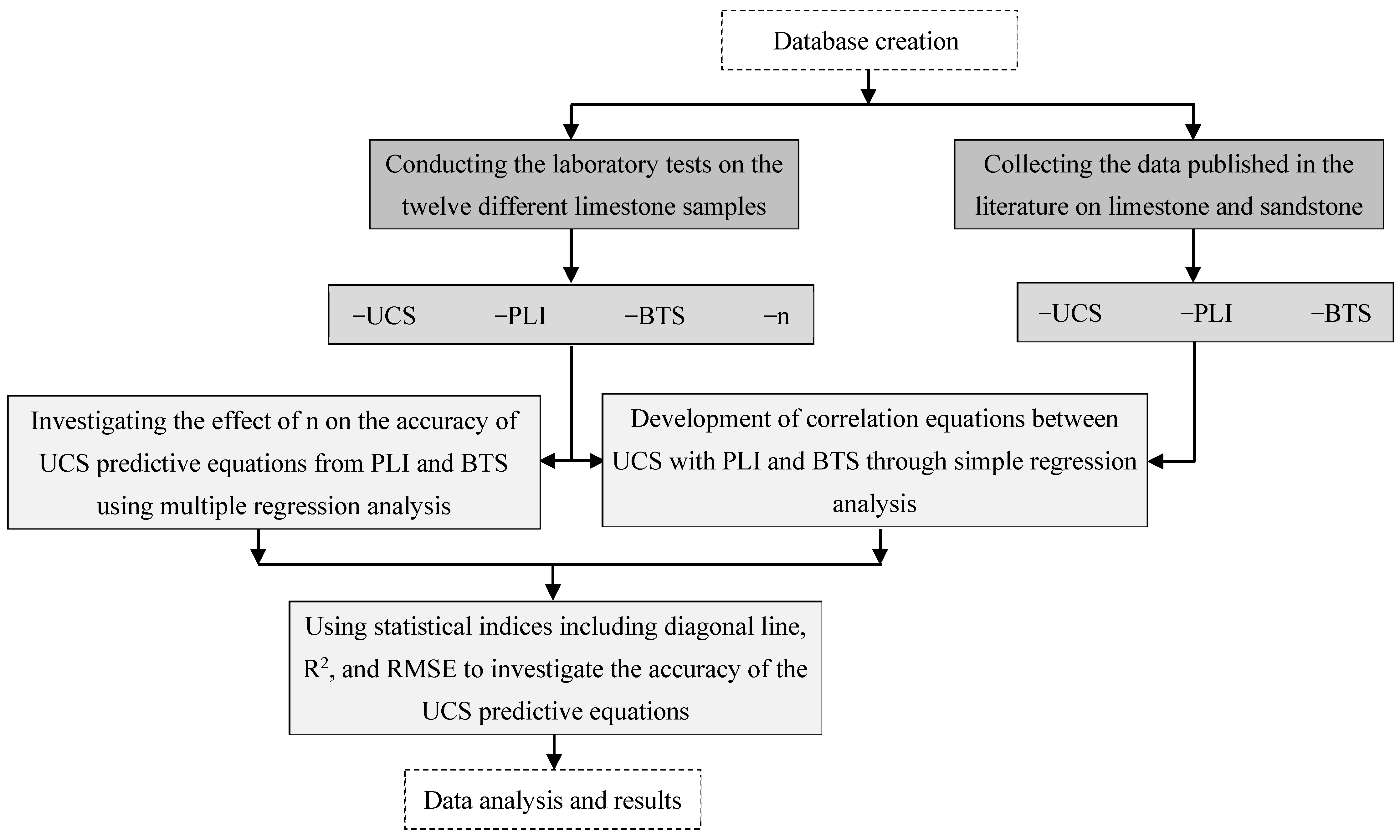
2. Materials and Methods

Two sets of data have been used in this paper. The first set was obtained by conducting laboratory tests and determining the UCS, PLI and BTS of twelve different limestone samples from the Lorestan province (western Iran). The other set was obtained by collecting data published in the literature on the UCS, PLI and BTS of limestones and sandstones. Correlation equations between UCS with PLI and BTS of the samples were developed by simple regression analysis. In addition, the role of n in the accuracy of UCS prediction equations based on PLI and BTS was investigated using multiple regression analysis. Some statistical indices including diagonal line (y = x), R2, and root mean square error (RMSE) were used to evaluate the accuracy of PLI and BTS in the UCS prediction. The flowchart of the present study is shown in Figure 1.

3. Database

3.1. Data Obtained from the Present Study

During several steps of field visits from some geotechnical projects in Khorramabad city (Lorestan Province, western Iran), blocks from twelve different limestone samples were collected. Figure 2 shows some of the geotechnical projects for the sampling. After transfer of block samples to the Engineering Geology Laboratory (Lorestan University), the cylindrical core specimens were prepared using a coring machine for various tests (Figure 2). The UCS, PLI, BTS, and n tests were performed on the specimens according to guidelines suggested by the International Society for Rock Mechanics [4]. Some information on the tests is presented in Table 3. Figure 3 shows the devices used in the present study to determine the UCS, PLI, and BTS of the specimens. The results are reported in Table 4. It can be seen from this table that the values of UCS, PLI, and BTS of the samples are different. These differences can be attributed to differences in photographical characteristics (i.e., mineralogical composition and textural features) and physical parameters such as density and porosity [6,7,10]. The UCS, PLI, and BTS of samples are a function of the climatic conditions prevailing in the region. Considering the climatic conditions, processes such as freezing–thawing, crystallization salt, heating–cooling, and wetting–drying can cause the deterioration of samples and, as a result, harmful effects on their UCS, PLI, and BTS [46,57].

3.2. Data Collected from Previous Studies

A literature review was conducted in order to collect the data required for the present study. Regarding the comparison of the accuracy of PLI and BTS in predicting the UCS of the rocks, only the papers that contained all these parameters simultaneously were applicable for the present study. For this, UCS, PLI, and BTS data published by Khajevand [18], Teymen and Menguc [56], Jamshidi et al. [59], and Lakirouhani, et al. [60] were extracted as a database for the present study. Table 5, Table 6, Table 7 and Table 8 present the UCS, PLI, and BTS data from these researchers.

4. Data Analysis and Results

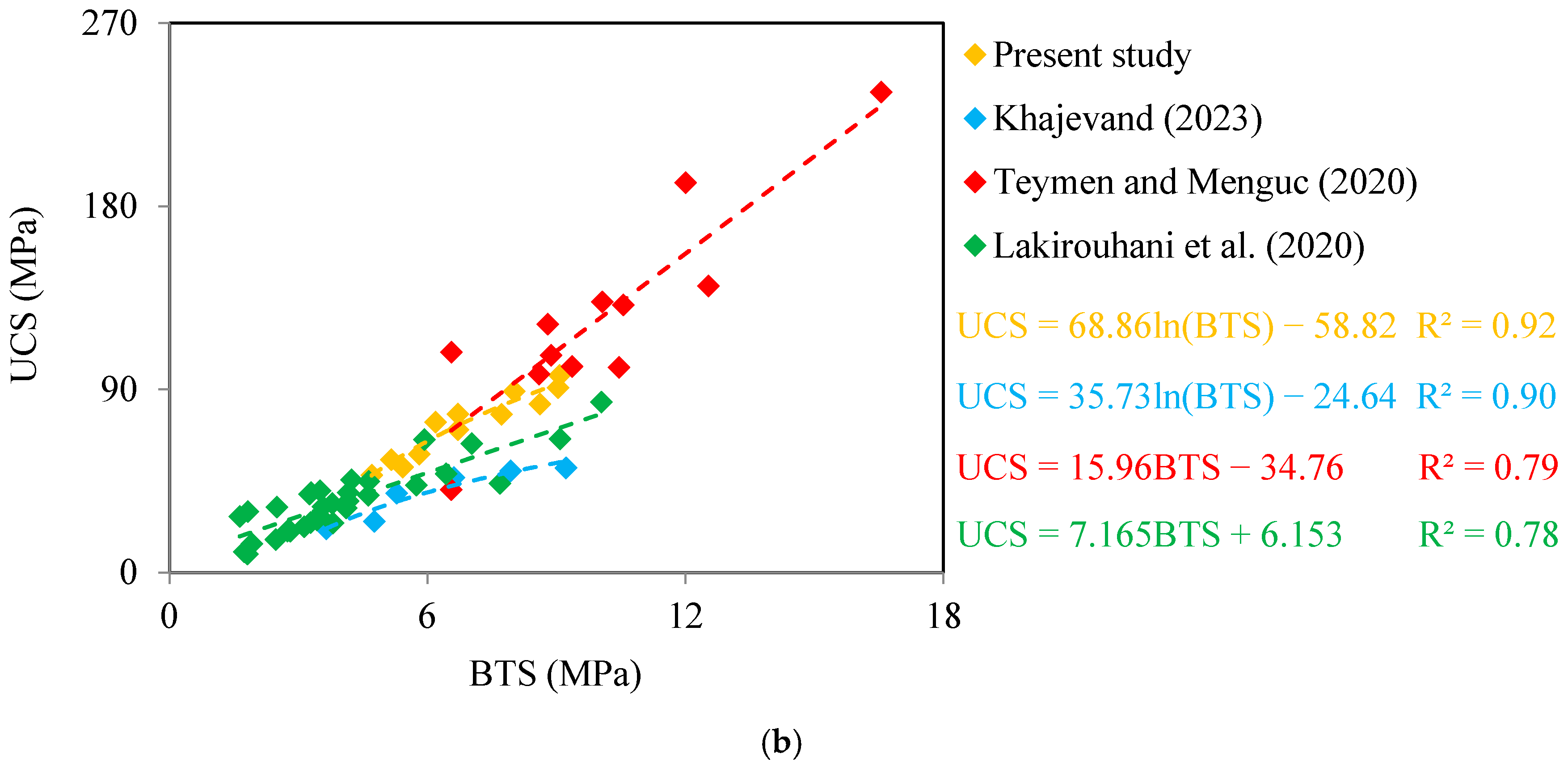
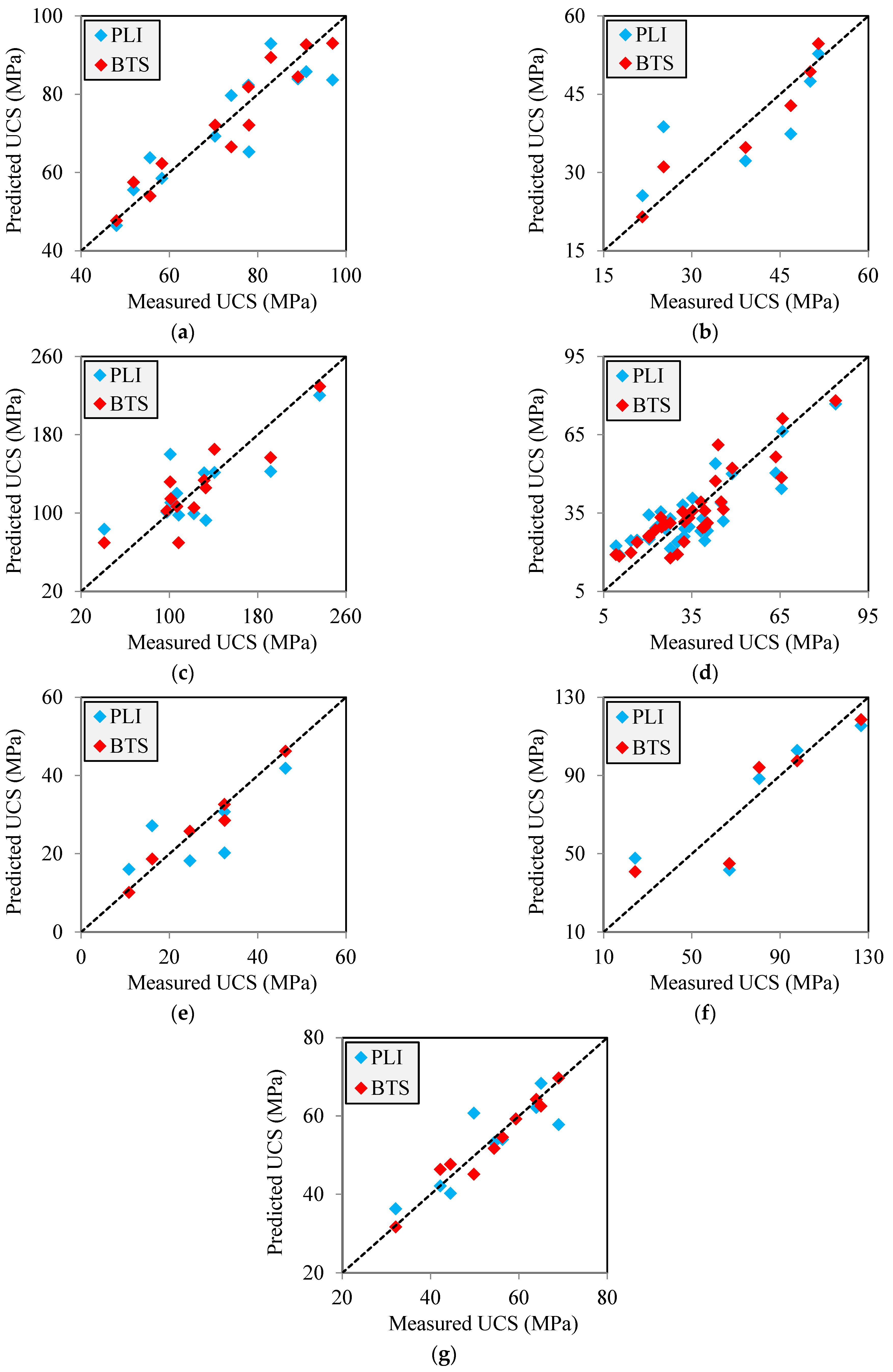
4.1. Comparing the Accuracy of PLI and BTS in Predicting the UCS

The data presented in Table 4, Table 5, Table 6, Table 7 and Table 8 were used to develop UCS predictive equations from PLI and BTS. For this, simple regression analyses were performed on the data. The four types of regression curves including linear (y = ax + b), power (y = axb), exponential (y = aex), and logarithmic (y = a + ln x) between UCS with PLI and BTS were fitted. The R2 value was used as a comparative measure to select the most appropriate regression curve. Among the regression curves, the one with the highest R2 was chosen as the correlation equation between UCS with PLI and BTS.
Figure 4 and Figure 5 show correlation equations between UCS with PLI and BTS for limestone and sandstone, respectively. It can be seen from these figures that the UCS of the samples shows an increasing trend with the increase of PLI and BTS. These results are in good agreement with the findings of Sadeghi et al. [2], Rajabzadeh et al. [12], Liu et al. [61], and Garrido et al. [62] on limestones. There are correlation equations in the forms of linear, power, exponential, and logarithmic equations between UCS with PLI and BTS with R2 values from 0.60 to 0.97. These values are acceptable, showing meaningful correlations between UCS with PLI and BTS. The PLI-based correlation equations have different R2 values than the BTS-based correlation equations, indicating that the PLI and BTS have different accuracies in predicting the UCS of the samples. The diagonal line (y = x) is a common qualitative measure and widely used by researchers to compare the accuracy between two correlation equations to predict an unknown parameter of rock [3,37,57]. The measured UCS values of the samples (Table 4, Table 5, Table 6, Table 7 and Table 8) were plotted versus predicted UCS using correlation equations shown in Figure 4 and Figure 5. The results of these analyses are shown in Figure 6. A data point on the diagonal line indicates an exact prediction of UCS using the PLI- or BTS-based correlation equations, i.e., the predicted UCS is in agreement with the measured UCS. Increasing the distance of the data points from the diagonal line increases the prediction error of UCS using the correlation equation. It can be seen from Figure 6 that for all databases, the predicted UCS values using the BTS are more concentrated around the diagonal line than those obtained using the PLI. The comparison of the scatter of the data points around the diagonal line indicates that the BTS is a more accurate parameter to predict the UCS of the samples.
As two quantitative indices, the R2 and RMSE were used for a deeper investigation of the accuracy of UCS predictive equations developed based on PLI and BTS. These two indices are among the most common and frequently used statistical parameters to assess the accuracy of a correlation equation [2,58,63]. The degree of fitting data to a regression curve can be measured by the R2 value, which measures the proportion of variation in the dependent variable. The RMSE, on the other hand, measures the average difference between the predicted values and the measured values. Mathematically, it is the standard deviation of the residuals. Residuals represent the distance between the regression curve and the data points. It should be mentioned that a correlation equation with a higher R2 has a smaller RMSE. In general, between two correlation equations, the one with the higher R2 and the smaller RMSE is more accurate in predicting an unknown parameter of rock. The R2 and RMSE values of correlation equations established between the UCS with PLI and BTS (Figure 4 and Figure 5) were calculated by Equations (1) and (2), respectively:
R 2 = ∑ i = 1 N y − y ¯ y ’ − y ¯ ’ ∑ i = 1 N ( y − y ¯ ) 2 ( y ’ − y ¯ ’ ) 2
R M S E = 1 N ∑ i = 1 N y − y ’ 2
where y and y’ are the measured and predicted values of the UCS, respectively, ȳ and ȳ’ are mean values of the y and y’, respectively, and N is the number of the dataset.
The R2 and RMSE values are presented in Figure 7. According to this figure, the correlation equations between UCS and PLI have values of R2 from 0.60 to 0.82, while the correlation equations between UCS and BTS show a higher R2, ranging from 0.78 to 0.97. The UCS predictive equations based on PLI and BTS have RMSE values between 5.49–29.77 MPa and 2.02–21.78 MPa, respectively. In regression analyses, R2 and RMSE values can range from 0 to 1 and 0 to positive infinity, respectively. The values of 1 and 0 values for the R2 and RMSE, respectively, obtained from a correlation equation means that the predicted values are in perfect agreement with the measured values. A correlation equation with the high R2 and a low RMSE indicates that the model fits the data well and has more accurate predictions. Conversely, lower R2 and higher RMSE values suggest more errors and a less accurate predictive equation. Comparing the values of R2 and RMSE of the correlation equations reveals that BTS, compared to PLI, is more accurate in predicting the rocks UCS. These results are in good agreement with the findings obtained from diagonal lines developed between the predicted and measured UCS values (Figure 6).
According to the International Society for Rock Mechanics [4], the shape and size of the rock specimen for PLI and BTS tests are similar, i.e., both were cylindrical cores with a diameter–thickness ratio of 2 (diameter = 54 mm). The findings showed that the BTS is a more accurate parameter than the PLI in predicting the UCS of the rocks. This can be attributed to the nature of the PLI device and its loading system on the rock specimen. In the PLI test, the loading on the specimen was carried out through two conical pieces with an apex angle of 60° (Figure 8). Therefore, the load applied on the rock specimen will be point. Rocks have a heterogeneous nature due to the variety in mineralogical composition, and the presence of pores and microcracks [64,65]. When the rock specimen is subjected to the PLI test, a pore or microcrack may be present along the axis of the loading between the conical pieces. This situation is shown schematically in Figure 8. The pores or microcrack will cause the specimen to failure at a lower load value, and therefore a lower PLI value compared to the actual PLI value. Figure 8 presents the premature failure of a specimen containing microcracks (Limestone 9 in the present study). According to this figure, it can be seen that the rupture surface of the specimen has passed across a microcrack. This will result in measurement error in the PLI, and therefore a prediction error of the UCS using the PLI-based correlation equation.

4.2. Effect of n on the Accuracy of UCS Predictive Equations

Multiple regression analyses were applied to the data to investigate the effect of n on the accuracy of UCS prediction from PLI and BTS. In these analyses, the UCS was regarded as the dependent variable, and PLI, BTS, and n were considered as independent variables. The general forms of the multiple correlation equations are as follows:
U C S = β 0 + β 1 P L I − β 2 n
U C S = β 0 + β 1 B T S − β 2 n
where UCS is the predicted value of the uniaxial compressive strength, PLI, BTS, and n are point load index, Brazilian tensile strength, and porosity, respectively, β0 is a constant, and β1 and β2 are the regression coefficients.
The data presented in Table 4 were analyzed using the SPSS®v.19 code statistical software. Multiple regression analyses were undertaken with the significance level of 5% and the best-fit curves were obtained between variables using the least squares method. The results of multiple regression analyses are given in Table 9 (Equations (6) and (8)). The significance and global usefulness of the multiple correlation equations were checked using the variance analysis for the regressions. F statistics test is frequently used in regression and variance analysis. The results of variance analysis for the multiple correlation equations are given in Table 9. For a significance level of 5%, the value of tabulated F with the degree of freedom υ1 = 2 and υ2 = 9 is 4.26. Since the F values computed for the multiple correlation equations are larger than the value of tabulated F, it can be concluded that the multiple correlation equations have good validity to predict UCS from PLI, BTS, and n.
The R2 and RMSE values of the simple and multiple correlation equations were used to investigate the role of n on the accuracy of UCS prediction. According to results given in Table 9, R2 and RMSE values equal to 0.82 and 7.25, respectively, were obtained for the simple correlation equation between UCS and PLI (Equation (5)), while these values were 0.92 and 4.69 for the multiple correlation equation between UCS with PLI and n (Equation (6)). The simple correlation equation between UCS and BTS (Equation (7)) had R2 and RMSE of 0.92 and 4.28, respectively. Also, R2 and RMSE values for multiple correlation equation between UCS with BTS and n (Equation (8)) were equal to 0.94 and 3.96, respectively. The comparison of these values shows that the multiple correlation equations rather than the simple ones have higher R2 and lower RMSE values, indicating that the n increases the accuracy of UCS prediction from PLI and BTS. As a result, prediction accuracy of the multiple correlation equations is higher than those of simple correlation equations. This is a significant finding regarding the more accurate evaluation of rocks UCS in the preliminary steps of the site investigation of a geotechnical project such as a tunnel, concrete dam, or rock slope. However, the correlation equations developed in the present study (Equations (5)–(8)) should be used with caution for limestones from other regions with a range of values for UCS, PLI, BTS and n similar to the samples tested in the present study (Table 4). This may be accompanied by some prediction errors.
Although our results revealed that multiple correlation equations compared to simple ones have higher accuracy in predicting the rocks UCS, a literature review was also conducted in this regard. Some researchers such as Gokceoglu and Zorlu [44], Teymen and Menguc [56], Mishra and Basu [66], Azimian [67], and Farhadian et al. [68] showed that compared with simple correlation equations, using the multiple correlation equations can provide a predictive model of UCS with a higher R2 value, and thus a more accurate prediction. However, the findings of Sadeghi et al. [2], Rajabzadeh et al. [12], Kamani and Ajalloeian [69], and Diamantis et al. [70] differ from those obtained by the above-mentioned researchers. Based on the regression analyses on the UCS, BTS, PLI, and n of the limestones, these researchers concluded that there is no significant difference between the accuracy of simple and multiple correlation equations in predicting the UCS.
In addition to the quantitative criteria of R2 and RMSE, a qualitative comparison was also carried out to evaluate the effect of n on the accuracy of the UCS predictor equations. For this, the measured UCS values were plotted versus predicted UCS values obtained from the simple and multiple correlation equations. As can be seen from Figure 9, the data points obtained based on the multiple correlation equations are closer to the diagonal line, which reveals that these equations compared to the simple correlation equations have higher accuracy for prediction of rocks UCS under study. These findings are in line with results obtained from R2 and RMSE values of the simple and multiple correlation equations. Based on Figure 9, a valuable point is that the data points are closer to the diagonal line for the BTS-based multiple correlation equation (Equation (8)) compared to the PLI-based ones (Equation (6)). Consequently, the BTS-based multiple correlation equation shows that it has a higher accuracy for predicting the UCS of rocks.

5. Conclusions

Based on laboratory tests in the present study and a literature review of previous studies, a database including uniaxial compressive strength (UCS), point load index (PLI), Brazilian tensile strength (BTS), and porosity (n) of different limestones and sandstones was created. Using data analyses, two goals were pursued: (1) investigating the accuracy of PLI and BTS in predicting UCS, and (2) the role of n in the prediction accuracy of UCS using of PLI and BTS-based correlation equations. The main findings of the present study are as follows:
-
The results of simple regression analyses showed that the BTS provides a more accurate prediction of the rock UCS than the PLI. This was verified by comparing the statistical indices (including diagonal line (y = x), coefficient of determination (R2), and root mean square error (RMSE)) obtained for PLI and BTS-based correlation equations.
-
The lower accuracy of PLI compared to the BTS in the indirect assessment of UCS is due to nature of the PLI device and its loading system on the rock specimen. The results showed that the specimen heterogeneity (caused by the presence of pores or microcracks) strongly affects the accuracy of PLI measurements and thus the performance of the UCS prediction equation.
-
Based on the comparison of the diagonal line results and the R2 and RMSE values obtained from the simple and multiple regression analyses, the n has a significant effect on the predictive accuracy of the UCS from the PLI and BTS-based correlation equations.
-
Considering the same size of the rock specimen for PLI and BTS tests, it is recommended that BTS measurements be preferred. As a result, a more accurate evaluation of the rock UCS can be obtained in the preliminary stages of the site investigation of a geotechnical project such as a tunnel, concrete dam or rock slope. A more accurate evaluation of the UCS will lead to a more appropriate design of the geotechnical project, thereby increasing its long-term success.
-
As an important point, it is necessary for researchers to carry out more studies in the future to investigate the accuracy of PLI and BTS for other types of rock.

Author Contributions

Conceptualization, A.J.; methodology, A.J.; validation, A.J. and L.S.; formal analysis, A.J. and L.S.; investigation, A.J. and L.S.; writing—original draft preparation, A.J. writing—review and editing, A.J. and L.S.; visualization, A.J. and L.S.; supervision, L.S. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the Fundação para a Ciência e a Tecnologia in the frame of the UIDB/00073/2020 and UIDP/00073/2020 projects of the I & D unit Geosciences Center (CGEO).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Acknowledgments

The authors acknowledge the official support of the Engineering Geology Laboratory of Lorestan University, Khorramabad, Iran, for performing all laboratory tests of the research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Heidari, M.; Khanlari, G.R.; Torabi-Kaveh, M.; Karegarian, S. Predicting the uniaxial compressive and tensile strengths of gypsum rock by point load testing. Rock Mech. Rock Eng. 2012, 45, 265–273. [Google Scholar] [CrossRef]
  2. Sadeghi, E.; Nikudel, M.R.; Khamehchiyan, M.; Kavussi, A. Estimation of unconfined compressive strength (UCS) of carbonate rocks by index mechanical tests and specimen size properties: Central Alborz Zone of Iran. Rock Mech. Rock Eng. 2022, 55, 125–145. [Google Scholar] [CrossRef]
  3. Fereidooni, D.; Karimi, Z.; Ghasemi, F. Non-destructive test-based assessment of uniaxial compressive strength and elasticity modulus of intact carbonate rocks using stacking ensemble models. PLoS ONE 2024, 19, e0302944. [Google Scholar] [CrossRef] [PubMed]
  4. ISRM. Rock characterization, testing and monitoring. In ISRM Suggested Methods; Brown, E.T., Ed.; Pergamon Press: New York, NY, USA, 1981. [Google Scholar]
  5. ASTM D7012–14; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures. ASTM International: West Conshohocken, PA, USA, 2014.
  6. Ulusay, R.; Tureli, K.; Ider, M.H. Prediction of engineering properties of a selected litharenite sandstone from its petrographic characteristics using correlation and multivariate statistical techniques. Eng. Geol. 1994, 37, 135–157. [Google Scholar] [CrossRef]
  7. Khajevand, R. Evaluating the influence of petrographic and textural characteristics on geotechnical properties of some carbonate rock samples by empirical equations. Innov. Infrastruct. Solut. 2021, 6, 113. [Google Scholar] [CrossRef]
  8. Chen, Z.-L.; Shi, H.-Z.; Xiong, C.; He, W.-H.; Wang, H.-Z.; Wang, B.; Dubinya, N.; Ge, K.-Q. Effects of mineralogical composition on uniaxial compressive strengths of sedimentary rocks. Pet. Sci. 2023, 20, 3062–3073. [Google Scholar] [CrossRef]
  9. Ajalloeian, R.; Jamshidi, A.; Khorasani, R. Evaluating the effects of mineral grain size and mineralogical composition on the correlated equations between strength and Schmidt hardness of granitic rocks. Geotech. Geol. Eng. 2024, 42, 675–685. [Google Scholar] [CrossRef]
  10. Jamshidi, A.; Zamanian, H.; Zarei Sahamieh, R. The effect of density and porosity on the correlation between uniaxial compressive strength and P-wave velocity. Rock Mech. Rock Eng. 2018, 51, 1279–1286. [Google Scholar] [CrossRef]
  11. Verma, R.K.; Singh, R.; Kumar, V.; Singh, T.N.; Umrao, R.K.; Mishra, P.; Sharma, P. Statistical estimation of uniaxial compressive strength in geotechnical projects using regression analysis: A comparative study. Int. J. Geomech. 2024, 24, 05024009. [Google Scholar] [CrossRef]
  12. Rajabzadeh, M.A.; Moosavinasab, Z.; Rakhshandehroo, G. Effects of rock classes and porosity on the relation between uniaxial compressive strength and some rock properties for carbonate rocks. Rock Mech. Rock Eng. 2012, 45, 113–122. [Google Scholar] [CrossRef]
  13. Valido, J.; Caceres, J.M.; Sousa, L. Mechanical properties of ignimbrites of Tenerife Island employed as building stone and their correlation with some physical properties. J. Build. Eng. 2024, 82, 108222. [Google Scholar] [CrossRef]
  14. Cobanoglu, I.; Celik, S.B. Estimation of uniaxial compressive strength from point load strength, Schmidt hardness and P-wave velocity. Bull. Eng. Geol. Environ. 2008, 67, 491–498. [Google Scholar] [CrossRef]
  15. Akbay, D. Investigating the accuracy of specimen shape for point load index test in predicting the uniaxial compressive strength for rocks using regression analysis and machine learning. Min. Metall. Explor. 2023, 40, 2107–2115. [Google Scholar]
  16. Karaman, K.; Cihangir, F.; Ercikdi, B.; Kesimal, A.; Demirel, S. Utilization of the Brazilian test for estimating the uniaxial compressive strength and shear strength parameters. J. South. Afr. Inst. Min. Metall. 2015, 115, 185–192. [Google Scholar] [CrossRef]
  17. Iyare, U.C.; Blake, O.O.; Ramsook, R. Estimating the uniaxial compressive strength of argillites using Brazilian tensile strength, ultrasonic wave velocities, and elastic properties. Rock Mech. Rock Eng. 2021, 54, 2067–2078. [Google Scholar] [CrossRef]
  18. Khajevand, R. Estimating geotechnical properties of sedimentary rocks based on physical parameters and ultrasonic P-Wave velocity using statistical methods and soft computing approaches. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 3785–3809. [Google Scholar] [CrossRef]
  19. Teymen, A. Statistical models for estimating the uniaxial compressive strength and elastic modulus of rocks from different hardness test methods. Heliyon 2021, 7, e06891. [Google Scholar] [CrossRef]
  20. Ahmed, W.; Ahmad, N.; Janjuhah, H.T.; Islam, I.; Sajid, M.; Kontakiotis, G. The evaluation of non-destructive tests for the strength and physical properties of granite, marble, and sandstone: A case study from North Pakistan. Quaternary 2023, 6, 4. [Google Scholar] [CrossRef]
  21. Jalali, S.H.; Heidari, M.; Zarrinshoja, M.; Mohseni, N. Predicting of uniaxial compressive strength of some igneous and metamorphic rocks by block punch index and cylindrical punch index test. Int. J. Rock Mech. Min. Sci. 2019, 119, 72–80. [Google Scholar] [CrossRef]
  22. Aladejare, A.E. Evaluation of empirical estimation of uniaxial compressive strength of rock using measurements from index and physical tests. J. Rock Mech. Geotech. 2020, 12, 256–268. [Google Scholar] [CrossRef]
  23. Koncagul, E.; Santi, P. Predicting the unconfined compressive strength of the Breathitt shale using slake durability, Shore hardness and rock structural properties. Int. J. Rock Mech. Min. Sci. 1999, 36, 139–153. [Google Scholar] [CrossRef]
  24. Kahraman, S.; Fener, M.; Gunaydin, O. Estimating the uniaxial compressive strength of pyroclastic rocks from the slake durability index. Bull. Eng. Geol. Environ. 2017, 76, 1107–1115. [Google Scholar] [CrossRef]
  25. Singh, V.K.; Singh, D.P. Correlation between point load index and compressive strength for quartzite rocks. Geotech. Geol. Eng. 1993, 11, 269–272. [Google Scholar] [CrossRef]
  26. Tugrul, A.; Zarif, I.H. Correlation of mineralogical and textural characteristics with engineering properties of selected granitic rocks from Turkey. Eng. Geol. 1999, 51, 303–317. [Google Scholar] [CrossRef]
  27. Lashkaripour, G.R. Predicting mechanical properties of mudrock from index parameters. Bull. Eng. Geol. Environ. 2002, 61, 73–77. [Google Scholar] [CrossRef]
  28. Tsiambaos, G.; Sabatakakis, N. Considerations on strength of intact sedimentary rocks. Eng. Geol. 2004, 72, 261–273. [Google Scholar] [CrossRef]
  29. Zorlu, K.; Ulusay, R.; Ocakoglu, F.; Gokceoglu, C.; Sonmez, H. Predicting intact rock properties of selected sandstones using petrographic thin-section data. Int. J. Rock Mech. Min. Sci. 2004, 41, 93–98. [Google Scholar] [CrossRef]
  30. Fener, M.; Kahraman, S.; Bilgil, A.; Gunaydin, O. A comparative evaluation of indirect methods to estimate the compressive strength of rocks. Rock Mech. Rock Eng. 2005, 38, 329–343. [Google Scholar] [CrossRef]
  31. Kahraman, S.; Gunaydin, O.; Fener, M. The effect of porosity on the relation between uniaxial compressive strength and point load index. Int. J. Rock Mech. Min. Sci. 2005, 42, 584–589. [Google Scholar] [CrossRef]
  32. Basu, A.; Aydin, A. Predicting uniaxial compressive strength by point load test: Significance of cone penetration. Rock Mech. Rock Eng. 2006, 39, 483–490. [Google Scholar] [CrossRef]
  33. Yilmaz, I.; Yuksek, G. Prediction of the strength and elasticity modulus of gypsum using multiple regression, ANN, and ANFIS models. Int. J. Rock. Mech. Min. Sci. 2009, 46, 803–810. [Google Scholar] [CrossRef]
  34. Mishra, D.A.; Basu, A. Use of the block punch test to predict the compressive and tensile strengths of rocks. Int. J. Rock Mech. Min. Sci. 2012, 51, 119–127. [Google Scholar] [CrossRef]
  35. Singh, T.N.; Kainthola, A.; Venkatesh, A. Correlation between point load index and uniaxial compressive strength for different rock types. Rock Mech. Rock Eng. 2012, 45, 259–264. [Google Scholar] [CrossRef]
  36. Palassi, M.; Emami, V. A new nail penetration test for estimation of rock strength. Int. J. Rock Mech. Min. Sci. 2014, 66, 124–127. [Google Scholar] [CrossRef]
  37. Azimian, A.; Ajalloeian, R. Empirical correlation of physical and mechanical properties of marly rocks with P wave velocity. Arab. J. Geosci. 2015, 8, 2069–2079. [Google Scholar] [CrossRef]
  38. Yin, J.H.; Wong, R.H.C.; Chau, K.T.; Lai, D.T.W.; Zhao, G.-S. Point load strength index of granitic irregular lumps: Size correction and correlation with uniaxial compressive strength. Tunn. Undergr. Space Technol. 2017, 70, 388–399. [Google Scholar] [CrossRef]
  39. Sadeghiamirshahidi, M.; Vitton, S.J. Mechanical properties of Michigan Basin’s gypsum before and after saturation. J. Rock Mech. Geotech. Eng. 2019, 11, 739–748. [Google Scholar]
  40. Rabat, A.; Cano, M.; Tomas, R.; Tamayo, A.E.; Alejano, L.R. Evaluation of strength and deformability of soft sedimentary rocks in dry and saturated conditions through needle penetration and point load tests: A comparative study. Rock Mech. Rock Eng. 2020, 53, 2707–2726. [Google Scholar] [CrossRef]
  41. Jamshidi, A. A comparative study of point load index test procedures in predicting the uniaxial compressive strength of sandstones. Rock Mech. Rock Eng. 2022, 55, 4507–4516. [Google Scholar] [CrossRef]
  42. Kong, F.; Xue, Y.; Shang, J.; Zhu, C.; Han, M.; Qu, Z.; Wang, B.; Yang, K. Predicting uniaxial compressive strength of building stone based on index tests: Correlations, validity, reliability, and unification. Constr. Build. Mater. 2024, 438, 137227. [Google Scholar] [CrossRef]
  43. Bell, F.G.; Lindsay, P. The petrographic and geomechanical properties of some sandstones from the newspaper member of the natal group near Durban, South Africa. Eng. Geol. 1999, 53, 57–81. [Google Scholar] [CrossRef]
  44. Gokceoglu, C.; Zorlu, K. A fuzzy model to predict the uniaxial compressive strength and the modulus of elasticity of a problematic rock. Eng. Appl. Artif. Intell. 2004, 17, 61–72. [Google Scholar] [CrossRef]
  45. Altindag, R.; Guney, A. Predicting the relationships between brittleness and mechanical properties (UCS, TS and SH) of rocks. Sci. Res. Essays. 2010, 5, 2107–2118. [Google Scholar]
  46. Farah, R. Correlations between Index Properties and Unconfined Compressive Strength of Weathered Ocala Limestone. Master’s Thesis, UNF College of Computing, Engineering and Construction, Jacksonville, FL, USA, 2011. [Google Scholar]
  47. Tahir, M.; Mohammad, N.; Din, F. Strength parameters and their inter-relationship for limestone of Cherat and Kohat areas of Khyber Pakhtunkhwa. J. Himal. Earth Sci. 2011, 44, 45–51. [Google Scholar]
  48. Kahraman, S.; Fener, M.; Kozman, E. Predicting the compressive and tensile strength of rocks from indentation hardness index. J. South. Afr. Inst. Min. Metall. 2012, 112, 331–339. [Google Scholar]
  49. Basu, A.; Mishra, D.A.; Roychowdhury, K. Rock failure modes under uniaxial compression, Brazilian, and point load tests. Bull. Eng. Geol. Environ. 2013, 72, 457–475. [Google Scholar] [CrossRef]
  50. Yesiloglu-Gultekin, N.; Gokceoglu, C.; Sezer, E.A. Prediction of uniaxial compressive strength of granitic rocks by various nonlinear tools and comparison of their performances. Int. J. Rock Mech. Min. Sci. 2013, 62, 13–122. [Google Scholar] [CrossRef]
  51. Kallu, R.; Roghanchi, P. Correlations between direct and indirect strength test methods. Int. J. Min. Sci. Technol. 2015, 25, 355–360. [Google Scholar] [CrossRef]
  52. Fereidooni, D. Determination of the geotechnical characteristics of hornfelsic rocks with a particular emphasis on the correlation between physical and mechanical properties. Rock Mech. Rock Eng. 2016, 49, 2595–2608. [Google Scholar] [CrossRef]
  53. Ribeiro, P.; Oliveira, M.; Nelson, P. Correlation between uniaxial compressive strength and Brazilian tensile strength using different rock types. In Proceedings of the XVIII Brazilian Conference on Soil Mechanics and Geotechnical Engineering, Belo Horizonte, Brazil, 19–22 October 2016. [Google Scholar]
  54. Masoumi, H.; Horne, J.; Timms, W. Establishing empirical relationships for the effects of water content on the mechanical behavior of Gosford sandstone. Rock Mech. Rock Eng. 2017, 50, 2235–2242. [Google Scholar] [CrossRef]
  55. Aliyu, M.M.; Shang, J.; Murphy, W.; Lawrence, J.A.; Collier, R.; Kong, F.; Zhao, Z. Assessing the uniaxial compressive strength of extremely hard cryptocrystalline flint. Int. J. Rock Mech. Min. Sci. 2019, 113, 310–321. [Google Scholar] [CrossRef]
  56. Teymen, A.; Menguc, E.C. Comparative evaluation of different statistical tools for the prediction of uniaxial compressive of rocks. Int. J. Min. Sci. Technol. 2020, 30, 785–797. [Google Scholar] [CrossRef]
  57. Arman, H. Correlation of uniaxial compressive strength with indirect tensile strength (Brazilian) and 2nd cycle of slake durability index for evaporitic rocks. Geotech. Geol. Eng. 2021, 39, 1583–1590. [Google Scholar] [CrossRef]
  58. Khajevand, R. Prediction of the uniaxial compressive strength of rocks by soft computing approaches. Geotech. Geol. Eng. 2023, 41, 3549–3574. [Google Scholar] [CrossRef]
  59. Jamshidi, A.; Abdi, Y.; Sarikhani, R. Prediction of brittleness indices of sandstones using a novel physico-mechanical parameter. Geotech. Geol. Eng. 2020, 38, 4651–4659. [Google Scholar] [CrossRef]
  60. Lakirouhani, A.; Asemi, F.; Zohdi, A.; Medzvieckas, J.; Kliukas, R. Physical parameters, tensile and compressive strength of dolomite rock samples: Influence of grain size. J. Civ. Eng. Manag. 2020, 26, 789–799. [Google Scholar] [CrossRef]
  61. Liu, Q.; Zhao, Y.; Zhang, X. Case study: Using the point load test to estimate rock strength of tunnels constructed by a tunnel boring machine. Bull. Eng. Geol. Environ. 2019, 78, 1727–1734. [Google Scholar] [CrossRef]
  62. Garrido, M.E.; Petnga, F.B.; Martínez-Ibanez, V.; JSeron, J.B.; Hidalgo-Signes, C.; Tomas, R. Predicting the uniaxial compressive strength of a limestone exposed to high temperatures by point load and leeb rebound hardness testing. Rock Mech. Rock Eng. 2022, 55, 1–17. [Google Scholar] [CrossRef]
  63. Ali, H.F.H. Utilizing several multivariable mathematical and M5P-tree models to predict uniaxial compressive strength of rocks. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 1737–1753. [Google Scholar] [CrossRef]
  64. Akin, M.; Ozsan, A. Evaluation of the long-term durability of yellow travertine using accelerated weathering tests. Bull. Eng. Geol. Environ. 2011, 70, 101–114. [Google Scholar] [CrossRef]
  65. Zalooli, A.; Khamehchiyan, M.; Nikudel, M.R. The quantification of total and effective porosities in travertines using PIA and saturation-buoyancy methods and the implication for strength and durability. Bull. Eng. Geol. Environ. 2018, 77, 1739–1751. [Google Scholar] [CrossRef]
  66. Mishra, D.A.; Basu, A. Estimation of uniaxial compressive strength of rock materials by index tests using regression analysis and fuzzy inference system. Eng. Geol. 2013, 160, 54–68. [Google Scholar] [CrossRef]
  67. Azimian, A. Application of statistical methods for predicting uniaxial compressive strength of limestone rocks using nondestructive tests. Acta Geotech. 2017, 12, 321–333. [Google Scholar] [CrossRef]
  68. Farhadian, A.; Ghasemi, E.; Hoseinie, S.H.; Bagherpour, R. Prediction of rock abrasivity index (RAI) and uniaxial compressive strength (UCS) of granite building stones using nondestructive tests. Geotech. Geol. Eng. 2022, 40, 3343–3356. [Google Scholar] [CrossRef]
  69. Kamani, M.; Ajalloeian, R. Evaluation of engineering properties of some carbonate rocks trough corrected texture coefficient. Geotech. Geol. Eng. 2019, 37, 599–614. [Google Scholar] [CrossRef]
  70. Diamantis, K.; Fereidooni, D.; Khajevand, R.; Migiros, G. Effect of textural characteristics on engineering properties of some sedimentary rocks. J. Cent. South Univ. 2021, 28, 926–938. [Google Scholar] [CrossRef]
Materials 17 05081 g001
Figure 1. Scheme showing how the present study was carried out.
Figure 1. Scheme showing how the present study was carried out.
Materials 17 05081 g001
Materials 17 05081 g002
Figure 2. (a) Sampling location in Iran (Lorestan Province). (b) Limestone sampling locations on the rock slope of a road and the foundation of a civil structure. (c) Some blocks collected from limestones. (d) Coring machine for preparation of test specimens. (e) Some specimens for UCS, PLI, BTS, and n tests.
Figure 2. (a) Sampling location in Iran (Lorestan Province). (b) Limestone sampling locations on the rock slope of a road and the foundation of a civil structure. (c) Some blocks collected from limestones. (d) Coring machine for preparation of test specimens. (e) Some specimens for UCS, PLI, BTS, and n tests.
Materials 17 05081 g002
Materials 17 05081 g003
Figure 3. Devices used in the present study: (a) UCS, (b) PLI, and (c) BTS.
Figure 3. Devices used in the present study: (a) UCS, (b) PLI, and (c) BTS.
Materials 17 05081 g003
Materials 17 05081 g004aMaterials 17 05081 g004b
Figure 4. Predictive equations of UCS for limestone using (a) PLI and (b) BTS (Khajevand [18], Teymen and Menguc [56], Lakirouhani et al. [60]).
Figure 4. Predictive equations of UCS for limestone using (a) PLI and (b) BTS (Khajevand [18], Teymen and Menguc [56], Lakirouhani et al. [60]).
Materials 17 05081 g004aMaterials 17 05081 g004b
Materials 17 05081 g005
Figure 5. Predictive equations of UCS for sandstone using (a) PLI and (b) BTS (Khajevand [18], Teymen and Menguc [56], Jamshidi et al. [59]).
Figure 5. Predictive equations of UCS for sandstone using (a) PLI and (b) BTS (Khajevand [18], Teymen and Menguc [56], Jamshidi et al. [59]).
Materials 17 05081 g005
Materials 17 05081 g006
Figure 6. Measured UCS versus predicted UCS using the PLI and BTS: (a) present study (limestone), (b) Khajevand [18] (limestone), (c) Teymen and Menguc [56] (limestone), (d) Lakirouhani et al. [60] (limestone), (e) Khajevand [18] (sandstone), (f) Teymen and Menguc [56] (sandstone), and (g) Jamshidi et al. [59] (sandstone).
Figure 6. Measured UCS versus predicted UCS using the PLI and BTS: (a) present study (limestone), (b) Khajevand [18] (limestone), (c) Teymen and Menguc [56] (limestone), (d) Lakirouhani et al. [60] (limestone), (e) Khajevand [18] (sandstone), (f) Teymen and Menguc [56] (sandstone), and (g) Jamshidi et al. [59] (sandstone).
Materials 17 05081 g006
Materials 17 05081 g007
Figure 7. The R2 and RMSE values of the correlation equations between UCS with PLI and BTS (Khajevand [18], Teymen and Menguc [56], Jamshidi et al. [59], Lakirouhani et al. [60]).
Figure 7. The R2 and RMSE values of the correlation equations between UCS with PLI and BTS (Khajevand [18], Teymen and Menguc [56], Jamshidi et al. [59], Lakirouhani et al. [60]).
Materials 17 05081 g007
Materials 17 05081 g008
Figure 8. Heterogeneity in the rock specimen and its premature failure during the PLI test.
Figure 8. Heterogeneity in the rock specimen and its premature failure during the PLI test.
Materials 17 05081 g008
Materials 17 05081 g009
Figure 9. Measured UCS versus predicted UCS using simple and multiple correlation equations: (a) PLI (Equations (5) and (6)), and (b) BTS (Equations (7) and (8)).
Figure 9. Measured UCS versus predicted UCS using simple and multiple correlation equations: (a) PLI (Equations (5) and (6)), and (b) BTS (Equations (7) and (8)).
Materials 17 05081 g009
Table 1. Prediction of the UCS from PLI.
Table 1. Prediction of the UCS from PLI.
ReferenceRock TypePredictive EquationR2
Ulusay et al. [6]SandstoneUCS = 19PLI + 12.70.81
Akbay [15]Limestone, MarbleUCS = 13.71PLI + 5.510.71
Singh and Singh [25]Quartzite UCS = 23.37PLI0.96
Tugrul and Zarif [26]Granitic rocksUCS = 15.25PLI0.96
Lashkaripour [27]MudrockUCS = 21.4PLI0.85
Tsiambaos and Sabatakakis [28]Different rock typesUCS = 7.3PLI1.710.82
Zorlu et al. [29]SandstoneUCS = 10.3PLI + 28.10.76
Fener et al. [30]Different rock typesUCS = 9.08PLI + 39.30.72
Kahraman et al. [31]Different rock typesUCS = 10.9PLI + 27.40.61
Basu and Aydin [32]GraniteUCS = 21PLI0.93
Yilmaz and Yuksek [33]GypsumUCS = 10.5PLI − 3.970.57
Mishra and Basu [34]SandstoneUCS = 13.0PLI − 5.190.84
Singh et al. [35]LimestoneUCS = 22.3PLI0.68
Palassi and Emami [36]Travertine, MarbleUCS = 20.1PLI − 17.10.80
Azimian and Ajalloeian [37]MarlUCS = 56.94 ln(PLI) − 1.660.93
Yin et al. [38]Granitic rocksUCS = 22.27PLI0.82
Sadeghiamirshahidi and Vitton [39]GypsumUCS = 6.58PLI0.91
Rabat et al. [40]SiltstoneUCS = 14.26PLI0.98
Jamshidi [41]SandstoneUCS = 4.94PLI + 33.030.85
Kong et al. [42]Different rock typesUCS = 16.19PLI0.90
Table 2. Prediction of the UCS from BTS.
Table 2. Prediction of the UCS from BTS.
ReferenceRock TypePredictive EquationR2
Sadeghi et al. [2]Carbonate rocksUCS = 7.26BTS0.95
Karman et al. [16]Different rock typesUCS = 4.87BTS + 24.300.90
Iyare et al. [17]ArgilliteUCS = 5.31BTS1.060.87
Tugrul and Zarif [26]Granite, GranodioriteUCS = 6.67BTS + 0.730.92
Bell and Lindsay [43]SandstoneUCS = 6.71BTS + 36.00.61
Gokceoglu and Zorlu [44]GraywackeUCS = 6.8BTS + 13.50.65
Altindag and Guney [45]Limestone, Granite, MarbleUCS = 2.38BTS1.0730.79
Farah [46]Sedimentary rocksUCS = 7.86BTS − 447.630.92
Tahir et al. [47]Sedimentary rocksUCS = 7.53BTS0.45
Kahraman et al. [48]Different rock typesUCS = 10.61BTS0.54
Basu et al. [49]SandstoneUCS = 10.53BTS − 10.230.83
Yesiloglu-Gultekin et al. [50]Granite, GranodioriteUCS = 7.22BTS + 40.080.61
Kallu and Roghanchi [51]Igneous rocksUCS = 6.75BTS1.080.80
Fereidooni [52]Hornfels schistUCS = 10.03BTS + 55.190.92
Ribeiro et al. [53]Sedimentary rocksUCS = 13.70BTS0.67
Masoumi et al. [54]SandstoneUCS = 9.29BTS + 3.910.68
Aliyu et al. [55]FlintUCS = 10.4BTS + 18.20.63
Teymen and Menguc [56]Andesite, Limestone, MarbleUCS = 7.73BTS1.1970.90
Arman [57]GypsumUCS = 4.233BTS + 13.640.53
Khajevand [58]LimestoneUCS = 40.09ln(BTS) − 36.140.94
Table 3. Information about the specimens used for UCS, PLI, BTS, and n tests.
Table 3. Information about the specimens used for UCS, PLI, BTS, and n tests.
TestSpecimen ShapeSpecimen SizeSpecimen StatusSpecimen NumberSource
Diameter (mm)Length (mm)D to L
UCSCylindrical core44882.0Dry5ISRM [4]
PLICylindrical core4430~1.5Dry5ISRM [4]
BTSCylindrical core4430~1.5Dry5ISRM [4]
nCylindrical core4430~1.5Dry5ISRM [4]
Table 4. The UCS, PLI, BTS, and n of limestone samples obtained in the present study.
Table 4. The UCS, PLI, BTS, and n of limestone samples obtained in the present study.
Sample CodeUCS (MPa)PLI (MPa)BTS (MPa)n (%)
Limestone 178.04 (3.72) 14.59 (0.39)6.70 (0.29)3.05 (0.20)
Limestone 251.90 (3.24)3.75 (0.38)5.42 (0.25)7.41 (0.17)
Limestone 374.00 (2.71)5.63 (0.36)6.18 (0.20)5.01 (0.19)
Limestone 458.33 (4.35)4.02 (0.43)5.81 (0.31)6.71 (0.24)
Limestone 577.90 (2.50)5.80 (0.37)7.72 (0.22)2.24 (0.18)
Limestone 648.00 (3.48)2.82 (0.38)4.70 (0.26)9.12 (0.21)
Limestone 789.12 (4.70)5.90 (0.45)8.01 (0.34)1.78 (0.23)
Limestone 855.60 (5.11)4.47 (0.48)5.15 (0.35)7.94 (0.19)
Limestone 991.00 (3.81)6.01 (0.41)9.03 (0.32)1.30 (0.25)
Limestone 1096.97 (2.98)5.88 (0.37)9.07 (0.24)1.47 (0.13)
Limestone 1170.35 (3.77)4.90 (0.39)6.70 (0.26)3.30 (0.24)
Limestone 1282.96 (4.02)6.43 (0.40)8.61 (0.29)2.07 (0.17)
1 The value in the bracket is standard deviation.
Table 5. The UCS, PLI, and BTS in the study of Khajevand [18].
Table 5. The UCS, PLI, and BTS in the study of Khajevand [18].
Rock TypeUCS (MPa)PLI (MPa)BTS (MPa)
Limestone50.1310.3250.13
Limestone25.198.2025.19
Limestone51.5111.8651.51
Limestone39.126.9039.12
Limestone21.605.7921.60
Limestone46.827.9146.82
Sandstone46.298.856.67
Sandstone32.466.545.38
Sandstone16.095.803.81
Sandstone32.514.364.95
Sandstone24.653.944.65
Sandstone10.823.492.61
Table 6. The UCS, PLI, and BTS in the study of Teymen and Menguc [56].
Table 6. The UCS, PLI, and BTS in the study of Teymen and Menguc [56].
Rock TypeUCS (MPa)PLI (MPa)BTS (MPa)
Limestone140.925.8912.53
Limestone236.199.6916.55
Limestone191.745.9412.00
Limestone97.623.938.59
Limestone40.893.096.55
Limestone108.403.796.55
Limestone133.003.5310.06
Limestone100.806.7910.45
Limestone101.354.409.36
Limestone131.585.8710.55
Limestone122.203.868.79
Limestone106.754.868.87
Sandstone97.645.848.56
Sandstone24.292.813.98
Sandstone80.485.058.29
Sandstone66.982.484.32
Sandstone126.606.5410.27
Table 7. The UCS, PLI, and BTS in the study of Jamshidi et al. [59].
Table 7. The UCS, PLI, and BTS in the study of Jamshidi et al. [59].
Rock TypeUCS (MPa)PLI (MPa)BTS (MPa)
Sandstone54.44.06.3
Sandstone65.06.17.0
Sandstone63.95.27.1
Sandstone42.22.75.9
Sandstone56.34.16.5
Sandstone44.52.56.0
Sandstone69.04.67.4
Sandstone49.85.05.8
Sandstone32.12.14.5
Sandstone59.34.86.8
Table 8. The UCS, PLI, and BTS in the study of Lakirouhani et al. [60].
Table 8. The UCS, PLI, and BTS in the study of Lakirouhani et al. [60].
Rock TypeUCS (MPa)PLI (MPa)BTS (MPa)
Limestone31.843.1531.84
Limestone27.622.5727.62
Limestone24.692.4124.69
Limestone22.652.1722.65
Limestone20.372.7320.37
Limestone16.381.6716.38
Limestone24.472.8624.47
Limestone25.972.1525.97
Limestone20.481.7120.48
Limestone14.261.6514.26
Limestone9.181.439.18
Limestone10.301.0510.30
Limestone43.935.6643.93
Limestone32.311.8332.31
Limestone39.372.9139.37
Limestone30.101.5930.10
Limestone34.012.2334.01
Limestone32.522.1532.52
Limestone35.223.4335.22
Limestone27.671.3227.67
Limestone43.004.8843.00
Limestone44.933.2344.93
Limestone63.514.4963.51
Limestone48.704.4548.70
Limestone45.662.4745.66
Limestone39.381.6539.38
Limestone40.312.0640.31
Limestone38.652.5738.65
Limestone38.062.0538.06
Limestone83.817.3883.81
Limestone65.826.2365.82
Limestone65.453.8365.45
Table 9. The statistical test results of the simple and multiple correlation equations developed in the present study (data from Table 4).
Table 9. The statistical test results of the simple and multiple correlation equations developed in the present study (data from Table 4).
Equation No.Equation TypeR2RMSE (MPa)F ValueF Sig.
ComputedTabulated
(5)UCS = 27.08e0.193PLI0.827.25--0.000
(6)UCS = 77.53 + 2.91PLI − 4.50n0.924.2854.964.260.000
(7)UCS = 68.86ln(BTS) − 58.820.924.49--0.000
(8)UCS = 54.96 + 4.54BTS − 3.17n0.943.9664.844.260.000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Jamshidi, A.; Sousa, L. Accuracy of Point Load Index and Brazilian Tensile Strength in Predicting the Uniaxial Compressive Strength of the Rocks: A Comparative Study. Materials 2024, 17, 5081. https://doi.org/10.3390/ma17205081

AMA Style

Jamshidi A, Sousa L. Accuracy of Point Load Index and Brazilian Tensile Strength in Predicting the Uniaxial Compressive Strength of the Rocks: A Comparative Study. Materials. 2024; 17(20):5081. https://doi.org/10.3390/ma17205081

Chicago/Turabian Style

Jamshidi, Amin, and Luís Sousa. 2024. "Accuracy of Point Load Index and Brazilian Tensile Strength in Predicting the Uniaxial Compressive Strength of the Rocks: A Comparative Study" Materials 17, no. 20: 5081. https://doi.org/10.3390/ma17205081

APA Style

Jamshidi, A., & Sousa, L. (2024). Accuracy of Point Load Index and Brazilian Tensile Strength in Predicting the Uniaxial Compressive Strength of the Rocks: A Comparative Study. Materials, 17(20), 5081. https://doi.org/10.3390/ma17205081

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop