Measuring the Electro-Optical Kerr Effect Against the Background of Electro-Absorption Modulation in Liquids
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Idea of the Measurement Method
2.2. Measurements with a Non-Ideal Quarter-Wave Plate
2.3. Experimental Material
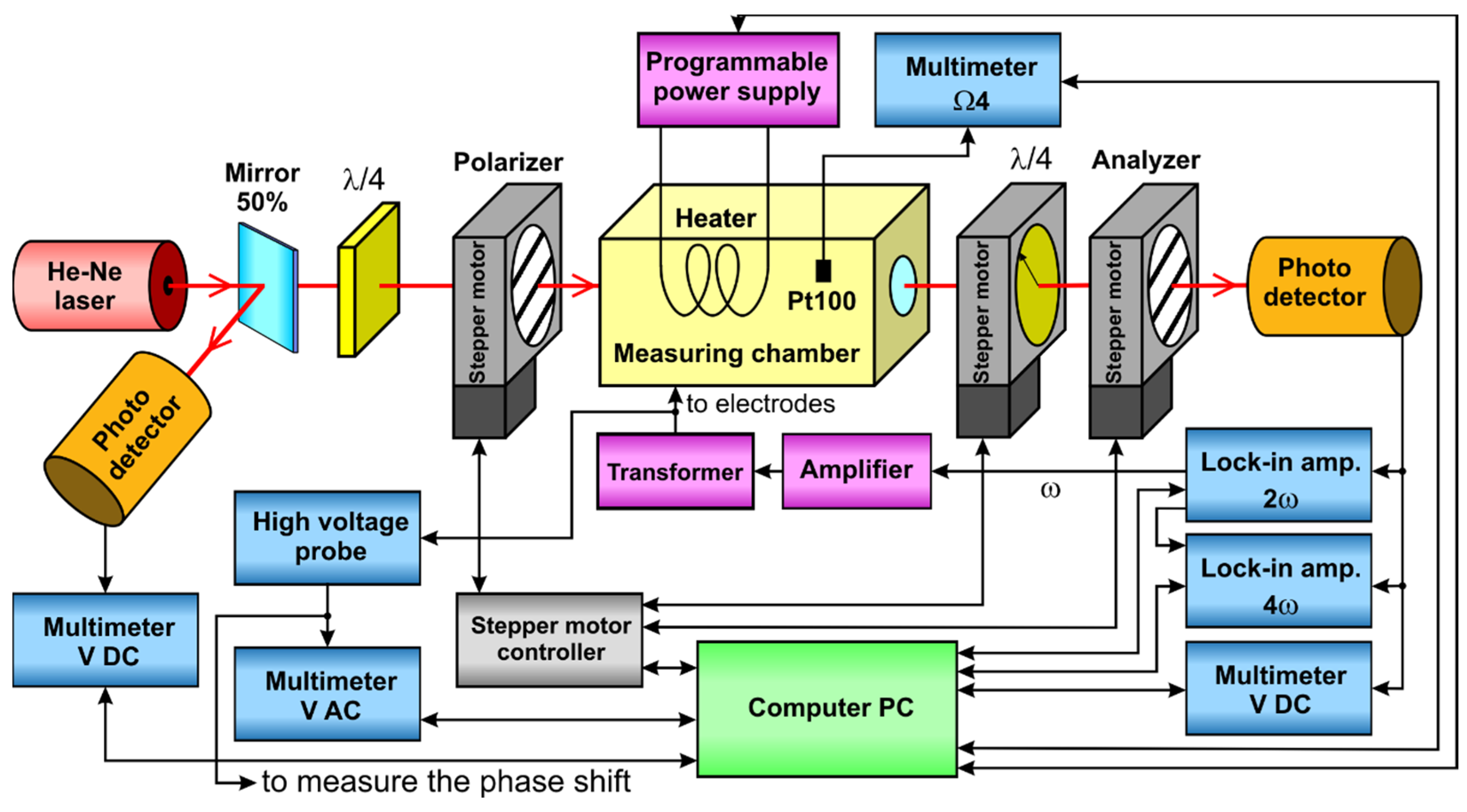
3. Experiment
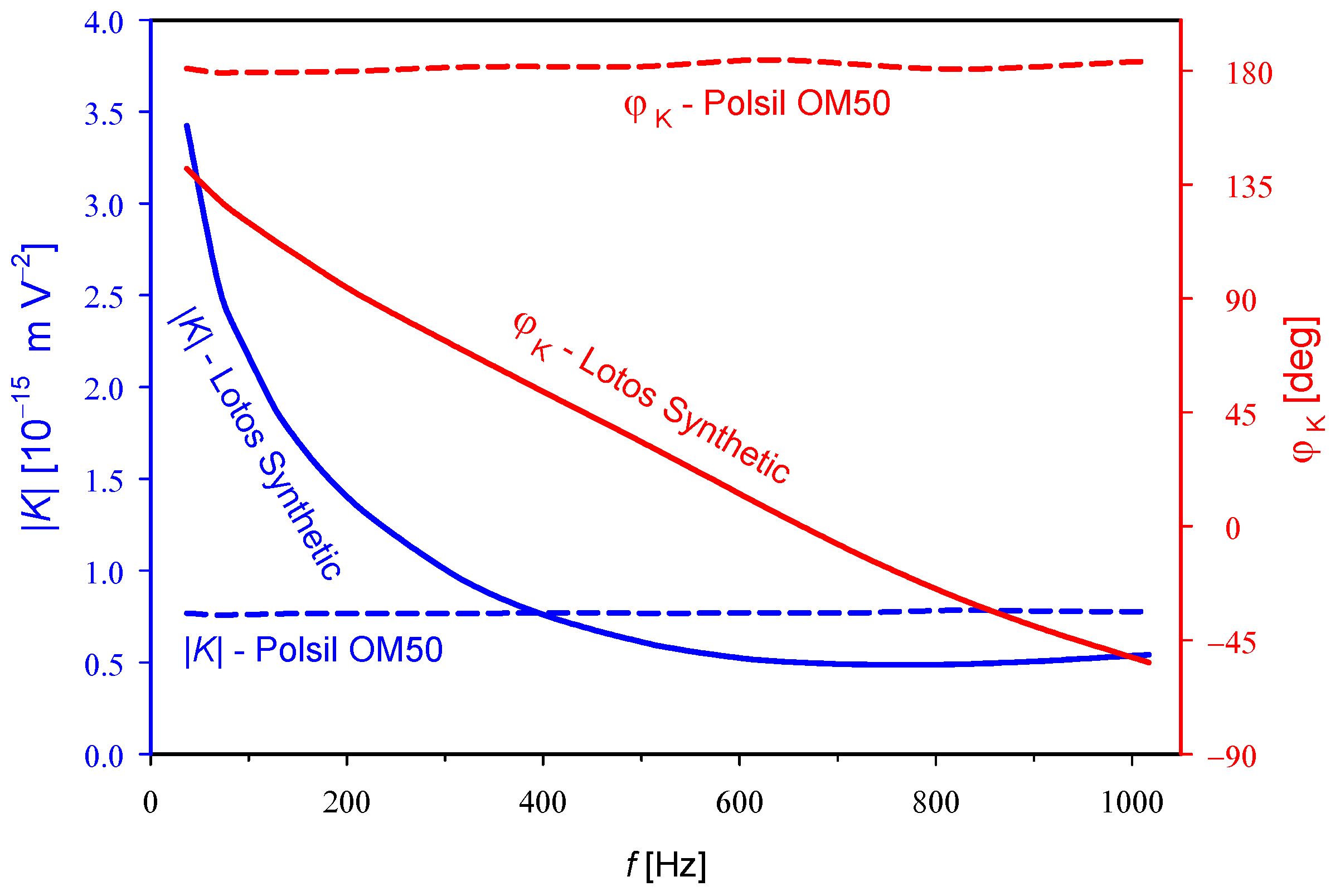
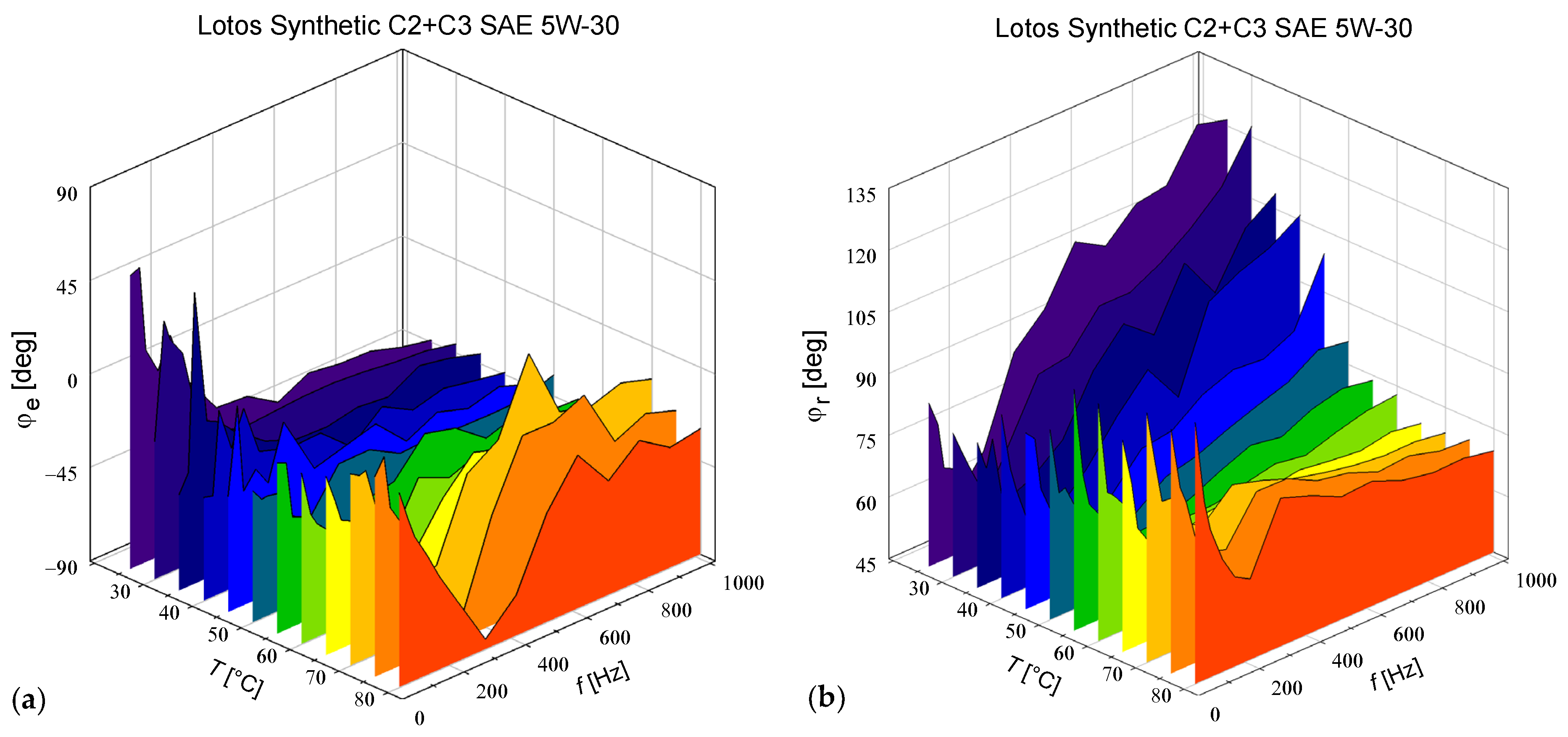
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Equation (37)
References
- Chartier, G. Introduction to Optics; Springer: New York, NY, USA, 2005; pp. 207–213. [Google Scholar]
- Abd-Elsalam, M.; Abdel-Salam, M.; Wiitanen, D.; Perger, W. A new laser voltmeter. Meas. Sci. Technol. 1993, 4, 311–320. [Google Scholar] [CrossRef]
- Zahn, M.; Hanaoka, R. Kerr electro-optic measurements of transformer oil in a point-plane geometry. In Proceedings of the 1994 4th International Conference on Properties and Applications of Dielectric Materials (ICPADM), Brisbane, QLD, Australia, 3–8 July 1994; Volume 2, pp. 697–700. [Google Scholar] [CrossRef]
- Nakamura, K.; Kato, K.; Koide, H.; Hatta, Y.; Okubo, H. Fundamental property of electric field in rapeseed ester oil based on Kerr electro-optic measurements. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 601–607. [Google Scholar] [CrossRef]
- Izdebski, M.; Ledzion, R.; Węgrzynowski, S. Extremely weak electro-optic Kerr effect in methyl silicone oils. Materials 2024, 17, 1850. [Google Scholar] [CrossRef] [PubMed]
- Ledzion, R.; Bondarczuk, K.; Górski, P.; Kucharczyk, W. Kerr constants of some mineral and silicone oils. Quantum. Electron. 1999, 29, 739–741. [Google Scholar] [CrossRef]
- Mousavi, Z.; Majles Ara, M.H.; Ghafary, B. Effect of time and frequency on the electro-optical Kerr constant of olive oil blended with natural turmeric dye. Opt. Mater. 2020, 100, 109609. [Google Scholar] [CrossRef]
- Kucharczyk, W.; Ledzion, R.; Górski, P. The effect of aging of transformer oil on the magnitude and temperature dependence of its Kerr constant. Przegląd Elektrotechniczny Electr. Rev. 2014, 12, 40–42. [Google Scholar] [CrossRef]
- Stępień, M.; Ledzion, R.; Górski, P.; Kucharczyk, W. Effect of ageing on the magnitude and temperature dependence of the Kerr constant in the castor oil used in pharmacy. Sci. Bulletin. Phys. 2012, 33, 89–95. [Google Scholar] [CrossRef]
- Hashempour-baltork, F.; Zade, S.V.; Mazaheri, Y.; Alizadeh, A.M.; Rastegar, H.; Abdian, Z.; Torbati, M.; Damirchi, S.A. Recent methods in detection of olive oil adulteration: State-of-the-Art. J. Agric. Food Res. 2024, 16, 101123. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Raab, R.E. A molecular theory of the electro-optical Kerr effect in liquids. J. Chem. Soc. 1957, 2341–2351. [Google Scholar] [CrossRef]
- Berne, B.J. A self-consistent theory of rotational diffusion. J. Chem. Phys. 1975, 62, 1154–1160. [Google Scholar] [CrossRef]
- Deshmukh, S.D.; Déjardin, P.M.; Kalmykov, Y.P. Dynamic Kerr effect in a strong uniform AC electric field for interacting polar and polarizable molecules in the mean field approximation. J. Chem. Phys. 2017, 147, 094501. [Google Scholar] [CrossRef] [PubMed]
- Aillerie, M.; Théofanous, N.; Fontana, M.D. Measurement of the electro-optic coefficients: Description and comparison of the experimental techniques. Appl. Phys. B 2000, 70, 317–334. [Google Scholar] [CrossRef]
- Aillerie, M.; Abdi, F.; Fontana, M.D.; Théofanous, N.; Abarkan, E. Accurate measurements of the electro-optic coefficients and birefringence changes using an external modulation signal. Rev. Sci. Instrum. 2000, 71, 1627–1634. [Google Scholar] [CrossRef]
- Izdebski, M. Precise measurements of the quadratic electro-optic effect in KH2PO4 crystals using a Sénarmont-type system. Materials 2021, 14, 5435. [Google Scholar] [CrossRef] [PubMed]
- Scierski, J.; Ratajczyk, F. The Jones matrix of the real dichroic elliptic object. Optik 1984, 68, 121–125. [Google Scholar]
- Izdebski, M.; Ledzion, R. Kerr constant measurement technique for liquids exhibiting orientational ordering of molecules. Optik 2017, 140, 812–822. [Google Scholar] [CrossRef]
- Wei, R.; Yang, B.; Ming, X.; Wang, S.; Cao, W.; Pan, R.; Zheng, K.; Sun, Z.; Liu, F.; He, X.; et al. Measurement of electro-optical coefficients based on the Stokes vectors. Measurement 2021, 167, 108287. [Google Scholar] [CrossRef]
- LOTOS SYNTHETIC C2+C3 SAE 5W-30, Material Safety Data Sheet. Available online: https://market.lotos.pl/sdscards/currentsds.aspx?number=LO/7/14&language=PL (accessed on 22 September 2024).
- Poborska, J.; Dąbrówka, D.; Chwirot, M.; Ledzion, R.; Izdebski, M.; Kucharczyk, W. Frequency dependence of the Kerr constant in Nynas Nytro 3000 oil determined by the polarimetric method. Sci. Bulletin. Phys. 2018, 39, 37–44. [Google Scholar] [CrossRef]
- Imai, K.; Kanematsu, A.; Nawata, M.; Zahn, M. Kerr constant frequency dependence in liquid nitrogen. In Proceedings of the 3rd International Conference on Properties and Applications of Dielectric Materials, Tokyo, Japan, 8–12 July 1991; Volume 1, pp. 280–283. [Google Scholar] [CrossRef]
- Hebner, R.E.; Misakian, M. Temperature dependence of the electro-optic Kerr coefficient of nitrobenzene. J. Appl. Phys. 1979, 50, 6016–6017. [Google Scholar] [CrossRef]
- Rajagopal, K.; Prasada Rao, T.A. Temperature dependence of Kerr coefficient of some homologous liquids. J. Mol. Liq. 1996, 68, 95–105. [Google Scholar] [CrossRef]
- Rajagopal, K.; Prasadarao, T.A. Temperature dependence of Kerr coefficient of binary liquid mixtures of aprotic-aprotic molecules. Phys. Chem. Liq. 2000, 38, 35–47. [Google Scholar] [CrossRef]
- Silicon Oils—Silikony Polskie Ltd. Technical Data Sheet. Available online: https://www.sklep.silikonypolskie.pl/pl/c/Oleje/332 (accessed on 22 September 2024).
- Buckingham, A.D. Frequency dependence of the Kerr constant. Proc. R. Soc. Lond. A 1962, 267, 271–282. [Google Scholar] [CrossRef]

| Measurement Model | Average CV(K) [-] | Average s(φK) [deg] | ||
| All Frequencies | at 37 Hz | All Frequencies | at 37 Hz | |
| Section 2.2, Equation (37) | 0.0056 | 0.011 | 0.14 | 0.26 |
| Section 2.1, Equation (33) | 0.044 | 0.050 | 0.31 | 0.63 |
| Section 3, Equation (45) | 0.045 | 0.063 | 2.22 | 6.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ledzion, R.; Izdebski, M.; Rambo, A. Measuring the Electro-Optical Kerr Effect Against the Background of Electro-Absorption Modulation in Liquids. Materials 2024, 17, 5346. https://doi.org/10.3390/ma17215346
Ledzion R, Izdebski M, Rambo A. Measuring the Electro-Optical Kerr Effect Against the Background of Electro-Absorption Modulation in Liquids. Materials. 2024; 17(21):5346. https://doi.org/10.3390/ma17215346
Chicago/Turabian StyleLedzion, Rafał, Marek Izdebski, and Anita Rambo. 2024. "Measuring the Electro-Optical Kerr Effect Against the Background of Electro-Absorption Modulation in Liquids" Materials 17, no. 21: 5346. https://doi.org/10.3390/ma17215346
APA StyleLedzion, R., Izdebski, M., & Rambo, A. (2024). Measuring the Electro-Optical Kerr Effect Against the Background of Electro-Absorption Modulation in Liquids. Materials, 17(21), 5346. https://doi.org/10.3390/ma17215346






