Study on the Characteristics of Circumferential and Longitudinal Flow of Vault Concrete during Tunnel Lining Pouring Processes
Abstract
:1. Introduction
2. Selection and Accuracy Verification of Rheological Parameters
2.1. Concrete Flow Test
2.1.1. Test Raw Materials
- 1
- Concrete
- 2
- Fine aggregate
- 3
- Coarse aggregate
- 4
- Fly ash
- 5
- Water reducing agent
- 6
- Water
2.1.2. Test Working Conditions
2.1.3. Brief Description of Tests and Results
- 1
- Rheometer test
- 2
- Slump extension test
- 3
- L-box flow test
2.2. Verification of the Accuracy of Rheological Parameters
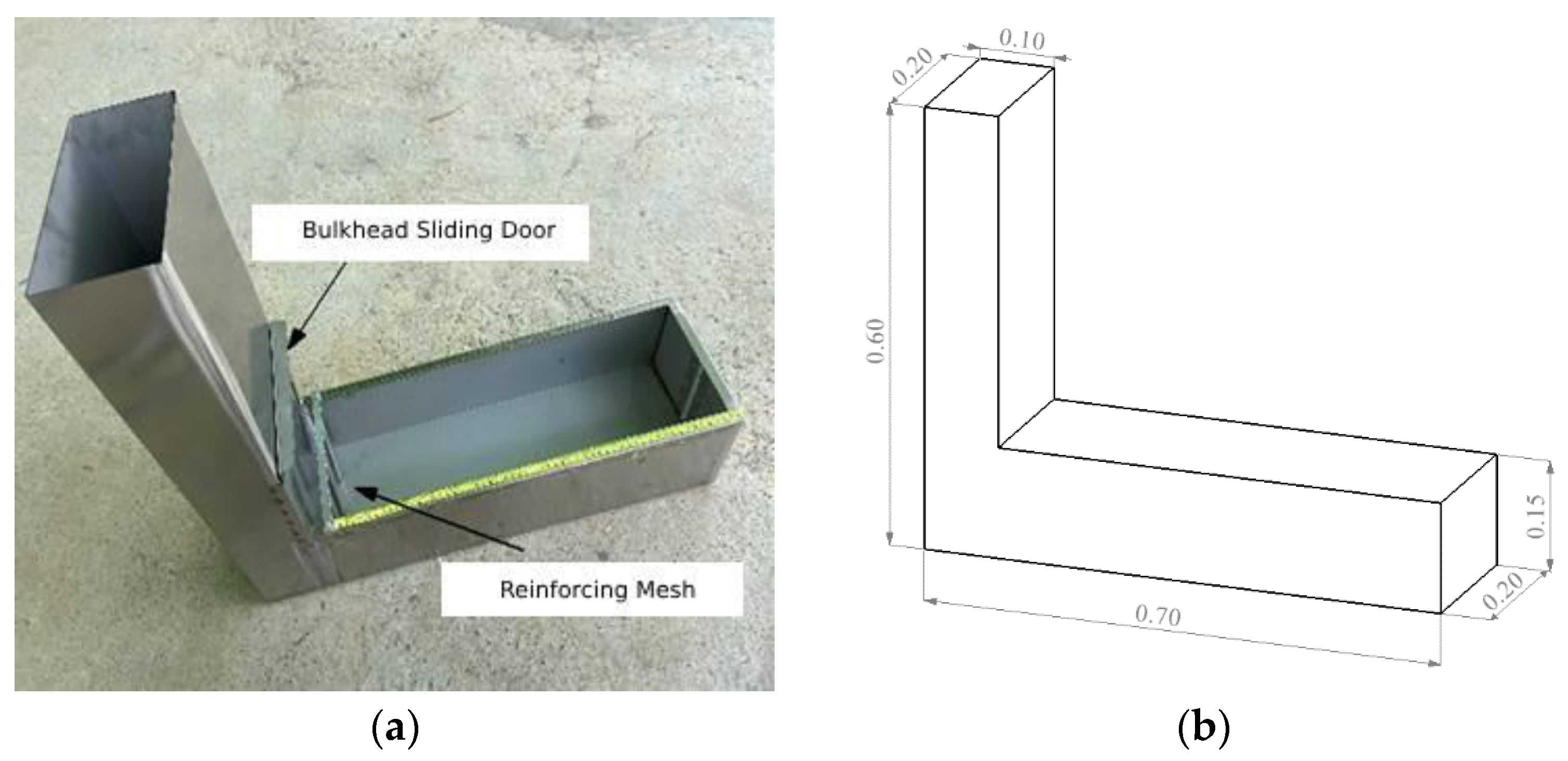
2.2.1. Numerical Simulation of Slump Test
2.2.2. Numerical Simulation of L-Box Tests
3. Simulation and Characterization of Circumferential Concrete Flow in Vaults
- (1)
- Considering the more realistic 2D simulation program, the vault area was divided into two regions: the vault ring direction and the vault longitudinal direction;
- (2)
- In the process of the pouring simulation, enhancing the concrete flow performance by inserting vibrating rods and attaching vibrators was not considered;
- (3)
- Only the effect of reinforcement perpendicular to the concrete flow direction in the lining on the concrete was considered.
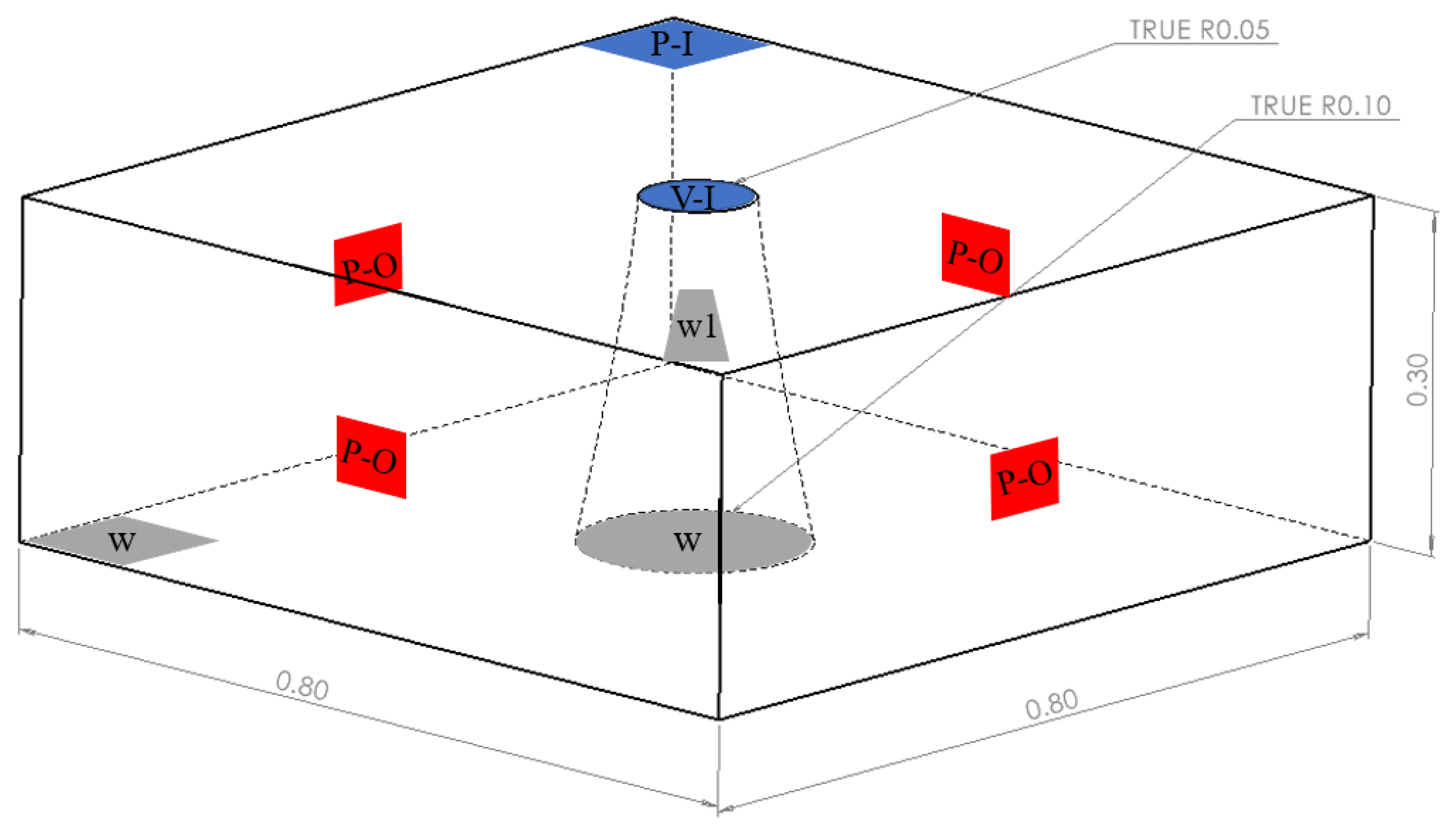
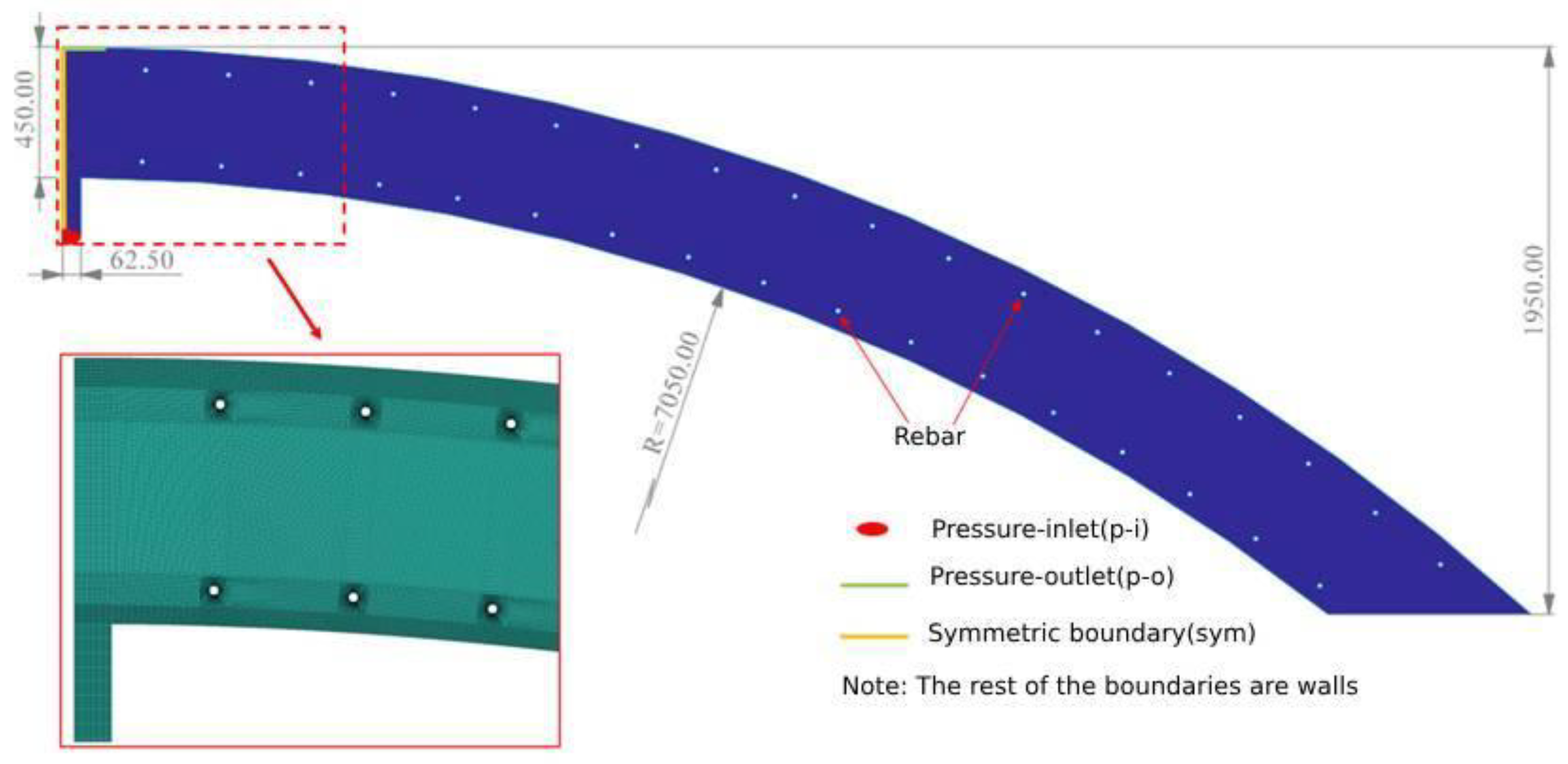
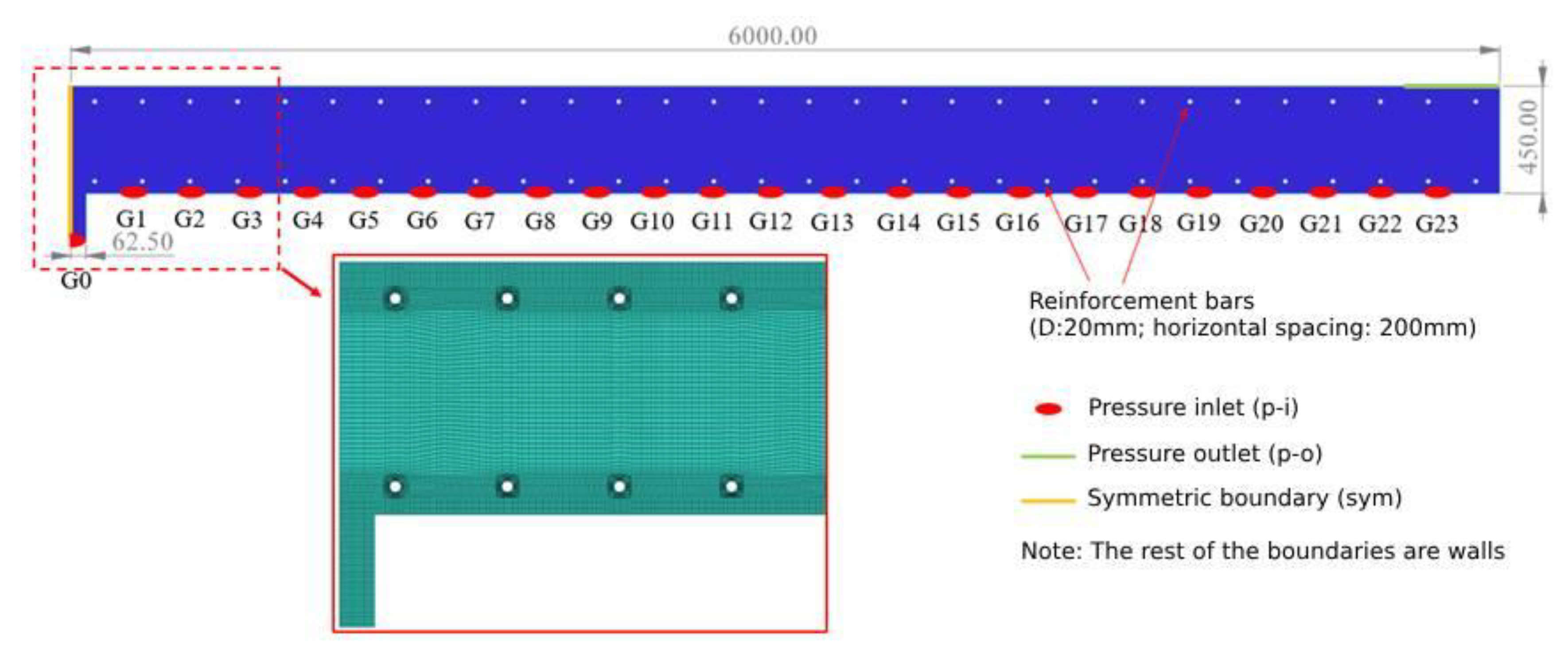
3.1. Model Introduction and Boundary Condition Setting
3.2. Selection of Calculation Working Conditions
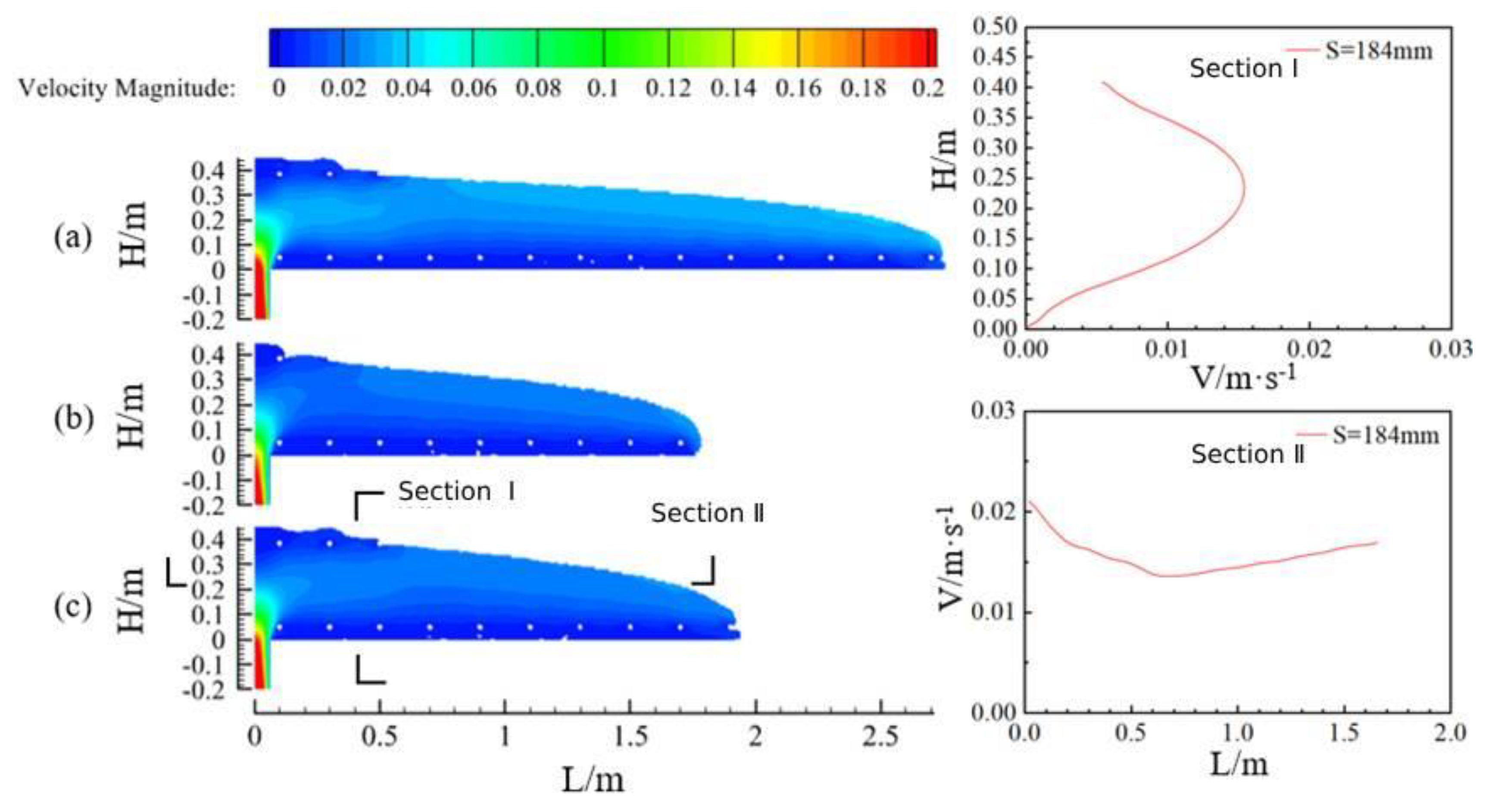
3.3. Concrete Flow Characteristics under Different Slumps
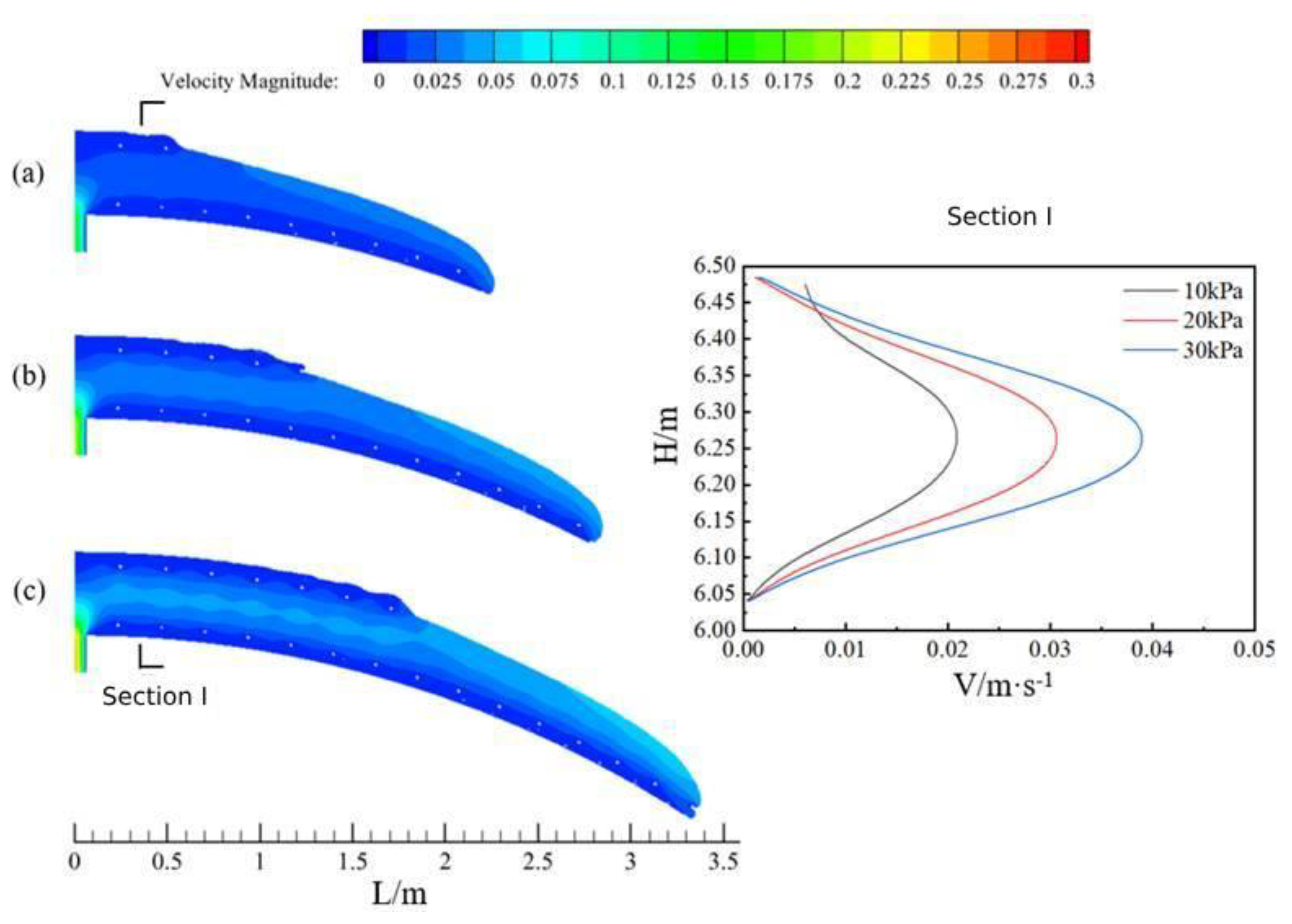
3.4. Characteristics of Concrete Circumferential Flow under Different Pumping Pressures
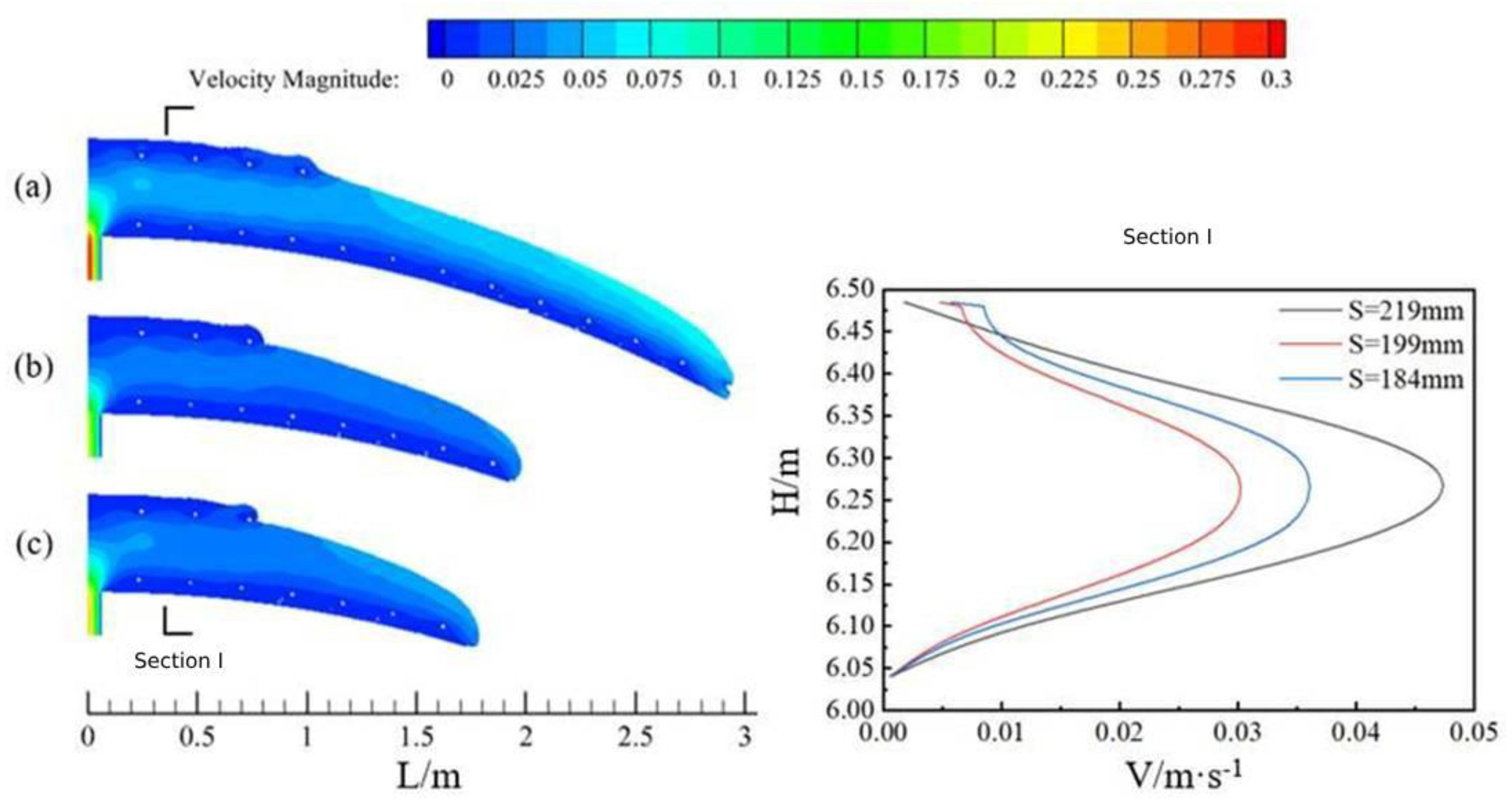
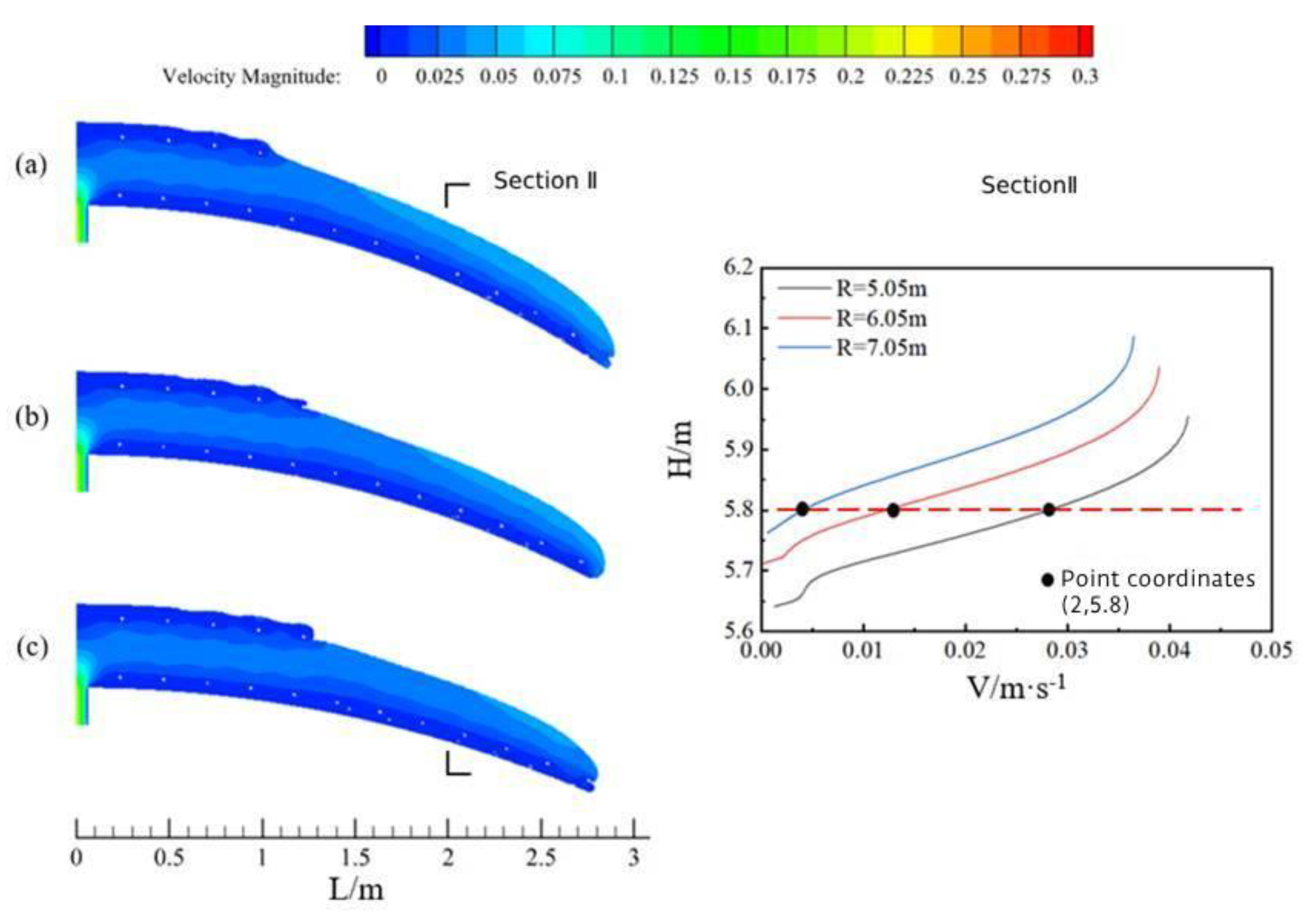
3.5. Concrete Circumferential Flow Characteristics under Different Lining Radius
4. Simulation and Characterization of Longitudinal Concrete Flow in Vaults
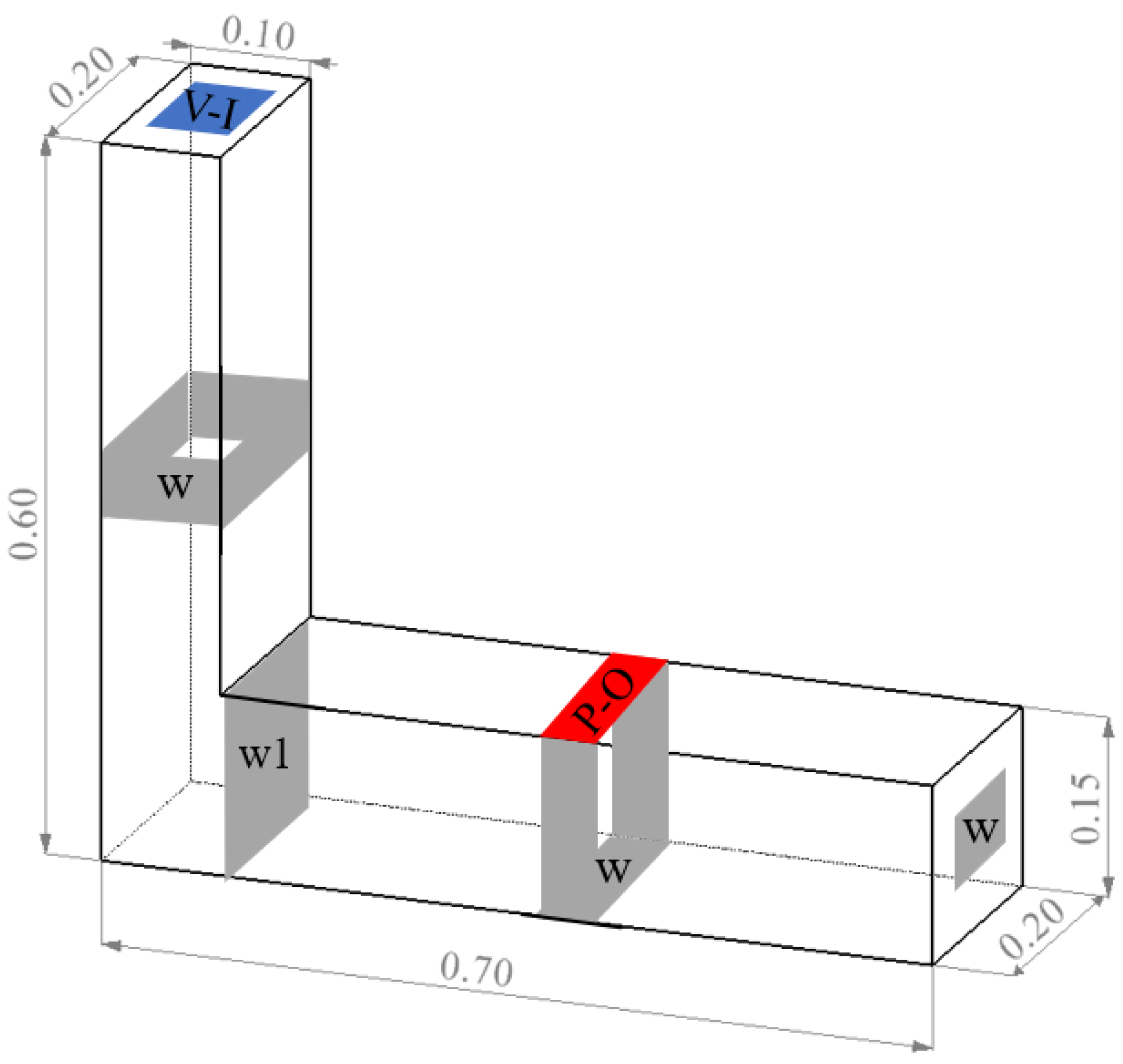
4.1. Model Introduction and Boundary Condition Setting
4.2. Selection of Calculation Working Conditions
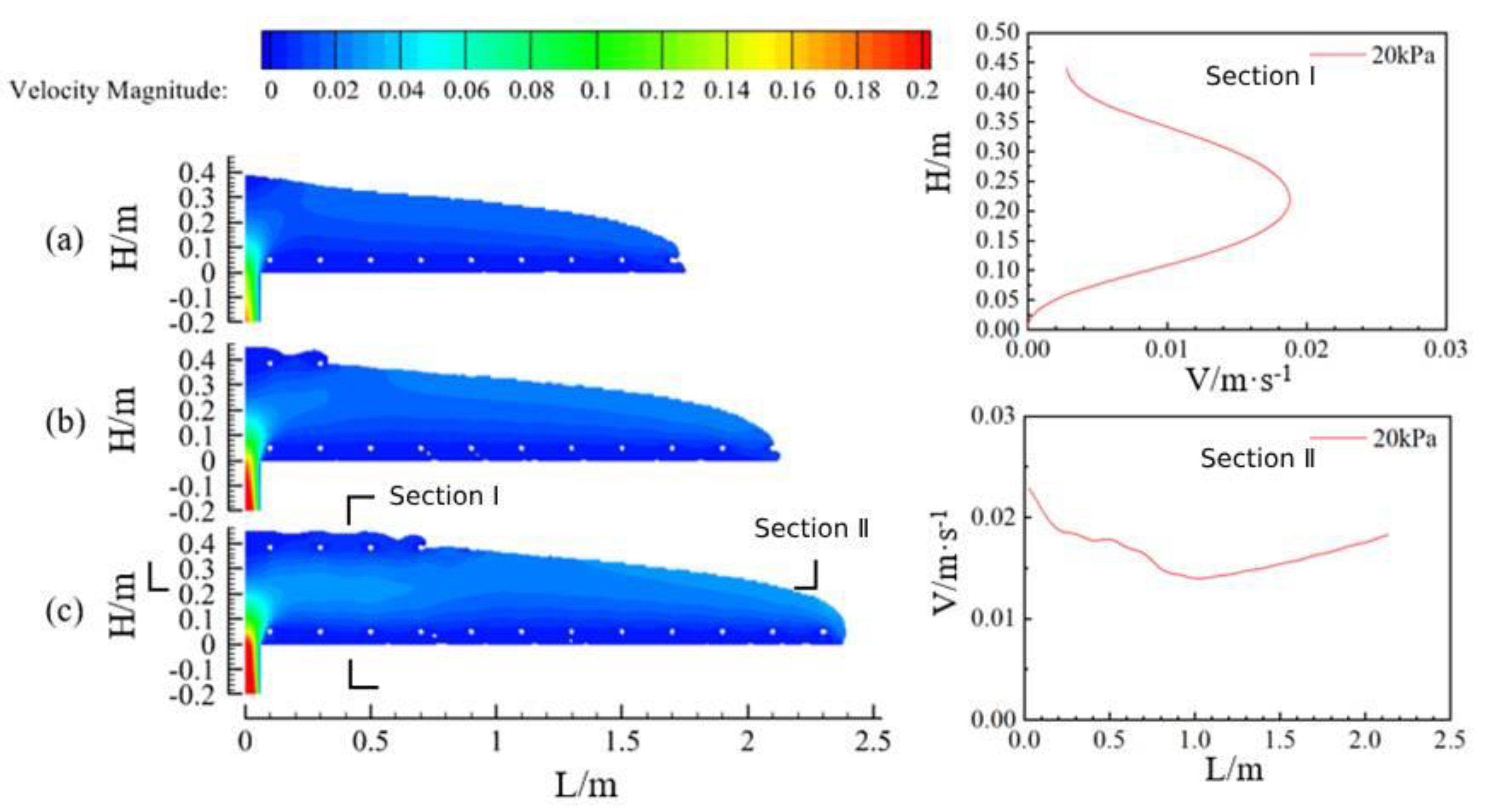
4.3. Longitudinal Flow Characteristics of Concrete under Different Slumps
4.4. Longitudinal Flow Characteristics of Concrete under Different Pumping Pressures
5. Conclusions
- The circumferential and longitudinal flow of concrete in the vault shows two major flow characteristics before and after. The flow characteristics near the filling hole area are similar to the flow characteristics of the concrete in the pumping pipe. The area between the lowest reinforcement and the bottom plate and the uppermost reinforcement and the top plate is the lubrication layer, and has a low flow rate. The middle is the core area, and has a high flow rate. The concrete at the front end presents a layered flow phenomenon as a whole, and the upper layer of the concrete has a higher speed. It gradually gets closer to the bottom plate and the speed is reduced during the forward pouring process and achieves the forward transport of concrete.
- In the process of vault casting, the larger the concrete slump, the larger the pumping pressure. The smaller the radius of the tunnel, the higher the flow rate of the overall cross-section at the same moment, and the farther the concrete movement. Therefore, in the actual project, according to the tunnel radius, concrete slump, pumping pressure, and other construction conditions can be the reasonable design of longitudinal filling hole spacing.
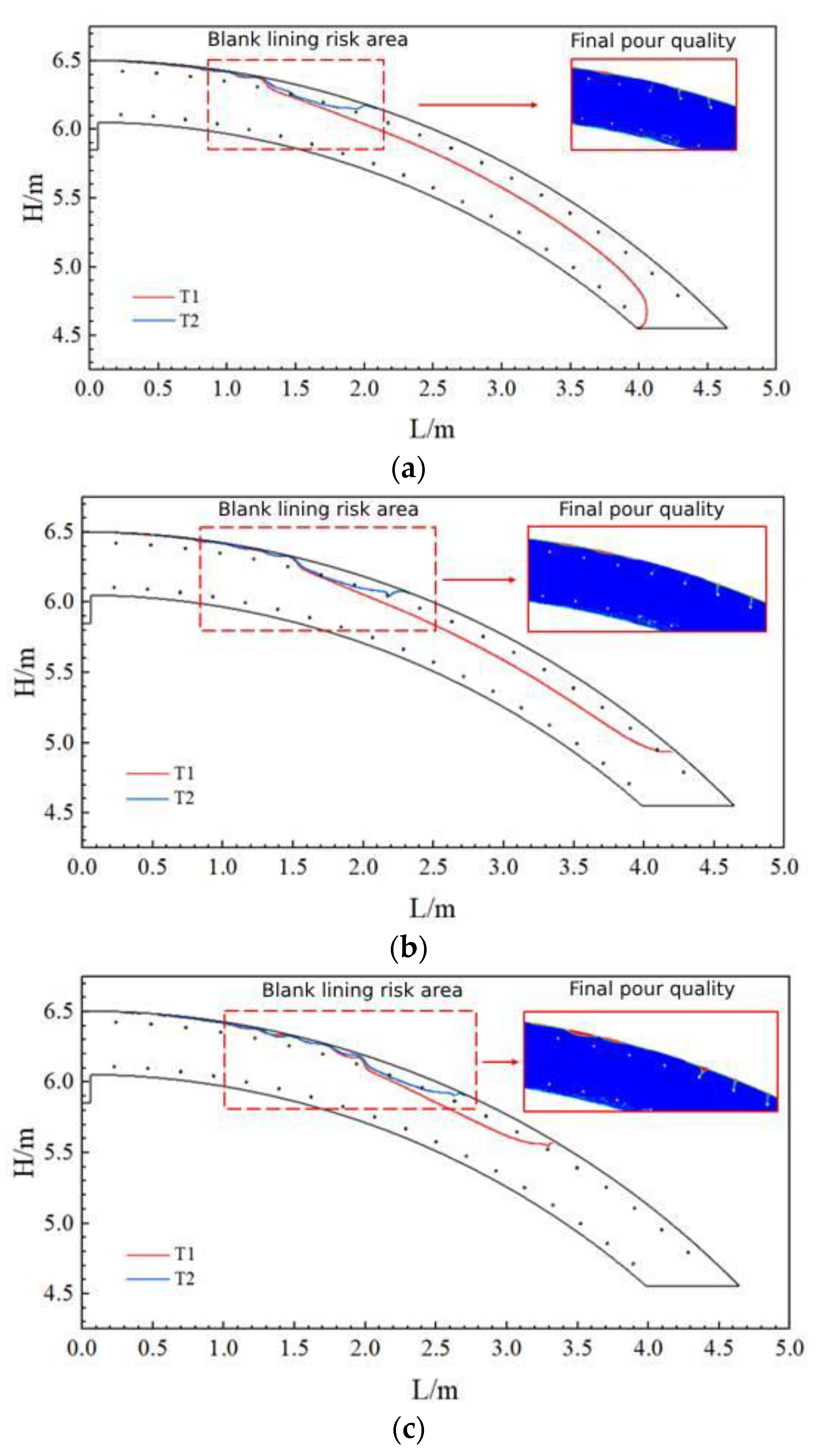
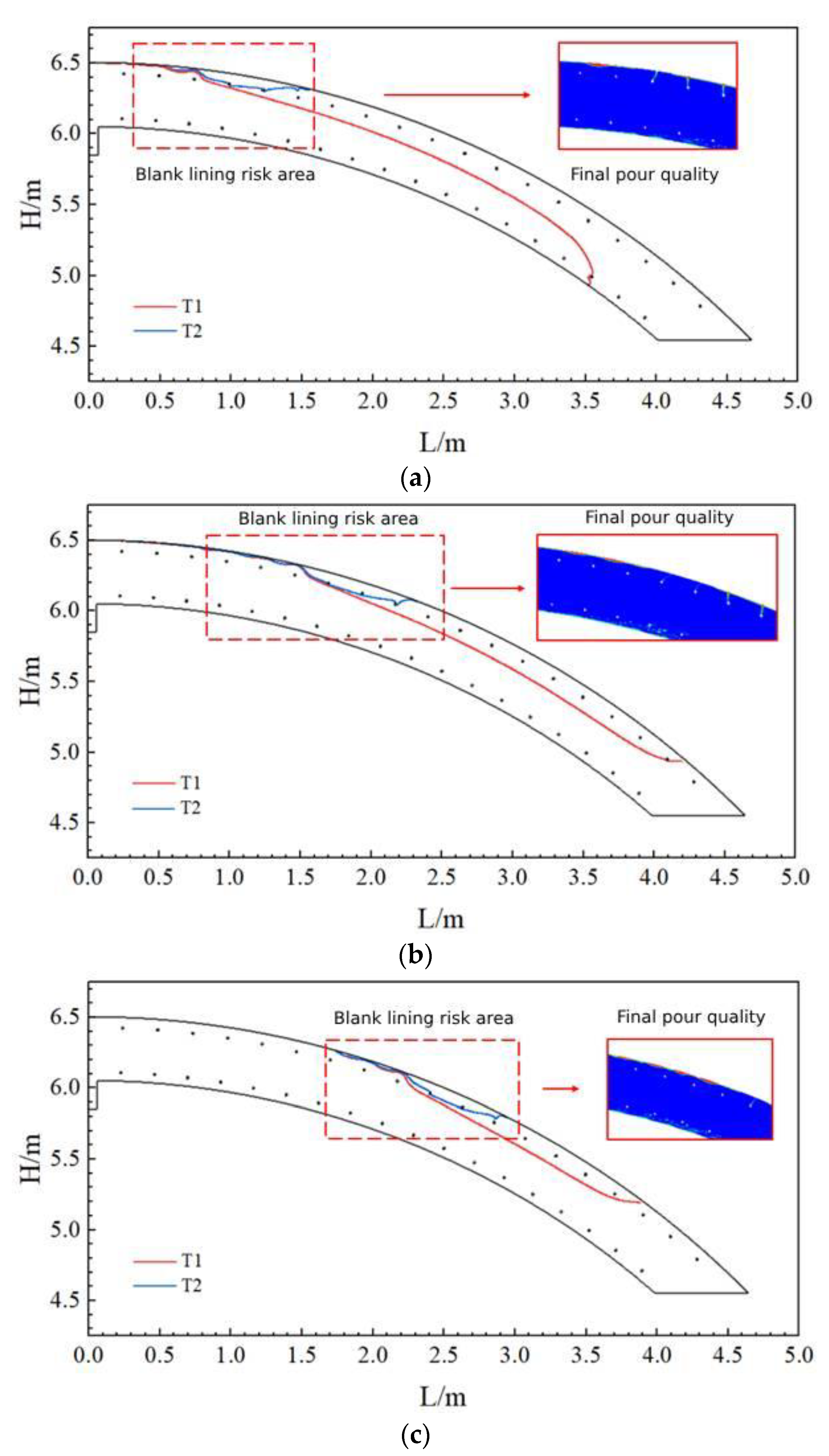
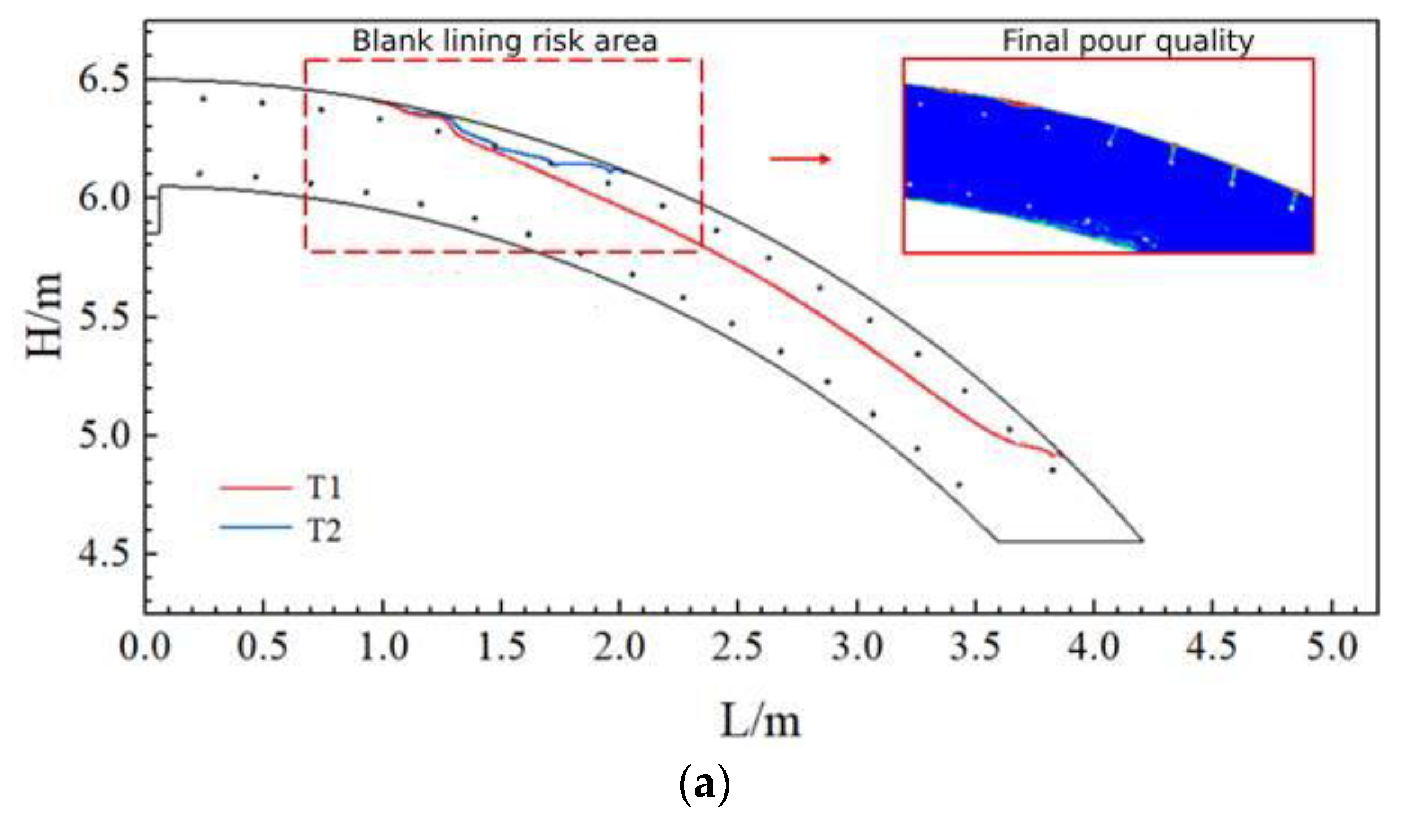
- During the casting process of the arch, the region from the arch to the arch shoulder was prone to the risk of blank lining. The higher the slump of the concrete, the lower the pumping pressure. Also, the smaller the radius of the tunnel cross-section, the higher the blank lining risk zone will be, and the closer it will be to the filling hole. Therefore, in order to avoid the phenomenon of blank lining during the casting of the secondary lining of the tunnel, optimization of the position of the uppermost pouring window of the lining trolley (by appropriately elevating the window position) must occur.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Afshani, A.; Kawakami, K.; Konishi, S.; Akagi, H. Study of Infrared Thermal Application for Detecting Defects within Tunnel Lining. Tunn. Undergr. Space Technol. 2019, 86, 186–197. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Zhang, B.; Dai, X.; Ye, J.; Sun, B.; Liu, N.; Wang, Z.; Zhao, Y. Tunnel Lining Detection and Retrofitting. Autom. Constr. 2023, 152, 104881. [Google Scholar] [CrossRef]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional Networks and Transformers for Intelligent Road Tunnel Investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Voulodimos, A.; Doulamis, A.; Doulamis, N.; Stathaki, T. Automatic Crack Detection for Tunnel Inspection Using Deep Learning and Heuristic Image Post-Processing. Appl. Intell. 2019, 49, 2793–2806. [Google Scholar] [CrossRef]
- Yao, Q.; Qi, S.; Wu, F.; Yang, X.; Li, H. Abrasion-Resistant and Temperature Control of Lining Concrete for Large-Sized Spillway Tunnels. Appl. Sci. 2020, 10, 7614. [Google Scholar] [CrossRef]
- Oreste, P.; Spagnoli, G.; Luna Ramos, C.A.; Hedayat, A. Assessment of the Safety Factor Evolution of the Shotcrete Lining for Different Curing Ages. Geotech. Geol. Eng. 2019, 37, 5555–5563. [Google Scholar] [CrossRef]
- Hao, S.; Fei, R. Optimisation Study on Crack Resistance of Tunnel Lining Concrete Under High Ground Temperature Environment. Geotech. Geol. Eng. 2022, 40, 3985–4006. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, B.; Li, H.; Zhang, H. The Performance of Mechanical Characteristics and Failure Mode for Tunnel Concrete Lining Structure in Water-Rich Layer. Tunn. Undergr. Space Technol. 2022, 121, 104335. [Google Scholar] [CrossRef]
- Han, W.; Jiang, Y.; Wang, G.; Liu, C.; Koga, D.; Luan, H. Review of Health Inspection and Reinforcement Design for Typical Tunnel Quality Defects of Voids and Insufficient Lining Thickness. Tunn. Undergr. Space Technol. 2023, 137, 105110. [Google Scholar] [CrossRef]
- Iskhakov, T.; Timothy, J.J.; Plückelmann, S.; Breitenbücher, R.; Meschke, G. Compressible Cementitious Composite Materials: Multiscale Modeling and Experimental Investigation. Cem. Concr. Compos. 2023, 142, 105174. [Google Scholar] [CrossRef]
- Moradi, P.; Asadi, M.J.; Ebrahimzadeh, N.; Yarahmadi, B. Ilam Tunnels Inspection, Maintenance, and Rehabilitation: A Case Study. Tunn. Undergr. Space Technol. 2021, 110, 103814. [Google Scholar] [CrossRef]
- Wu, Y.; Shao, S.; Fu, H.; Liu, D.; Liu, C.; Ma, Z. Analysis of Tunnel Lining Vault Void and Methods of Active Monitoring and Prevention. China Saf. Sci. J. 2019, 29, 186–191. [Google Scholar]
- Krenzer, K.; Mechtcherine, V.; Palzer, U. Simulating Mixing Processes of Fresh Concrete Using the Discrete Element Method (DEM) under Consideration of Water Addition and Changes in Moisture Distribution. Cem. Concr. Res. 2019, 115, 274–282. [Google Scholar] [CrossRef]
- Kolařík, F.; Patzák, B.; Zeman, J. Computational Homogenization of Fresh Concrete Flow around Reinforcing Bars. Comput. Struct. 2018, 207, 37–49. [Google Scholar] [CrossRef]
- Haustein, M.A.; Eslami Pirharati, M.; Fataei, S.; Ivanov, D.; Jara Heredia, D.; Kijanski, N.; Lowke, D.; Mechtcherine, V.; Rostan, D.; Schäfer, T.; et al. Benchmark Simulations of Dense Suspensions Flow Using Computational Fluid Dynamics. Front. Mater. 2022, 9, 874144. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Bos, F.P.; Perrot, A.; Da Silva, W.R.L.; Nerella, V.N.; Fataei, S.; Wolfs, R.J.M.; Sonebi, M.; Roussel, N. Extrusion-Based Additive Manufacturing with Cement-Based Materials—Production Steps, Processes, and Their Underlying Physics: A Review. Cem. Concr. Res. 2020, 132, 106037. [Google Scholar] [CrossRef]
- Caliendo, C.; Russo, I. A 3D Computational Fluid Dynamics Model for Assessing the Concrete Spalling of a Tunnel Lining in the Event of a Fire. Comput. Geotech. 2022, 152, 105041. [Google Scholar] [CrossRef]
- Chen, J.; Martin, P.; Xu, Z.; Manzano, H.; Dolado, J.S.; Ye, G. A Dissolution Model of Alite Coupling Surface Topography and Ions Transport under Different Hydrodynamics Conditions at Microscale. Cem. Concr. Res. 2021, 142, 106377. [Google Scholar] [CrossRef]
- Sassi, R.; Jelidi, A.; Montassar, S. Numerical Simulation of Fresh Concrete Flow in the L-Box Test Using Computational Fluid Dynamics. Mag. Concr. Res. 2023, 75, 1189–1201. [Google Scholar] [CrossRef]
- Gu, Q. Investigation on Flow Characteristics of Wet Concrete Conveyed by Compressed Gas and Anti-Blocking of Pipeline Vibration. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2022. [Google Scholar]




| Density (g/cm3) | Specific Surface Area (m2/kg) | Water Consumption for Standard Consistency (%) | Condensation Time (min) | Stability | 28 d Compressive Strength (Mpa) | |
|---|---|---|---|---|---|---|
| Initial Setting | Final Setting | |||||
| 3.15 | 360 | 28 | 175 | 235 | Eligible | 49 |
| Modulus of Fineness | Mud Content (%) | Apparent Density (kg/m3) | Stacking Density (kg/m3) | Dense Voids (%) |
|---|---|---|---|---|
| 2.73 | 1.61 | 2602.6 | 1670.8 | 35.8 |
| Density (g/cm3) | Specific Surface Area (m2/kg) | Water Requirement Ratio (%) | 45 μm Sieve Residue (%) | Stability | Loss on Burnout (%) |
|---|---|---|---|---|---|
| 2.15 | 450 | 103 | 18 | Eligible | 6.73 |
| Grouping Number | Cement | Admixture | Fine Aggregate | Coarse Aggregate 1 | Coarse Aggregate 2 | Additives | Water | Water-Cement Ratio | Sand Ratio | Water Reducing Agent Dosage |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 291 | 125 | 749 | 323 | 749 | 4.16 | 178 | 0.43 | 0.41 | 1% |
| M2 | 299 | 128 | 749 | 323 | 749 | 4.16 | 167 | 0.39 | 0.41 | 1% |
| M3 | 294 | 127 | 749 | 323 | 749 | 4.16 | 173 | 0.41 | 0.41 | 1% |
| M4 | 287 | 123 | 749 | 323 | 749 | 4.16 | 184 | 0.45 | 0.41 | 1% |
| M5 | 283 | 122 | 749 | 323 | 749 | 4.16 | 189 | 0.47 | 0.41 | 1% |
| M6 | 291 | 125 | 674 | 345 | 802 | 4.16 | 178 | 0.43 | 0.37 | 1% |
| M7 | 291 | 125 | 710 | 334 | 777 | 4.16 | 178 | 0.43 | 0.39 | 1% |
| M8 | 291 | 125 | 783 | 312 | 726 | 4.16 | 178 | 0.43 | 0.43 | 1% |
| Grouping Number | (Pa) | (Pa·s) |
|---|---|---|
| M1 | 140 | 136 |
| M2 | 687 | 139 |
| M3 | 447 | 142 |
| M4 | 188 | 127 |
| M5 | 126 | 107 |
| M6 | 926 | 438 |
| M7 | 544 | 176 |
| M8 | 312 | 225 |
| Grouping Number | Mean Value of Slump S (mm) | (mm) |
|---|---|---|
| M1 | 201 | 503 |
| M2 | 165 | 459 |
| M3 | 181 | 477 |
| M4 | 208 | 515 |
| M5 | 219 | 529 |
| M6 | 173 | 470 |
| M7 | 184 | 491 |
| M8 | 199 | 517 |
| Grouping Number | T200 (s) | T300 (s) | T400 (s) | T500 (s) | T600 (s) | T700 (s) |
|---|---|---|---|---|---|---|
| M1 | 2.5 | 3.9 | 5.3 | 6.0 | 8.2 | 11.5 |
| M2 | 3.1 | 5.4 | 7.3 | 10.9 | 19.1 | 32.2 |
| M3 | 2.5 | 3.4 | 4.7 | 7.5 | 12.4 | 23.7 |
| M4 | 2.2 | 3.1 | 4.3 | 5.8 | 8.1 | 11.4 |
| M5 | 1.8 | 2.7 | 3.8 | 5.0 | 6.1 | 7.3 |
| M6 | 3.4 | 6.3 | 11.5 | 21.0 | 35.8 | - |
| M7 | 3.3 | 5.1 | 8.7 | 13.9 | 21.5 | 30.4 |
| M8 | 2.6 | 4.5 | 6.8 | 10.6 | 16.1 | 22.3 |
| Test Condition | Slump (mm) | Extension (mm) | ||||
|---|---|---|---|---|---|---|
| Test Value | Numerical Solution | Error (%) | Test Value | Numerical Solution | Error (%) | |
| M1 | 201 | 218 | 8.5 | 503 | 523 | 4.0 |
| M2 | 165 | 190 | 15.2 | 459 | 479 | 4.4 |
| M3 | 181 | 202 | 11.6 | 477 | 490 | 2.7 |
| M4 | 208 | 223 | 7.2 | 515 | 522 | 1.4 |
| M5 | 219 | 229 | 4.6 | 529 | 524 | 0.9 |
| M6 | 173 | 194 | 12.1 | 470 | 478 | 1.7 |
| M7 | 184 | 199 | 8.2 | 491 | 521 | 6.1 |
| M8 | 199 | 208 | 4.5 | 517 | 537 | 3.9 |
| Condition | Projects | T200 (s) | T300 (s) | T400 (s) | T500 (s) | T600 (s) | T700 (s) |
|---|---|---|---|---|---|---|---|
| M1 | Test Value | 2.5 | 3.9 | 5.3 | 6.0 | 8.2 | 11.5 |
| Numerical Solution | 0.6 | 1.3 | 2.4 | 3.5 | 5.3 | 9.4 | |
| M2 | Test Value | 3.1 | 5.4 | 7.3 | 10.9 | 19.1 | 32.2 |
| Numerical Solution | 0.9 | 2.1 | 3.8 | 7.7 | 15.4 | 26.8 | |
| M3 | Test Value | 2.5 | 3.4 | 4.7 | 7.5 | 12.4 | 23.7 |
| Numerical Solution | 0.8 | 1.8 | 3.1 | 5.4 | 10.4 | 19.0 | |
| M4 | Test Value | 2.2 | 3.1 | 4.3 | 5.8 | 8.1 | 11.4 |
| Numerical Solution | 0.6 | 1.3 | 2.3 | 3.5 | 5.6 | 10.3 | |
| M5 | Test Value | 1.8 | 2.7 | 3.8 | 5.0 | 6.1 | 7.3 |
| Numerical Solution | 0.5 | 1.1 | 1.9 | 2.9 | 4.3 | 7.6 | |
| M6 | Test Value | 3.4 | 6.3 | 11.5 | 21.0 | 35.8 | - |
| Numerical Solution | 1.6 | 4.2 | 8.3 | 15.2 | 26.1 | 41.1 | |
| M7 | Test Value | 3.3 | 5.1 | 8.7 | 13.9 | 21.5 | 30.4 |
| Numerical Solution | 0.9 | 2.1 | 3.7 | 7.1 | 13.8 | 24.2 | |
| M8 | Test Value | 2.6 | 4.5 | 6.8 | 10.6 | 16.1 | 22.3 |
| Numerical Solution | 0.9 | 2.0 | 3.3 | 5.6 | 10.3 | 18.0 |
| Grouping Number | Yield Stress (Pa) | (Pa·s) | Slump (mm) | Extension (mm) |
|---|---|---|---|---|
| M5 | 126 | 107 | 219 | 529 |
| M7 | 544 | 176 | 184 | 491 |
| M8 | 312 | 225 | 199 | 517 |
| Cases | (Pa) | (Pa·s) | Model Radius (m) | Pumping Pressure (kpa) |
|---|---|---|---|---|
| Case1 | 126 | 107 | 6.05 | 20 |
| Case2 | 312 | 225 | 6.05 | 20 |
| Case3 | 544 | 176 | 6.05 | 20 |
| Case4 | 312 | 225 | 6.05 | 10 |
| Case5 | 312 | 225 | 6.05 | 30 |
| Case6 | 312 | 225 | 5.05 | 20 |
| Case7 | 312 | 225 | 7.05 | 20 |
| Cases | (Pa) | Pumping Pressure (kpa) | |
|---|---|---|---|
| Case1 | 126 | 107 | 20 |
| Case2 | 312 | 225 | 20 |
| Case3 | 544 | 176 | 20 |
| Case4 | 312 | 225 | 10 |
| Case5 | 312 | 225 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Wu, Y.; Zhou, Z. Study on the Characteristics of Circumferential and Longitudinal Flow of Vault Concrete during Tunnel Lining Pouring Processes. Materials 2024, 17, 678. https://doi.org/10.3390/ma17030678
Yang S, Wu Y, Zhou Z. Study on the Characteristics of Circumferential and Longitudinal Flow of Vault Concrete during Tunnel Lining Pouring Processes. Materials. 2024; 17(3):678. https://doi.org/10.3390/ma17030678
Chicago/Turabian StyleYang, Shuai, Yimin Wu, and Zhuangzhuang Zhou. 2024. "Study on the Characteristics of Circumferential and Longitudinal Flow of Vault Concrete during Tunnel Lining Pouring Processes" Materials 17, no. 3: 678. https://doi.org/10.3390/ma17030678




