Next Article in Journal
Ductility Variation and Improvement of Strain-Hardening Cementitious Composites in Structural Utilization
Next Article in Special Issue
First-Principles Investigation into the Interaction of H2O with α-CsPbI3 and the Intrinsic Defects within It
Previous Article in Journal
Machining Surface Improvement through Electric- and Flow-Field Adjustments in Flying Electrochemical Milling of AA 2219
Previous Article in Special Issue
Revealing the Influence of SiC Particle Size on the Hot Workability of SiCp/6013 Aluminum Matrix Composites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 17
Issue 4
10.3390/ma17040830
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants

by
Veronica Manescu (Paltanea)
1,2,
Gheorghe Paltanea
2,
Aurora Antoniac
1,*,
Lucian Gheorghe Gruionu
3,
Alina Robu
1,
Marius Vasilescu
1,
Stefan Alexandru Laptoiu
1,
Ana Iulia Bita
1,*,
Georgiana Maria Popa
4,
Andreea Liliana Cocosila
4,
Vlad Silviu
4 and
Anca Porumb
5
1
Faculty of Material Science and Engineering, National University of Science and Technology Politehnica Bucharest, 313 Splaiul Independentei, District 6, RO-060042 Bucharest, Romania
2
Faculty of Electrical Engineering, National University of Science and Technology Politehnica Bucharest, 313 Splaiul Independentei, District 6, RO-060042 Bucharest, Romania
3
Faculty of Mechanics, University of Craiova, 13 Alexandru Ioan Cuza, RO-200585 Craiova, Romania
4
Department of Surgical Disciplines, Faculty of Medicine and Pharmacy, University of Oradea, 10 P-ta 1 December Street, RO-410073 Oradea, Romania
5
Department of Dental Medicine, Faculty of Medicine and Pharmacy, University of Oradea, 10 P-ta 1 December Street, RO-410073 Oradea, Romania
*
Authors to whom correspondence should be addressed.
Materials 2024, 17(4), 830; https://doi.org/10.3390/ma17040830
Submission received: 16 December 2023 / Revised: 26 January 2024 / Accepted: 3 February 2024 / Published: 8 February 2024
(This article belongs to the Special Issue Study on Advanced Metal Matrix Composites (2nd Edition))
Browse Figures
Versions Notes

Abstract

:
Today, mechanical properties and fluid flow dynamic analysis are considered to be two of the most important steps in implant design for bone tissue engineering. The mechanical behavior is characterized by Young’s modulus, which must have a value close to that of the human bone, while from the fluid dynamics point of view, the implant permeability and wall shear stress are two parameters directly linked to cell growth, adhesion, and proliferation. In this study, we proposed two simple geometries with a three-dimensional pore network dedicated to a manufacturing route based on a titanium wire waving procedure used as an intermediary step for Mg-based implant fabrication. Implant deformation under different static loads, von Mises stresses, and safety factors were investigated using finite element analysis. The implant permeability was computed based on Darcy’s law following computational fluid dynamic simulations and, based on the pressure drop, was numerically estimated. It was concluded that both models exhibited a permeability close to the human trabecular bone and reduced wall shear stresses within the biological range. As a general finding, the proposed geometries could be useful in orthopedics for bone defect treatment based on numerical analyses because they mimic the trabecular bone properties.

1. Introduction

Lately, one can notice that the continuous development of the tissue engineering domain is growing fast and becoming appealing for researchers investigating biocompatible material manufacture and artificial bone substitutes. It is estimated that man-made grafts will cover an important part of the worldwide tissue demand, so a reduction in the number of autografts and allografts, which are considered today as the “gold standard”, could be foreseen [1,2]. Three-dimensional (3D) porous implants or scaffolds exhibiting various geometries are used to treat patients who need a complex and difficult surgical intervention generated by a hard tissue absence due to an accident, infections of the primary endoprosthesis, or bone oncological pathologies. Schemitsch et al. [3] classified bone defects. They considered small defects as those that present a size lower than 2 cm and a cortical bone circumference loss below 50%. Intermediate bone defects have geometrical dimensions between 2 cm and 6 cm and a circumference loss higher than 50%, and large bone defects with a minimum size of 6 cm are considered critical-size defects. It is well known that such defects cannot spontaneously heal during the patients’ lives. On the other hand, for defects smaller than 2.5 cm, a natural healing process with no scars is observed [4,5]. When a bone substitute is present, the bone healing mechanism consists of new bone formation around the implant, stabilizing its position at the bone defect place. The osteogenesis process strongly depends on the implant’s chemical composition and surface topography [6]. Starting with the moment when the implant is inserted into the patient’s body, it enters into contact with human blood, leading to platelet apparition and activation on the implant surface. This phenomenon simultaneously occurs with an inflammatory process generated by the macrophages and neutrophils that ends with hematoma formation. Thrombocytes and leucocytes create a beneficial medium for mesenchymal stem cell (MSC) recruitment. This type of cell will differentiate into osteoblasts through the contact osteogenesis process. The osteoblasts will later form a layer-by-layer substrate at the bone defect zone along the bone edges [7]. The new bone formation also occurs in the opposite direction, oriented from bone edges to implant, in the framework of a phenomenon known in the literature as distance osteogenesis [6]. Contact and distance osteogenesis are important in new and immature bone formation, filling the free space between the implant and the bone. The bone remodeling process in the peri-implant zone substitutes the immature bone with a mature one, resulting in increased mechanical resistance of the bond between the human bone and implant. This process is continuous and has an important contribution to securing the connections that occur at the bone–implant interface. However, in some cases, implant demobilization and failure are present due to insufficient development of the bone in the peri-implant area caused by a specific disease or the stress shielding effect, which consists of a mismatch between the Young’s modulus value of bone and implant.
Different production techniques for implants were developed based on an additive manufacturing process, which permits obtaining anatomical configurations and using many biocompatible materials [8,9]. In addition, designing an implant with adequate architecture similar to the human bone is a complex procedure. One should consider the pore size, shape, and implant total porosity [10]. The literature research evidenced that the implant porosity must be between 25% and 90%, and the pore size has to be included in the following interval, starting with 10 μm and ending with 1000 μm [11,12,13]. All these parameters exhibit an important influence on the implant’s mechanical properties and biocompatibility. A high porosity must be considered when the implant is populated with cells, and beneficial conditions with properties characteristic for increased cell viability are necessary [14]. Concomitantly with the abovementioned advantage, highly porous structures are associated with decreased mechanical properties. As a direct consequence, implant porosity must be correctly chosen to entirely respect bone’s mechanical properties and the application for which it is designed. The medical performance of an implant depends on material properties, topological requirements, and production parameters. Generally, after the implants are manufactured, they are populated with cells developed and multiplied inside a bioreactor before the implantation step.
The most important mechanical properties of orthopedic implants are the elasticity modulus and the yield strength because these implants are usually used in load-bearing zones [15,16]. The human bone has a Young’s modulus between 0.5 GPa and 20 GPa [17,18]. This parameter is essential and must be considered when an implant dedicated to orthopedics is designed. For high-elasticity modulus values, it can be noticed that the implant porosity is reduced and can be useful for intense mechanical solicitation zones [19]. The beneficial effect of mechanical stimuli against the differentiation and proliferation of living cells inside the implant is well known, so the elasticity modulus can be considered one of the most adequate mechanical properties for cell activity monitoring. Finite element analysis (FEA) is considered one of the most important steps in orthopedic implant design today because its geometry can be controlled and modified without the involvement of expensive and invasive experimental mechanical tests, which are usually based on many samples.
The design method and fabrication parameters are chosen as a function of fluid transport capabilities through the implant because the flow of blood or simulated body fluid used in bioreactors for cell development is essential for oxygen and nutrient delivery and also to eliminate the carbon dioxide and waste through blood circulation [20,21]. The biological behavior strongly depends on the fluid–implant interaction, resulting in the wall shear stress (WSS) that is of utmost importance for the cell’s overall viability. Experimental fluid flow analyses are expensive and characterized by numerous limitations, such as high costs, long observation time, and precise results without fluid flow perturbations. An easy solution consists of computational fluid dynamics (CFD) analysis, which is considered an appropriate way to understand and predict the in vivo performance of an implant. This method permits the implant permeability computation [22,23]. The fluid pressure and the wall shear stress have a major impact on the mechanical stimulation of the cells by influencing the level of nitric oxide, which is an important parameter in the human body [24]. Different studies [24,25,26,27,28] proved that WSS influenced the pluripotent stem cells’ differentiation into osteoblasts, cardiac cells, or endothelial cells. It was noticed that values of WSS below 30 mPa had a positive effect on MSC activity, proliferation, and differentiation. At the same time, for values between 0.11 and 10 mPa, increased differentiation of stem cells into osteogenic cells was evidenced, while for WSS comprising a 0.55–24 mPa interval, an accelerated hard tissue mineralization was noticed [29]. The literature revealed that WSS values higher than 60 mPa are in a direct relationship with cellular death [30,31,32,33,34].
Implant material plays an important role in establishing its mechanical and biological performance. Many investigations reported as adequate for bone tissue engineering various biodegradable materials from different classes, such as polymers (polycaprolactone, polyglycolic acid, polylactic acid) [35,36,37], ceramics (tricalcium phosphate, bioglasses) [38,39,40], and metals (zinc and magnesium-based alloys) [4,41,42,43,44,45].
In the present study, we have chosen a biodegradable commercial Mg-based alloy (Mg-Nd-Y-Zr-Zn) produced by Dead See Magnesium Be’er Sheva, Israel, and traded under the name MRI201S. This paper’s aim consists of designing and analyzing two geometrical configurations, which will be practically manufactured as a future study based on a combination of an additive-manufactured polymeric matrix and titanium wire orthogonal waving procedure. Firstly, we will print the two proposed geometries based on fused deposition modeling technology using biodegradable and biocompatible polymers. Then, inside the matrix pores, we will insert and wave Ti6Al4V (medical Ti Grade 5) wires with different diameters. After that, the polymer matrix will be dissolved based on the immersion of Ti-polymer structures in dedicated solvents. The resulting titanium waving will be introduced in a liquid magnesium alloy, and a biocompatible bi-metallic structure will be obtained. We will eliminate the Ti6Al4V wires by introducing the structure mentioned above in hydrofluoric acid, and the Mg parts will be unaffected [46], so we expect to obtain similar geometries to those analyzed in this paper.
Many studies were conducted in the literature that analyzed the mechanical and fluid flow behaviors of implants with different geometric architectures. They found that Young’s modulus and porosity values are very important and must be considered together when the mechanical properties are analyzed. Hutmacher et al. [10] underlined that designing and manufacturing an ideal scaffold could be very complicated, and many parameters must be considered. They recommended that analyzing composite materials and simple implant geometries is the easiest way to modify and consider adequate bone tissue engineering (BTE) geometries. Boccaccio et al. [14] developed a mechanobiology-based algorithm to optimize BTE implant microstructure. The authors considered mechanical analyses expensive and destructive, and performing an FEA during the first stage of implant design compulsory. They searched for an ideal geometry by considering parameters such as pore shapes, their spatial positions, and the number of pores per unit area. Based on Young’s modulus computation and comparing these values with those of human bone, the authors concluded that the rectangular pore structure was characterized by a more considerable predicted amount of new bone compared to the square pores. In addition, elliptic pores proved to be much more beneficial to cell development than circular ones. It can be noticed that the implant geometry features are very important, and simple geometries are preferable over complicated ones because they are much more practically realizable. Nune et al. [16] chose a mesh structure made of biocompatible Ti alloy that proved to sustain the cell development and viability. The implant showed a Young’s modulus of about 4.36 GPa and a porosity of 70%. Ali and Sen [47] designed gyroid- and lattice-based architecture implants with regulated and commonly used geometries. They performed FEA and CFD analysis by choosing Ti6Al4V as the implant material and water as the fluid. They concluded that the mechanical properties of the implant were in the biological range. Still, regarding the CFD analysis, higher permeability and lower WSS values were obtained for the lattice-based models. Zhao et al. [48] investigated the fluid shear stress in BTE implants with cubical and spherical pore architectures. They provided a mathematical approach that can be followed in experiments to estimate the wall shear stress as a function of pore size, total porosity, and entire architecture. One can also notice that simple and regulated geometries were preferred in this case. The authors concluded that combining the FEA and CFD analysis is of utmost importance in implant design and offered information regarding the biological range for WSS, implant materials, and mechanical testing conditions. Much more complex structures were developed by Li et al. [49], which were based on patient medical images of vertebral cancellous tissue. Although the implant design is much more realistic in this case, precise control, optimization, and modification of the geometrical parameters are hard to obtain, and expensive devices are needed, so as a direct consequence, much more effort must be conducted to achieve adequate mechanical properties and fluid flow behavior in the biological range. Fallah et al. [50] designed and made practical innovative designs of BTE implants. Unfortunately, these structures are very hard to implement for Mg-based scaffolds due to the necessity of expensive printing devices, which are suitable in most cases for the additive manufacturing of polymeric scaffolds. Considering the state of the art in the literature, we designed and analyzed two simple implant geometries that can be practically implemented as described above to validate the proposed design through future experimental testing. In our opinion, our implants can be manufactured through an innovative method that does not involve expensive and complicated devices, and their properties are similar to those produced through additive manufacturing of magnesium. Our method can avoid some dangerous situations that can occur in other cases due to the magnesium powder’s pyrophoric character.
Figure 1 presents a general process diagram that must be followed when 3D implants for bone tissue engineering are designed.

2. Modeling and Simulation

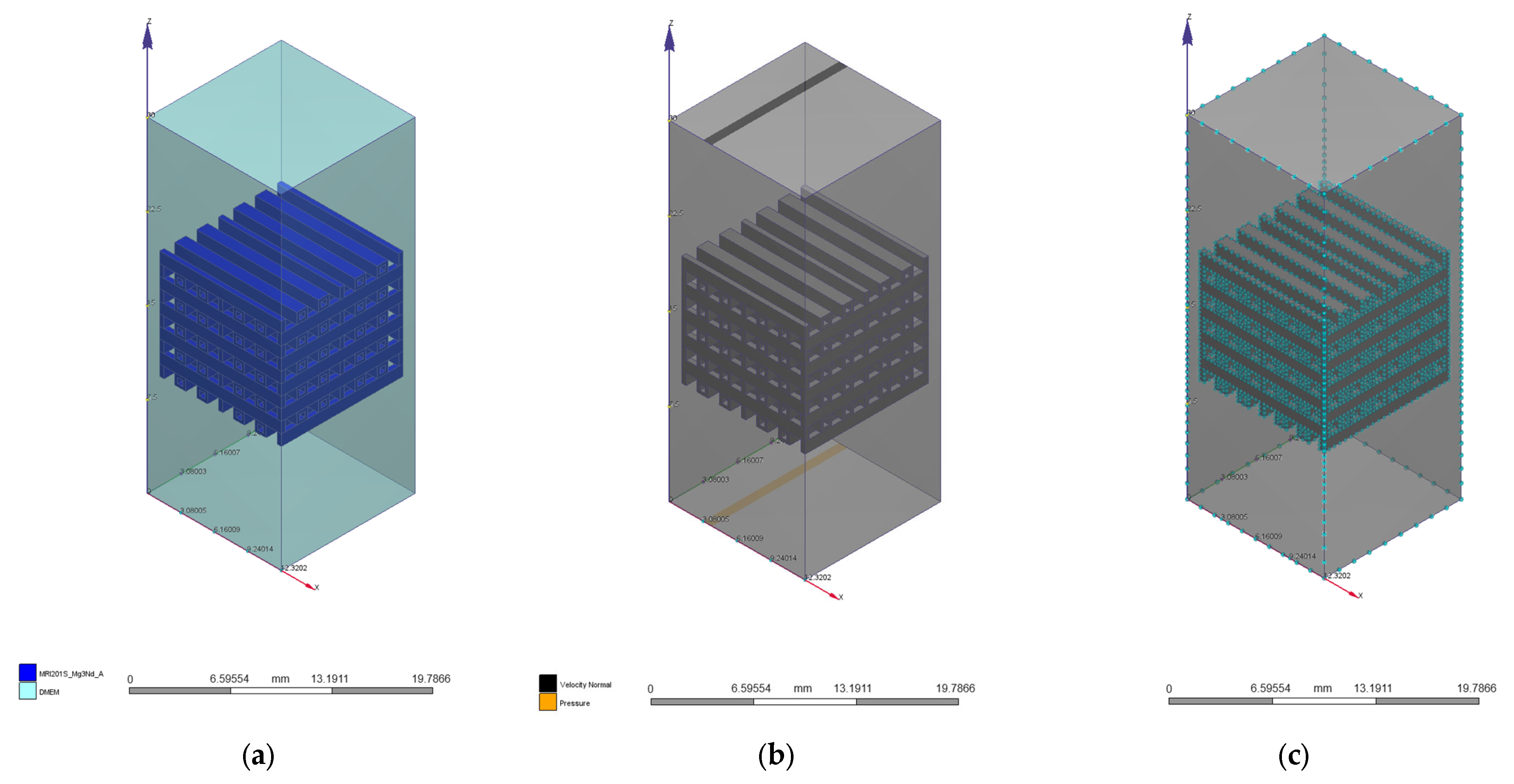
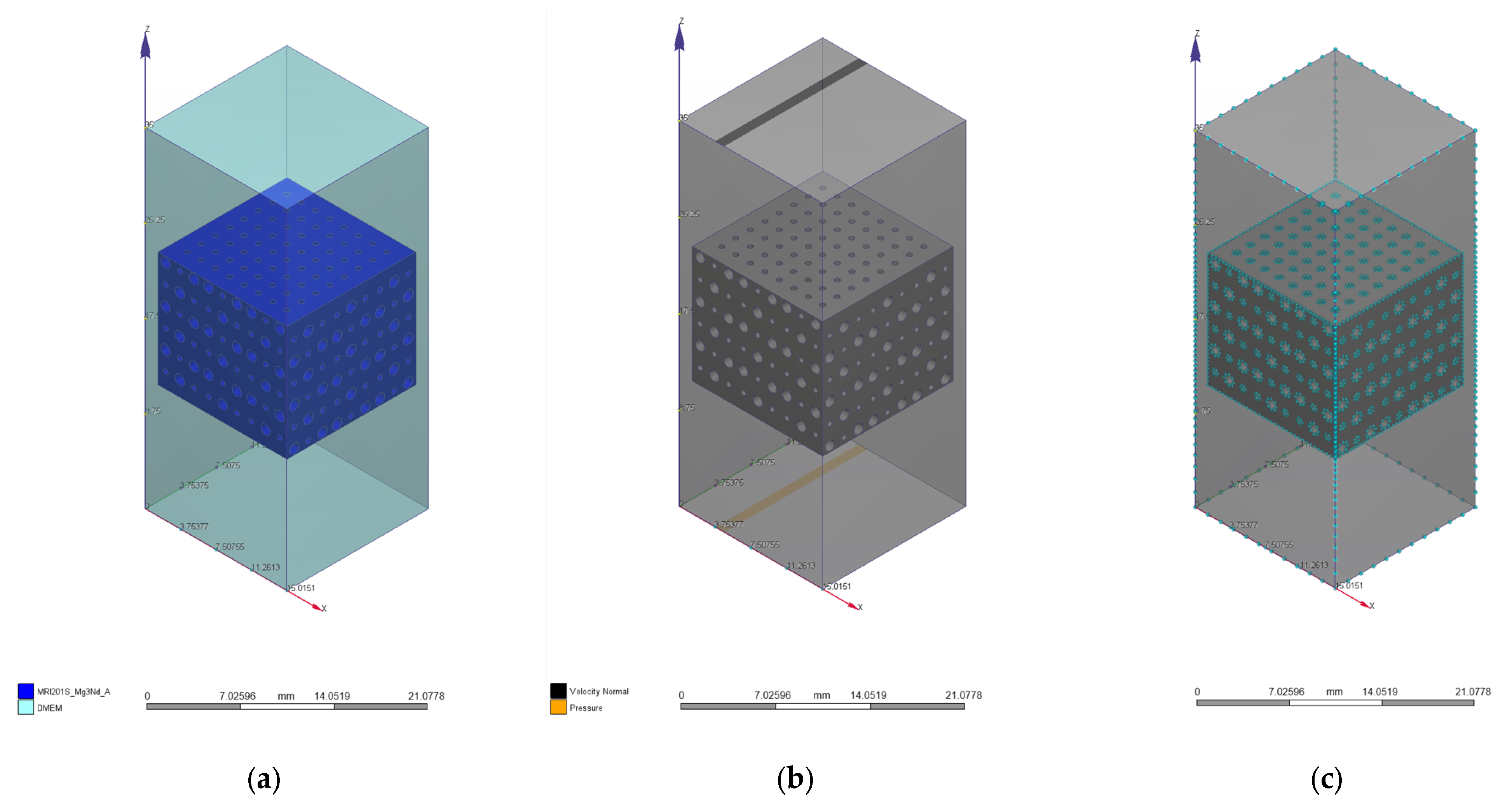
2.1. Scaffold Design

Computer-aided design (CAD) models were developed using Autodesk Inventor® Professional 2021 mechanical design software. The first geometrical configuration (PP) corresponds to an implant with a base area of 11.20 mm × 11.20 mm, height of 10 mm, and two types of pores with square shapes of the cross-sectional area, having edge dimensions of 1 mm and 0.5 mm, respectively. The second implant exhibited a base area of 13.65 mm × 13.65 mm, a height of 12 mm, and circular-shaped pores with diameters of 1 mm and 0.5 mm. Figure 2 shows the two CAD models developed in the study.
The implants’ porosity P was computed based on the following equation:
P = V s − V t V t ⋅ 100 ,
where VS represents the total volume of a cuboid considered in the absence of a pore network, and Vt is the implant volume. The obtained results are presented in Table 1.
In the case of the CAD model with square-shaped pores, we developed a layered geometry with elements drawn in the XZ and YZ planes, respectively, which were then extruded in Y and X directions with a length of 11.2 mm for each case. Regarding the geometrical configuration based on pores with round-shaped cross-sections, we considered a superposed distribution in YZ and XY planes with an extrusion of 13.65 mm along the X and Z directions. To ensure the possibility of vertical fluid flow inside the implants, circular pores were designed with a diameter of 0.5 mm along the entire structure height. In Figure 3 is presented an axial view of the PP geometry and a coronal view in the case of the PC model.

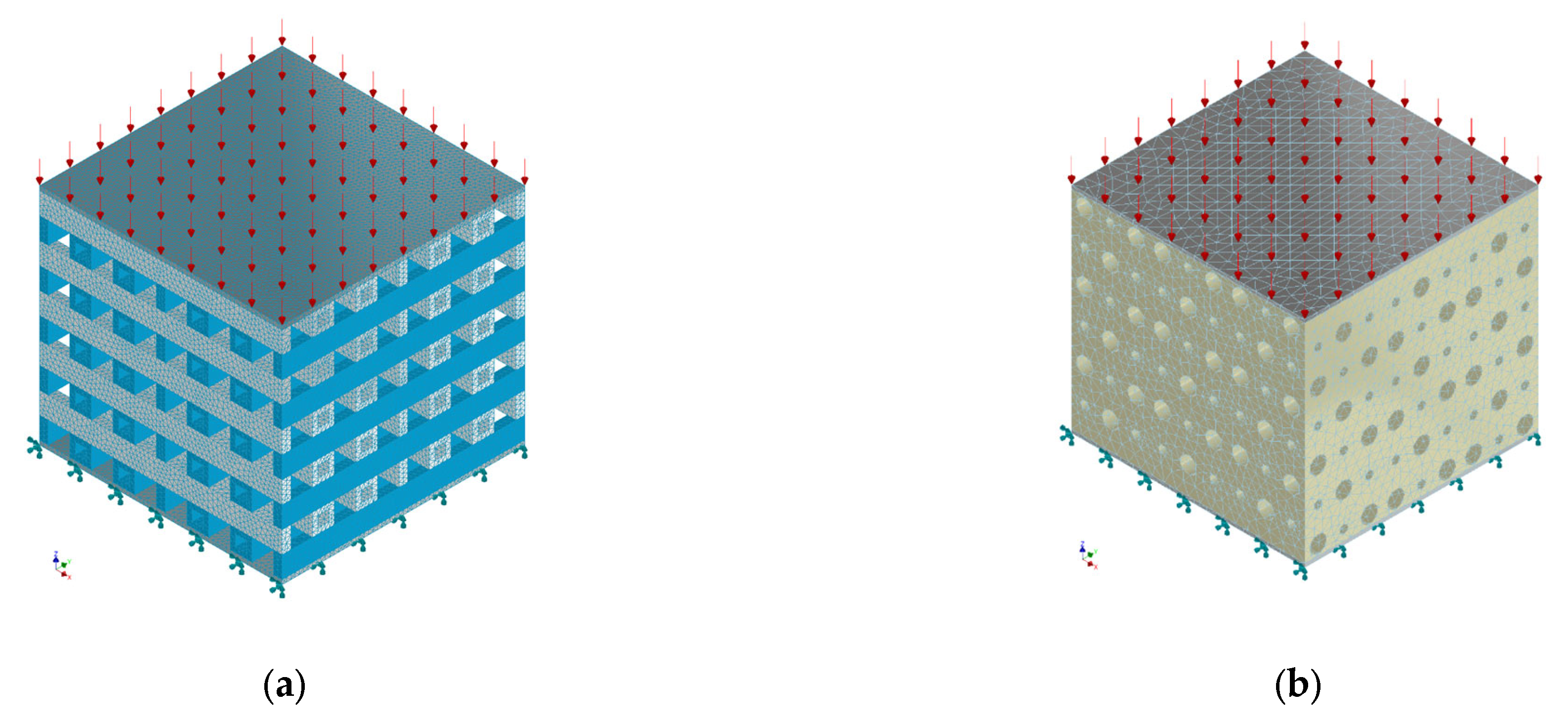
2.2. Mechanical Simulation

In implant design and practical manufacturing, the mechanical properties must be known and well-tuned in accordance with medical applications. Of all these properties, one of the most investigated is Young’s modulus, which must have values close to those of human bone. The analysis of the elastic region was performed using Autodesk Inventor Nastran® 2021 stress analysis software, assuming that the load has a constant value and the dependence between stress and strain is linear. This type of investigation can be considered adequate in the case of medical implants because, inside the human body in non-loading zones, the stress–strain curve evolves in most cases in the linear region.
To compute Young’s modulus, estimate the mechanical stress, and measure the displacement, the two designed CAD models were placed between two rigid bodies with thicknesses of 0.2 mm and areas equal to the base area of the implants. The applied mechanical test was compression in accordance with many literature studies [47,51,52,53,54,55,56]. To model the real behavior of a universal testing machine, we applied a surface-distributed force on the Z axis on the superior rigid body. In contrast, the inferior rigid body was fixed, with all freedom degrees blocked. Regarding the implant material, a Young’s modulus of 44.2 GPa, Poisson ratio of 0.27, compressive yield strength of 190 MPa, and density of 1.79 g/cm3 were adopted in good accordance with the mechanical properties of Mg-Nd-Y-Zr-Zn manufactured using the gravity casting method [41,42,57,58,59,60,61,62,63].
We used a mesh with 761,490 nodes and 399,714 tetrahedral second-order elements with a maximum size of 0.2 mm for the PP geometry. In the case of the PC model, the mesh had 646,295 nodes and 401,617 tetrahedral second-order elements with a 0.7 mm maximum size. All the mechanical simulations presented in the Results and Discussion section were performed by keeping constant mesh for both implants, respectively. In Figure 4 are presented the applied mechanical boundary conditions and the mesh for the two CAD models.

2.3. Computational Fluid Dynamics Simulation

Computational fluid dynamics represents a simple numerical analysis necessary for investigating the hemodynamic and biological performance of 3D implants characterized by different porosity grades and pore shapes. In the framework of our study, we adopted some idealizations. Firstly, we considered that the fluid has Newtonian behavior by assuming its viscosity has a constant value. This simplification is important because non-Newtonian fluids could have a different effect relative to the wall shear stress that acts on the implant wall and highly influences cell viability [64,65]. Secondly, we adopted different values for the fluid flow velocity. These values were similar to those of blood flow in the case of bone defects located in the long bones of the human body and to those in bioreactors [66,67]. Lastly, the implant surface was supposed to be smooth by considering the wall roughness equal to zero. When the wall roughness is not null, the interactions between implant walls and fluid flows change compared to the ideal case we considered [68].
The numerical CFD simulation was performed with Autodesk® CFD 2021. Based on the computed results, it is possible to determine the implant permeability and the wall shear stress, which are of utmost importance in CFD analysis. By investigating some literature studies, we have chosen the fluid Dullbecco’s Modified Eagle Medium (DMEM) with a density of 1 g/cm3 and a viscosity of 0.00145 Pas [51,69]. We assumed that DMEM is uncompressible and has a Newtonian character, and the implants are rigid bodies inside the fluid domain [34,66]. In the idealizations’ case mentioned above, the Navier–Stokes equation (Equation (2)) for incompressible fluids is adequate to solve the problem of mass and momentum conservation along the implants based on the finite volume elements’ method (FVM) [70].
ρ ∂ u ∂ t − μ ∇ 2 u + ρ u · ∇ u + ∇ p = F , u · ∇ = 0 ,
where ρ is the fluid density, u represents the fluid flow velocity, t is the time variable, μ is the fluid viscosity, ∇ is the Del operator, p is the fluid pressure, and F represents a gravitational or centrifugal force. According to Vossenberg et al. [70] and Xue et al. [71], we imposed F = 0. The implant permeability k was computed as described by Truscello et al. [72] by taking into account the Darcy relationship:
k = u μ L P max − P min ,
where L represents the implant height, Pmax is the maximum pressure determined after the CFD analysis, and Pmin is the minimum pressure in all cases equal to zero. It was noticed that for high values of fluid flow velocity, the Darcy law does not correctly estimate the implant permeability [28,65,67,73]. When the Reynolds number (Re) is higher than 8.6, the classical Darcy relationship becomes inapplicable [65,67]. To estimate the applicability of Darcy’s law, we computed the Reynolds number following [26,65]:
R e = ρ u d μ ,
where d is the maximum pore size. In our study, because the proposed structure has different pore sizes, we considered in Equation (4) the maximum pore size to be a significative geometrical dimension, as mentioned in [26,65,67].
By considering a laminar flow for the Newtonian fluids, the wall shear stress (WSS τw) can be defined to be equal to the first derivative of the fluid flow velocity in the perpendicular direction to the wall, as presented by Eagger et al. [74]:
τ w = μ ∂ u ∂ n ,
where n is the normal wall direction.
The boundary conditions for the CFD simulations consisted of an imposed variable velocity value on the inlet surface and null pressure on the outlet surface. The implant walls were set for hydrophilic material behavior and modeled in Autodesk® CFD as implicit “no slip” boundary conditions [72,75,76]. The fluid domain was designed as a cuboid (12.32 mm × 12.32 mm × 30 mm) around the Mg alloy implants. Regarding the Mg-Nd-Y-Zr-Zn, we considered the following values for thermal conductivity 91 W/(mK) in a homogenous distribution along X, Y, and Z axes, specific heat 1050 J/(kg K), and electrical resistivity 6.20 × 10−8 Ωm [57,58,59,60,61,62]. The fluid and implant temperature was established at 37 °C to simulate the physiological conditions inside the human body. In addition, we have chosen a shear stress transport turbulence model (SST) of the K-Omega type with an average value of 0.05 for turbulence stated by Bozzi et al. [77], due to the fact that turbulence is a physiological property of the biological fluids and occurs in the case of bone injuries and other pathologies that involve blood flow [78,79,80].
In Figure 5 and Figure 6 are presented the fluid domain, boundary conditions, and the mesh used for the analyzed problems developed in the case of two CAD models.

3. Results and Discussion

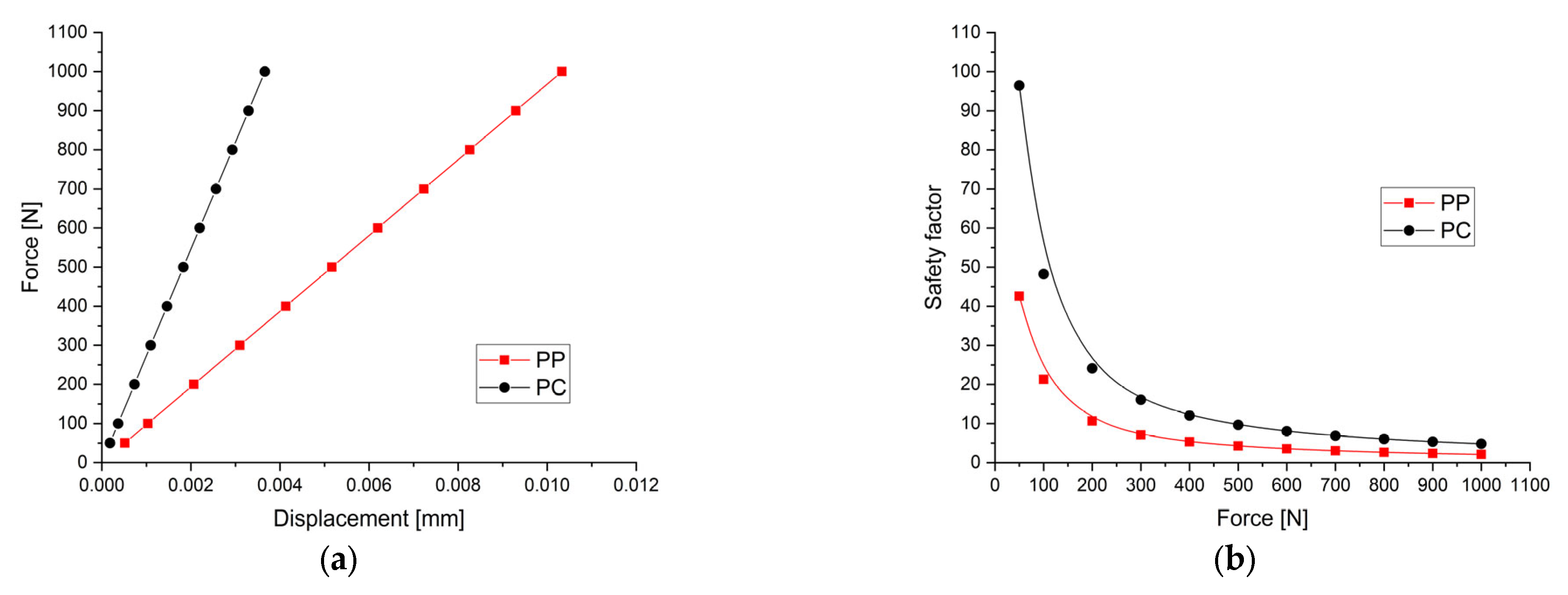
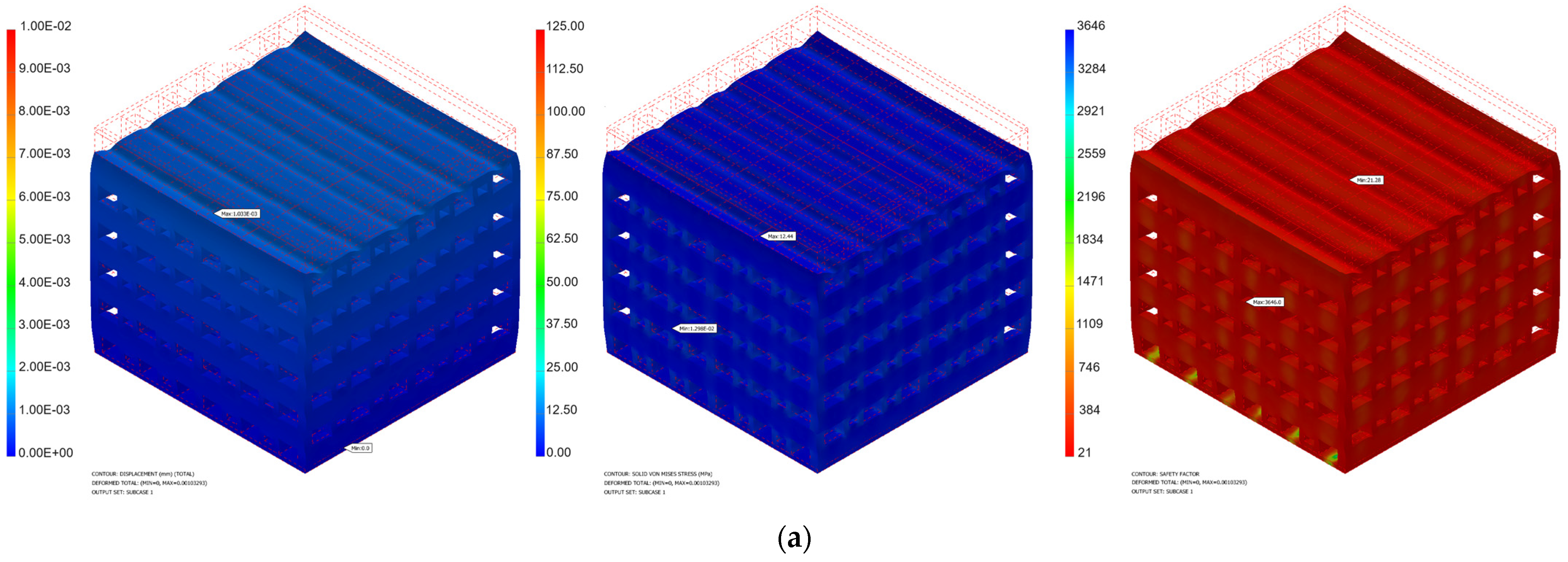
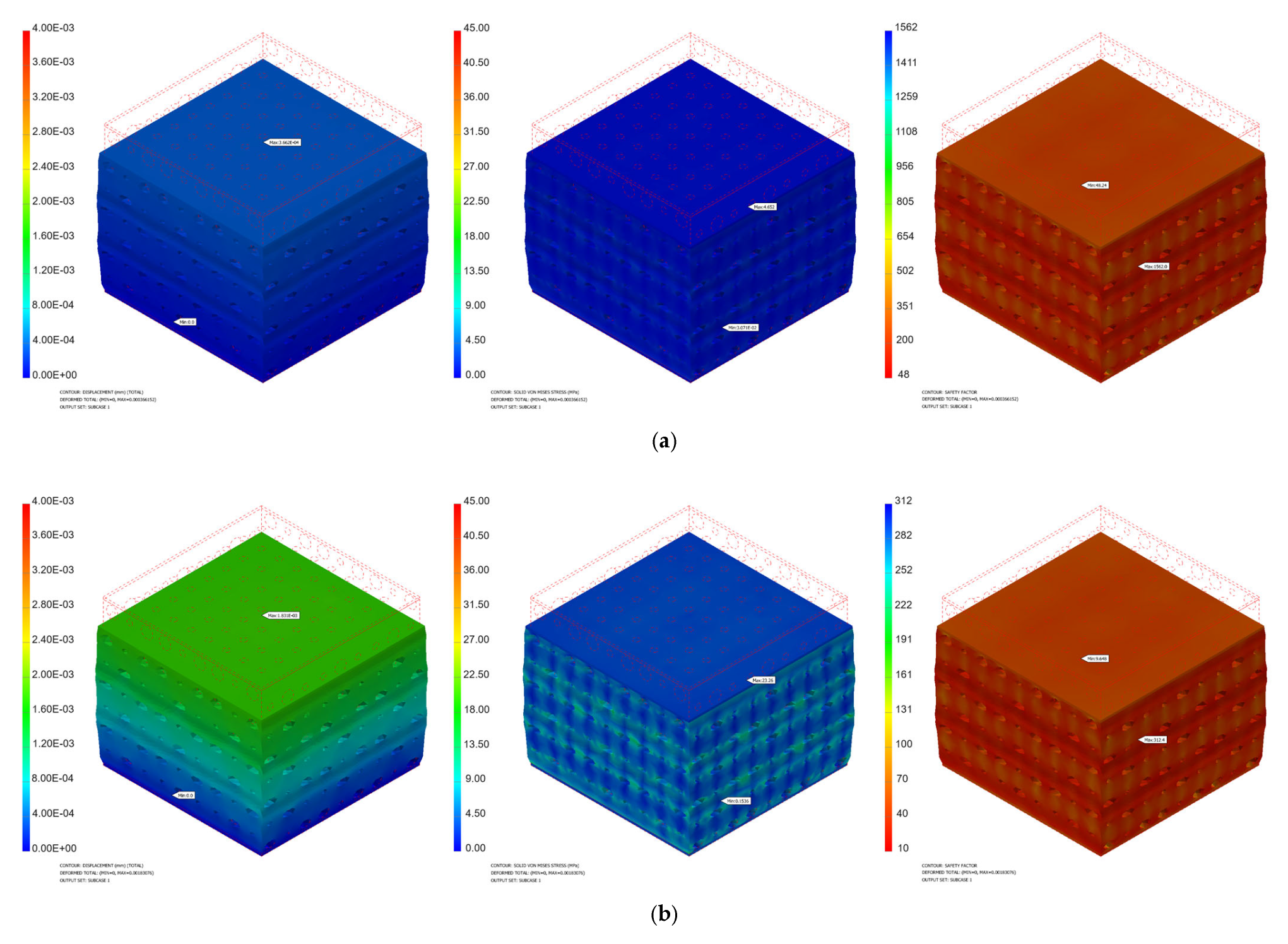
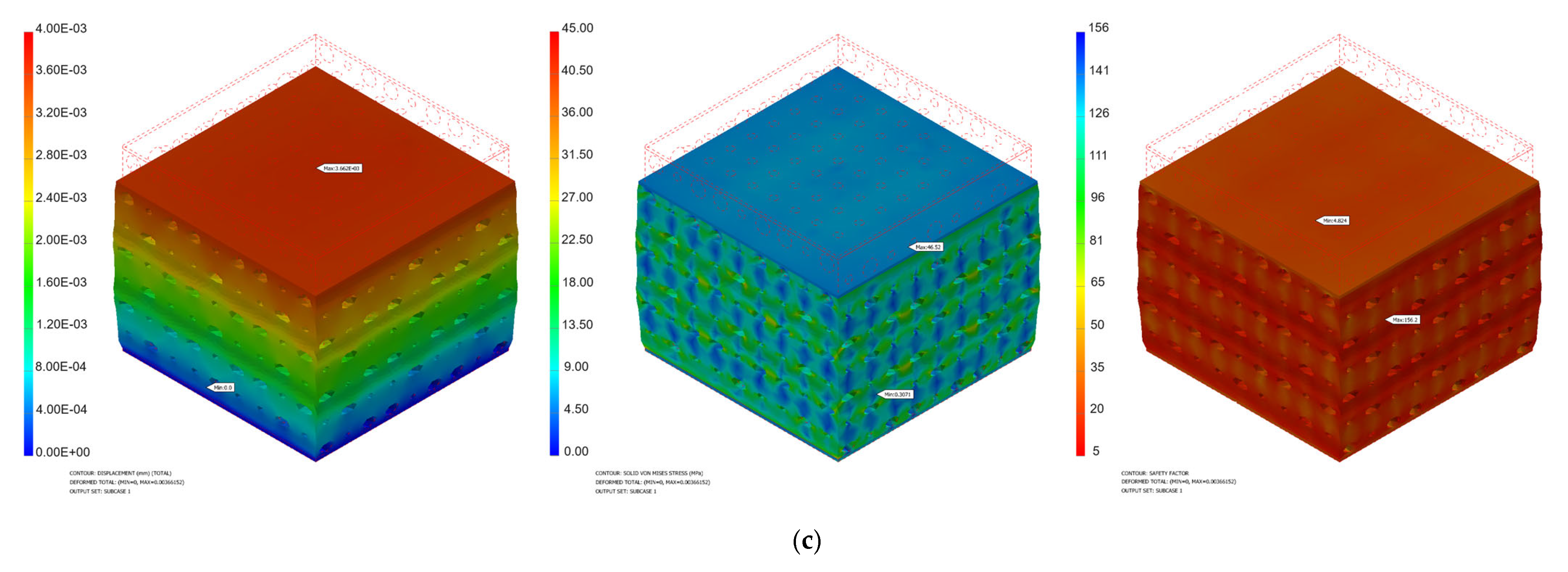
3.1. Mechanical Simulation Results

The Young’s modulus of the implants was computed based on results obtained from the mechanical simulations. The applied force was variated between 50 N and 1000 N with a step of 100 N. This type of load was chosen by the following criteria: it was supposed that the implants would be placed into a patient’s femur to treat a bone defect, the patient has an average body mass index, and against the leg would be applied a maximum force equal to 10% of body weight. Table 2 presents the results of mechanical simulations for PP and PC geometries used in the elasticity modulus computation (Equation (6) [47]).
E t = F L d A ,
where F represents the applied force distributed on the superior rigid body surface, L is the implant height, d is associated with the maximum displacement value computed with Autodesk Inventor Nastran®, and A is the cross-sectional area (for PP model 125.44 mm2, for PC model 186.33 mm2).
For the PP implant, the theoretical elasticity modulus computed based on Equation (6) was equal to 7.71 GPa, and a very good convergence of the results presented in Table 2 was evidenced. The implant rigidity was estimated at 96,837.38 N/mm and mathematically determined as the slope of force–displacement variation (Figure 7a). The safety factor is an important parameter that is usually used to see if an implant is correctly designed for different applied loads. In the case of a good mechanical resistance, its value must be higher than 1. A Young’s modulus of about 17.88 GPa was obtained for the PC configuration. Using Equation (6) and the data presented in Table 2, it can be noted that all the computed values were equal to the elasticity modulus mentioned above. The implant rigidity was determined as in the other case and was estimated at 273,125 N/mm (Figure 7a). In addition, the safety factor for the PC design exhibited values higher than 4.82 in comparison with 2.12 in the case of the PP model. Both values were obtained for an applied force of 1000 N (Figure 7b).
As a general conclusion, both developed implants have Young’s modulus values between 0.5 and 20 GPa, which are adequate for bone defect treatment in good accordance with the literature [17]. The differences between elasticity modulus are due to the porosity grade and pore shape variation. The PC model can be used in intense load-bearing zones, exhibiting a higher elasticity modulus value. However, this value is lower than the upper limit of 20 GPa determined for the human bone. For the PP model, one can notice an excellent value for Young’s modulus and we suggest using this implant for patients with trabecular bone defects. In both cases, the minimum value of the safety factor is higher than 1, a fact that is linked to good mechanical resistance, so we do not foresee implant failure. Figure 7 presents the variation of force versus maximum implant displacement and the safety factor as a function of the applied load.
Figure 8 and Figure 9 present some numerical results obtained for different values of the applied force.

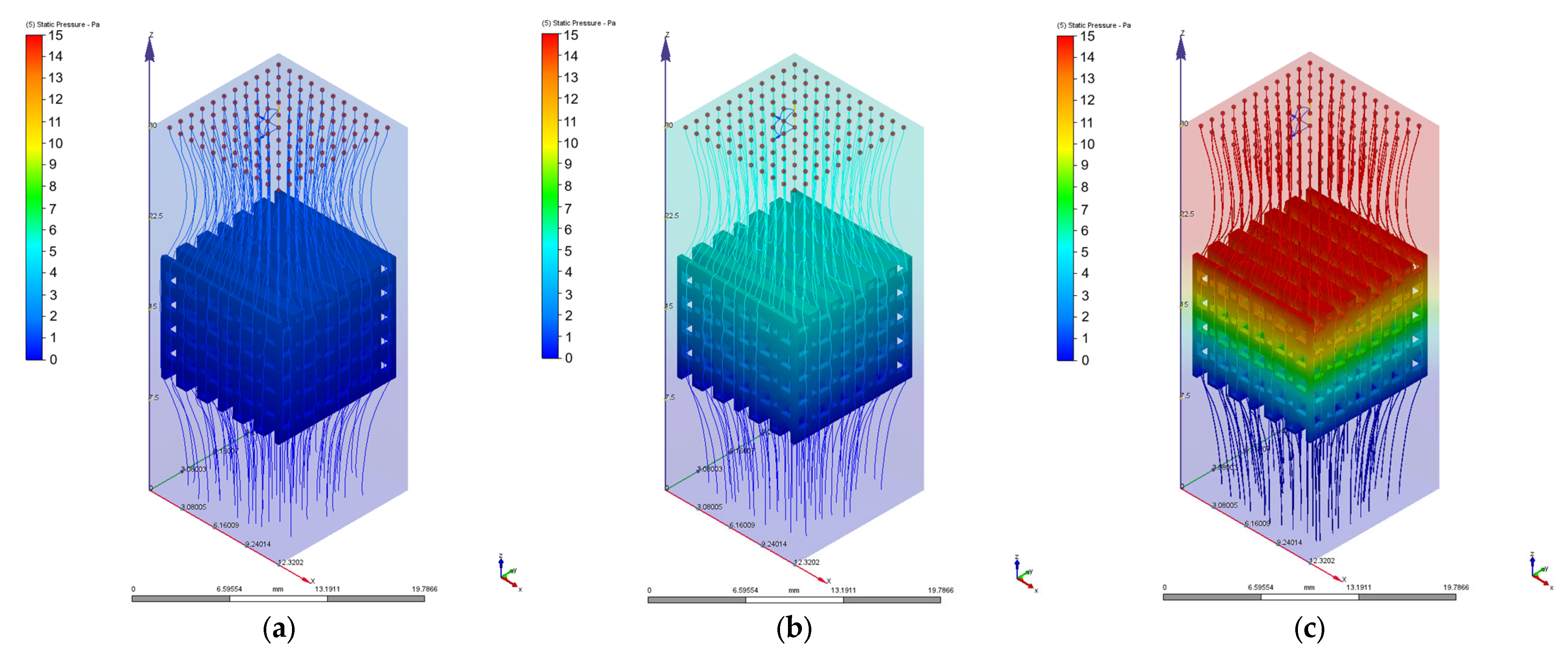
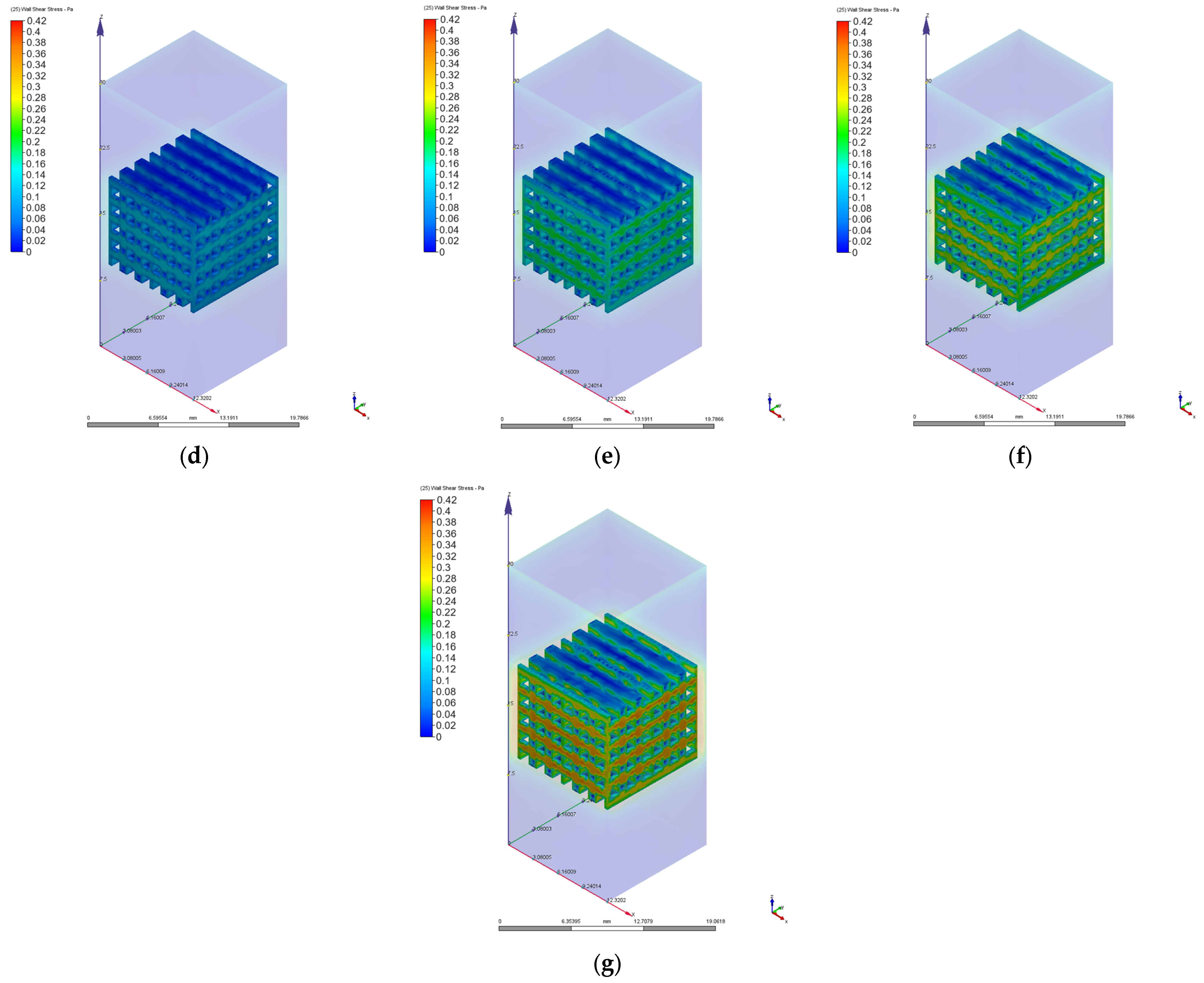
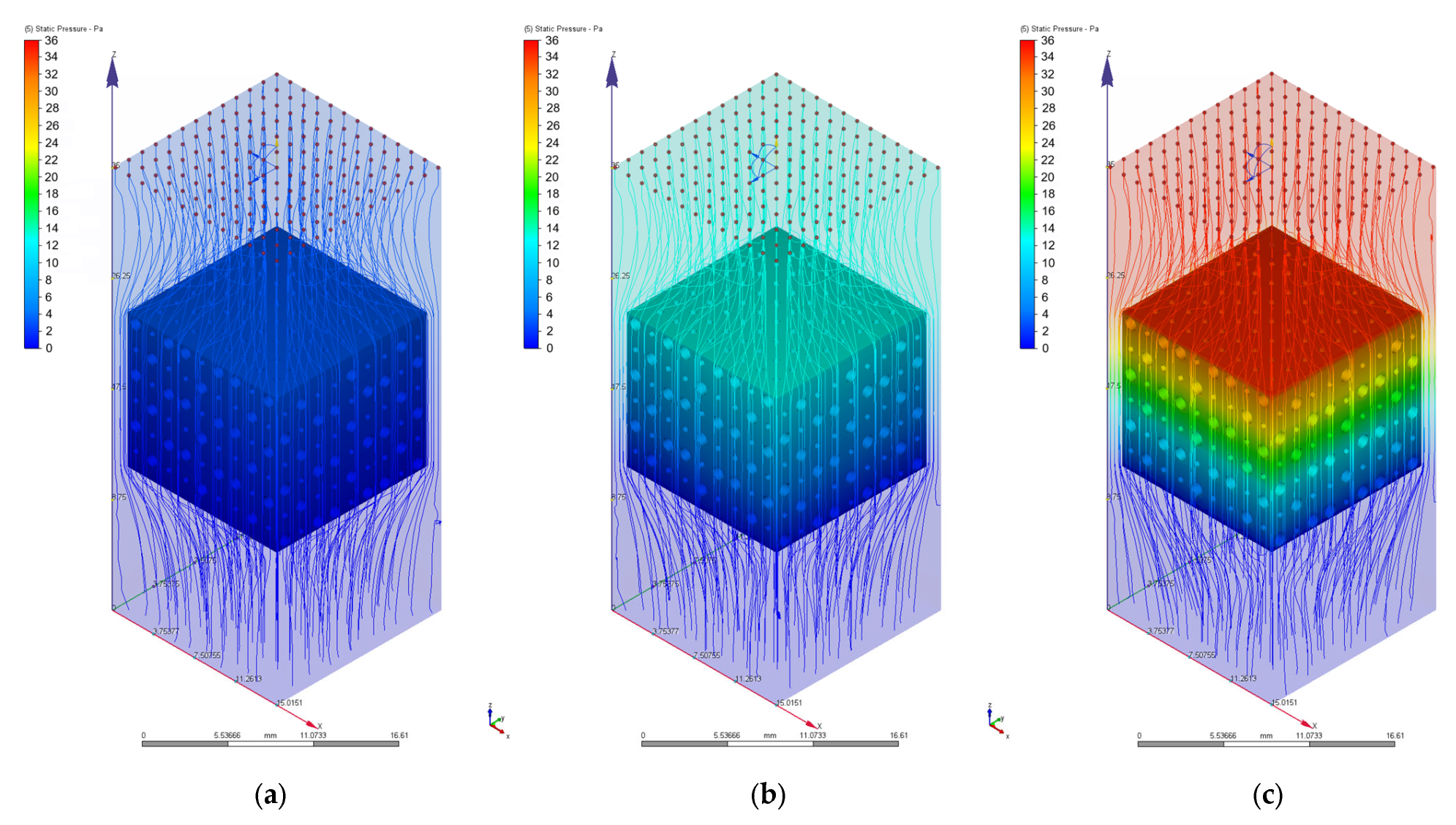
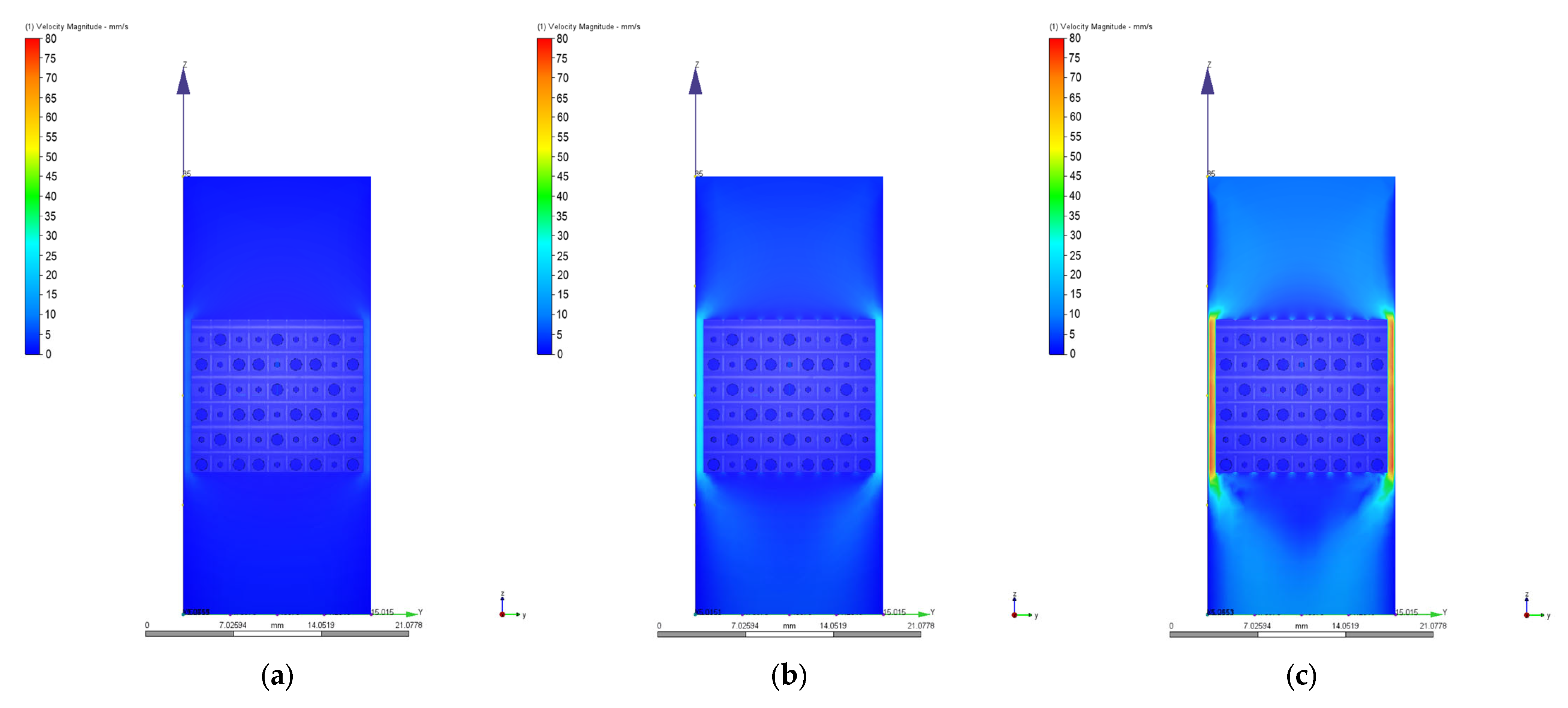
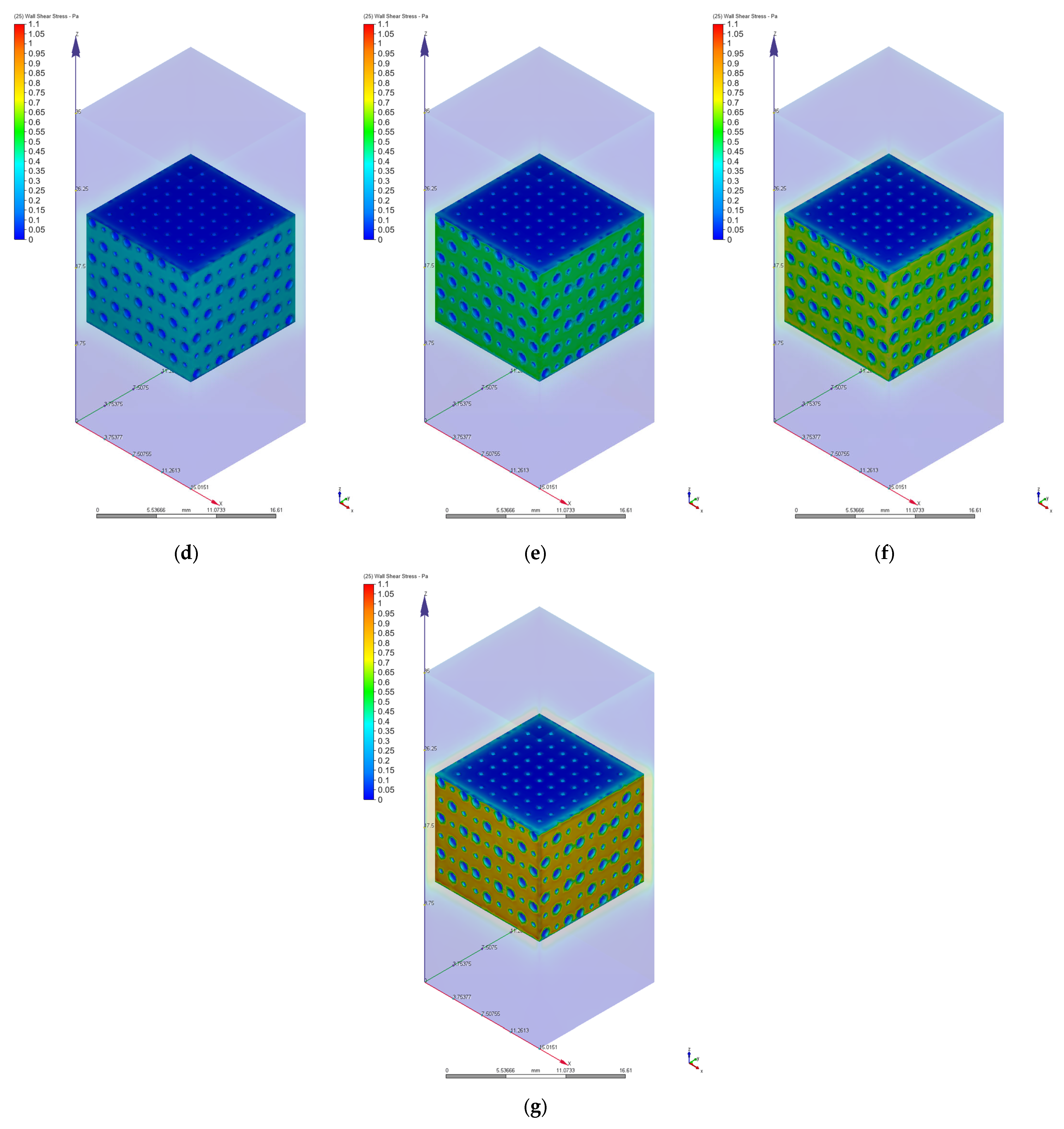
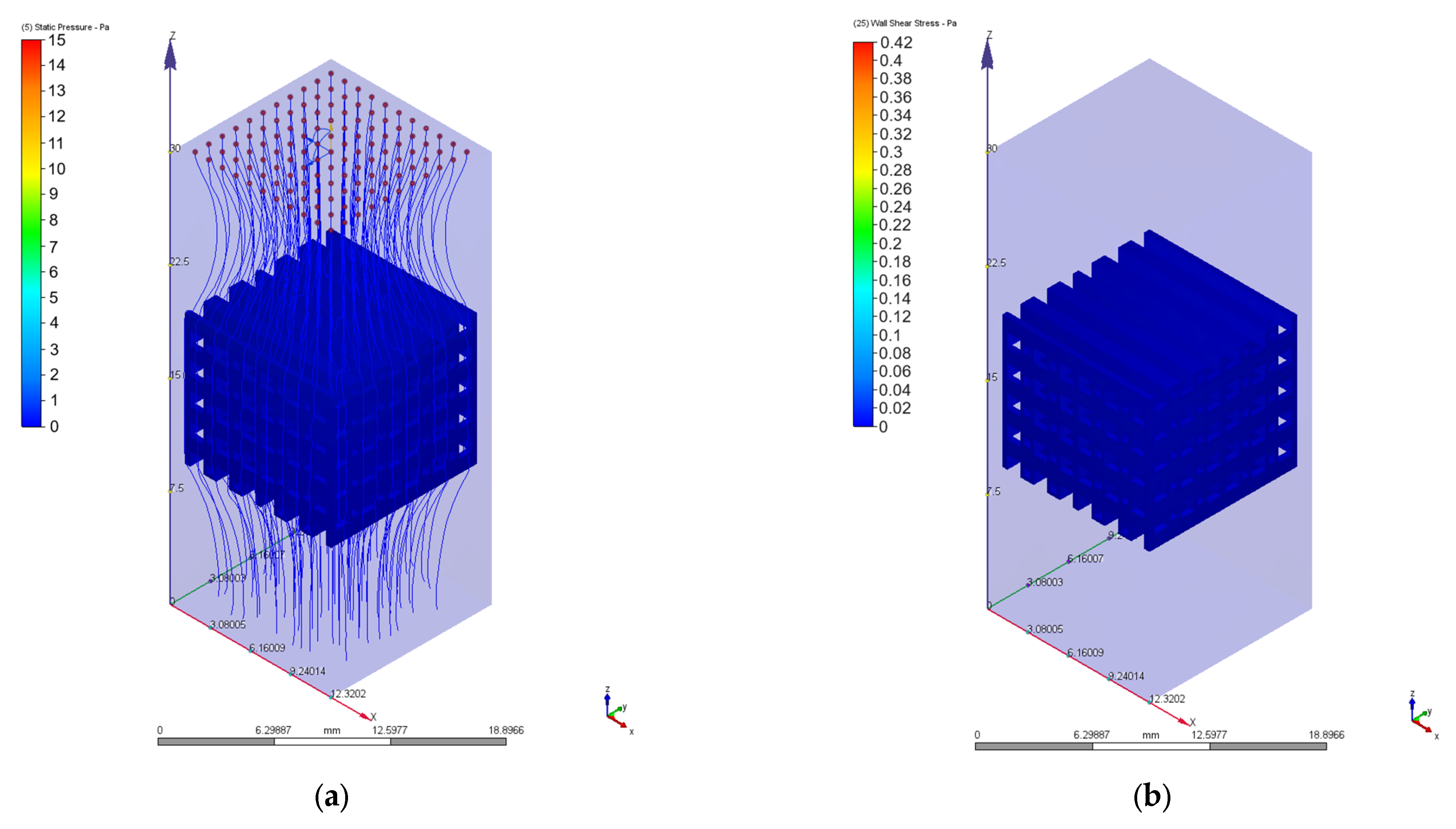
3.2. Computational Fluid Dynamics Simulation Results

As we mentioned in Section 2.3, different values of 0.1 mm/s, 1 mm/s, 2 mm/s, 3 mm/s, 4 mm/s, 6 mm/s, 8 mm/s, and 10 mm/s were chosen for the velocity value on the inlet surface during the CFD simulations. Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 present numerical results obtained for the PP and PC models used for implant permeability calculation based on Equation (3).
In Table 3 are summarized the main numerical results used for implant permeability computation and the Reynolds number obtained in the case of the two CAD models.
In Figure 16a is presented the pressure drop dependence determined between the inlet and outlet surfaces of the implants as a function of the fluid flow velocity. It can be noticed that the pressure drop varies linearly with the velocity increase (Figure 10, Figure 11, Figure 13 and Figure 14). The highest value of 35.39 Pa was achieved for the PC implant at a velocity of 10 mm/s compared to 15.624 Pa in the case of the PP implant. This difference can be explained based on the fact that the pore dimensions and implant architecture are different. The high value of the pressure drop numerically computed could be attributed to the important fluid dynamic interactions between implant and fluid due to an increased value of the specific area and a reduced porosity of about 38%. In the case of the PP implant, the higher porosity of about 62% and square-shaped pores determine much more reduced interactions between fluid and implant, so as a direct consequence, a lower pressure drop was achieved. It was observed that the Reynolds number had a maximum value of 6.89 for all the imposed fluid velocity values, and the implant permeability can be correctly estimated by Darcy’s law. Figure 16b shows that the implant permeability decreases when the fluid velocity increases, showing a much more pronounced effect of the pore geometry and implant architecture for the low value of the fluid velocity. In addition, we must mention that this observation remains valid for both designed implants. The implant PP has a maximum permeability of 10.67 × 10−9 m2 at a velocity of 1 mm/s compared with 5.363 × 10−9 m2 obtained for the PC implant. Regarding the wall shear stress values for the PP implant (Figure 12), it can be noticed that for a velocity u = 1 mm/s, the maximum value is about 20 mPa, which can be considered an optimal value for the biological range, ensuring cell viability. As long as the flow velocity increases, the following values for WSS placed on the implant are achieved: 60 mPa (u = 2 mm/s), 80 mPa (u = 3 mm/s), 100 mPa (u = 4 mm/s), 180 mPa (u = 6 mm/s), 280 mPa (u = 8 mm/s), and 340 mPa (u = 10 mm/s). These high values of the maximum WSS are located exclusively around the implant’s exterior walls. Meanwhile, in the interior of the implant the fluid flows can be considered a beneficial medium for cell adhesion and proliferation, that, according to the literature [24,25,26,27,28], occur in the case of a WSS below a 30 mPa limit. In addition, we can estimate that cell adhesion is difficult on the implant’s exterior surface while it is enhanced on the interior. For the PC implant (Figure 15), a similar behavior was evidenced by the CFD simulations, and the following values for WSS measured on the implant exterior surface were detected: 50 mPa (u = 1 mm/s), 200 mPa (u = 2 mm/s), 300 mPa (u = 3 mm/s), 360 mPa (u = 4 mm/s), 450 mPa (u = 6 mm/s), 700 mPa (u = 8 mm/s), and 800 mPa (u = 10 mm/s). The same conclusion regarding the increased cell viability on the implant’s inner volume can be foreseen.
We tested a very low fluid velocity of 0.1 mm/s and found that below this value specific to bioreactors, the WSS values are much lower than 30 mPa on both implants’ exterior surfaces and interior volumes. It can be concluded that implant cell population should be performed in bioreactor conditions at such reduced values of fluid velocity because values of WSS higher than 60 mPa were not observed (Figure 17).

4. Conclusions

Permeability and Young’s modulus of implants dedicated to bone defect treatment must be in accordance with trabecular bone properties (Young’s modulus of 20 GPa and permeability of 5.13 × 10−9 m2 [18,81,82]). The theoretical values of these physical properties obtained for the two designed implants in conformity with the numerical simulations evidenced that our models are adequate for regenerative implants in bone tissue engineering. Following the WSS analysis, we can conclude that in the case of the low fluid flow velocities met in bioreactors, the cell viability is increased on the inner volume and on the outer surface of the implant. On the other hand, for velocity values close to those of blood flow, which occur in the case of a fracture, one must consider that the cell viability is enhanced on the implant interior and decreased on the exterior surface. It can be recommended that the implant cell population be made in conditions close to those of bioreactors and then implanted at the defect site.
The FEA-CFD simulations permit the mathematical reproduction of linear compression and fluid circulation natural phenomena. The FEA revealed that both implants have mechanical properties close to those of trabecular bone that are adequate for bone defect treatment. It can be noticed that the PC implant has a higher value of Young’s modulus than the PP model, but both values are in the biological range of trabecular bone, helping reconstruct the hard tissue in different parts of the human body.
Current implant design considers that the implant materials have a specific and constant biodegradation rate. Future analysis will be made to validate both implants’ experimental designs for bone defect treatment. In addition, looking to future studies, we want to use non-Newtonian fluids and transient simulations because developing numerical strategies for bone tissue engineering is very important to ensure the success or failure of the designed implants by modifying the mechanical properties and controlling the cell viability.

Author Contributions

Conceptualization, V.M., G.P., L.G.G. and M.V.; methodology, A.A., A.R., S.A.L., G.M.P. and V.S.; software, G.P., V.M., A.L.C., L.G.G., V.S. and S.A.L.; validation, A.I.B., M.V. and L.G.G.; formal analysis, A.A., G.M.P., A.L.C. and A.P.; investigation, V.M., A.R., M.V., S.A.L., A.I.B., G.M.P., A.L.C. and G.P.; resources, V.M., A.P., L.G.G. and S.A.L.; writing—original draft preparation, V.M. and G.P.; writing—review and editing, A.A.; visualization, A.R., V.S., A.I.B. and A.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by a grant from the National Program for Research of the National Association of Technical Universities—GNAC ARUT 2023 (Project number 29/9.10.2023, Project ID 220235050). In addition, this work was supported by a grant from Norwegian Financial Mechanism 2014–2021 under the project RO-NO-2019-0138, 19/2020 “Improving Cancer Diagnostics in Flexible Endoscopy using Artificial Intelligence and Medical Robotics” IDEAR, Contract No. 19/2020.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sohn, H.-S.; Oh, J.-K. Review of Bone Graft and Bone Substitutes with an Emphasis on Fracture Surgeries. Biomater. Res. 2019, 23, 9. [Google Scholar] [CrossRef]
  2. Fernandez de Grado, G.; Keller, L.; Idoux-Gillet, Y.; Wagner, Q.; Musset, A.-M.; Benkirane-Jessel, N.; Bornert, F.; Offner, D. Bone Substitutes: A Review of Their Characteristics, Clinical Use, and Perspectives for Large Bone Defects Management. J. Tissue Eng. 2018, 9, 2041731418776819. [Google Scholar] [CrossRef]
  3. Schemitsch, E.H. Size Matters: Defining Critical in Bone Defect Size! J. Orthop. Trauma 2017, 31, S20–S22. [Google Scholar] [CrossRef]
  4. Antoniac, I.; Manescu (Paltanea), V.; Antoniac, A.; Paltanea, G. Magnesium-Based Alloys with Adapted Interfaces for Bone Implants and Tissue Engineering. Regen. Biomater. 2023, 10, rbad095. [Google Scholar] [CrossRef]
  5. Paltanea, G.; Manescu (Paltanea), V.; Antoniac, I.; Antoniac, A.; Nemoianu, I.V.; Robu, A.; Dura, H. A Review of Biomimetic and Biodegradable Magnetic Scaffolds for Bone Tissue Engineering and Oncology. Int. J. Mol. Sci. 2023, 24, 4312. [Google Scholar] [CrossRef]
  6. Kuzyk, P.R.; Schemitsch, E.H. The Basic Science of Peri-Implant Bone Healing. Indian J. Orthop. 2011, 45, 108–115. [Google Scholar] [CrossRef] [PubMed]
  7. Li, Z.; Müller, R.; Ruffoni, D. Bone Remodeling and Mechanobiology around Implants: Insights from Small Animal Imaging. J. Orthop. Res. 2018, 36, 584–593. [Google Scholar] [CrossRef] [PubMed]
  8. Ahmadi, S.M.; Yavari, S.A.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Additively Manufactured Open-Cell Porous Biomaterials Made from Six Different Space-Filling Unit Cells: The Mechanical and Morphological Properties. Materials 2015, 8, 1871–1896. [Google Scholar] [CrossRef] [PubMed]
  9. Shirazi, S.F.S.; Gharehkhani, S.; Mehrali, M.; Yarmand, H.; Metselaar, H.S.C.; Adib Kadri, N.; Osman, N.A.A. A Review on Powder-Based Additive Manufacturing for Tissue Engineering: Selective Laser Sintering and Inkjet 3D Printing. Sci. Technol. Adv. Mater. 2015, 16, 033502. [Google Scholar] [CrossRef] [PubMed]
  10. Hutmacher, D.W.; Schantz, J.T.; Lam, C.X.F.; Tan, K.C.; Lim, T.C. State of the Art and Future Directions of Scaffold-Based Bone Engineering from a Biomaterials Perspective. J. Tissue Eng. Regen. Med. 2007, 1, 245–260. [Google Scholar] [CrossRef] [PubMed]
  11. Zhang, L.; Song, B.; Yang, L.; Shi, Y. Tailored Mechanical Response and Mass Transport Characteristic of Selective Laser Melted Porous Metallic Biomaterials for Bone Scaffolds. Acta Biomater. 2020, 112, 298–315. [Google Scholar] [CrossRef] [PubMed]
  12. Li, J.; Zhao, Z.; Yan, R.; Yang, Y. Mechanical Properties of Graded Scaffolds Developed by Curve Interference Coupled with Selective Laser Sintering. Mater. Sci. Eng. C Mater. Biol. Appl. 2020, 116, 111181. [Google Scholar] [CrossRef]
  13. Pałka, K.; Pokrowiecki, R. Porous Titanium Implants: A Review. Adv. Eng. Mater. 2018, 20, 1700648. [Google Scholar] [CrossRef]
  14. Boccaccio, A.; Uva, A.E.; Fiorentino, M.; Lamberti, L.; Monno, G. A Mechanobiology-Based Algorithm to Optimize the Microstructure Geometry of Bone Tissue Scaffolds. Int. J. Biol. Sci. 2016, 12, 1–17. [Google Scholar] [CrossRef] [PubMed]
  15. Čapek, J.; Machová, M.; Fousová, M.; Kubásek, J.; Vojtěch, D.; Fojt, J.; Jablonská, E.; Lipov, J.; Ruml, T. Highly Porous, Low Elastic Modulus 316L Stainless Steel Scaffold Prepared by Selective Laser Melting. Mater. Sci. Eng. C 2016, 69, 631–639. [Google Scholar] [CrossRef]
  16. Nune, K.C.; Misra, R.D.K.; Li, S.J.; Hao, Y.L.; Yang, R. Cellular Response of Osteoblasts to Low Modulus Ti-24Nb-4Zr-8Sn Alloy Mesh Structure. J. Biomed. Mater. Res. Part A 2017, 105, 859–870. [Google Scholar] [CrossRef]
  17. Li, G.; Wu, Y.; Zhang, Y.; Zhi, R.; Wang, J.; Ma, C. Performance Study on a Single-Screw Expander for a Small-Scale Pressure Recovery System. Energies 2017, 10, 6. [Google Scholar] [CrossRef]
  18. Goldstein, S.A. The Mechanical Properties of Trabecular Bone: Dependence on Anatomic Location and Function. J. Biomech. 1987, 20, 1055–1061. [Google Scholar] [CrossRef]
  19. Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical Evaluation of Porous Titanium (Ti6Al4V) Structures with Electron Beam Melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef]
  20. Pennings, S.; Liu, K.J.; Qian, H. The Stem Cell Niche: Interactions between Stem Cells and Their Environment. Stem Cells Int. 2018, 2018, e4879379. [Google Scholar] [CrossRef]
  21. Chen, J.; Hendriks, M.; Chatzis, A.; Ramasamy, S.K.; Kusumbe, A.P. Bone Vasculature and Bone Marrow Vascular Niches in Health and Disease. J. Bone Miner. Res. 2020, 35, 2103–2120. [Google Scholar] [CrossRef]
  22. Daskalakis, E.; Liu, F.; Huang, B.; Acar, A.A.; Cooper, G.; Weightman, A.; Blunn, G.; Koç, B.; Bartolo, P. Investigating the Influence of Architecture and Material Composition of 3D Printed Anatomical Design Scaffolds for Large Bone Defects. Int. J. Bioprinting 2021, 7, 43–52. [Google Scholar] [CrossRef]
  23. Hendrikson, W.; van Blitterswijk, C.; Rouwkema, J.; Moroni, L. The Use of Finite Element Analyses to Design and Fabricate Three-Dimensional Scaffolds for Skeletal Tissue Engineering. Front. Bioeng. Biotechnol. 2017, 5, 30. [Google Scholar] [CrossRef]
  24. Schipani, R.; Nolan, D.R.; Lally, C.; Kelly, D.J. Integrating Finite Element Modelling and 3D Printing to Engineer Biomimetic Polymeric Scaffolds for Tissue Engineering. Connect. Tissue Res. 2020, 61, 174–189. [Google Scholar] [CrossRef]
  25. Wang, Z.; Huang, C.; Wang, J.; Wang, P.; Bi, S.; Abbas, C.A. Design and Simulation of Flow Field for Bone Tissue Engineering Scaffold Based on Triply Periodic Minimal Surface. Chin. J. Mech. Eng. 2019, 32, 19. [Google Scholar] [CrossRef]
  26. Chabanon, M.; Duval, H.; Grenier, J.; Beauchesne, C.; Goyeau, B.; David, B. Histological Method to Study the Effect of Shear Stress on Cell Proliferation and Tissue Morphology in a Bioreactor. Tissue Eng. Regen. Med. 2019, 16, 225–235. [Google Scholar] [CrossRef]
  27. Melke, J.; Zhao, F.; Van Rietbergen, B.; Ito, K.; Hofmann, S. Localisation of Mineralised Tissue in a Complex Spinner Flask Environment Correlates with Predicted Wall Shear Stress Level Localisation. eCM 2018, 36, 57–68. [Google Scholar] [CrossRef] [PubMed]
  28. Zhao, F.; van Rietbergen, B.; Ito, K.; Hofmann, S. Flow Rates in Perfusion Bioreactors to Maximise Mineralisation in Bone Tissue Engineering in Vitro. J. Biomech. 2018, 79, 232–237. [Google Scholar] [CrossRef] [PubMed]
  29. Salinas, E.Y.; Aryaei, A.; Paschos, N.; Berson, E.; Kwon, H.; Hu, J.C.; Athanasiou, K.A. Shear Stress Induced by Fluid Flow Produces Improvements in Tissue-Engineered Cartilage. Biofabrication 2020, 12, 045010. [Google Scholar] [CrossRef] [PubMed]
  30. Seddiqi, H.; Saatchi, A.; Amoabediny, G.; Helder, M.N.; Abbasi Ravasjani, S.; Safari Hajat Aghaei, M.; Jin, J.; Zandieh-Doulabi, B.; Klein-Nulend, J. Inlet Flow Rate of Perfusion Bioreactors Affects Fluid Flow Dynamics, but Not Oxygen Concentration in 3D-Printed Scaffolds for Bone Tissue Engineering: Computational Analysis and Experimental Validation. Comput. Biol. Med. 2020, 124, 103826. [Google Scholar] [CrossRef] [PubMed]
  31. Moradkhani, M.; Vahidi, B.; Ahmadian, B. Finite Element Study of Stem Cells under Fluid Flow for Mechanoregulation toward Osteochondral Cells. J. Mater. Sci. Mater. Med. 2021, 32, 84. [Google Scholar] [CrossRef] [PubMed]
  32. Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Finite Element Analysis of Mechanical Behavior, Permeability of Irregular Porous Scaffolds and Lattice-Based Porous Scaffolds. Mater. Res. Express 2019, 6, 105407. [Google Scholar] [CrossRef]
  33. Zhao, F.; Melke, J.; Ito, K.; van Rietbergen, B.; Hofmann, S. A Multiscale Computational Fluid Dynamics Approach to Simulate the Micro-Fluidic Environment within a Tissue Engineering Scaffold with Highly Irregular Pore Geometry. Biomech. Model. Mechanobiol. 2019, 18, 1965–1977. [Google Scholar] [CrossRef] [PubMed]
  34. Zhao, F.; Lacroix, D.; Ito, K.; van Rietbergen, B.; Hofmann, S. Changes in Scaffold Porosity during Bone Tissue Engineering in Perfusion Bioreactors Considerably Affect Cellular Mechanical Stimulation for Mineralization. Bone Rep. 2020, 12, 100265. [Google Scholar] [CrossRef]
  35. Abdelaziz, A.G.; Nageh, H.; Abdo, S.M.; Abdalla, M.S.; Amer, A.A.; Abdal-hay, A.; Barhoum, A. A Review of 3D Polymeric Scaffolds for Bone Tissue Engineering: Principles, Fabrication Techniques, Immunomodulatory Roles, and Challenges. Bioengineering 2023, 10, 204. [Google Scholar] [CrossRef] [PubMed]
  36. Prasad, A. State of Art Review on Bioabsorbable Polymeric Scaffolds for Bone Tissue Engineering. Mater. Today Proc. 2021, 44, 1391–1400. [Google Scholar] [CrossRef]
  37. Hu, X.; Lin, Z.; He, J.; Zhou, M.; Yang, S.; Wang, Y.; Li, K. Recent Progress in 3D Printing Degradable Polylactic Acid-Based Bone Repair Scaffold for the Application of Cancellous Bone Defect. MedComm–Biomater. Appl. 2022, 1, e14. [Google Scholar] [CrossRef]
  38. Panseri, S.; Montesi, M.; Hautcoeur, D.; Dozio, S.M.; Chamary, S.; De Barra, E.; Tampieri, A.; Leriche, A. Bone-like Ceramic Scaffolds Designed with Bioinspired Porosity Induce a Different Stem Cell Response. J. Mater. Sci. Mater. Med. 2021, 32, 3. [Google Scholar] [CrossRef]
  39. Suárez, M.; Fernández-García, E.; Fernández, A.; López-Píriz, R.; Díaz, R.; Torrecillas, R. Novel Antimicrobial Phosphate-Free Glass–Ceramic Scaffolds for Bone Tissue Regeneration. Sci. Rep. 2020, 10, 13171. [Google Scholar] [CrossRef]
  40. Ribas, R.G.; Schatkoski, V.M.; do Amaral Montanheiro, T.L.; de Menezes, B.R.C.; Stegemann, C.; Leite, D.M.G.; Thim, G.P. Current Advances in Bone Tissue Engineering Concerning Ceramic and Bioglass Scaffolds: A Review. Ceram. Int. 2019, 45, 21051–21061. [Google Scholar] [CrossRef]
  41. Antoniac, I.; Manescu (Paltanea), V.; Paltanea, G.; Antoniac, A.; Nemoianu, I.V.; Petrescu, M.I.; Dura, H.; Bodog, A.D. Additive Manufactured Magnesium-Based Scaffolds for Tissue Engineering. Materials 2022, 15, 8693. [Google Scholar] [CrossRef]
  42. Antoniac, I.; Miculescu, M.; Mănescu (Păltânea), V.; Stere, A.; Quan, P.H.; Păltânea, G.; Robu, A.; Earar, K. Magnesium-Based Alloys Used in Orthopedic Surgery. Materials 2022, 15, 1148. [Google Scholar] [CrossRef]
  43. Cockerill, I.; Su, Y.; Sinha, S.; Qin, Y.-X.; Zheng, Y.; Young, M.L.; Zhu, D. Porous Zinc Scaffolds for Bone Tissue Engineering Applications: A Novel Additive Manufacturing and Casting Approach. Mater. Sci. Eng. C Mater. Biol. Appl. 2020, 110, 110738. [Google Scholar] [CrossRef]
  44. Wu, H.; Xie, X.; Wang, J.; Ke, G.; Huang, H.; Liao, Y.; Kong, Q. Biological Properties of Zn–0.04Mg–2Ag: A New Degradable Zinc Alloy Scaffold for Repairing Large-Scale Bone Defects. J. Mater. Res. Technol. 2021, 13, 1779–1789. [Google Scholar] [CrossRef]
  45. Zhuang, Y.; Liu, Q.; Jia, G.; Li, H.; Yuan, G.; Yu, H. A Biomimetic Zinc Alloy Scaffold Coated with Brushite for Enhanced Cranial Bone Regeneration. ACS Biomater. Sci. Eng. 2021, 7, 893–903. [Google Scholar] [CrossRef] [PubMed]
  46. Cheng, M.; Wahafu, T.; Jiang, G.; Liu, W.; Qiao, Y.; Peng, X.; Cheng, T.; Zhang, X.; He, G.; Liu, X. A Novel Open-Porous Magnesium Scaffold with Controllable Microstructures and Properties for Bone Regeneration. Sci. Rep. 2016, 6, 24134. [Google Scholar] [CrossRef] [PubMed]
  47. Ali, D.; Sen, S. Finite Element Analysis of Mechanical Behavior, Permeability and Fluid Induced Wall Shear Stress of High Porosity Scaffolds with Gyroid and Lattice-Based Architectures. J. Mech. Behav. Biomed. Mater. 2017, 75, 262–270. [Google Scholar] [CrossRef]
  48. Zhao, F.; Vaughan, T.J.; McNamara, L.M. Quantification of Fluid Shear Stress in Bone Tissue Engineering Scaffolds with Spherical and Cubical Pore Architectures. Biomech. Model. Mechanobiol. 2016, 15, 561–577. [Google Scholar] [CrossRef] [PubMed]
  49. Li, X.; Wang, Y.; Zhang, B.; Yang, H.; Mushtaq, R.T.; Liu, M.; Bao, C.; Shi, Y.; Luo, Z.; Zhang, W. The Design and Evaluation of Bionic Porous Bone Scaffolds in Fluid Flow Characteristics and Mechanical Properties. Comput. Methods Programs Biomed. 2022, 225, 107059. [Google Scholar] [CrossRef]
  50. Fallah, A.; Altunbek, M.; Bartolo, P.; Cooper, G.; Weightman, A.; Blunn, G.; Koc, B. 3D Printed Scaffold Design for Bone Defects with Improved Mechanical and Biological Properties. J. Mech. Behav. Biomed. Mater. 2022, 134, 105418. [Google Scholar] [CrossRef]
  51. Gómez, S.; Vlad, M.D.; López, J.; Fernández, E. Design and Properties of 3D Scaffolds for Bone Tissue Engineering. Acta Biomater. 2016, 42, 341–350. [Google Scholar] [CrossRef] [PubMed]
  52. Jayasathyakawin, S.; Ravichandran, M.; Baskar, N.; Anand Chairman, C.; Balasundaram, R. Mechanical Properties and Applications of Magnesium Alloy—Review. Mater. Today Proc. 2020, 27, 909–913. [Google Scholar] [CrossRef]
  53. Arjunan, A.; Demetriou, M.; Baroutaji, A.; Wang, C. Mechanical Performance of Highly Permeable Laser Melted Ti6Al4V Bone Scaffolds. J. Mech. Behav. Biomed. Mater. 2020, 102, 103517. [Google Scholar] [CrossRef] [PubMed]
  54. Daroonparvar, M.; Yajid, M.A.M.; Gupta, R.K.; Yusof, N.M.; Bakhsheshi-Rad, H.R.; Ghandvar, H.; Ghasemi, E. Antibacterial Activities and Corrosion Behavior of Novel PEO/Nanostructured ZrO2 Coating on Mg Alloy. Trans. Nonferrous Met. Soc. China 2018, 28, 1571–1581. [Google Scholar] [CrossRef]
  55. Hussein, N.A.K.; Mohtar, N.A.J.; Neza, L.H.; Noordin, M.A.; Saad, A.P. Pore Size Effect on Mechanical Response and Fluid Permeability for Bone Scaffold Regeneration. Malays. J. Med. Health Sci. 2021, 17, 34–39. [Google Scholar]
  56. Perevoshchikova, N.; Moerman, K.M.; Akhbari, B.; Bindra, R.; Maharaj, J.N.; Lloyd, D.G.; Gomez Cerezo, M.; Carr, A.; Vaquette, C.; Saxby, D.J. Finite Element Analysis of the Performance of Additively Manufactured Scaffolds for Scapholunate Ligament Reconstruction. PLoS ONE 2021, 16, e0256528. [Google Scholar] [CrossRef]
  57. Bronfin, B.; Aghion, A.; Fantetti, N.; Von Buch, F.; Schumann, S.; Friedrich, H. High Temperature Mg Alloys for Sand and Permanent Mold Casting Applications. SAE Trans. 2004, 113, 266–270. [Google Scholar]
  58. Bronfin, B.; Moscovitch, N. New Magnesium Alloys for Transmission Parts. Met. Sci. Heat Treat. 2006, 48, 479–486. [Google Scholar] [CrossRef]
  59. Zengin, H.; Turen, Y. Effect of Y Addition on Microstructure and Corrosion Behavior of Extruded Mg–Zn–Nd–Zr Alloy. J. Magnes. Alloys 2020, 8, 640–653. [Google Scholar] [CrossRef]
  60. Aghion, E.; Moscovitch, N.; Arnon, A. Mechanical Properties of Die-Cast Magnesium Alloy MRI 230D. J. Mater. Eng. Perform. 2009, 18, 912–916. [Google Scholar] [CrossRef]
  61. Wang, P.; Gammer, C.; Brenne, F.; Prashanth, K.G.; Mendes, R.G.; Rümmeli, M.H.; Gemming, T.; Eckert, J.; Scudino, S. Microstructure and Mechanical Properties of a Heat-Treatable Al-3.5Cu-1.5Mg-1Si Alloy Produced by Selective Laser Melting. Mater. Sci. Eng. A 2018, 711, 562–570. [Google Scholar] [CrossRef]
  62. Gaon, O.; Dror, G.; Davidi, O.; Lugovskoy, A. The Effect of the Local Microstructure of MRI 201S Magnesium Alloy on Its Corrosion Rate. Corros. Sci. 2015, 93, 167–171. [Google Scholar] [CrossRef]
  63. Streza, A.; Antoniac, A.; Manescu (Paltanea), V.M.; Ciocoiu, R.; Cotrut, C.-M.; Miculescu, M.; Miculescu, F.; Antoniac, I.; Fosca, M.; Rau, J.V.; et al. In Vitro Studies Regarding the Effect of Cellulose Acetate-Based Composite Coatings on the Functional Properties of the Biodegradable Mg3Nd Alloys. Biomimetics 2023, 8, 526. [Google Scholar] [CrossRef] [PubMed]
  64. Liu, Y.; Nelson, T.; Chakroff, J.; Cromeens, B.; Johnson, J.; Lannutti, J.; Besner, G.E. Comparison of Polyglycolic Acid, Polycaprolactone, and Collagen as Scaffolds for the Production of Tissue Engineered Intestine. J. Biomed. Mater. Res. 2019, 107, 750–760. [Google Scholar] [CrossRef] [PubMed]
  65. Ali, D.; Sen, S. Permeability and Fluid Flow-Induced Wall Shear Stress of Bone Tissue Scaffolds: Computational Fluid Dynamic Analysis Using Newtonian and Non-Newtonian Blood Flow Models. Comput. Biol. Med. 2018, 99, 201–208. [Google Scholar] [CrossRef]
  66. Matos, S.; Guerra, F.; Krauser, J.T.; Figueiredo, H.; Marcelino, J.P.; Sanz, M. Evaluation of an Anorganic Bovine-Derived Mineral with P-15 Hydrogel Bone Graft: Preliminary Study in a Rabbit Cranial Bone Model. Clin. Oral Implant. Res. 2012, 23, 698–705. [Google Scholar] [CrossRef]
  67. Falacho, R.I.; Palma, P.J.; Marques, J.A.; Figueiredo, M.H.; Caramelo, F.; Dias, I.; Viegas, C.; Guerra, F. Collagenated Porcine Heterologous Bone Grafts: Histomorphometric Evaluation of Bone Formation Using Different Physical Forms in a Rabbit Cancellous Bone Model. Molecules 2021, 26, 1339. [Google Scholar] [CrossRef]
  68. Ali, D.; Sen, S. Computational Fluid Dynamics Study of the Effects of Surface Roughness on Permeability and Fluid Flow-Induced Wall Shear Stress in Scaffolds. Ann. Biomed. Eng. 2018, 46, 2023–2035. [Google Scholar] [CrossRef]
  69. Olivares, A.L.; Marsal, È.; Planell, J.A.; Lacroix, D. Finite Element Study of Scaffold Architecture Design and Culture Conditions for Tissue Engineering. Biomaterials 2009, 30, 6142–6149. [Google Scholar] [CrossRef]
  70. Vossenberg, P.; Higuera, G.A.; van Straten, G.; van Blitterswijk, C.A.; van Boxtel, A.J.B. Darcian Permeability Constant as Indicator for Shear Stresses in Regular Scaffold Systems for Tissue Engineering. Biomech. Model. Mechanobiol. 2009, 8, 499–507. [Google Scholar] [CrossRef] [PubMed]
  71. Xue, X.; Patel, M.K.; Kersaudy-Kerhoas, M.; Desmulliez, M.P.Y.; Bailey, C.; Topham, D. Analysis of Fluid Separation in Microfluidic T-Channels. Appl. Math. Model. 2012, 36, 743–755. [Google Scholar] [CrossRef]
  72. Truscello, S.; Kerckhofs, G.; Van Bael, S.; Pyka, G.; Schrooten, J.; Van Oosterwyck, H. Prediction of Permeability of Regular Scaffolds for Skeletal Tissue Engineering: A Combined Computational and Experimental Study. Acta Biomater. 2012, 8, 1648–1658. [Google Scholar] [CrossRef]
  73. Liu, H.; Lan, L.; Abrigo, J.; Ip, H.L.; Soo, Y.; Zheng, D.; Wong, K.S.; Wang, D.; Shi, L.; Leung, T.W.; et al. Comparison of Newtonian and Non-Newtonian Fluid Models in Blood Flow Simulation in Patients With Intracranial Arterial Stenosis. Front. Physiol. 2021, 12, 718540. [Google Scholar] [CrossRef]
  74. Egger, D.; Fischer, M.; Clementi, A.; Ribitsch, V.; Hansmann, J.; Kasper, C. Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture. Bioengineering 2017, 4, 51. [Google Scholar] [CrossRef]
  75. Lesman, A.; Blinder, Y.; Levenberg, S. Modeling of Flow-Induced Shear Stress Applied on 3D Cellular Scaffolds: Implications for Vascular Tissue Engineering. Biotechnol. Bioeng. 2010, 105, 645–654. [Google Scholar] [CrossRef]
  76. Marín, F.; Roldán, V. GDF-15 and Risk Stratification in Atrial Fibrillation. Nat. Rev. Cardiol. 2015, 12, 8–9. [Google Scholar] [CrossRef] [PubMed]
  77. Bozzi, S.; Dominissini, D.; Redaelli, A.; Passoni, G. The Effect of Turbulence Modelling on the Assessment of Platelet Activation. J. Biomech. 2021, 128, 110704. [Google Scholar] [CrossRef]
  78. Saqr, K.M.; Tupin, S.; Rashad, S.; Endo, T.; Niizuma, K.; Tominaga, T.; Ohta, M. Physiologic Blood Flow Is Turbulent. Sci. Rep. 2020, 10, 15492. [Google Scholar] [CrossRef]
  79. Andersson, M. Turbulence Descriptors in Arterial Flows Patient-Specific Computational Hemodynamics; Linköping Studies in Science and Technology; Linköping University Electronic Press: Linköping, Sweden, 2021; Volume 2129, ISBN 978-91-7929-686-5. [Google Scholar]
  80. Salles, S.; Shepherd, J.; Vos, H.J.; Renaud, G. Revealing Intraosseous Blood Flow in the Human Tibia with Ultrasound. JBMR Plus 2021, 5, e10543. [Google Scholar] [CrossRef] [PubMed]
  81. Ochoa, I.; Sanz-Herrera, J.A.; García-Aznar, J.M.; Doblaré, M.; Yunos, D.M.; Boccaccini, A.R. Permeability Evaluation of 45S5 Bioglass®-Based Scaffolds for Bone Tissue Engineering. J. Biomech. 2009, 42, 257–260. [Google Scholar] [CrossRef] [PubMed]
  82. Grimm, M.J.; Williams, J.L. Measurements of Permeability in Human Calcaneal Trabecular Bone. J. Biomech. 1997, 30, 743–745. [Google Scholar] [CrossRef] [PubMed]
Materials 17 00830 g001
Figure 1. Process diagram comprised of CAD design, mechanical FEA simulation, and CFD analysis for 3D implant manufacturing.
Figure 1. Process diagram comprised of CAD design, mechanical FEA simulation, and CFD analysis for 3D implant manufacturing.
Materials 17 00830 g001
Materials 17 00830 g002
Figure 2. Architecture of the two developed implants: (a) PP geometrical configuration; (b) PC geometrical configuration.
Figure 2. Architecture of the two developed implants: (a) PP geometrical configuration; (b) PC geometrical configuration.
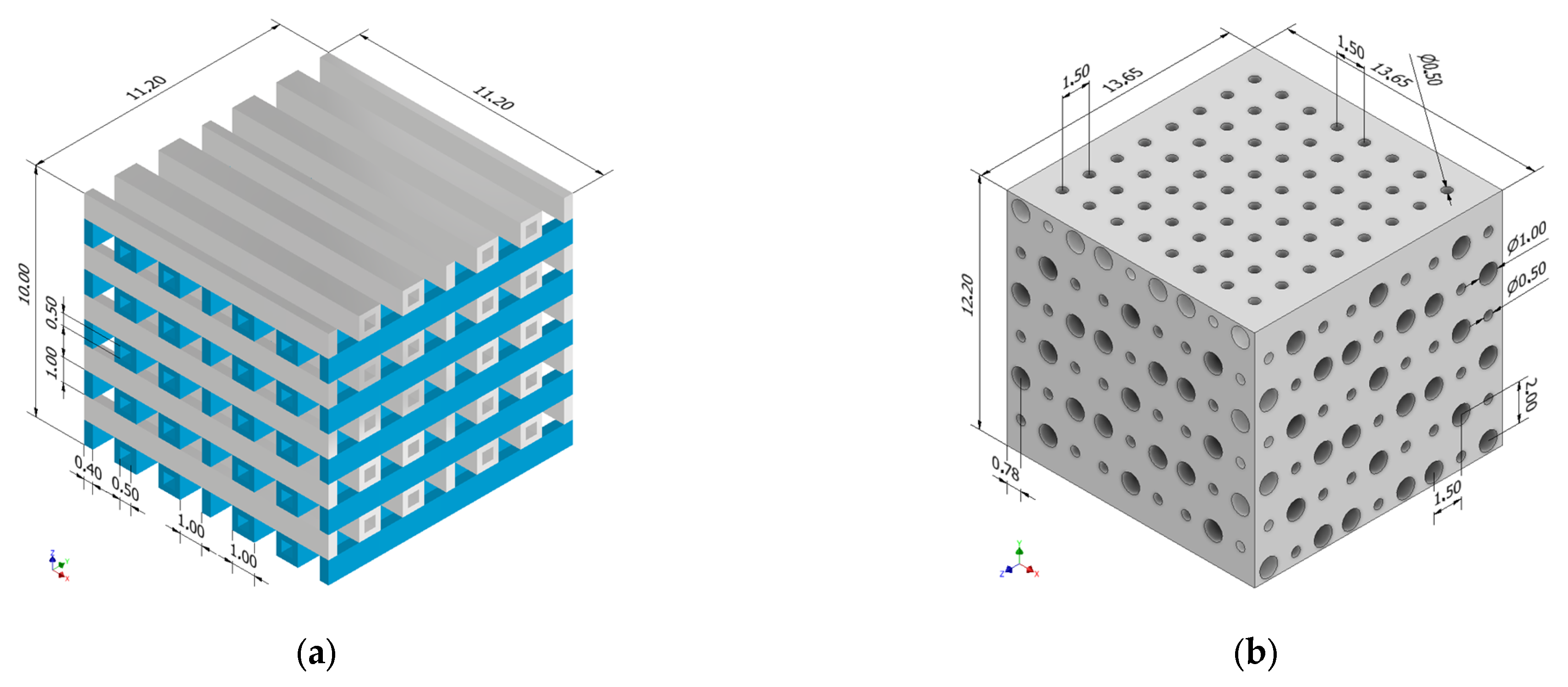
Materials 17 00830 g002
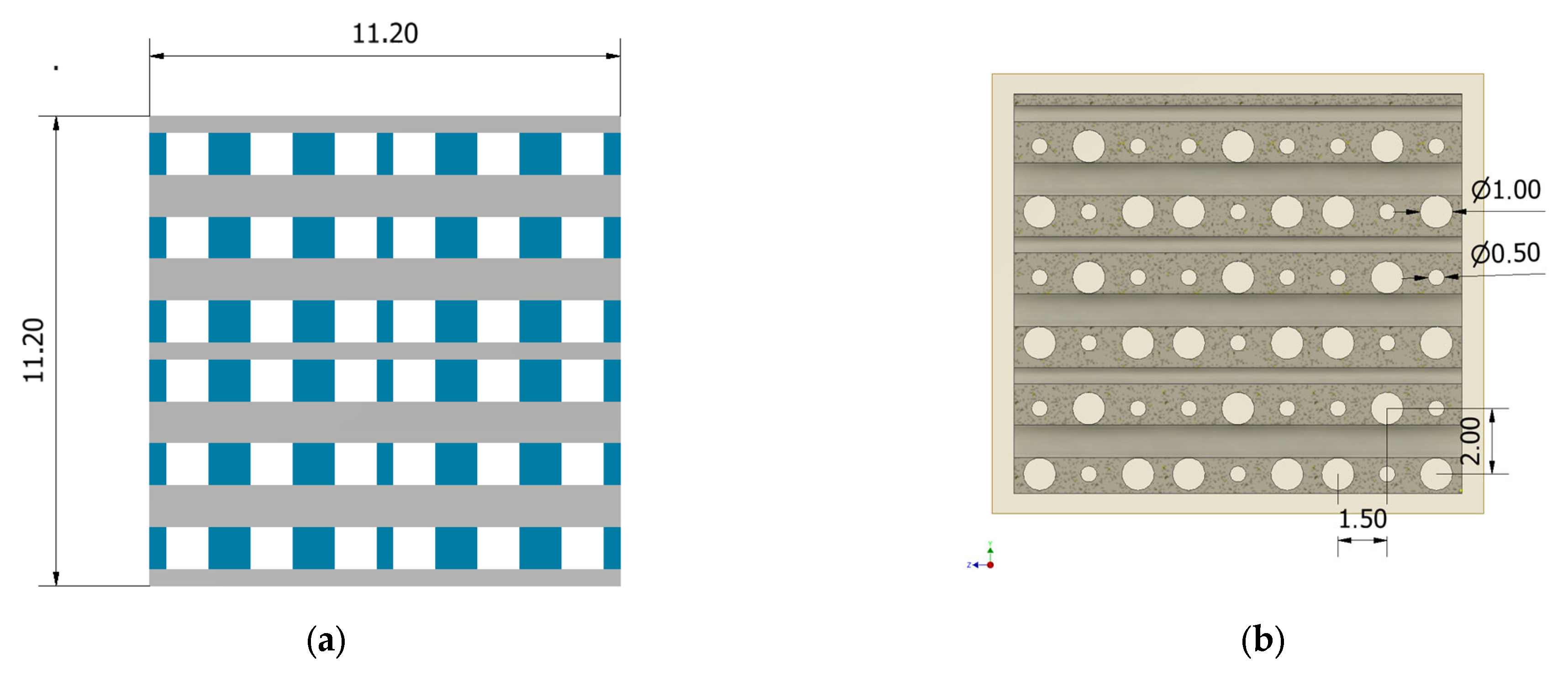
Materials 17 00830 g003
Figure 3. Geometric details of the two developed implants: (a) axial view for PP geometry; (b) coronal view for PC geometry.
Figure 3. Geometric details of the two developed implants: (a) axial view for PP geometry; (b) coronal view for PC geometry.
Materials 17 00830 g003
Materials 17 00830 g004
Figure 4. CAD geometries with imposed mechanical load (red arrows) and fixed rigid surface (green fixators): (a) PP geometry; (b) PC geometry.
Figure 4. CAD geometries with imposed mechanical load (red arrows) and fixed rigid surface (green fixators): (a) PP geometry; (b) PC geometry.
Materials 17 00830 g004
Materials 17 00830 g005
Figure 5. CFD simulation for the PP implant: (a) fluid domain; (b) boundary conditions; (c) mesh with 340,000 volume elements.
Figure 5. CFD simulation for the PP implant: (a) fluid domain; (b) boundary conditions; (c) mesh with 340,000 volume elements.
Materials 17 00830 g005
Materials 17 00830 g006
Figure 6. CFD simulation for the PC implant: (a) fluid domain; (b) boundary conditions; (c) mesh with 1,275,053 volume elements.
Figure 6. CFD simulation for the PC implant: (a) fluid domain; (b) boundary conditions; (c) mesh with 1,275,053 volume elements.
Materials 17 00830 g006
Materials 17 00830 g007
Figure 7. Graphical dependencies obtained after the mechanical simulations made for the two implants: (a) force versus displacement variation used in the computation of mechanical rigidity of the implants; (b) safety factor dependence on the applied load.
Figure 7. Graphical dependencies obtained after the mechanical simulations made for the two implants: (a) force versus displacement variation used in the computation of mechanical rigidity of the implants; (b) safety factor dependence on the applied load.
Materials 17 00830 g007
Materials 17 00830 g008aMaterials 17 00830 g008b
Figure 8. Numerical simulation results obtained for the PP implant (displacement, von Misses stress, safety factor) in the cases of different applied loads: (a) 100 N; (b) 500 N; (c) 1000 N.
Figure 8. Numerical simulation results obtained for the PP implant (displacement, von Misses stress, safety factor) in the cases of different applied loads: (a) 100 N; (b) 500 N; (c) 1000 N.
Materials 17 00830 g008aMaterials 17 00830 g008b
Materials 17 00830 g009aMaterials 17 00830 g009b
Figure 9. Numerical simulation results obtained for the PC implant (displacement, von Misses stress, safety factor) in the cases of different applied loads: (a) 100 N; (b) 500 N; (c) 1000 N.
Figure 9. Numerical simulation results obtained for the PC implant (displacement, von Misses stress, safety factor) in the cases of different applied loads: (a) 100 N; (b) 500 N; (c) 1000 N.
Materials 17 00830 g009aMaterials 17 00830 g009b
Materials 17 00830 g010
Figure 10. Pressure drops in the case of PP implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Figure 10. Pressure drops in the case of PP implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Materials 17 00830 g010
Materials 17 00830 g011
Figure 11. Variation of the fluid flow velocity in the case of PP implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Figure 11. Variation of the fluid flow velocity in the case of PP implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Materials 17 00830 g011
Materials 17 00830 g012aMaterials 17 00830 g012b
Figure 12. Wall shear stress variation for the PP implant at different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 2 mm/s; (c) 3 mm/s; (d) 4 mm/s; (e) 6 mm/s; (f) 8 mm/s; (g) 10 mm/s.
Figure 12. Wall shear stress variation for the PP implant at different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 2 mm/s; (c) 3 mm/s; (d) 4 mm/s; (e) 6 mm/s; (f) 8 mm/s; (g) 10 mm/s.
Materials 17 00830 g012aMaterials 17 00830 g012b
Materials 17 00830 g013
Figure 13. Pressure drops in the case of PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Figure 13. Pressure drops in the case of PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Materials 17 00830 g013
Materials 17 00830 g014
Figure 14. Variation of the fluid flow velocity in the case of PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Figure 14. Variation of the fluid flow velocity in the case of PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 4 mm/s; (c) 10 mm/s.
Materials 17 00830 g014
Materials 17 00830 g015aMaterials 17 00830 g015b
Figure 15. Wall shear stress variation for the PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 2 mm/s; (c) 3 mm/s; (d) 4 mm/s; (e) 6 mm/s; (f) 8 mm/s; (g) 10 mm/s.
Figure 15. Wall shear stress variation for the PC implant for different values of the inlet velocity set as boundary conditions: (a) 1 mm/s; (b) 2 mm/s; (c) 3 mm/s; (d) 4 mm/s; (e) 6 mm/s; (f) 8 mm/s; (g) 10 mm/s.
Materials 17 00830 g015aMaterials 17 00830 g015b
Materials 17 00830 g016
Figure 16. Graphical dependencies obtained after the CFD simulations made for the two implants: (a) pressure drop–velocity dependence; (b) implant permeability variation as a function of fluid flow velocity.
Figure 16. Graphical dependencies obtained after the CFD simulations made for the two implants: (a) pressure drop–velocity dependence; (b) implant permeability variation as a function of fluid flow velocity.
Materials 17 00830 g016
Materials 17 00830 g017aMaterials 17 00830 g017b
Figure 17. Specific conditions for bioreactors (u = 0.1 mm/s): (a) pressure drop for the PP implant; (b) WSS map for the PP implant; (c) pressure drop for the PC implant; (d) WSS map for the PC implant.
Figure 17. Specific conditions for bioreactors (u = 0.1 mm/s): (a) pressure drop for the PP implant; (b) WSS map for the PP implant; (c) pressure drop for the PC implant; (d) WSS map for the PC implant.
Materials 17 00830 g017aMaterials 17 00830 g017b
Table 1. Volume and porosity data for the CAD models.
Table 1. Volume and porosity data for the CAD models.
Geometrical ConfigurationVS [mm3]Vt [mm3]P [%]
PP1254.40470.4062
PC2273.131396.1838
Table 2. Numerical results obtained after mechanical simulations for the CAD models.
Table 2. Numerical results obtained after mechanical simulations for the CAD models.
Force [N]Pressure [MPa]Minimum von Mises Stress [MPa]Maximum von Mises Stress [MPa]Maximum Displacement [mm]Safety
Factor
PPPCPPPCPPPCPPPC
500.396.49 × 10−31.54 × 10−26.2222.3265.16 × 10−41.83 × 10−442.5796.46
1000.791.30 × 10−23.07 × 10−212.444.6521.03 × 10−33.66 × 10−421.2848.24
2001.592.60 × 10−26.14 × 10−224.899.3032.07 × 10−37.32 × 10−410.6424.12
3002.393.89 × 10−29.21 × 10−237.3313.953.10 × 10−31.10 × 10−37.0916.08
4003.185.19 × 10−21.23 × 10−149.7818.614.13 × 10−31.47 × 10−35.3212.06
5003.986.49 × 10−21.54 × 10−162.2223.265.17 × 10−31.83 × 10−34.259.64
6004.787.79 × 10−21.84 × 10−174.6627.916.20 × 10−32.20 × 10−33.548.04
7005.589.09 × 10−22.15 × 10−187.1132.567.23 × 10−32.56 × 10−33.046.89
8006.371.04 × 10−22.46 × 10−199.5537.218.26 × 10−32.93 × 10−32.666.03
9007.171.17 × 10−12.76 × 10−111241.869.30 × 10−33.30 × 10−32.365.36
10007.971.30 × 10−13.07 × 10−1124.446.521.03 × 10−23.66 × 10−22.124.82
The pressure was computed as F/A for each implant, respectively.
Table 3. Numerical results obtained after CFD simulations for the two CAD models.
Table 3. Numerical results obtained after CFD simulations for the two CAD models.
Velocity [mm/s]Pressure Drops [Pa]Permeability [m2]Reynolds NumberMaximum Wall Shear Stress [Pa]
PPPCPPPCPP/PCPPPC
11.353.291.06 × 10−85.36 × 10−90.680.040.10
22.736.631.06 × 10−85.33 × 10−91.370.080.20
34.1510.021.05 × 10−85.29 × 10−92.070.120.31
45.6113.491.03 × 10−85.24 × 10−92.750.160.42
68.7720.579.91 × 10−95.16 × 10−94.140.250.64
812.1027.789.58 × 10−95.09 × 10−95.520.340.87
1015.6235.399.28 × 10−94.99 × 10−96.890.431.10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Manescu, V.; Paltanea, G.; Antoniac, A.; Gruionu, L.G.; Robu, A.; Vasilescu, M.; Laptoiu, S.A.; Bita, A.I.; Popa, G.M.; Cocosila, A.L.; et al. Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants. Materials 2024, 17, 830. https://doi.org/10.3390/ma17040830

AMA Style

Manescu V, Paltanea G, Antoniac A, Gruionu LG, Robu A, Vasilescu M, Laptoiu SA, Bita AI, Popa GM, Cocosila AL, et al. Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants. Materials. 2024; 17(4):830. https://doi.org/10.3390/ma17040830

Chicago/Turabian Style

Manescu (Paltanea), Veronica, Gheorghe Paltanea, Aurora Antoniac, Lucian Gheorghe Gruionu, Alina Robu, Marius Vasilescu, Stefan Alexandru Laptoiu, Ana Iulia Bita, Georgiana Maria Popa, Andreea Liliana Cocosila, and et al. 2024. "Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants" Materials 17, no. 4: 830. https://doi.org/10.3390/ma17040830

APA Style

Manescu, V., Paltanea, G., Antoniac, A., Gruionu, L. G., Robu, A., Vasilescu, M., Laptoiu, S. A., Bita, A. I., Popa, G. M., Cocosila, A. L., Silviu, V., & Porumb, A. (2024). Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants. Materials, 17(4), 830. https://doi.org/10.3390/ma17040830

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop