Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures
Abstract
:1. Introduction
2. Experiments
2.1. Materials
2.2. Experimental Methods
2.2.1. Sample Preparation
2.2.2. Sensors Arrangement and Monitoring
3. Numerical Simulation
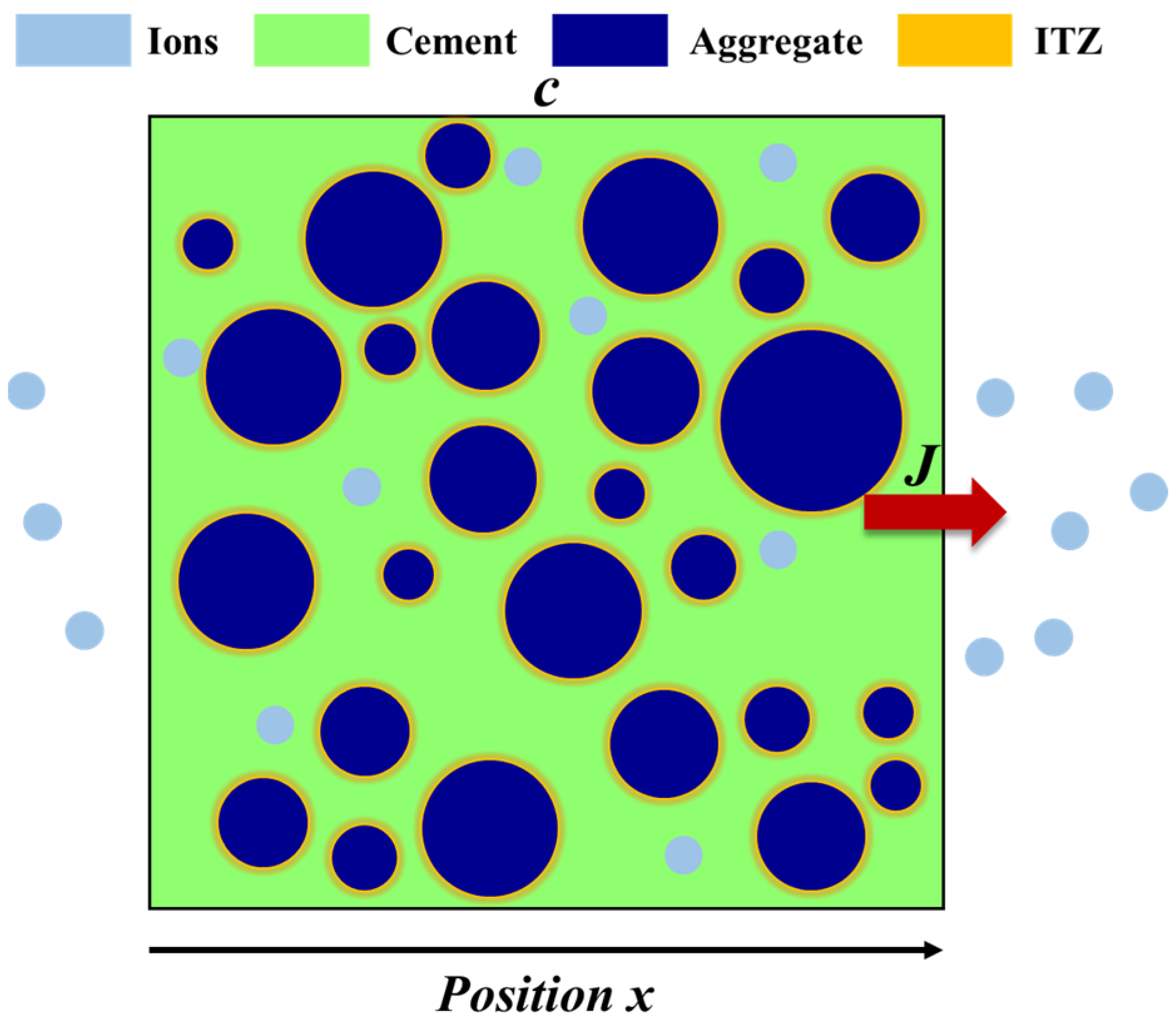
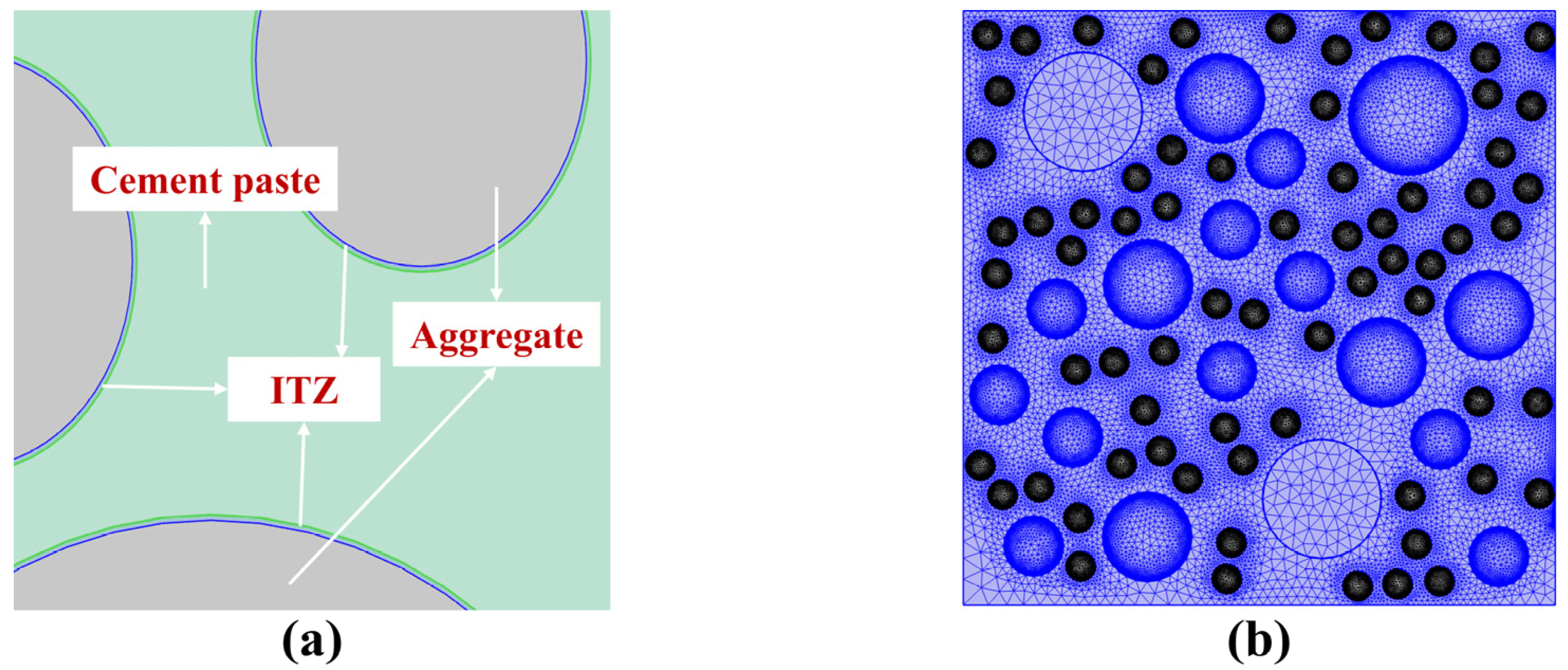
3.1. Theoretical Models
3.2. Model Establishment
4. Results and Discussion
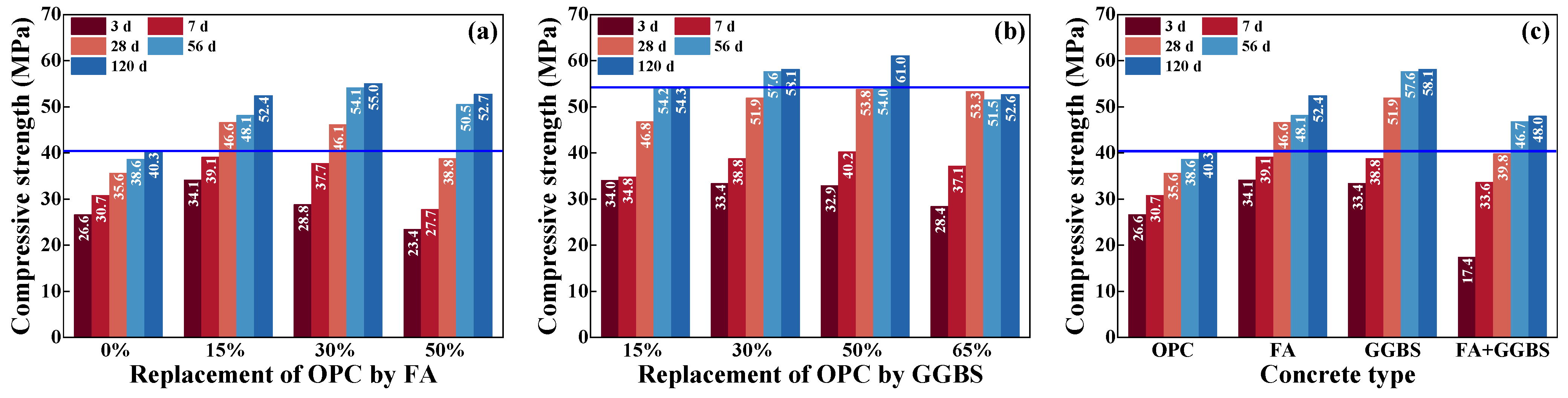
4.1. Compressive Strength of Concrete
4.2. Chloride Transport in Unsaturated Concrete
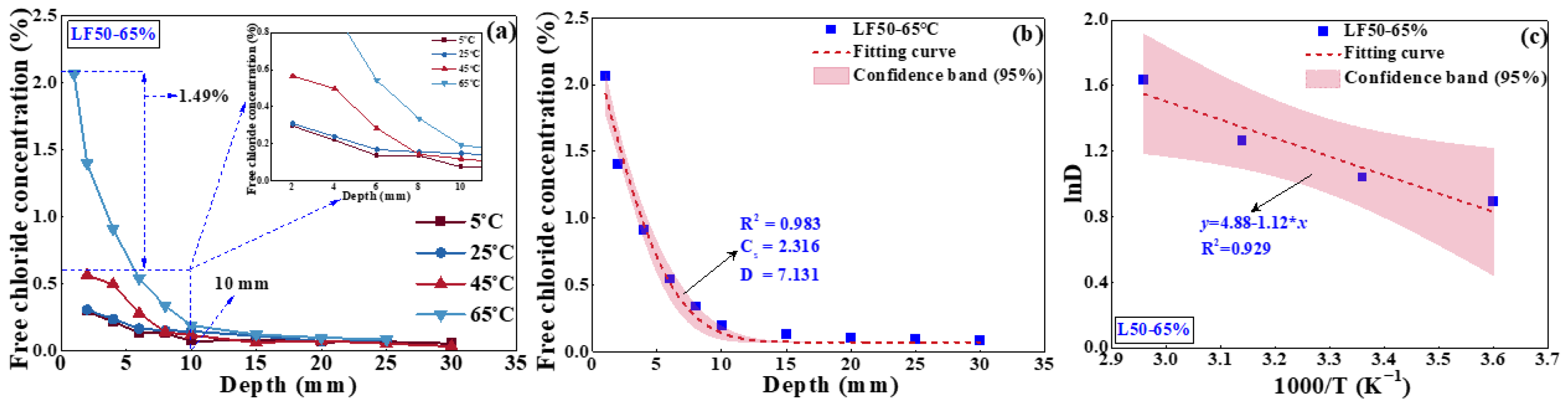
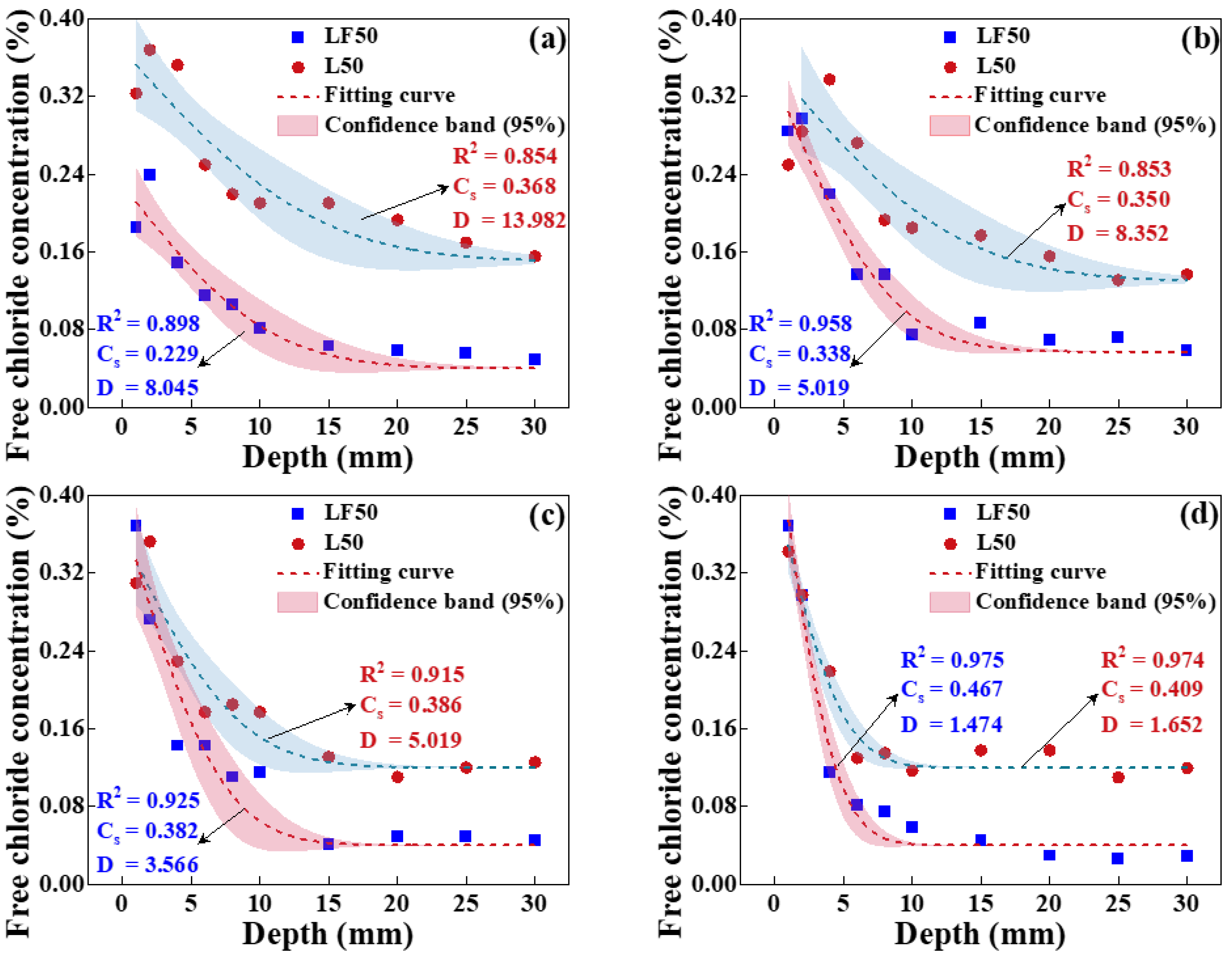
4.2.1. Effect of Temperature on Chloride Transport
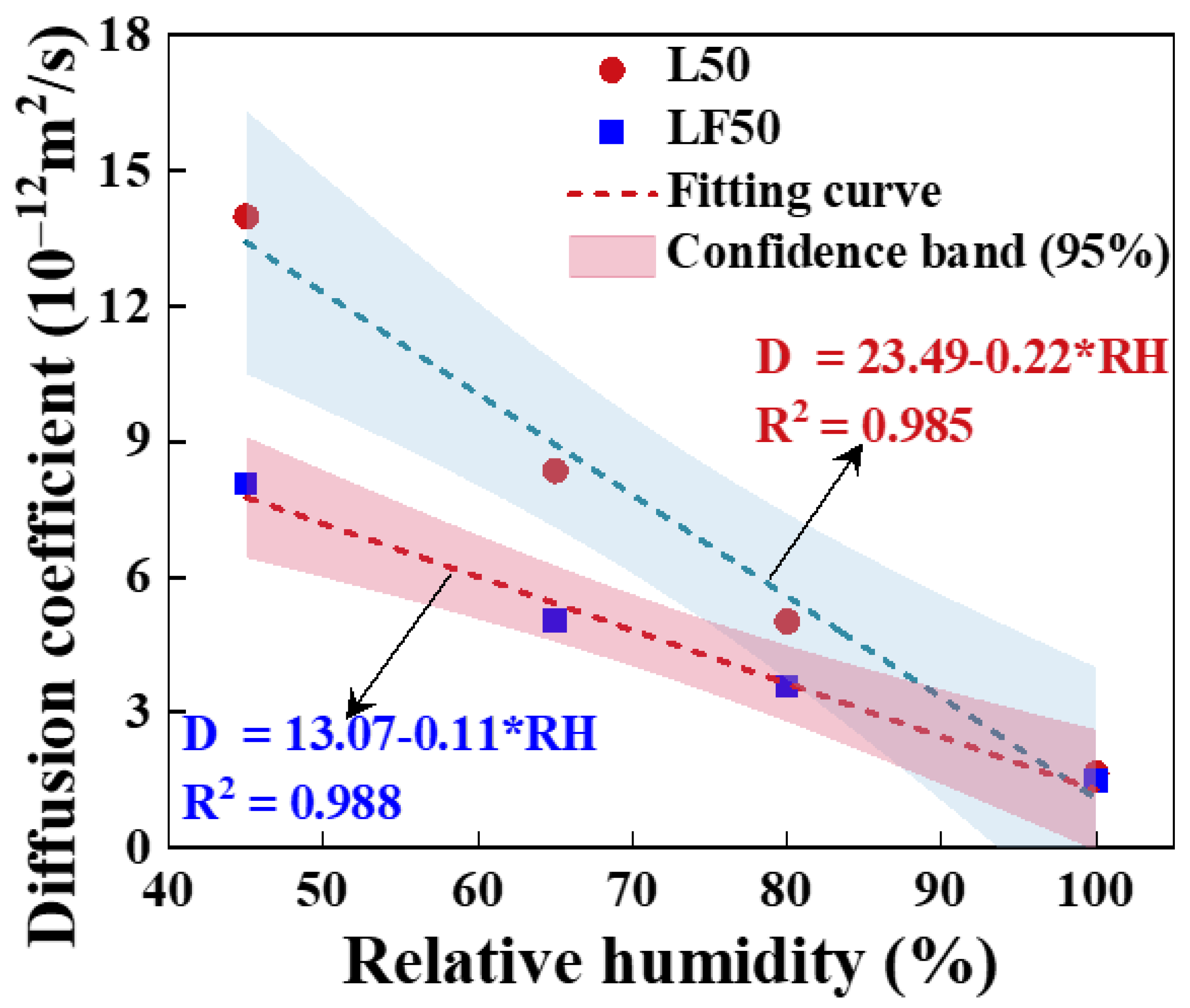
4.2.2. Effect of Relative Humidity on Chloride Transport
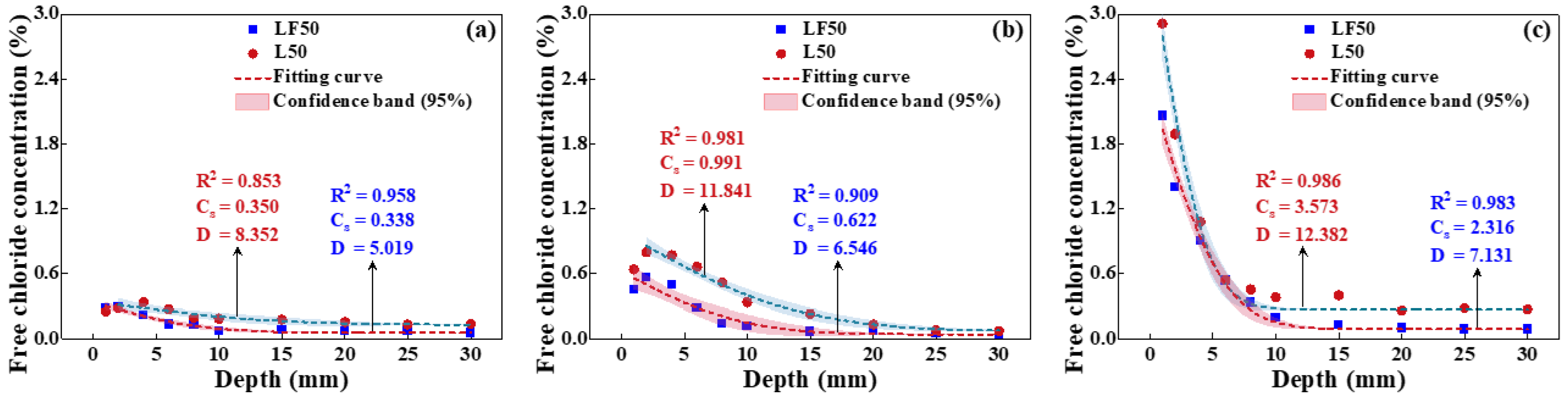
4.2.3. Effect of Mineral Admixtures on Chloride Transport
- (1)
- Effect of adding FA on chloride transport
- (2)
- Effect of adding GGBS on chloride transport
- (3)
- Effect of compounding FA and GGBS on chloride transport
4.3. Numerical Simulation
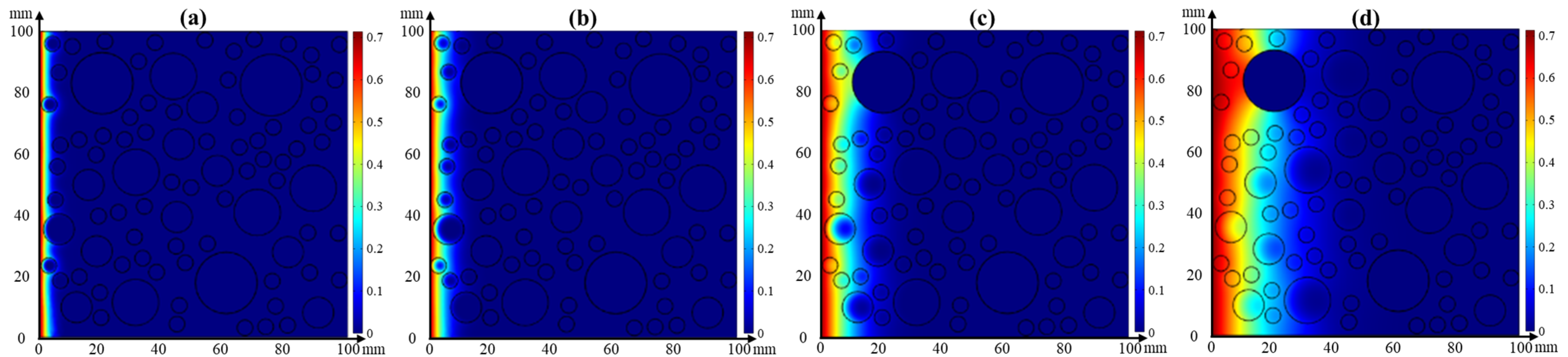
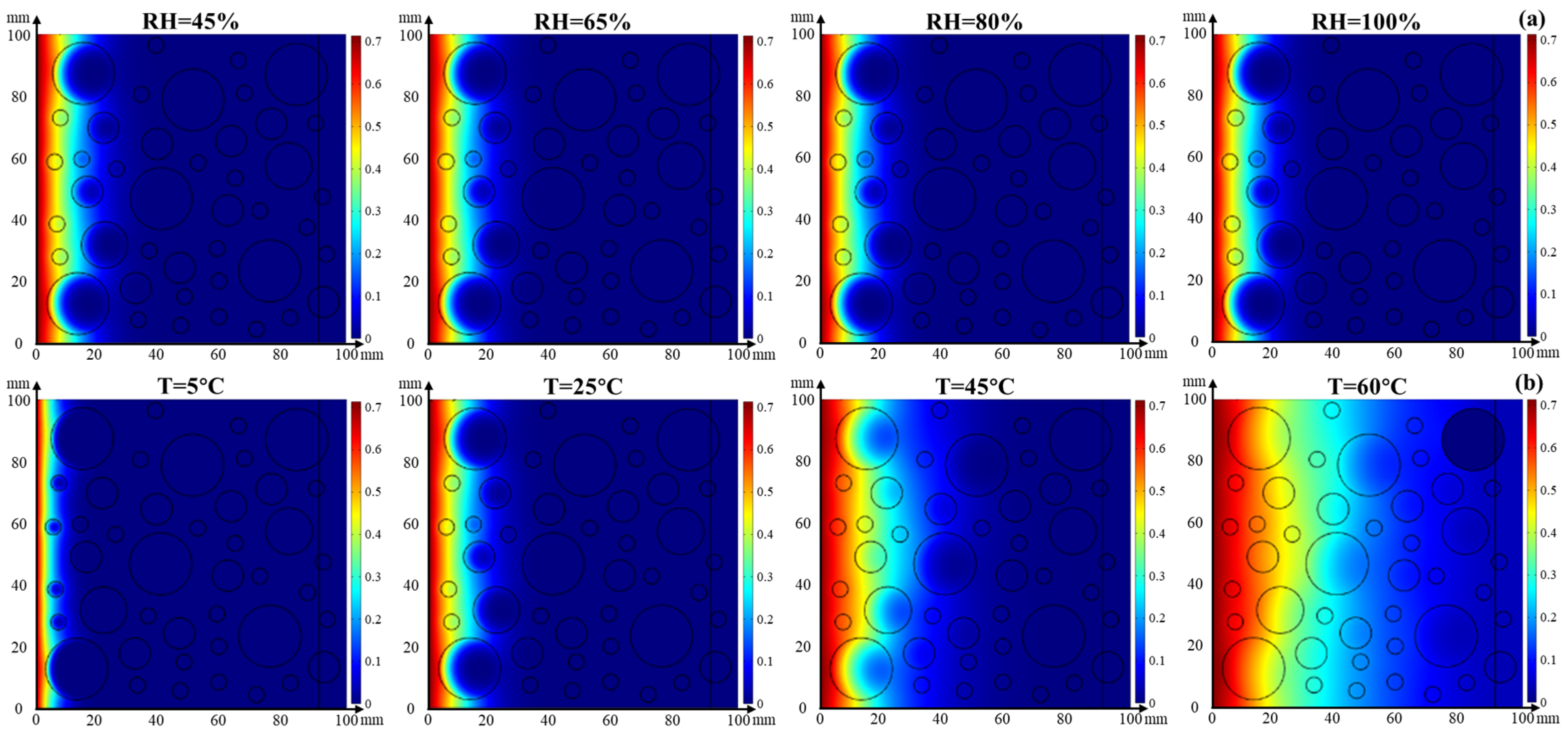
4.3.1. Single Effect of Temperature or Relative Humidity on Chloride Transport
- (1)
- Effect of temperature on chloride transport
- (2)
- Effect of relative humidity on chloride transport
4.3.2. Coupled Effect of Temperature and Relative Humidity on Chloride Transport
5. Conclusions
- The replacement of OPC by FA and GGBS is beneficial for improving the strength and capacity of antichloride, and its best dosage is suggested as compounding about 15% FA and 30% GGBS.
- The chloride diffusion coefficient is decreased with the decreased temperature and growth of relative humidity; however, the chloride concentration on the concrete surface is increased with the growth of temperature and relative humidity. Moreover, the chloride migrates to the deeper interior as the temperature increases.
- The effect tendency of temperature and relative humidity on chloride distribution in concrete obtained from the numerical simulation is consistent with the experimental result. Moreover, its accuracy is improved when considering the coupled effect of temperature or relative humidity on chloride transport.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balestra, C.E.T.; Reichert, T.A.; Savaris, G. Contribution for durability studies based on chloride profiles analysis of real marine structures in different marine aggressive zones. Constr. Build. Mater. 2019, 206, 140–150. [Google Scholar] [CrossRef]
- Lun, P.Y.; Zhang, X.G.; Jiang, C.; Ma, Y.F.; Fu, L. Modelling of Corrosion-Induced Concrete Cover Cracking Due to Chloride Attacking. Materials 2021, 14, 1440. [Google Scholar] [CrossRef]
- Oh, B.H.; Jang, S.Y. Effects of material and environmental parameters on chloride penetration profiles in concrete structures. Cem. Concr. Res. 2007, 37, 47–53. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Z.L.; Zhao, Y.L.; Zhou, H.; Wang, X.D.; Zhou, H.J.; Xing, F.; Li, S.L.; Zhu, J.H.; Liu, W. Chloride Distribution and Steel Corrosion in a Concrete Bridge after Long-Term Exposure to Natural Marine Environment. Materials 2020, 13, 3900. [Google Scholar] [CrossRef] [PubMed]
- Bui, H.T.; Tan, K.H. Time-dependent nonuniform numerical model of corrosion process and consequent corrosion-induced concrete cracking under chloride attack. Structures 2023, 52, 332–347. [Google Scholar] [CrossRef]
- Petcherdchoo, A. Closed-form solutions for modeling chloride transport in unsaturated concrete under wet-dry cycles of chloride attack. Constr. Build. Mater. 2018, 176, 638–651. [Google Scholar] [CrossRef]
- Ragab, A.M.; Elgammal, M.A.; Hodhod, O.A.; Ahmed, T. Evaluation of field concrete deterioration under real conditions of seawater attack. Constr. Build. Mater. 2016, 119, 130–144. [Google Scholar] [CrossRef]
- Rochanavibhata, U.; Punthutaecha, K.; Petcherdchoo, A. Time-dependent chloride transport models for predicting service life of bridge decks under chloride attack. Mater. Today Proc. 2022, 52, 2361–2364. [Google Scholar] [CrossRef]
- Osio-Norgaard, J.; Gevaudan, J.P.; Srubar, W.V. A review of chloride transport in alkali-activated cement paste, mortar, and concrete. Constr. Build. Mater. 2018, 186, 191–206. [Google Scholar] [CrossRef]
- Homan, L.; Ababneh, A.N.; Xi, Y. The effect of moisture transport on chloride penetration in concrete. Constr. Build. Mater. 2016, 125, 1189–1195. [Google Scholar] [CrossRef]
- Jin, H.; Liu, J.; Zhong, D.; Tang, L. Experimental study on chloride ion diffusion behavior and microstructure in concrete under alternating ambient humidity conditions. Constr. Build. Mater. 2023, 401, 132886. [Google Scholar] [CrossRef]
- Li, S.; Jin, Z.; Chang, H.; Gao, Y. Oxygen diffusion into unsaturated seawater and sea sand concrete and its effect on non-uniform corrosion of steel bars. J. Build. Eng. 2024, 84, 108665. [Google Scholar] [CrossRef]
- Ortolan, T.L.P.; Borges, P.M.; Silvestro, L.; Da Silva, S.R.; Possan, E.; Andrade, J.J.O. Durability of concrete incorporating recycled coarse aggregates: Carbonation and service life prediction under chloride-induced corrosion. Constr. Build. Mater. 2023, 404, 133267. [Google Scholar] [CrossRef]
- Li, S.; Jin, Z.; Pang, B.; Li, J. Durability performance of an RC beam under real marine all corrosion zones exposure for 7 years. Case Stud. Constr. Mater. 2022, 17, e01516. [Google Scholar] [CrossRef]
- Gašpárek, J.; Húlek, L.; Paulík, P.; Janotka, I. Theoretical prediction of chloride diffusion into concrete compared to natural chloride contamination of existing bridges. Structures 2023, 57, 105080. [Google Scholar] [CrossRef]
- Reichert, T.A.; Balestra, C.E.T.; Medeiros-Junior, R.A.D. Coupled model on the variation of diffusion coefficient and surface chloride concentration in reinforced concrete structures over time. Constr. Build. Mater. 2024, 411, 134715. [Google Scholar] [CrossRef]
- Homayoonmehr, R.; Rahai, A.; Ramezanianpour, A.A. Predicting the chloride diffusion coefficient and surface electrical resistivity of concrete using statistical regression-based models and its application in chloride-induced corrosion service life prediction of RC structures. Constr. Build. Mater. 2022, 357, 129351. [Google Scholar] [CrossRef]
- Jin, H.; Fan, X.; Li, Z.; Zhang, W.; Liu, J.; Zhong, D.; Tang, L. An experimental study on the influence of continuous ambient humidity conditions on relative humidity changes, chloride diffusion and microstructure in concrete. J. Build. Eng. 2022, 59, 105112. [Google Scholar] [CrossRef]
- Wu, L.; Gao, X.; Xia, Y. Randomness and time-varying characteristics of chloride ion transport in existing harbor concrete structures. Constr. Build. Mater. 2024, 412, 134839. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, Y.; Liu, P.; Wang, W. Accelerated simulation of chloride ingress into concrete under drying–wetting alternation condition chloride environment. Constr. Build. Mater. 2015, 93, 205–213. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Yan, B.; Liu, Z.; Wang, Y.; Yuan, C. Experimental and analytical investigation on chloride ions transport in concrete considering the effect of dry-exposure ratio under diurnal tidal environment. Constr. Build. Mater. 2022, 328, 127138. [Google Scholar] [CrossRef]
- Al-Sodani, K.A.A.; Al-Zahrani, M.M.; Maslehuddin, M.; Al-Amoudi, O.S.B.; Al-Dulaijan, S.U. Chloride diffusion models for plain and blended cement concretes exposed to laboratory and atmospheric marine conditions. J. Mater. Res. Technol. 2022, 17, 125–138. [Google Scholar] [CrossRef]
- Pansera, W.A.; Reichert, T.A.; Savaris, G.; Balestra, C.E.T. Nonlinear regression using Gaussian-Lorentzian functions to empirical modeling of convective-diffusive chloride transport in concrete. Constr. Build. Mater. 2022, 341, 127770. [Google Scholar] [CrossRef]
- Korec, E.; Jirásek, M.; Wong, H.S.; Martínez-Pañeda, E. Phase-field chemo-mechanical modelling of corrosion-induced cracking in reinforced concrete subjected to non-uniform chloride-induced corrosion. Theor. Appl. Fract. Mech. 2024, 129, 104233. [Google Scholar] [CrossRef]
- Sun, C.; Yuan, L.; Zhai, X.; Qu, F.; Li, Y.; Hou, B. Numerical and experimental study of moisture and chloride transport in unsaturated concrete. Constr. Build. Mater. 2018, 189, 1067–1075. [Google Scholar] [CrossRef]
- Dehwah, O.H.A.; Xi, Y. Theoretical model for the coupling effect of moisture transport on chloride penetration in concrete. Cem. Concr. Res. 2024, 177, 107431. [Google Scholar] [CrossRef]
- Lian, S.; Meng, T.; Zhao, Y.; Liu, Z.; Zhou, X.; Ruan, S. Experimental and theoretical analyses of chloride transport in recycled concrete subjected to a cyclic drying-wetting environment. Structures 2023, 52, 1020–1034. [Google Scholar] [CrossRef]
- Liu, Q.-F.; Cai, Y.; Peng, H.; Meng, Z.; Mundra, S.; Castel, A. A numerical study on chloride transport in alkali-activated fly ash/slag concretes. Cem. Concr. Res. 2023, 166, 107094. [Google Scholar] [CrossRef]
- Lee, J.M.; Hong, S.I.; Yang, H.J.; Jung, D.H. Numerical Modeling of Chloride Transport in Concrete under Cyclic Exposure to Chloride. Materials 2022, 15, 5966. [Google Scholar] [CrossRef]
- Jain, A.; Gencturk, B. Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete. Materials 2021, 14, 885. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Wang, J.; Liu, C.; Jiang, J.; Li, H. Experiment and simulation of chloride ion transport and binding in concrete under the coupling of diffusion and convection. J. Build. Eng. 2022, 45, 103610. [Google Scholar] [CrossRef]
- Vieira, D.R.; Moreira, A.L.R.; Calmon, J.L.; Dominicini, W.K. Service life modeling of a bridge in a tropical marine environment for durable design. Constr. Build. Mater. 2018, 163, 315–325. [Google Scholar] [CrossRef]
- da Costa, A.; Fenaux, M.; Fernández, J.; Sánchez, E.; Moragues, A. Modelling of chloride penetration into non-saturated concrete: Case study application for real marine offshore structures. Constr. Build. Mater. 2013, 43, 217–224. [Google Scholar] [CrossRef]
- Violetta, B.K. Life-365 Service Life Prediction Model. Concr. Int. 2002, 24, 53–57. [Google Scholar]
- Xi, Y.; Zdeněk, P.B. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Ababneh, A.; Benboudjema, F.; Xi, Y. Chloride Penetration in Nonsaturated Concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
- Chen, D.; Guo, W.; Wu, B.; Ye, T. Mesoscopic characteristics and spatiotemporal variability of chloride transport in concrete. Constr. Build. Mater. 2024, 415, 135081. [Google Scholar] [CrossRef]
- Kang, X.; Tong, X.-Y.; Chen, R.-P.; Chen, Y.-Q. Effect of ITZ on chloride ion transport in recycled aggregate concrete: Analytical and numerical studies. J. Build. Eng. 2024, 83, 108443. [Google Scholar] [CrossRef]




| Constituent | SiO2 | Al2O3 | Fe2O3 | CaO | MgO | Na2O | K2O | SO3 | P2O5 |
|---|---|---|---|---|---|---|---|---|---|
| OPC | 21.58 | 4.95 | 3.29 | 64.84 | 3.48 | 0.56 | 0.48 | 0.53 | 0.12 |
| GGBS | 29.05 | 12.51 | 1.30 | 48.34 | 5.72 | 0.56 | 0.08 | 1.18 | 0.54 |
| FA | 56.90 | 13.70 | 4.46 | 1.90 | 0.37 | 0.12 | 1.55 | 0.12 | 0.11 |
| NO. | Cement | GGBS | FA | Sand | Aggregate | Water | Superplasticizer | Air-Entraining Agent |
|---|---|---|---|---|---|---|---|---|
| L50 | 470 | – | – | 760 | 1090 | 165 | 8 | 0.19 |
| L51 | 399.5 | – | 70.5 | 760 | 1090 | 165 | 8 | 0.25 |
| L52 | 329 | – | 141 | 760 | 1090 | 165 | 8 | 0.25 |
| L53 | 235 | – | 235 | 760 | 1090 | 165 | 8 | 0.25 |
| F51 | 399.5 | 70.5 | – | 760 | 1090 | 165 | 8 | 0.12 |
| F52 | 329 | 141 | – | 760 | 1090 | 165 | 8 | 0.12 |
| F53 | 235 | 235 | – | 760 | 1090 | 165 | 8 | 0.12 |
| F54 | 165 | 305 | – | 760 | 1090 | 165 | 8 | 0.12 |
| LF50 | 240 | 150 | 80 | 760 | 1090 | 165 | 8 | 0.25 |
| Parameter | Value | Units |
|---|---|---|
| D1 | 4 × 10−12 | m2/s |
| D2 | 4 × 10−10 | m2/s |
| D3 | 4 × 10−13 | m2/s |
| Tref | 293.15 | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Z.; Jin, Z.; Li, S.; Xue, H.; Zhao, R. Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures. Materials 2024, 17, 930. https://doi.org/10.3390/ma17040930
Du Z, Jin Z, Li S, Xue H, Zhao R. Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures. Materials. 2024; 17(4):930. https://doi.org/10.3390/ma17040930
Chicago/Turabian StyleDu, Zhantao, Zuquan Jin, Shicai Li, Huan Xue, and Rui Zhao. 2024. "Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures" Materials 17, no. 4: 930. https://doi.org/10.3390/ma17040930
APA StyleDu, Z., Jin, Z., Li, S., Xue, H., & Zhao, R. (2024). Experimental and Numerical Study on Chloride Transport in Unsaturated Concrete: Highlighting Temperature, Humidity, and Mineral Admixtures. Materials, 17(4), 930. https://doi.org/10.3390/ma17040930







