Plasticity-Induced Heating: Revisiting the Energy-Based Variational Model
Abstract
:1. Introduction
2. State-of-the-Art Works
3. Objective
4. The Energy-Based Variational Model
4.1. Derivation for General Dissipative Solids
4.2. Adjustment to Thermo-Visco-Plasticity
4.3. Adjustment to the Johnson–Cook Plasticity Model
4.4. Implications of Given Displacement Fields
4.5. Calculation of the Taylor–Quinney Coefficient
5. Analysis of the Energy-Based Variational Model
5.1. Examination with the Johnson–Cook Constitutive Model
5.2. Examination with the Stainier–Ortiz Constitutive Model
6. Alternative Approach
7. Discussion and Conclusions
8. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Derivation of the Resulting Adiabatic Heat
Appendix A.2. Derivation of Equivalent Strain and Stress for Uni-Axial Loading
Appendix A.3. Examined Influences on the Issues of the Energy-Based Variational Model
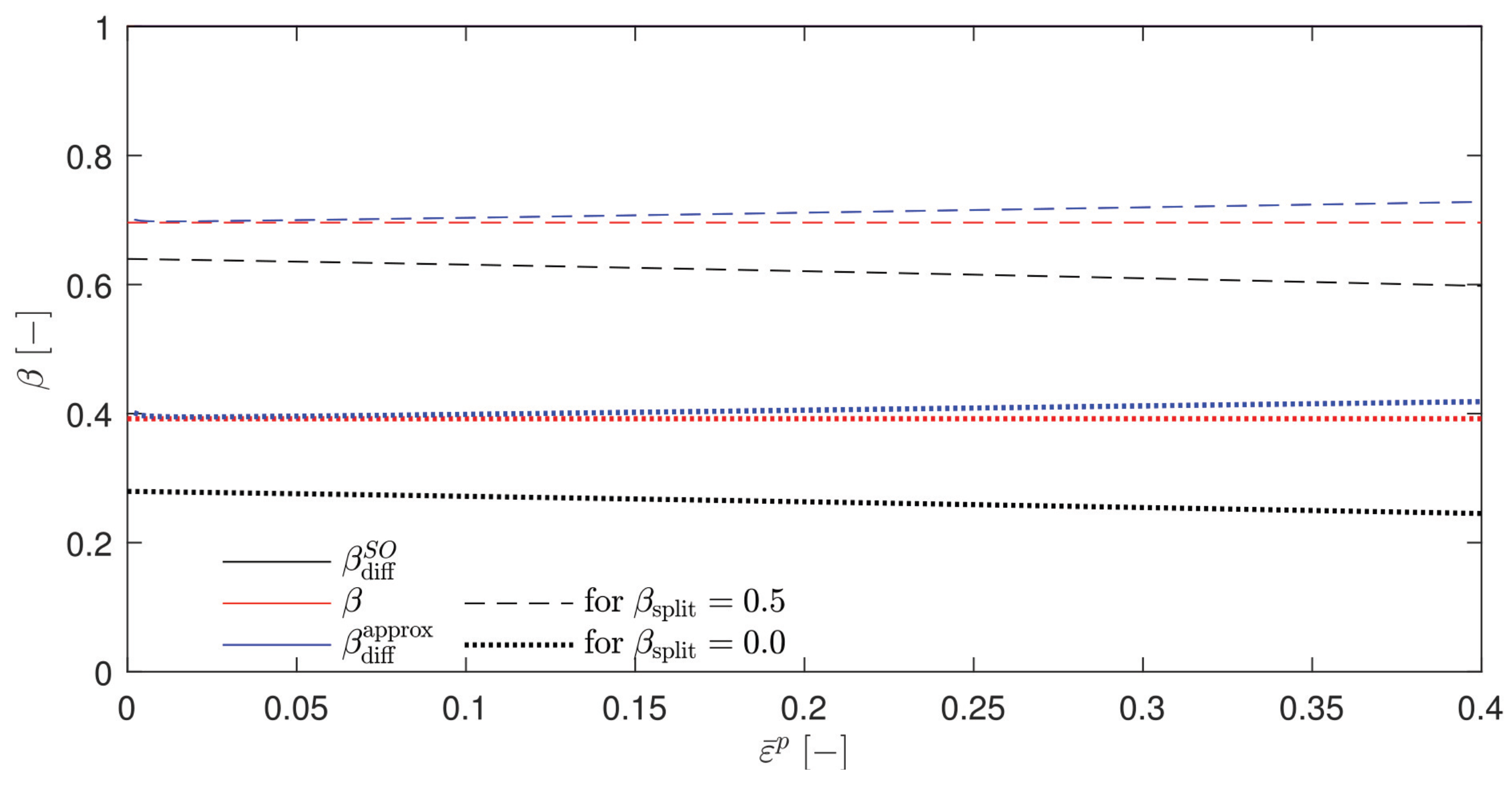
Appendix A.4. β Plots for the Review of the Energy-Based Variational Model with the Johnson–Cook Constitutive Model
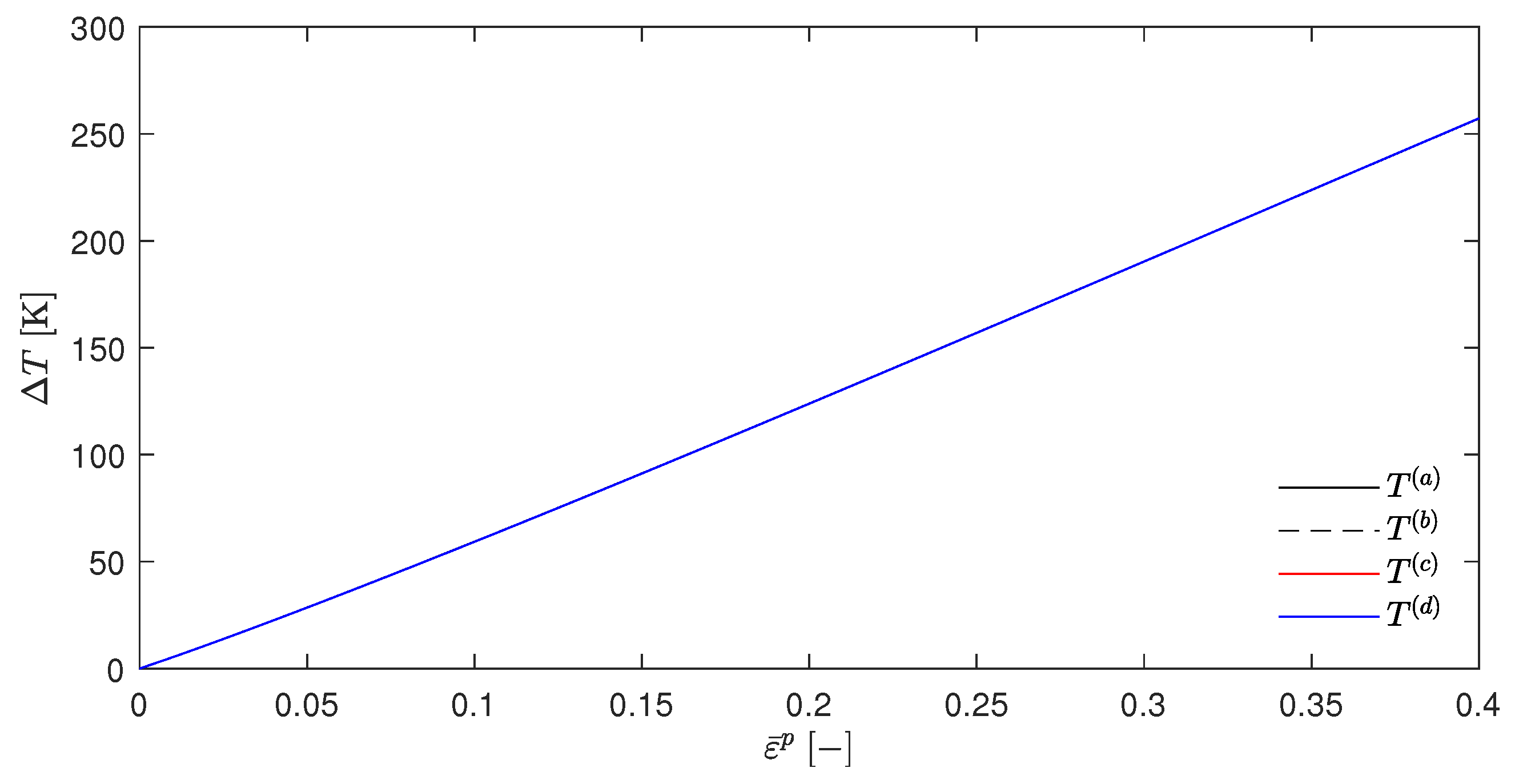
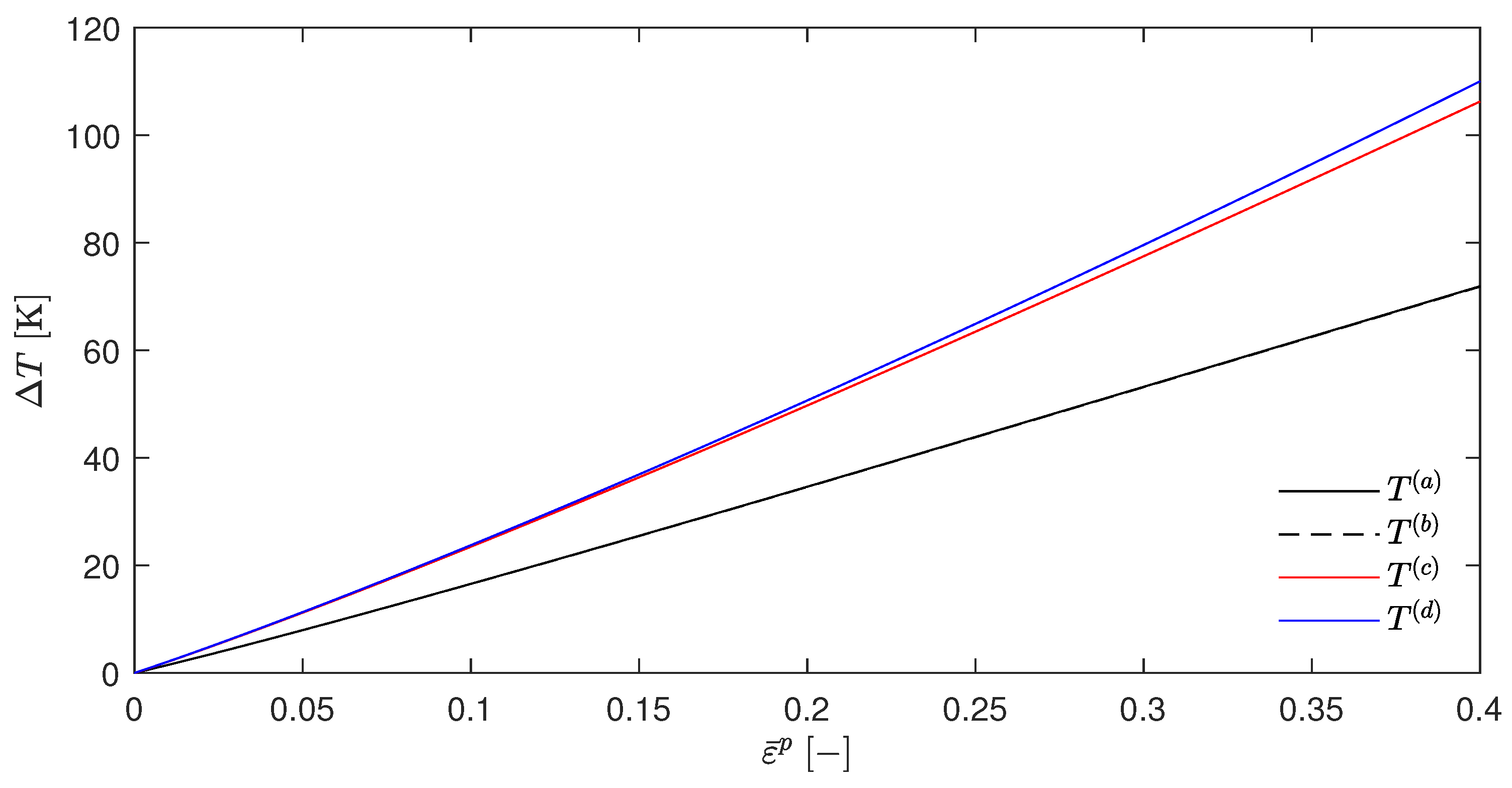
Appendix A.5. Temperature Evolution for the Review of the Energy-Based Variational Model with the Johnson–Cook Constitutive Model with Parameter q ≠ 1

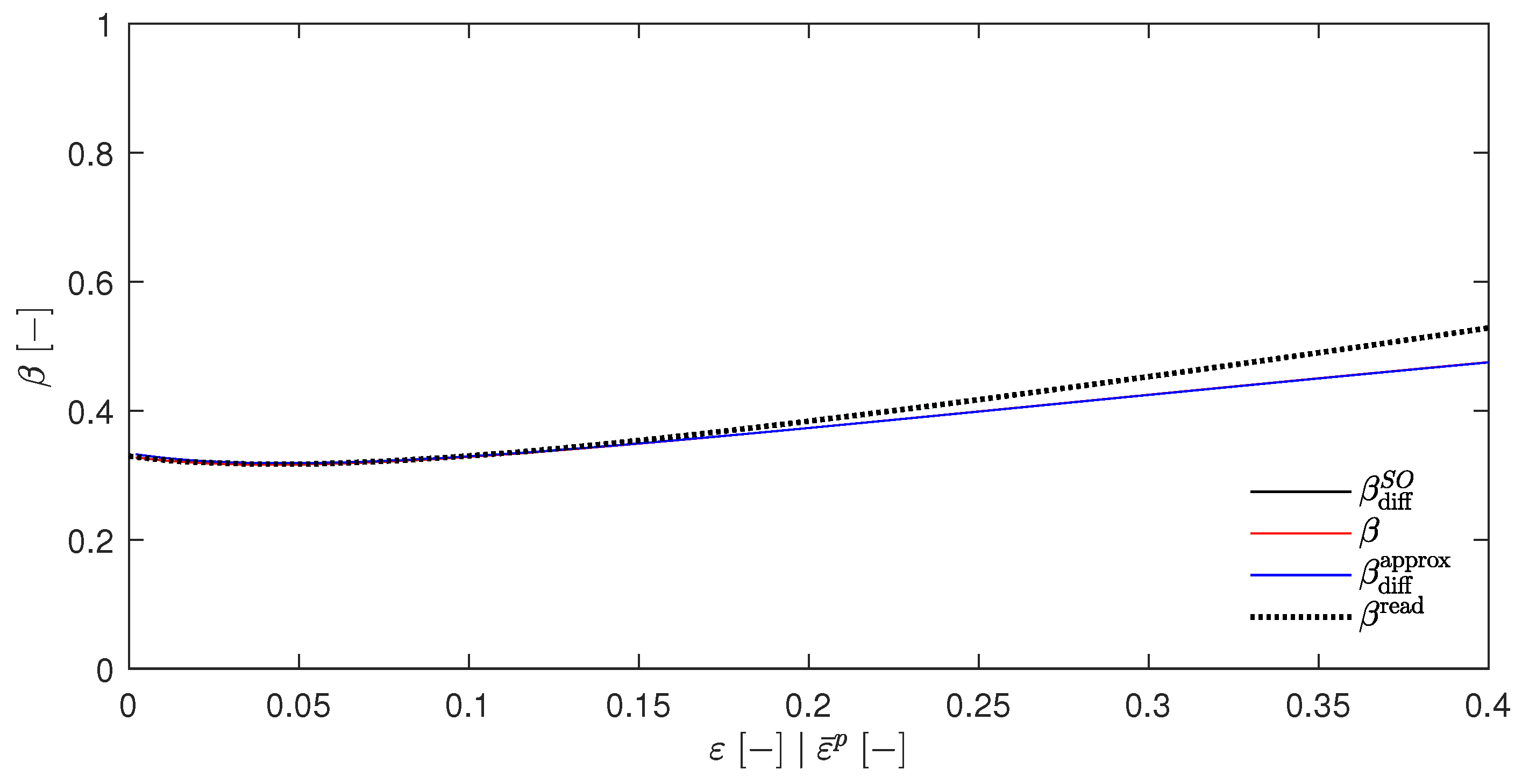
Appendix A.6. Stainier–Ortiz Model for an α-Titanium Alloy

Appendix A.7. On Possible Boundary Conditions
References
- Farren, W.S.; Taylor, G.I. The heat developed during plastic extension of metals. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1925, 107, 422–451. [Google Scholar] [CrossRef]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1934, 849, 307–326. [Google Scholar]
- Bever, M.B.; Holt, D.L.; Titchener, A.L. The stored energy of cold work. Prog. Mater. Sci. 1973, 17, 5–177. [Google Scholar] [CrossRef]
- Rosakis, P.; Rosakis, A.J.; Ravichandran, G.; Hodowany, J. A thermodynamic internal variable model for the partition of plastic work into heat and stored energy in metals. J. Mech. Phys. Solids 2000, 48, 581–607. [Google Scholar] [CrossRef]
- Vitzthum, S.; Hartmann, C.; Eder, M.; Volk, W. Temperature-based determination of the onset of yielding using a new clip-on device for tensile tests. Procedia Manuf. 2019, 29, 490–497. [Google Scholar] [CrossRef]
- Hodowany, J.; Ravichandran, G.; Rosakis, A.J.; Rosakis, P. Partition of plastic work into heat and stored energy in metals. Exp. Mech. 2000, 40, 113–123. [Google Scholar] [CrossRef]
- Nicholas, J. The dissipation of energy during plastic deformation. Acta Metall. 1959, 7, 544–548. [Google Scholar] [CrossRef]
- Nakada, Y. Orientation dependence of energy dissipation during plastic deformation of f.c.c. crystals. Philos. Mag. 1965, 11, 251–261. [Google Scholar] [CrossRef]
- Belytschko, T.; Moran, B.; Kulkarni, M. On the Crucial Role of Imperfections in Quasi-static Viscoplastic Solutions. J. Appl. Mech. 1991, 58, 658–665. [Google Scholar] [CrossRef]
- Simo, J.C.; Miehe, C. Associative coupled thermoplasticity at finite strains: Formulation, numerical analysis and implementation. Comput. Methods Appl. Mech. Eng. 1992, 98, 41–104. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. Analysis of a brittle-ductile transition under dynamic shear loading. Int. J. Solids Struct. 1995, 32, 2571–2590. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Isaacs, J.B. Direct measurement of isothermal flow stress of metals at elevated temperatures and high strain rates with application to Ta and TaW alloys. Acta Mater. 1997, 45, 907–919. [Google Scholar] [CrossRef]
- Rusinek, A.; Zaera, R.; Klepaczko, J.R. Constitutive relations in 3-D for a wide range of strain rates and temperatures—Application to mild steels. Int. J. Solids Struct. 2007, 44, 5611–5634. [Google Scholar] [CrossRef]
- Chrysochoos, A.; Maisonneuve, O.; Martin, G.; Caumon, H.; Chezeaux, J.C. Plastic and dissipated work and stored energy. Nuclear Eng. Des. 1989, 114, 323–333. [Google Scholar] [CrossRef]
- Chrysochoos, A.; Belmahjoub, F. Thermographic analysis of thermomechanical couplings. Arch. Mech. 1992, 44, 55–68. [Google Scholar]
- Mason, J.J.; Rosakis, A.J.; Ravichandran, G. On the strain and strain rate dependence of the fraction of plastic work converted to heat: An experimental study using high speed infrared detectors and the Kolsky bar. Mech. Mater. 1994, 17, 135–145. [Google Scholar] [CrossRef]
- Zehnder, A.T.; Babinsky, E.; Palmer, T. Hybrid method for determining the fraction of plastic work converted to heat. Exp. Mech. 1998, 38, 295–302. [Google Scholar] [CrossRef]
- Chaboche, J.L. Cyclic Viscoplastic Constitutive Equations, Part II: Stored Energy—Comparison Between Models and Experiments. J. Appl. Mech. 1993, 60, 822–828. [Google Scholar] [CrossRef]
- Longère, P.; Dragon, A. Plastic work induced heating evaluation under dynamic conditions: Critical assessment. Mech. Res. Commun. 2008, 35, 135–141. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J.R. Experiments on heat generated during plastic deformation and stored energy for TRIP steels. Mater. Des. 2009, 30, 35–48. [Google Scholar] [CrossRef]
- Aravas, N.; Kim, K.S.; Leckie, F.A. On the Calculations of the Stored Energy of Cold Work. J. Eng. Mater. Technol. 1990, 112, 465–470. [Google Scholar] [CrossRef]
- Zehnder, A.T. A model for the heating due to plastic work. Mech. Res. Commun. 1991, 18, 23–28. [Google Scholar] [CrossRef]
- Benzerga, A.A.; Bréchet, Y.; Needleman, A.; van der Giessen, E. The stored energy of cold work: Predictions from discrete dislocation plasticity. Acta Mater. 2005, 53, 4765–4779. [Google Scholar] [CrossRef]
- Yang, Q.; Stainier, L.; Ortiz, M. A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. J. Mech. Phys. Solids 2006, 54, 401–424. [Google Scholar] [CrossRef]
- Rittel, D. On the conversion of plastic work to heat during high strain rate deformation of glassy polymers. Mech. Mater. 1999, 31, 131–139. [Google Scholar] [CrossRef]
- Kapoor, R.; Nemat-Nasser, S. Determination of temperature rise during high strain rate deformation. Mech. Mater. 1998, 27, 1–12. [Google Scholar] [CrossRef]
- Stainier, L.; Ortiz, M. Study and validation of a variational theory of thermo-mechanical coupling in finite visco-plasticity. Int. J. Solids Struct. 2010, 47, 705–715. [Google Scholar] [CrossRef]
- Hartmann, C.; Lechner, P.; Volk, W. In-situ measurement of higher-order strain derivatives for advanced analysis of forming processes using spatio-temporal optical flow. CIRP Ann. 2021, 70, 251–254. [Google Scholar] [CrossRef]
- Hartmann, C.; Volk, W. Full-Field Strain Measurement in Multi-stage Shear Cutting: High-Speed Camera Setup and Variational Motion Estimation. In Forming the Future; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; Springer: Cham, Switzerland, 2021; pp. 1605–1615. [Google Scholar] [CrossRef]
- Hartmann, C.; Wang, J.; Opristescu, D.; Volk, W. Implementation and evaluation of optical flow methods for two-dimensional deformation measurement in comparison to digital image correlation. Opt. Lasers Eng. 2018, 107, 127–141. [Google Scholar] [CrossRef]
- Smith, J.L.; Seidt, J.D.; Gilat, A. Full-Field Determination of the Taylor-Quinney Coefficient in Tension Tests of Ti-6Al-4V at Strain Rates up to 7000s-1. In Advancement of Optical Methods & Digital Image Correlation in Experimental Mechanics, Volume 3; Lamberti, L., Lin, M.T., Furlong, C., Sciammarella, C., Reu, P.L., Sutton, M.A., Eds.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer International Publishing: Cham, Switzerland, 2019; Volume A107, pp. 133–139. [Google Scholar] [CrossRef]
- Bauer, A.; Hartmann, C. Spatio-Trajectorial Optical Flow for Higher-Order Deformation Analysis in Solid Experimental Mechanics. Sensors 2023, 23, 4408. [Google Scholar] [CrossRef]
- Bauer, A.; Volk, W.; Hartmann, C. Application of Fractal Image Analysis by Scale-Space Filtering in Experimental Mechanics. J. Imaging 2022, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Stainier, L. A Variational Approach to Modeling Coupled Thermo-Mechanical Nonlinear Dissipative Behaviors. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 46, pp. 69–126. [Google Scholar] [CrossRef]
- Su, S.; Stainier, L. Energy-based variational modeling of adiabatic shear bands structure evolution. Mech. Mater. 2015, 80, 219–233. [Google Scholar] [CrossRef]
- Levine, I.N. Physical Chemistry, 6th ed.; McGraw-Hill Higher Education: Boston, MA, USA, 2009. [Google Scholar]
- Coleman, B.D.; Noll, W. The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal. 1963, 13, 167–178. [Google Scholar] [CrossRef]
- Biot, M. Linear thermodynamics and the mechanics of solids. In Proceedings of the Third US National Congress of Applied Mechanics; Cornell Aeronautical Lab., Inc.: Buffalo, NY, USA, 1958; pp. 1–18. [Google Scholar]
- Ortiz, M.; Stainier, L. The variational formulation of viscoplastic constitutive updates. Comput. Methods Appl. Mech. Eng. 1999, 171, 419–444. [Google Scholar] [CrossRef]
- Li, Y.M.; Peng, Y.H. Fine-blanking process simulation by rigid viscous-plastic FEM coupled with void damage. Finite Elements Anal. Des. 2003, 39, 457–472. [Google Scholar] [CrossRef]
- Zhao, P.J.; Chen, Z.H.; Dong, C.F. Experimental and numerical analysis of micromechanical damage for DP600 steel in fine-blanking process. J. Mater. Process. Technol. 2016, 236, 16–25. [Google Scholar] [CrossRef]
- Su, S. Energy-Based Variational Modelling of Adiabatic Shear Band Structure. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes, France, 2012. [Google Scholar]
- Miehe, C. Entropic thermoelasticity at finite strains. Aspects of the formulation and numerical implementation. Comput. Methods Appl. Mech. Eng. 1995, 120, 243–269. [Google Scholar] [CrossRef]
- Halphen, B.; Nguyen, Q.S. On Generalized Standard Materials [Sur les matériaux standard généralisés]. J. Mécanique 1975, 14, 39–63. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L.; Shrivastava, B. Mechanics of Solid Materials, 1st ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Stainier, L. Consistent incremental approximation of dissipation pseudo-potentials in the variational formulation of thermo-mechanical constitutive updates. Mech. Res. Commun. 2011, 38, 315–319. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Lee, W.S.; Lin, C.F. Plastic deformation and fracture behaviour of Ti–6Al–4V alloy loaded with high strain rate under various temperatures. Mater. Sci. Eng. A 1998, 241, 48–59. [Google Scholar] [CrossRef]
- Ziegler, H.; Wehrli, C. The Derivation of Constitutive Relations from the Free Energy and the Dissipation Function. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1987; Volume 25, pp. 183–238. [Google Scholar] [CrossRef]
- Ziegler, H. Grundprobleme der Thermomechanik. Z. Angew. Math. Phys. ZAMP 1977, 28, 965–977. [Google Scholar] [CrossRef]
- Hartmann, C.; Weiss, H.A.; Lechner, P.; Volk, W.; Neumayer, S.; Fitschen, J.H.; Steidl, G. Measurement of strain, strain rate and crack evolution in shear cutting. J. Mater. Process. Technol. 2021, 288, 116872. [Google Scholar] [CrossRef]
- Klopp, R.W.; Clifton, R.J.; Shawki, T.G. Pressure-shear impact and the dynamic viscoplastic response of metals. Mech. Mater. 1985, 4, 375–385. [Google Scholar] [CrossRef]
- Khan, A.S.; Sung Suh, Y.; Kazmi, R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys. Int. J. Plast. 2004, 20, 2233–2248. [Google Scholar] [CrossRef]
- Khan, A.S.; Yu, S. Deformation induced anisotropic responses of Ti–6Al–4V alloy. Part I: Experiments. Int. J. Plast. 2012, 38, 1–13. [Google Scholar] [CrossRef]
- The Mathworks, Inc. MATLAB R2018b; The Mathworks, Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Valbruna Edel Inox GmbH. Werkstoffdatenblatt Valbruna GR5/Ti6Al4V; Valbruna Edel Inox GmbH: Nürtingen, Germany, 2020. [Google Scholar]
- Ranc, N.; Chrysochoos, A. Calorimetric consequences of thermal softening in Johnson–Cook’s model. Mech. Mater. 2013, 65, 44–55. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements for Continua and Structures, 2nd ed.; Wiley: Chichester, UK, 2006. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J. The Finite Element Method, 6th ed.; Elsevier Butterworth-Heinemann: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Knabner, P.; Angermann, L. Numerical Methods for Elliptic and Parabolic Partial Differential Equations; Texts in Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 44. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Faragó, I. Qualitative Analysis of the Crank-Nicolson Method for the Heat Conduction Equation. In Numerical Analysis and Its Applications; Lecture Notes in Computer Science; Margenov, S., Vulkov, L.G., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5434, pp. 44–55. [Google Scholar] [CrossRef]
- Langtangen, H.P.; Linge, S. Finite Difference Computing with PDEs; Springer: Cham, Switzerland, 2017; Volume 16. [Google Scholar] [CrossRef]
- Canadija, M.; Mosler, J. On the thermomechanical coupling in finite strain plasticity theory with non-linear kinematic hardening by means of incremental energy minimization. Int. J. Solids Struct. 2011, 48, 1120–1129. [Google Scholar] [CrossRef]
- Gaskell, D.R.; Laughlin, D.E. Introduction to the Thermodynamics of Materials, 6th ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2018. [Google Scholar]
- Colby, R.B. Equivalent Plastic Strain for the Hill’s Yield Criterion under General Three-Dimensional Loading. Bachelor’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]



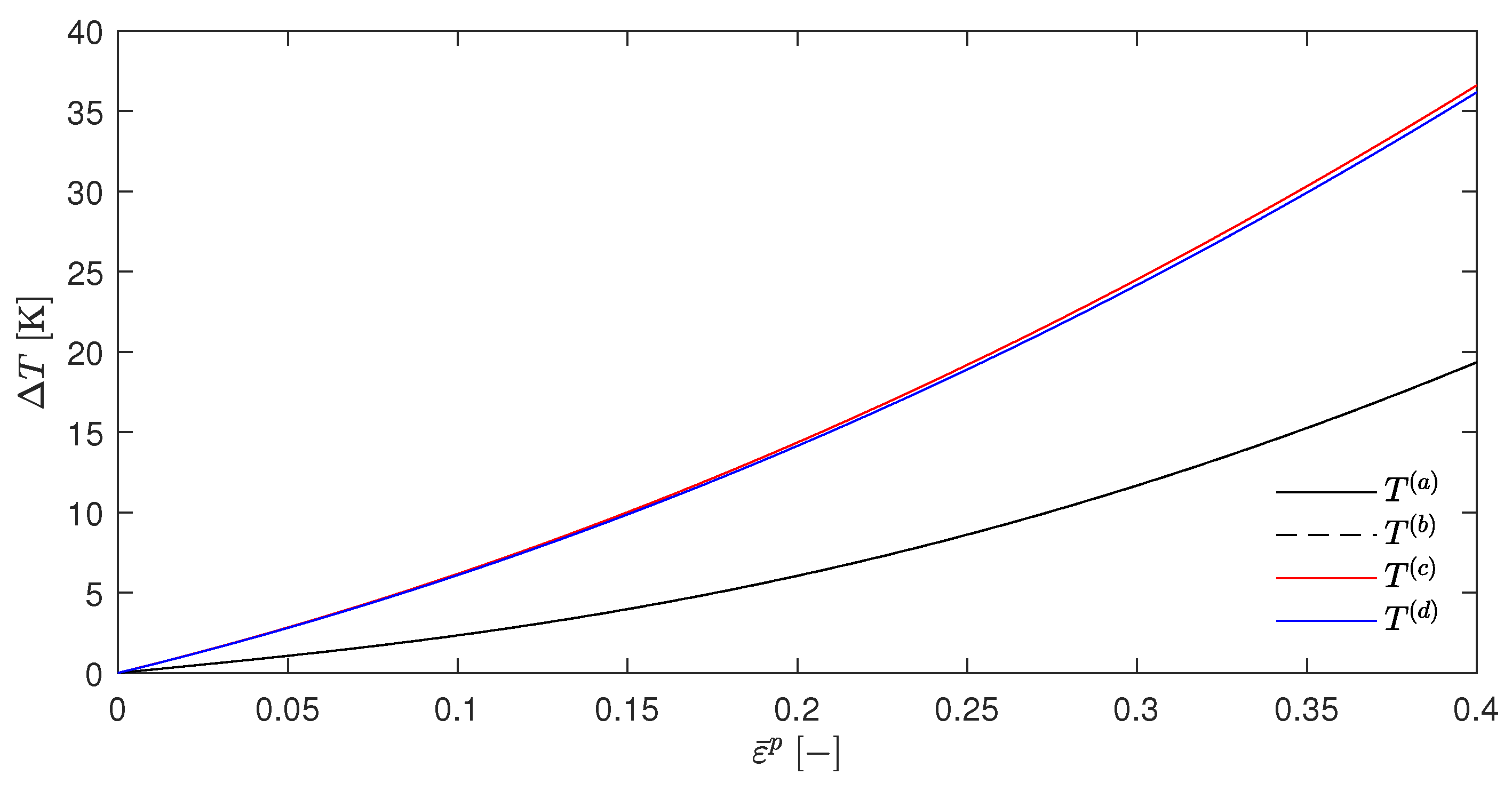
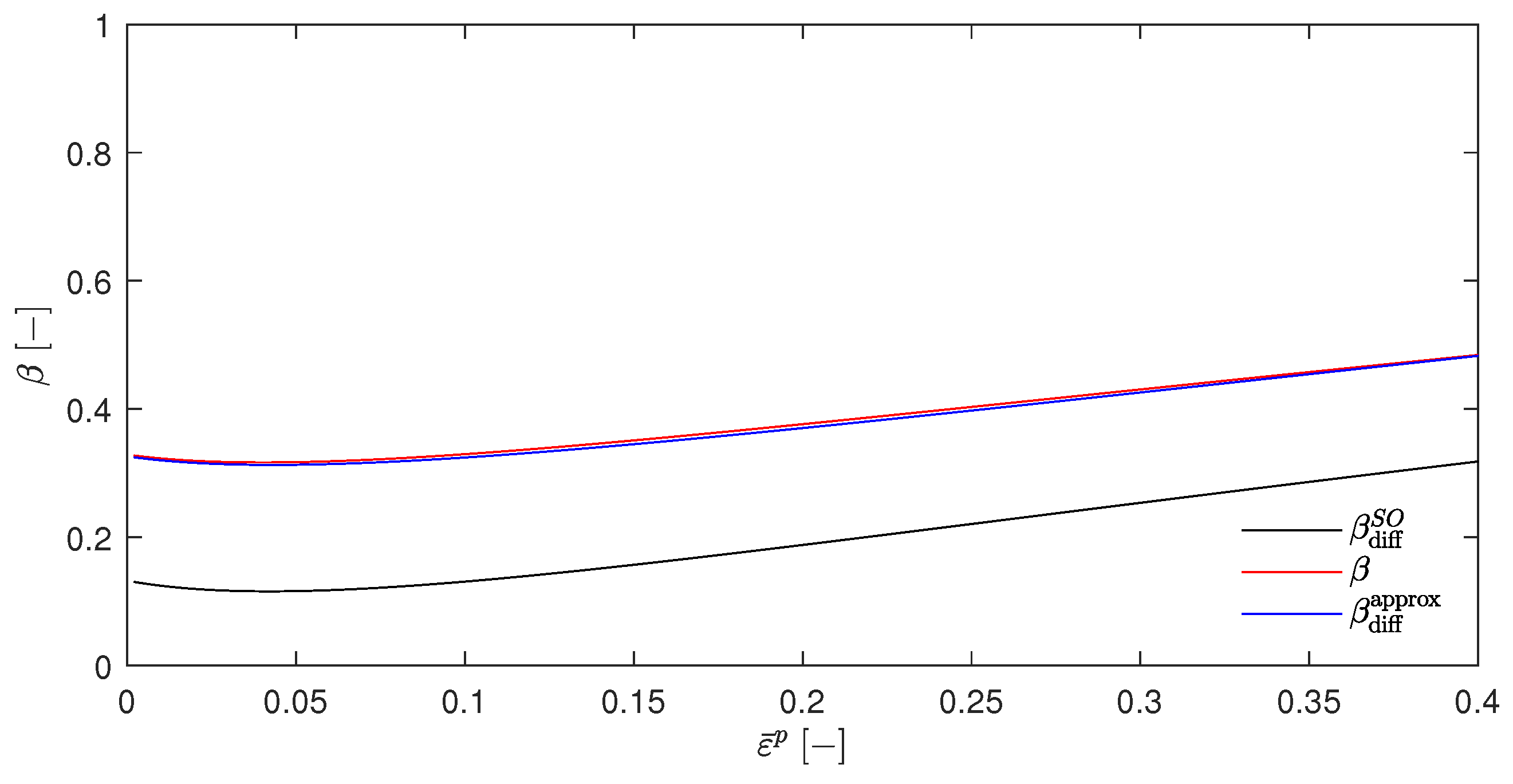
| − | ||||
| − | − | |||
| − | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartmann, C.; Obermeyer, M. Plasticity-Induced Heating: Revisiting the Energy-Based Variational Model. Materials 2024, 17, 1078. https://doi.org/10.3390/ma17051078
Hartmann C, Obermeyer M. Plasticity-Induced Heating: Revisiting the Energy-Based Variational Model. Materials. 2024; 17(5):1078. https://doi.org/10.3390/ma17051078
Chicago/Turabian StyleHartmann, Christoph, and Michael Obermeyer. 2024. "Plasticity-Induced Heating: Revisiting the Energy-Based Variational Model" Materials 17, no. 5: 1078. https://doi.org/10.3390/ma17051078
APA StyleHartmann, C., & Obermeyer, M. (2024). Plasticity-Induced Heating: Revisiting the Energy-Based Variational Model. Materials, 17(5), 1078. https://doi.org/10.3390/ma17051078






