Pulsed Optical Vortex Array Generation in a Self-Q-Switched Tm:YALO3 Laser
Abstract
:1. Introduction
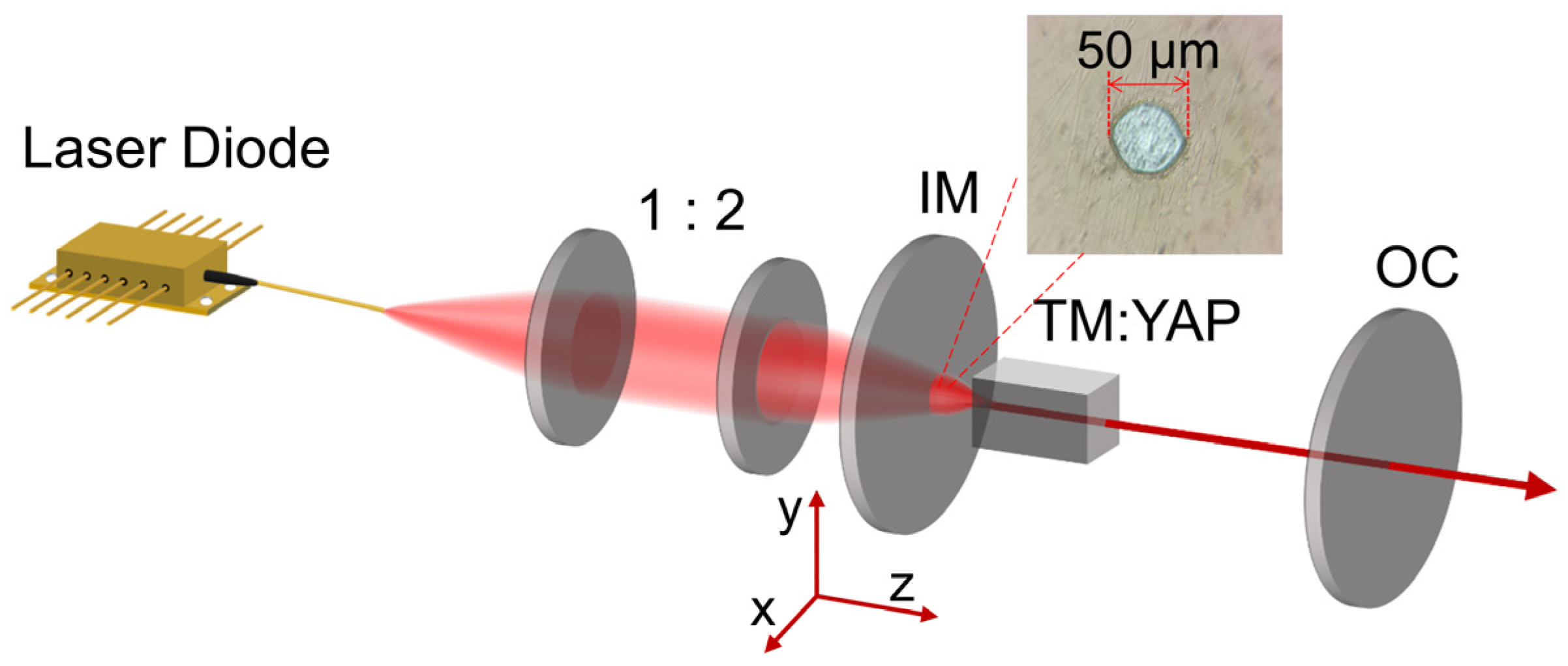
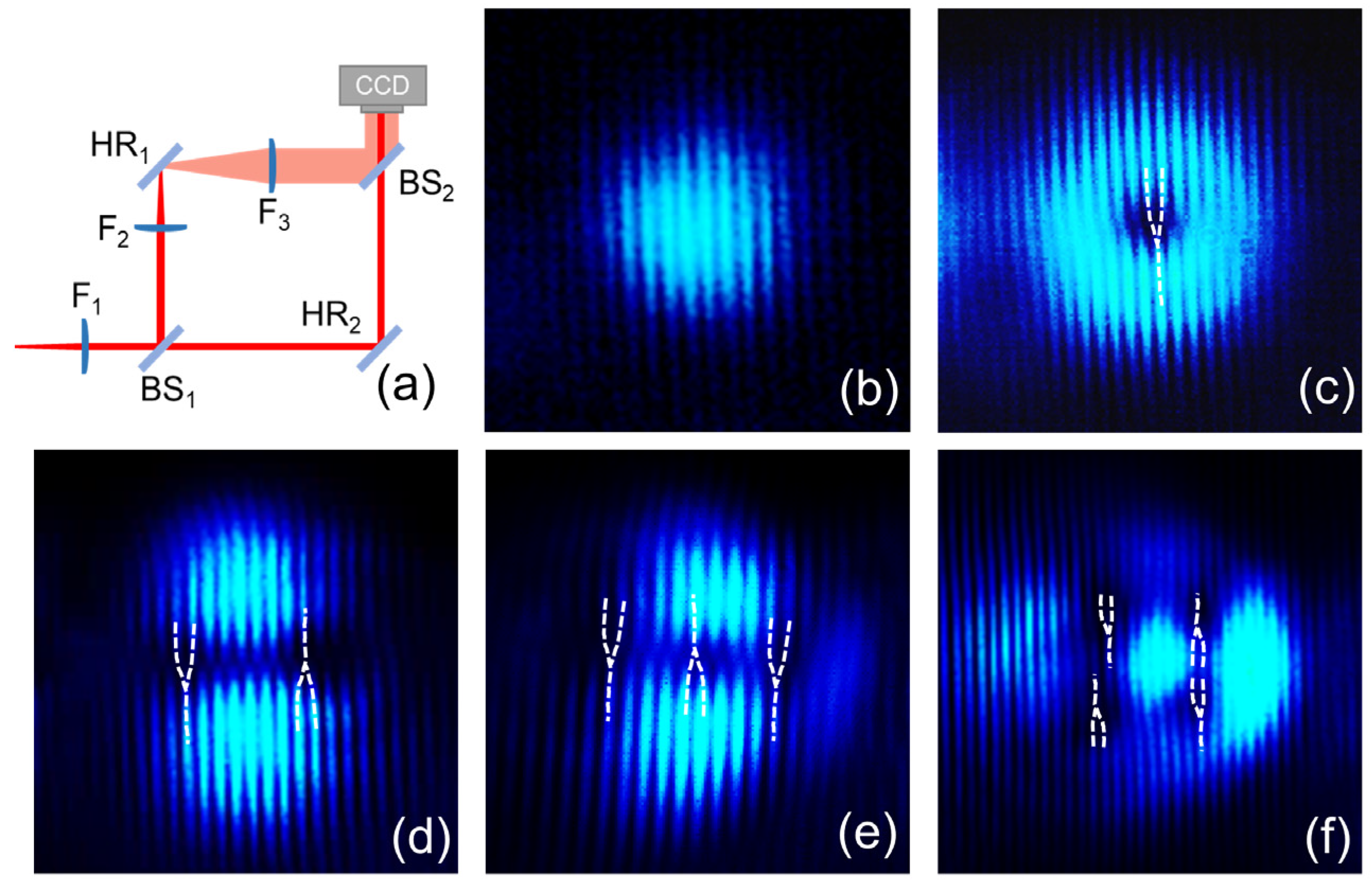
2. Materials and Methods
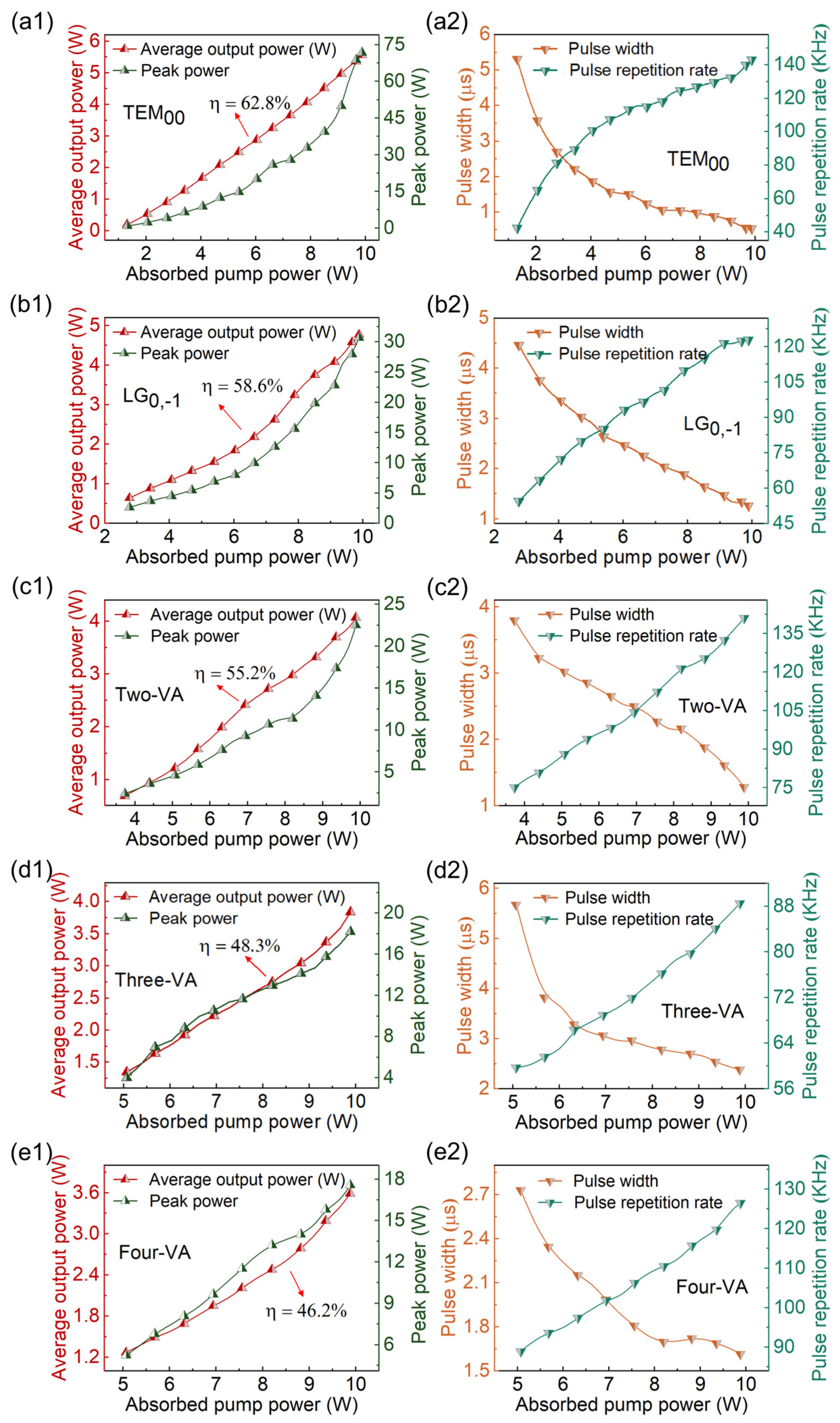
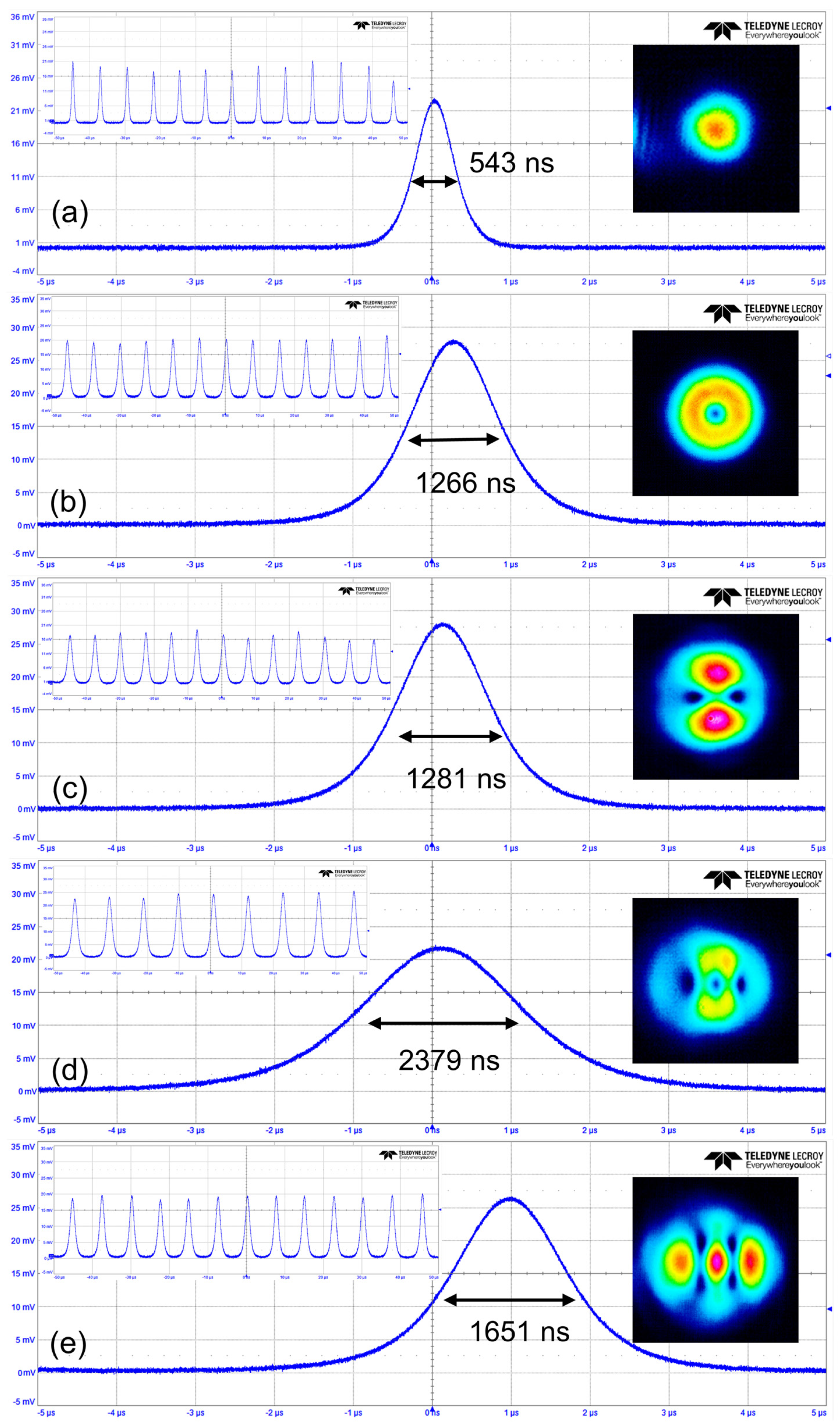
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 2008, 4, 282–286. [Google Scholar] [CrossRef]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Allegre, O.J.; Jin, Y.; Perrie, W.; Ouyang, J.; Fearon, E.; Edwardson, S.P.; Dearden, G. Complete wavefront and polarization control for ultrashort-pulse laser microprocessing. Opt. Express 2013, 21, 21198–21207. [Google Scholar] [CrossRef]
- Toyoda, K.; Takahashi, F.; Takizawa, S.; Tokizane, Y.; Miyamoto, K.; Morita, R.; Omatsu, T. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 2013, 110, 143603. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef] [PubMed]
- Woerdemann, M.; Alpmann, C.; Esseling, M.; Denz, C. Advanced optical trapping by complex beam shaping. Laser Photonics Rev. 2013, 7, 839–854. [Google Scholar] [CrossRef]
- Ladavac, K.; Grier, D. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt. Express 2004, 12, 1144–1149. [Google Scholar] [CrossRef] [PubMed]
- Li, X.K.; Li, Y.; Zeng, X.N.; Han, Y.H. Perfect optical vortex array for optical communication based on orbital angular momentum shift keying. J. Opt. 2018, 20, 125604. [Google Scholar] [CrossRef]
- Lobo, C.; Castin, Y. Nonclassical scissors mode of a vortex lattice in a Bose-Einstein condensate. Phys. Rev. A 2005, 72, 043606. [Google Scholar] [CrossRef]
- Anguita, J.A.; Herreros, J.; Djordjevic, I.B. Coherent Multimode OAM Superpositions for Multidimensional Modulation. IEEE Photon. J. 2014, 6, 1–11. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N. Simple method for efficient reconfigurable optical vortex beam splitting. Opt. Express 2017, 25, 18722–18735. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Chang, C.L.; Yuan, X.Z.; Yuan, C.J.; Feng, S.T.; Nie, S.P.; Ding, J.P. Generation of optical vortex array along arbitrary curvilinear arrangement. Laser Photonics Rev. 2018, 26, 9798–9812. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Wang, L.; Chen, W.D.; Loiko, P.; Mateos, X.; Xu, X.D.; Liu, Y.; Shen, D.Y.; Wang, Z.P.; Xu, X.G.; et al. Structured laser beams: Toward 2-μm femtosecond laser vortices. Photonics Res. 2021, 9, 357–363. [Google Scholar] [CrossRef]
- Chen, D.M.; Miao, Y.J.; Wang, H.J.; Dong, J. Vortex arrays directly generated from an efficient diode-pumped microchip laser. J. Phys. Photonics 2020, 2, 035002. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Wang, Z.P.; Yu, H.H.; Zhuang, S.D.; Zhang, H.J.; Xu, X.D.; Xu, J.; Xu, X.G.; Wang, J.Y. Direct generation of optical vortex pulses. Appl. Phys. Lett. 2012, 101, 031113. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, S.; Yang, H.; Xie, J.; Jiang, S.; Feng, G.; Zhou, S. Direct emission of chirality controllable femtosecond LG01 vortex beam. Appl. Phys. Lett. 2018, 112, 201110. [Google Scholar] [CrossRef]
- Liang, H.C.; Huang, Y.J.; Lin, Y.C.; Lu, T.H.; Chen, Y.F.; Huang, K.F. Picosecond optical vortex converted from multigigahertz self-mode-locked high-order Hermite-Gaussian Nd:GdVO4 lasers. Opt. Lett. 2009, 34, 3842–3844. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhao, Z.G.; Ito, I.; Kobayashi, Y. Direct generation of femtosecond vortex beam from a Yb:KYW oscillator featuring a defect-spot mirror. OSA Continuum 2019, 2, 523–530. [Google Scholar] [CrossRef]
- Qiao, Z.; Xie, G.; Wu, Y.; Yuan, P.; Ma, J.; Qian, L.; Fan, D. Generating High-Charge Optical Vortices Directly from Laser Up to 288th Order. Laser Photonics Rev. 2018, 12, 1800019. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Y.Y.; Sheng, Q.; He, X.; Liu, J.J.; Shi, W.; Yao, J.Q.; Omatsu, T. Laguerre-Gaussian beam generation via enhanced intracavity spherical aberration. Opt. Express 2021, 29, 27783. [Google Scholar] [CrossRef] [PubMed]
- Brambilla, M.; Battipede, F.; Lugiato, L.A.; Penna, V.V.; Prati, F.; Tamm, C.; Weiss, C.O. Transverse laser patterns. I. Phase singularity crystals. Phys. Rev. A 1991, 43, 5090–5113. [Google Scholar] [CrossRef]
- Scheuer, J.; Orenstein, M. Optical vortices crystals: Spontaneous generation in nonlinear semiconductor microcavities. Science 1999, 285, 230–233. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lan, Y.P. Formation of optical vortex lattices in solid-state microchip lasers: Spontaneous transverse mode locking. Phys. Rev. A 2001, 64, 063807. [Google Scholar] [CrossRef]
- Dong, J.; Ueda, K.I. Observation of repetitively nanosecond pulse-width transverse patterns in microchip self-Q-switched laser. Phys. Rev. A 2006, 73, 053824. [Google Scholar] [CrossRef]
- Otsuka, K.; Chu, S.C. Generation of vortex array beams from a thin-slice solid-state laser with shaped wide-aperture laser-diode pumping. Opt. Lett. 2009, 34, 10–12. [Google Scholar] [CrossRef]
- Kong, W.P.; Sugita, A.; Taira, T. Generation of Hermite–Gaussian modes and vortex arrays based on two-dimensional gain distribution controlled microchip laser. Opt. Lett. 2012, 37, 2661–2663. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Wang, X.L.; Zhang, M.M.; Wang, X.J.; He, H.S. Structured optical vortices with broadband comb-like optical spectra in Yb:Y3Al5O12/YVO4 Raman microchip laser. Appl. Phys. Lett. 2018, 112, 161108. [Google Scholar] [CrossRef]
- Shen, Y.J.; Wan, Z.S.; Fu, X.; Liu, Q.; Gong, M.L. Vortex lattices with transverse-mode-locking states switching in a large-aperture off-axis-pumped solid-state laser. J. Opt. Soc. Am. B 2018, 35, 2940–2944. [Google Scholar] [CrossRef]
- Tong, L.Y.; Yuan, Y.; Zhang, W.Y.; Chen, C.D.; Cai, Y.J.; Zhao, L.N. High-power picosecond structured optical vortices directly generated in an all-solid-state laser. Opt. Laser Technol. 2022, 155, 108396. [Google Scholar] [CrossRef]
- Niu, Z.K.; Tong, L.Y.; Cao, X.H.; Chen, C.D.; Cai, Y.J.; Zhao, L.N. Inner-cavity generation of mid-infrared optical vortex arrays from an Er:CaF2 laser. Infrared Phys. Technol. 2023, 133, 104863. [Google Scholar] [CrossRef]
- Hutfilz, A.; Theisen-Kunde, D.; Bonsanto, M.M.; Brinkmann, R. Pulsed thulium laser blood vessel haemostasis as an alternative to bipolar forceps during neurosurgical tumour resection. Lasers Med. Sci. 2023, 38, 94. [Google Scholar] [CrossRef] [PubMed]
- Steinlechner, J.; Martin, I.W.; Bell, A.S.; Hough, J.; Fletcher, M.; Murray, P.G.; Robie, R.; Rowan, S.; Schnabel, R. Silicon-Based Optical Mirror Coatings for Ultrahigh Precision Metrology and Sensing. Phys. Rev. Lett. 2018, 120, 263602. [Google Scholar] [CrossRef] [PubMed]
- Petrovich, M.N.; Poletti, F.; Wooler, J.P.; Heidt, A.M.; Baddela, N.K.; Li, Z.; Gray, D.R.; Slavík, R.; Parmigiani, F.; Wheeler, N.V.; et al. Demonstration of amplified data transmission at 2 µm in a low-loss wide bandwidth hollow core photonic bandgap fiber. Opt. Express 2013, 21, 28559–28569. [Google Scholar] [CrossRef]
- Titterton, D.H.; Elder, I.; Thorne, D.; Jones, I.; Bell, D. Thulium fibre laser pumped mid-IR source. In Technologies for Optical Countermeasures III; SPIE: Zürich, Switzerland, 2006; Volume 6397, p. 639703. [Google Scholar]
- Razdobreev, I.; Shestakov, A. Self-pulsing of a monolithic Tm-doped YAlO3 microlaser. Phys. Rev. A 2006, 73, 053815. [Google Scholar] [CrossRef]
- Wu, K.S.; Henderson-Sapir, O.; Veitch, P.J.; Hamilton, M.; Munch, J.; Ottaway, D.J. Self-pulsing in Tm-doped YAlO3 lasers: Excited-state absorption and chaos. Phys. Rev. A 2015, 91, 043819. [Google Scholar] [CrossRef]
- Cai, W.; Liu, J.; Li, C.; Zhu, H.T.; Ge, P.G.; Zheng, L.H.; Su, L.B.; Xu, J. Compact self-Q-switched laser near 2 μm. Opt. Commun. 2015, 334, 287–289. [Google Scholar] [CrossRef]
- Zhang, B.; Li, L.; He, C.J.; Tian, F.J.; Yang, X.T.; Cui, J.H.; Zhang, J.Z.; Sun, W.M. Compact self-Q-switched Tm:YLF laser at 1.91 μm. Opt. Laser Technol. 2018, 100, 103–108. [Google Scholar] [CrossRef]
- Feng, X.Y.; Li, F.; Wang, C.; Zhang, Z.; Liu, J.J.; Liu, J.; Su, L.B.; Zhang, H. Broadband MIR SnSe nanosheets nonlinear saturable absorber for high peak power pulsed lasers. Opt. Laser Technol. 2023, 163, 109343. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, M.M.; Wang, J.L.; Wang, L.; Liu, Q.Y.; Zhao, Y.G.; Liu, Y.; Shen, D.Y.; Wang, Z.P.; Xu, X.G.; et al. High-energy 2 microm pulsed vortex beam excitation from a Q-switched Tm:LuYAG laser. Opt. Lett. 2020, 45, 722–725. [Google Scholar] [CrossRef] [PubMed]

| X1 (μm) | Y1 (μm) | X2 (μm) | Y2 (μm) | |
|---|---|---|---|---|
| LG0,−1 | 0 | 0 | 0 | 0 |
| Two-VA | 80 | 0 | 0 | 0 |
| Three-VA | 160 | 0 | 50 | 0 |
| Four-VA | 120 | 90 | 70 | 0 |
| Laser Medium | Output Mode | Q-Switch Approach | Output Power (W) | Pulse Width (ns) | Repetition Rate (kHz) | Peak Power (W) | Single-Pulse Energy (μJ) | Ref. |
|---|---|---|---|---|---|---|---|---|
| Tm:YAP | TEM00 | SQS | 5.6 | 543 | 143 | 71.7 | 38.9 | This work |
| Tm:YAP | LG0,−1 | SQS | 4.8 | 1266 | 122.8 | 30.6 | 38.8 | |
| Tm:YAP | Two-VA | SQS | 4.07 | 1281 | 141 | 22.5 | 28.8 | |
| Tm:YAP | Three-VA | SQS | 3.84 | 2379 | 88.5 | 18.2 | 43.3 | |
| Tm:YAP | Four-VA | SQS | 3.59 | 1615 | 126.5 | 17.6 | 28.3 | |
| Tm:YAP | TEM00 | SQS | 1.68 | 1640 | 82.25 | 15.64 | 25.7 | [43] |
| Tm:YLF | TEM00 | SQS | 0.61 | 1500 | 21 | 19.36 | 29 | [44] |
| Tm:YAP | TEM00 | SA | 0.72 | 1090 | 82.25 | 7.11 | 8.86 | [45] |
| Tm:LuYAG | LG0,−1 | A-O | 0.74 | 366 | 0.5 | 3800 | 1510 | [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, L.; Chen, C.; Cai, Y.; Zhao, L. Pulsed Optical Vortex Array Generation in a Self-Q-Switched Tm:YALO3 Laser. Materials 2024, 17, 1144. https://doi.org/10.3390/ma17051144
Tong L, Chen C, Cai Y, Zhao L. Pulsed Optical Vortex Array Generation in a Self-Q-Switched Tm:YALO3 Laser. Materials. 2024; 17(5):1144. https://doi.org/10.3390/ma17051144
Chicago/Turabian StyleTong, Luyang, Changdong Chen, Yangjian Cai, and Lina Zhao. 2024. "Pulsed Optical Vortex Array Generation in a Self-Q-Switched Tm:YALO3 Laser" Materials 17, no. 5: 1144. https://doi.org/10.3390/ma17051144







