Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates
Abstract
:1. Introduction
- Mechanical model which is based on the assumption that the cutting process depends on cutting force and that compressive stress is induced in the surface layer, while tensile stress is induced in the core;
- Thermal model which focuses on only the cutting process, assuming that tensile stress is induced in the surface layer, while compressive stress is induced in the core.
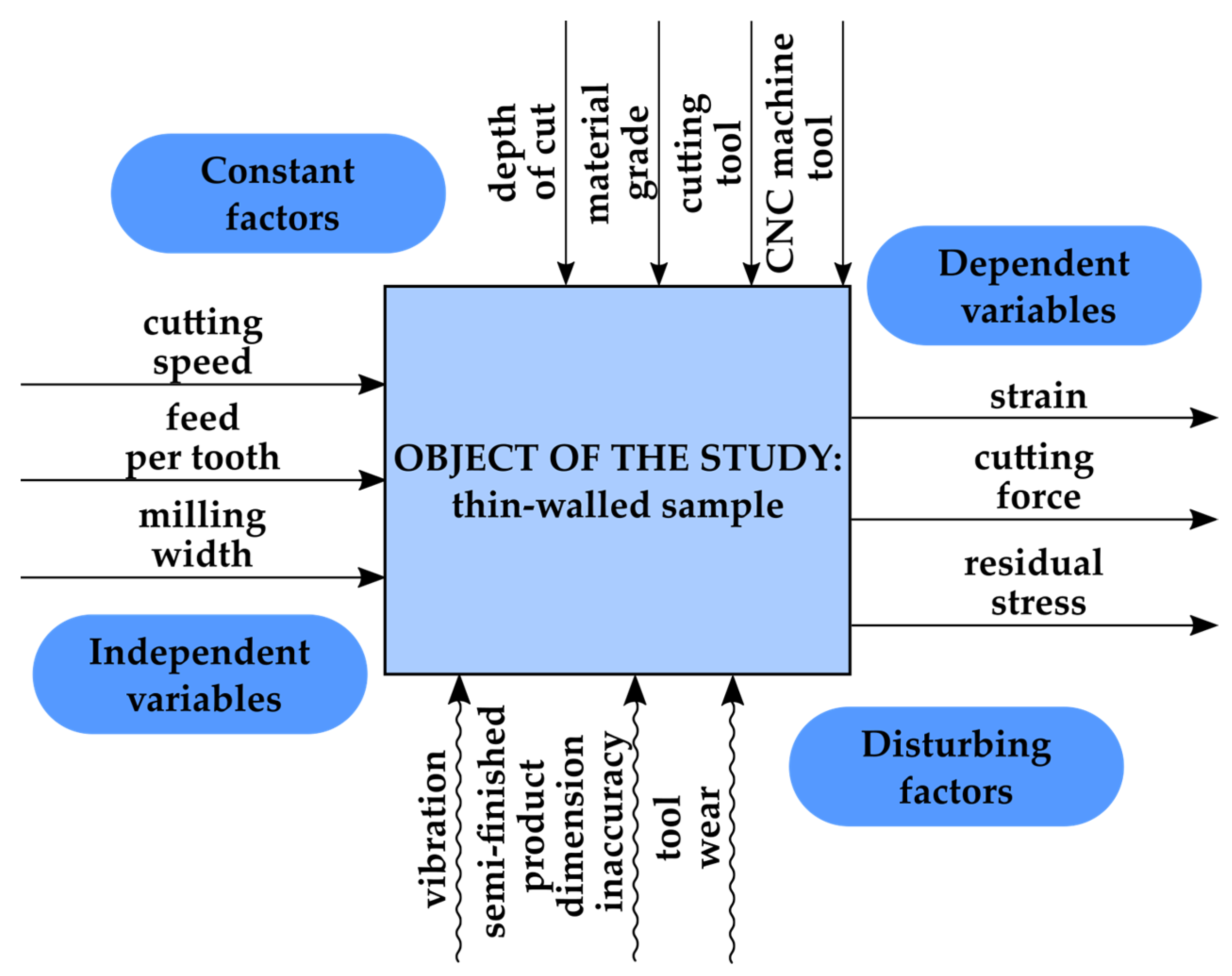
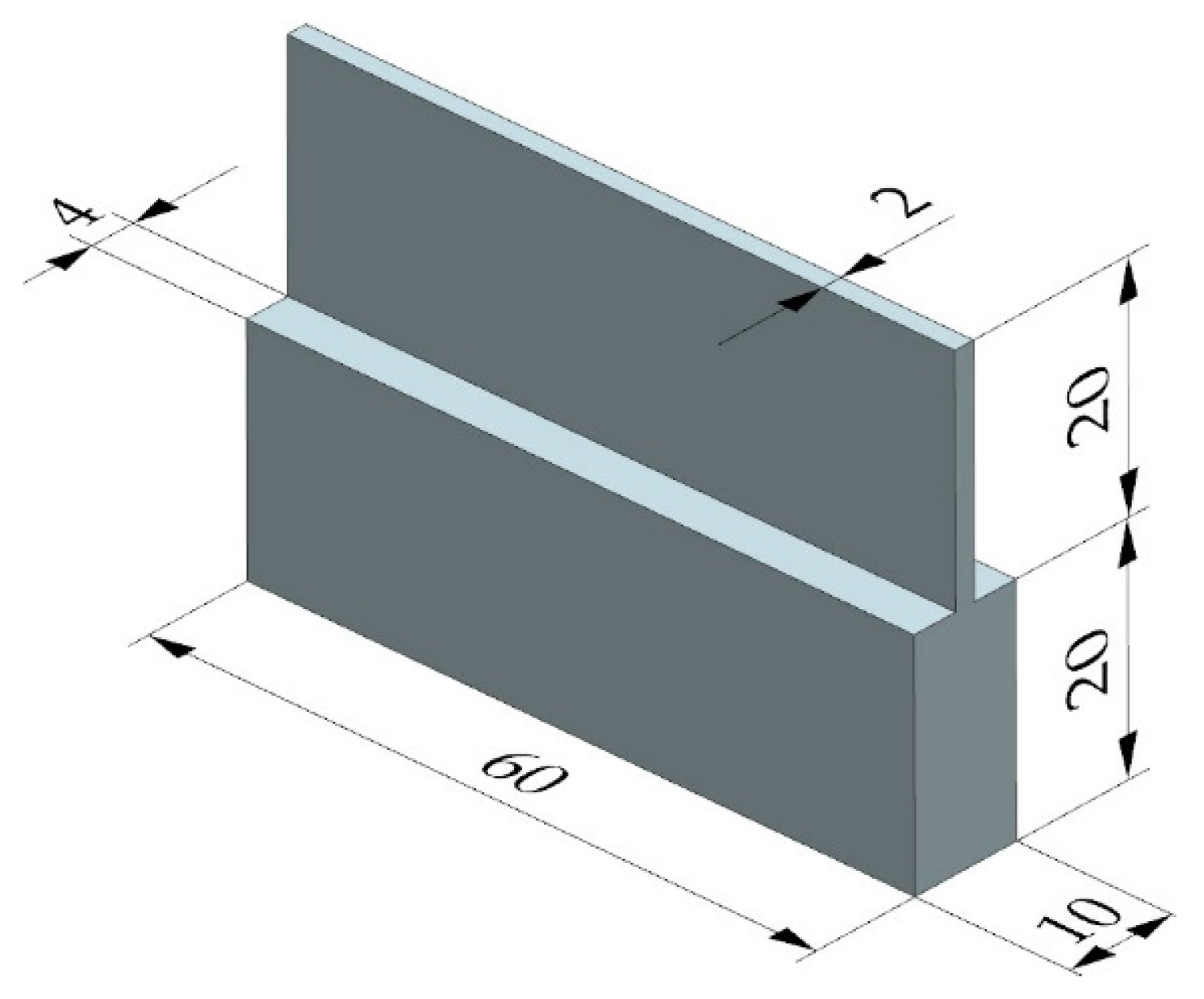
2. Materials and Methods
3. Results
- H0: ;
- H1: .
- H0: ;
- H1: .
4. Discussion
- Increased cutting speed results in a local increase in temperature, which reduces cutting resistance due to a decrease in the coefficient of friction;
- Increased temperature improves the plasticization of the material in the shear zone, which also leads to reduced cutting resistance;
- Reduced friction as a result of increased chip flow rate.
5. Conclusions
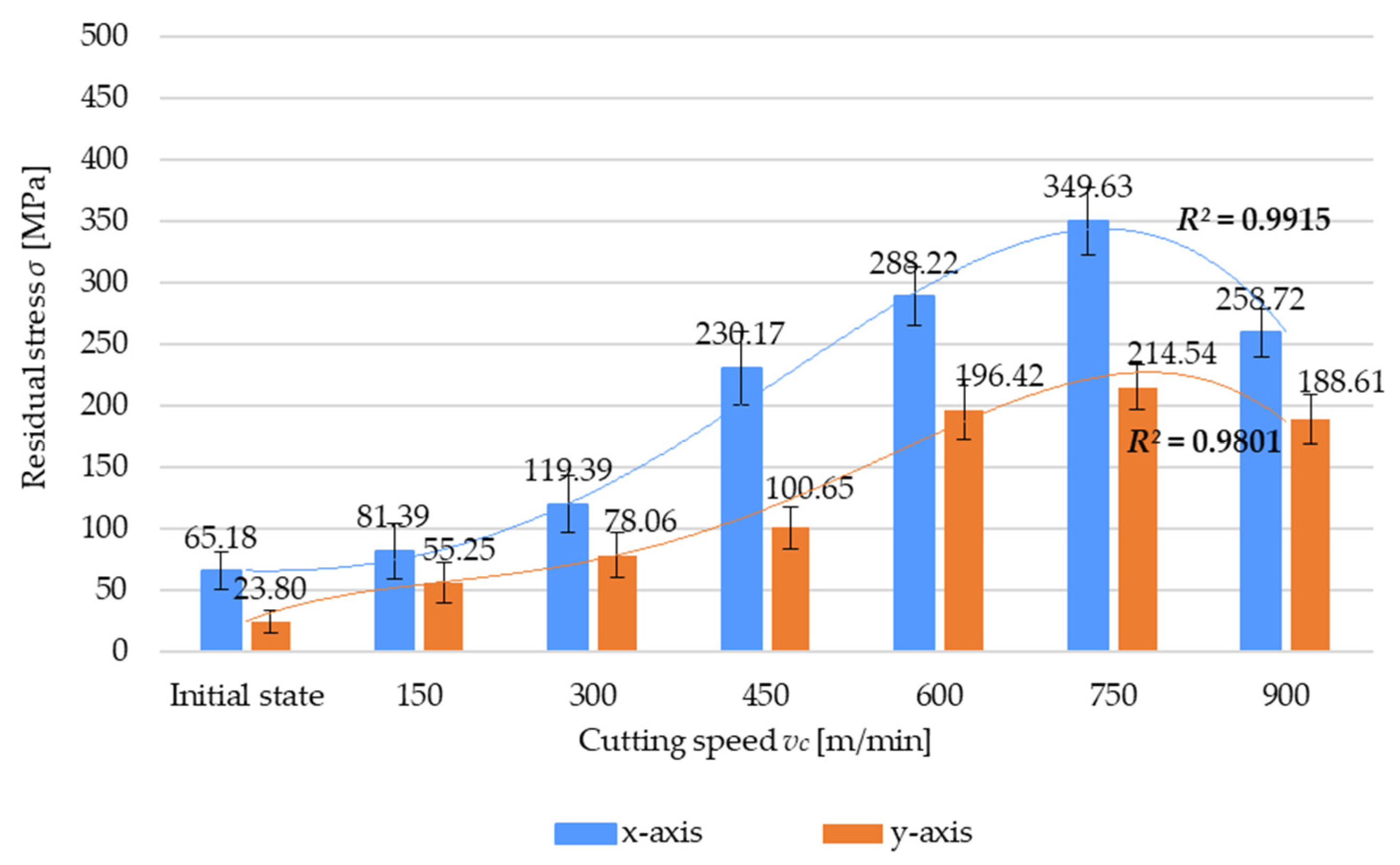
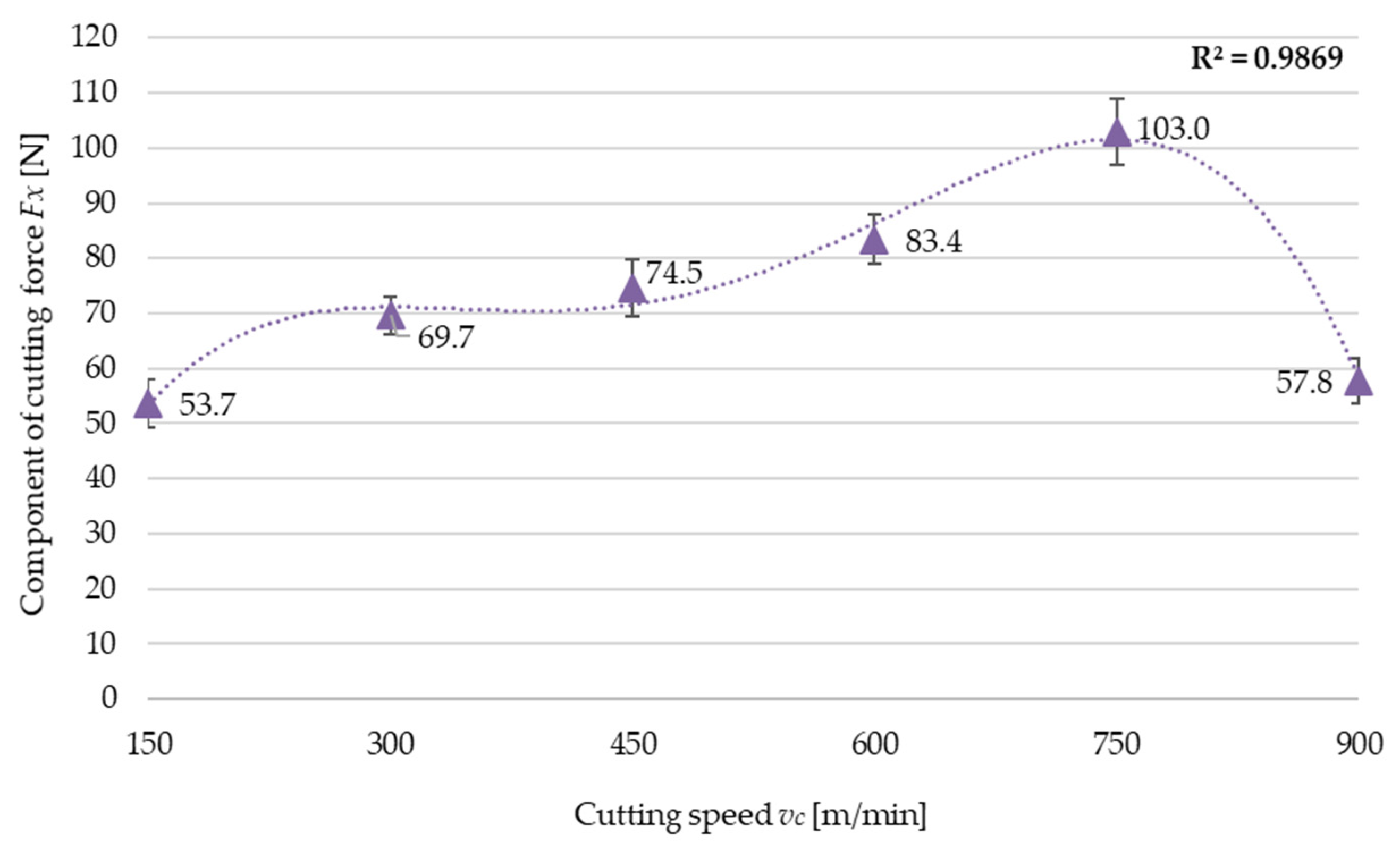
- The variable cutting speed has the most significant effect on machining-induced residual stress;
- Regarding the variable cutting speed, the pattern of residual stress variations is closely correlated with the cutting force variations;
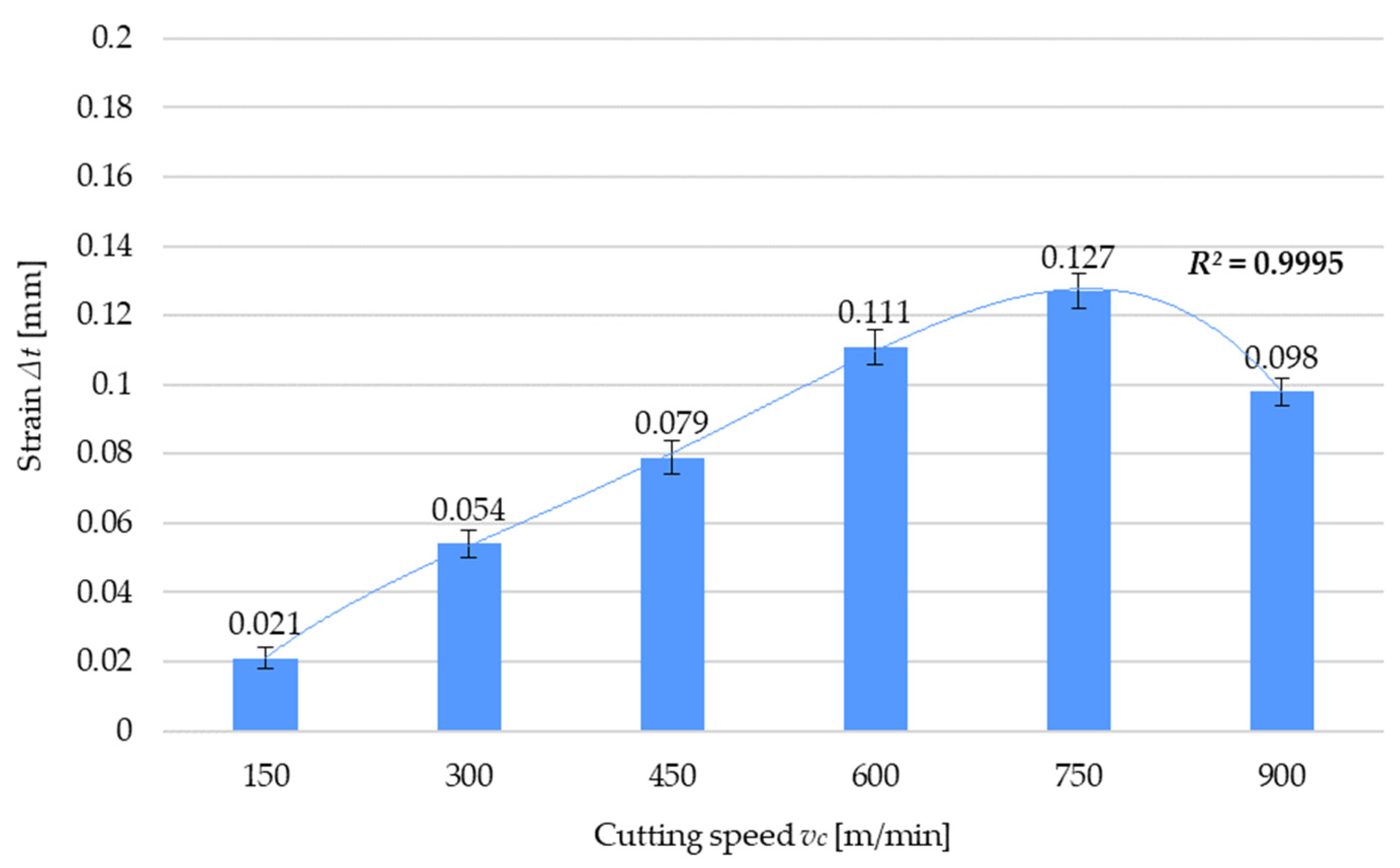
- Reduced machining resistance under HSC conditions leads to reduced values of cutting force and residual stress, which results in the reduced strain of the thin walls;
- Given the reduction in residual stress, cutting force, and strain, it is recommended that HSC be used for machining thin-walled parts;
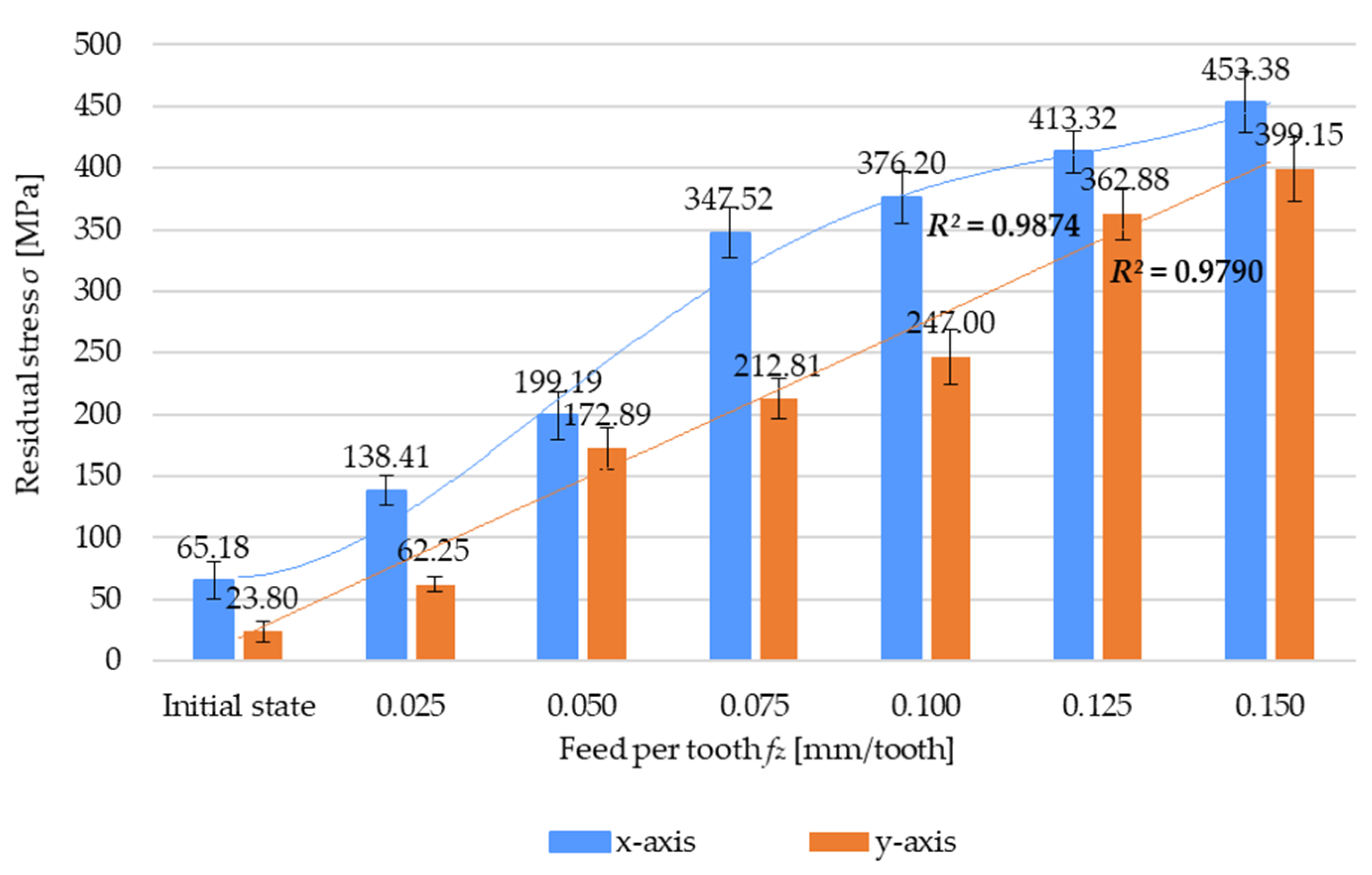
- Residual stress is also significantly affected by variations in the feed per tooth and milling width, so the pattern of variations observed for both cases is similar, i.e., increasing the values of these parameters leads to an increase in residual stress, which is related to higher machining resistance due to an increased cross-section of the cut layer;
- It has been noted that out of the two abovementioned parameters, residual stress depends more significantly on feed per tooth;
- In general, residual stress increases with increasing the milling width, and this may be related to a greater effect of thermal interactions for low wall thicknesses. The exception is the result obtained for the greatest milling width value, i.e., ae = 4.5 mm;
- A residual stress decrease in the lowest-thickness wall leads to reduced strain, which demonstrates the importance of the effect exerted by the induced stress on the strain of machined parts, especially thin-walled ones;
- It should be noted that tensile and compressive stress occurs simultaneously, albeit with varying intensity. In the cases under study, tensile residual stress prevailed, thus indicating the dominance of the thermal stress model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bałon, P.; Rejman, E.; Świątoniowski, A.; Kiełbasa, B.; Smusz, R.; Szostak, J.; Cieślik, J.; Kowalski, Ł. Thin-walled Integral Constructions in Aircraft Industry. Proc. Manuf. 2020, 47, 498–504. [Google Scholar] [CrossRef]
- Nowakowski, L.; Bartoszuk, M.; Skrzyniarz, M.; Blasiak, S.; Vasileva, D. Influence of the Milling Conditions of Aluminium Alloy 2017A on the Surface Roughness. Materials 2022, 15, 3626. [Google Scholar] [CrossRef] [PubMed]
- Park, S.H.; Nam, E.; Gang, M.G.; Min, B.K. Post-machining Deformation Analysis for Virtual Machining of Thin Aluminium Alloy Parts. Int. J. Precis. Eng. Manuf. 2019, 20, 687–691. [Google Scholar] [CrossRef]
- Twardowski, P.; Wieczorowski, M. Monitoring of Cutting Process and Tool Condition of Metal and Metal Composite. Materials 2023, 16, 3660. [Google Scholar] [CrossRef] [PubMed]
- Bałon, P.; Rejman, E.; Kiełbasa, B.; Smusz, R. Using HSM Technology in Machining of Thin-Walled Aircraft Structures. Acta Mech. Autom. 2022, 16, 27–33. [Google Scholar] [CrossRef]
- Bałon, P.; Rejman, E.; Smusz, R.; Szostak, J.; Kiełbasa, B. Implementation of high speed machining in thin-walled aircraft integral elements. Open Eng. 2018, 8, 162–169. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Kuczmaszewski, J.; Legutko, S.; Pieśko, P. Techniques for Thin-Walled Element Milling with Respect to Minimising Post-Machining Deformations. Materials 2020, 13, 4723. [Google Scholar] [CrossRef] [PubMed]
- Zawada-Michałowska, M.; Pieśko, P.; Józwik, J.; Legutko, S.; Kukiełka, L. A Comparison of the Geometrical Accuracy of Thin-Walled Elements Made of Different Aluminum Alloys. Materials 2021, 14, 7242. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, Y.; Zhou, J.; Zhan, K.; Ding, Z.; Liang, Z.D. Residual stress generation and evaluation in milling: A review. Int. J. Adv. Manuf. Technol. 2023, 126, 3783–3812. [Google Scholar] [CrossRef]
- Kuczmaszewski, J.; Pieśko, P.; Zawada-Michałowska, M. Evaluation of the impact of the natural seasoning process on post-machining deformation of thin-walled elements made of aluminium alloy EN AW-2024. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 012102. [Google Scholar] [CrossRef]
- Borojević, S.; Lukić, D.; Milošević, M.; Vukman, J.; Kramar, D. Optimization of process parameters for machining of Al 7075 thin-walled structures. Adv. Prod. Eng. Manag. 2018, 13, 125–135. [Google Scholar] [CrossRef]
- Czyżycki, J.; Twardowski, P.; Znojkiewicz, N. Analysis of the Displacement of Thin-Walled Workpiece Using a High-Speed Camera during Peripheral Milling of Aluminum Alloys. Materials 2021, 14, 4771. [Google Scholar] [CrossRef]
- Kuji, C.; Chighizola, C.R.; Hill, M.R.; Aurich, J.C.; Soyama, H. Experimental study on the effect of the milling condition of an aluminum alloy on subsurface residual stress. Int. J. Adv. Manuf. Technol. 2023, 127, 5487–5501. [Google Scholar] [CrossRef]
- Olszak, W. Machining; Wydawnictwa Naukowo-Techniczne: Warszawa, Poland, 2009. (In Polish) [Google Scholar]
- Outeiro, J. Residual stresses in machining operations. In CIRP Encyclopedia of Production Engineering; Laperrière, L., Reinhart, G., Eds.; Springer: Berlin, Germany, 2018; pp. 1–13. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Kuczmaszewski, J.; Pieśko, P. Pre-Machining of Rolled Plates as an Element of Minimising the Post-Machining Deformations. Materials 2020, 13, 4777. [Google Scholar] [CrossRef] [PubMed]
- Kuczmaszewski, J.; Łogin, W.; Pieśko, P.; Zagórski, I. State of Residual Stresses after the Process of Milling Selected Aluminium Alloys. Adv. Sci. Technol. Res. J. 2018, 12, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Childerhouse, T.; M’Saoubi, R.; Franca, L.; Weston, N.; Crawforth, P.; Jackson, M. The influence of machining induced surface integrity and residual stress onthe fatigue performance of Ti-6Al-4V following polycrystalline diamond andcoated cemented carbide milling. Int. J. Fatigue 2022, 163, 107054. [Google Scholar] [CrossRef]
- Królczyk, G.; Legutko, S.; Niesłony, P.; Gajek, M. Study of the surface integrity microhardness of austenitic stainless steel after turning. Teh. Vjesn. 2014, 21, 1307–1311. [Google Scholar]
- Franceschi, A.; Kaffenberger, M.; Schork, B.; Hoche, H.; Oechsner, M.; Groche, P. Observations on the stability of the residual stresses after cold forming and unidirectional loading. Prod. Eng. 2019, 13, 157–167. [Google Scholar] [CrossRef]
- Fu, W.-E.; Cohen, P.H.; Ruud, C.O. Experimental investigation of the machining induced residual stress tensor under mechanical loading. J. Manuf. Process. 2009, 11, 88–96. [Google Scholar] [CrossRef]
- Niesłony, P.; Grzesik, W.; Laskowski, P.; Sieniawski, J. Numerical and experimental analysis of residual stresses generated in the machining of Ti6Al4V titanium alloy. Procedia CIRP 2014, 13, 78–83. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; Chighizola, C.R.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Analysis of machining-induced residual stresses of milled aluminum workpieces, their repeatability, and their resulting distortion. Int. J. Adv. Manuf. Technol. 2021, 115, 1089–1110. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Wu, Q.; Song, J. An analytical model for predicting the machining deformation of a plate blank considers biaxial initial residual stresses. Int. J. Adv. Manuf. Technol. 2017, 93, 1473–1486. [Google Scholar] [CrossRef]
- Li, B.; Jiang, X.; Yang, J.; Liang, S.Y. Effects of depth of cut on the redistribution of residual stress and distortion during the milling of thin-walled part. J. Mater. Process. Technol. 2015, 216, 223–233. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, P.; Zhang, J.; Wu, Z.; Yu, D. Prediction of surface residual stress after end milling based on cutting force and temperature. J. Mater. Process. Technol. 2016, 235, 41–48. [Google Scholar] [CrossRef]
- Shet, C.; Deng, X. Residual stresses and strains in orthogonal metal cutting. Int. J. Mach. Tool. Manuf. 2003, 43, 573–587. [Google Scholar] [CrossRef]
- Jiang, X.H.; Kong, X.J.; Zhang, Z.Y.; Wu, Z.P.; Ding, Z.S.; Guo, M.X. Modeling the effects of Undeformed Chip Volume (UCV) on residual stresses during the milling of curved thin-walled parts. Int. J. Mech. Sci. 2020, 167, 105162. [Google Scholar] [CrossRef]
- Song, Y.; Chen, H.; Tang, Y.; Huang, S.; Yin, G.; Yin, M. Study on surface morphology and residual stress in inclined milling of titanium alloy TC11. Int. J. Adv. Manuf. Technol. 2022, 122, 3411–3423. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; Jonsson, J.E.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Simulation based compensation techniques to minimize distortion of thin-walled monolithic aluminum parts due to residual stresses. CIRP J. Manuf. Sci. Technol. 2022, 38, 427–441. [Google Scholar] [CrossRef]
- Li, J.; Wang, S. Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances. Int. J. Adv. Manuf. Technol. 2017, 89, 997–1012. [Google Scholar] [CrossRef]
- Chighizola, C.R.; D’Elia, C.R.; Jonsson, J.E.; Weber, D.; Kirsch, B.; Aurich, J.C.; Linke, B.S.; Hill, M.R. The Effect of Bulk Residual Stress on Milling-Induced Residual Stress and Distortion. Exp. Mech. 2022, 62, 1437–1459. [Google Scholar] [CrossRef]
- Masoudi, S.; Amini, S.; Saeidi, E.; Eslami-Chalander, H. Effect of machining-induced residual stress on the distortion of thin-walled parts. Int. J. Adv. Manuf. Technol. 2015, 76, 597–608. [Google Scholar] [CrossRef]
- Yi, S.; Wu, Y.; Gong, H.; Peng, C.; He, Y. Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys. Appl. Sci. 2021, 11, 5881. [Google Scholar] [CrossRef]
- Shan, C.; Zhang, M.; Zhang, S.; Dang, J. Prediction of machining-induced residual stress in orthogonal cutting of Ti6Al4V. Int. J. Adv. Manuf. Technol. 2020, 107, 2375–2385. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Feng, L.; Qiu, T.; Wang, X.; Zhang, B. Prediction of surface residual stress in end milling with Gaussian process regression. Measurement 2021, 178, 109333. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Q.; Qing, L.; Chen, S. 3D coupled thermo-mechanical simulation of surface roughness and residual stress in end milling aluminum alloy. Int. J. Adv. Manuf. Technol. 2022, 123, 4489–4504. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, L.; Cui, R.; Liu, J.; Zhang, Q. Machining-induced residual stress analysis and multi-objective optimization for milling process of Mg–Li alloy. Measurement 2022, 204, 112127. [Google Scholar] [CrossRef]
- Jiang, X.; Cai, Y.; Liu, W.; Guo, M.; Zhou, H.; Xu, Z.; Kong, X.; Ju, P. Residual compressive stress prediction determined by cutting-edge radius and feed rate during milling of thin-walled parts. Int. J. Adv. Manuf. Technol. 2023, 124, 773–788. [Google Scholar] [CrossRef]
- Xu, Y.; Yue, C.; Chen, Z.; Li, M.; Wang, L.; Liu, X. Finite element simulation of residual stress in milling of aluminum alloy with different passes. Int. J. Adv. Manuf. Technol. 2023, 127, 4199–4210. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, D.; Agmell, M.; M’Saoubi, R.; Ahadi, A.; Stahl, J.-E.; Zhou, J. Numerical and experimental investigation of tool geometry effect on residual stresses in orthogonal machining of Inconel 718. Simul. Model. Pract. Theory 2021, 106, 102187. [Google Scholar] [CrossRef]
- Meng, L.; Khan, A.M.; Zhang, H.; Fang, C.; He, N. Research on surface residual stresses generated by milling Ti6Al4V alloy under different pre-stresses. Int. J. Adv. Manuf. Technol. 2020, 107, 2597–2608. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, W. Analytical modeling of machining-induced residual stresses in milling of complex surface. Int. J. Adv. Manuf. Technol. 2019, 105, 565–577. [Google Scholar] [CrossRef]
- Jiang, X.; Kong, X.; He, S.; Wu, K. Modeling the superposition of residual stresses induced by cutting force and heat during the milling of thin-walled parts. J. Manuf. Process. 2021, 68, 356–370. [Google Scholar] [CrossRef]
- Ji, C.; Sun, S.; Lin, B.; Fei, J. Effect of cutting parameters on the residual stress distribution generated by pocket milling of 2219 aluminum alloy. Adv. Mech. Eng. 2018, 10, 12. [Google Scholar] [CrossRef]
- Sivam, S.P.S.S.; Bhat, M.D.J.; Natarajan, S.; Chauhan, N. Analysis of residual stresses, thermal stresses, cutting forces and other output responses of face milling operation on ZE41 Magnesium alloy. Int. J. Mod. Manuf. Technol. 2018, 10, 92–101. [Google Scholar]
- Berry, L.; Wheatley, G.; Ma, W.; Nejad, R.M.; Berto, F. The influence of milling induced residual stress on fatigue life of aluminum alloys. Forces Mech. 2022, 7, 100096. [Google Scholar] [CrossRef]
- Matuszak, J.; Zaleski, K.; Zyśko, A. Investigation of the Impact of High-Speed Machining in the Milling Process of Titanium Alloy on Tool Wear, Surface Layer Properties, and Fatigue Life of the Machined Object. Materials 2023, 16, 5361. [Google Scholar] [CrossRef] [PubMed]
- De Paula Oliveira, G.; Cindra Fonseca, M.; Araujo, A.C. Residual stresses and cutting forces in cryogenic milling of Inconel 718. Proc. CIRP 2018, 77, 211–214. [Google Scholar] [CrossRef]
- Wika, K.K.; Litwa, P.; Hitchens, C. Impact of supercritical carbon dioxide cooling with Minimum Quantity Lubrication on tool wear and surface integrity in the milling of AISI 304L stainless steel. Wear 2019, 426–427, 1691–1701. [Google Scholar] [CrossRef]
- Lostado Lorza, R.; Escribano García, R.; Martínez Calvo, M.Á.; Múgica Vidal, R. Improvement in the Design of Welded Joints of EN 235JR Low Carbon Steel by Multiple Response Surface Methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- PN-EN 573-1:2006; Aluminium and Aluminium Alloys—Chemical Composition and Form of Wrought Products—Part 1: Numerical Designation System. Polish Committee for Standardization: Warsaw, Poland, 2006.
- PN-EN 485-2+A1:2018-12; Aluminium and Aluminium Alloys—Sheet, Tape, Plate—Part 2: Mechanical Properties. Polish Committee for Standardization: Warsaw, Poland, 2018.
- ISO 1940-1:2003; Mechanical Vibrations—Balancing of Rigid Rotors—Determination of Permissible Residual Unbalance. ISO Standard: Geneva, Switzerland, 2003.
- SGS Tool Catalogue. Available online: https://www.kyocera-sgstool.com/digital-catalog (accessed on 10 October 2023).
- PN-EN ISO/IEC 17025:2018-02; General Requirements for the Competence of Testing and Calibration Laboratories. Polish Committee for Standardization: Warsaw, Poland, 2018.
- ASTM E1426-14(2019)E1; Standard Test Method for Determining the X-ray Elastic Constants for Use in the Measurement of Residual Stress Using X-ray Diffraction Techniques. ASTM: West Conshohocken, PA, USA, 2019.






| Chemical Composition [%] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Si | Fe | Mg | Cu | Mn | Zn | Cr | Zr+Ti | Ti | Others | Al | ||||
| ≤0.5 | ≤0.5 | 1.2–1.8 | 3.8–4.9 | 0.3–0.9 | ≤0.25 | ≤0.1 | ≤0.2 | ≤0.15 | ≤0.15 | The rest | ||||
| Properties | ||||||||||||||
| Density ρ [g/cm3] | Young’s Modulus E [Gpa] | Tensile Strength Rm [Mpa] | Yield Strength Rp0,2 [Mpa] | Brinell Hardness Number [HB] | ||||||||||
| 2.78 | 73 | 469 | 324 | 120 | ||||||||||
| Parameter | Value |
|---|---|
| Cutting diameter [mm] | 12 |
| Overall length [mm] | 100 |
| Length of cut [mm] | 48 |
| Shrank diameter [mm] | 12 |
| Corner radius [mm] | 2 |
| Number of flutes [-] | 4 |
| No. | Cutting Speed vc [m/min] | Feed per Tooth fz [mm/tooth] | Milling Width ae [mm] | |
|---|---|---|---|---|
| Case 1 | 1 | 150 | 0.075 | 4.0 |
| 2 | 300 | |||
| 3 | 450 | |||
| 4 | 600 | |||
| 5 | 750 | |||
| 6 | 900 | |||
| Case 2 | 7 | 750 | 0.025 | 4.0 |
| 8 | 0.050 | |||
| 9 | 0.075 | |||
| 10 | 0.100 | |||
| 11 | 0.125 | |||
| 12 | 0.150 | |||
| Case 3 | 13 | 750 | 0.075 | 2.0 |
| 14 | 2.5 | |||
| 15 | 3.0 | |||
| 16 | 3.5 | |||
| 17 | 4.0 | |||
| 18 | 4.5 |
| Constant Parameters | Cutting Speed vc [m/min] | Residual Stress σ [MPa] | Strain Δt [mm] | |
|---|---|---|---|---|
| x-Axis | y-Axis | |||
| fz = 0.075 mm/tooth ae = 4.0 mm | 150 | 81.39 | 55.25 | 0.021 |
| 300 | 119.39 | 78.06 | 0.054 | |
| 450 | 230.17 | 100.65 | 0.079 | |
| 600 | 288.22 | 196.42 | 0.111 | |
| 750 | 349.63 | 214.54 | 0.127 | |
| 900 | 258.72 | 188.61 | 0.098 | |
| Tests | F | Fcr | Result | t | tcr | Result |
|---|---|---|---|---|---|---|
| Initial state – vc = 150 m/min | 2.1943 | 3.1789 | −1.8164 | 2.1009 | ||
| vc = 150 m/min– vc = 300 m/min | 1.0959 | 3.1789 | −3.5486 | 2.1009 | ||
| vc = 300 m/min– vc = 450 m/min | 1.6545 | 3.1789 | −8.7810 | 2.1009 | ||
| vc = 450 m/min– vc = 600 m/min | 1.5539 | 3.1789 | −4.5462 | 2.1009 | ||
| vc = 600 m/min– vc = 750 m/min | 1.2810 | 3.1789 | −5.0889 | 2.1009 | ||
| vc = 750 m/min– vc = 900 m/min | 2.0239 | 3.1789 | 8.2242 | 2.1009 |
| Tests | F | Fcr | Result | t | tcr | Result |
|---|---|---|---|---|---|---|
| Initial state – fz = 0.025 mm/tooth | 1.5378 | 3.1789 | −11.4161 | 2.1009 | ||
| fz = 0.025 mm/tooth– fz = 0.050 mm/tooth | 2.5632 | 3.1789 | −7.9964 | 2.1009 | ||
| fz = 0.050 mm/tooth– fz = 0.075 mm/tooth | 1.1589 | 3.1789 | −15.6595 | 2.1009 | ||
| fz = 0.075 mm/tooth– fz = 0.100 mm/tooth | 1.0222 | 3.1789 | −2.9061 | 2.1009 | ||
| fz = 0.100 mm/tooth– fz = 0.125 mm/tooth | 1.5189 | 3.1789 | −4.1081 | 2.1009 | ||
| fz = 0.125 mm/tooth– fz = 0.150 mm/tooth | 2.1100 | 3.1789 | −3.9899 | 2.1009 |
| Tests | F | Fcr | Result | t | tcr | Result |
|---|---|---|---|---|---|---|
| Initial state– ae = 2.0 mm | 1.1294 | 3.1789 | −19.6993 | 2.1009 | ||
| ae = 2.0 mm– ae = 2.5 mm | 1.4169 | 3.1789 | −0.2570 | 2.1009 | ||
| ae = 2.5 mm– ae = 3.0 mm | 1.0986 | 3.1789 | −5.2128 | 2.1009 | ||
| ae = 3.0 mm– ae = 3.5 mm | 1.2090 | 3.1789 | −2.2719 | 2.1009 | ||
| ae = 3.5 mm– ae = 4.0 mm | 1.1326 | 3.1789 | −5.4778 | 2.1009 | ||
| ae = 4.0 mm– ae = 4.5 mm | 1.3858 | 3.1789 | 8.4656 | 2.1009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawada-Michałowska, M.; Pieśko, P.; Mrówka-Nowotnik, G.; Nowotnik, A.; Legutko, S. Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates. Materials 2024, 17, 1193. https://doi.org/10.3390/ma17051193
Zawada-Michałowska M, Pieśko P, Mrówka-Nowotnik G, Nowotnik A, Legutko S. Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates. Materials. 2024; 17(5):1193. https://doi.org/10.3390/ma17051193
Chicago/Turabian StyleZawada-Michałowska, Magdalena, Paweł Pieśko, Grażyna Mrówka-Nowotnik, Andrzej Nowotnik, and Stanisław Legutko. 2024. "Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates" Materials 17, no. 5: 1193. https://doi.org/10.3390/ma17051193
APA StyleZawada-Michałowska, M., Pieśko, P., Mrówka-Nowotnik, G., Nowotnik, A., & Legutko, S. (2024). Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates. Materials, 17(5), 1193. https://doi.org/10.3390/ma17051193










