Utilizing Crushed Limestone as a Sustainable Alternative in Shotcrete Applications
Abstract
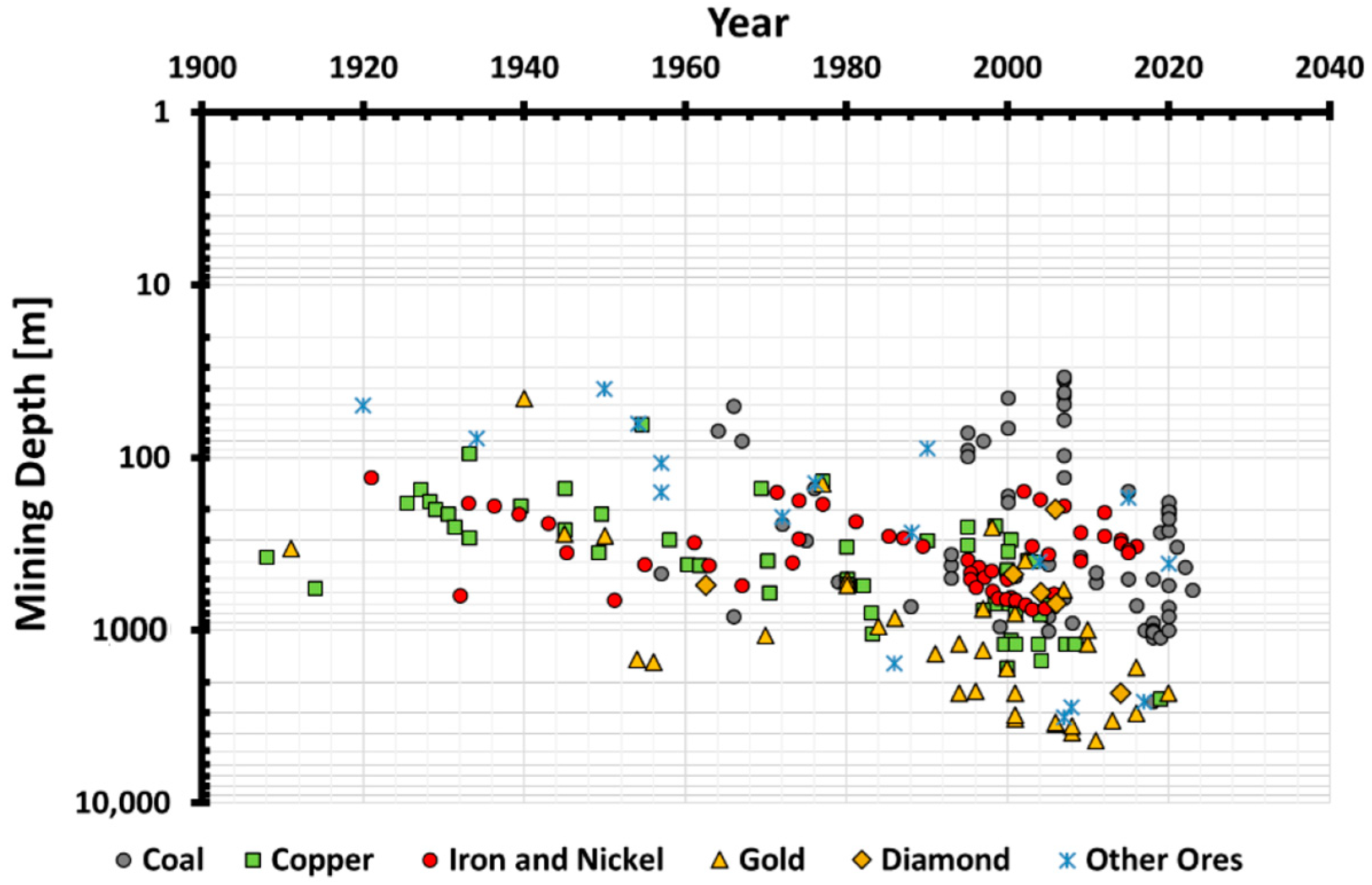
1. Introduction
1.1. Background and Overview
1.2. Shotcrete and Grout in Tunneling
| Model | Crack Initiation Stress () Determination |
|---|---|
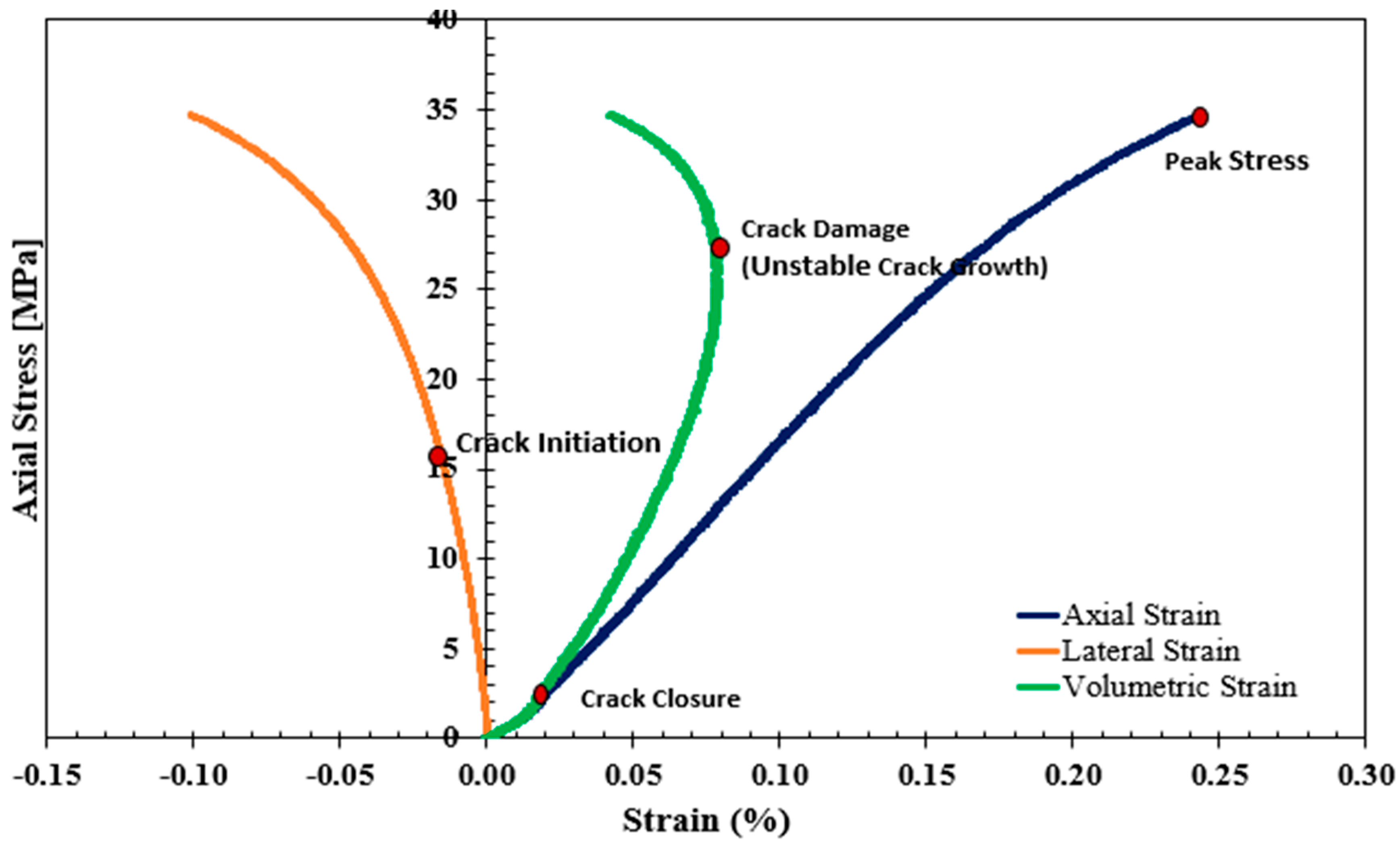
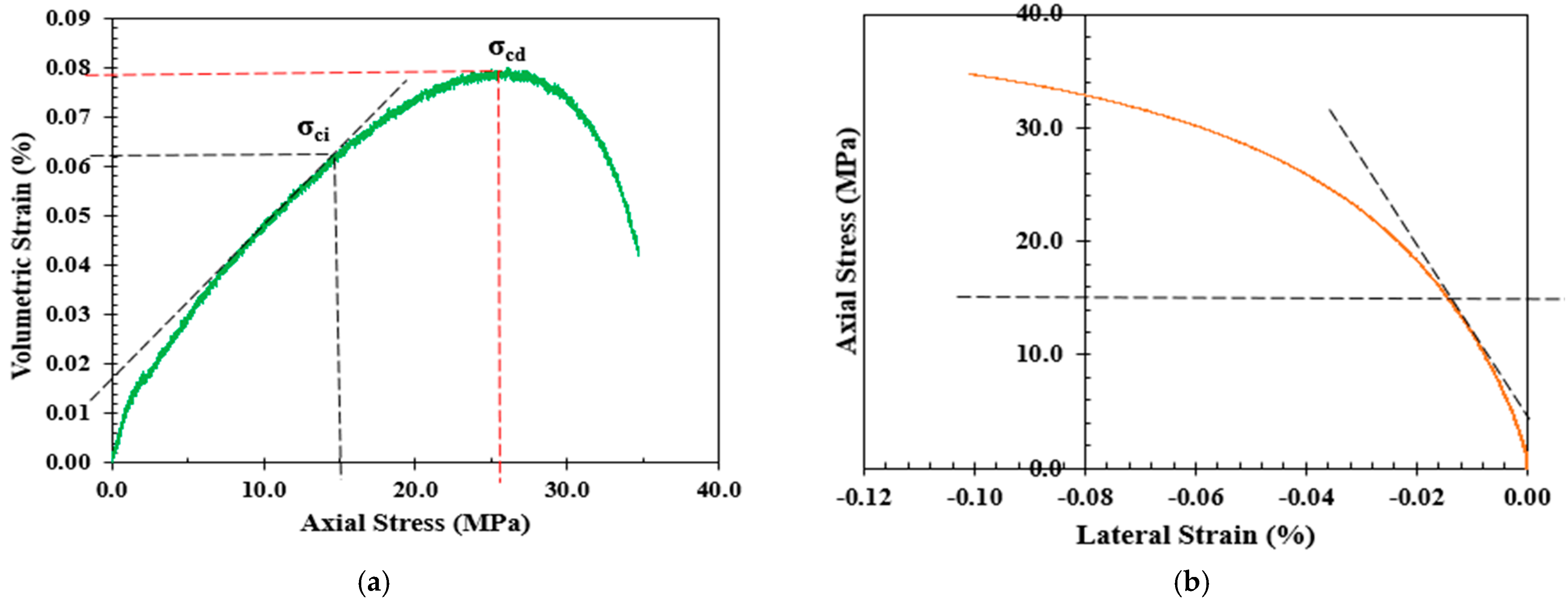
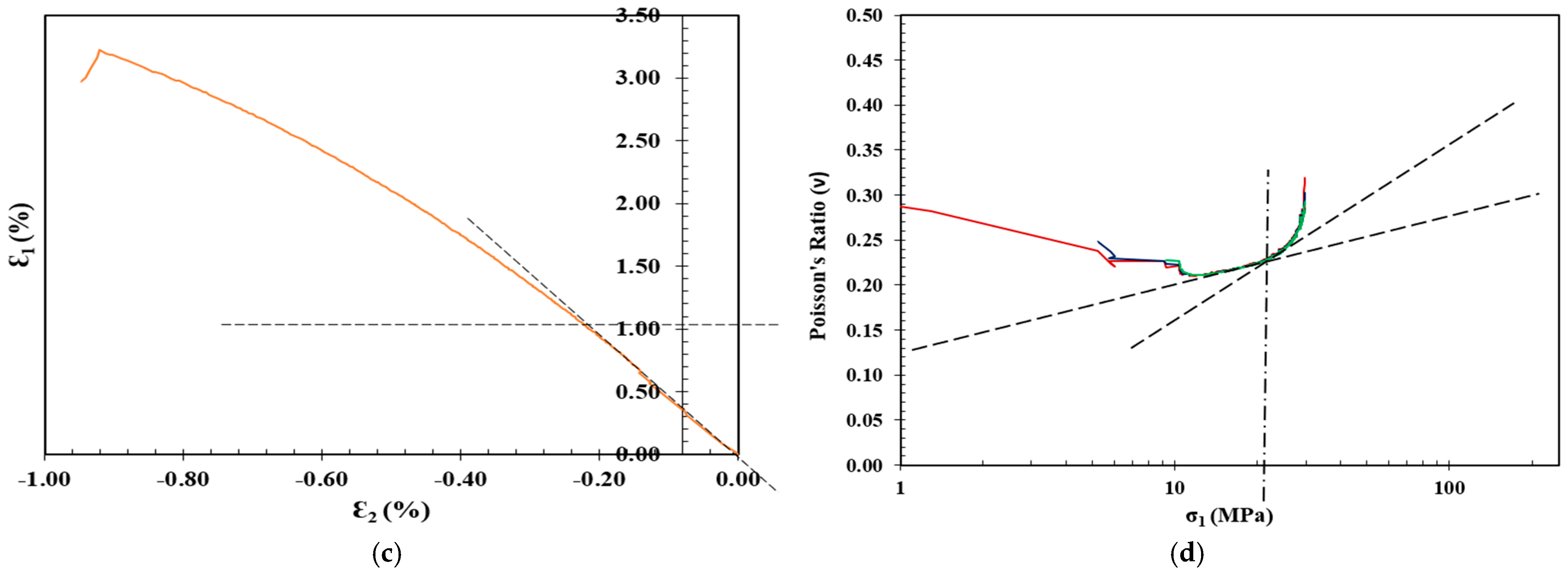
| Volumetric Strain Method [28] | The volumetric strain () is the summation of axial () and lateral strains () and () in the direction of the major, intermediate, and minor principal stresses, respectively. The crack initiation () in this model is defined as the point where the volumetric strain curve deviates from its linearity. |
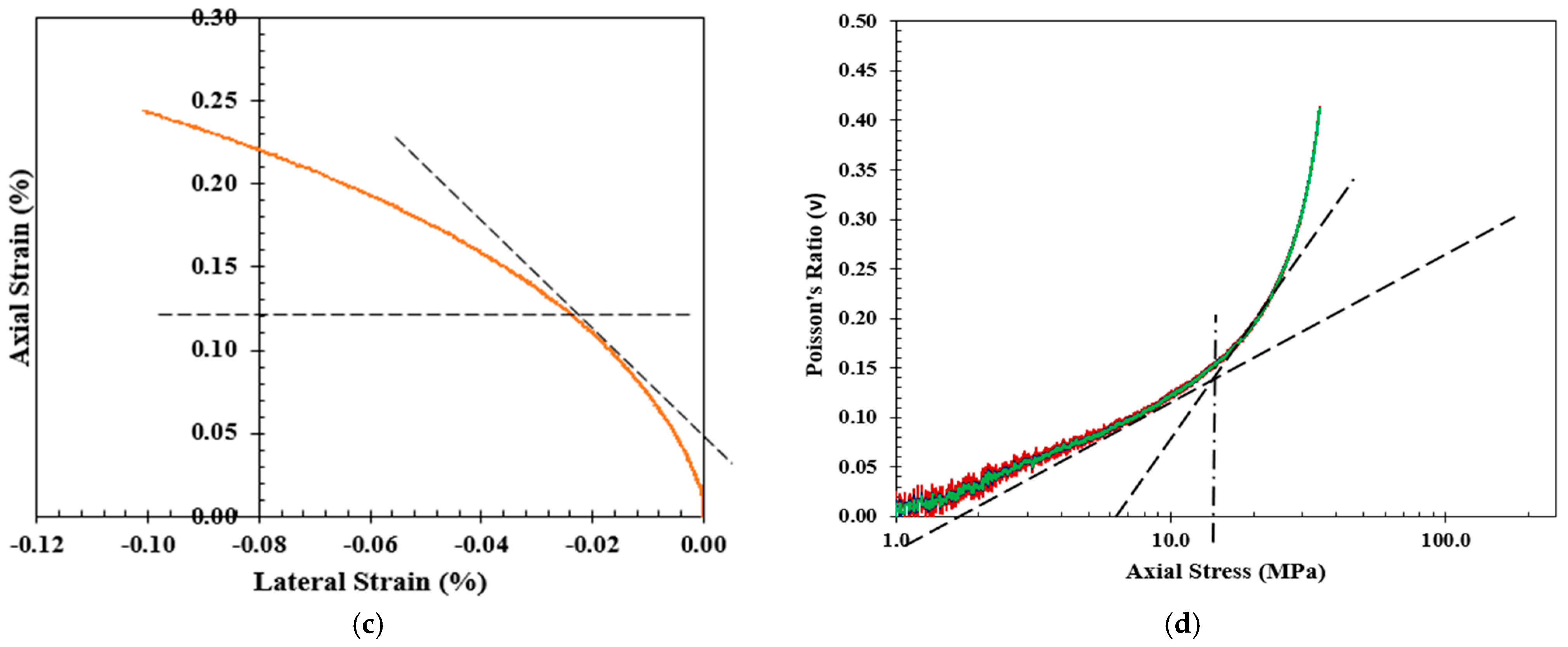
| Lateral Strain Method [29] | This model suggests that the lateral strain is more sensitive than axial strain to the growth of cracks before the onset of unstable crack growth on the stress–strain response. Therefore, the crack initiation () is determined as the point where the lateral strain deviates from the linearity of the axial stress () vs. lateral strain curve. |
| Extensional Strain Method [30] | The extensional strain method was proposed suggesting that the extensional strain could be determined experimentally by plotting the lateral strain versus axial strain. Therefore, the crack initiation () is determined as the point where the axial strain tends to deviate from its linearity on the axial strain versus lateral strain curve. |
| Poisson’s Ratio Method [17] | In this model, Poisson’s ratio is plotted against the log of axial stress, and the intersection of the tangents to the linear portions of the curve are determined to calculate the crack initiation stress (). |
| Parameter | Crack Initiation Stress () | Crack Initiation Ratio (CIR) |
|---|---|---|
| Elastic Modulus () | Increases with an increase in elastic modulus | Independent of elastic modulus |
| Poisson’s Ratio () | Independent of Poisson’s ratio; at the same Poisson’s ratio, is a function of rock type | Independent of Poisson’s ratio |
| Porosity () | Decreases with an increase in porosity | Decreases with an increase in porosity |
| Tensile Strength | Increases with an increase in tensile strength | Increases with an increase in tensile strength |
2. Experimental Setup and Methodology
2.1. Material Characteristics and Sample Preparation
2.2. Crack Initiation Setup
3. Crack Initiation Determination
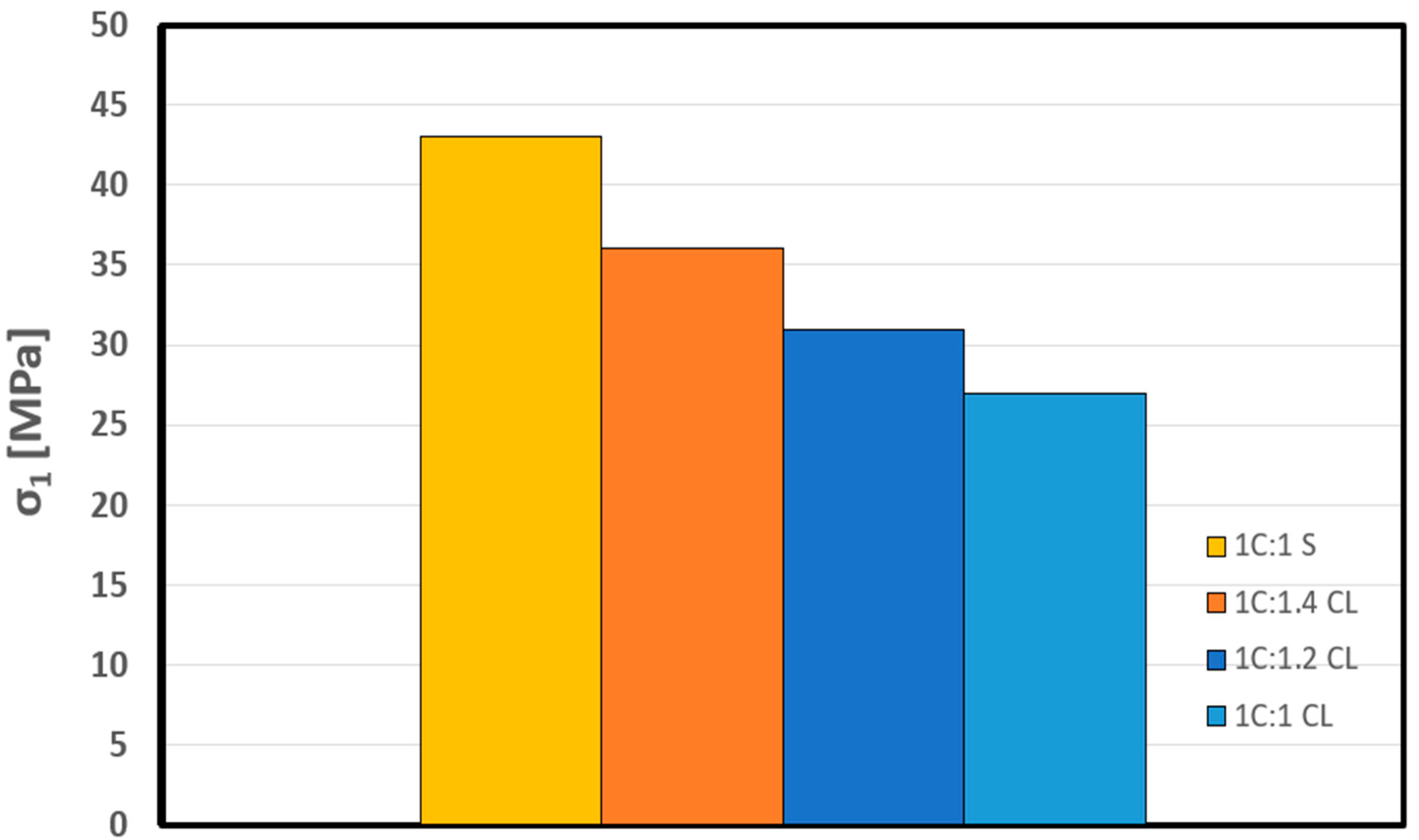
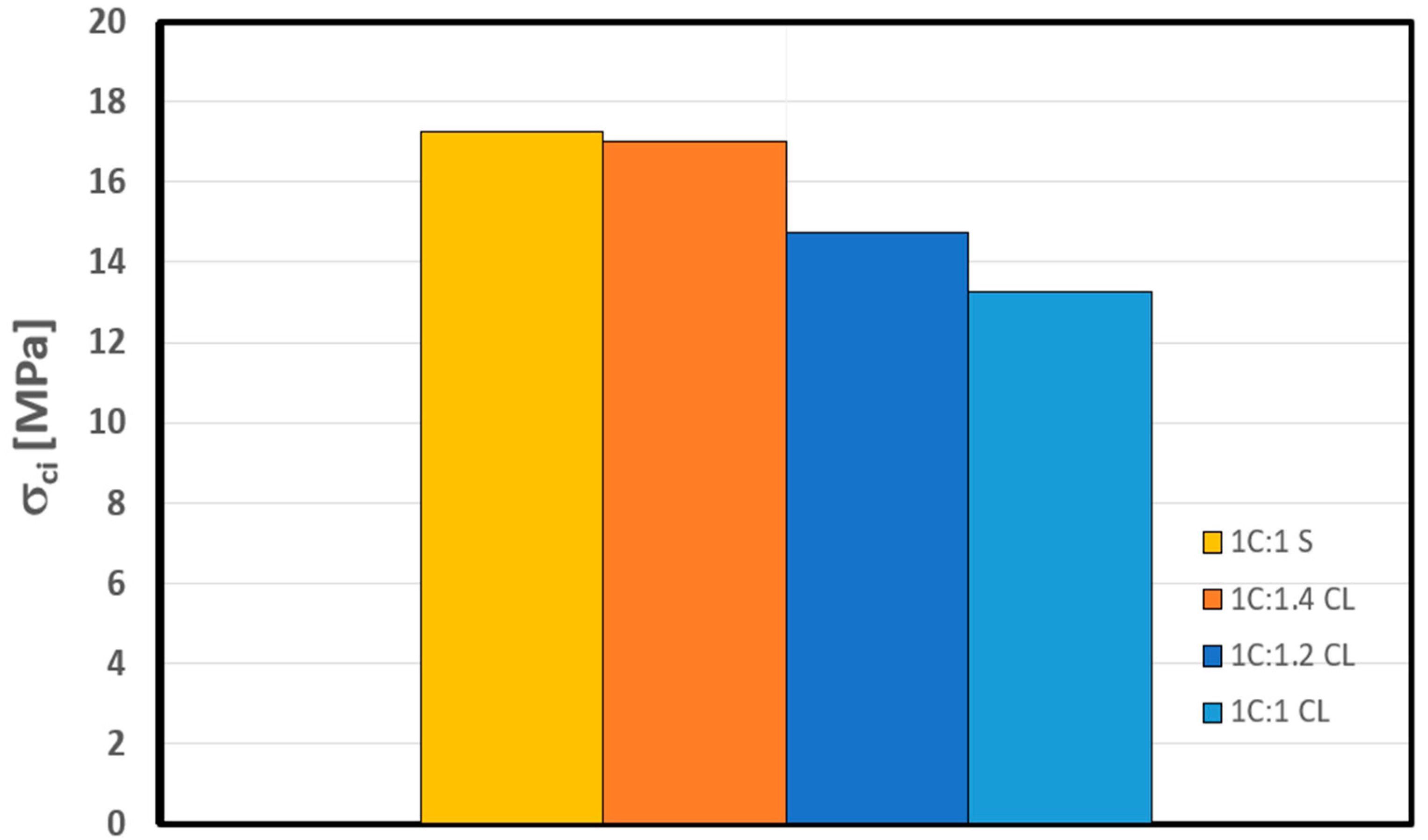
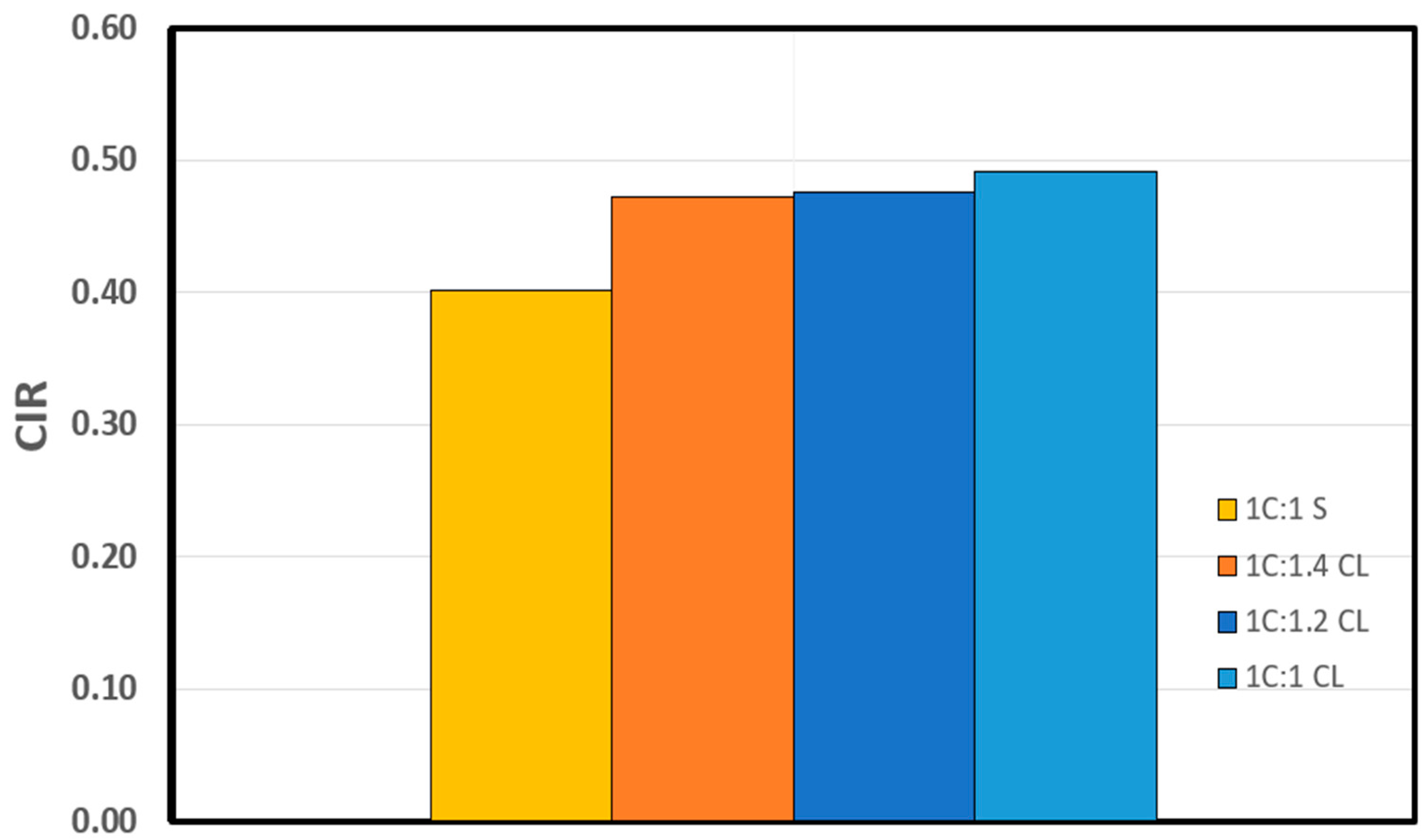
4. Effect of Crushed Limestone on the Strength and Crack Initiation
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, H.; Gao, F.; Ju, Y.; Gao, M.; Zhang, R.; Gao, Y.; Liu, J.; Xie, L. Quantitative definition and investigation of deep mining. J. China Coal Soc. 2015, 40, 1–10. [Google Scholar]
- Xie, H. Research framework and anticipated results of deep rock mechanics and mining theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar]
- Ranjith, P.G.; Zhao, J.; Ju, M.; De Silva, R.V.; Rathnaweera, T.D.; Bandara, A.K. Opportunities and challenges in deep mining: A brief review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Manzi, M.; Cooper, G.; Malehmir, A.; Durrheim, R.; Nkosi, Z. Integrated interpretation of 3D seismic data to enhance the detection of the gold-bearing reef: Mponeng Gold mine, Witwatersrand Basin (South Africa). Geophys. Prospect. 2015, 63, 881–902. [Google Scholar] [CrossRef]
- Woo, K.-S.; Eberhardt, E.; Elmo, D.; Stead, D. Empirical investigation and characterization of surface subsidence related to block cave mining. Int. J. Rock Mech. Min. Sci. 2013, 61, 31–42. [Google Scholar] [CrossRef]
- Xie, H.; Konietzky, H.; Zhou, H. Special Issue “Deep Mining”; Springer: Berlin/Heidelberg, Germany, 2019; Volume 52, pp. 1415–1416. [Google Scholar]
- Mahmoud, M. Physical Modelling of Spalling Failure in Underground Structures. Ph.D. Thesis, The University of Queensland, St. Lucia, Australia, 2023. [Google Scholar]
- Shiyong, W.; Manbin, S.; Jian, W. Jinping hydropower project: Main technical issues on engineering geology and rock mechanics. Bull. Eng. Geol. Environ. 2010, 69, 325–332. [Google Scholar] [CrossRef]
- Brown, L.; Hudyma, M. Canadian Seismicity and Rockburst Database; Technical Report; January 2017.
- Whyatt, J.; Blake, W.; Williams, T.; White, B. 60 years of rockbursting in the Coeur d’Alene District of Northern Idaho, USA: Lessons learned and remaining issues. In Proceedings of the 2002 SME Annual Meeting and Exhibit, Phoenix, AZ, USA, 25–27 February 2002. [Google Scholar]
- Carlsson, A.; Olsson, T. Rock bursting phenomena in a superficial rock mass in southern central Sweden. Rock Mech. 1982, 15, 99–110. [Google Scholar] [CrossRef]
- Fujii, Y.; Ishijima, Y.; Deguchi, G. Prediction of coal face rockbursts and microseismicity in deep longwall coal mining. Int. J. Rock Mech. Min. Sci. 1997, 34, 85–96. [Google Scholar] [CrossRef]
- Mutaz, E.; Serati, M.; Bahaaddini, M.; Williams, D. On the evaluation of crack initiation stress threshold. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Virtual, 18–25 June 2021. [Google Scholar]
- Terzaghi, K. Rock defects and loads on tunnel supports. In Rock Tunneling with Steel Supports; Commercial Shearing and Stamping Company: Youngstown, OH, USA, 1946. [Google Scholar]
- Martin, C.; Christiansson, R. Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock. Int. J. Rock Mech. Min. Sci. 2009, 46, 219–228. [Google Scholar] [CrossRef]
- Gong, F.-q.; Luo, Y.; Li, X.-b.; Si, X.-f.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Diederichs, M.S. The 2003 Canadian Geotechnical Colloquium: Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling. Can. Geotech. J. 2007, 44, 1082–1116. [Google Scholar] [CrossRef]
- Martin, C.D. Seventeenth Canadian geotechnical colloquium: The effect of cohesion loss and stress path on brittle rock strength. Can. Geotech. J. 1997, 34, 698–725. [Google Scholar] [CrossRef]
- Blake, W.; Hedley, D. Rockbursts: Case Studies from North American Hard-Rock Mines; Society for Mining, Metallurgy, and Exploration, Inc.: Littleton, CO, USA, 2003. [Google Scholar]
- Karekal, S.; Rao, M.; Chinnappa, S. Mining-associated seismicity in kolar gold mines: Some case studies using multifractals. In RaSiM6: Proceedings of the Sixth International Symposium on Rockburst and Seismicity in Mines Proceedings; Australian Centre for Geomechanics: Perth, Australia, 2005. [Google Scholar]
- Catrin, E. Strength, Fallouts and Numerical Modelling of Hard Rock Masses. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2008. [Google Scholar]
- Matti, H.; John, A.; John, P.; Erik, J. Assessment of the Potential for Rock Spalling at the Olkiluoto Site Posiva OY; Working Report; Posiva: Eurajoki, Finland, 2008; Volume 38. [Google Scholar]
- Rojat, F.; Labiouse, V.; Kaiser, P.K.; Descoeudres, F. Brittle rock failure in the Steg lateral adit of the Lötschberg base tunnel. Rock Mech. Rock Eng. 2009, 42, 341–359. [Google Scholar] [CrossRef]
- Doghozlou, H.; Goodarzi, M.; Rafiei Renani, H.; Salmi, E. Analysis of spalling failure in marble rock slope: A case study of Neyriz marble mine, Iran. Environ. Earth Sci. 2016, 75, 1478. [Google Scholar] [CrossRef]
- Zhao, X.; Li, H.; Zhang, S. Analysis of the spalling process of rock mass around a deep underground ramp based on numerical modeling and in-situ observation. Geomat. Nat. Hazards Risk 2020, 11, 1619–1637. [Google Scholar] [CrossRef]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Sjölander, A. Structural Behaviour of Shotcrete in Hard Rock Tunnels. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2020. [Google Scholar]
- Brace, W.; Paulding, B., Jr.; Scholz, C. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Lajtai, E. Brittle fracture in compression. Int. J. Fract. 1974, 10, 525–536. [Google Scholar] [CrossRef]
- Stacey, T. A simple extension strain criterion for fracture of brittle rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 469–474. [Google Scholar] [CrossRef]
- Mohajerani, A.; Rodrigues, D.; Ricciuti, C.; Wilson, C. Early-age strength measurement of shotcrete. J. Mater. 2015, 2015, 470160. [Google Scholar] [CrossRef][Green Version]
- Balck, L. Guide to Shotcrete. Concr. Int. 2017, 39, 35–37. [Google Scholar]
- Bernard, E.S. Early-age load resistance of fibre reinforced shotcrete linings. Tunn. Undergr. Space Technol. 2008, 23, 451–460. [Google Scholar] [CrossRef]
- Thompson, A.; Villaescusa, E.; Windsor, C. Ground support terminology and classification: An update. Geotech. Geol. Eng. 2012, 30, 553–580. [Google Scholar] [CrossRef]
- Drover, C.; Villaescusa, E. Performance of shotcrete surface support following dynamic loading of mining excavations. In Proceedings of the Shotcrete for Underground Support XII, Singapore, 11–13 October 2015. [Google Scholar]
- Chen, D.; Wang, L.; Sun, C.; Jia, C.; Zheng, L. Investigation of the support constraint effect and failure instability law of tunnels constructed using the New Austrian tunneling method. Sci. Rep. 2022, 12, 5811. [Google Scholar] [CrossRef]
- Saw, H.; Villaescusa, E.; Windsor, C.; Thompson, A. Laboratory testing of steel fibre reinforced shotcrete. Int. J. Rock Mech. Min. Sci. 2013, 57, 167–171. [Google Scholar] [CrossRef]
- Barrett, S.; McCreath, D. Shortcrete support design in blocky ground: Towards a deterministic approach. Tunn. Undergr. Space Technol. 1995, 10, 79–89. [Google Scholar] [CrossRef]
- Villaescusa, E.; Kusui, A.; Drover, C. Ground support design for sudden and violent failures in hard rock tunnels. In Proceedings of the 9th Asian Rock Mechanics Symposium, Bali, Indonesia, 18–20 October 2016. [Google Scholar]
- Thompson, A.; Windsor, C. A classification system for reinforcement and its use in design. In Proceedings of the Western Australian Conference on Mining Geomechanics, Kalgoorlie, Australia, 8–10 June 1992; pp. 115–125. [Google Scholar]
- Heltzen, A. Shotcrete-An Effective Resource Against Rock Fall In Spalling Rock. In Proceedings of the 20th US Symposium on Rock Mechanics (USRMS), Austin, TX, USA, 4–6 June 1979. [Google Scholar]
- Zhang, C.; Feng, X.-T.; Zhou, H.; Qiu, S.; Wu, W. Case histories of four extremely intense rockbursts in deep tunnels. Rock Mech. Rock Eng. 2012, 45, 275–288. [Google Scholar] [CrossRef]
- Serati, M.; Jakson, N.; Asche, H.; Basireddy, S.; Malgotra, G. Sustainable shotcrete production with waste glass aggregates. SN Appl. Sci. 2022, 4, 82. [Google Scholar] [CrossRef]
- Villaescusa, E. Geotechnical Design for Sublevel Open Stoping; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Zhou, G.; Zhao, Z.; Song, Z.; Wang, H. Stability analysis and protection measures of large section tunnel in coal rich weak rock stratum. Geofluids 2021, 2021, 9394145. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Y.; Chen, L.; Hu, W.; Chen, S. The prevention and control mechanism of rockburst hazards and its application in the construction of a deeply buried tunnel. Appl. Sci. 2019, 9, 3629. [Google Scholar] [CrossRef]
- El-Kelesh, A.M.; Matsui, T. Compaction Grouting and Soil Compressibility. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; p. ISOPE-I-02-221. [Google Scholar]
- Alokili, T.; Dafalla, M.; Al-Mahbashi, A.; Alnuaim, A.; Mutaz, E. Tunnel Boring Machine Crushed Limestone as a Cement Grout. In Proceedings of the Geo-Congress, Los Angeles, CA, USA, 26–29 March 2023; pp. 45–54. [Google Scholar]
- Holmstrom, O.C.; Swan, C.W. Geotechnical properties of innovative, synthetic lightweight aggregates. In Proceedings of the 1999 International Ash Utilization Symposium; University of Kentucky: Lexington, KY, USA, 1999; pp. 18–20. [Google Scholar]
- Kazmi, D.; Serati, M.; Williams, D.J.; Qasim, S.; Cheng, Y.P. The potential use of crushed waste glass as a sustainable alternative to natural and manufactured sand in geotechnical applications. J. Clean. Prod. 2021, 284, 124762. [Google Scholar] [CrossRef]
- Koehnken, L.; Rintoul, M. Impacts of Sand Mining on Ecosystem Structure, Process and Biodiversity in Rivers; World Wildlife Fund International: Gland, Switzerland, 2018. [Google Scholar]
- Bravo, M.; De Brito, J.; Pontes, J.; Evangelista, L. Mechanical performance of concrete made with aggregates from construction and demolition waste recycling plants. J. Clean. Prod. 2015, 99, 59–74. [Google Scholar] [CrossRef]
- Hebhoub, H.; Aoun, H.; Belachia, M.; Houari, H.; Ghorbel, E. Use of waste marble aggregates in concrete. Constr. Build. Mater. 2011, 25, 1167–1171. [Google Scholar] [CrossRef]
- Kazmi, D.; Williams, D.J.; Serati, M. Waste glass in civil engineering applications—A review. Int. J. Appl. Ceram. Technol. 2020, 17, 529–554. [Google Scholar] [CrossRef]
- Dom, A.A.M.; Jamaluddin, N.; Hamid, N.A.A.; Hoon, C.S. A Review: GGBS as a Cement Replacement in Concrete. IOP Conf. Ser. Earth Environ. Sci. 2022, 1022, 012044. [Google Scholar]
- Yifru, B.W.; Mitikie, B.B. Partial replacement of sand with marble waste and scoria for normal strength concrete production. SN Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Bertoldo, N.; Qureshi, T.; Simpkins, D.; Arrigoni, A.; Dotelli, G. Concrete with Organic Waste Materials as Aggregate Replacement. Appl. Sci. 2023, 14, 108. [Google Scholar] [CrossRef]
- Singh, J.; Mukherjee, A.; Dhiman, V.K. Impact of crushed limestone dust on concrete’s properties. Mater. Today Proc. 2021, 43, 341–347. [Google Scholar] [CrossRef]
- Djedid, T.; Mani, M.; Ouakouak, A.; Guettala, A. Effect of varying silica-limestone sand fines on the physical-mechanical performance of concrete. Frat. Ed Integrità Strutt. 2022, 16, 580–591. [Google Scholar] [CrossRef]
- Alnuaim, A.; Dafalla, M.; Al-Mahbashi, A. Enhancement of Clay–Sand Liners Using Crushed Limestone Powder for Better Fluid Control. Arab. J. Sci. Eng. 2020, 45, 367–380. [Google Scholar] [CrossRef]
- Alnuaim, A.; Abbas, Y.M.; Khan, M.I. Sustainable application of processed TBM excavated rock material as green structural concrete aggregate. Constr. Build. Mater. 2021, 274, 121245. [Google Scholar] [CrossRef]
- Dafalla, M.; Al-Mahbashi, A.; Alnuaim, A. Characterization and assessment of crushed limestone powder and its environmental applications. IOP Conf. Ser. Earth Environ. Sci. 2021, 727, 012013. [Google Scholar] [CrossRef]
- Omar, O.M.; Abd Elhameed, G.D.; Sherif, M.A.; Mohamadien, H.A. Influence of limestone waste as partial replacement material for sand and marble powder in concrete properties. HBRC J. 2012, 8, 193–203. [Google Scholar] [CrossRef]
- Al-Mahbashi, A.M.; Dafalla, M. Shear strength prediction for an unsaturated Sand Clay Liner. Int. J. Geotech. Eng. 2022, 16, 282–292. [Google Scholar] [CrossRef]
- Mutaz, E.; Serati, M.; Williams, D. Crack Initiation Evolution Under Triaxial Loading Conditions. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012012. [Google Scholar] [CrossRef]
- Nicksiar, M.; Martin, C. Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks. Rock Mech. Rock Eng. 2012, 45, 607–617. [Google Scholar] [CrossRef]








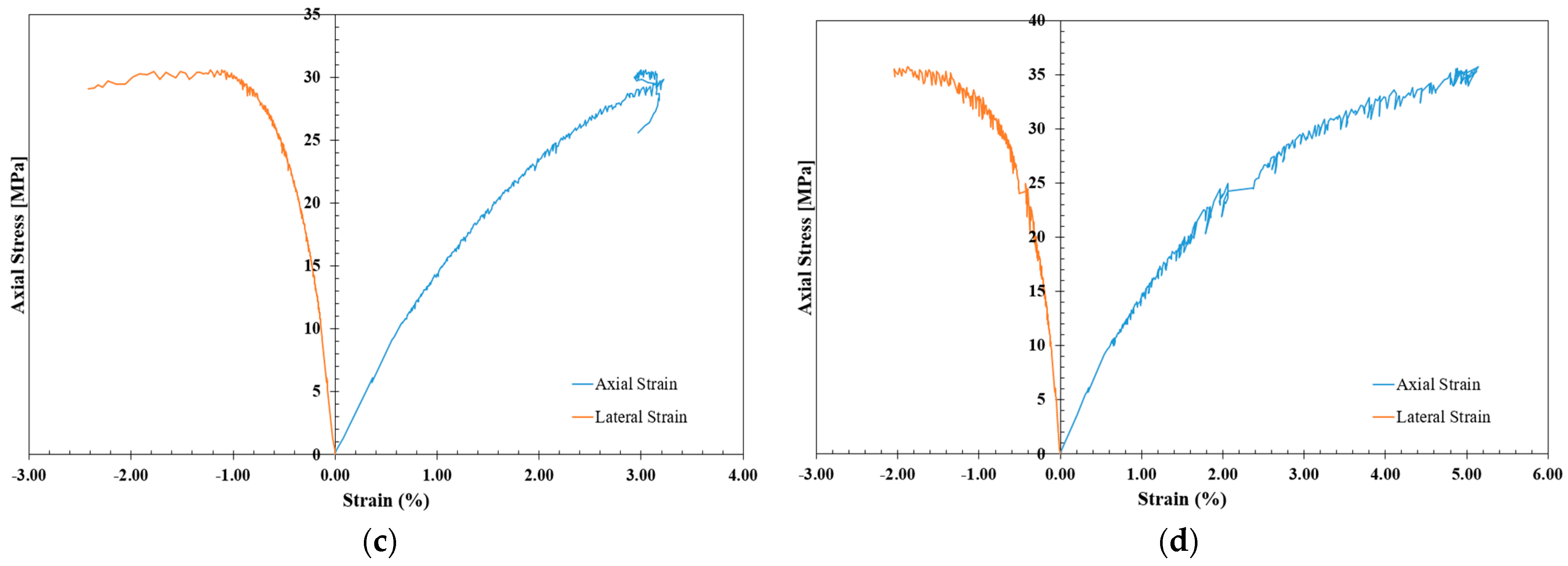
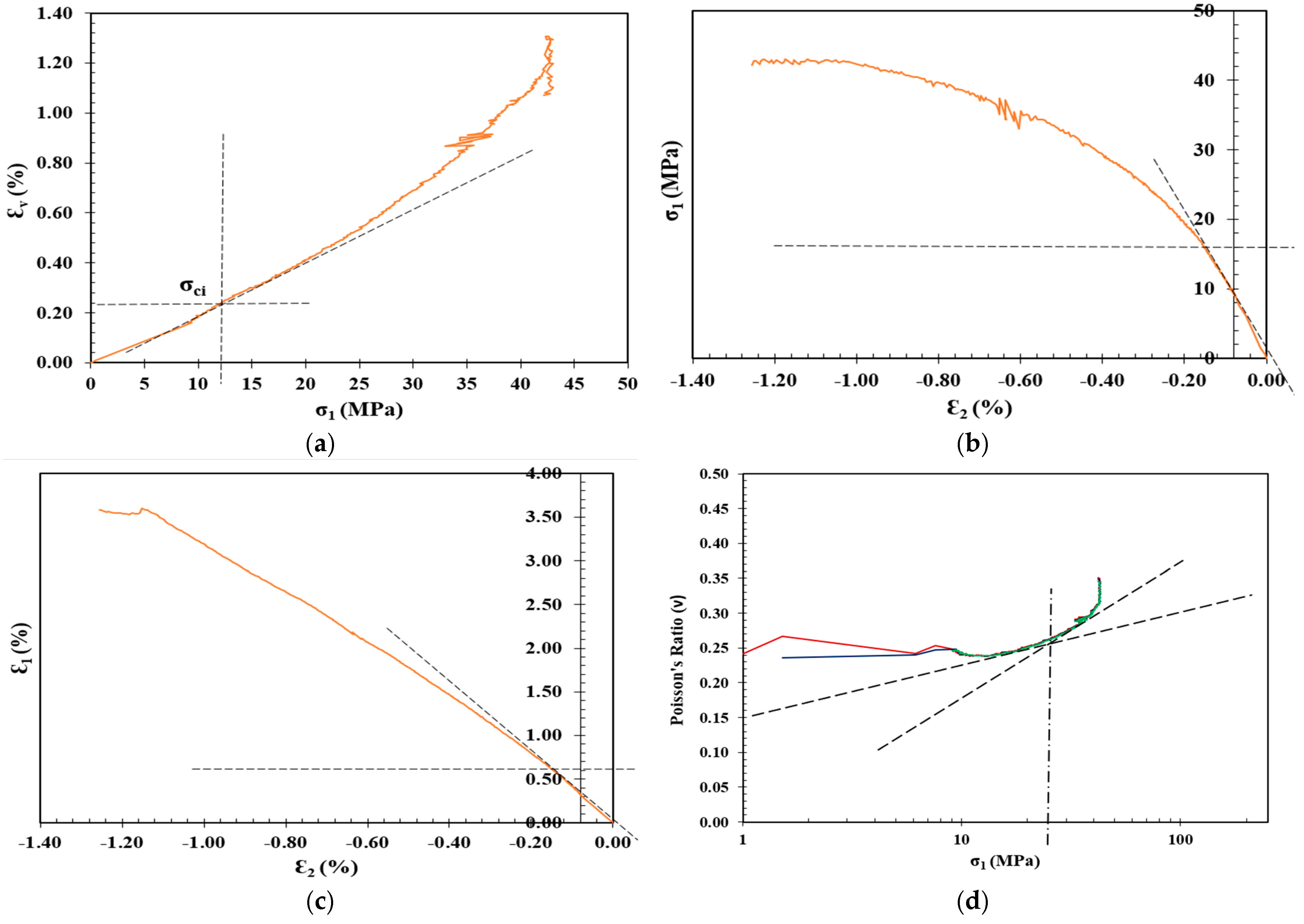
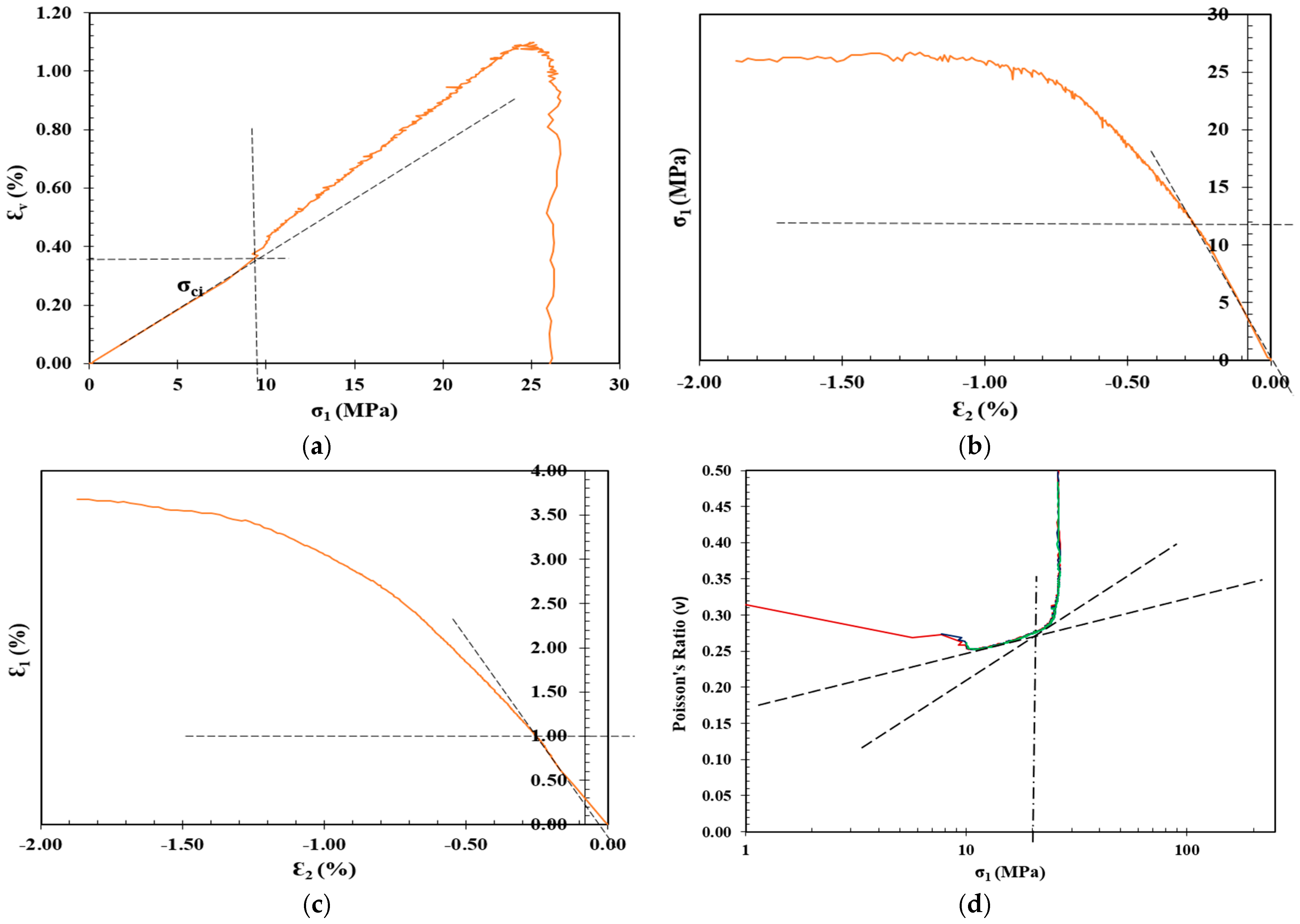
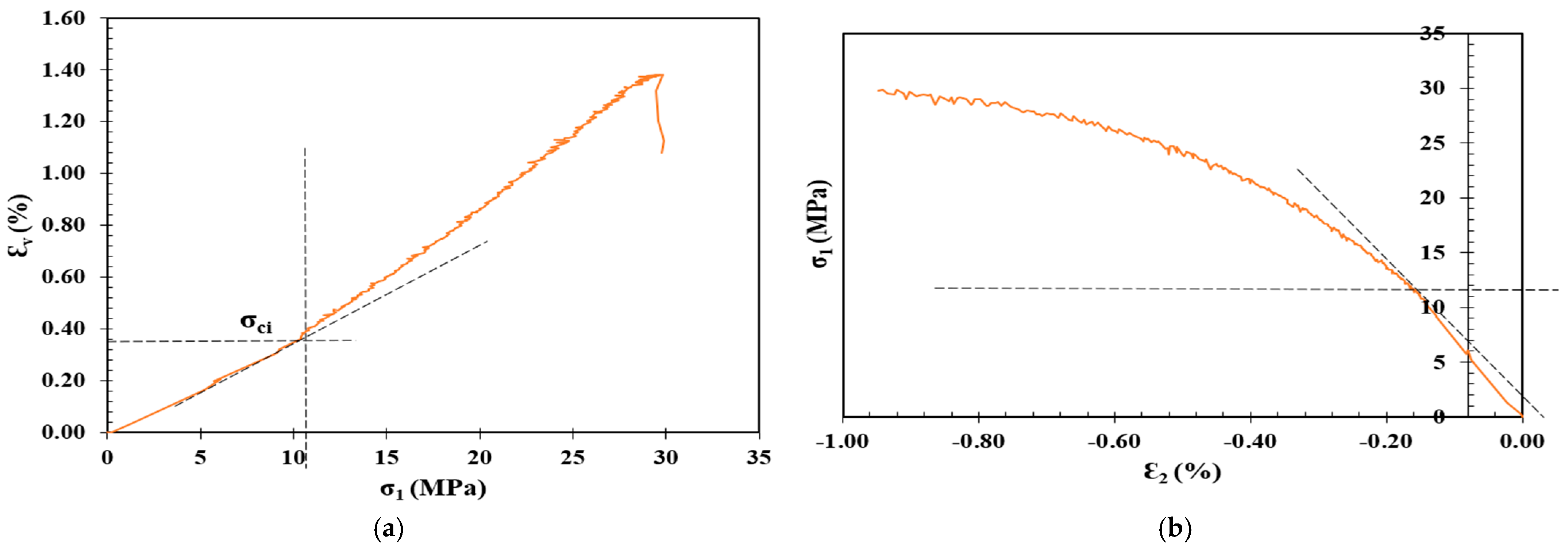

| Shotcrete Mix No. | Materials Ratio | |||
|---|---|---|---|---|
| Cement (C) | Crushed Limestone (CL) | Sand (S) | Water–Cement Ratio (w/c) | |
| 1 | 1 | - | 1 | 0.50 |
| 2 | 1 | 1 | - | 0.60 |
| 3 | 1 | 1.2 | - | 0.60 |
| 4 | 1 | 1.4 | - | 0.60 |
| MPa | Shotcrete Mix | Crack Initiation Stress () [MPa] | SD | CoV (%) | Average of All CI Methods [MPa] | CIR | |||
|---|---|---|---|---|---|---|---|---|---|
| Volumetric Strain Method | Lateral Strain Method | Extensional Strain Method | Poisson’s Ratio Method | ||||||
| 43 | 1C:1S | 12 | 16 | 16 | 25 | 5.5 | 31.9 | 17.25 | 0.40 |
| 27 | 1C:1CL | 10 | 12 | 11 | 20 | 4.6 | 34.5 | 13.25 | 0.49 |
| 31 | 1C:1.2CL | 11 | 13 | 14 | 21 | 4.4 | 29.5 | 14.75 | 0.48 |
| 36 | 1C:1.4CL | 16 | 14 | 16 | 22 | 3.5 | 20.4 | 17.00 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mutaz, E.; Dafalla, M.; Al-Mahbashi, A.M.; Serati, M. Utilizing Crushed Limestone as a Sustainable Alternative in Shotcrete Applications. Materials 2024, 17, 1486. https://doi.org/10.3390/ma17071486
Mutaz E, Dafalla M, Al-Mahbashi AM, Serati M. Utilizing Crushed Limestone as a Sustainable Alternative in Shotcrete Applications. Materials. 2024; 17(7):1486. https://doi.org/10.3390/ma17071486
Chicago/Turabian StyleMutaz, Elamin, Muawia Dafalla, Ahmed M. Al-Mahbashi, and Mehdi Serati. 2024. "Utilizing Crushed Limestone as a Sustainable Alternative in Shotcrete Applications" Materials 17, no. 7: 1486. https://doi.org/10.3390/ma17071486
APA StyleMutaz, E., Dafalla, M., Al-Mahbashi, A. M., & Serati, M. (2024). Utilizing Crushed Limestone as a Sustainable Alternative in Shotcrete Applications. Materials, 17(7), 1486. https://doi.org/10.3390/ma17071486





