Enhanced Microwave Deicing Capacity of Cement Pavement with Carbon Fiber Screens
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Preparation of Composite Specimens
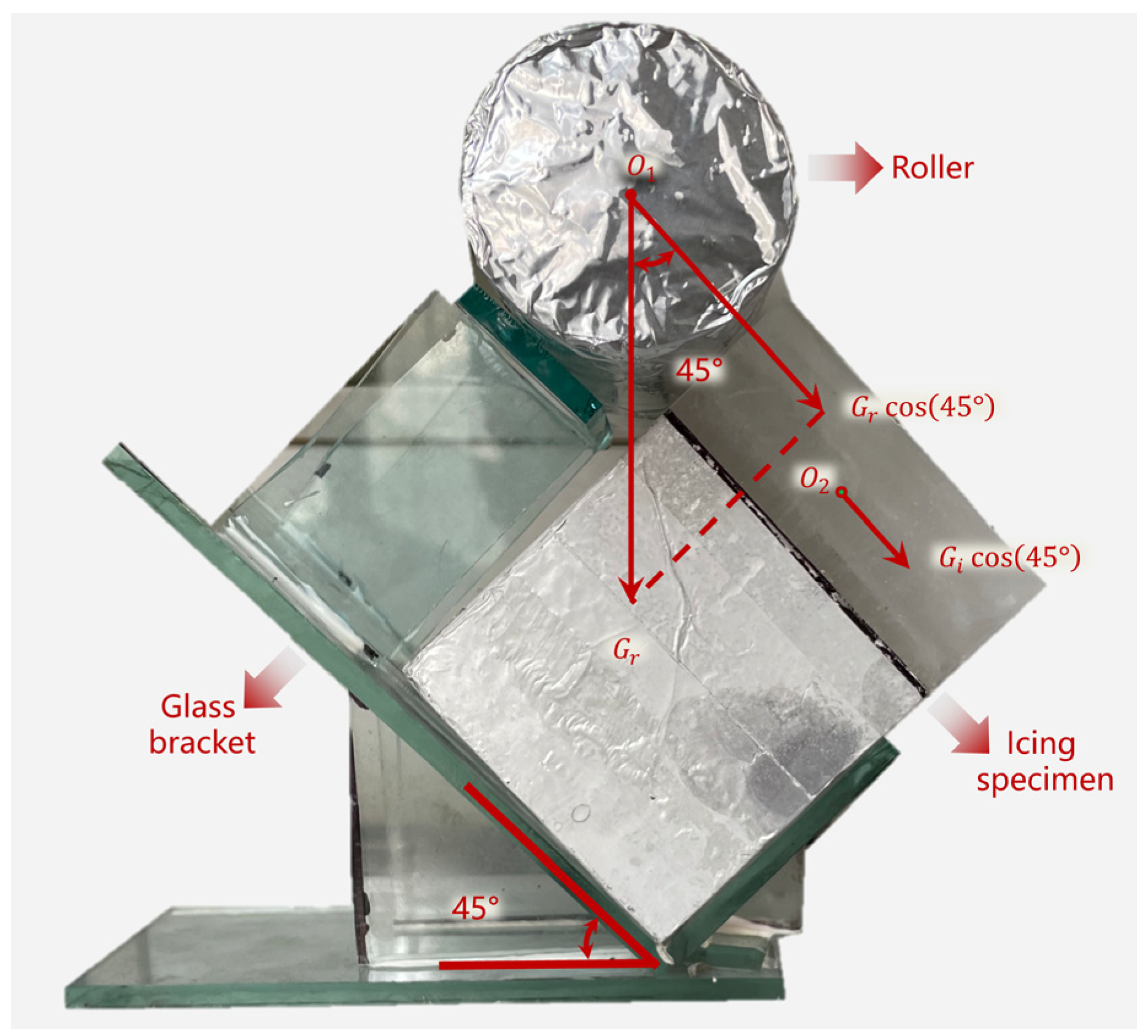
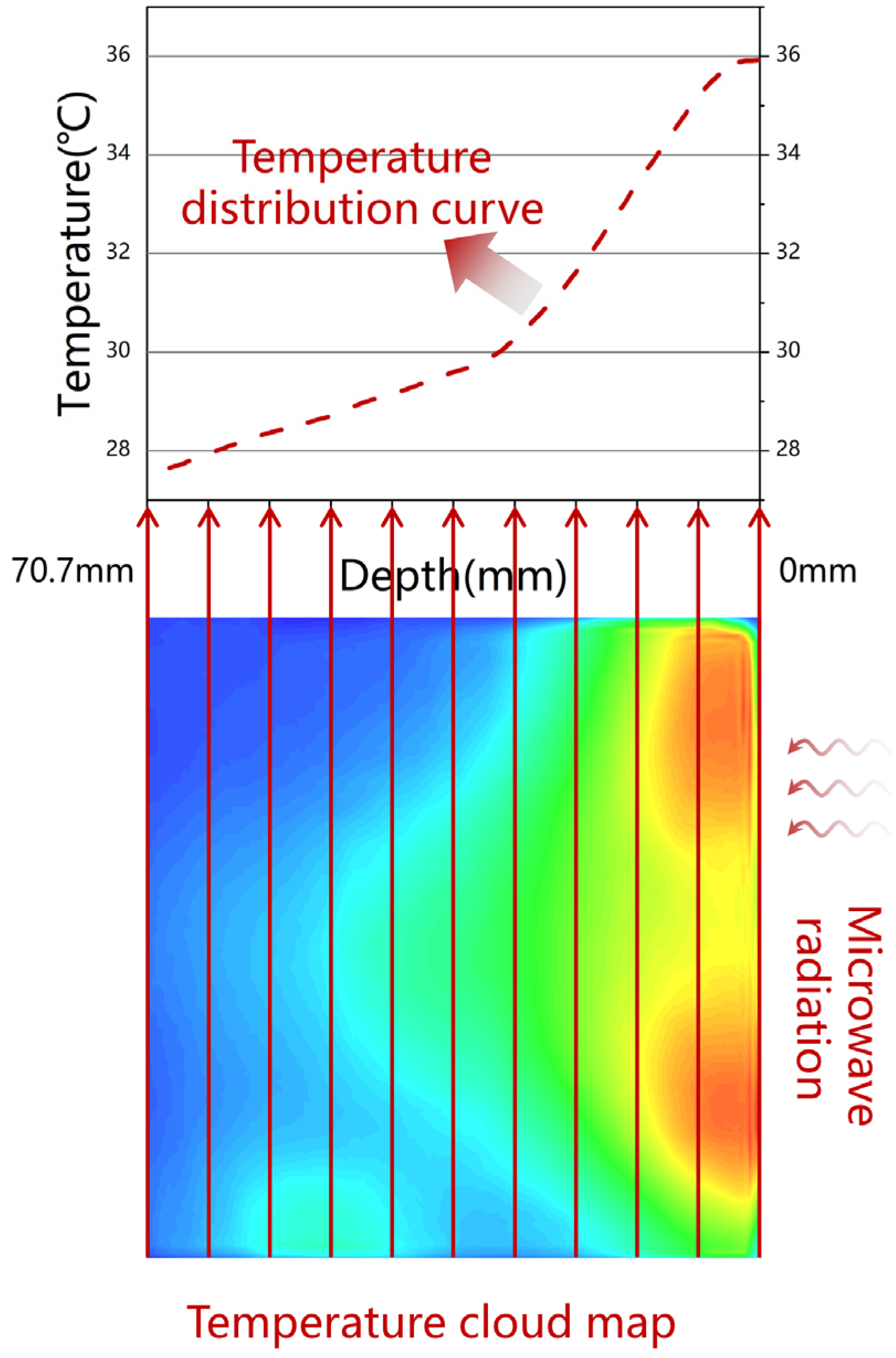
2.2.2. Temperature Test
2.2.3. Microwave Deicing Test
2.2.4. Optimization of the Surface Heating Rate (SHR)
3. Results
3.1. The SHR of the CFS/CM Composite Specimen
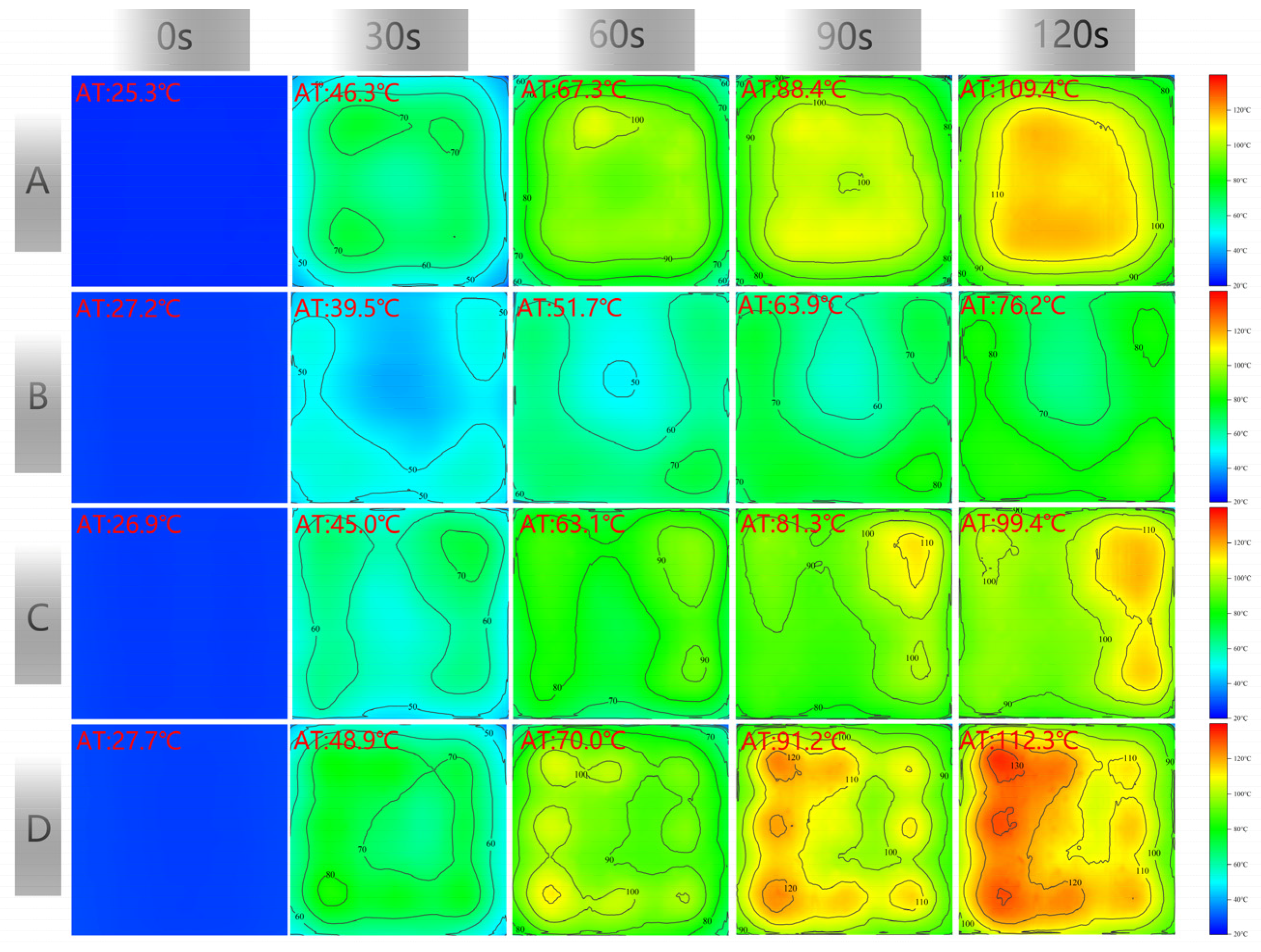
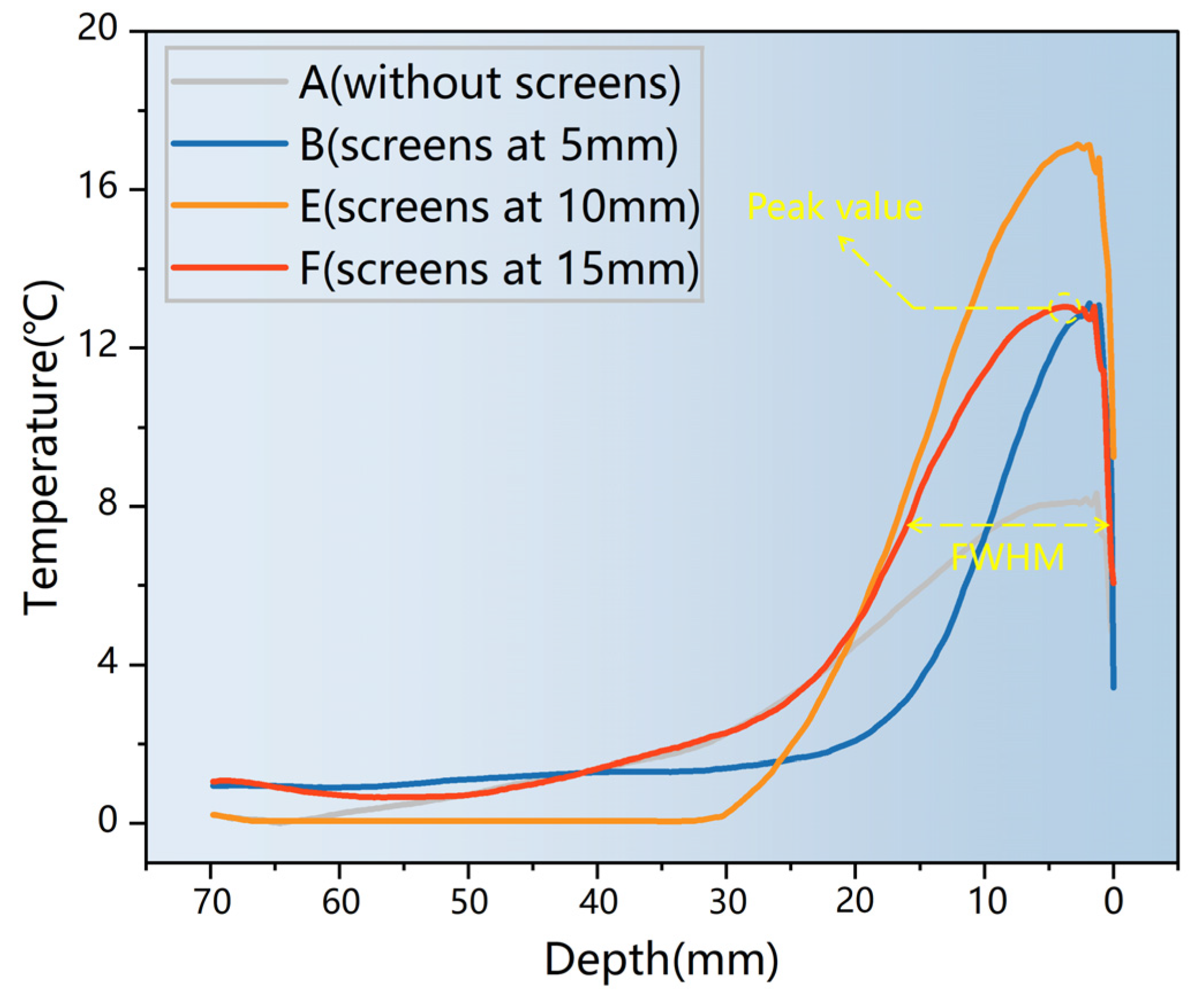
3.1.1. Effect of CFS Size on the SHR
3.1.2. Effect of CFS Depth on the SHR
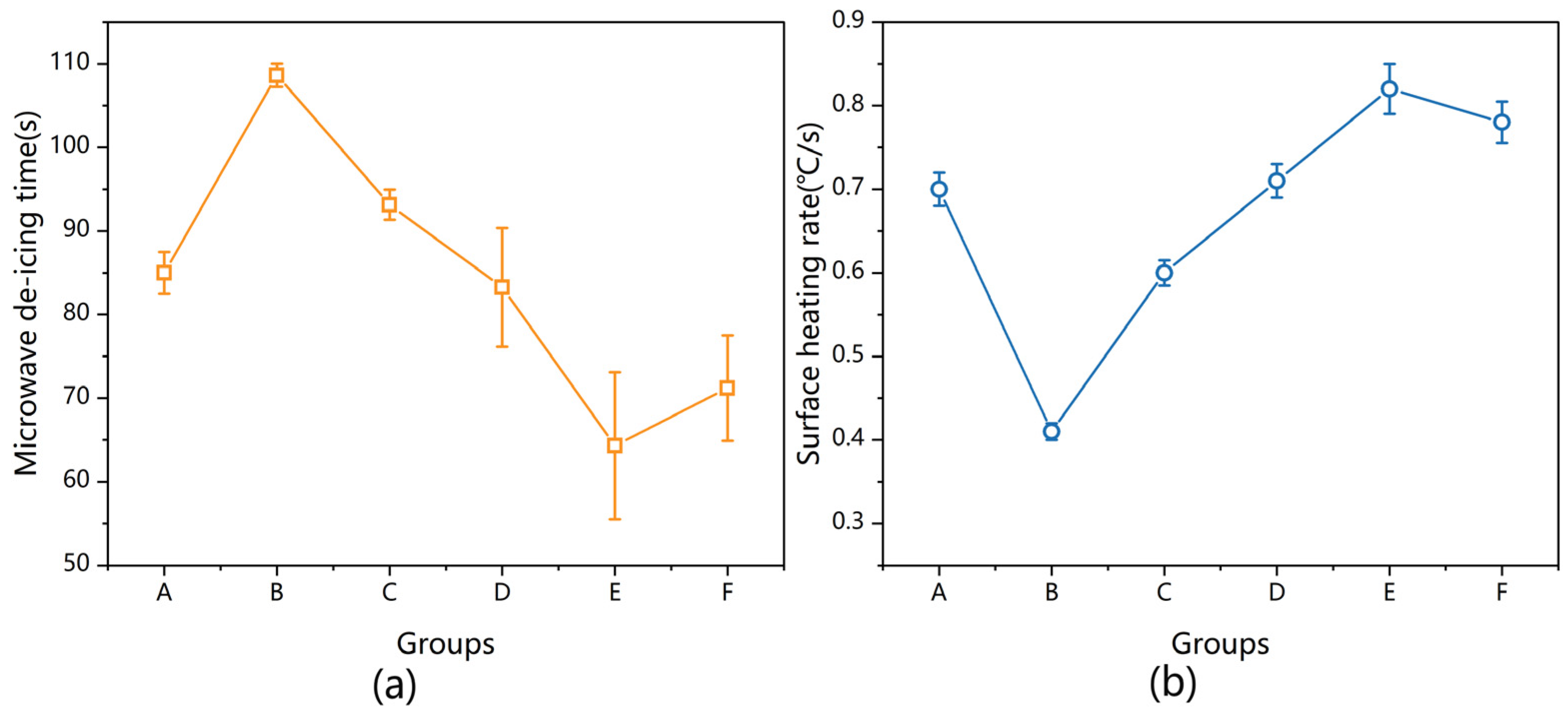
3.2. Microwave Deicing Time
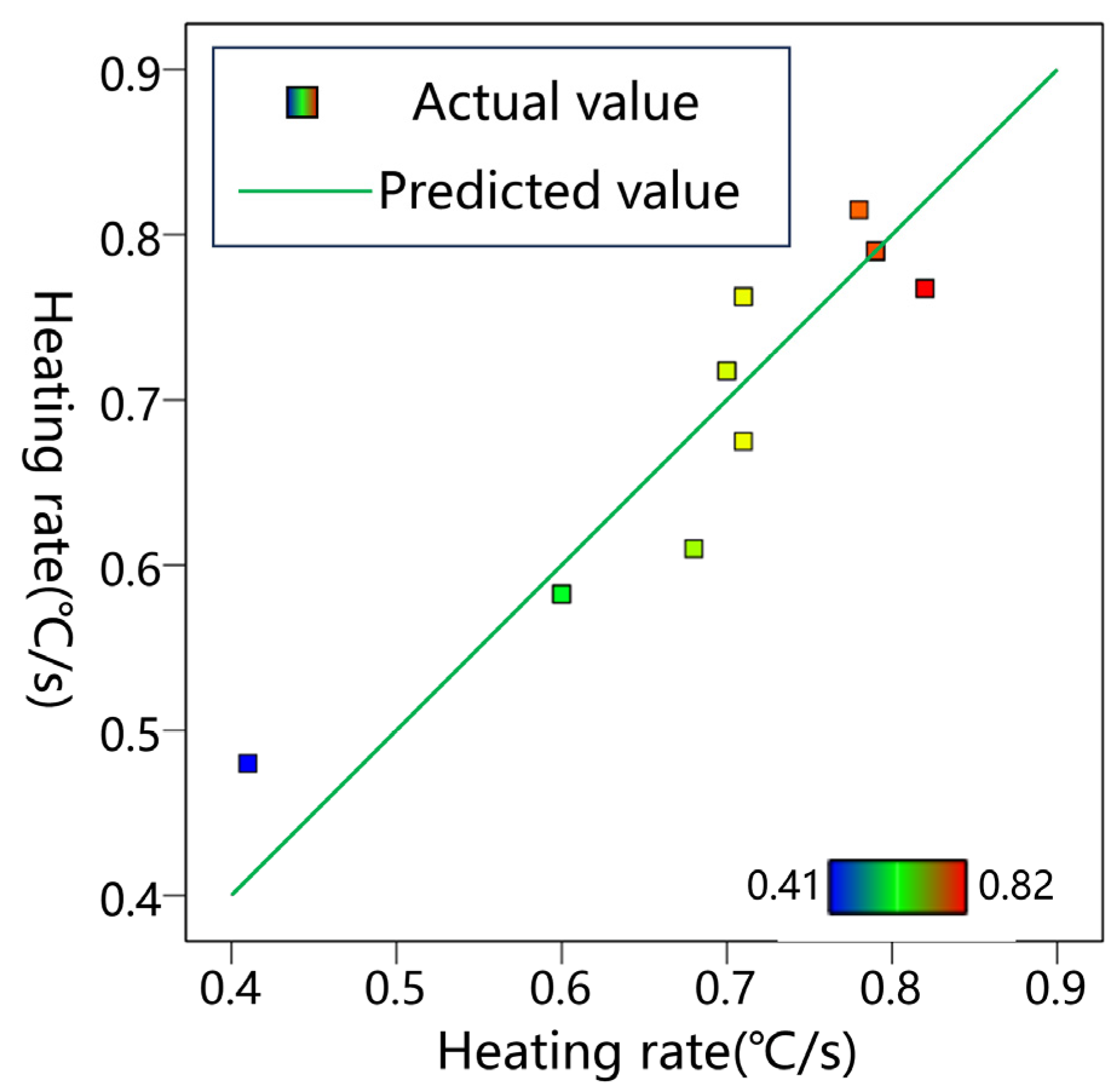
3.3. Optimization of the SHR Based on RSM
3.3.1. Variance Analyses
3.3.2. Optimization of the SHR
4. Discussion
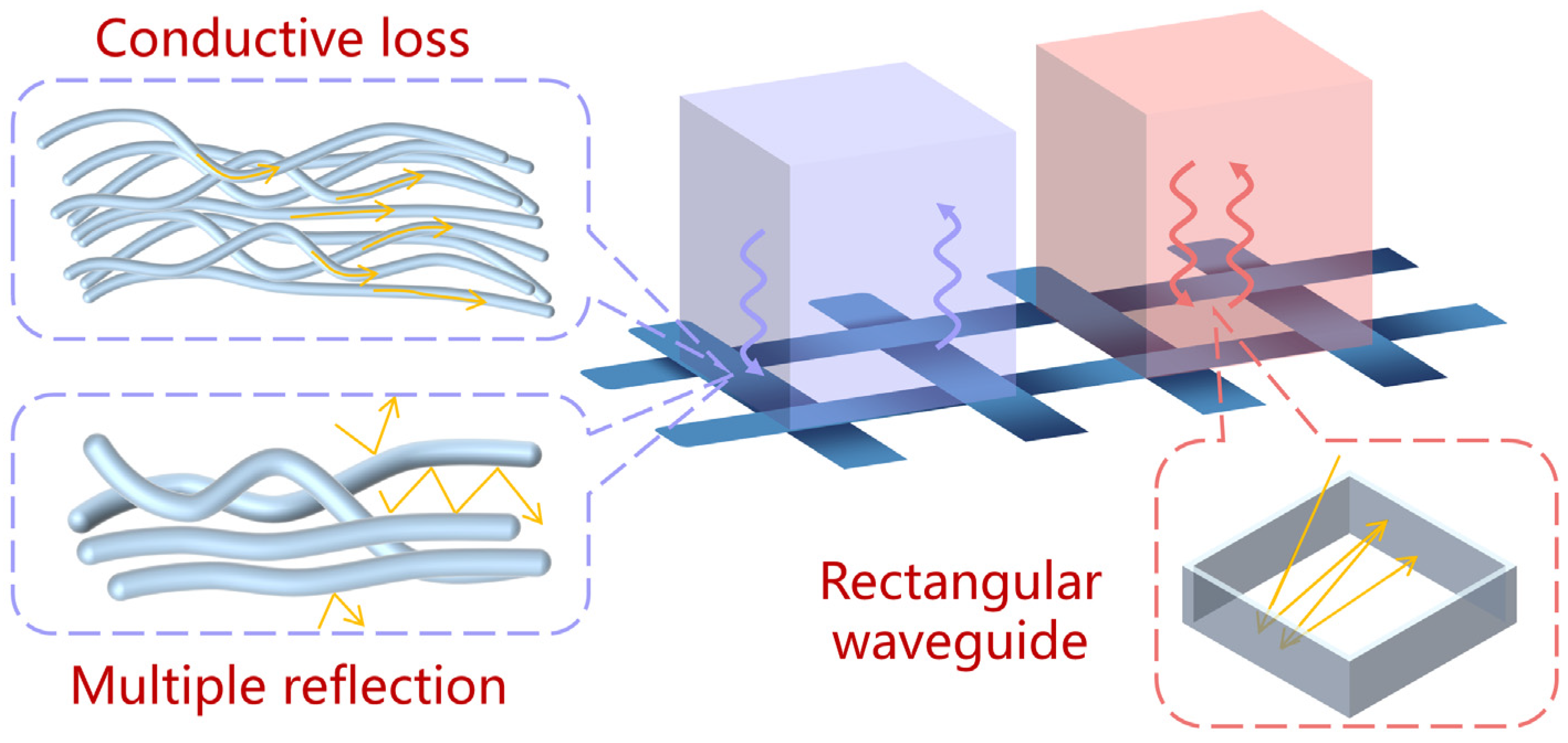
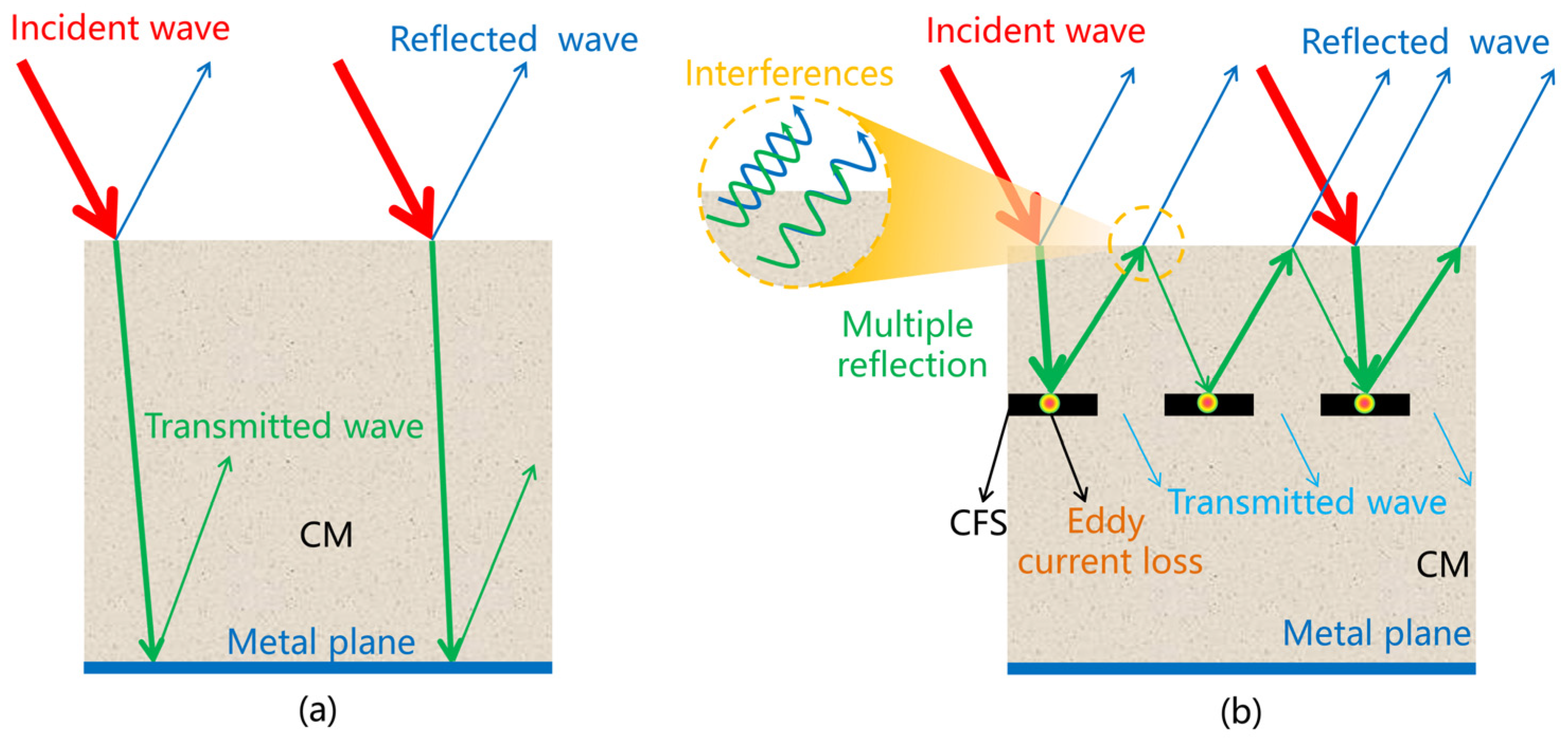
4.1. Interaction between Microwaves and CFS
4.2. Effect of CFS on Microwave Propagation
5. Conclusions and Recommendations
5.1. Conclusions
- A combination of heating efficiency, heating position, and heating range resulted in the effective surface heating of the CFS/CM composite specimens.
- The surface heating rate of the CFS/CM composite specimen could be used to characterize the deicing efficiency because the surface heating rate had a consistent negative correlation with the MDT.
- The carbon fiber bundle of the CFS consumed some microwaves, and the size of the CFS determined the reflection and transmission of microwaves.
- The effective surface heating of the CFS/CM specimens was mainly caused by the destructive interference produced by the CFS.
5.2. Importance and Further Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rocha Segundo, I.; Freitas, E.; Castelo Branco, V.T.F.; Landi, S., Jr.; Costa, M.F.; Carneiro, J.O. Review and analysis of advances in functionalized, smart, and multifunctional asphalt mixtures. Renew. Sustain. Energy Rev. 2021, 151, 111552. [Google Scholar] [CrossRef]
- Guzik, P.; Szymkowiak, A.; Kulawik, P.; Zając, M.; Migdał, W. The confrontation of consumer beliefs about the impact of microwave-processing on food and human health with existing research. Trends Food Sci. Technol. 2022, 119, 110–121. [Google Scholar] [CrossRef]
- Gulisano, F.; Gallego, J.; Trigos, L.; Apaza, F.R.A. Dielectric characterisation of asphalt mortars for microwave heating applications. Constr. Build. Mater. 2021, 308, 125048. [Google Scholar] [CrossRef]
- Ding, L.; Wang, X.; Cui, X.; Zhang, M.; Chen, B. Development and performance research of new sensitive materials for microwave deicing pavement at different frequencies. Cold Reg. Sci. Technol. 2021, 181, 103176. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Deng, Y.; Guo, Y.; Zhao, J.; Li, M. Study on Microwave Deicing Efficiency of Microwave-Absorbing Concrete Pavements and Its Influencing Factors. Materials 2022, 15, 8923. [Google Scholar] [CrossRef]
- Huang, H.; Xu, J.; Yao, A.; Xia, W.; Bai, E.; Ning, Y. Study on Microwave Deicing of Carbon-Fiber-Modified Concrete under Multi-Factor Coupling Effect. Appl. Sci. 2022, 12, 5551. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Z.; Huo, J.; Wang, X.; Liu, Z.; Li, G. Microwave heating improvement of asphalt mixtures through optimizing layer thickness of magnetite and limestone aggregates. J. Clean. Prod. 2020, 273, 123090. [Google Scholar] [CrossRef]
- Bakbolat, B.; Daulbayev, C.; Sultanov, F.; Taurbekov, A.; Tolynbekov, A.; Yeleuov, M.; Korobeinyk, A.V.; Mansurov, Z. Effectiveness of bio-waste-derived carbon doping on de-icing performance of an electrically resistant concrete. Coatings 2022, 12, 1629. [Google Scholar] [CrossRef]
- Li, J.; Zhao, P.; Jing, M.; Zhu, J.; Guo, J. Microwave heating characteristics and energy utilisation efficiency of the double-layer magnetite cement concrete (DLMCC). Int. J. Pavement Eng. 2023, 24, 2176497. [Google Scholar] [CrossRef]
- Liu, X.; Chang, F.; Zhao, Y. An Ultra-Thin, Microwave-Absorbing Wear Layer for Pavement Deicing. Materials 2023, 16, 3080. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Xin, L.; Ren, J.; Cao, Y.; Tian, Y. Concrete pavement with microwave heating enhancement functional layer for efficient de-icing: Design and case study. Cold Reg. Sci. Technol. 2023, 210, 103846. [Google Scholar] [CrossRef]
- Seman, F.C.; Cahill, R. Performance enhancement of Salisbury screen absorber using resistively loaded spiral FSS. Microw. Opt. Technol. Lett. 2011, 53, 1538–1541. [Google Scholar] [CrossRef]
- Medvedev, V.V. An epsilon-near-zero-based Dallenbach absorber. Opt. Mater. 2022, 123, 111899. [Google Scholar] [CrossRef]
- Akram, S.; Ashraf, M.; Javid, A.; Abid, H.A.; Ahmad, S.; Nawab, Y.; Rasheed, A.; Xue, Z.; Nosheen, A. Recent advances in electromagnetic interference (EMI) shielding textiles: A comprehensive review. Synth. Met. 2023, 294, 117305. [Google Scholar] [CrossRef]
- Abdalla, I.; Cai, J.; Lu, W.; Yu, J.; Li, Z.; Ding, B. Recent progress on electromagnetic wave absorption materials enabled by electrospun carbon nanofibers. Carbon 2023, 213, 118300. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, S.Y.; Zhang, Y.; Park, S.J.; Gu, J. Carbon-Based Radar Absorbing Materials toward Stealth Technologies. Adv. Sci. 2023, 10, 2303104. [Google Scholar] [CrossRef]
- Zhao, N.; Zou, T.; Shi, C.; Li, J.; Guo, W. Microwave absorbing properties of activated carbon-fiber felt screens (vertical-arranged carbon fibers)/epoxy resin composites. Mater. Sci. Eng. B-Adv. 2006, 127, 207–211. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, P.; Zhou, W.; Hong, W.; Luo, H. Preparation and microwave absorbing properties of carbon fibers/epoxy composites with grid structure. J. Mater. Sci.-Mater. Electron. 2015, 26, 651–658. [Google Scholar] [CrossRef]
- Shah, A.; Ding, A.; Wang, Y.; Zhang, L.; Wang, D.; Muhammad, J.; Zhang, Z. Enhanced microwave absorption by arrayed carbon fibers and gradient dispersion of Fe nanoparticles in epoxy resin composites. Carbon 2016, 96, 987–997. [Google Scholar] [CrossRef]
- Li, X.; Zhu, L.; Sun, D.; Yang, Q.; Liu, Y.; Yu, W.; Lv, C. Preparation, microstructure and performance of interference microwave absorbing cermet composites with frequency–selective screens. Ceram. Int. 2022, 48, 34199–34209. [Google Scholar] [CrossRef]
- Lai, Y.; Liu, Y.; Ma, D. Automatically melting snow on airport cement concrete pavement with carbon fiber grille. Cold Reg. Sci. Technol. 2014, 103, 57–62. [Google Scholar] [CrossRef]
- Haghnejad, M.; Modarres, A. Effect of freeze-thaw cycles on the response of roller compacted concrete pavement reinforced by recycled polypropylene fibre under monotonic and cyclic loadings. Road Mater. Pavement 2021, 22, 2704–2720. [Google Scholar] [CrossRef]
- Sun, J.; Wang, W.; Yue, Q. Review on microwave-matter interaction fundamentals and efficient microwave-associated heating strategies. Materials 2016, 9, 231. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y. Research on Design of Components and Walking Synchronization System Based on Microwave Heating Snow Removal Deicing Vehicle. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2013. [Google Scholar]
- Gencel, O.; Karadag, O.; Oren, O.H.; Bilir, T. Steel slag and its applications in cement and concrete technology: A review. Constr. Build. Mater. 2021, 283, 122783. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wires Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Elkelawy, M.; Bastawissi, H.A.E.; Esmaeil, K.K.; Radwan, A.M.; Panchal, H.; Sadasivuni, K.K.; Israr, M. Maximization of biodiesel production from sunflower and soybean oils and prediction of diesel engine performance and emission characteristics through response surface methodology. Fuel 2020, 266, 117072. [Google Scholar] [CrossRef]
- Beg, S.; Akhter, S. Box–Behnken designs and their applications in pharmaceutical product development. In Design of Experiments for Pharmaceutical Product Development; Beg, S., Ed.; Springer: Singapore, 2021; Volume 1, pp. 77–85. [Google Scholar] [CrossRef]
- Zanko, L.M.; Hopstock, D.M. Minnesota Taconite as a Microwave-Absorbing Road Aggregate Material for Deicing and Pothole Patching Applications; University of Minnesota Duluth: Duluth, MN, USA, 2004. [Google Scholar]
- Karimi, M.M.; Amani, S.; Jahanbakhsh, H.; Jahangiri, B.; Alavi, A.H. Induced heating-healing of conductive asphalt concrete as a sustainable repairing technique: A review. Clean. Eng. Technol. 2021, 4, 100188. [Google Scholar] [CrossRef]
- Huang, H.; Xu, J. Effect of magnetite on concrete mechanics and microwave deicing performance. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042019. [Google Scholar] [CrossRef]
- Thomson, L.I.; Osinski, G.R.; Pollard, W.H. Application of the Brewster angle to quantify the dielectric properties of ground ice formations. J. Appl. Geophys. 2013, 99, 12–17. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Kim, S.; Kim, M.J.; Kim, D.; Shin, H.O. Self-healing capability of asphalt concrete with carbon-based materials. J. Mater. Res. Technol. 2019, 8, 827–839. [Google Scholar] [CrossRef]
- Gulisano, F.; Buasiri, T.; Apaza, F.R.A.; Cwirzen, A.; Gallego, J. Piezoresistive behavior of electric arc furnace slag and graphene nanoplatelets asphalt mixtures for self-sensing pavements. Autom. Constr. 2022, 142, 104534. [Google Scholar] [CrossRef]
- Witek-Krowiak, A.; Chojnacka, K.; Podstawczyk, D.; Dawiec, A.; Pokomeda, K. Application of response surface methodology and artificial neural network methods in modelling and optimization of biosorption process. Bioresour. Technol. 2014, 160, 150–160. [Google Scholar] [CrossRef]
- Méndez, A.A.; Pena, L.B.; Curto, L.M.; Sciorra, M.D.; Ulloa, R.M.; Aguilar, S.M.G.; Gallego, S.M. Optimization of recombinant maize CDKA; 1 and CycD6; 1 production in Escherichia coli by response surface methodology. Protein Expr. Purif. 2020, 165, 105483. [Google Scholar] [CrossRef]
- Notani, M.A.; Arabzadeh, A.; Ceylan, H.; Kim, S.; Gopalakrishnan, K. Effect of carbon-fiber properties on volumetrics and ohmic heating of electrically conductive asphalt concrete. J. Mater. Civ. Eng. 2019, 31, 04019200. [Google Scholar] [CrossRef]
- Luukkonen, O.; Simovski, C.; Granet, G.; Goussetis, G.; Lioubtchenko, D.; Raisanen, A.V.; Tretyakov, S.A. Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Trans. Antennas Propag. 2008, 56, 1624–1632. [Google Scholar] [CrossRef]
- Anu, K.S.; Vishnumurthy, K.A.; Mahesh, A.; Natarajan, K. Carbon fiber-reinforced, activated carbon-embedded copper oxide nanoparticles/epoxy hybrid composites for EMI shielding in aircraft applications. Polym. Bull. 2024, 1–28. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Fathy, I.N.; Tayeh, B.A.; Almeshal, I. Using artificial neural networks for predicting mechanical and radiation shielding properties of different nano-concretes exposed to elevated temperature. Constr. Build. Mater. 2022, 324, 126663. [Google Scholar] [CrossRef]




| Properties | Values | |
|---|---|---|
| Density/(g/cm3) | 3.20 | |
| Average particle size/µm | 20.80 | |
| Setting time/min | Initial | 141.00 |
| Final | 233.00 | |
| Flexural strength/MPa | 3 d | 3.80 |
| 28 d | 6.20 | |
| Compressive strength/MPa | 3 d | 18.90 |
| 28 d | 35.80 | |
| Main chemical composition/% | CaO | 60.10 |
| SiO2 | 20.80 | |
| Aggregates | Bulk Density/(g/cm3) | Apparent Density/(g/cm3) | Water Absorption/% | Soil Content/% | Fineness Modulus |
|---|---|---|---|---|---|
| Sand | 1.54 | 2.36 | 0.58 | 0.60 | 1.8 |
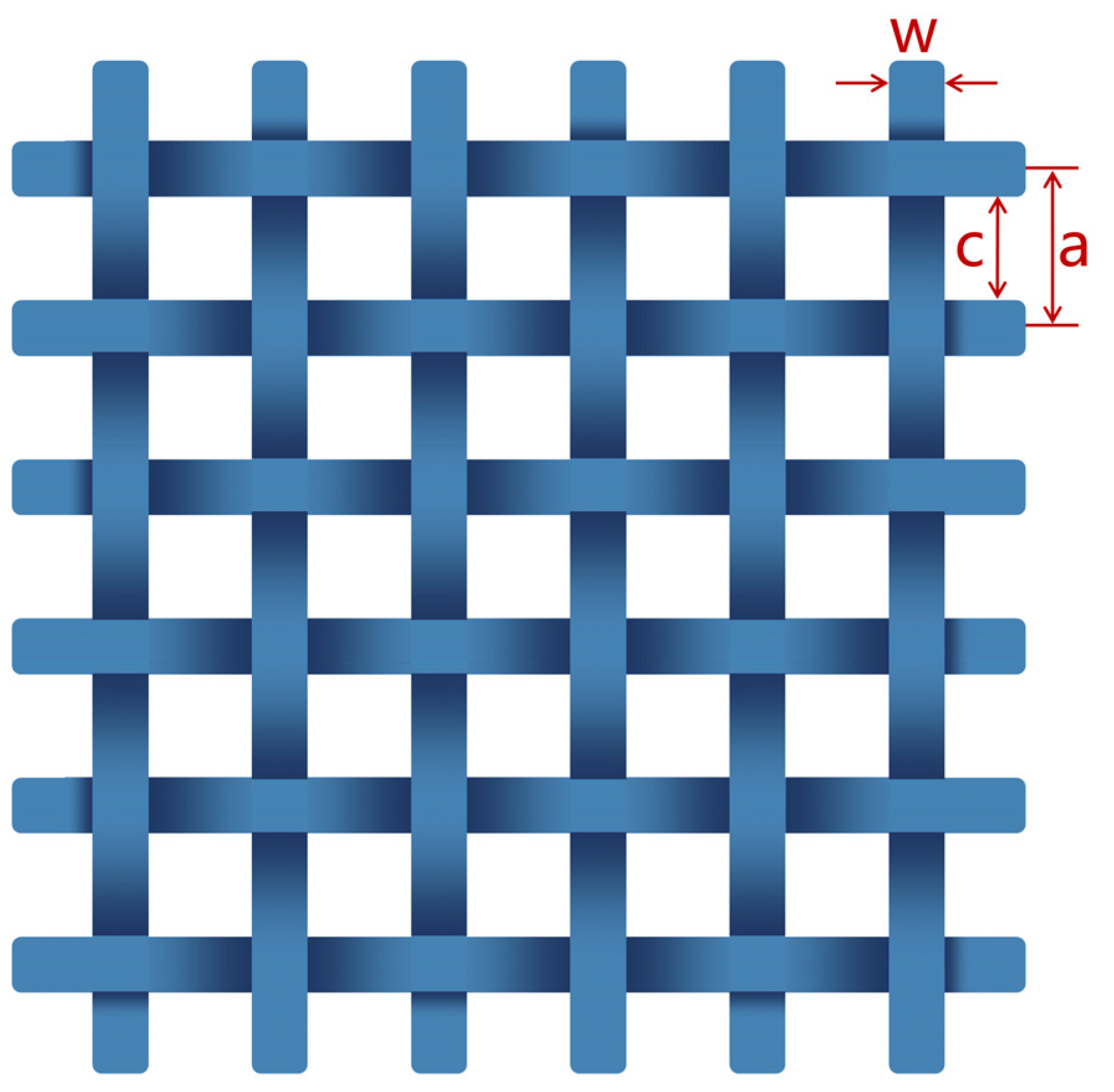
| Type | Period (a)/mm | Space (c)/mm | Width (w)/mm |
|---|---|---|---|
| CFS-1 | 10 | 5 | 5 |
| CFS-2 | 12 | 10 | 2 |
| CFS-3 | 20 | 15 | 5 |
| Group | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Depth of CFS(d)/mm | / | 5 | 5 | 5 | 10 | 15 |
| Type of CFS | / | CFS-1 | CFS-2 | CFS-3 | CFS-1 | CFS-1 |
| Variable | Code | Levels | ||
|---|---|---|---|---|
| −1.0 | 0 | +1.0 | ||
| Space/mm | A | 5 | 10 | 15 |
| Depth/mm | B | 5 | 10 | 15 |
| Width/mm | C | 2 | 3.5 | 5 |
| No. | Variable | Response | ||
|---|---|---|---|---|
| A | B | C | SHR/(°C/s) | |
| 1 | 0 | 0 | 0 | 0.79 |
| 2 | 0 | 0 | 0 | 0.79 |
| 3 | 0 | 0 | 0 | 0.79 |
| 4 | 0 | 0 | 0 | 0.79 |
| 5 | 0 | 1.0 | −1.0 | 0.7 |
| 6 | 1.0 | 1.0 | 0 | 0.68 |
| 7 | 0 | 0 | 0 | 0.79 |
| 8 | 0 | −1.0 | 1.0 | 0.6 |
| 9 | −1.0 | 0 | −1.0 | 0.82 |
| 10 | −1.0 | 1.0 | 0 | 0.78 |
| 11 | 0 | −1.0 | −1.0 | 0.6 |
| 12 | 1.0 | 0 | −1.0 | 0.71 |
| 13 | −1.0 | −1.0 | 0 | 0.41 |
| 14 | 1.0 | −1.0 | 0 | 0.71 |
| 15 | 0 | 1.0 | 1.0 | 0.7 |
| 16 | 1.0 | 0 | 1.0 | 0.71 |
| 17 | −1.0 | 0 | 1.0 | 0.82 |
| Specimen | Peak Value/°C | Position of Peak Value/mm | FWHM/mm |
|---|---|---|---|
| A | 8.19 | 2.05 | 21.5 |
| B | 13.08 | 1.12 | 10.63 |
| E | 17.13 | 2.8 | 15.68 |
| F | 13.05 | 3.55 | 17.17 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Remark |
|---|---|---|---|---|---|---|
| Model | 0.1511 | 9 | 0.0168 | 4.80 | 0.0254 | significant |
| A | 0.0000 | 1 | 0.0000 | 0.0143 | 0.9082 | |
| B | 0.0364 | 1 | 0.0364 | 10.41 | 0.0145 | |
| AB | 0.0400 | 1 | 0.0400 | 11.43 | 0.0117 | |
| AC | 0.0000 | 1 | 0.0000 | 0.0000 | 1.0000 | |
| BC | 0.0000 | 1 | 0.0000 | 0.0000 | 1.0000 | |
| A2 | 0.0009 | 1 | 0.0009 | 0.2707 | 0.6189 | |
| B2 | 0.0712 | 1 | 0.0712 | 20.33 | 0.0028 | |
| C2 | 0.0004 | 1 | 0.0004 | 0.1203 | 0.7389 | |
| Residual | 0.0245 | 7 | 0.0035 | |||
| Lack of fit | 0.0245 | 3 | 0.0082 | |||
| Pure error | 0.0000 | 4 | 0.0000 | |||
| Cor total | 0.1756 | 16 | 0.1756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhao, P.; Jing, M.; Luo, X.; Guo, J.; Zhang, F. Enhanced Microwave Deicing Capacity of Cement Pavement with Carbon Fiber Screens. Materials 2024, 17, 1488. https://doi.org/10.3390/ma17071488
Li J, Zhao P, Jing M, Luo X, Guo J, Zhang F. Enhanced Microwave Deicing Capacity of Cement Pavement with Carbon Fiber Screens. Materials. 2024; 17(7):1488. https://doi.org/10.3390/ma17071488
Chicago/Turabian StyleLi, Jiangjiang, Peng Zhao, Minghai Jing, Xiao Luo, Jiaqi Guo, and Fei Zhang. 2024. "Enhanced Microwave Deicing Capacity of Cement Pavement with Carbon Fiber Screens" Materials 17, no. 7: 1488. https://doi.org/10.3390/ma17071488
APA StyleLi, J., Zhao, P., Jing, M., Luo, X., Guo, J., & Zhang, F. (2024). Enhanced Microwave Deicing Capacity of Cement Pavement with Carbon Fiber Screens. Materials, 17(7), 1488. https://doi.org/10.3390/ma17071488






