Crashworthiness of 3D Lattice Topologies under Dynamic Loading: A Comprehensive Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Lattice Geometry and Design
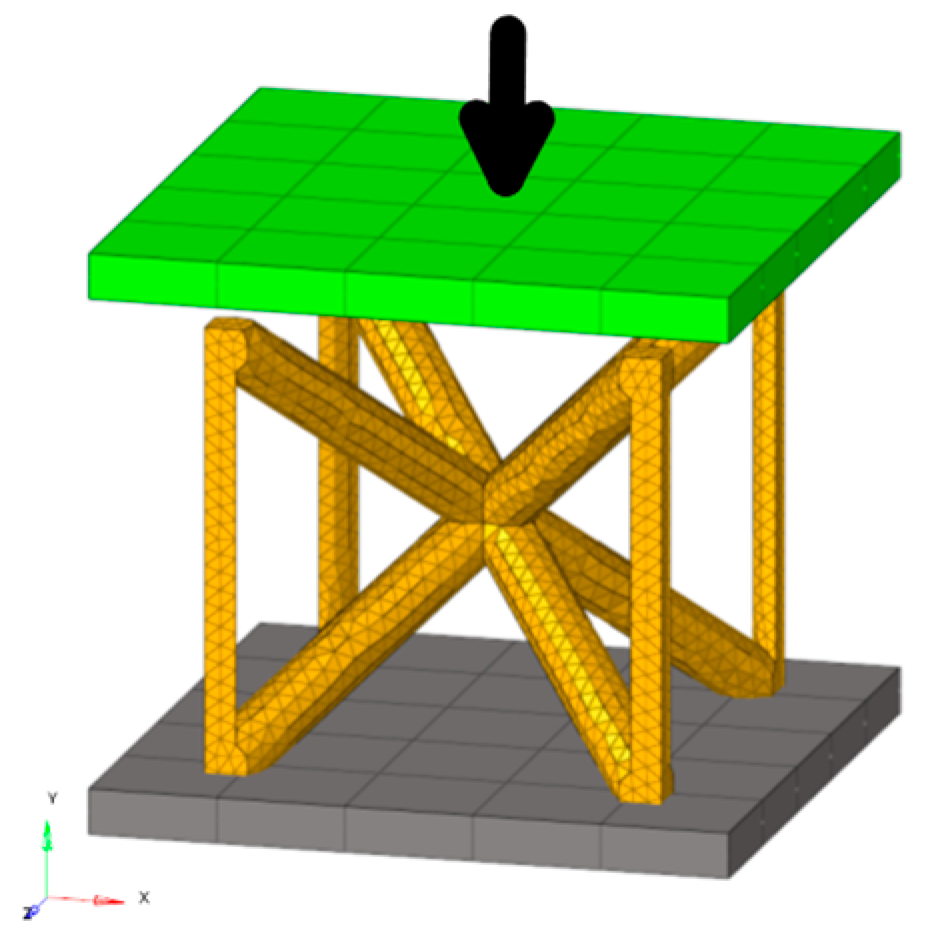
2.2. Finite Element Model
2.2.1. Initial Model Creation
2.2.2. Unit Cell Model
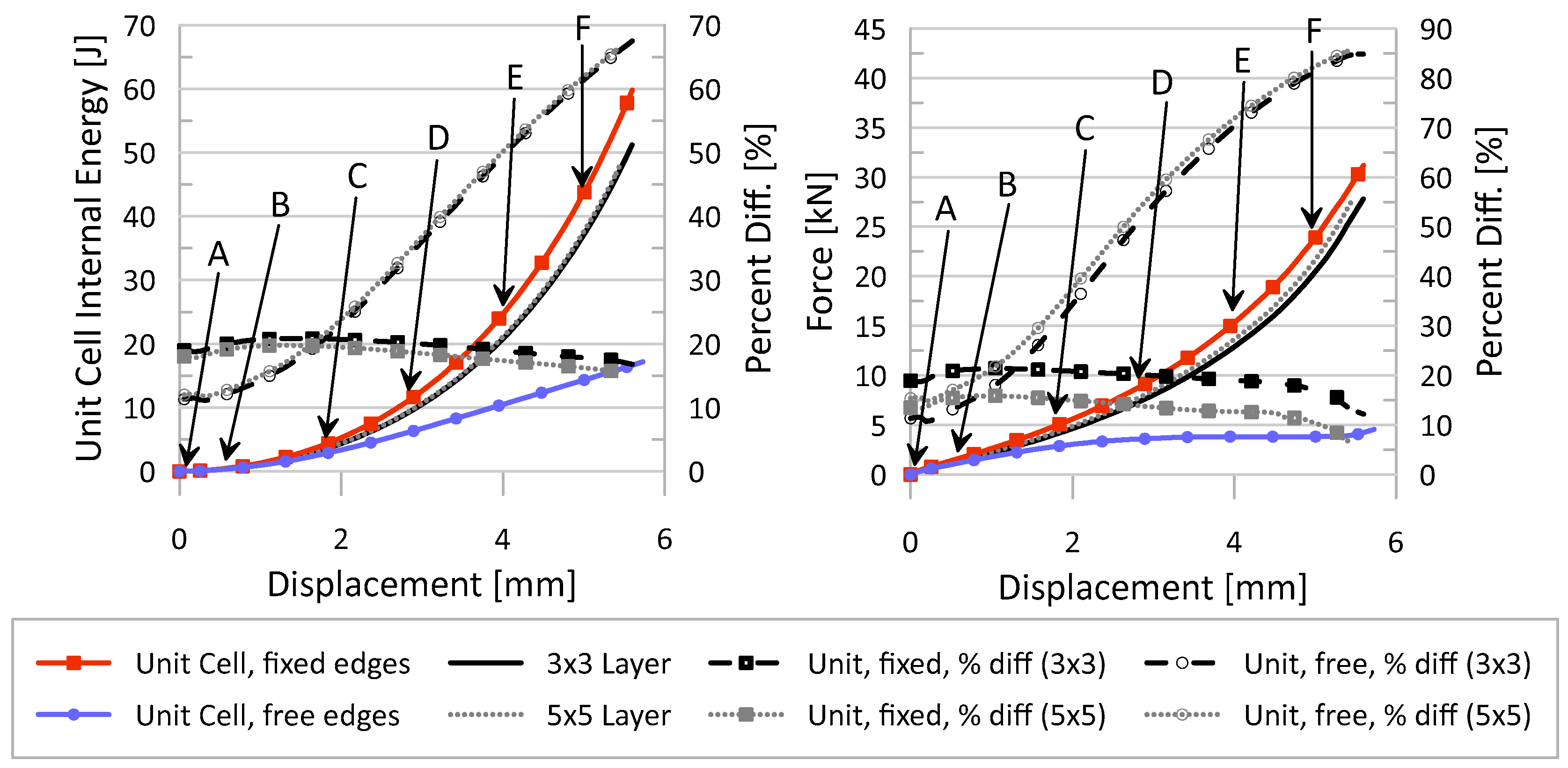
2.2.3. Boundary Conditions
2.2.4. Material and Failure Model
2.3. Design of Experiments
3. Results
3.1. Data Analysis and Crashworthiness Parameters
3.2. Numerical Model Results and Discussion
3.2.1. Effect of Initial KE
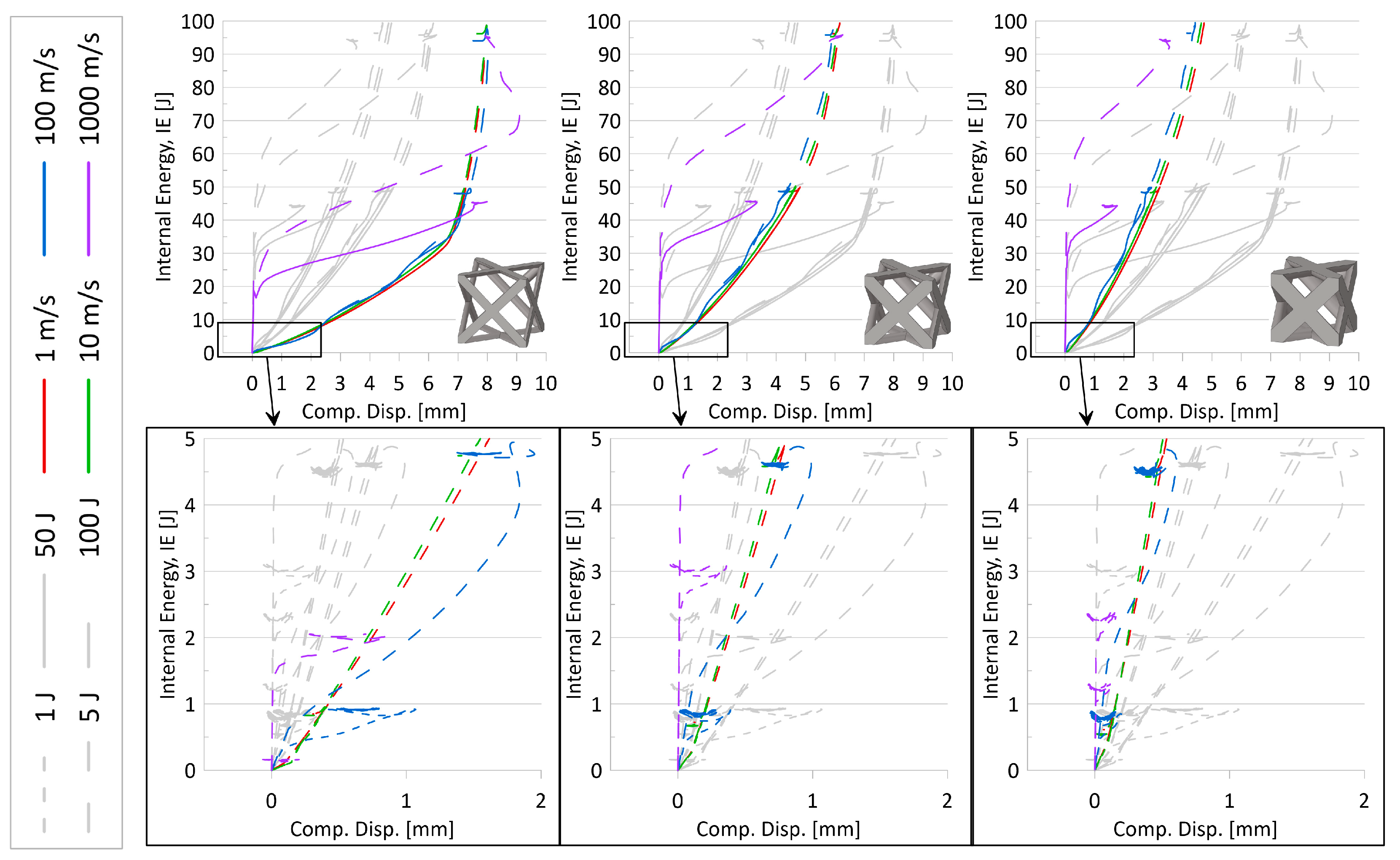
- It was noted that simulations with lower initial impactor kinetic energies mimicked the initial behavior of the larger initial KE, particularly for simulations with initial impactor speeds of 100 m/s or less. That is, the results suggest that running simulations at a larger initial KE could still predict the behavior of the simulations at a lower initial KE. A set of internal energy over compression displacement curves for the AFCC topology (at all three relative densities) is provided in Figure 7 to illustrate such a phenomenon. In the top graphs of this figure, it is evidently seen that the lower initial impact energy curves (solid lines) follow the path of the higher initial internal energy curves (dashed lines) up until the system limit is reached and the higher energy curves continue.
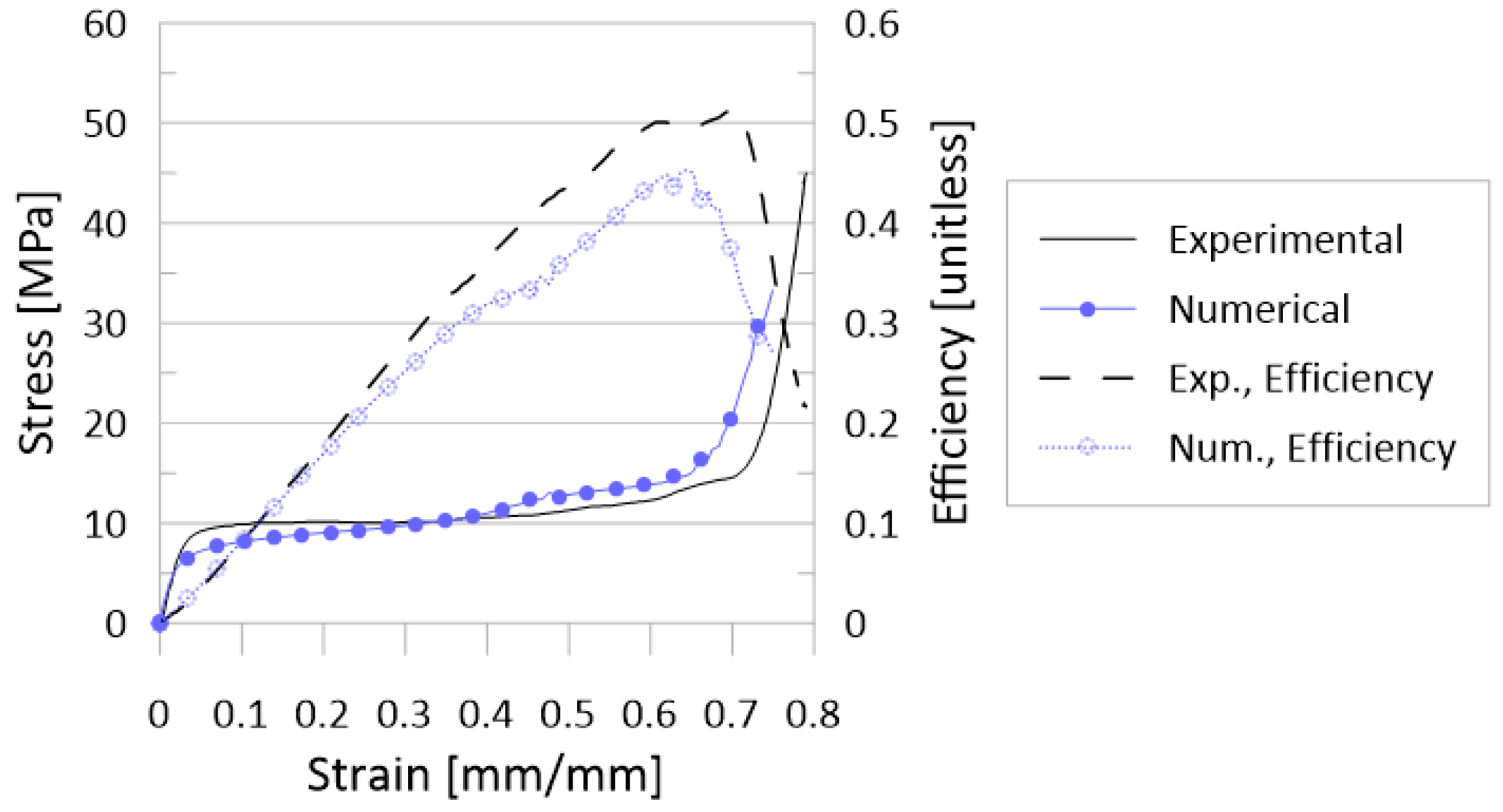
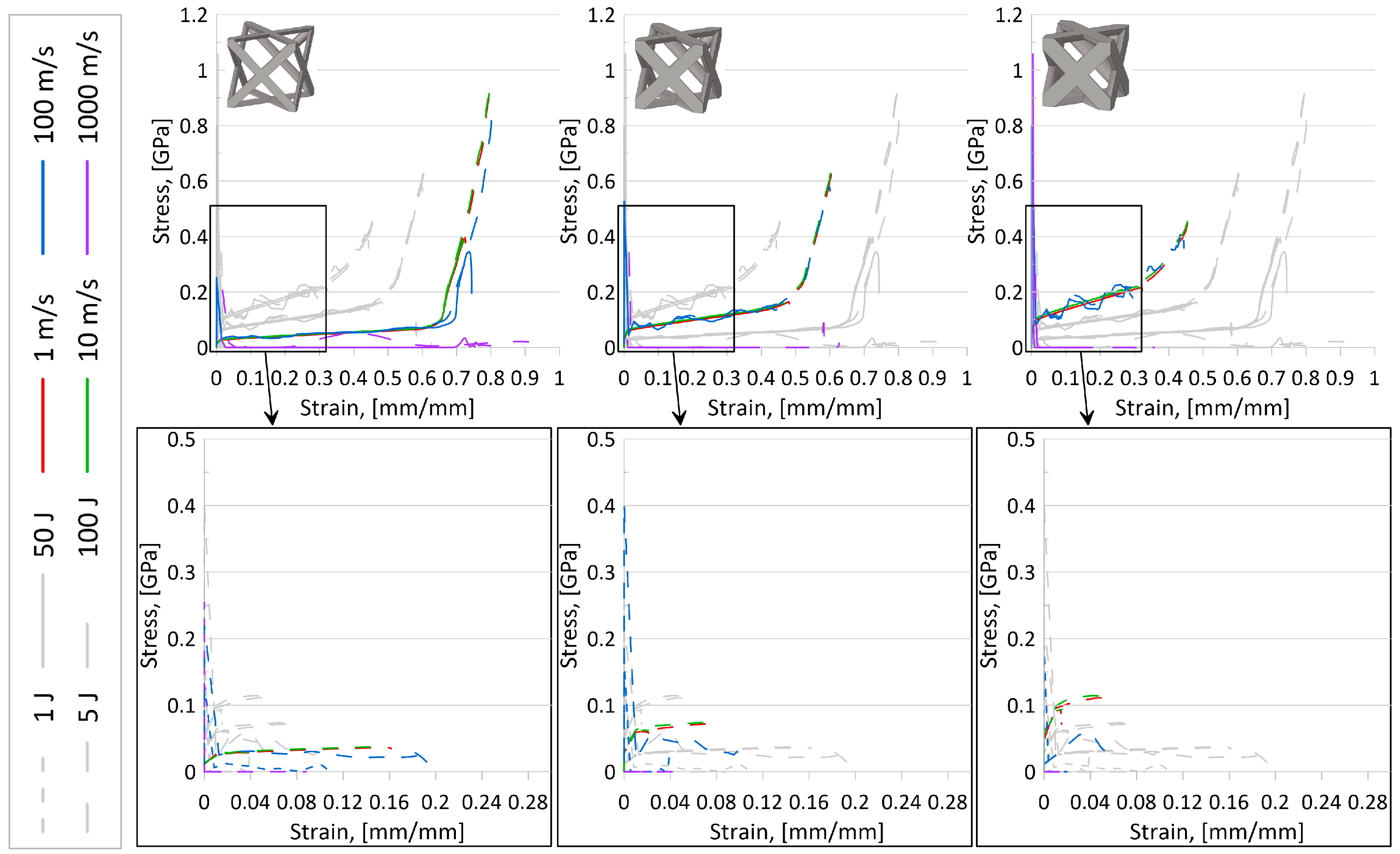
- In looking at stress–strain results, it was revealed that initial impactor KE of 1 J and 5 J was not sufficiently large to reveal complete elastic-plateau-densification stress–strain curves and a demonstratory set of stress–strain curves for the AFCC topology is provided in Figure 8. As a result, calculated crashworthiness parameters—such as densification strain or energy absorption—for the simulations with those lower initial KE would not accurately reflect the behavior and capabilities of the topology. It should be noted that for some topologies, even an initial impactor KE of 50 J was not always sufficient to reveal the complete elastic-plateau-densification characteristics expected of a stress–strain curve for lattice materials, particularly at higher relative densities.
3.2.2. Effect of Speed
- As illustrated in Figure 7, despite the strain-sensitivity of the material, up to initial impactor speeds of approximately 10 m/s, there is very little difference in results, suggesting that at those low speeds, the sensitivity of the material to strain rate variations is negligible. While it also appears that data from simulations with initial impactor speeds of 100 m/s is also insignificantly different from the two lower speed levels in those plots, stress–strain plots for certain topologies (as an example, in Figure 8) did suggest that results from 10 m/s could not always be used to accurately predict results for a speed of 100 m/s.
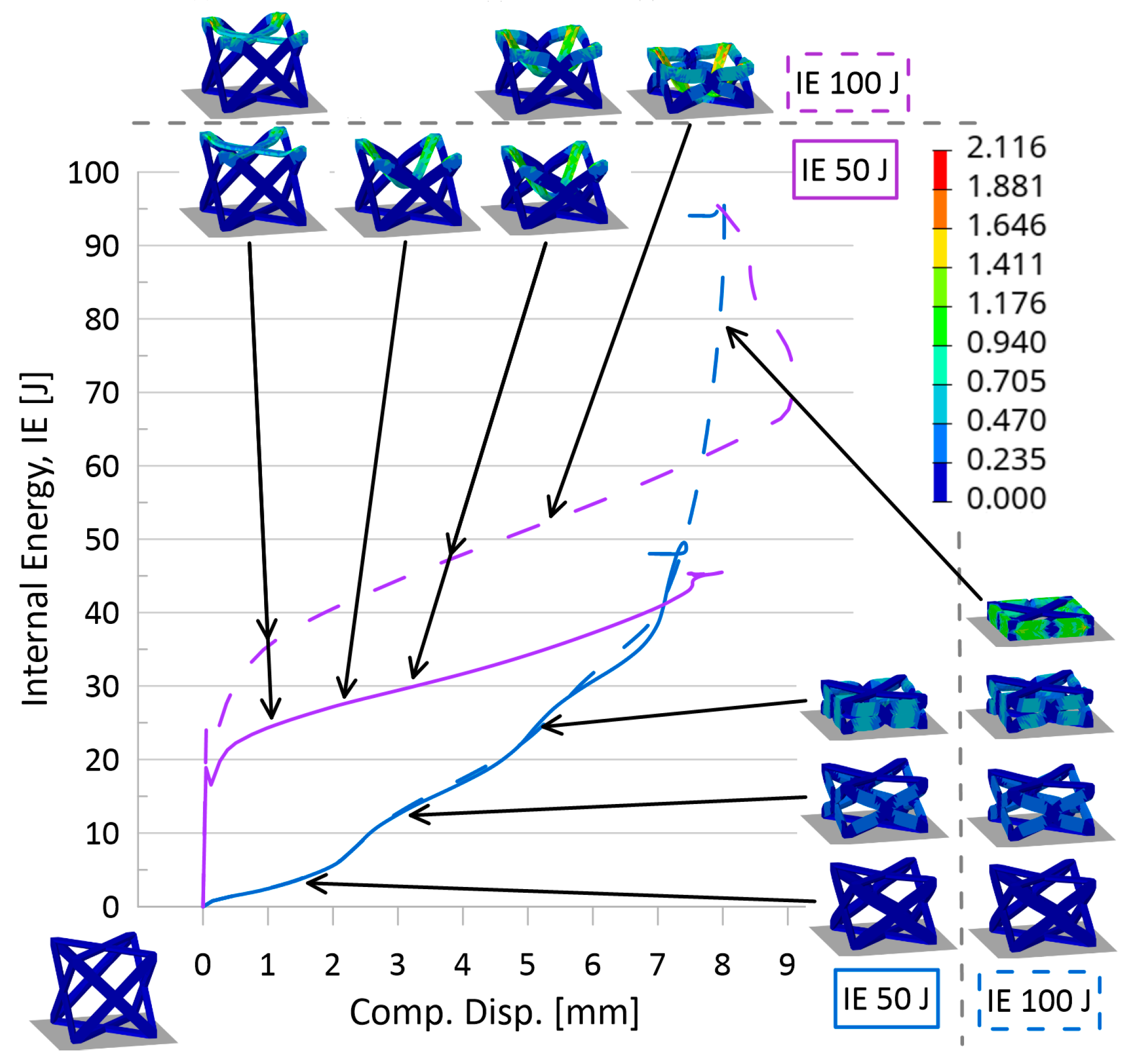
- Also seen from stress–strain results was the indication that the current model setup was insufficient to appropriately reveal topology behavior at an initial impactor speed of 1000 m/s. While the internal energy over the compression event curves (Figure 7) and associated simulation animations (Figure 9) for numerical models at initial impactor speeds at 1000 m/s appear to illustrate the phenomenon of layer-by-layer collapse at high impact speeds (versus all layers deforming in the same or similar manner during a quasi-static or low-speed compression event), the jump in magnitude from 100 m/s to 1000 m/s results in erratic time-history behavior, bringing into question the reliability and credibility of the data. Additionally, with only one unit cell contained in this model, such a conclusion would realistically require multiple layers. Coupled with the stress–strain result observations, data for numerical models with impact speeds of 1000 m/s were perceived to have a high level of uncertainty.
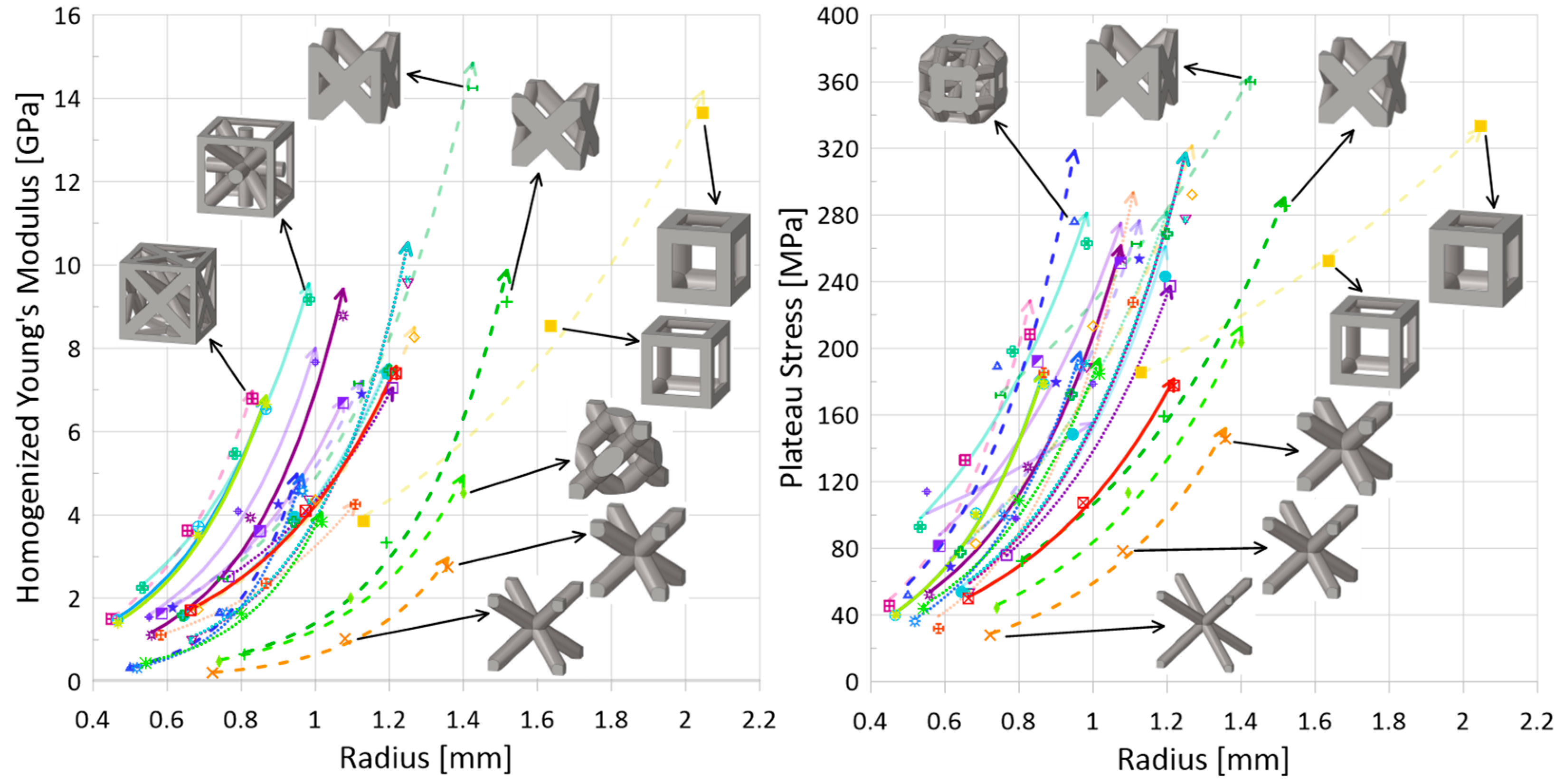
3.2.3. Effect of Relative Density
 ) and FCC-Z (
) and FCC-Z ( ), that have higher homogenized strengths for a given relative density also have higher resulting plateau stresses, and understandably, as relative density increases, the plateau stress increases as well. Notably, the rate of increase for the tesseract topology (
), that have higher homogenized strengths for a given relative density also have higher resulting plateau stresses, and understandably, as relative density increases, the plateau stress increases as well. Notably, the rate of increase for the tesseract topology ( ) is lower in comparison to other topologies. While the data for the 10 m/s speed and initial impact energy of 100 J is presented in Figure 10, it is noted that, except for actual numerical result values, the trends and relations between topologies are generally the same for a speed of 100 m/s.
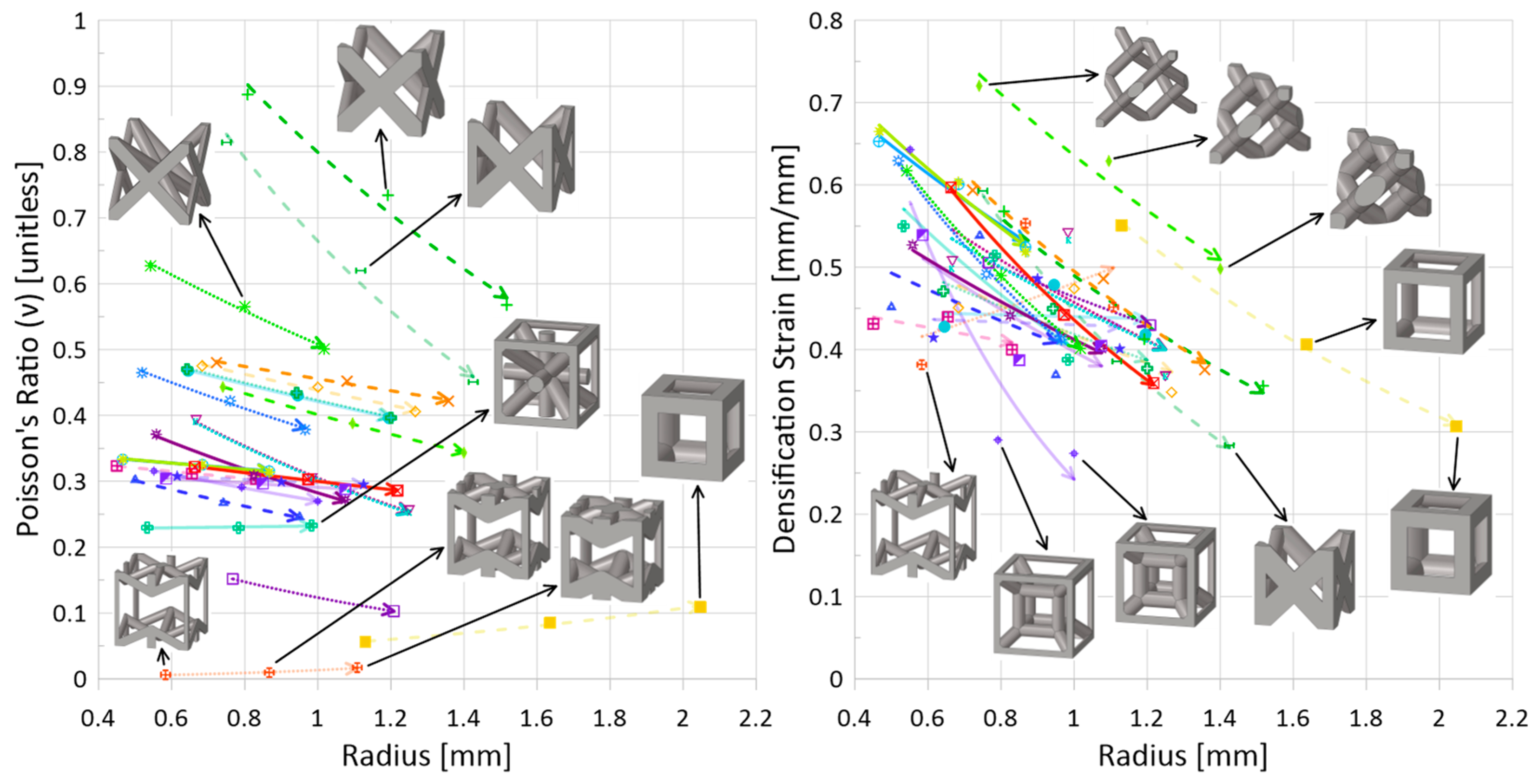
) is lower in comparison to other topologies. While the data for the 10 m/s speed and initial impact energy of 100 J is presented in Figure 10, it is noted that, except for actual numerical result values, the trends and relations between topologies are generally the same for a speed of 100 m/s.- Decrease in densification strain. Shown in Figure 11 (right), this statement is true for all topologies, except auxetic (
). The expectation for this decrease with an increase in relative density is understandable if one considers densification strain to represent the point at which the lattice has been compressed and begins behaving like the solid parent material; at lower relative densities, the lattice must be compressed more before it self-contacts and can behave as a monolithic material. Thus, the auxetic behavior is intriguing and will be discussed further in the following subsection.
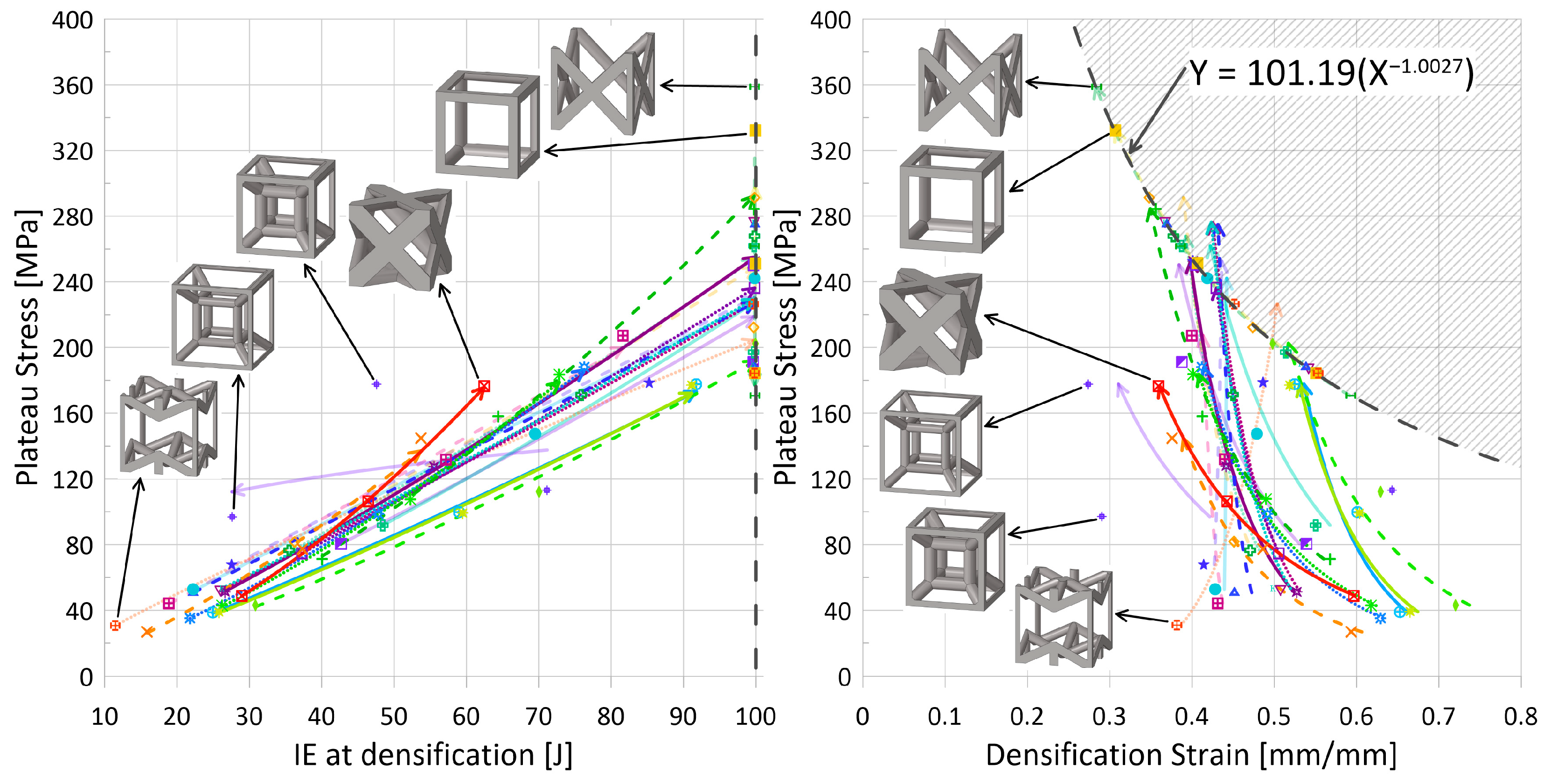
- Increase in absorbed energy up to densification strain. Such a trend can be seen in Figure 12 (left). Since absorbed energy is related to both stress and strain, and it has been observed that the plateau stress increased with increasing relative density, this result is also unsurprising. However, given that the rate at which the plateau stress increased for the tesseract topology was notably lower in comparison to other topologies, the absorbed energy actually decreased with an increase in relative density from 0.1 to 0.2; its decrease in densification strain was enough to cause a shift in direction. Additionally, the two highest-strength (and highest plateau-stress) topologies—cubic and FCC-Z—had a consistent internal energy at densification regardless of relative density; had the initial impact energy been increased beyond 100 J, it may have been possible for the trend of increasing IE for increasing relative density to be observed.
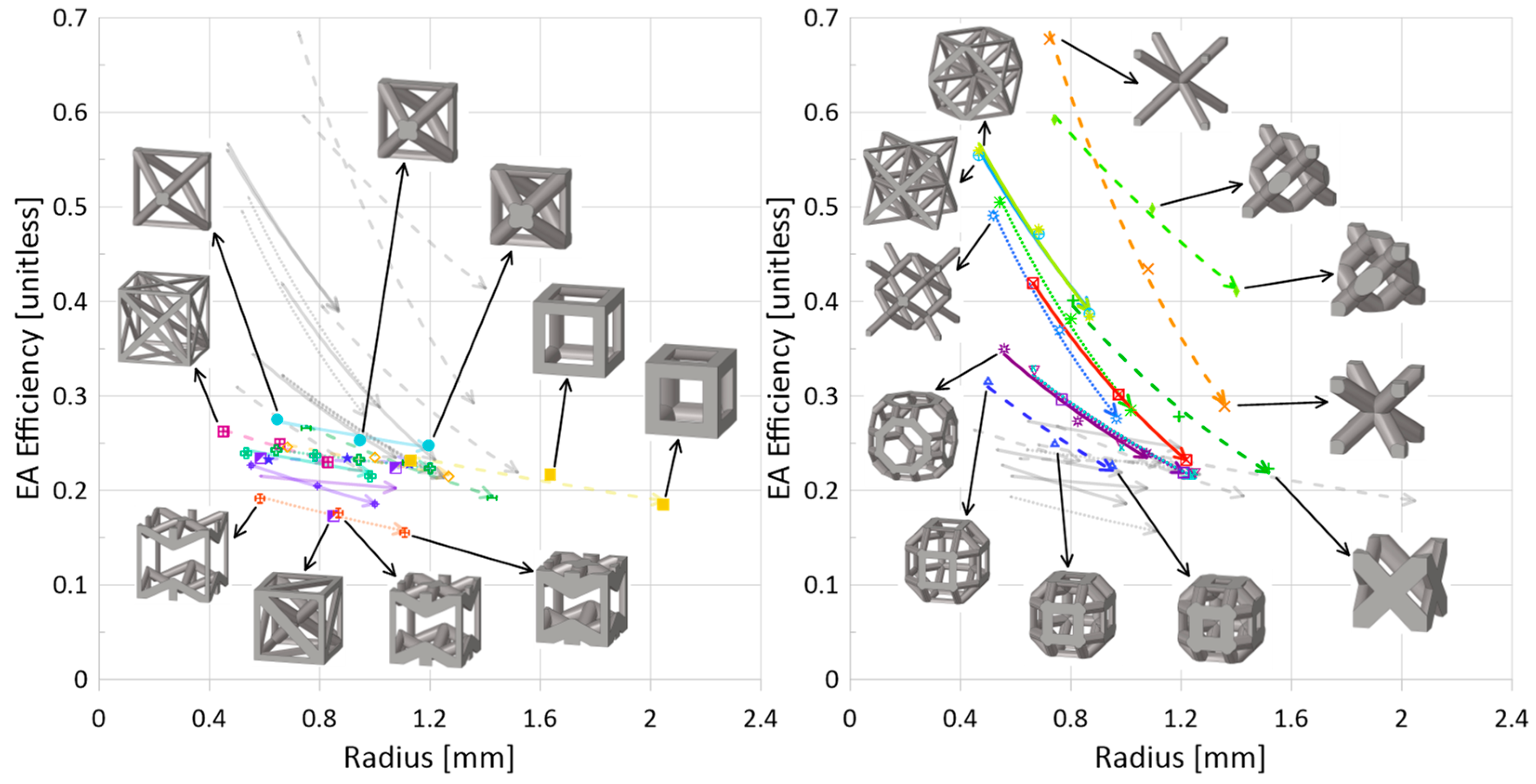
- Decrease in energy absorption efficiency. This decreasing trend can be seen in Figure 13, and more discussion regarding the EA efficiency is provided in the following subsection with regards to whether there are struts aligned in the loading direction.
3.2.4. Effect of Topology
- Bending versus Stretching. While bending-dominated cellular materials are known to be better energy absorbers and be compliant (lower strength and stiffness), and stretching-dominated cellular materials have higher stiffness and strength, the dynamic data collected for this work using the numerical model set up described suggests no noticeable delineation between these two categories of topologies (nor mixed-mode topologies), though it is noted that absorbed energy is measured up to the densification of the given topology, not up to a stationary strain point. Additionally, as has been noted by others in the literature, it appears that there is a non-negligible influence of the strut orientation with respect to the loading direction when it comes to deformation modes, which is not accounted for in Maxwell’s criterion and can increase the strength of otherwise bending-dominated topologies.
- Strut(s) aligned in loading direction. With regards to energy absorption efficiency (Figure 13), there is, quite interestingly, a clear separation of performance when it comes to a topology having strut(s) aligned in the loading direction versus a topology not having any struts aligned in that direction. For those topologies with struts aligned in the loading direction—
, Figure 13 (left)—the resulting maximum energy absorption efficiency during impact is lower than for topologies that do not have struts aligned in that direction (Figure 13 (right),
). For plateau stress (Figure 10 (right)), it is obvious that the cubic unit cell—which has struts aligned in the compression direction and fewer struts, leading to a larger overall strut radius to reach a given relative density—has a greater strength than other topologies when considering only a given relative density. Indeed, the topology that has the next highest plateau stress for a given relative density is FCC-Z, which also has struts aligned in the impact direction and has a similarly large radius for struts given the fewer total number of struts compared to other topologies (not including cubic). The BCC (
) topology, which has no struts aligned in the compression direction and is generally bending-dominated, has the lowest strength.
- Topology Highlight: Auxetic (
). Unlike other topologies, the densification strain increased with an increase in relative density for the auxetic topology. The Poisson’s ratio of this topology in relation to other topologies—Figure 11 (left)—is notably significantly smaller, almost equal to zero (generally, auxetic materials are those materials with negative Poisson’s ratio, unlike other types of topologies).
- Topology Highlight: Cubic (
) and FCC-Z (
). These two topologies had noticeably larger plateau stresses for a given relative density than other topologies. For a constant relative density and unit cell height, these two topologies have the largest strut radius as compared to other topologies with struts aligned in the impact direction. Thus, the combination of large strut radius and struts aligned in the loading direction seems to have allowed for an increase in overall strength and higher plateau stress during impact. Notably, observing the response of the FCC-Z, FCC (
), diamond (
), and BCC (
) topologies at a constant strut radius of approximately 1.4 mm in Figure 10 (left or right), it is the topology with struts aligned directly in the loading direction (FCC-Z) that has the highest Young’s modulus and plateau stress, whereas the others reach less than 70% of those properties of the FCC-Z topology. Also interesting is that the cubic topology requires a larger strut radius to reach a similar strength and plateau stress as compared to the FCC-Z topology; at a radius of approximately 1.4 mm, it yields similar results to the FCC, diamond, and BCC topologies.
- Topology Highlight: Tesseract (
). The tesseract topology was noted to have a lower rate of increase in plateau stress for an increase in strut radius (thus, relative density) (Figure 10 (right)). Together with a decrease in densification strain from a relative density of 0.1 to 0.2, the absorbed energy up to densification actually decreased with the increase in relative density (71.2 J vs. 27.6 J). However, with an additional 10% relative density from 0.2 to 0.3, the absorbed energy also increased (to 47.6 J), the results of which are plotted in Figure 12 (left).
- Topology Highlight: Octahedron (
), Truncated Cube (
), Truncatedcuboctahedron (
), Rhombicuboctahedron (
). Of the topologies with struts aligned in the impact direction, the octahedron topology is the only one that has two half-struts aligned in that direction, as opposed to four-quarter struts. Interestingly, the energy absorption efficiency results from Figure 13 (left) place the octahedron topology along the strut-no strut division. Also close to this split are the truncated cube, truncatedcuboctahedron, and rhombicuboctahedron (Figure 13 (right)), which do not have full struts aligned in the impact direction (i.e., a strut with a length equal to the unit height) but do have smaller-length struts aligned in the impact direction. Such an observation seems to suggest that while it is possible to observe a generally distinct division between the energy absorption efficiency results of Figure 13 based on whether or not there are struts aligned directly in the loading direction, the amount and length of those struts can shift the efficiency.
3.2.5. Discussion Concluding Remarks
 ) at a relative density of 10% is almost equivalent to the plateau stress of an AFCC topology (
) at a relative density of 10% is almost equivalent to the plateau stress of an AFCC topology ( ) at a relative density of 30%, allowing for a reduction in structure weight; Figure 11 (right) indicates that there is a minimal change in densification strain for changing relative density for the Xgrid topology (
) at a relative density of 30%, allowing for a reduction in structure weight; Figure 11 (right) indicates that there is a minimal change in densification strain for changing relative density for the Xgrid topology ( ); and Figure 13 shows that by simply removing the struts aligned in the impact direction, the energy absorption increases.
); and Figure 13 shows that by simply removing the struts aligned in the impact direction, the energy absorption increases.4. Conclusions
- Despite the strain-rate-sensitive material properties of the SLM steel alloy, changes in impact performance from 1 m/s to 10 m/s were negligible (for the same initial impact energy). There were some changes between speeds of 10 m/s and 100 m/s, but general trends were similar regardless of the data set observed. At speeds of 1000 m/s, significant performance changes were observed, but it was determined that there was a large amount of uncertainty in results given the current numerical model setup—single unit cell with periodic boundary conditions—and that a multi-layered, larger cluster of cells would probably be better suited to illustrate the layer-by-layer collapse observed for high impact speeds with lattice materials.
- Increasing initial impact energy allowed for a better representation of the elastic-plateau-densification stress–strain curve characteristic of lattice materials. Lower impact energies whose stress–strain curves did not reach densification simply revealed a portion of the stress–strain curve; higher energies were better for performance comparison, given more representative values for densification strain and energy absorption up to densification.
- For increasing relative density, it was generally seen that the plateau stress increased, the densification strain decreased, the energy absorbed at densification increased, and the energy absorption efficiency decreased. A few exceptions include the auxetic and tesseract topologies.
- It was clear that topologies with struts aligned in the impact direction had lower energy absorption efficiencies as compared to topologies that had no struts aligned in that direction.
- Based on the numerical model setup, there was no clear separation in performance based on bending, stretching, or mixed deformation modes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashby, M.F. The Properties of Foams and Lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 9780521499118. [Google Scholar]
- Helou, M.; Kara, S. Design, Analysis and Manufacturing of Lattice Structures: An Overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Tsopanos, S.; Mines, R.A.W.; McKown, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The Influence of Processing Parameters on the Mechanical Properties of Selectively Laser Melted Stainless Steel Microlattice Structures. J. Manuf. Sci. Eng. 2010, 132, 0410111–04101112. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical Evaluation of Porous Titanium (Ti6Al4V) Structures with Electron Beam Melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Banhart, J. Manufacture, Characterisation and Application of Cellular Metals and Metal Foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Ashby, M.F. The Mechanical Properties of Cellular Solids. Metall. Trans. 1983, 14A, 1755–1769. [Google Scholar] [CrossRef]
- Bhate, D.; Penick, C.A.; Ferry, L.A.; Lee, C. Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs 2019, 3, 19. [Google Scholar] [CrossRef]
- Fleck, N.A.; Deshpande, V.S.; Ashby, M.F. Micro-Architectured Materials: Past, Present and Future. Proc. R. Soc. A 2010, 466, 2495–2516. [Google Scholar] [CrossRef]
- Mueller, J.; Matlack, K.H.; Shea, K.; Daraio, C. Energy Absorption Properties of Periodic and Stochastic 3D Lattice Materials. Adv. Theory Simul. 2019, 2, 1900081. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective Properties of the Octet-Truss Lattice Material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Evans, A.G.; Hutchinson, J.W.; Fleck, N.A.; Ashby, M.F.; Wadley, H.N.G. The Topological Design of Multifunctional Cellular Metals. Prog. Mater. Sci. 2001, 46, 309–327. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Raymont, D. Advanced Lightweight 316L Stainless Steel Cellular Lattice Structures Fabricated via Selective Laser Melting. Mater. Des. 2014, 55, 533–541. [Google Scholar] [CrossRef]
- Park, K.-M.; Min, K.-S.; Roh, Y.-S. Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials 2022, 15, 97. [Google Scholar] [CrossRef] [PubMed]
- Bhate, D. Four Questions in Cellular Material Design. Materials 2019, 12, 1060. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Ren, X.; Zhao, T.; Li, Y.; Xiao, D.; Fang, D. Numerical and Theoretical Analysis of the Dynamic Mechanical Behaviour of a Modified Rhombic Dodecahedron Lattice Structure. Int. J. Mech. Mater. Des. 2020, 17, 271–283. [Google Scholar] [CrossRef]
- Cao, X.; Xiao, D.; Li, Y.; Wen, W.; Zhao, T.; Chen, Z.; Jiang, Y.; Fang, D. Dynamic Compressive Behavior of a Modified Additively Manufactured Rhombic Dodecahedron 316L Stainless Steel Lattice Structure. Thin-Walled Struct. 2020, 148, 106586. [Google Scholar] [CrossRef]
- Wadley, H.N.G. Cellular Metals Manufacturing. Adv. Eng. Mater. 2002, 4, 726–733. [Google Scholar] [CrossRef]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.W.; Hazell, P.J. Metallic Microlattice Materials: A Current State of the Art on Manufacturing, Mechanical Properties and Applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Yuan, S.; Chua, C.K.; Zhou, K. 3D-Printed Mechanical Metamaterials with High Energy Absorption. Adv. Mater. Technol. 2019, 4, 1800419. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical Properties and Energy Absorption Capability of Functionally Graded F2BCC Lattice Fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Mieszala, M.; Hasegawa, M.; Guillonneau, G.; Bauer, J.; Raghavan, R.; Frantz, C.; Kraft, O.; Mischler, S.; Michler, J.; Philippe, L. Micromechanics of Amorphous Metal/Polymer Hybrid Structures with 3D Cellular Architectures: Size Effects, Buckling Behavior, and Energy Absorption Capability. Small 2017, 13, 1602514. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy Absorption in Lattice Structures in Dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.M. Advanced Lattice Material with High Energy Absorption Based on Topology Optimisation. Mech. Mater. 2020, 148, 103536. [Google Scholar] [CrossRef]
- Nasrullah, A.I.H.; Santosa, S.P.; Dirgantara, T. Design and Optimization of Crashworthy Components Based on Lattice Structure Configuration. Structures 2020, 26, 969–981. [Google Scholar] [CrossRef]
- Wang, P.; Bian, Y.; Yang, F.; Fan, H.; Zheng, B. Mechanical Properties and Energy Absorption of FCC Lattice Structures with Different Orientation Angles. Acta Mech. 2020, 231, 3129–3144. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Tyas, A.; Goodall, R.; Askes, H. Energy Absorption in Lattice Structures in Dynamics: Nonlinear FE Simulations. Int. J. Impact Eng. 2017, 102, 1–15. [Google Scholar] [CrossRef]
- Jin, N.; Wang, F.; Wang, Y.; Zhang, B.; Cheng, H.; Zhang, H. Failure and Energy Absorption Characteristics of Four Lattice Structures under Dynamic Loading. Mater. Des. 2019, 169, 107655. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of Compressive Properties of SLM-Fabricated Multi-Layer Lattice Structures by Experimental Test and μ-CT-Based Finite Element Analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-Manufactured Metallic Micro-Lattice Materials for High Specific Energy Absorption under Static and Dynamic Loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Giorgio, I.; dell’Isola, F.; Steigmann, D.J. Second-Grade Elasticity of Three-Dimensional Pantographic Lattices: Theory and Numerical Experiments. Contin. Mech. Thermodyn. 2023, 1–13. [Google Scholar] [CrossRef]
- Tran, L.V.; Niiranen, J. A Geometrically Nonlinear Euler–Bernoulli Beam Model within Strain Gradient Elasticity with Isogeometric Analysis and Lattice Structure Applications. Math. Mech. Complex Syst. 2020, 8, 345–371. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in MATLAB. J. Eng. Mater. Technol. 2019, 141, 011005. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and Specific Energy Absorption of Additively-Manufactured Metallic BCC Metamaterials Composed of Tapered Beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical Behaviors of SLM Additive Manufactured Octet-Truss and Truncated-Octahedron Lattice Structures with Uniform and Taper Beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical Response of Ti-6Al-4V Octet-Truss Lattice Structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D Printed Stretching-Dominated Micro-Trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Z.; Lu, Z.; Liao, B.; He, X. Effective Elastic Properties and Initial Yield Surfaces of Two 3D Lattice Structures. Int. J. Mech. Sci. 2018, 138–139, 146–158. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical Properties of an Improved 3D-Printed Rhombic Dodecahedron Stainless Steel Lattice Structure of Variable Cross Section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.J.; Chen, D.H. Prediction of the Mechanical Properties of Micro-Lattice Structures Subjected to Multi-Axial Loading. Int. J. Mech. Sci. 2013, 68, 47–55. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.; Mines, R.; Tsopanos, S.; Smith, M. An Investigation into the Compressive Properties of Stainless Steel Micro-Lattice Structures. J. Sandw. Struct. Mater. 2011, 13, 303–329. [Google Scholar] [CrossRef]
- Parisien, A. Characterization and Design Optimization of Periodic Cellular Solids for Optimal Bone Ingrowth in Osseointegration Implants; Carleton University: Ottawa, ON, Canada, 2021. [Google Scholar]
- Altair Engineering Inc. Altair Radioss 2022: Theory Manual; Altair Engineering Inc.: Troy, MI, USA, 2022. [Google Scholar]
- Altair Engineering Inc. Altair Radioss 2022: Reference Guide; Altair Engineering Inc.: Troy, MI, USA, 2022. [Google Scholar]
- Labeas, G.N.; Sunaric, M.M. Investigation on the Static Response and Failure Process of Metallic Open Lattice Cellular Structures. Strain 2010, 46, 195–204. [Google Scholar] [CrossRef]
- Bernard, A.R.; Elsayed, M.S.A. Impact Resistance and Specific Energy Absorption Efficiency Limits of Periodic Cellular Solids. In AIAA SCITECH 2022 Forum; AIAA Inc.: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Zhou, S.; Shao, J.; Wu, X. Novel Negative Poisson’s Ratio Lattice Structures with Enhanced Stiffness and Energy Absorption Capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive Strain at the Onset of Densification of Cellular Solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Lu, G.; Yu, T. Energy Absorption of Structures and Materials; Woodhead Publishing Limited: Cambridge, UK, 2003; ISBN 0849317681. [Google Scholar]
- Xu, P.; Yang, C.; Peng, Y.; Yao, S.; Xing, J.; Li, B. Cut-out Grooves Optimization to Improve Crashworthiness of a Gradual Energy-Absorbing Structure for Subway Vehicles. Mater. Des. 2016, 103, 132–143. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. Thin-Walled Corrugated Structures: A Review of Crashworthiness Designs and Energy Absorption Characteristics. Thin-Walled Struct. 2020, 157, 106995. [Google Scholar] [CrossRef]
- Maxwell, J.C. On the Calculation of the Equilibrium and Stiffness of Frames. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 294–299. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective Laser Melting (SLM) of AlSi12Mg Lattice Structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Williams, H.; Yang, E.; Alghamdi, A.; Lozanovski, B.; Zhang, X.; Shidid, D.; Farahbod-Sternahl, L.; Witt, G.; et al. Inconel 625 Lattice Structures Manufactured by Selective Laser Melting (SLM): Mechanical Properties, Deformation and Failure Modes. Mater. Des. 2018, 157, 179–199. [Google Scholar] [CrossRef]
- Calladine, C.R. Buckminster Fuller’s “Tensegrity” Structures and Clerk Maxwell’s Rules for the Construction of Stiff Frames. Int. J. Solids Struct. 1978, 14, 161–172. [Google Scholar] [CrossRef]
- Pellegrino, S.; Calladine, C.R. Matrix Analysis of Statically and Kinematically Indeterminate Frameworks. Int. J. Solids Struct. 1986, 22, 409–428. [Google Scholar] [CrossRef]
- Tarnai, T. Simultaneous Static and Kinematic Indeterminacy of Space Trusses with Cyclic Symmetry. Int. J. Solids Struct. 1980, 16, 347–359. [Google Scholar] [CrossRef]
- Altamimi, S.; Lee, D.W.; Barsoum, I.; Rowshan, R.; Jasiuk, I.M.; Abu Al-Rub, R.K. On Stiffness, Strength, Anisotropy, and Buckling of 30 Strut-Based Lattices with Cubic Crystal Structures. Adv. Eng. Mater. 2022, 24, 2101379. [Google Scholar] [CrossRef]
- Parisien, A.; ElSayed, M.S.A.; Frei, H. Mechanoregulation Modelling of Stretching versus Bending Dominated Periodic Cellular Solids. Mater. Today Commun. 2022, 33, 104315. [Google Scholar] [CrossRef]
- Wagner, M.A.; Lumpe, T.S.; Chen, T.; Shea, K. Programmable, Active Lattice Structures: Unifying Stretch-Dominated and Bending-Dominated Topologies. Extreme Mech. Lett. 2019, 29, 100461. [Google Scholar] [CrossRef]
- Bauer, J.; Hengsbach, S.; Tesari, I.; Schwaiger, R.; Kraft, O. High-Strength Cellular Ceramic Composites with 3D Microarchitecture. Proc. Natl. Acad. Sci. USA 2014, 111, 2453–2458. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Xu, Q.S.; Wang, Z.; Hou, W.T.; Hao, Y.L.; Yang, R.; Murr, L.E. Influence of Cell Shape on Mechanical Properties of Ti–6Al–4V Meshes Fabricated by Electron Beam Melting Method. Acta Biomater. 2014, 10, 4537–4547. [Google Scholar] [CrossRef] [PubMed]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of Polymeric Lattice Structures for Optimum Energy Absorption Using Multi Jet Fusion Technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, Ultrastiff Mechanical Metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.; Liu, G.; Zong, H.; Zhang, C. Stiffness and Energy Absorption of Additive Manufactured Hybrid Lattice Structures. Virtual Phys. Prototyp. 2021, 16, 428–443. [Google Scholar] [CrossRef]
- Athanker, P.; Singh, A.K. Elastic and Elasto-Plastic Analysis of Ti6Al4V Micro-Lattice Structures under Compressive Loads. Math. Mech. Solids 2021, 26, 591–615. [Google Scholar] [CrossRef]
- Arabnejad, S.; Burnett Johnston, R.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-Strength Porous Biomaterials for Bone Replacement: A Strategy to Assess the Interplay between Cell Morphology, Mechanical Properties, Bone Ingrowth and Manufacturing Constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef] [PubMed]
- Nordmann, J.; Aßmus, M.; Altenbach, H. Visualising Elastic Anisotropy: Theoretical Background and Computational Implementation. Contin. Mech. Thermodyn. 2018, 30, 689–708. [Google Scholar] [CrossRef]
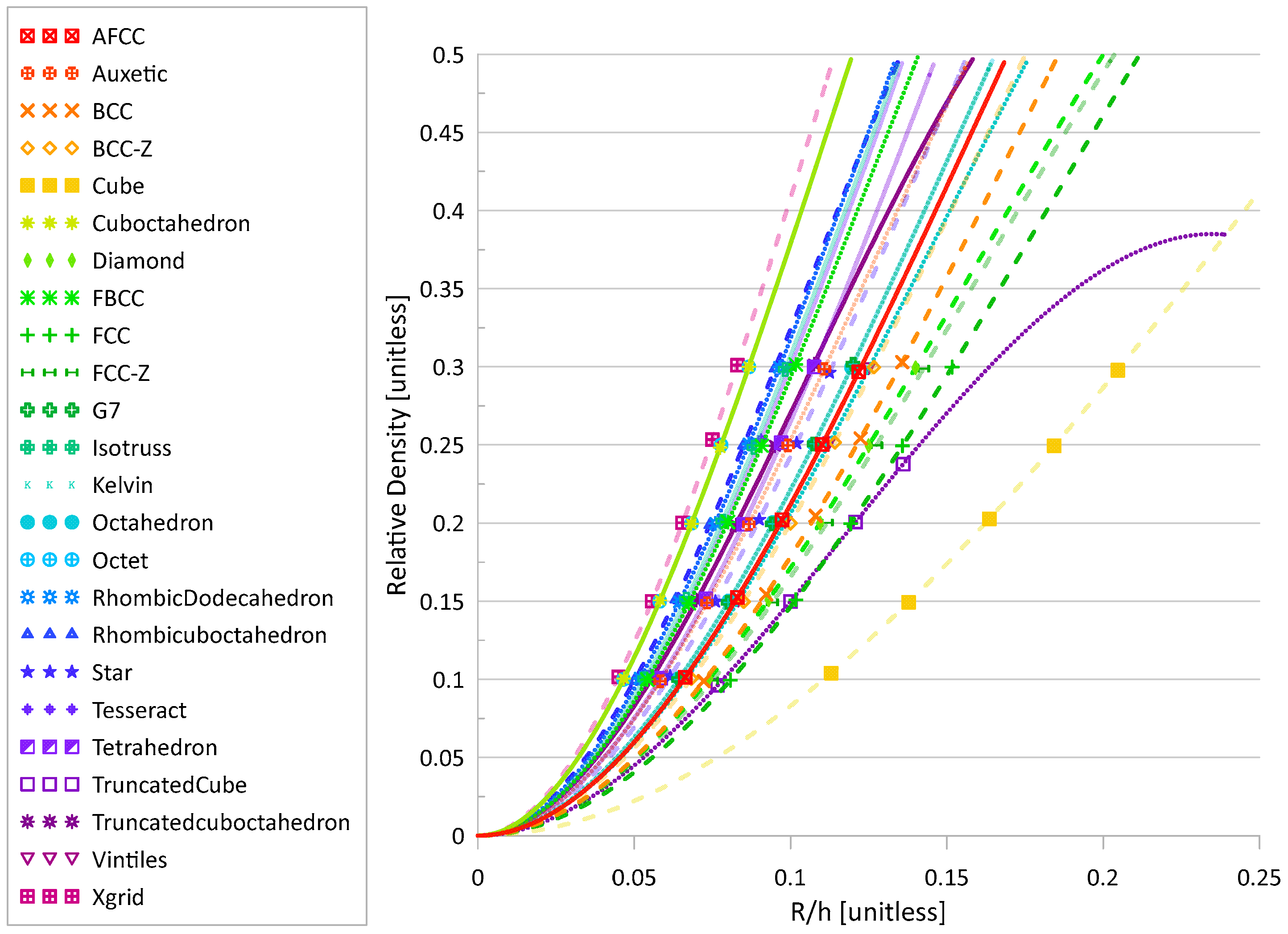


| Topo. | Geometry | R [mm] | Topo. | Geometry | R [mm] | ||
|---|---|---|---|---|---|---|---|
| AFCC |  | 0.1 | 0.663 | Kelvin |  | 0.1 | 0.665 |
| 0.2 | 0.973 | 0.2 | 0.985 | ||||
| 0.3 | 1.218 | 0.3 | 1.250 | ||||
| Auxetic |  | 0.1 | 0.583 | Octahedron |  | 0.1 | 0.645 |
| 0.2 | 0.867 | 0.2 | 0.945 | ||||
| 0.3 | 1.108 | 0.3 | 1.195 | ||||
| BCC |  | 0.1 | 0.723 | Octet |  | 0.1 | 0.466 |
| 0.2 | 1.080 | 0.2 | 0.684 | ||||
| 0.3 | 1.357 | 0.3 | 0.867 | ||||
| BCC-Z |  | 0.1 | 0.683 | Rhombic Dodecahedron |  | 0.1 | 0.519 |
| 0.2 | 1.000 | 0.2 | 0.760 | ||||
| 0.3 | 1.267 | 0.3 | 0.965 | ||||
| Cube |  | 0.1 | 1.130 | Rhombi-cuboctahedron |  | 0.1 | 0.500 |
| 0.2 | 1.636 | 0.2 | 0.742 | ||||
| 0.3 | 2.047 | 0.3 | 0.950 | ||||
| Cuboctahedron |  | 0.1 | 0.467 | Star |  | 0.1 | 0.615 |
| 0.2 | 0.683 | 0.2 | 0.900 | ||||
| 0.3 | 0.867 | 0.3 | 1.125 | ||||
| Diamond |  | 0.1 | 0.740 | Tesseract |  | 0.1 | 0.551 |
| 0.2 | 1.095 | 0.2 | 0.792 | ||||
| 0.3 | 1.400 | 0.3 | 1.000 | ||||
| FBCC |  | 0.1 | 0.542 | Tetrahedron |  | 0.1 | 0.585 |
| 0.2 | 0.800 | 0.2 | 0.850 | ||||
| 0.3 | 1.017 | 0.3 | 1.075 | ||||
| FCC |  | 0.1 | 0.808 | Truncated Cube 1 |  | 0.1 | 0.767 |
| 0.2 | 1.192 | 0.2 | 1.208 | ||||
| 0.3 | 1.517 | ||||||
| FCC-Z |  | 0.1 | 0.750 | Truncatedcuboctahedron |  | 0.1 | 0.558 |
| 0.2 | 1.117 | 0.2 | 0.825 | ||||
| 0.3 | 1.425 | 0.3 | 1.075 | ||||
| G7 |  | 0.1 | 0.642 | Vintiles |  | 0.1 | 0.667 |
| 0.2 | 0.942 | 0.2 | 0.983 | ||||
| 0.3 | 1.200 | 0.3 | 1.250 | ||||
| IsoTruss |  | 0.1 | 0.533 | Xgrid |  | 0.1 | 0.450 |
| 0.2 | 0.783 | 0.2 | 0.655 | ||||
| 0.3 | 0.983 | 0.3 | 0.830 |
| Topology | Topology | ||||
|---|---|---|---|---|---|
| AFCC | 26.656 | 54.618 | Kelvin | 26.657 | 60.331 |
| Auxetic | 34.381 | 90.751 | Octahedron | 28.049 | 59.170 |
| BCC | 21.765 | 39.187 | Octet | 53.313 | 154.493 |
| BCC-Z | 24.907 | 49.179 | Rhombic Dodecahedron | 43.530 | 117.566 |
| Cube | 9.425 | 11.311 | Rhombicuboctahedron | 46.847 | 144.491 |
| Cuboctahedron | 53.313 | 154.493 | Star | 31.190 | 69.157 |
| Diamond | 21.765 | 46.361 | Tesseract | 39.156 | 90.673 |
| FBCC | 39.542 | 102.212 | Tetrahedron | 33.635 | 71.375 |
| FCC | 17.774 | 31.282 | Truncated Cube | 20.919 | 59.354 |
| FCC-Z | 20.913 | 43.497 | Truncatedcuboctahedron | 39.391 | 123.597 |
| G7 | 28.048 | 59.169 | Vintiles | 26.657 | 60.330 |
| IsoTruss | 40.614 | 99.127 | Xgrid | 170.547 | 57.846 |
| Model | Num. Elem. | Output File Size [MB] | Run Time [min] | Percent Reduction 1 [%] | ||
|---|---|---|---|---|---|---|
| Num. Elem. | Output File Size | Run Time | ||||
| Free BC | 3139 | 74 | 15 | 89 | 85 | 72 |
| Fixed BC | 3139 | 74 | 16 | 89 | 84 | 70 |
| 3 × 3 Single-Layer Cluster | 27,520 | 498 | 53 | - | - | - |
| 5 × 5 Single-Layer Cluster | 77,547 | 1010 | 339 | - | - | - |
| 7960 kg/m3 | 93 GPa | 0.3 | ||
| 310 MPa | 622 | 0.1 | 0.8 | 0.001 |
| 0.1152 | 1.0116 | −1.7684 | −0.05279 | 0.5256 |
| Strain Rate 1 [1/s] | Speed [m/s] | Initial Kinetic Energy [J] | |||
|---|---|---|---|---|---|
| 1 | 5 | 50 | 100 | ||
| 100 | 1 | 2 | 10 | 100 | 200 |
| 1000 | 10 | 0.02 | 0.1 | 1 | 2 |
| 10,000 | 100 | 0.0002 | 0.001 | 0.01 | 0.02 |
| 100,000 | 1000 | 0.000002 | 0.00001 | 0.0001 | 0.0002 |
| Topology | b 1 | j 2 | M 3 | S/B 4 | S/B 5 | Ref. | LD? 6 | ||
|---|---|---|---|---|---|---|---|---|---|
 | AFCC |  | 24 | 12 | −6 | B | S | [59] | N |
 | Auxetic |  | 36 | 18 | −12 | B | B | [60,61] | Y |
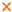 | BCC |  | 8 | 9 | −13 | B | S/B | [14,29,54,55] | N |
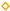 | BCC-Z |  | 12 | 9 | −9 | B | S/B | [54,55] | Y |
 | Cube |  | 12 | 8 | −6 | B | S/B | [10,14,26,62] | Y |
 | Cuboctahedron |  | 36 | 13 | 3 | S | S | [60] | N |
 | Diamond |  | 16 | 14 | −20 | B | S/B | [14,24,28] | N |
 | FBCC |  | 24 | 13 | −9 | B | B | [60] | N |
 | FCC |  | 16 | 12 | −14 | B | S/B | [54,55] | N |
 | FCC-Z |  | 20 | 12 | −10 | B | S/B | [54,55] | Y |
 | G7 |  | 16 | 9 | −5 | B | B | [60,63] | Y |
 | IsoTruss |  | 26 | 15 | −13 | B | S | [10,59] | Y |
 | Kelvin |  | 36 | 24 | −30 | B | B | [10,14,64,65] | N |
 | Octahedron |  | 12 | 6 | 0 | S | S | [26,59] | Y |
 | Octet |  | 36 | 14 | 0 | S | S | [10,26,29,59,65] | N |
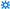 | Rhombic Dodecahedron |  | 32 | 20 | −22 | B | B | [16,40] | N |
 | Rhombicuboctahedron |  | 48 | 24 | −18 | B | S/B | [14,26,64] | N |
 | Star |  | 20 | 9 | −1 | B | S/B | [14,59] | Y |
 | Tesseract |  | 32 | 16 | −10 | B | S | [60,66,67] | Y |
 | Tetrahedron |  | 22 | 9 | 1 | S | S | [68] | Y |
 | Truncated Cube |  | 36 | 24 | −30 | B | B | [14] | N |
 | Truncatedcuboctahedron |  | 72 | 48 | −66 | B | S | [60] | N |
 | Vintiles |  | 36 | 28 | −42 | B | B | [10] | N |
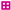 | Xgrid |  | 44 | 15 | 5 | S | S/B | [59] | Y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernard, A.R.; ElSayed, M.S.A. Crashworthiness of 3D Lattice Topologies under Dynamic Loading: A Comprehensive Study. Materials 2024, 17, 1597. https://doi.org/10.3390/ma17071597
Bernard AR, ElSayed MSA. Crashworthiness of 3D Lattice Topologies under Dynamic Loading: A Comprehensive Study. Materials. 2024; 17(7):1597. https://doi.org/10.3390/ma17071597
Chicago/Turabian StyleBernard, Autumn R., and Mostafa S. A. ElSayed. 2024. "Crashworthiness of 3D Lattice Topologies under Dynamic Loading: A Comprehensive Study" Materials 17, no. 7: 1597. https://doi.org/10.3390/ma17071597
APA StyleBernard, A. R., & ElSayed, M. S. A. (2024). Crashworthiness of 3D Lattice Topologies under Dynamic Loading: A Comprehensive Study. Materials, 17(7), 1597. https://doi.org/10.3390/ma17071597







