Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials
Abstract
:1. Introduction
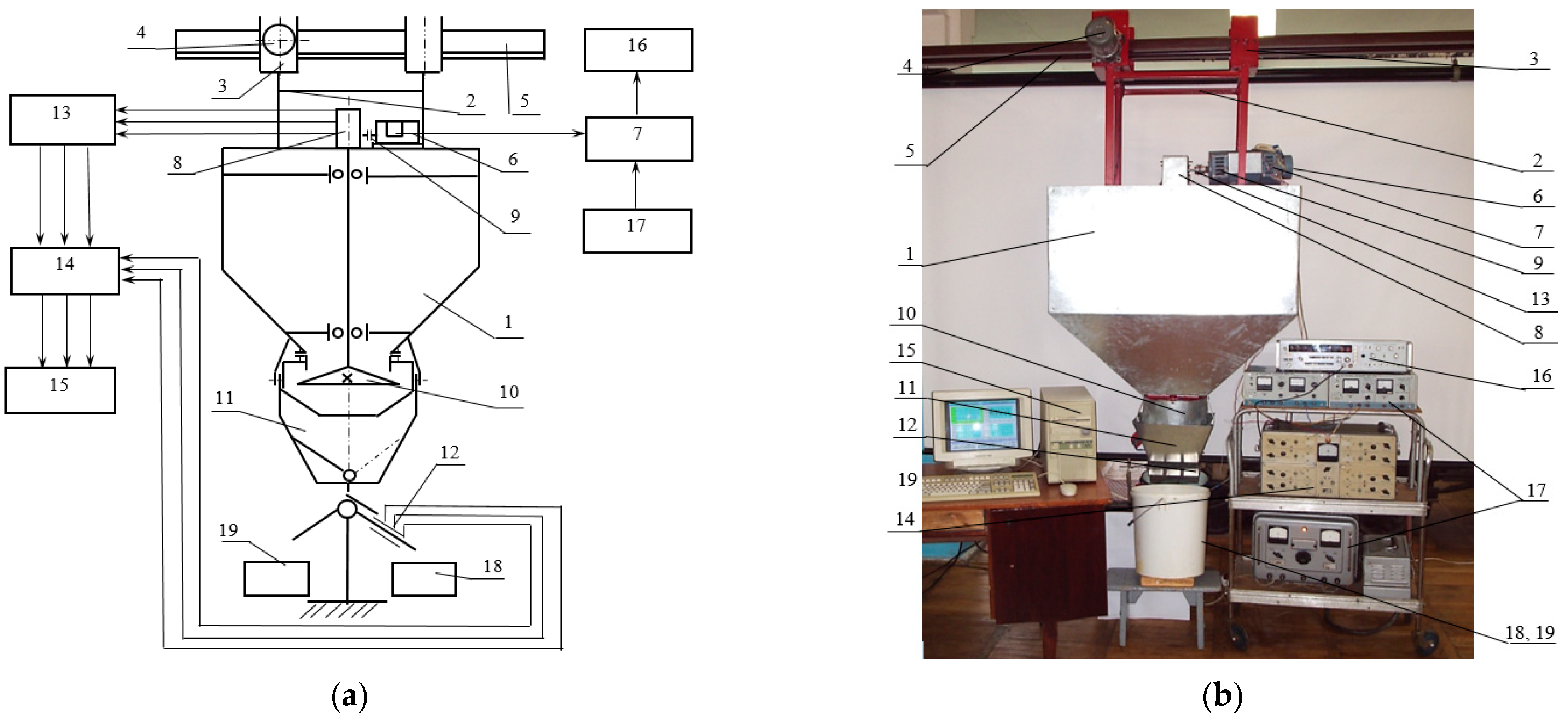
2. Materials and Methods
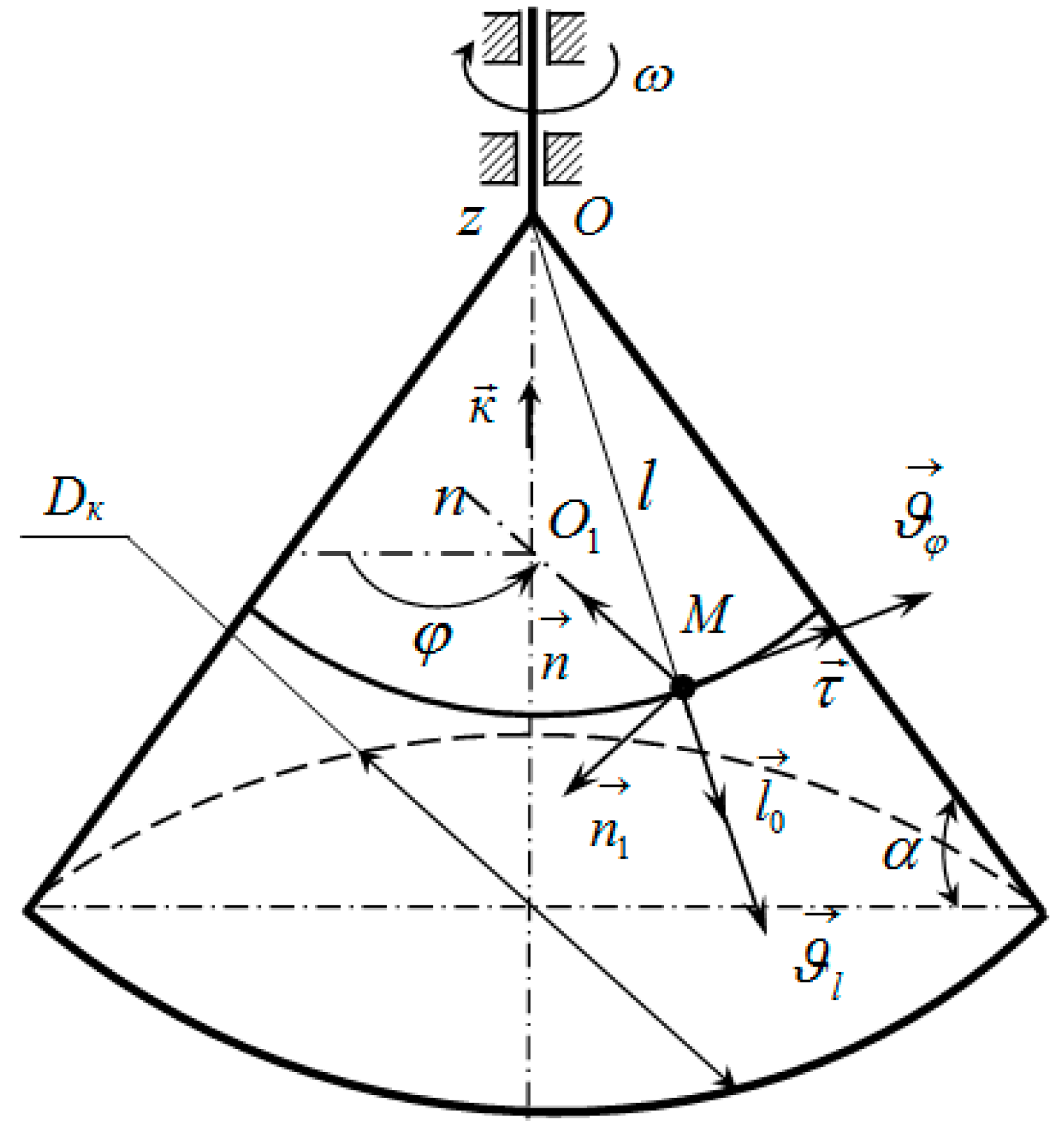
2.1. Analytical Model of the Productivity of a Centrifugal Conical Disk Bulk Material Dispenser
- —radial component of velocity (velocity along the generator) [m/s];
- —a unit vector directed along the generating OM;
- —transverse component of velocity [m/s]:
- l—distance from the top of the conical dosing working body to point M [m];
- —a unit vector directed along the tangent to the parallel (perpendicular to and O1M);
- —angular speed of rotation of the moving plane [rad/s];
- α—angle of the truncated cone at its base [°].
- —density of the material [kg/m3];
- —gravitational acceleration [m/s2];
- h—height of the elementary volume of the dispersed material [m];
- —cross-sectional area of the volume of the dispersed material in a plan view [m2].
- —the diameter of the disk above which the bulk material is located;
- f—coefficient of friction of the material sliding against the walls of the bunker;
- β—angle of packing of particles of the bulk material [°].
- , —the absolute and relative speed of movement of a material particle of dispersed materials:
- —diameter of the disk above which there is bulk material [mm];
- h—height of the elementary volume of the bulk material, corresponding to the height of the annular gap between the discharge neck of the hopper and the dosing cone disk [mm];
- —density of loose material [g/mm3];
- —radial velocity of the loose material at the exit from the disk [mm/s].
2.2. Factorial Planned Experiment
- Xi—natural value of the factor;
- Xi0—natural value of the factor at zero level;
- —variation interval.
3. Results and Discussion
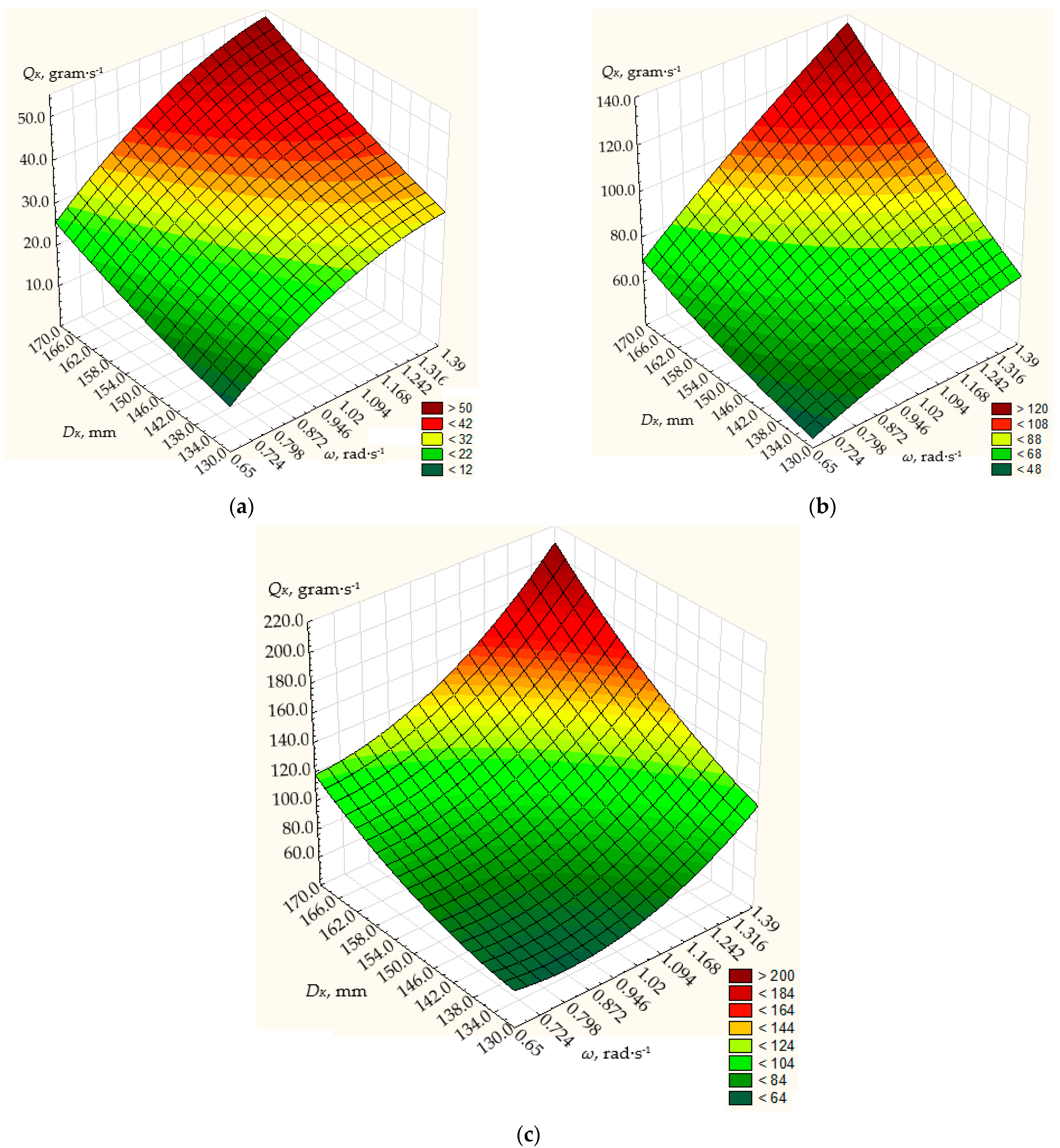
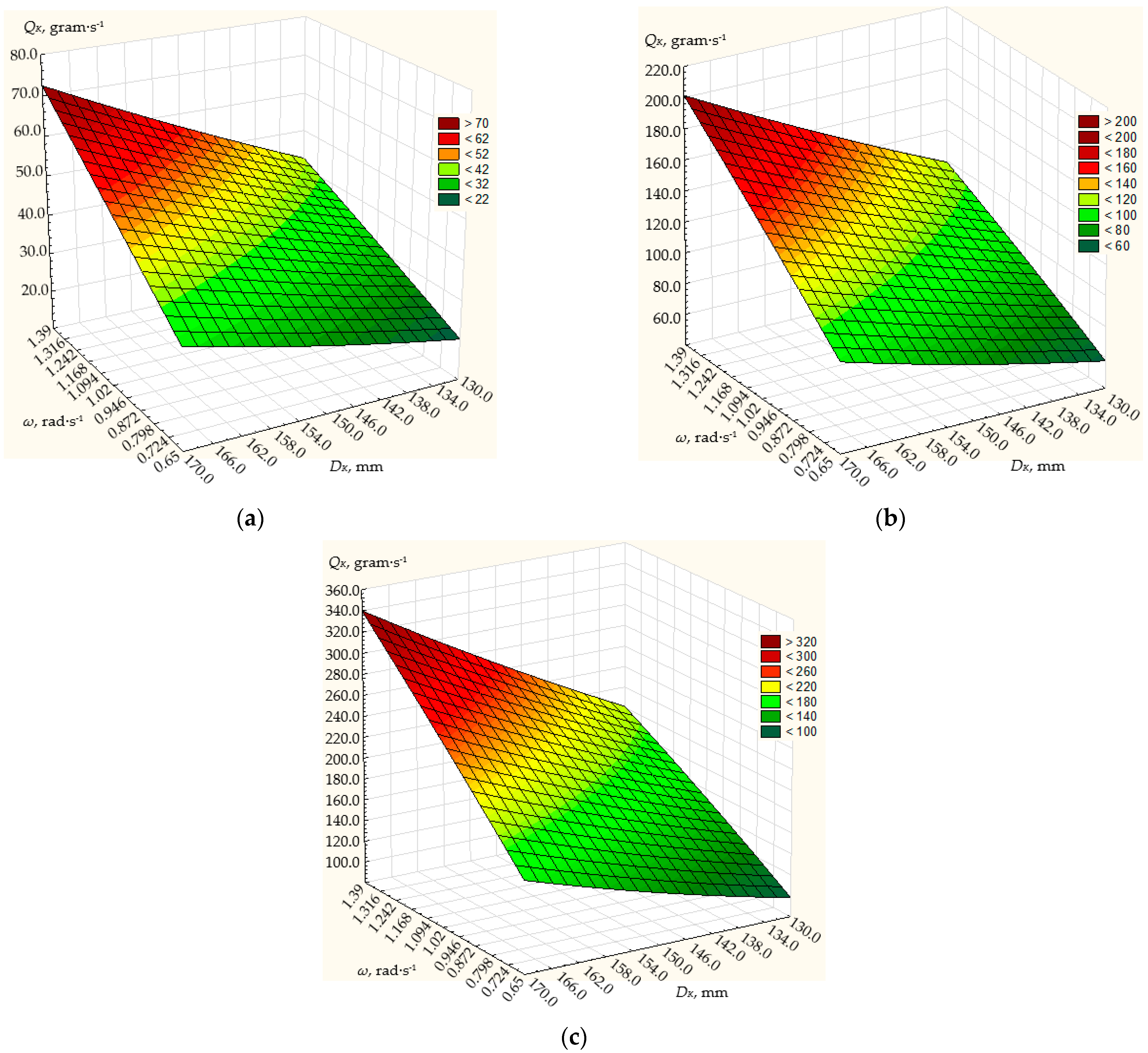
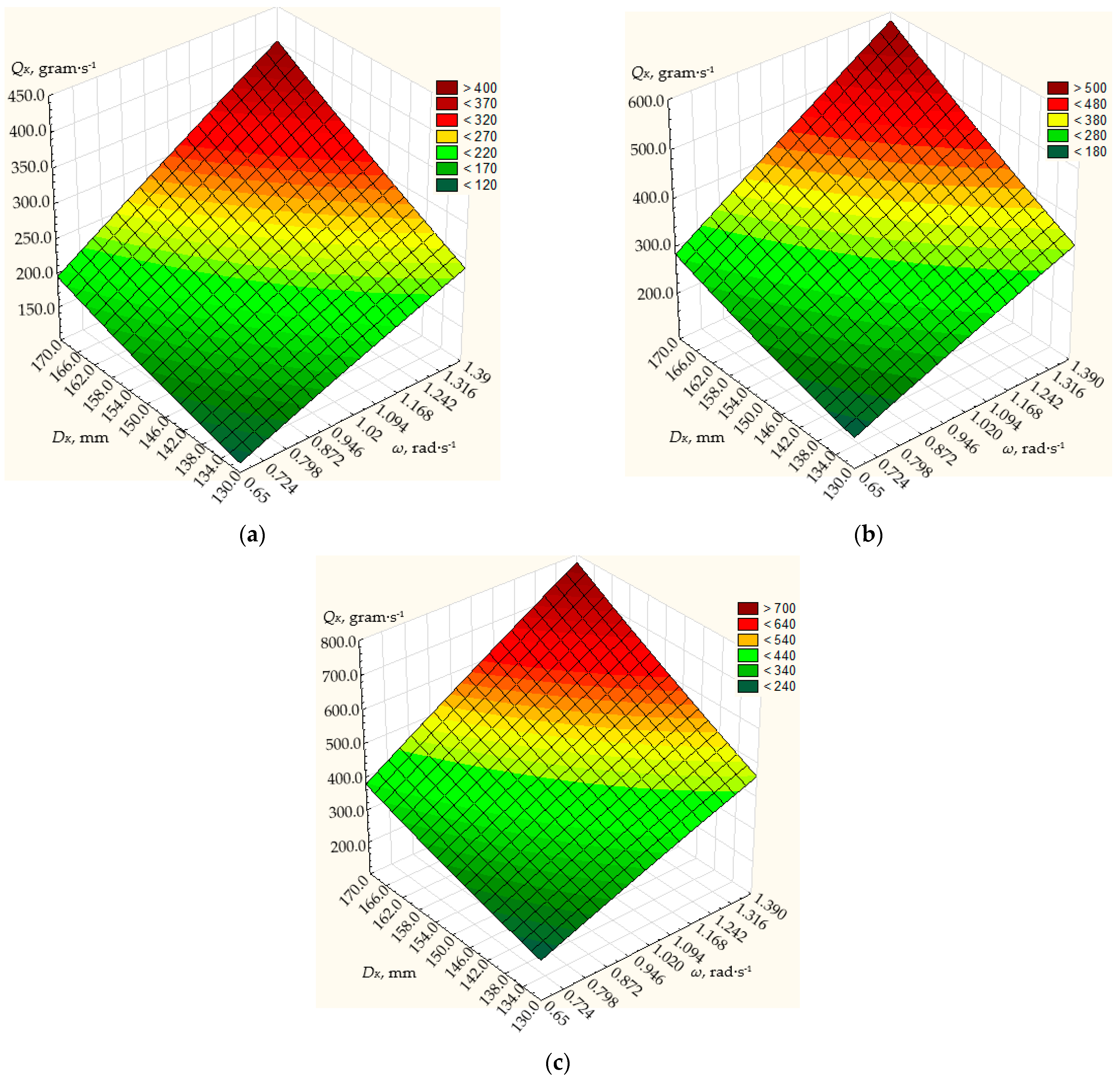
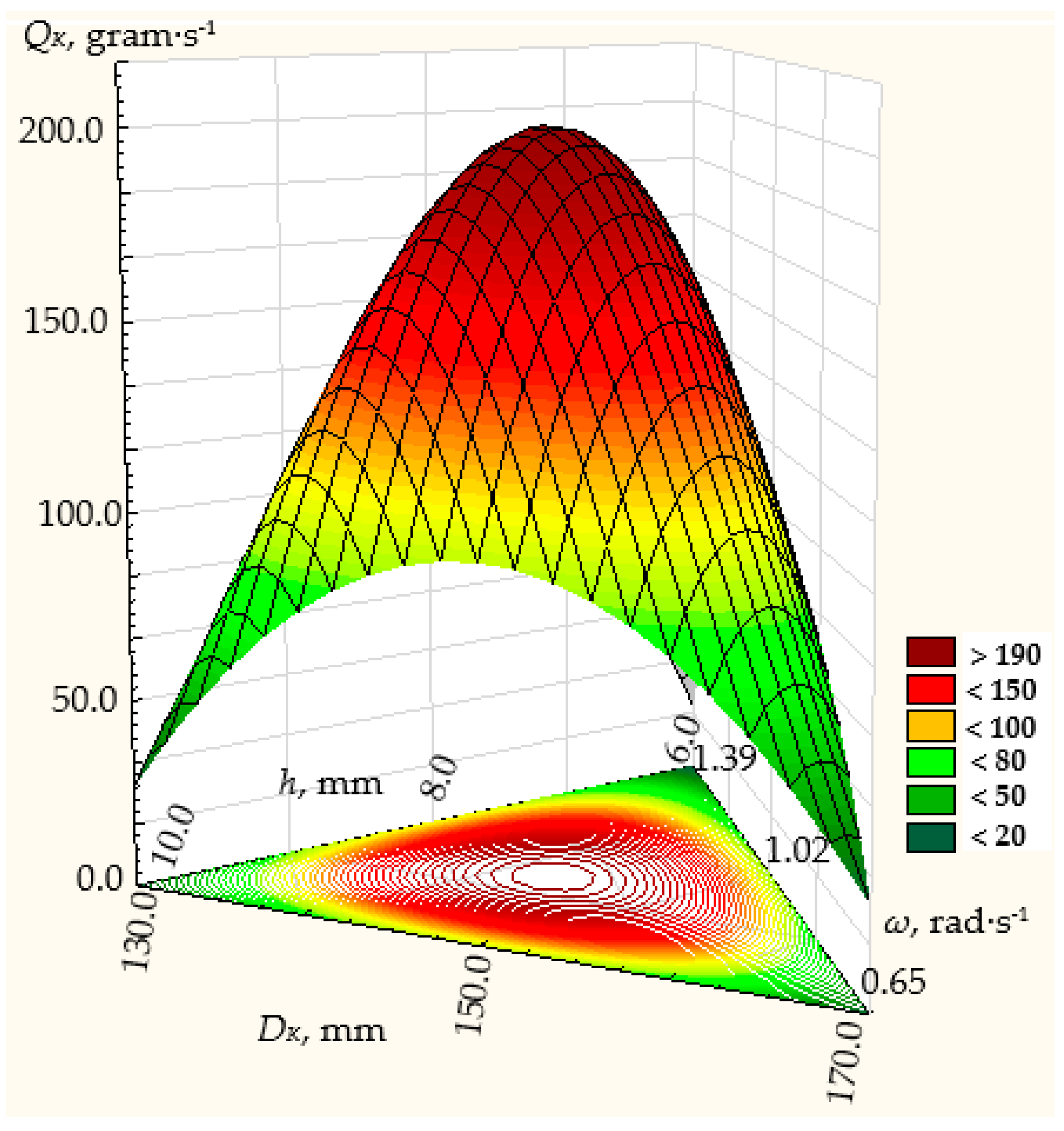
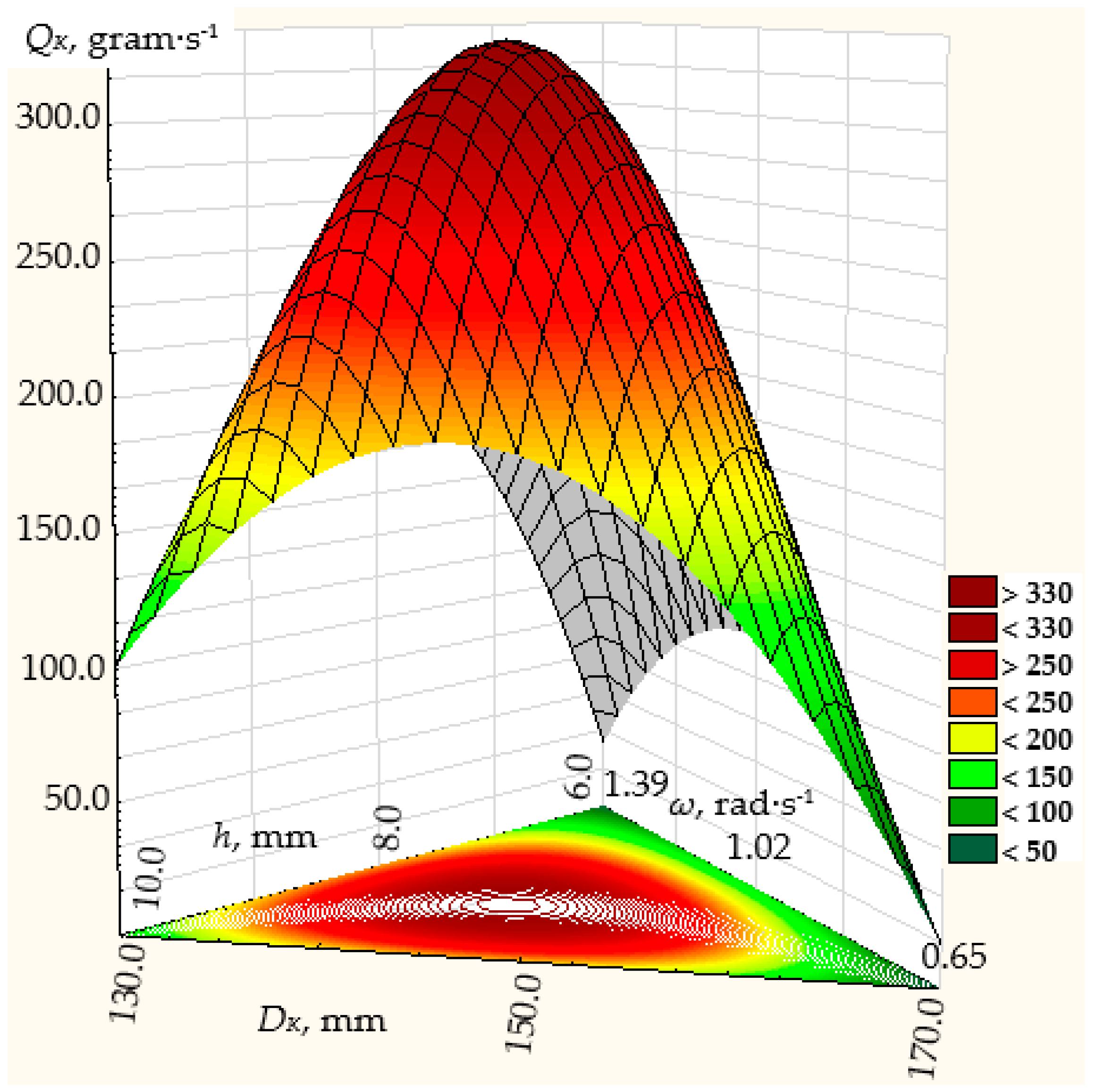
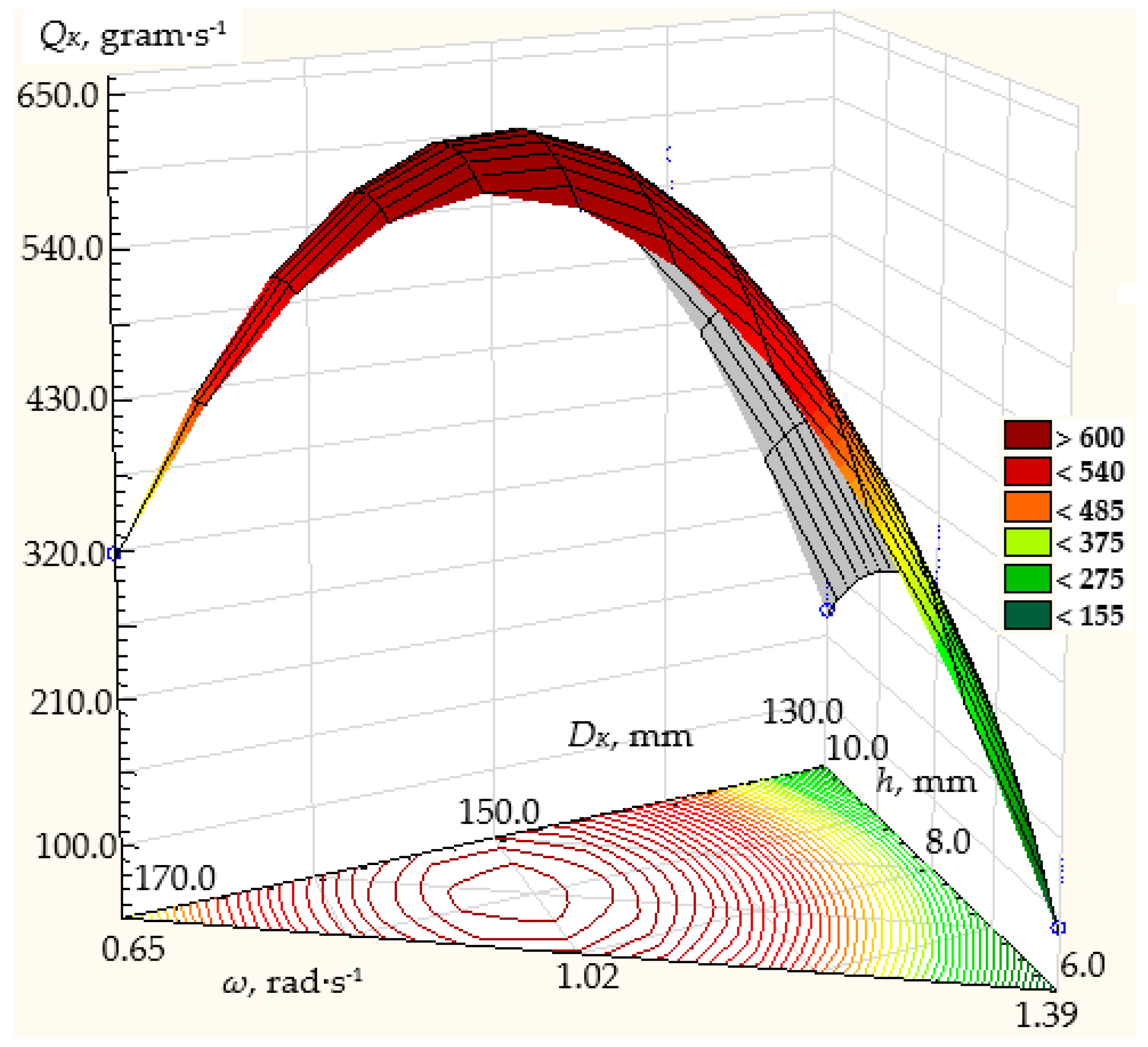
3.1. Results of Modeling Dosing Efficiency
3.2. Results of Experimental Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, V.K.; Singh, S.B.; Chandrawat, H.N.; Ray, S. Modeling of creep behavior of a rotating disc in the presence of both composition and thermal gradients. J. Eng. Mater. Technol. 2005, 127, 97–105. [Google Scholar] [CrossRef]
- Hojjati, M.H.; Hassani, A. Theoretical and numerical analysis of rotating discs of nonuniform thickness and density. Int. J. Press. Vessel. Pip. 2008, 85, 694–700. [Google Scholar] [CrossRef]
- Singh, S.B.; Ray, S. Modeling the anisotropy and creep in orthotropic aluminum-silicon carbide composite rotating disc. Mech. Mater. 2002, 34, 363–372. [Google Scholar] [CrossRef]
- Sutowski, P.; Plichta, J.; Kałduński, P. Determining kinetic energy distribution of the working medium in a centrifugal disc finishing process—Part 1: Theoretical and numerical analysis with DEM method. Int. J. Adv. Manuf. Technol. 2019, 104, 1345–1355. [Google Scholar] [CrossRef]
- Sutowski, P.; Plichta, J.; Kałduński, P. Determining kinetic energy distribution of the working medium in centrifugal disc finishing process—Part 2: Experimental analysis with the use of acoustic emission signal. Int. J. Adv. Manuf. Technol. 2019, 104, 687–704. [Google Scholar] [CrossRef]
- Yildirim, V.A. Parametric Study on the Centrifugal Force-Induced Stress and Displacements in Power-Law Graded Hyperbolic Discs. Lat. Am. J. Solids Struct. 2018, 15, e34. [Google Scholar] [CrossRef]
- Madadelahi, M.; Acosta-Soto, L.F.; Hosseini, S.; Martinez-Chapa, S.O.; Madou, M.J. Mathematical modeling and computational analysis of centrifugal microfluidic platforms: A review. Lab Chip 2020, 20, 1318–1357. [Google Scholar] [CrossRef] [PubMed]
- Khudher, A.Y.; Himoud, M.S.; Almaliki, S.A. Modulating a Centrifuge Spreader Disc and Evaluating Performance Under Some Different Operating Factors. Int. J. Agric. Stat. Sci. 2020, 16, 1799–1805. [Google Scholar]
- Marano, S.; Barker, S.A.; Raimi-Abraham, B.T.; Missaghi, S.; Rajabi-Siahboomi, A.; Craig, D.Q.M. Development of micro-fibrous solid dispersions of poorly water-soluble drugs in sucrose using temperature-controlled centrifugal spinning. Eur. J. Pharm. Biopharm. 2016, 103, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Huo, X. Multiobjective Optimization Design and Performance Prediction of Centrifugal Pump Based on Orthogonal Test. Adv. Mater. Sci. Eng. 2018, 10, 6218178. [Google Scholar] [CrossRef]
- Strohmeier, O.; Keller, M.; Schwemmer, F.; Zehnle, S.; Mark, D.; Stetten, F.; Zengerle, R.; Paust, N. Centrifugal microfluidic platforms: Advanced unit operations and applications. Chem. Soc. Rev. 2015, 44, 6187–6229. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.; Wang, N.; Zhou, C.; Li, J.A. Simplified Analysis Method for the Piezo Jet Dispenser with a Diamond Amplifier. Sensors 2018, 18, 2115. [Google Scholar] [CrossRef] [PubMed]
- Villette, S.; Piron, E.; Miclet, D. Hybrid centrifugal spreading model to study the fertilizer spatial distribution and its assessment using the transverse coefficient of variation. Comput. Electron. Agric. 2017, 137, 115–129. [Google Scholar] [CrossRef]
- Yinyan, S.; Mann, C.; Xiaochan, W.; Odhiambo, M.O.; Weimin, D. Numerical Simulation of Spreading Performance and Distribution Pattern of Centrifugal Variable-Rate Fertilizer Applicator Based on DEM Software. Comput. Electron. Agric. 2018, 144, 249–259. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P.; Ristić, M. Vibrations and stability analysis of multiple rectangular plates coupled with elastic layers based on different plate theories. Int. J. Mech. Sci. 2015, 92, 233–244. [Google Scholar] [CrossRef]
- Stojanović, V.; Petković, M.D.; Deng, J. Stability and vibrations of an overcritical speed moving multiple discrete oscillators along an infinite continuous structure. Eur. J. Mech.-A/Solids 2019, 75, 367–380. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, Y. Simulation of soil-micropenetrometer interaction using the discrete element method (DEM). Trans. ASABE 2016, 59, 1157–1163. [Google Scholar] [CrossRef]
- Song, X.F.; Dai, F.; Zhang, F.W.; Wang, D.M.; Liu, Y.C. Calibration of DEM models for fertilizer particles based on numerical simulations and granular experiments. Comput. Electron. Agric. 2023, 204, 107507. [Google Scholar] [CrossRef]
- Liu, J.S.; Gao, C.Q.; Nie, Y.J.; Xu, Z.H. Numerical simulation of fertilizer shunt-plate with uniformity based on EDEM software. Comput. Electron. Agric. 2020, 178, 105737. [Google Scholar] [CrossRef]
- Bembenek, M.; Buczak, M.; Baiul, K. Modeling of the Fine-Grained Materials Briquetting Process in a Roller Press with the Discrete Element Method. Materials 2022, 15, 4901. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.F.; Chen, H.C.; Duan, J.L.; Liu, Z.; Zhu, Q.C. Mechanical properties of the grooved-wheel drilling particles under multivariate interaction influence based on 3d printing and EDEM simulation. Comput. Electron. Agric. 2020, 172, 105329. [Google Scholar] [CrossRef]
- Du, J.; Yang, Q.; Xia, J.F.; Li, G. Discrete element modeling and verification of an outer groove wheel fertilizer applicator with helical teeth. Trans. ASABE 2020, 63, 659–665. [Google Scholar] [CrossRef]
- Xu, L.; Luo, K.; Zhao, Y.Z. Numerical prediction of wear in SAG mills based on DEM simulations. Powder Technol. 2018, 329, 353–363. [Google Scholar] [CrossRef]
- Bembenek, M.; Krawczyk, J.; Pa´ncikiewicz, K. The wear mechanism of mill beaters for coal grinding made-up from high manganese cast steel. Eng. Fail. Anal. 2022, 142, 106843. [Google Scholar] [CrossRef]
- Villette, S.; Piron, E.; Miclet, D.; Martin, R.; Jones, G.; Paoli, J.N.; Gée, C. How mass flow and rotational speed affect fertilizer centrifugal spreading: Potential interpretation in terms of the amount of fertilizer per vane. Biosyst. Eng. 2012, 111, 133–138. [Google Scholar] [CrossRef]
- Gao, X.; Cui, T.; Zhou, Z.; Yu, Y.; Song, W. DEM study of particle motion in novel high-speed seed metering device. Adv. Powder Technol. 2021, 32, 1438–1449. [Google Scholar] [CrossRef]
- Yildirim, Y. Effect of cone angle and revolution speed of disc on fertilizer distribution uniformity in single-disc rotary fertilizer spreaders. J. Appl. Sci. 2006, 6, 2875–2881. [Google Scholar] [CrossRef]
- Van Liedekerke, P.; Tijskens, E.; Dintwa, E.; Anthony, J.; Ramon, H. A discrete element model for simulation of a spinning disc fertilizer spreader I. Single particle simulations. Powder Technol. 2006, 170, 71–85. [Google Scholar] [CrossRef]
- Kruszelnicka, W.; Macko, M.; Łączny, D.; Bałdowska-Witos, P.; Lewandowski, J. The Use of Simulation Software using the Discrete Element Method (DEM) for the Process of Materials Comminution. MATEC Web Conf. 2022, 357, 07005. [Google Scholar] [CrossRef]
- Karwat, B.; Machnik, R.; Niedźwiedzki, J.; Nogaj, M.; Rubacha, P.; Stańczyk, E. Calibration of bulk material model in Discrete Element Method on example of perlite D18-DN. Maint. Reliab.-Maint. Reliab. 2019, 21, 351–357. [Google Scholar] [CrossRef]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A. DEM Calibration Approach: Design of experiment. J. Phys. Conf. Ser. 2018, 1015, 032017. [Google Scholar] [CrossRef]
- Hlosta, J.; Jezerská, L.; Rozbroj, J.; Žurovec, D.; Nečas, J.; Zegzulka, J. DEM Investigation of the Influence of Particulate Properties and Operating Conditions on the Mixing Process in Rotary Drums: Part 1- Determination of the DEM Parameters and Calibration Process. Processes 2020, 8, 222. [Google Scholar] [CrossRef]
- Wang, X.; Yi, J.; Zhou, Z.; Yang, C. Optimal Speed Control for a Semi-Autogenous Mill Based on Discrete Element Method. Processes 2020, 8, 233. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; De-Carvalho, R.M.; Kwade, A.; Tavares, L.M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technol. 2013, 248, 84–93. [Google Scholar] [CrossRef]
- Artur, P. The impact of structural and operational parameters of the centrifugal disc spreader on the spatial distribution of fertilizer. Agric. Agric. Sci. Procedia 2015, 7, 215–222. [Google Scholar] [CrossRef]
- Statsenko, V.; Burmistenkov, O.; Bila, T.; Statsenko, D. Determining the motion character of loose materials in the system of continuous action “hopper-reciprocating plate feeder”. East.-Eur. J. Enterp. Technol. 2019, 2, 21–28. [Google Scholar] [CrossRef]
- An, X.; Cheng, X.; Wang, X.; Han, Y.; Li, H.; Liu, L.; Liu, M.; Liu, M.; Zhang, X. Design and Experimental Testing of a Centrifugal Wheat Strip Seeding Device. Agriculture 2023, 13, 1883. [Google Scholar] [CrossRef]
- Symons, D.D. Frictional flow of damp granular material in a conical centrifuge. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 94–103. [Google Scholar] [CrossRef]
- Cool, S.; Pieters, J.; Mertens, K.C.; Hijazi, B.; Vangeyte, J. A simulation of the influence of spinning on the ballistic flight of spherical fertilizer grains. Comput. Electron. Agric. 2014, 105, 121–131. [Google Scholar] [CrossRef]
- Karwat, B.; Rubacha, P.; Stańczyk, E. Optimization of a screw conveyor’s exploitation parameters. Maint. Reliab.-Maint. Reliab. 2021, 23, 285–293. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Horodetskyy, I.M.; Horodniak, R.V.; Dmytriv, T.V. Method of theory of dimensions in experimental research of systems and processes. INMATEH-Agric. Eng. 2021, 65, 233–240. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Horodetskyy, I.M.; Yatsunskyi, P.P. Adaptive cyber-physical system of the milk production process. INMATEH-Agric. Eng. 2020, 61, 199–208. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Yatsunskyi, P.P. Experimental pulse generator combined with the milking machine collector. INMATEH-Agric. Eng. 2019, 59, 219–226. [Google Scholar] [CrossRef]

| Factors | Designation | Dimension | Levels of Factors | Variation Interval | ||
|---|---|---|---|---|---|---|
| Upper | Null | Lower | ||||
| Code Values | ||||||
| +1 | 0 | −1 | ||||
| Rotational frequency of the conical disk, n | x1 | rad/s | 1.39 | 1.02 | 0.65 | 0.37 |
| Height of the annular gap, h | x2 | mm | 10.0 | 8.0 | 6.0 | 2.0 |
| Diameter of the conical disk, DK | x3 | mm | 170.0 | 150.0 | 130.0 | 20.0 |
| No. of the Experiment | x1 | x2 | x3 | x1·x2 | x1·x3 | x2·x3 | (x1′)2 | (x2′)2 | (x3′)2 | x1·x2·x3 | y1 (QK), α = 10° [g/s] | y1 (QK), α = 20° [g/s] | y1 (QK), α = 30° [g/s] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | +1 | +1 | +1 | +1 | +1 | +1 | 0.3333 | 0.3333 | 0.3333 | +1 | 200.00 | 335.00 | 745.4 |
| 2 | 0 | +1 | +1 | 0 | 0 | +1 | −0.6667 | 0.3333 | 0.3333 | 0 | 138.33 | 250.46 | 580.5 |
| 3 | −1 | +1 | +1 | −1 | −1 | +1 | 0.3333 | 0.3333 | 0.3333 | −1 | 115.00 | 165.36 | 362.36 |
| 4 | +1 | +1 | −1 | +1 | −1 | −1 | 0.3333 | 0.3333 | 0.3333 | −1 | 105.67 | 200.00 | 449.50 |
| 5 | 0 | +1 | −1 | 0 | 0 | −1 | −0.6667 | 0.3333 | 0.3333 | 0 | 68.63 | 149.73 | 358.43 |
| 6 | −1 | +1 | −1 | −1 | +1 | −1 | 0.3333 | 0.3333 | 0.3333 | +1 | 62.43 | 97.00 | 171.46 |
| 7 | +1 | +1 | 0 | +1 | 0 | 0 | 0.3333 | 0.3333 | −0.6667 | 0 | 145.00 | 260.30 | 601.46 |
| 8 | 0 | +1 | 0 | 0 | 0 | 0 | −0.6667 | 0.3333 | −0.6667 | 0 | 96.00 | 200.30 | 445.40 |
| 9 | −1 | +1 | 0 | −1 | 0 | 0 | 0.3333 | 0.3333 | −0.6667 | 0 | 76.53 | 129.60 | 278.50 |
| 10 | +1 | −1 | +1 | −1 | +1 | −1 | 0.3333 | 0.3333 | 0.3333 | −1 | 50.60 | 72.36 | 400.20 |
| 11 | 0 | −1 | +1 | 0 | 0 | −1 | −0.6667 | 0.3333 | 0.3333 | 0 | 42.50 | 52.13 | 310.00 |
| 12 | −1 | −1 | +1 | +1 | −1 | −1 | 0.3333 | 0.3333 | 0.3333 | +1 | 23.90 | 33.86 | 180.00 |
| 13 | +1 | −1 | −1 | −1 | −1 | +1 | 0.3333 | 0.3333 | 0.3333 | +1 | 31.40 | 41.53 | 240.00 |
| 14 | 0 | −1 | −1 | 0 | 0 | +1 | −0.6667 | 0.3333 | 0.3333 | 0 | 23.80 | 30.20 | 173.30 |
| 15 | −1 | −1 | −1 | +1 | +1 | +1 | 0.3333 | 0.3333 | 0.3333 | −1 | 11.40 | 19.56 | 112.56 |
| 16 | +1 | −1 | 0 | −1 | 0 | 0 | 0.3333 | 0.3333 | −0.6667 | 0 | 40.46 | 55.40 | 304.50 |
| 17 | 0 | −1 | 0 | 0 | 0 | 0 | −0.6667 | 0.3333 | −0.6667 | 0 | 33.80 | 41.43 | 226.00 |
| 18 | −1 | −1 | 0 | +1 | 0 | 0 | 0.3333 | 0.3333 | −0.6667 | 0 | 14.86 | 26.00 | 148.33 |
| 19 | +1 | 0 | +1 | 0 | +1 | 0 | 0.3333 | −0.6667 | 0.3333 | 0 | 135.70 | 199.50 | 581.4 |
| 20 | 0 | 0 | +1 | 0 | 0 | 0 | −0.6667 | −0.6667 | 0.3333 | 0 | 95.80 | 149.50 | 418.50 |
| 21 | −1 | 0 | +1 | 0 | −1 | 0 | 0.3333 | −0.6667 | 0.3333 | 0 | 69.20 | 97.40 | 458.60 |
| 22 | +1 | 0 | −1 | 0 | −1 | 0 | 0.3333 | −0.6667 | 0.3333 | 0 | 68.80 | 118.53 | 353.26 |
| 23 | 0 | 0 | −1 | 0 | 0 | 0 | −0.6667 | −0.6667 | 0.3333 | 0 | 57.43 | 88.40 | 248.50 |
| 24 | −1 | 0 | −1 | 0 | +1 | 0 | 0.3333 | −0.6667 | 0.3333 | 0 | 40.60 | 56.30 | 163.16 |
| 25 | +1 | 0 | 0 | 0 | 0 | 0 | 0.3333 | −0.6667 | −0.6667 | 0 | 91.40 | 156.80 | 452.46 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | −0.6667 | −0.6667 | −0.6667 | 0 | 81.16 | 117.20 | 342.80 |
| 27 | −1 | 0 | 0 | 0 | 0 | 0 | 0.3333 | −0.6667 | −0.6667 | 0 | 53.40 | 75.13 | 218.00 |
| ∑ | 18 | 18 | 18 | 12 | 12 | 12 | — | — | — | 8 | — | — | — |
| Coefficient of the Regression Equation | Coded Coefficient | Real Coefficient |
|---|---|---|
| b0 | 71.9648 | 165.5043 |
| b1 | 22.3172 | 106.1478 |
| b2 | 40.8261 | 23.1952 |
| b3 | 22.2706 | −3.4021 |
| b12 | 10.3675 | 24.9371 |
| b13 | 7.23 | −1.4815 |
| b23 | 13.85 | 0.0105 |
| b11 | 3.4138 | −30.4071 |
| b22 | −5.9261 | −1.3918 |
| b33 | 4.2205 | 0.0442 |
| b123 | 4.3825 | 0.2961 |
| Coefficient of the Regression Equation | Coded Coefficient | Real Coefficient |
|---|---|---|
| b0 | 117.9648 | 164.5176 |
| b1 | 41.0672 | 144.4081 |
| b2 | 78.6266 | −15.5005 |
| b3 | 30.7955 | −1.7246 |
| b12 | 26.1225 | −7.7388 |
| b13 | 10.2533 | 0.5931 |
| b23 | 19.7525 | 0.0045 |
| b11 | −1.0594 | −28.1833 |
| b22 | 2.3722 | −2.0002 |
| b33 | 1.8055 | 0.0621 |
| b123 | 6.2637 | 0.4232 |
| Coefficient of the Regression Equation | Coded Coefficient | Real Coefficient |
|---|---|---|
| b0 | 380.457 | −2815.578 |
| b1 | 6.7094 | 6830.101 |
| b2 | 17.9322 | 577.7693 |
| b3 | −20.5883 | 1.4054 |
| b12 | −0.5691 | −607.203 |
| b13 | −16.8317 | −4.9544 |
| b23 | 47.3491 | 0.0867 |
| b11 | −83.1261 | −654.011 |
| b22 | −19.8178 | −37.1962 |
| b33 | 34.7138 | −3.2687 |
| b123 | 64.605 | 4.3652 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmytriv, V.; Bembenek, M.; Banha, V.; Dmytriv, I.; Dzienniak, D.; Nurkusheva, S. Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials. Materials 2024, 17, 1815. https://doi.org/10.3390/ma17081815
Dmytriv V, Bembenek M, Banha V, Dmytriv I, Dzienniak D, Nurkusheva S. Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials. Materials. 2024; 17(8):1815. https://doi.org/10.3390/ma17081815
Chicago/Turabian StyleDmytriv, Vasyl, Michał Bembenek, Vasyl Banha, Ihor Dmytriv, Damian Dzienniak, and Saltanat Nurkusheva. 2024. "Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials" Materials 17, no. 8: 1815. https://doi.org/10.3390/ma17081815
APA StyleDmytriv, V., Bembenek, M., Banha, V., Dmytriv, I., Dzienniak, D., & Nurkusheva, S. (2024). Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials. Materials, 17(8), 1815. https://doi.org/10.3390/ma17081815







