Thermal and Mechanical Stress Analysis in Aircraft Hybrid Panels with Multi-Bolt Joints
Abstract
1. Introduction
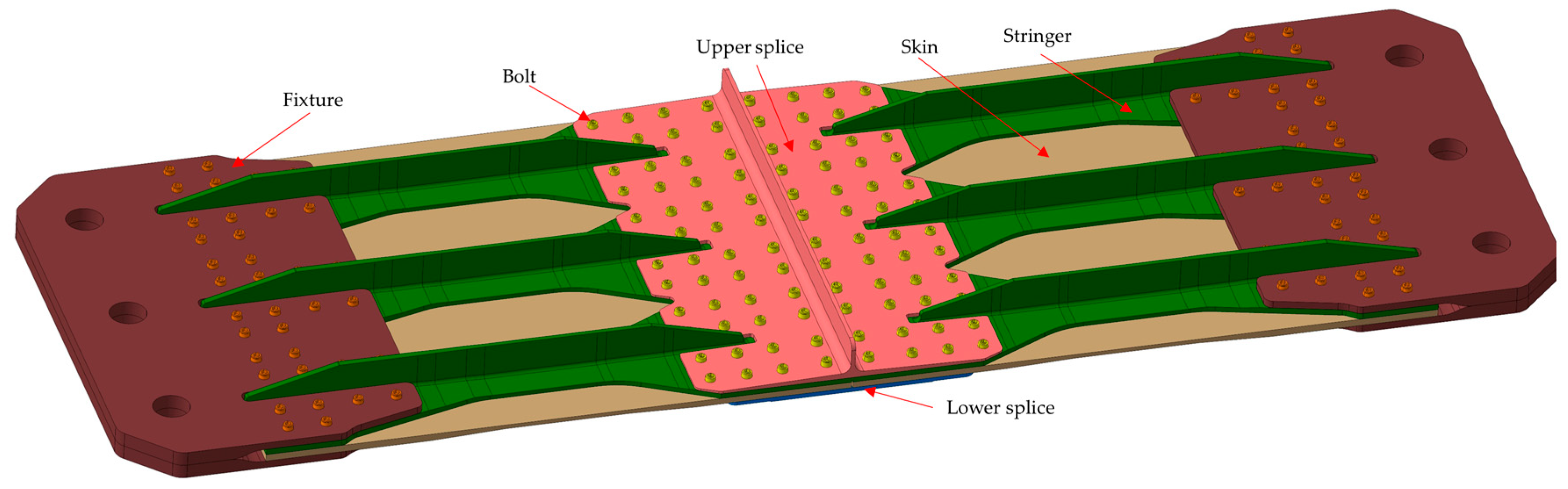
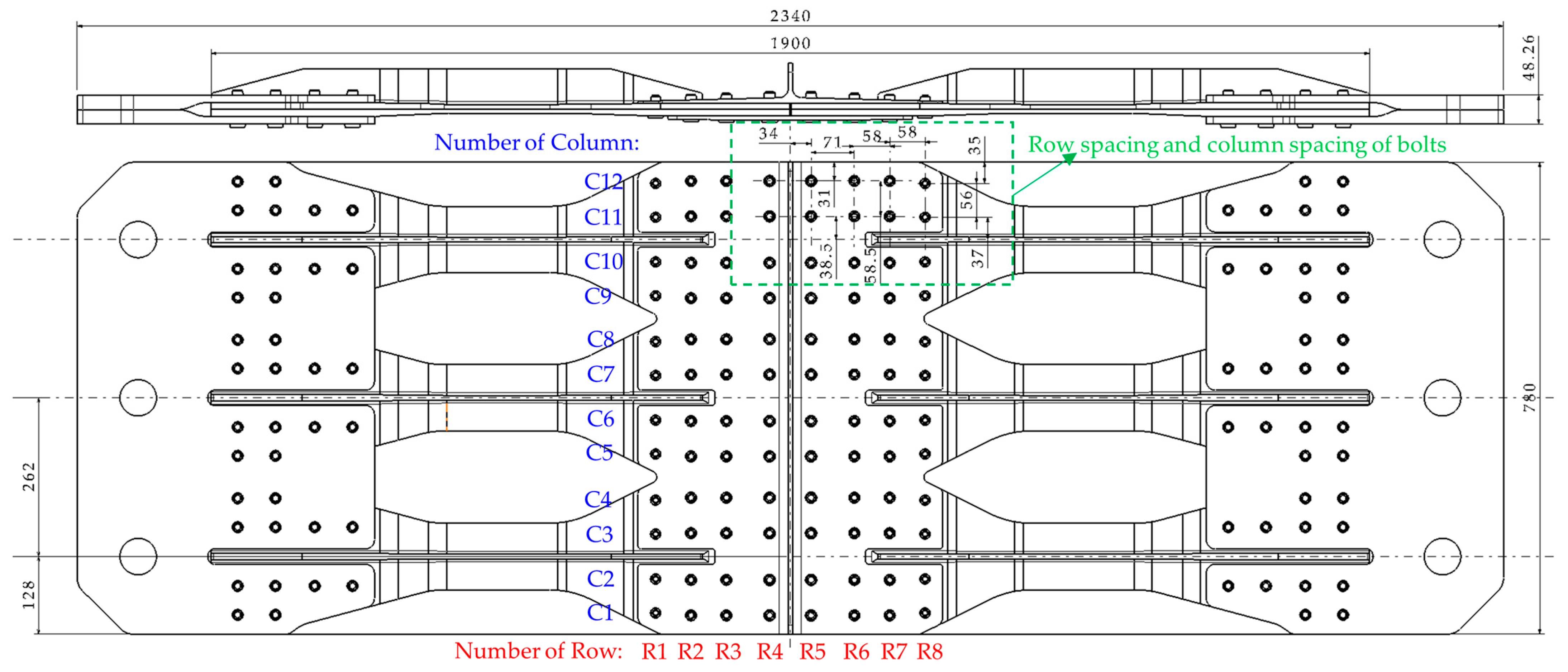
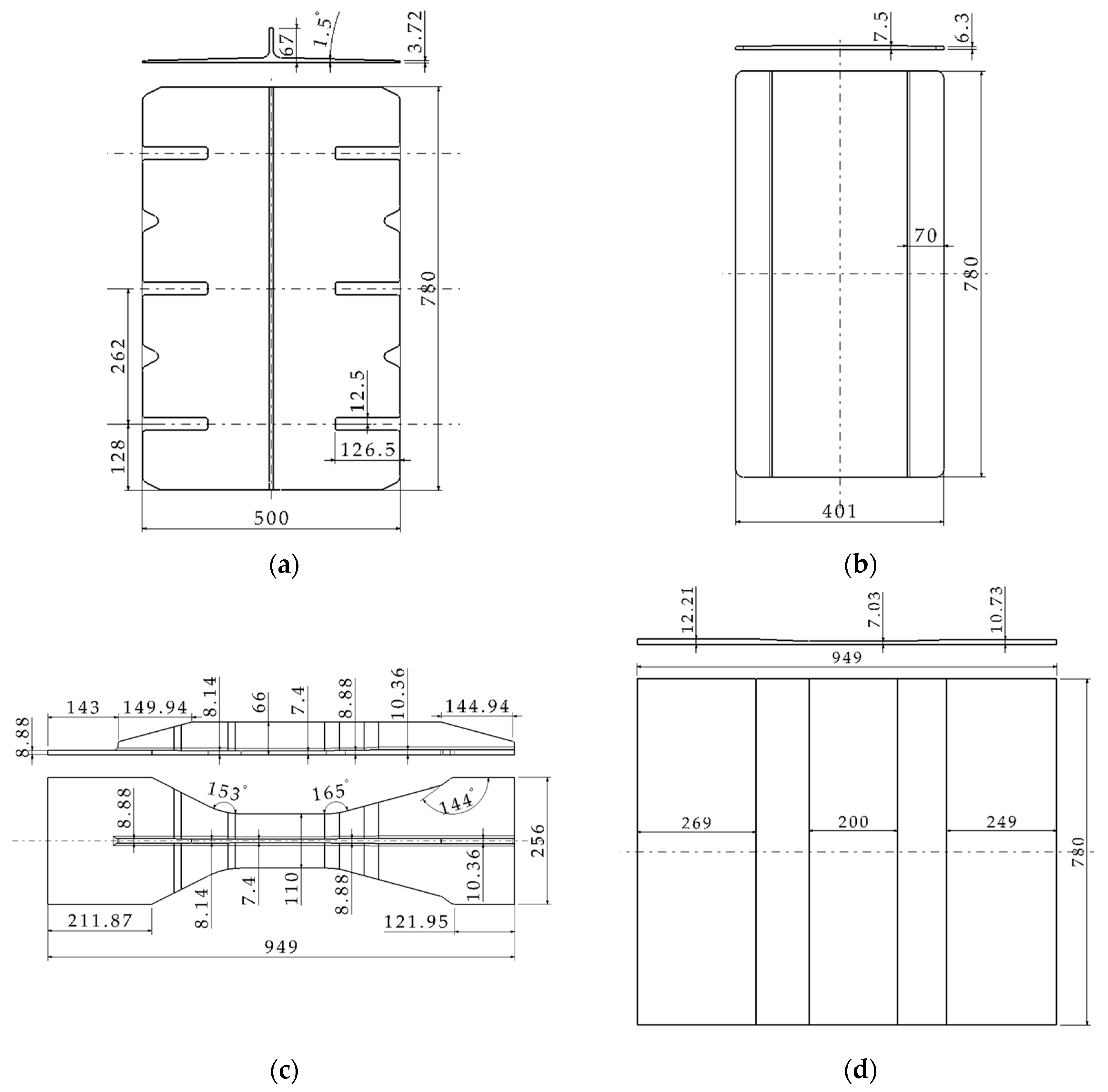
2. The Hybrid Panel Structure
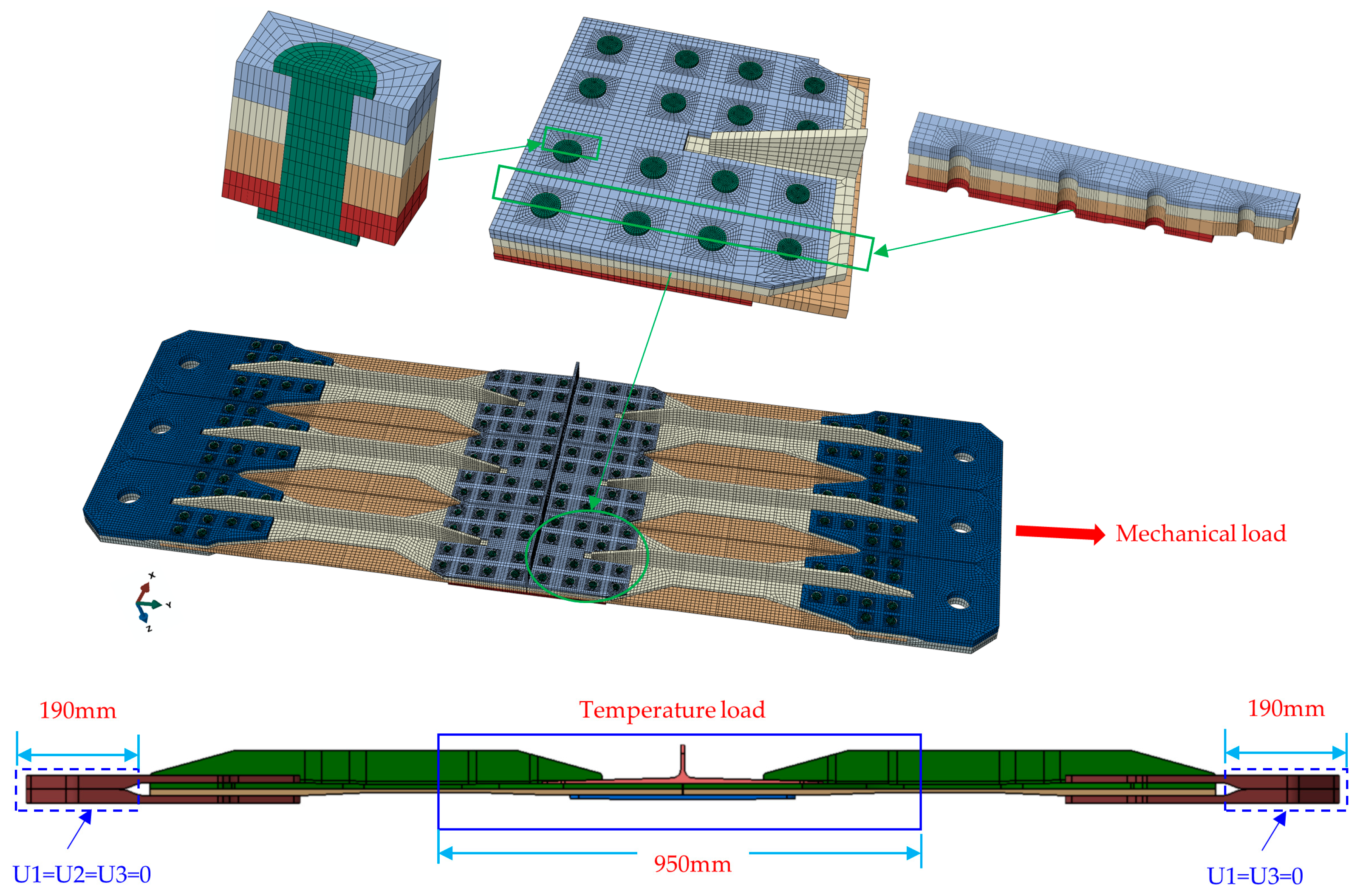
3. Finite Element Simulation of Hybrid Panel under Temperature Field
4. Experimental Design of Hybrid Panel
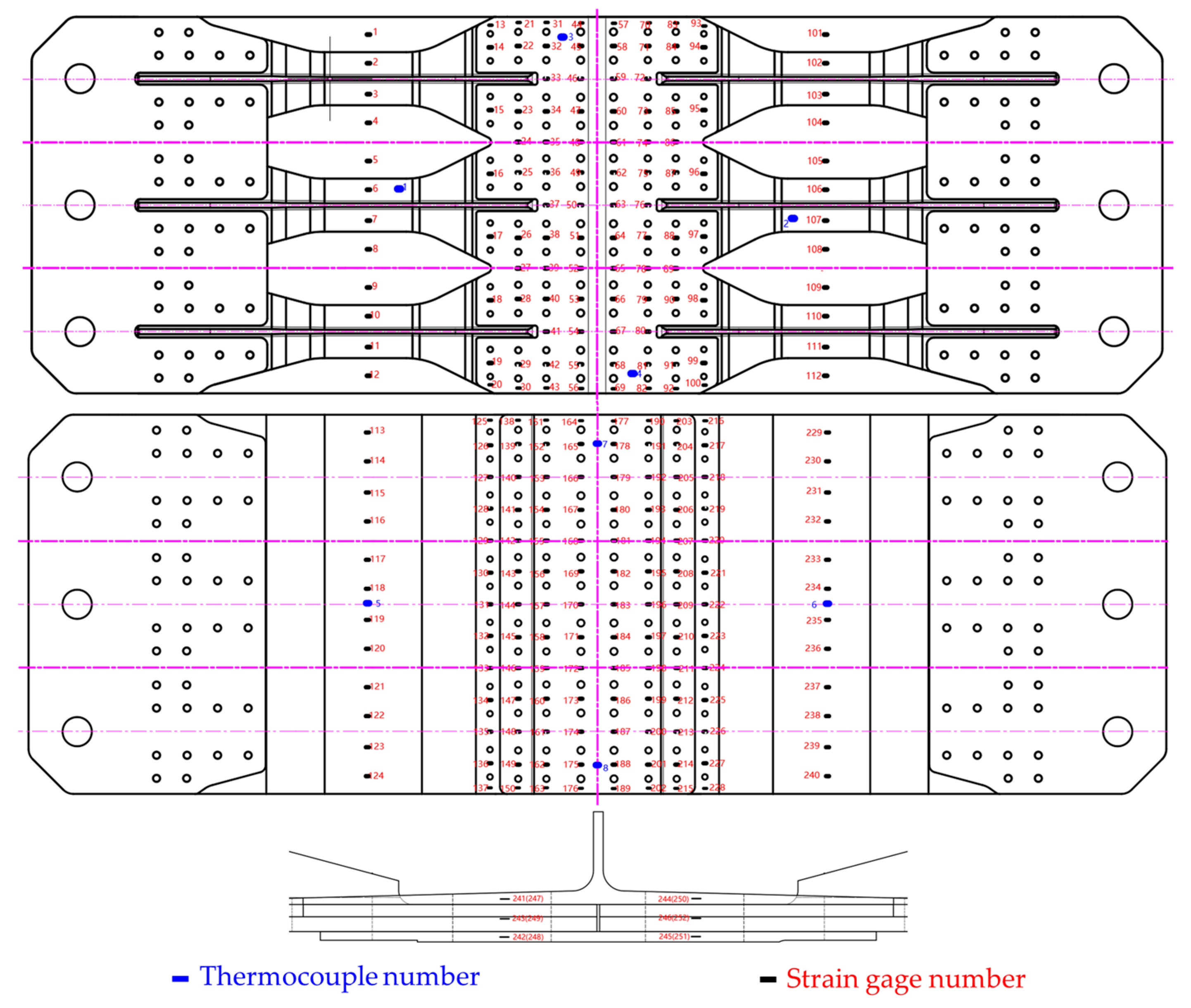
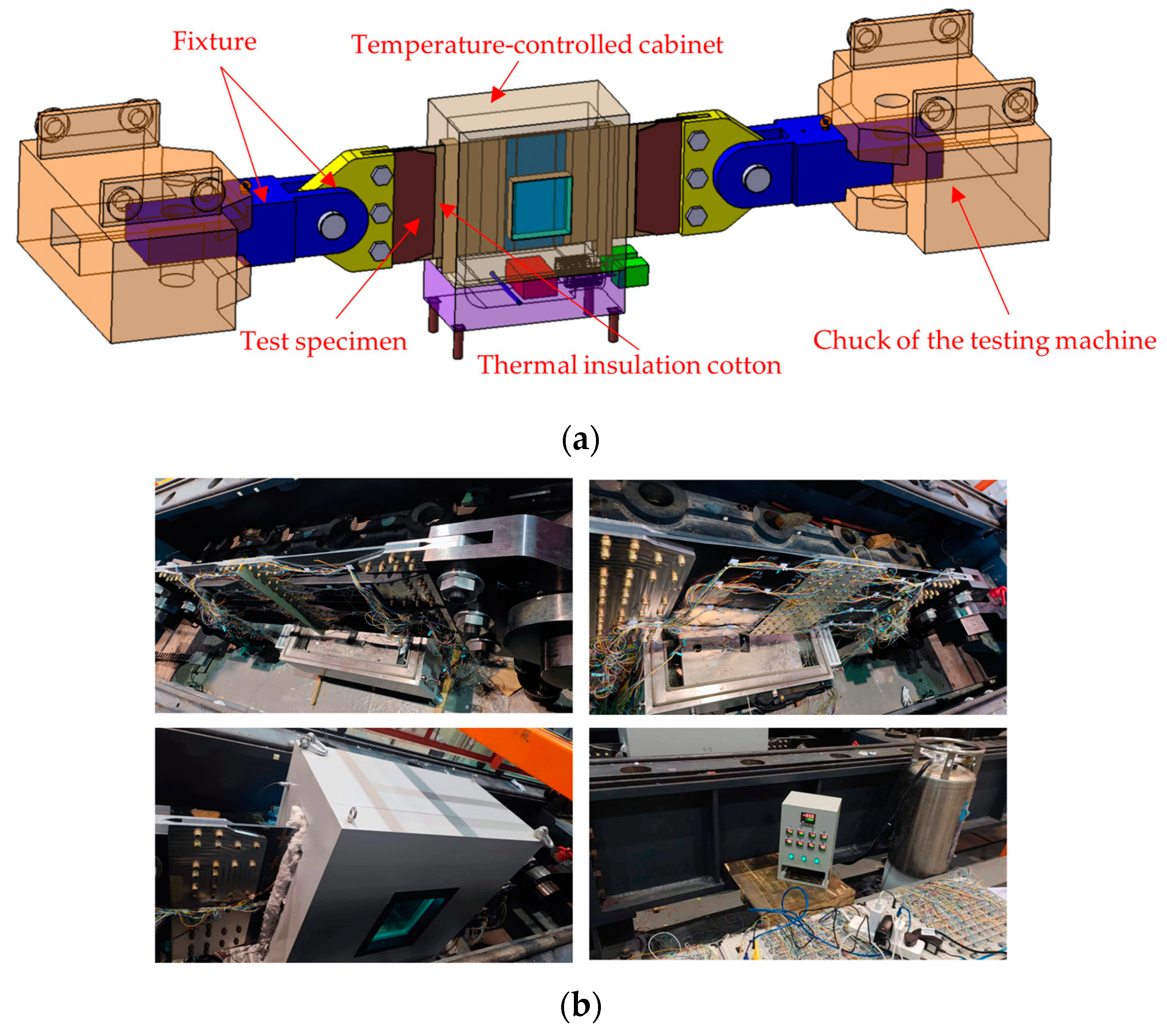
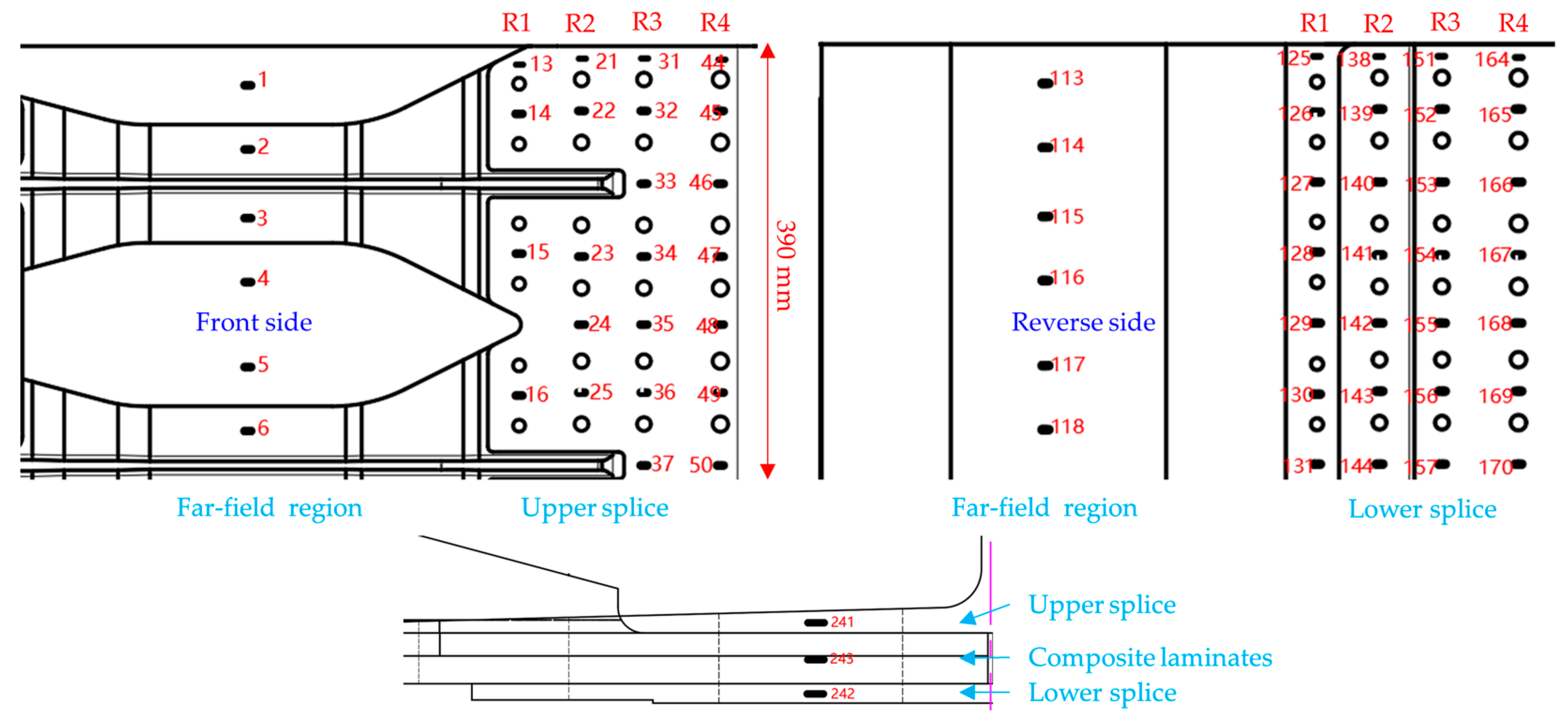
4.1. Test Design
4.2. Test Procedure
5. Comparison between Measured Results and Simulation Results
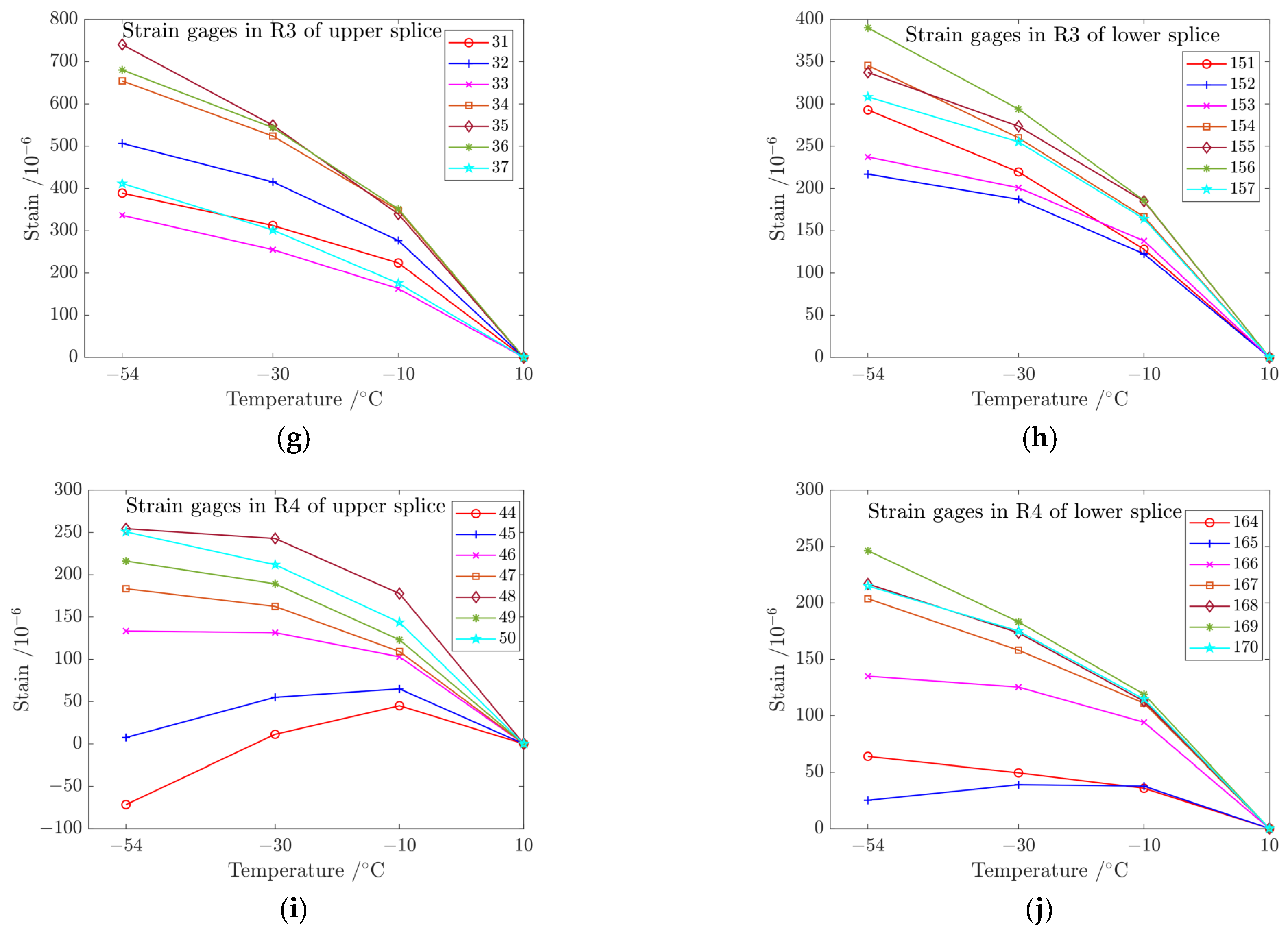
5.1. Strain Distribution with the Decrease in Temperature
5.2. Strain Distribution Included by Thermal Stress at a Working Temperature of −54 ℃
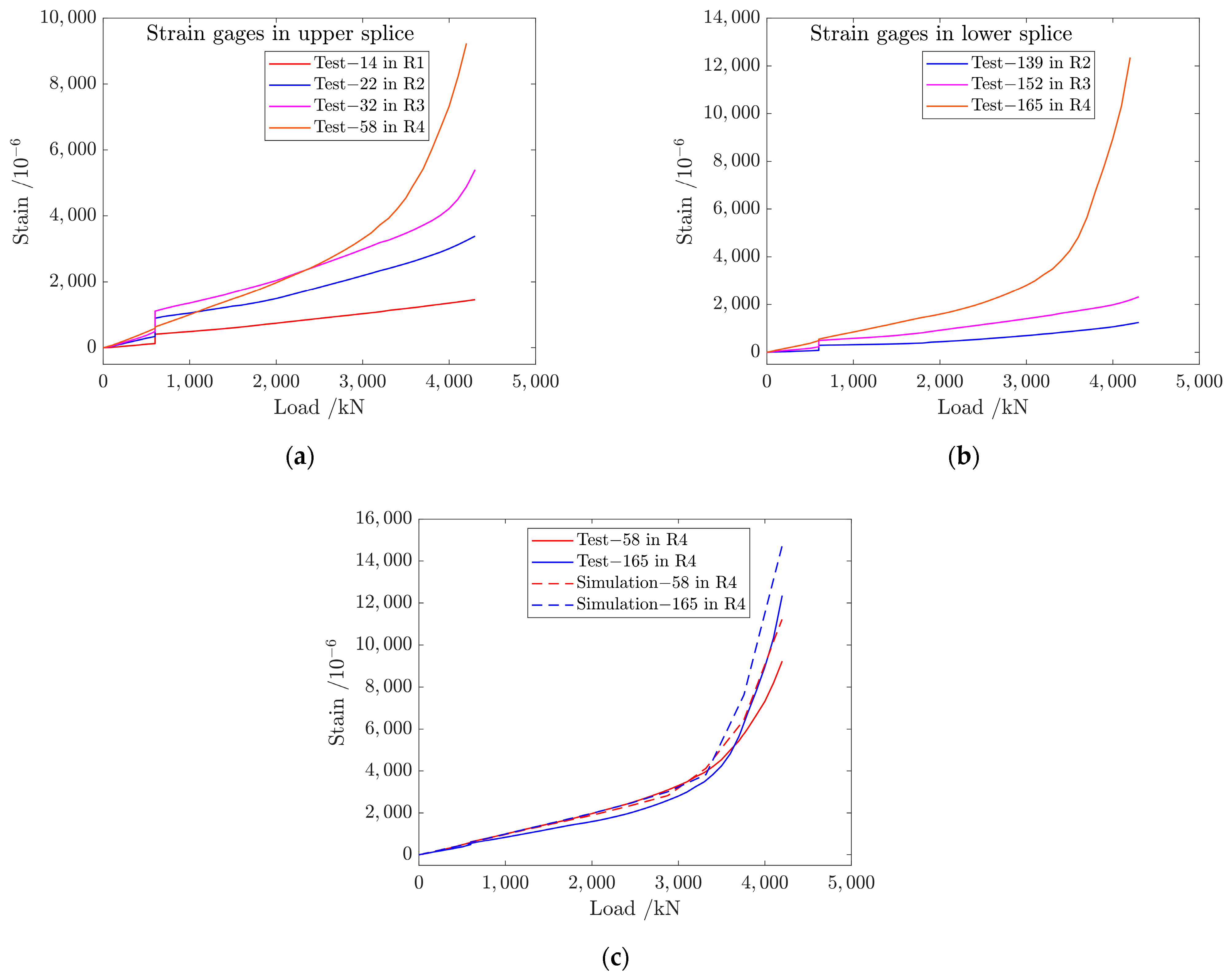
5.3. Fracture Load and Mode at a Working Temperature of −54 ℃
6. Effects of Temperature and Mechanical Load on Bolt Load Distribution of Hybrid Panel
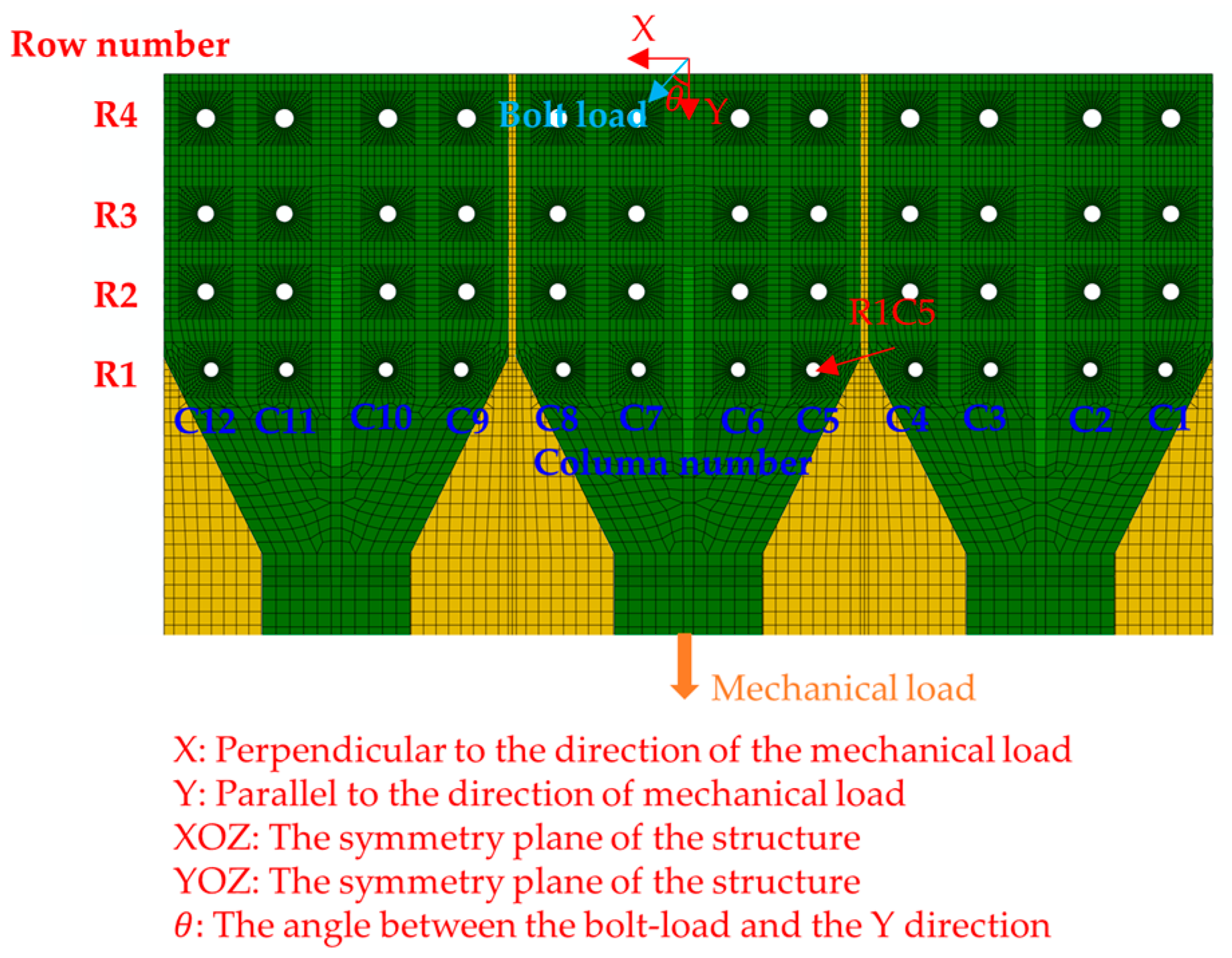
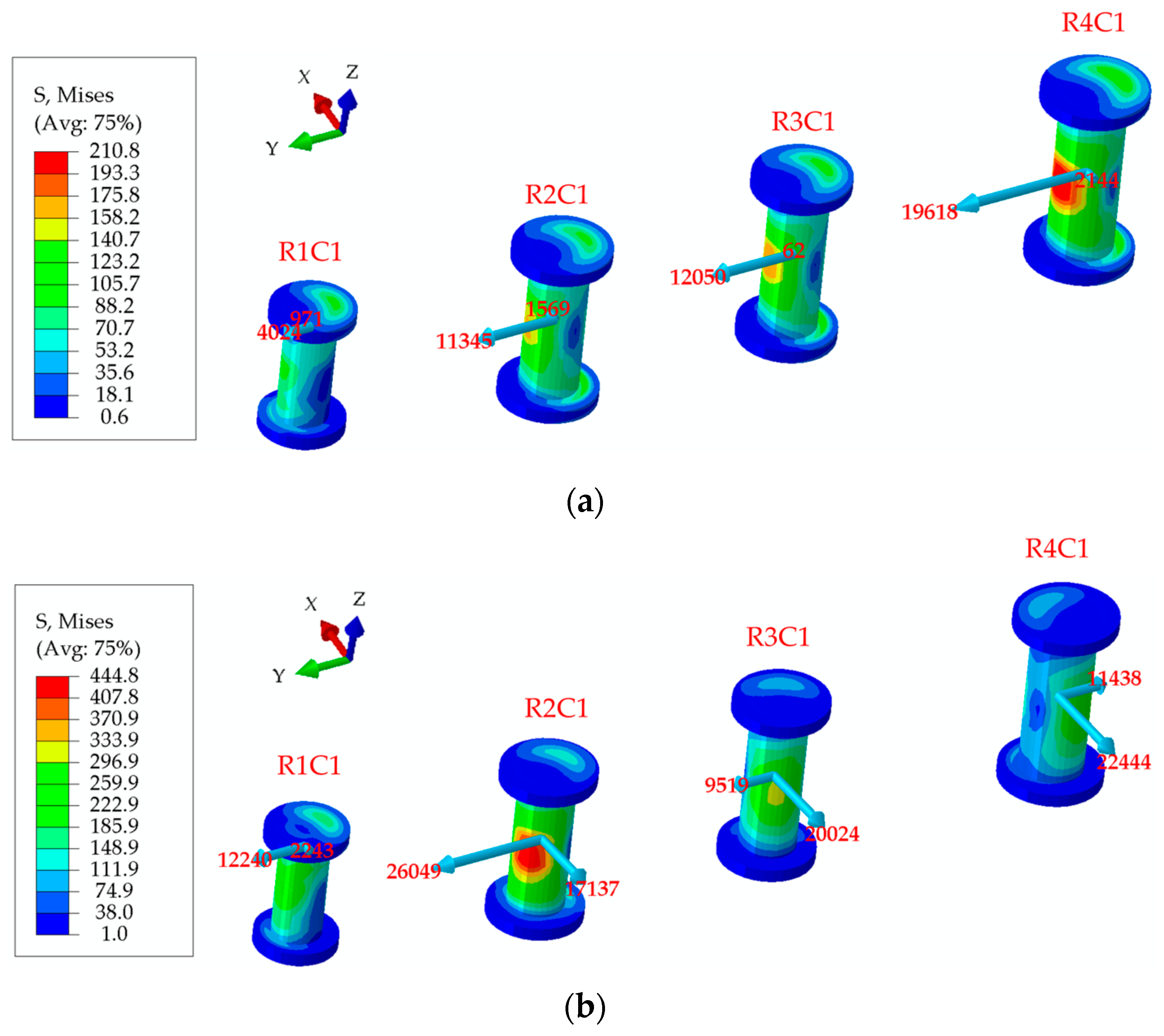
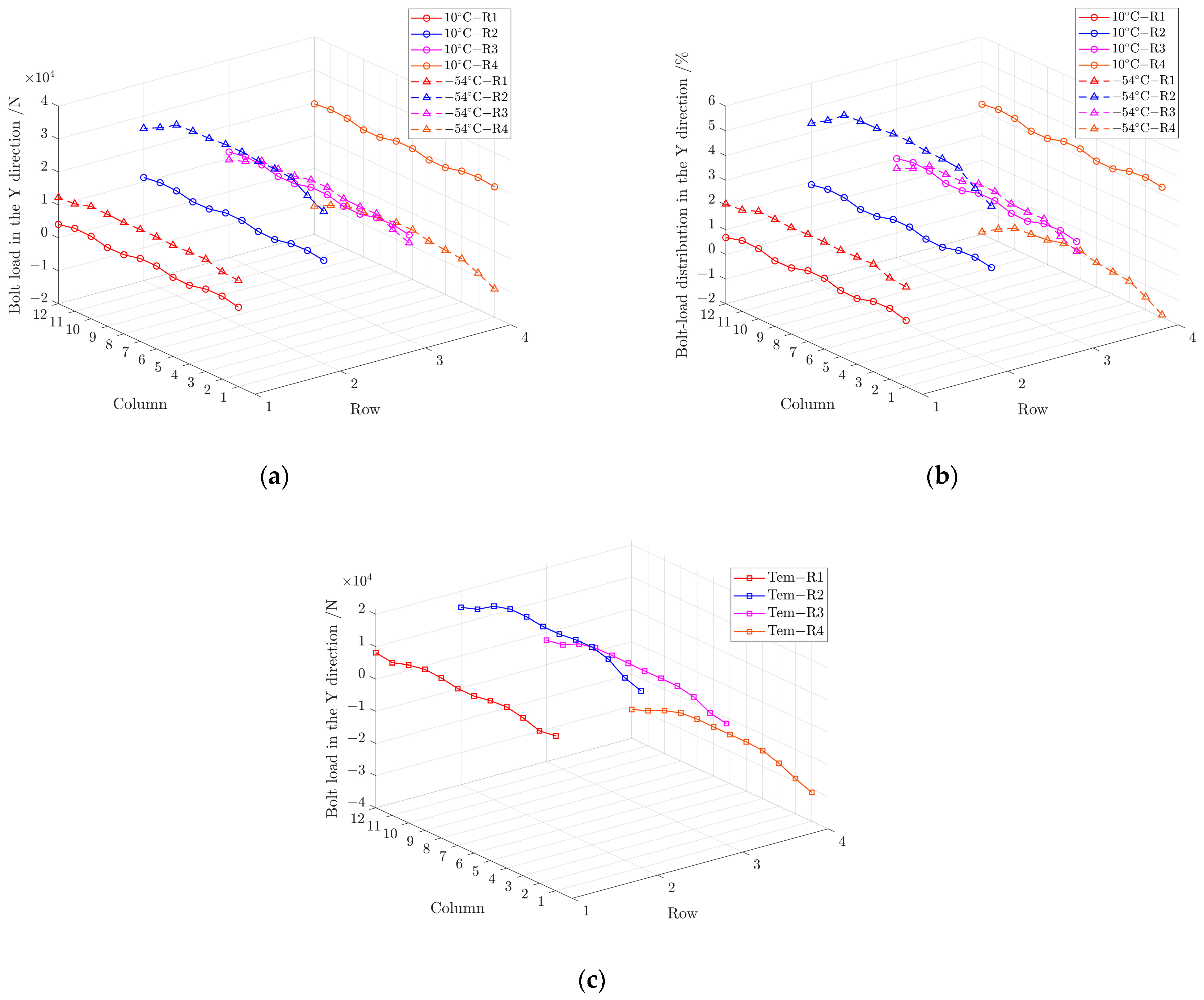
6.1. Analysis of Bolt-Load Distribution at a Working Temperature of −54 ℃
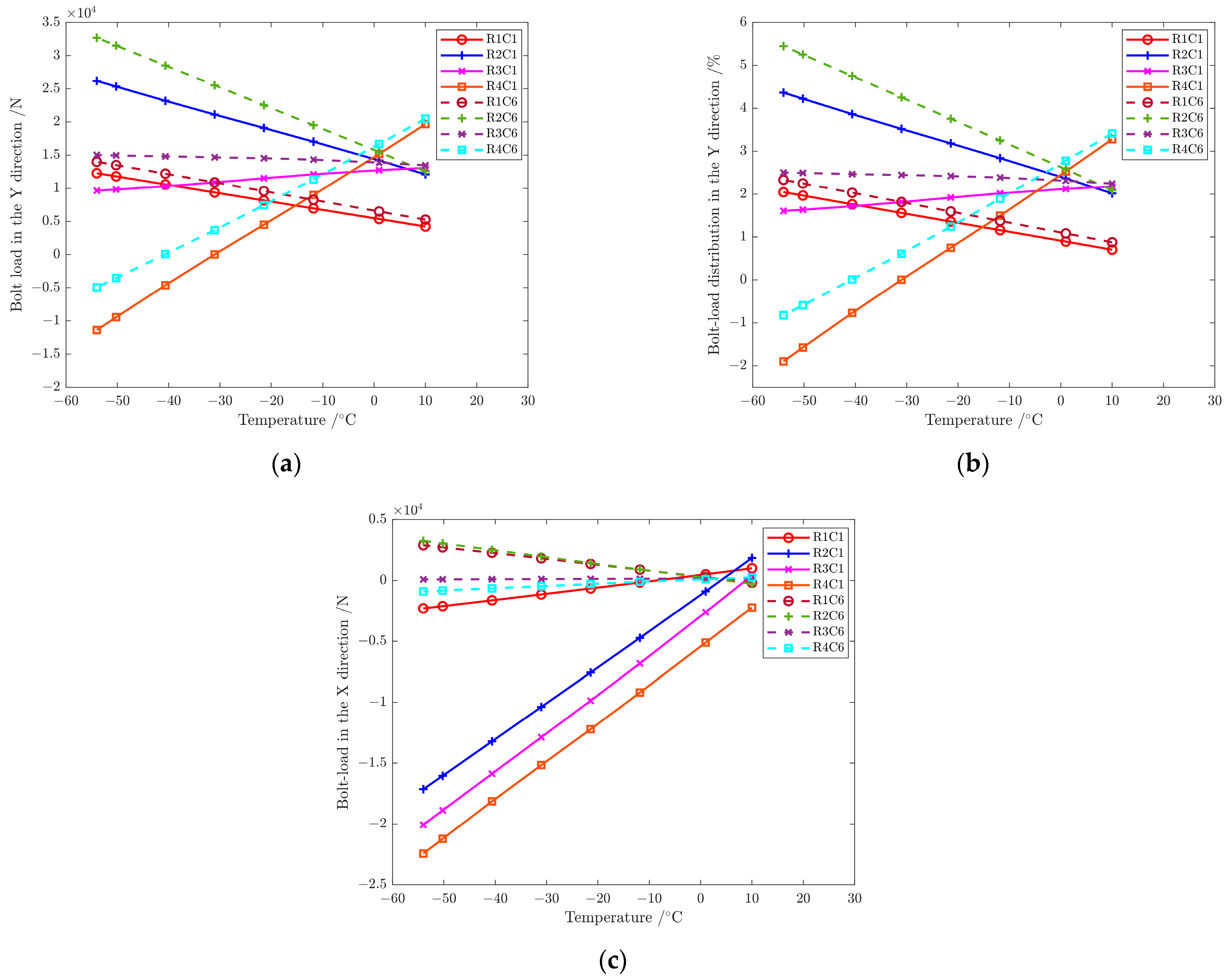
6.2. Influence of Temperature Change on Bolt-Load Distribution
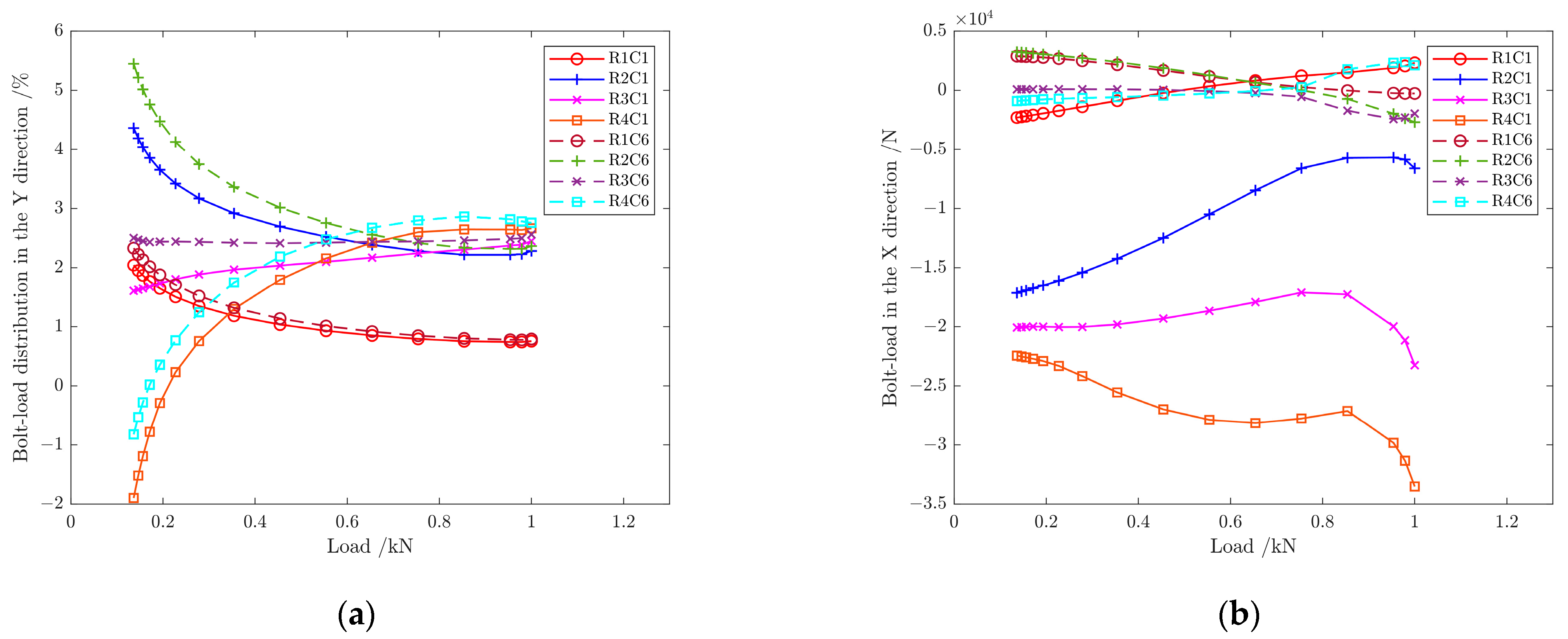
6.3. Influence of Mechanical Load Change on Bolt-Load Distribution
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Materials | Temperature/°C | E/MPa | /() |
|---|---|---|---|
| Ti-6Al-4V | 21.11 | 116,521 | 8.82 |
| −55 | 118,851 | 8.46 | |
| 2024-T351 | 21.11 | 73,777 | 22.17 |
| −55 | 76,728 | 21.78 |
| Seed Numbers | Maximum Stress at the Hole Edge/MPa | Bolt Load/kN | Calculation Time/s |
|---|---|---|---|
| 24 | 195.4 | 19.2 | 5164 |
| 28 | 203.5 | 19.5 | 6230 |
| 32 | 210.6 | 19.7 | 7489 |
| 36 | 212.3 | 19.8 | 9024 |
| 40 | 213.5 | 19.8 | 10,326 |
| Diameter/mm | Torque/Nm | Preload Value/kN |
|---|---|---|
| 11.1125 | 63.55 | 19.1 |
| 12.7 | 87.56 | 23.0 |
| 14.2875 | 121.46 | 28.3 |

Appendix B
- fiber tensile failure :
- fiber compression failure :
- matrix tensile failure :
- matrix tensile failure :
References
- Sun, Z.Q.; Wu, A.R. Application of advanced composite in aircraft structures. J. Mater. Rev. 2015, 29, 61–64. [Google Scholar]
- Dun, S.Y. Advanced composite materials and aerospace engineering. Acta Mater. Compos. Sin. 2007, 204, 1–12. [Google Scholar]
- Ma, L.M.; Zhang, J.Z.; Yue, G.Q. Application of composites in new generation of large civil aircraft. Acta Mater. Compos. Sin. 2015, 32, 317–322. [Google Scholar]
- Xie, S.S.; Wang, S.W.; Cheng, W.Z. The Manual for Air Frame Design: Volume 9. Master’s Thesis, Beijing Aviation Industry Press, Beijing, China, 2003. [Google Scholar]
- Gray, P.J.; Mccarthy, C.T. A global bolted joint model for finite element analysis of load distributions in multi-bolt composite joints. Compos. Part B Eng. 2010, 41, 317–325. [Google Scholar] [CrossRef]
- Liu, F.; Yao, W.; Zhao, L. An improved 2D finite element model for bolt load distribution analysis of composite multi-bolt single-lap joints. Compos. Struct. 2020, 253, 112770. [Google Scholar] [CrossRef]
- Sharos, P.A.; Mccarthy, C.T. Novel finite element for near real-time design decisions in multi-fastener composite bolted joints under various loading rates. Compos. Struct. 2020, 240, 112005. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Comparative analysis of FE modeling techniques for single-lap multi-column composite bolted joints. Int. Conf. Chem. Sci. Eng. 2023, 21, 121–128. [Google Scholar]
- Matthews, F.L.; Wong, C.M.; Chryssafitis, S. Stress distribution around a single bolt in fiber-reinforced plastic. Composites 1982, 13, 2623–2651. [Google Scholar] [CrossRef]
- Walker, S.P. Thermal effects on pin-bearing behavior of IM7/PETI5 composite joints. J. Compos. Mater. 2002, 13, 2623–2651. [Google Scholar] [CrossRef]
- Goswami, S. A finite element investigation on progressive failure analysis of composite bolted joints under thermal environment. J. Reinf. Plast. Compos. 2005, 24, 161–171. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, J.C.; Kang, B.S. Finite element analysis and modeling of structure with bolted joints. J. Appl. Math. Model. 2007, 31, 895–911. [Google Scholar] [CrossRef]
- Zhu, Z.X. Thermal Effect Analysis of Composite Laminates and Metal Connections for Aircraft. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Deng, W.L.; Tang, H.; Cheng, Z. Influence of temperature on bolt load distribution of composite and metal structures. J. Eng. Test 2018, 58, 27–30. [Google Scholar]
- Cai, Q.Y.; Zhang, Q. Effects of temperature and clearance fit on the load distribution of composite-metal hybrid structures. J. Acta Mater. Compos. Sin. 2021, 38, 4228–4238. [Google Scholar]
- Eriksson, I.; Backlund, J.; Moller, R. Design of multiple-row bolted composite joints under general in-plane loading. Compos. Eng. 1995, 5, 1051–1068. [Google Scholar] [CrossRef]
- Kradinov, V.; Barut, A.; Madenci, E. Bolted double-lap composite joints under mechanical and thermal loading. Int. J. Solids Struct. 2001, 38, 7801–7837. [Google Scholar] [CrossRef]
- Ekha, J.; Schon, J. Load transfer in multirow, single shear, composite-to-aluminum lap joints. Compos. Sci. Technol. 2006, 66, 875–885. [Google Scholar] [CrossRef]
- Ekha, J.; Schon, J.; Melin, L.G. Secondary bending in multi fastener, composite-to-aluminum single shear lap joints. Compos. Part B Eng. 2005, 66, 195–208. [Google Scholar] [CrossRef]
- Ekha, J.; Schon, J. Finite element modeling and optimization of load transfer in multi-fastener joints using structural element. J. Compos. Part 2008, 82, 245–246. [Google Scholar] [CrossRef]
- Yang, C.; Sun, W.; Seneviratne, W. Thermally induced loads of fastened hybrid composite/aluminum structures. J. Aircr. 2008, 45, 569–580. [Google Scholar] [CrossRef]
- Lei, K.; Wang, B.W.; Wu, J.T. Temperature-included load of bolted hybrid composite /metal joint. In Proceedings of the 32nd Congress of the International Council of the Aeronautical Sciences (ICAS 2021), Shanghai, China, 6–10 September 2021; pp. 1–11. [Google Scholar]
- Lei, K.; Wang, B.W.; Cheng, Z. Thermal stress analysis and verification of aircraft multi-bolt hybrid panel structure. Chin. J. Appl. Mech. 2023, 40, 41–47. [Google Scholar]
- Kapidzic, Z.; Nilsson, L.; Ansell, H. Finite element modeling of mechanically fastened composite-aluminum joints in aircraft structures. J. Compos. Struct. 2014, 109, 198–210. [Google Scholar] [CrossRef]
- Cheng, D.; Chen, Z.H. Mechanical properties of pure aluminum alloys at cryogenic temperatures. J. Aerosp. Mater. Technol. 2014, 41, 34–48. [Google Scholar]
- Ireman, T. Three-dimensional stress analysis of bolted single-lap composite joints. Compos. Struct. 1998, 43, 195–216. [Google Scholar] [CrossRef]
- Schon, J. Coefficient of friction for aluminum in contact with a carbon fiber epoxy composite. Tribol. Int. 2004, 3157, 385–404. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A fatigue failure criterion for fiber reinforced materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composite. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A progressive damage model for mechanically fastened joints in composite laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]








| Part | Thickness of Region/mm | Ply Information |
|---|---|---|
| Skin | 12.21 | [45/90/−45/90/−45/0/45/0/−45/0/45/0/0/−45/0/0/45/0/0/45/0/0/−45/0/0/45/0/0/−45/−45/0/0/45]s |
| 7.03 | [45/90/−45/90/−45/0/0/45/0/0/45/0/0/−45/0/0/−45/0/45]s | |
| 10.73 | [45/90/−45/90/−45/0/45/0/−45/0/45/0/0/−45/0/0/45/0/0/45/0/0/−45/0/0/−45/0/0/45]s | |
| Stringer | 10.36 | [45/90/−45/0/0/−45/0/0/45/90/45/0/0/−45/0/0/−45/0/0/45/0/45/0/−45/0/−45/0/45]s |
| 8.88 | [45/90/−45/0/0/−45/0/0/45/90/45/0/0/−45/0/0/−45/0/45/0/0/−45/0/45]s | |
| 7.4 | [45/90/−45/0/0/−45/0/0/45/0/0/−45/0/0/45/0/0/−45/0/45]s | |
| 8.14 | [45/90/−45/0/0/−45/0/0/45/90/45/0/0/−45/0/0/45/0/0/−45/0/45]s |
| /MPa | /MPa | /MPa | /() | /() | /() | |
|---|---|---|---|---|---|---|
| 163,500 | 9000 | 0.319 | 4140 | 3.5 | 32 | 32 |
| Part | Material | /MPa | /MPa | /MPa | /% | ) | |
|---|---|---|---|---|---|---|---|
| Splice | 2024-T351 | 73,777 | 344.7 | 475.2 | 12 | 0.33 | 22 |
| Bolt | Ti-6Al-4V | 116,521 | 820.5 | 951.5 | 10 | 0.31 | 8.8 |
| Fixture | 4130 | 199,810 | 985.9 | 1031.8 | 12 | 0.32 | 11 |
| Row Number | Column Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | ||
| R1 | load/kN | 4.1 | 5.1 | 5.0 | 3.9 | 4.0 | 5.1 | 5.1 | 4.0 | 3.9 | 5.0 | 5.1 | 4.1 |
| /° | 13.5 | −0.5 | 4.9 | −5.3 | 9.1 | −1.9 | 1.9 | −9.1 | 5.3 | −4.9 | 0.5 | −13.5 | |
| R2 | load/kN | 11.4 | 12.1 | 11.9 | 10.8 | 11.0 | 12.1 | 12.1 | 11.0 | 10.8 | 11.9 | 12.1 | 11.4 |
| /° | 7.9 | 2.8 | 4.7 | 2.5 | 1.0 | −1.2 | 1.2 | −1.0 | −2.5 | −4.7 | −2.8 | −7.9 | |
| R3 | load/kN | 12.1 | 12.9 | 12.7 | 11.5 | 11.6 | 12.8 | 12.8 | 11.6 | 11.5 | 12.7 | 12.9 | 12.1 |
| /° | 0.3 | 1.2 | 0.5 | 1.0 | 0.3 | 0.6 | −0.6 | −0.3 | −1.0 | −0.5 | −1.2 | −0.3 | |
| R4 | load/kN | 19.7 | 20.2 | 19.8 | 18.6 | 18.6 | 19.8 | 19.8 | 18.6 | 18.6 | 19.8 | 20.2 | 19.7 |
| /° | −6.2 | −1.6 | −1.0 | 0.1 | 0.1 | 0.7 | −0.7 | −0.1 | −0.1 | 1.0 | 1.6 | 6.2 | |
| R5 | load/kN | 19.7 | 20.2 | 19.8 | 18.6 | 18.6 | 19.8 | 19.8 | 18.6 | 18.6 | 19.8 | 20.2 | 19.7 |
| /° | −173.8 | −178.4 | −179.0 | 179.9 | 179.9 | 179.3 | −179.3 | −179.9 | −179.9 | 179.0 | 178.4 | 173.8 | |
| R6 | load/kN | 12.1 | 12.9 | 12.7 | 11.5 | 11.6 | 12.8 | 12.8 | 11.6 | 11.5 | 12.7 | 12.9 | 12.1 |
| /° | 179.7 | 178.8 | 179.5 | 179.0 | 179.7 | 179.4 | −179.4 | −179.7 | −179.0 | −179.5 | −178.8 | −179.7 | |
| R7 | load/kN | 11.4 | 12.1 | 11.9 | 10.8 | 11.0 | 12.1 | 12.1 | 11.0 | 10.8 | 11.9 | 12.1 | 11.4 |
| /° | 172.1 | 177.2 | 175.3 | 177.5 | 179.0 | −178.8 | 178.8 | −179.0 | −177.5 | −175.3 | −177.2 | −172.1 | |
| R8 | load/kN | 4.1 | 5.1 | 5.0 | 3.9 | 4.0 | 5.1 | 5.1 | 4.0 | 3.9 | 5.0 | 5.1 | 4.1 |
| /° | 166.5 | −179.5 | 175.1 | −174.7 | 170.9 | −178.1 | 178.1 | −170.9 | 174.7 | −175.1 | 179.5 | −166.5 | |
| Row Number | Column Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | ||
| R1 | load/kN | 12.4 | 12.7 | 14.7 | 14.0 | 13.8 | 14.2 | 14.2 | 13.8 | 14.0 | 14.6 | 12.7 | 12.4 |
| /° | −10.4 | 8.1 | −16.6 | −3.7 | −1.4 | 11.6 | −11.6 | 1.5 | 3.7 | 16.6 | −8.1 | 10.4 | |
| R2 | load/kN | 31.2 | 29.0 | 32.6 | 32.1 | 32.2 | 32.8 | 32.8 | 32.2 | 32.1 | 32.6 | 29.0 | 31.2 |
| /° | −33.3 | −10.4 | −14.1 | −2.6 | −3.9 | 5.7 | −5.7 | 3.8 | 2.6 | 14.0 | 10.4 | 33.3 | |
| R3 | load/kN | 22.2 | 14.6 | 14.5 | 13.7 | 14.1 | 15.0 | 15.0 | 14.1 | 13.7 | 14.5 | 14.6 | 22.2 |
| /° | −64.6 | −37.9 | −17.0 | −1.3 | −9.9 | 0.3 | −0.3 | 9.9 | 1.3 | 17.0 | 37.9 | 64.6 | |
| R4 | load/kN | 25.2 | 14.1 | 7.6 | 6.4 | 6.7 | 5.0 | 5.0 | 6.7 | 6.4 | 7.6 | 14.1 | 25.2 |
| /° | −117.0 | −129.0 | −152.7 | 177.5 | −152.7 | −169.7 | 170.0 | 152.9 | −177.2 | 152.9 | 129.1 | 117.0 | |
| R5 | load/kN | 25.2 | 14.1 | 7.6 | 6.4 | 6.7 | 5.0 | 5.0 | 6.7 | 6.4 | 7.6 | 14.1 | 25.2 |
| /° | −63.0 | −51.0 | −27.3 | 2.5 | −27.3 | −10.3 | 10.0 | 27.1 | −2.8 | 27.1 | 50.9 | 63.0 | |
| R6 | load/kN | 22.2 | 14.6 | 14.5 | 13.7 | 14.1 | 15.0 | 15.0 | 14.1 | 13.7 | 14.5 | 14.6 | 22.2 |
| /° | −115.4 | −142.1 | −163.0 | −178.7 | −170.1 | 179.7 | −179.7 | 170.1 | 178.7 | 163.0 | 142.1 | 115.4 | |
| R7 | load/kN | 31.2 | 29.0 | 32.6 | 32.1 | 32.2 | 32.8 | 32.8 | 32.2 | 32.1 | 32.6 | 29.0 | 31.2 |
| /° | −146.7 | −169.6 | −165.9 | −177.4 | −176.1 | 174.3 | −174.3 | 176.2 | 177.4 | 166.0 | 169.6 | 146.7 | |
| R8 | load/kN | 12.4 | 12.7 | 14.7 | 14.0 | 13.8 | 14.2 | 14.2 | 13.8 | 14.0 | 14.6 | 12.7 | 12.4 |
| /° | −169.6 | 171.9 | −163.4 | −176.3 | −178.6 | 168.4 | −168.4 | 178.5 | 176.3 | 163.4 | −171.9 | 169.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zheng, J.; Zeng, J.; Yang, G.; Tong, M. Thermal and Mechanical Stress Analysis in Aircraft Hybrid Panels with Multi-Bolt Joints. Materials 2024, 17, 1872. https://doi.org/10.3390/ma17081872
Zhang J, Zheng J, Zeng J, Yang G, Tong M. Thermal and Mechanical Stress Analysis in Aircraft Hybrid Panels with Multi-Bolt Joints. Materials. 2024; 17(8):1872. https://doi.org/10.3390/ma17081872
Chicago/Turabian StyleZhang, Junhua, Jie Zheng, Jianjiang Zeng, Guang Yang, and Mingbo Tong. 2024. "Thermal and Mechanical Stress Analysis in Aircraft Hybrid Panels with Multi-Bolt Joints" Materials 17, no. 8: 1872. https://doi.org/10.3390/ma17081872
APA StyleZhang, J., Zheng, J., Zeng, J., Yang, G., & Tong, M. (2024). Thermal and Mechanical Stress Analysis in Aircraft Hybrid Panels with Multi-Bolt Joints. Materials, 17(8), 1872. https://doi.org/10.3390/ma17081872








