Study on the Damage of Fiber-Reinforced Seawater Sea Sand Concrete by Freezing and Thawing of Seawater
Abstract
1. Introduction
2. Experimental Design
2.1. Raw Material
2.2. Mixing Ratio Design
2.3. Instrumentation
2.4. Specimen Preparation
2.5. Performance Test
2.5.1. Test Procedure
- (1)
- We removed the specimen from the curing room, selected the specimen with a flat surface and no missing corners, and soaked it in a white bucket filled with seawater at a temperature of 18–22 °C. The distance between the liquid surface of the bucket and the top surface of the specimen was 4 cm, and the soaking time was 4 days. This ensured that the water retention state was reached, as shown in Figure 7a.
- (2)
- We placed the soaked specimen into a stainless-steel groove measuring 120 mm × 120 mm × 480 mm and poured the original seawater into the stainless-steel groove. During the test, we ensured that the distance between the side of the specimen and the side wall of the stainless-steel groove was 2 cm, and that the seawater exceeded the top surface of the specimen by 2 cm.
- (3)
- We placed the stainless-steel tank containing seawater and test specimens into the freeze–thaw box, as shown in Figure 7b. We carried out 25, 50, and 75 cycles of freezing and thawing cycles of seawater. When the melting and freezing time exceeded 4 h, we poured distilled water into the external automatic water melting cycle box and maintained the melting temperature within the range of 18–20 °C, while ensuring that the temperature in the box remained within the range of −20 °C to −18 °C. We replaced the seawater solution used for soaking every other week.
- (4)
- Once the required number of cycles had been reached, we removed the specimen from the freeze–thaw machine and noted the changes in compressive strength, mass and dynamic elastic modulus of the concrete cube before and after the freeze–thaw cycles. If the mass loss rate exceeded 5% or the strength loss rate exceeded 25%, we discarded the specimen.
2.5.2. Data Acquisition
3. Results and Analysis
3.1. Experimental Phenomena
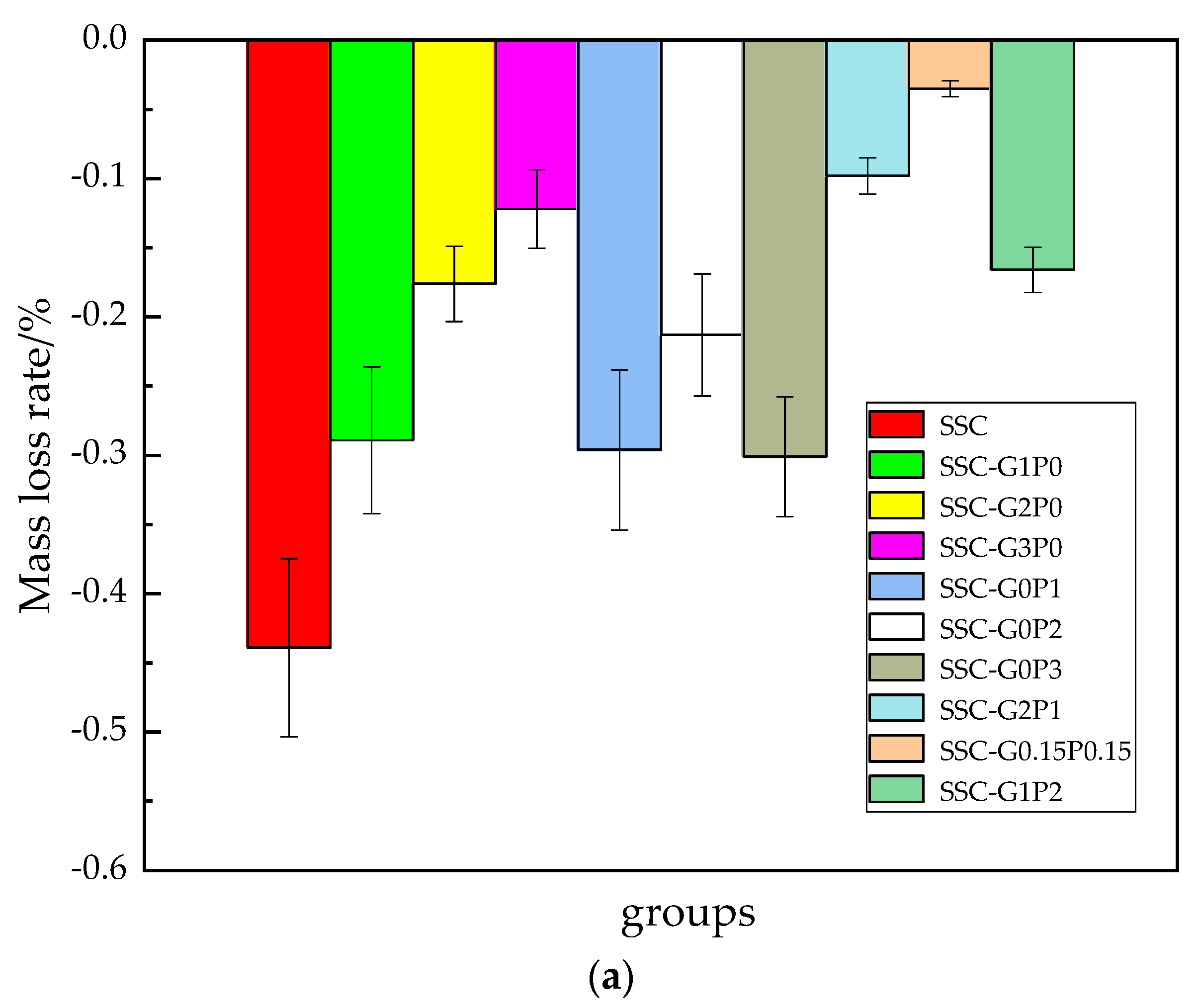
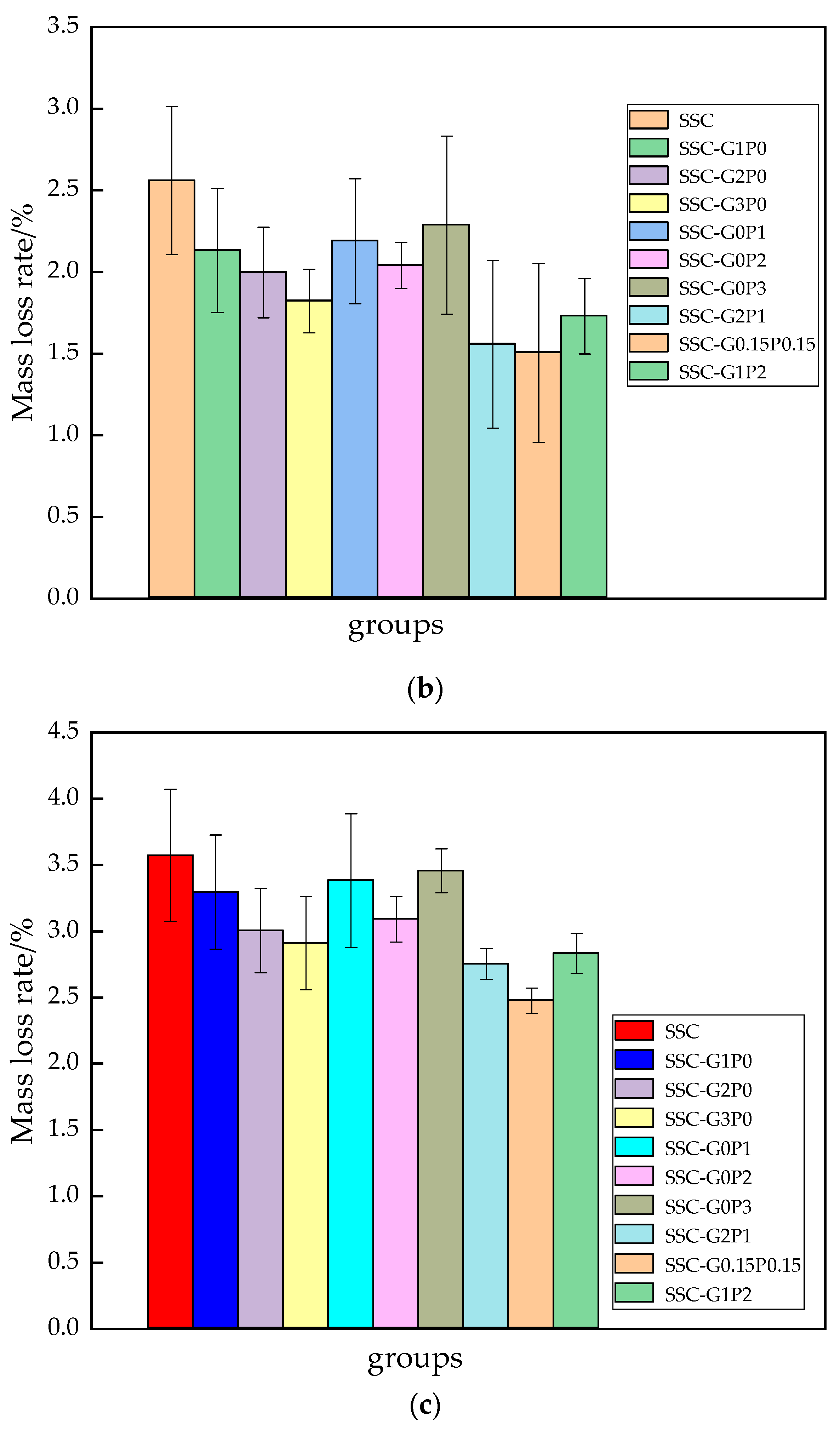
3.2. Rate of Quality Loss
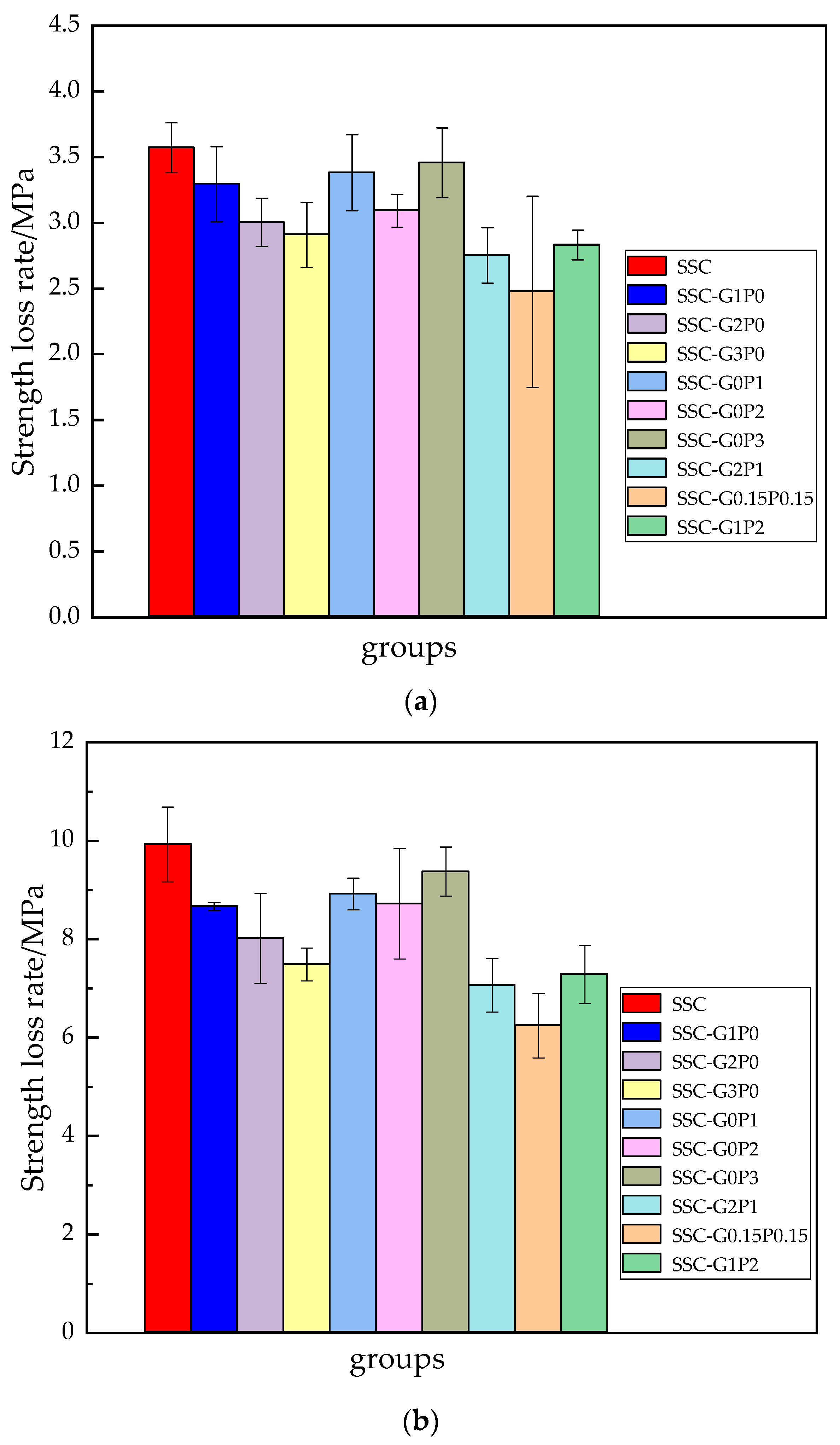
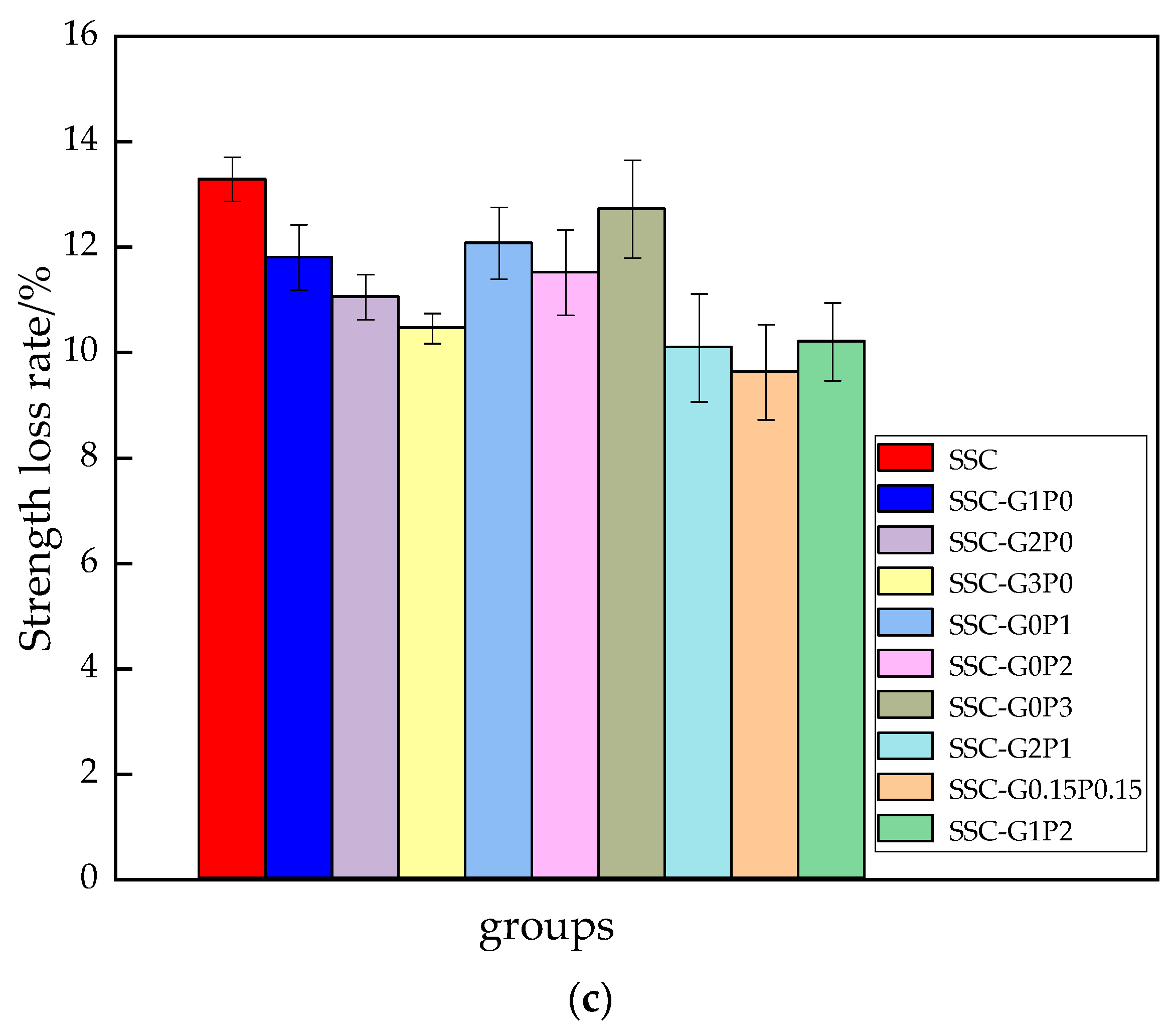
3.3. Rate of Strength Loss
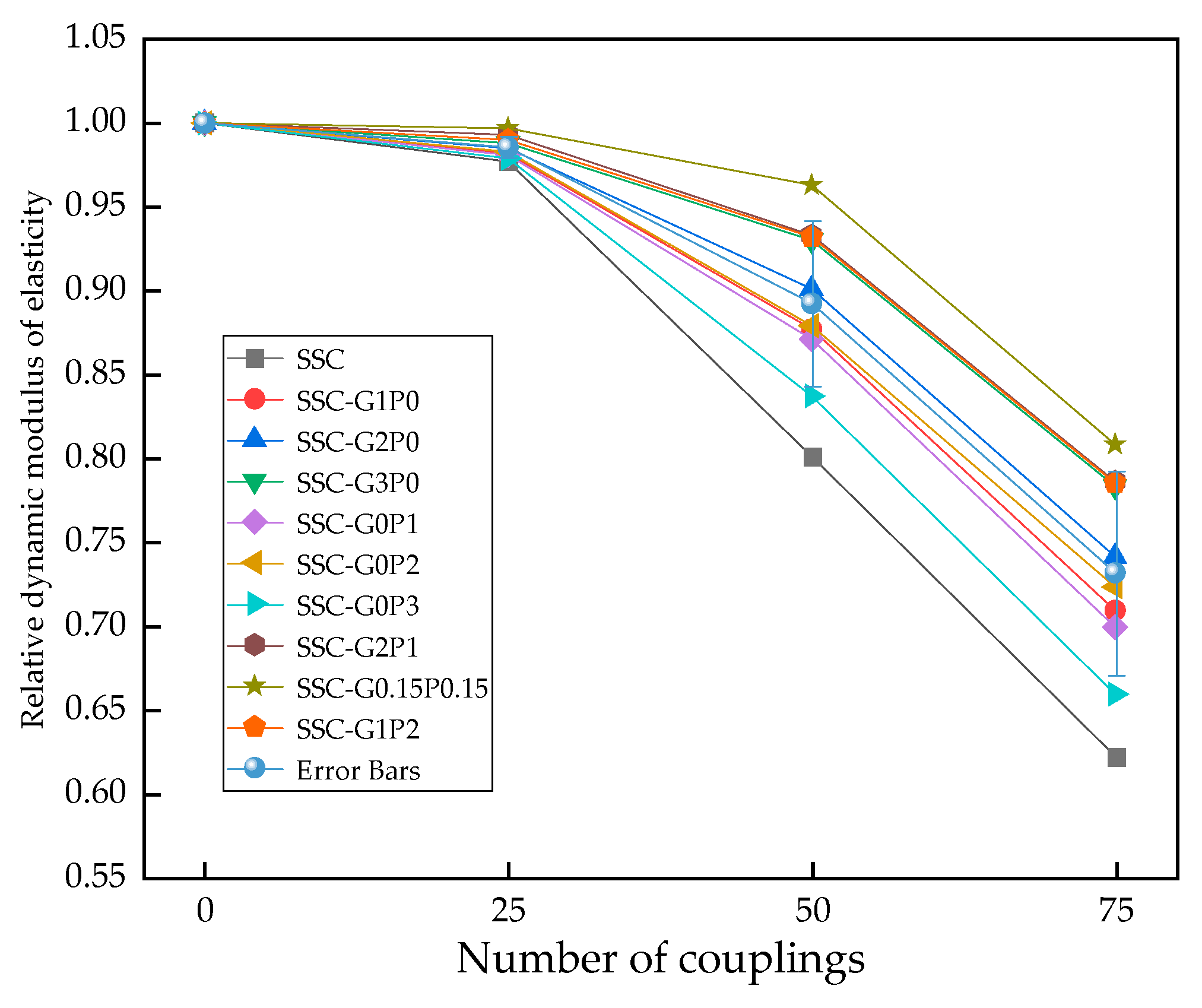
3.4. Relative Modulus of Elasticity
4. Microanalysis
5. NSGM(1,N)-Based Damage Prediction Models
5.1. Model Building
5.2. Accuracy Prediction
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Monteiro, P.J.M.; Miller, S.A.; Horvath, A. Towards sustainable concrete. Nat. Mater. 2017, 16, 698–699. [Google Scholar] [CrossRef] [PubMed]
- Wijayasundara, M.; Mendis, P.; Crawford, R.H. Integrated assessment of the use of recycled concrete aggregate replacing natural aggregate in structural concrete. J. Clean. Prod. 2018, 174, 591–604. [Google Scholar] [CrossRef]
- Sun, C.; Chen, Q.; Xiao, J.; Liu, W. Utilization of waste concrete recycling materials in self-compacting concrete. Resour. Conserv. Recycl. 2020, 161, 104930. [Google Scholar] [CrossRef]
- Xiong, Z.; Wei, W.; Liu, F.; Cui, C.; Li, L.; Zou, R.; Zeng, Y. Bond behaviour of recycled aggregate concrete with basalt fibre-reinforced polymer bars. Compos. Struct. 2021, 256, 113078. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Xiong, Z.; Lu, Z.; Li, L. Bond performance between fibre-reinforced polymer bars and concrete under pull-out tests. Constr. Build. Mater. 2019, 227, 116803. [Google Scholar] [CrossRef]
- Ebead, U.; Lau, D.; Lollini, F.; Nanni, A.; Suraneni, P.; Yu, T. A review of recent advances in the science and technology of seawater-mixed concrete. Cem. Concr. Res. 2022, 152, 106666. [Google Scholar] [CrossRef]
- Nishida, T.; Otsuki, N.; Ohara, H.; Garba-Say, Z.M.; Nagata, T. Some considerations for applicability of seawater as mixing water in concrete. J. Mater. Civ. Eng. 2015, 27, B4014004. [Google Scholar] [CrossRef]
- Priyadharshini, P.; Ramamurthy, K.; Robinson, R.G. Sustainable reuse of excavation soil in cementitious composites. J. Clean. Prod. 2018, 176, 999–1011. [Google Scholar] [CrossRef]
- Zhou, J.K.; He, X.; Wang, Z.Y. Research Progress on Seawater and Sea Sand Concrete and Its Potentia Hazards. Sci. Technol. Eng. 2018, 18, 179–187. [Google Scholar]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef]
- Xiong, Z.; Zeng, Y.; Li, L.G.; Kwan, A.K.; He, S.H. Experimental study on the effects of glass fibres and expansive agent on the bond behaviour of glass/basalt FRP bars in seawater sea-sand concrete. Constr. Build. Mater. 2021, 274, 122100. [Google Scholar] [CrossRef]
- Li, L.G.; Xiao, B.F.; Fang, Z.Q.; Xiong, Z.; Chu, S.H.; Kwan, A.K. Feasibility of glass/basalt fiber reinforced seawater coral sand mortar for 3D printing. Addit. Manuf. 2021, 37, 101684. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhao, X.L.; Raman, R.K.S.; Al-Saadi, S. Thermal and mechanical properties of alkali-activated slag paste, mortar and concrete utilising seawater and sea sand. Constr. Build. Mater. 2018, 159, 704–724. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, Y.; Li, P.D.; Li, H. Shear behaviour of seawater sea-sand coral aggregate concrete beams reinforced with FRP strip stirrups. Eng. Struct. 2023, 290, 116332. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.S.; Al-Saadi, S.; Haque, A. Long-term durability of basalt-and glass-fibre reinforced polymer (BFRP/GFRP) bars in seawater and sea sand concrete environment. Constr. Build. Mater. 2017, 139, 467–489. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, J.; Zhang, P.; Zhang, K. Mechanical behaviour of seawater sea-sand recycled coarse aggregate concrete columns under axial compressive loading. Constr. Build. Mater. 2019, 229, 117050. [Google Scholar] [CrossRef]
- Sun, J.; Ding, Z.; Li, X.; Wang, Z. Bond behavior between BFRP bar and basalt fiber reinforced seawater sea-sand recycled aggregate concrete. Constr. Build. Mater. 2021, 285, 122951. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Xiong, Z.; Yang, F.; Li, L.; Luo, H. Effect of loading rates on bond behaviour between basalt fibre-reinforced polymer bars and concrete. Constr. Build. Mater. 2020, 231, 117138. [Google Scholar] [CrossRef]
- Ge, L.; Feng, Z.; Sayed, U.; Li, H. Research on the performance of seawater sea-sand concrete: A review. Constr. Build. Mater. 2023, 409, 133921. [Google Scholar] [CrossRef]
- Sun, N.; Yang, L.; Liu, X. Analysis of creep process of marine concrete. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Florence, Italy, 24–27 September 2019; IOP Publishing: Bristol, UK, 2020; Volume 446, p. 052004. [Google Scholar]
- Ahmed, A.; Guo, S.; Zhang, Z.; Shi, C.; Zhu, D. A review on durability of fiber reinforced polymer (FRP) bars reinforced seawater sea sand concrete. Constr. Build. Mater. 2020, 256, 119484. [Google Scholar] [CrossRef]
- Zhang, W.; Ye, F.P. Problems and countermeasures of sea sand concrete in coastal cities. Technol. Mark. 2013, 20, 104–106. [Google Scholar]
- Hasanzade-Inallu, A.; Zarfam, P.; Nikoo, M. Modified imperialist competitive algorithm-based neural network to determine shear strength of concrete beams reinforced with FRP. J. Cent. South Univ. 2019, 26, 3156–3174. [Google Scholar] [CrossRef]
- Ashraf, M.; Iqbal, M.F.; Rauf, M.; Ashraf, M.U.; Ulhaq, A.; Muhammad, H.; Liu, Q.F. Developing a sustainable concrete incorporating bentonite clay and silica fume: Mechanical and durability performance. J. Clean. Prod. 2022, 337, 130315. [Google Scholar] [CrossRef]
- Liu, Q.; Iabal, M.F.; Yang, J.; Lu, X.Y.; Zhang, P.; Rauf, M. Prediction of chloride diffusivity in concrete using artificial neural network: Modelling and performance evaluation. Constr. Build. Mater. 2021, 268, 121082. [Google Scholar] [CrossRef]
- Li, S.; Zhu, D.; Guo, S.; Yi, Y.; Feng, G. Experimental study on the effects of dynamic loading and seawater attack on bond behavior between basalt fiber reinforced polymer bars and seawater sea-sand concrete. J. Build. Eng. 2023, 72, 106505. [Google Scholar] [CrossRef]
- Fu, X.; Zhao, G.; Wang, M.; Wang, J.; Xu, Y.; Gu, C. Comprehensive evaluation method for structural behavior of concrete dams in cold regions. Eng. Struct. 2023, 278, 115435. [Google Scholar] [CrossRef]
- Chen, K.; Wu, D.; Xia, L.; Cai, Q.; Zhang, Z. Geopolymer concrete durability subjected to aggressive environments—A review of influence factors and comparison with ordinary Portland cement. Constr. Build. Mater. 2021, 279, 122496. [Google Scholar] [CrossRef]
- Mari, A.; Mirambell, E.; Estrada, I. Effects of construction process and slab prestressing on the serviceability behaviour of composite bridges. J. Constr. Steel Res. 2003, 59, 135–163. [Google Scholar] [CrossRef]
- Shi, T.; Deng, C.; Zhao, J.; Ding, P.; Fan, Z. Temperature field of concrete cured in winter conditions using thermal control measures. Adv. Mater. Sci. Eng. 2022, 2022, 7255601. [Google Scholar] [CrossRef]
- Alsaif, A.; Bernal, S.A.; Guadagnini, M.; Pilakoutas, K. Freeze-thaw resistance of steel fibre reinforced rubberised concrete. Constr. Build. Mater. 2019, 195, 450–458. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, J.; Xu, C.; Dang, F.; Zhou, H.; Shi, L. Experimental study and evaluation of bonding properties between fiber and cement matrix under sulfate attack. J. Build. Eng. 2023, 76, 107306. [Google Scholar] [CrossRef]
- Su, Y.; Xiong, Z.; Hu, Z.; Zhu, W.; Zhou, K.; Wang, J.; Liu, F.; Li, L. Dynamic bending study of glass fiber reinforced seawater and sea-sand concrete incorporated with expansive agents. Constr. Build. Mater. 2022, 358, 129415. [Google Scholar] [CrossRef]
- Chen, J.; Jia, J.; Zhu, M. Development of admixtures on seawater sea sand concrete: A critical review on Concrete hardening, chloride ion penetration and steel corrosion. Constr. Build. Mater. 2024, 411, 134219. [Google Scholar] [CrossRef]
- Ganesan, N.; Indira, P.V.; Sabeena, M.V. Bond stress slip response of bars embedded in hybrid fibre reinforced high performance concrete. Constr. Build. Mater. 2014, 50, 108–115. [Google Scholar] [CrossRef]
- Guo, M.; Hu, B.; Xing, F.; Zhou, X.; Sun, M.; Sui, L.; Zhou, Y. Characterization of the mechanical properties of eco-friendly concrete made with untreated sea sand and seawater based on statistical analysis. Constr. Build. Mater. 2020, 234, 117339. [Google Scholar] [CrossRef]
- Xiao, J.; Qiang, C.; Nanni, A.; Zhang, K. Use of sea-sand and seawater in concrete construction: Current status and future opportunities. Constr. Build. Mater. 2017, 155, 1101–1111. [Google Scholar] [CrossRef]
- Xu, G.; Gong, C.; Liu, J.; Gao, D.J.; Zeng, Z. Correlation between Water Freeze-Thaw Resistance and Salt Thaw Resistance of Concrete. J. Build. Mater. 2020, 23, 552–556+562. [Google Scholar]
- GB/T50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Construction of the People’s Republic of China: Beijing, China, 2019.
- GB/T50082-2009; Standard for Long-term Performance and Durability Test Methods for Ordinary Concrete. Ministry of Housing and Urban-Rural Development of PRC: Beijing, China, 2009.
- Zeng, B. Grey Prediction Theory and Its Application; Science Press: Beijing, China, 2020. [Google Scholar]
- Liu, S.F.; Guo, T.B.; Dang, H.G. Grey System Theory and Its Application, 2nd ed.; Science Press: Beijing, China, 1999. [Google Scholar]
- Deng, J.L. Grey Prediction and Decision Making; Huazhong University of Science and Technology Press: Wuhan, China, 1988. [Google Scholar]
- Liu, S.F.; Yang, Y.J.; Wu, L.W. Grey System Theory and Its Application, 7th ed.; Science Press: Beijing, China, 2014. [Google Scholar]










| Chemical Composition | SiO2 | Al2O3 | Fe2O3 | CaO | K2O | MgO |
|---|---|---|---|---|---|---|
| Quantity contained (%) | 19.1 | 6.2 | 3.31 | 64.6 | 5.91 | 2.93 |
| Cement | Densities (g·cm−3) | Incipient Condensation Time (min) | Final Setting Time (min) | Flexural Strength (MPa) | Compressive Strength (MPa) | ||
|---|---|---|---|---|---|---|---|
| 3 d | 28 d | 3 d | 28 d | ||||
| P-O42.5 | 3.1 | 160.5 | 260.5 | 5.18 | 8.88 | 24.59 | 49.87 |
| Aggregate | Apparent Density (g·cm−3) | Packing Density (g·cm−3) | Mud Content (%) | Grain Size Grading (mm) | Needle and Flake Content (%) |
|---|---|---|---|---|---|
| Coarse aggregate | 2658 | 1445 | 0.29 | 5–20 | 15 |
| Ion Type | CI− | Ca2+ | Mg2+ | K+ | Na2+ | |
|---|---|---|---|---|---|---|
| Ionic concentration | 2116 | 15,723 | 257 | 7699 | 231 | 958 |
| Fiber Type | Lengths (mm) | Densities (g·cm−3) | Modulus of Elasticity (GPa) | Ultimate Elongation (%) | Tensile Strength (MPa) | Geometry |
|---|---|---|---|---|---|---|
| GF | 12 | 2.65 | 80 | 2.47 | 2300 | Slub yarn |
| PVA | 12 | 1.29 | 40 | - | 1750 | Fasciculated |
| Coarse Aggregate (kg·m−3) | Fine Aggregate (kg·m−3) | Cement (kg·m−3) | Sea Water (kg·m−3) | Water–Cement Ratio | Sand Rate (%) |
|---|---|---|---|---|---|
| 1173 | 660 | 417 | 200 | 0.48 | 36 |
| Test Grouping | Fiber Doping/% | Quality Loss Rate/% | Strength Loss Rate/% | Relative Modulus of Elasticity | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GF | PVA | 25 Times | 50 Times | 75 Times | 25 Times | 50 Times | 75 Times | 25 Times | 50 Times | 75 Times | |
| SSC | 0 | 0 | −0.439 | 1.315 | 2.559 | 3.572 | 9.926 | 13.287 | 0.977 | 0.801 | 0.622 |
| SSC-G1P0 | 0.1 | 0 | −0.289 | 1.107 | 2.131 | 3.295 | 8.667 | 11.802 | 0.982 | 0.877 | 0.709 |
| SSC-G2P0 | 0.2 | 0 | −0.176 | 0.942 | 1.996 | 3.004 | 8.02 | 11.051 | 0.985 | 0.901 | 0.741 |
| SSC-G3P0 | 0.3 | 0 | −0.122 | 0.769 | 1.821 | 2.909 | 7.485 | 10.456 | 0.988 | 0.930 | 0.783 |
| SSC-G0P1 | 0 | 0.1 | −0.296 | 1.121 | 2.188 | 3.382 | 8.917 | 12.073 | 0.981 | 0.871 | 0.699 |
| SSC-G0P2 | 0 | 0.2 | −0.213 | 0.999 | 2.039 | 3.092 | 8.721 | 11.515 | 0.983 | 0.879 | 0.723 |
| SSC-G0P3 | 0 | 0.3 | −0.301 | 1.243 | 2.286 | 3.457 | 9.374 | 12.718 | 0.979 | 0.837 | 0.659 |
| SSC-G2P1 | 0.2 | 0.1 | −0.098 | 0.695 | 1.556 | 2.753 | 7.064 | 10.089 | 0.993 | 0.933 | 0.786 |
| SSC-G0.15P0.15 | 0.15 | 0.15 | −0.035 | 0.447 | 1.504 | 2.476 | 6.241 | 9.626 | 0.997 | 0.963 | 0.808 |
| SSC-G1P2 | 0.1 | 0.2 | −0.166 | 0.718 | 1.728 | 2.832 | 7.282 | 10.203 | 0.990 | 0.932 | 0.785 |
| Number of Seawater Freeze–Thaw Couplings | Predictive Model |
|---|---|
| 25 | |
| 50 | |
| 75 |
| Number of Seawater Freeze–Thaw Couplings | Predictive Model |
|---|---|
| 25 | |
| 50 | |
| 75 |
| Number of Seawater Freeze–Thaw Couplings | Strength Loss Rate Prediction Model | Relative Dynamic Elastic Modulus Prediction Model | ||
|---|---|---|---|---|
| a | Average Relative Error | a | Average Relative Error | |
| 25 | −0.1733 | 4.9498% | −0.1639 | 0.3806% |
| 50 | −0.0366 | 4.7651% | −0.0233 | 0.9743% |
| 75 | −0.2125 | 3.4281% | −0.2094 | 0.9890% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Wang, X.; Xin, M.; He, J. Study on the Damage of Fiber-Reinforced Seawater Sea Sand Concrete by Freezing and Thawing of Seawater. Materials 2024, 17, 1910. https://doi.org/10.3390/ma17081910
Sun C, Wang X, Xin M, He J. Study on the Damage of Fiber-Reinforced Seawater Sea Sand Concrete by Freezing and Thawing of Seawater. Materials. 2024; 17(8):1910. https://doi.org/10.3390/ma17081910
Chicago/Turabian StyleSun, Chuanwu, Xuezhi Wang, Ming Xin, and Jingjing He. 2024. "Study on the Damage of Fiber-Reinforced Seawater Sea Sand Concrete by Freezing and Thawing of Seawater" Materials 17, no. 8: 1910. https://doi.org/10.3390/ma17081910
APA StyleSun, C., Wang, X., Xin, M., & He, J. (2024). Study on the Damage of Fiber-Reinforced Seawater Sea Sand Concrete by Freezing and Thawing of Seawater. Materials, 17(8), 1910. https://doi.org/10.3390/ma17081910





