A Study on the Critical Saturation Response Characteristics of Simple and Sandwich Cylindrical Shells under Long-Duration Blast Loading
Abstract
:1. Introduction
2. Finite Element Model
3. Results and Discussion
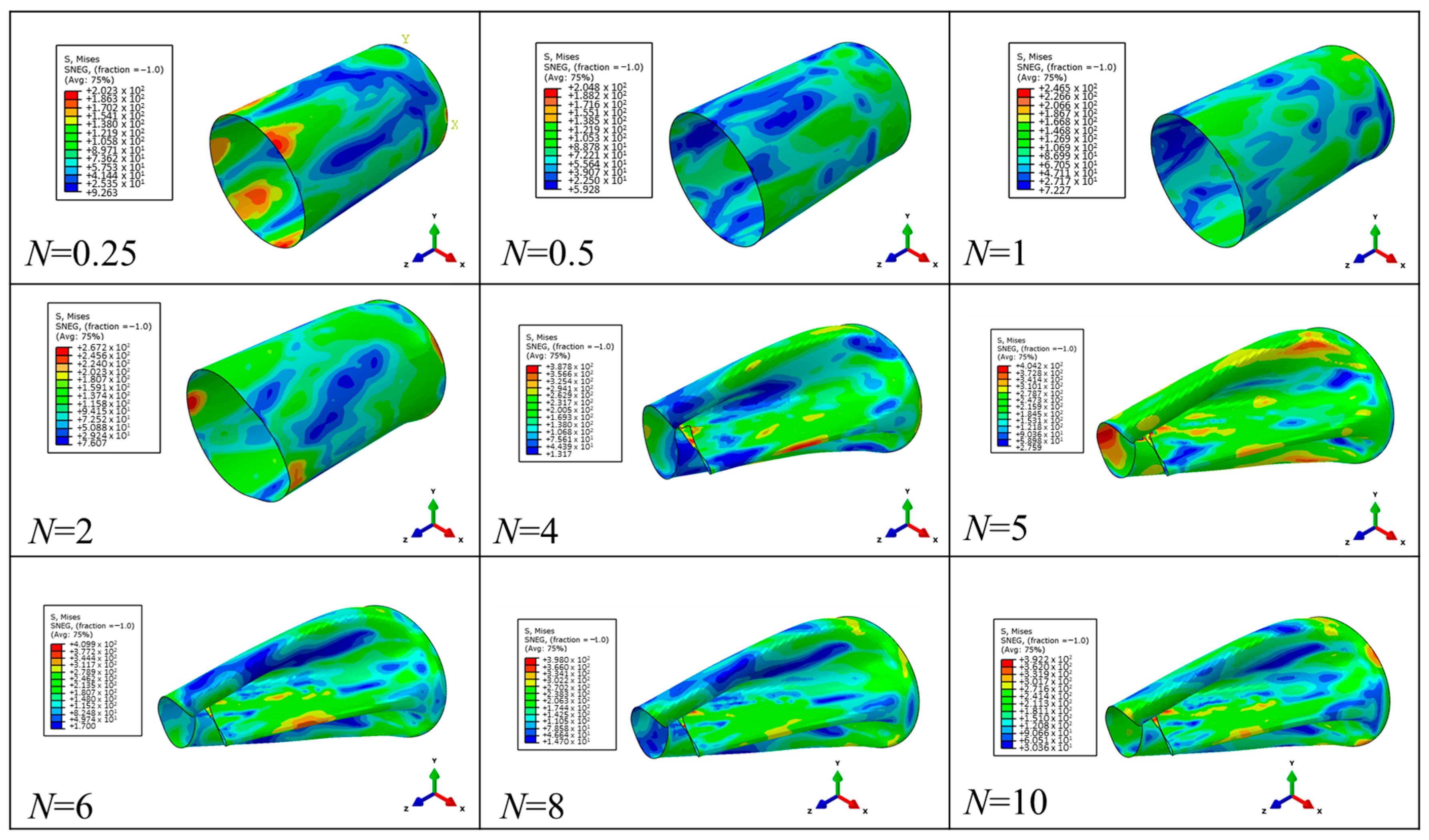
3.1. A Preliminary Exploration of the Saturation Effect
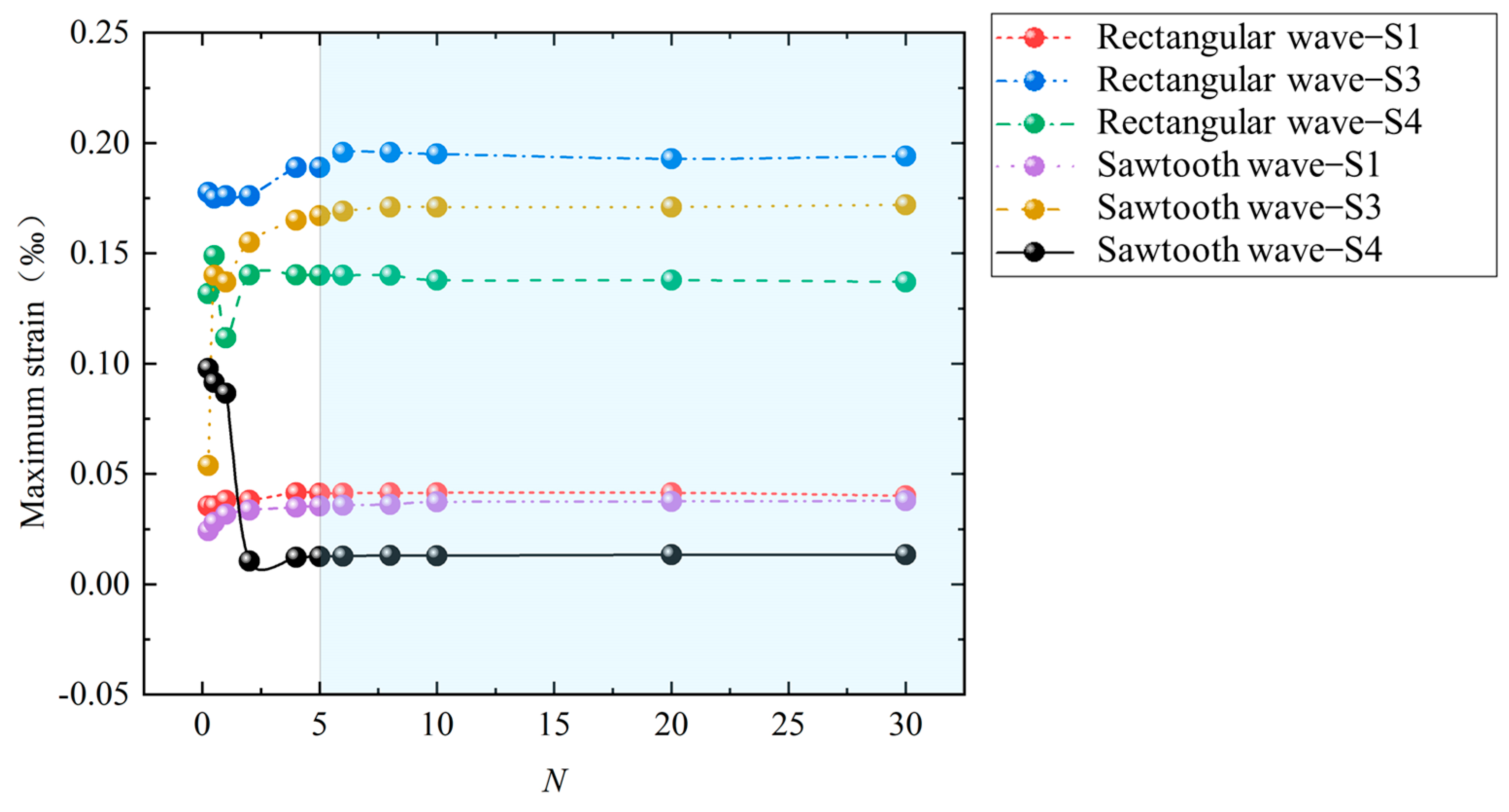
3.2. Influence of Structural Vibration Shape and Load Waveform
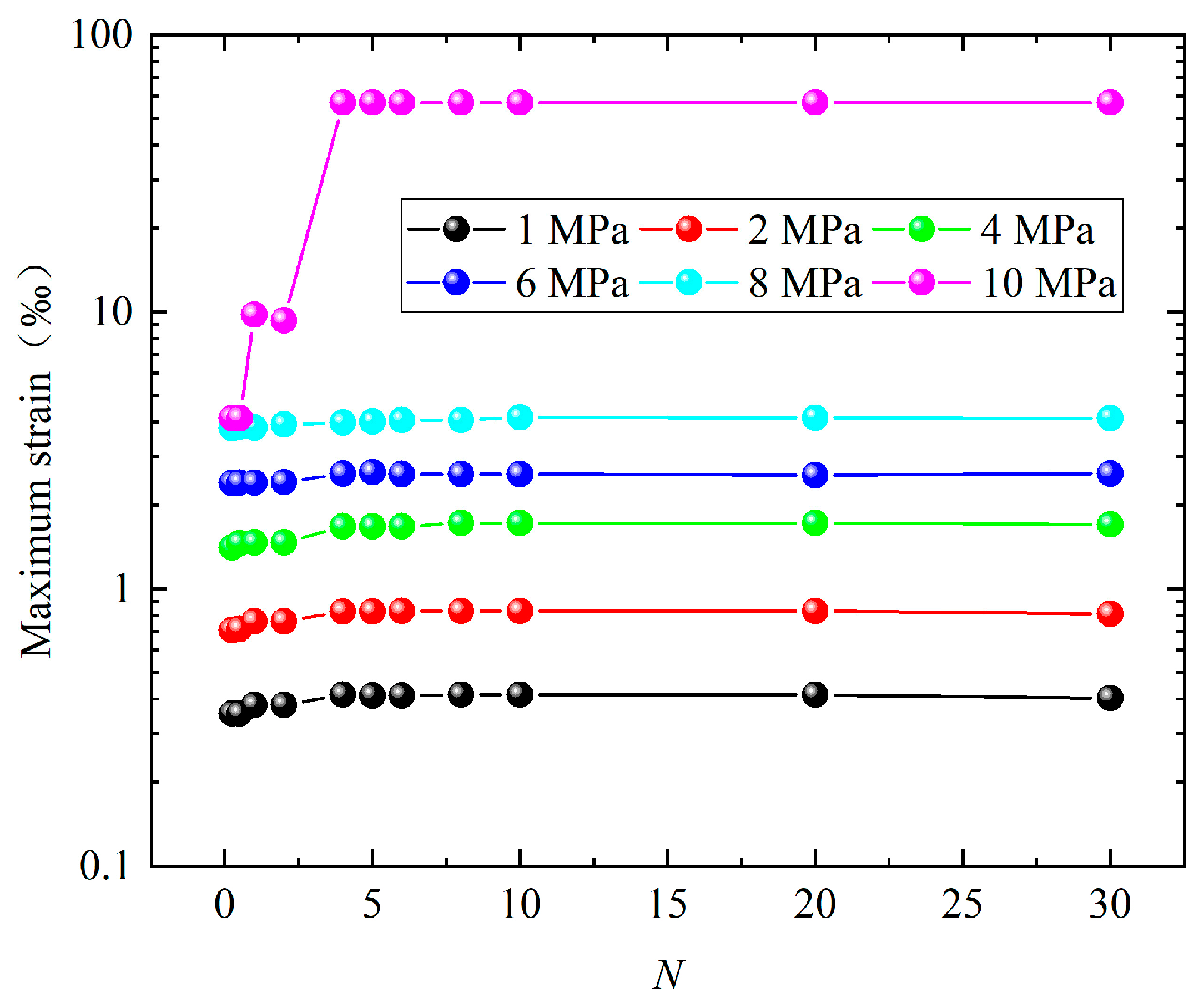
3.3. Influence of Load Amplitude
3.4. Sandwich Shells
4. Conclusions
- When the pulse duration of the load is greater than or equal to four to five times the first-order period of the structure, the maximum response of the structure tends to be consistent. That is, the maximum response of the cylindrical shell of different vibration modes (the breathing mode, bending mode, and triangle mode) shows a saturation effect as the pulse duration increases.
- When the load waveform is a typical rectangular wave or sawtooth wave, the above saturation effect is applicable.
- Whether the structure undergoes elastic deformation or large plastic deformation, the above saturation effect is applicable.
- The above saturation effect applies to both simple single-layer cylindrical shells and relatively complex structures (i.e., corrugated sandwich cylindrical shells).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| T | First-order period of cylindrical shells |
| td | The pulse duration |
| N | td = NT |
| L | The height of the sandwich cylindrical shell |
| Ri | The radius of the inner panel of the sandwich cylindrical shell |
| Ro | The radius of the outer panel of the sandwich cylindrical shell |
| α | A single corrugation corresponds to the central angle |
| t | The wall thickness of the sandwich cylindrical shell |
References
- Clubley, S.K. Non-linear long duration blast loading of cylindrical shell structures. Eng. Struct. 2014, 59, 113–126. [Google Scholar] [CrossRef]
- Clubley, S.K. Long duration blast loading of cylindrical shell structures with variable fill level. Thin-Walled Struct. 2014, 85, 234–249. [Google Scholar] [CrossRef]
- Børvik, T.; Burbach, A.; Langberg, H.; Langseth, M. On the ballistic and blast load response of a 20ft ISO container protected with aluminum panels filled with a local mass-Phase II: Validation of protective system. Eng. Struct. 2008, 30, 1621–1631. [Google Scholar] [CrossRef]
- Keys, R.A.; Clubley, S.K. Experimental analysis of debris distribution of masonry panels subjected to long duration blast loading. Eng. Struct. 2017, 130, 229–241. [Google Scholar] [CrossRef]
- Clough, L.G.; Clubley, S.K. Steel column response to thermal and long duration blast loads inside an air blast tunnel. Struct. Infrastruct. Eng. 2019, 15, 1510–1528. [Google Scholar] [CrossRef]
- Denny, J.W.; Clubley, S.K. Evaluating long-duration blast loads on steel columns using computational fluid dynamics. Struct. Infrastruct. Eng. 2019, 15, 1419–1435. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Yu, T.X.; Fang, J. Large dynamic plastic deflection of a simply supported beam subjected to rectangular pressure pulse. Arch. Appl. Mech. 1994, 64, 223–232. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Yu, T.; Fang, J.; Zheng, Z.M.; Tan, Q.M. Dynamic plastic response of structures with finite deflection and saturation impulse. In Proceedings of the Iutam Symposium on Impact Dynamics, Iutam Symposium on Impact Dynamics, Beijing, China, 11–15 October 1993. [Google Scholar]
- Zhu, L.; Yu, T.X. Saturated impulse for pulse-loaded elastic-plastic square plates. Int. J. Solids Struct. 1997, 34, 1709–1718. [Google Scholar] [CrossRef]
- Zhu, L.; He, X.; Yu, T.X.; Chen, F.L. Scaling effect on saturated impulse for square plates under rectangular pulse loading. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2016), Busan, Republic of Korea, 19–24 June 2016. [Google Scholar]
- Xi, F.; Yang, J.L. Dynamic Response Analysis of Elastic-plastic Thin Circular Plates under Impulse Loading with Considenration of Large Deflection. Explos. Shock. Waves 2000, 20, 379–384. [Google Scholar]
- Xi, F.; Zhang, Y. The effects of strain rate on the dynamic response and abnormal behavior of steel beams under pulse loading. Explos. Shock. Waves 2012, 32, 34–42. [Google Scholar]
- Bai, X.Y.; Zhu, L.; Yu, T.X. Saturated impulse for pulse-loaded rectangular plates with various boundary conditions. Thin-Walled Struct. 2017, 119, 166–177. [Google Scholar] [CrossRef]
- Zhu, L.; He, X.; Chen, F.L.; Bai, X. Effects of the strain rate sensitivity and strain hardening on the saturated impulse of plates. Lat. Am. J. Solids Struct. 2017, 14, 1273–1292. [Google Scholar] [CrossRef]
- Zhu, L.; Bai, X.Y.; Yu, T.X. The saturated impulse of fully clamped square plates subjected to linearly decaying pressure pulse. Int. J. Impact Eng. 2017, 110, 198–207. [Google Scholar] [CrossRef]
- Bai, X.Y.; Zhu, L.; Yu, T.X. Saturated impulse for fully clamped square plates under blast loading. Int. J. Mech. Sci. 2018, 146–147, 417–431. [Google Scholar] [CrossRef]
- Tian, L.R.; Chen, F.L.; Zhu, L.; Yu, T.X. Saturated analysis of pulse-loaded beams based on membrane factor method. Int. J. Impact Eng. 2019, 131, 17–26. [Google Scholar] [CrossRef]
- Nurick, G.N.; Martin, J.B. Deformation of thin plates subjected to impulsive loading: A review Part II: Experimental studies. Int. J. Impact Eng. 1989, 8, 171–186. [Google Scholar] [CrossRef]
- Nurick, G.N.; Martin, J.B. Deformation of thin plates subjected to impulsive loading: A review: Part I: Theoretical considerations. Int. J. Impact Eng. 1989, 8, 159–170. [Google Scholar] [CrossRef]
- Guo, Z.; Gao, B.; Guo, Z.; Zhang, W. Dynamic constitutive relation based on J-C model of Q235steel. Explos. Shock. Waves 2018, 38, 804–810. [Google Scholar]
- Pham, T.T.; Changsoo, K.; Hyounseung, J.; Kim, T.; Kim, J. Buckling behavior analysis of hybrid-honeycomb sandwich cylindrical shells. Ocean. Eng. 2023, 276, 114214. [Google Scholar]
- Shahgholian-Ghahfarokhi, D.; Rahimi, G. A sensitivity study of the free vibration of composite sandwich cylindrical shells with grid cores. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 149–162. [Google Scholar] [CrossRef]
- Ghahfarokhi, D.S.; Rahimi, G. An analytical approach for global buckling of composite sandwich cylindrical shells with lattice cores. Int. J. Solids Struct. 2018, 146, 69–79. [Google Scholar] [CrossRef]
- Zarei, M.; Rahimi, G.H. Buckling resistance of joined composite sandwich conical–cylindrical shells with lattice core under lateral pressure. Thin-Walled Struct. 2022, 174, 109027. [Google Scholar] [CrossRef]
- Tho Hung, V.; Thuy Dong, D.; Thi Phuong, N.; Ngoc Ly, L.; Quang Minh, T.; Trung, N.-T.; Hoai Nam, V. Nonlinear buckling behavior of spiral corrugated sandwich FGM cylindrical shells surrounded by an elastic medium. Materials 2020, 13, 1984. [Google Scholar] [CrossRef] [PubMed]
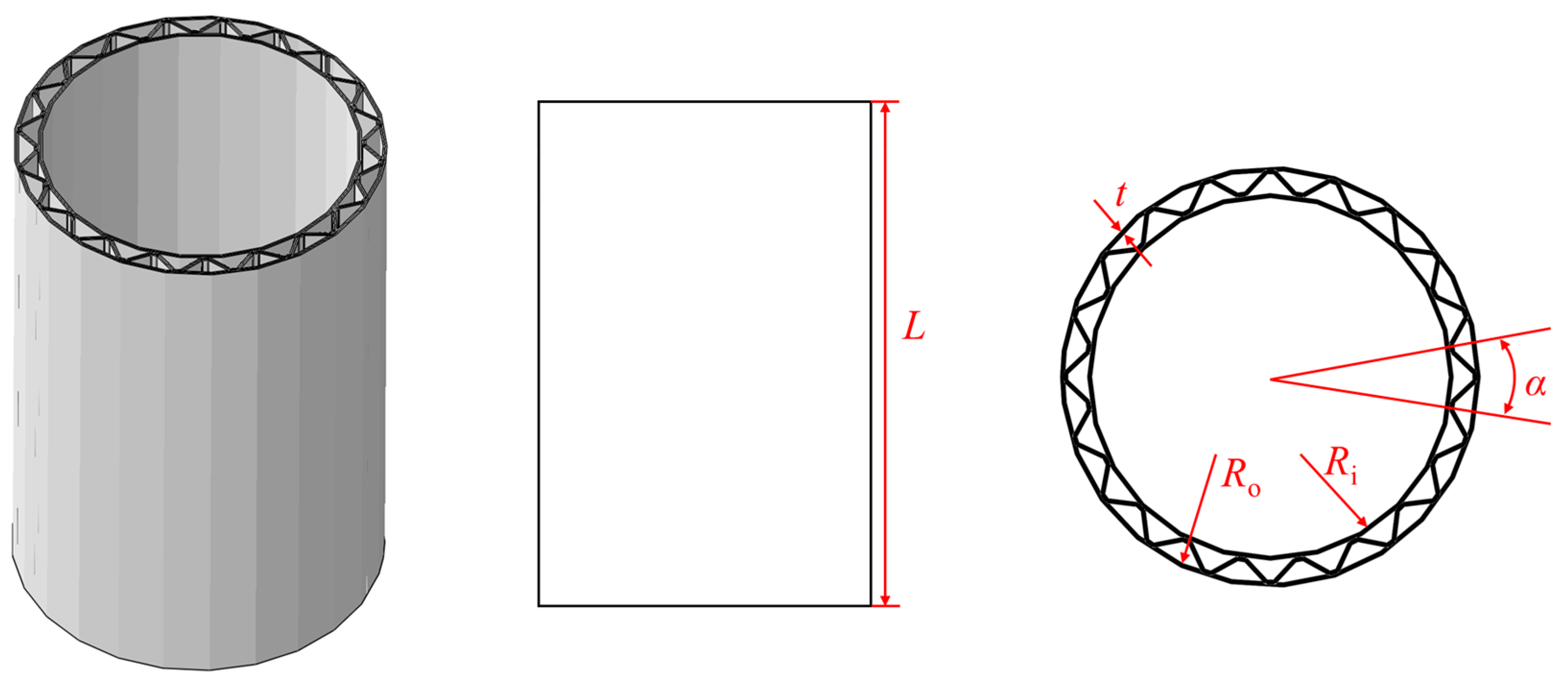
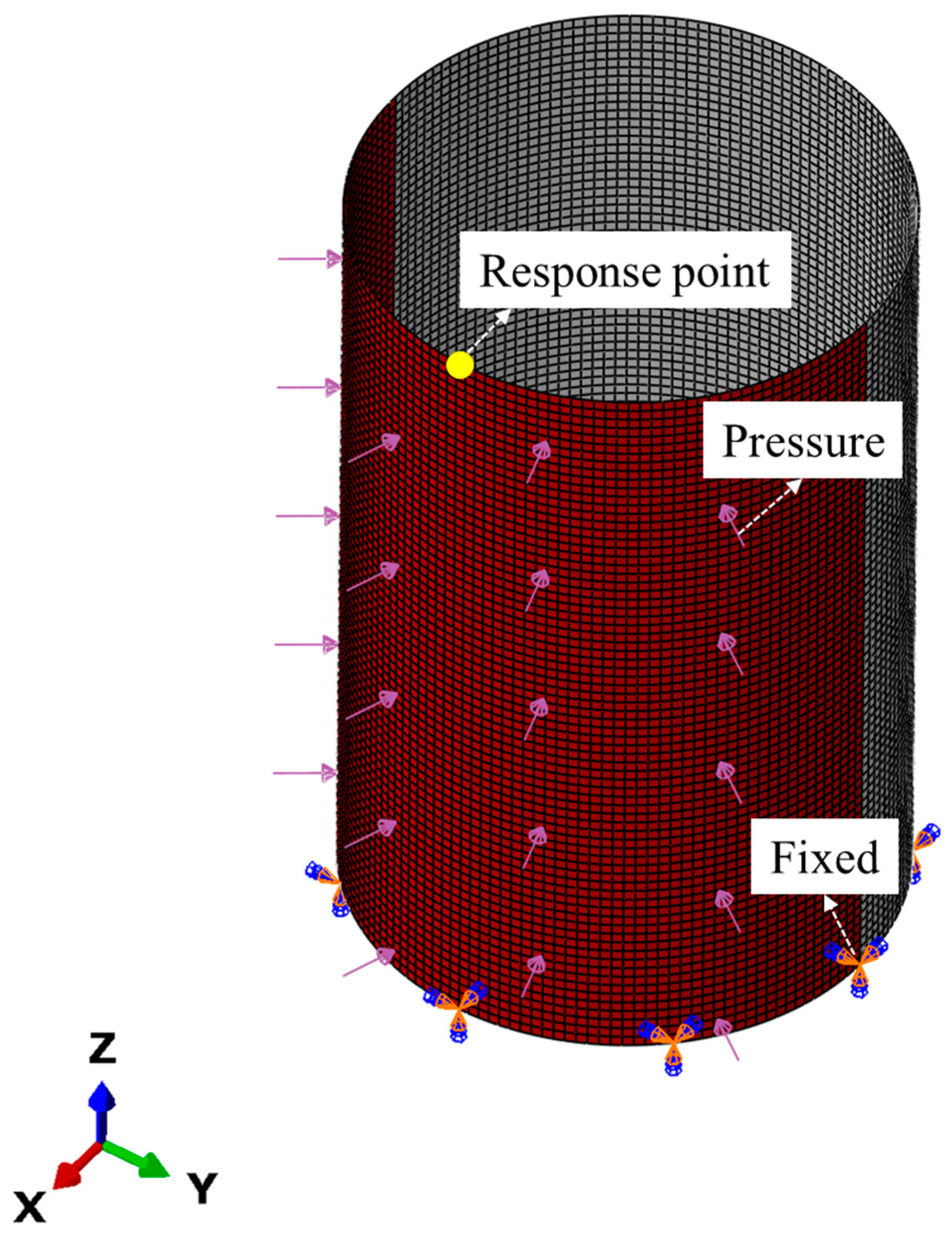
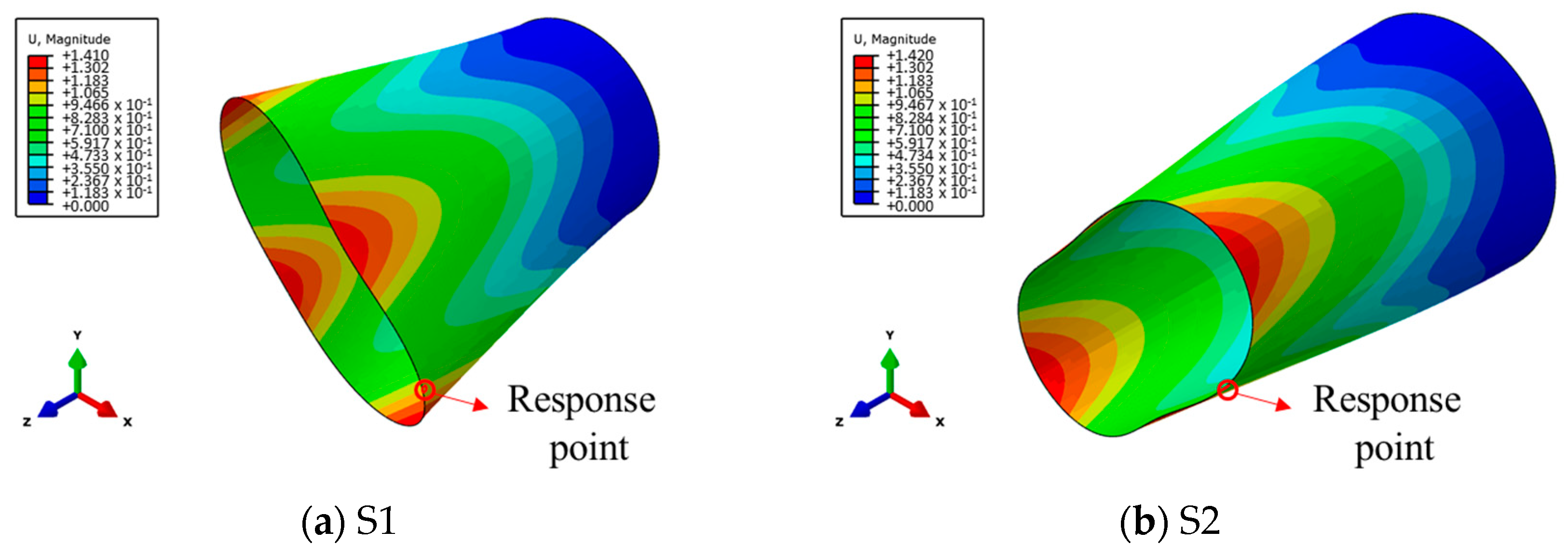
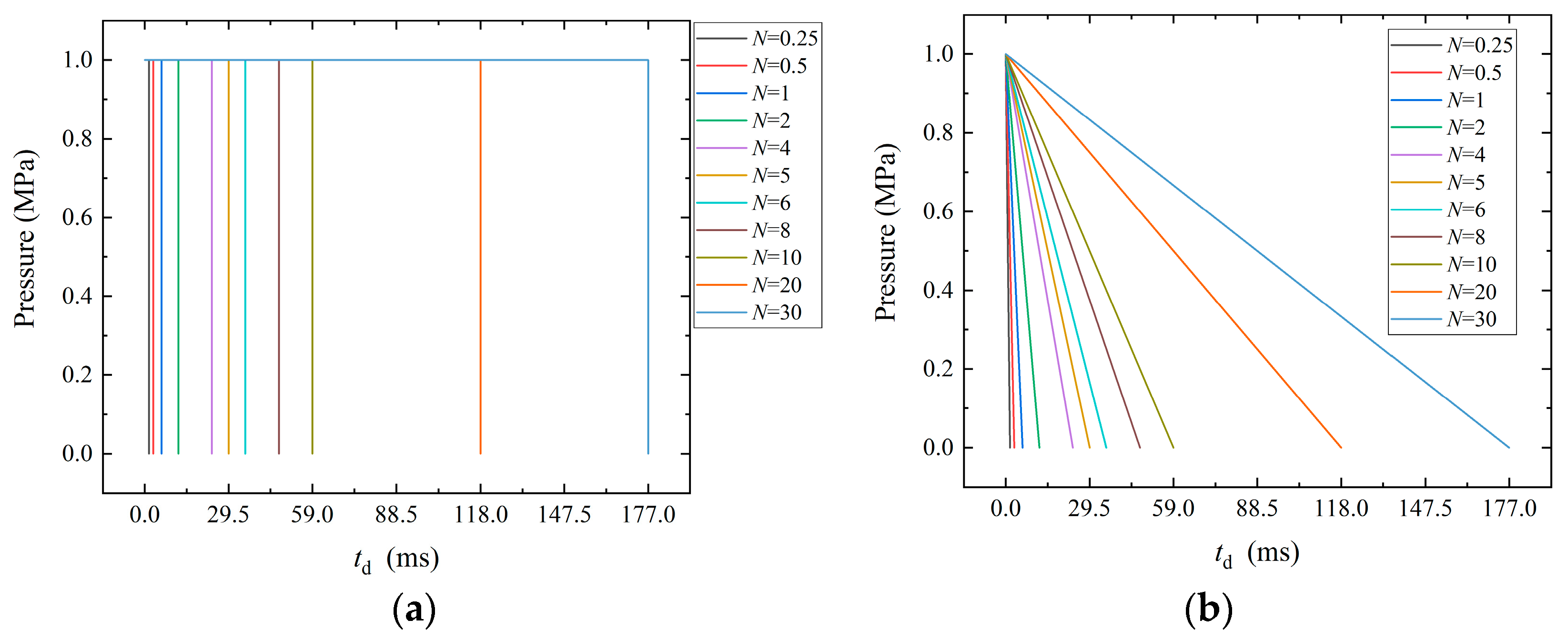




| Num. | Diameter (mm) | Height (mm) | Wall Thickness (mm) |
|---|---|---|---|
| S1 | 1000 | 1500 | 40 |
| S2 | 1000 | 1500 | 80 |
| S3 | 3000 | 1000 | 40 |
| S4 | 2000 | 1500 | 40 |
| Num. | L (mm) | Ri (mm) | Ro (mm) | α (°) | t (mm) |
|---|---|---|---|---|---|
| CSCS | 1500 | 450 | 500 | 18 | 10 |
| ρ (g/cm−3) | E (MPa) | ν | A (MPa) | B (MPa) | n | m |
|---|---|---|---|---|---|---|
| 7.8 | 2 × 105 | 0.33 | 293.8 | 230.2 | 0.578 | 0.706 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Zhang, J.; Mu, Y.; Huang, H.; Han, B.; Mao, Y. A Study on the Critical Saturation Response Characteristics of Simple and Sandwich Cylindrical Shells under Long-Duration Blast Loading. Materials 2024, 17, 1990. https://doi.org/10.3390/ma17091990
Yang M, Zhang J, Mu Y, Huang H, Han B, Mao Y. A Study on the Critical Saturation Response Characteristics of Simple and Sandwich Cylindrical Shells under Long-Duration Blast Loading. Materials. 2024; 17(9):1990. https://doi.org/10.3390/ma17091990
Chicago/Turabian StyleYang, Mao, Jun Zhang, Yunfei Mu, Hanjun Huang, Bin Han, and Yongjian Mao. 2024. "A Study on the Critical Saturation Response Characteristics of Simple and Sandwich Cylindrical Shells under Long-Duration Blast Loading" Materials 17, no. 9: 1990. https://doi.org/10.3390/ma17091990
APA StyleYang, M., Zhang, J., Mu, Y., Huang, H., Han, B., & Mao, Y. (2024). A Study on the Critical Saturation Response Characteristics of Simple and Sandwich Cylindrical Shells under Long-Duration Blast Loading. Materials, 17(9), 1990. https://doi.org/10.3390/ma17091990







