Integrating Experimental and Computational Analyses for Mechanical Characterization of Titanium Carbide/Aluminum Metal Matrix Composites
Abstract
:1. Introduction
2. Materials and Methods
3. Results
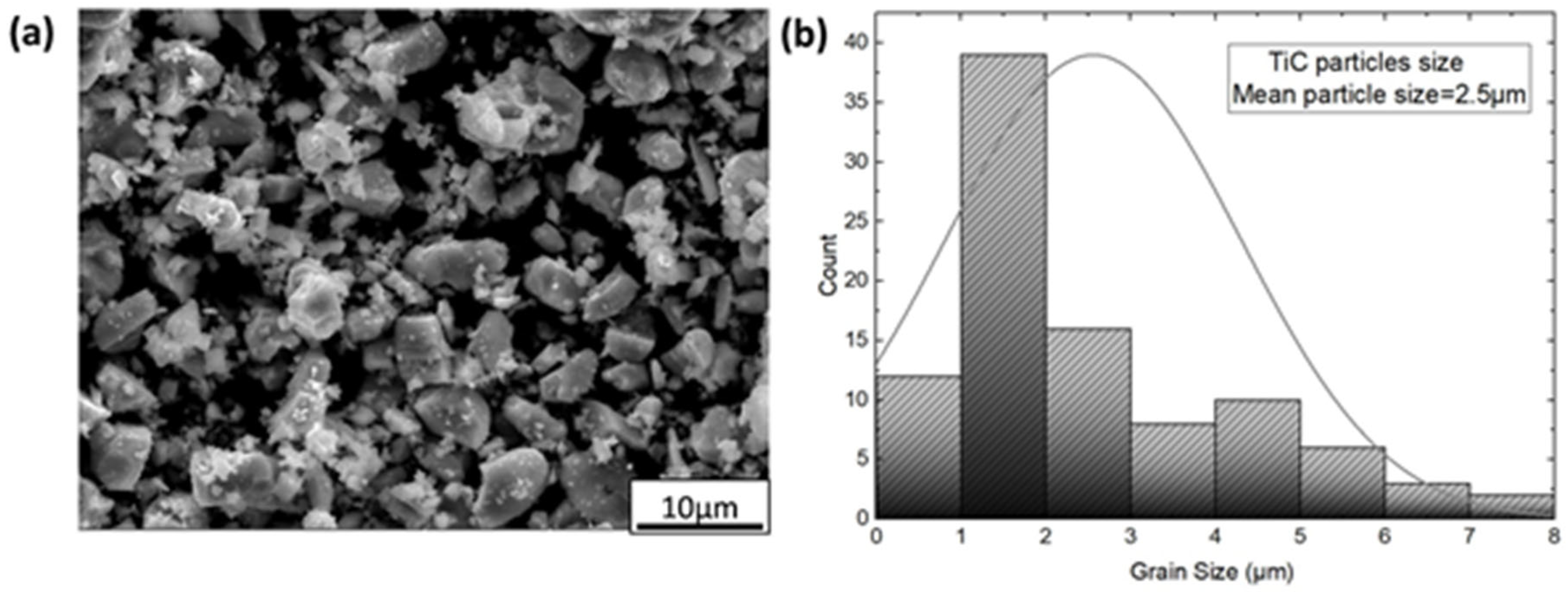
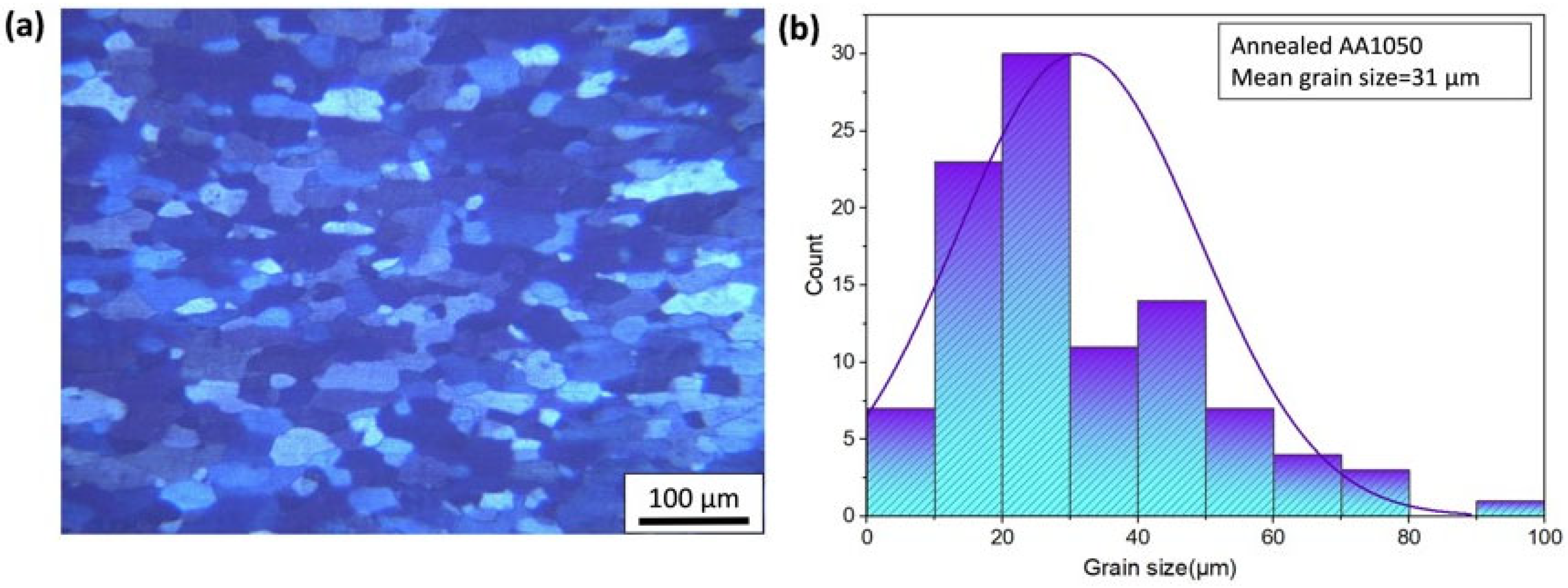
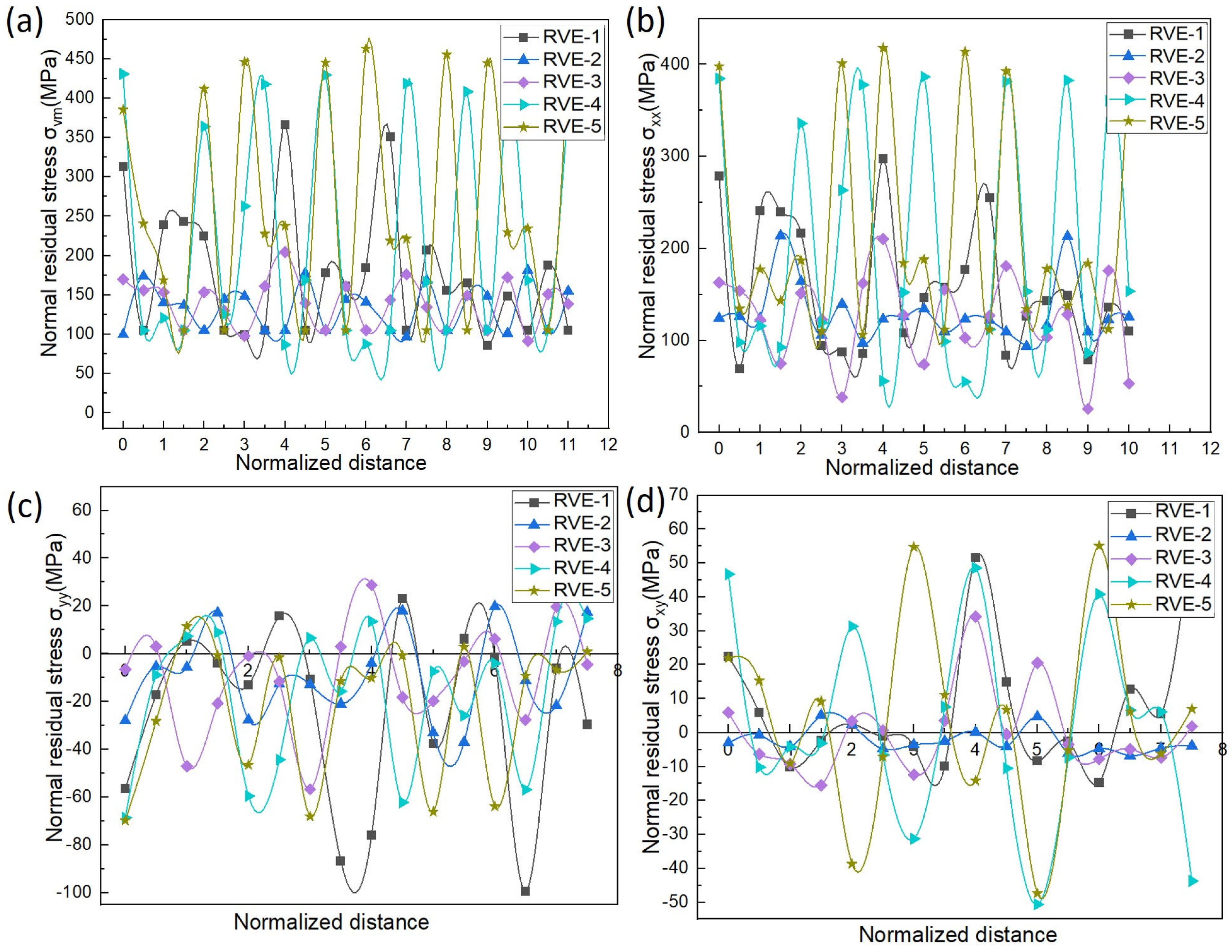
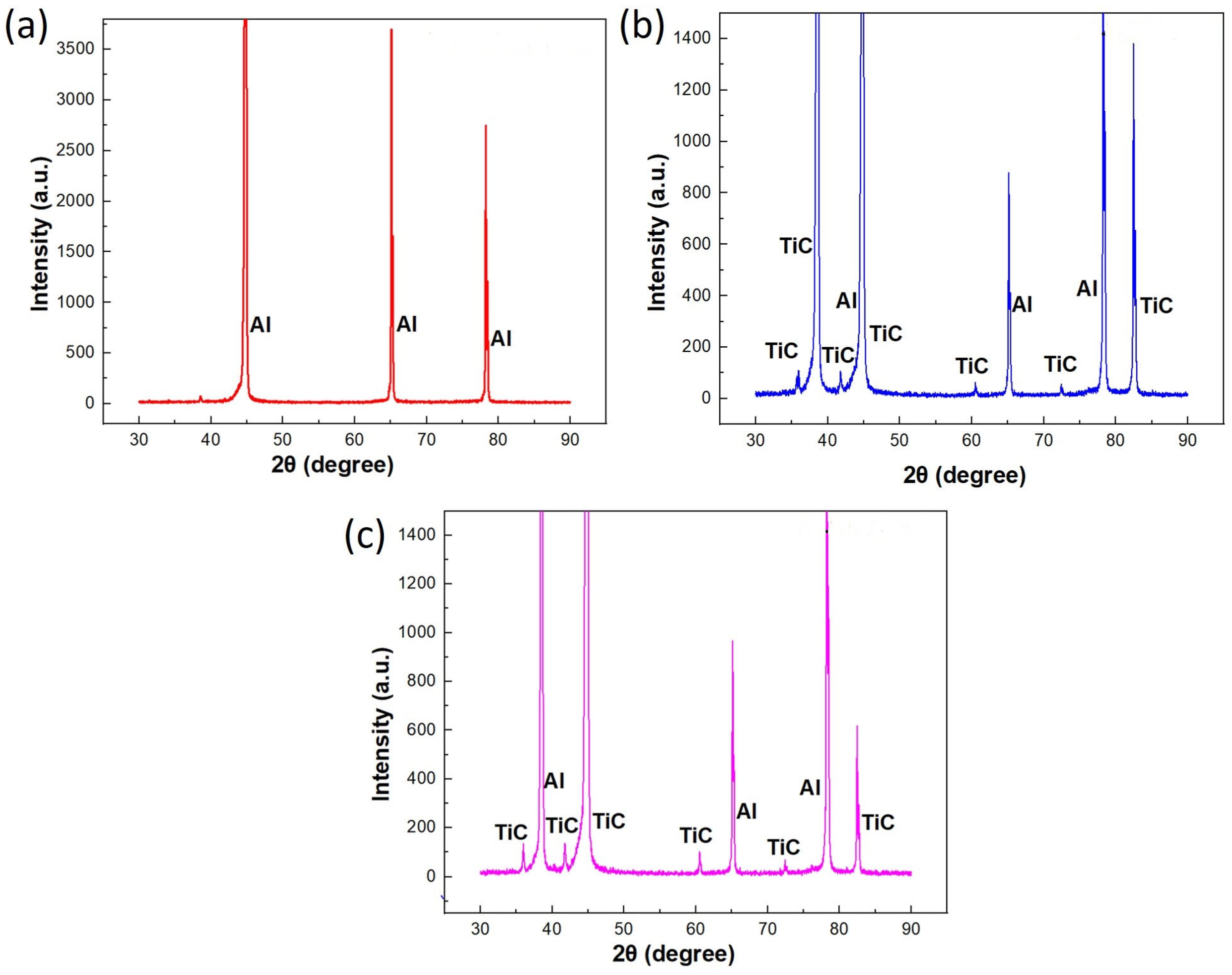
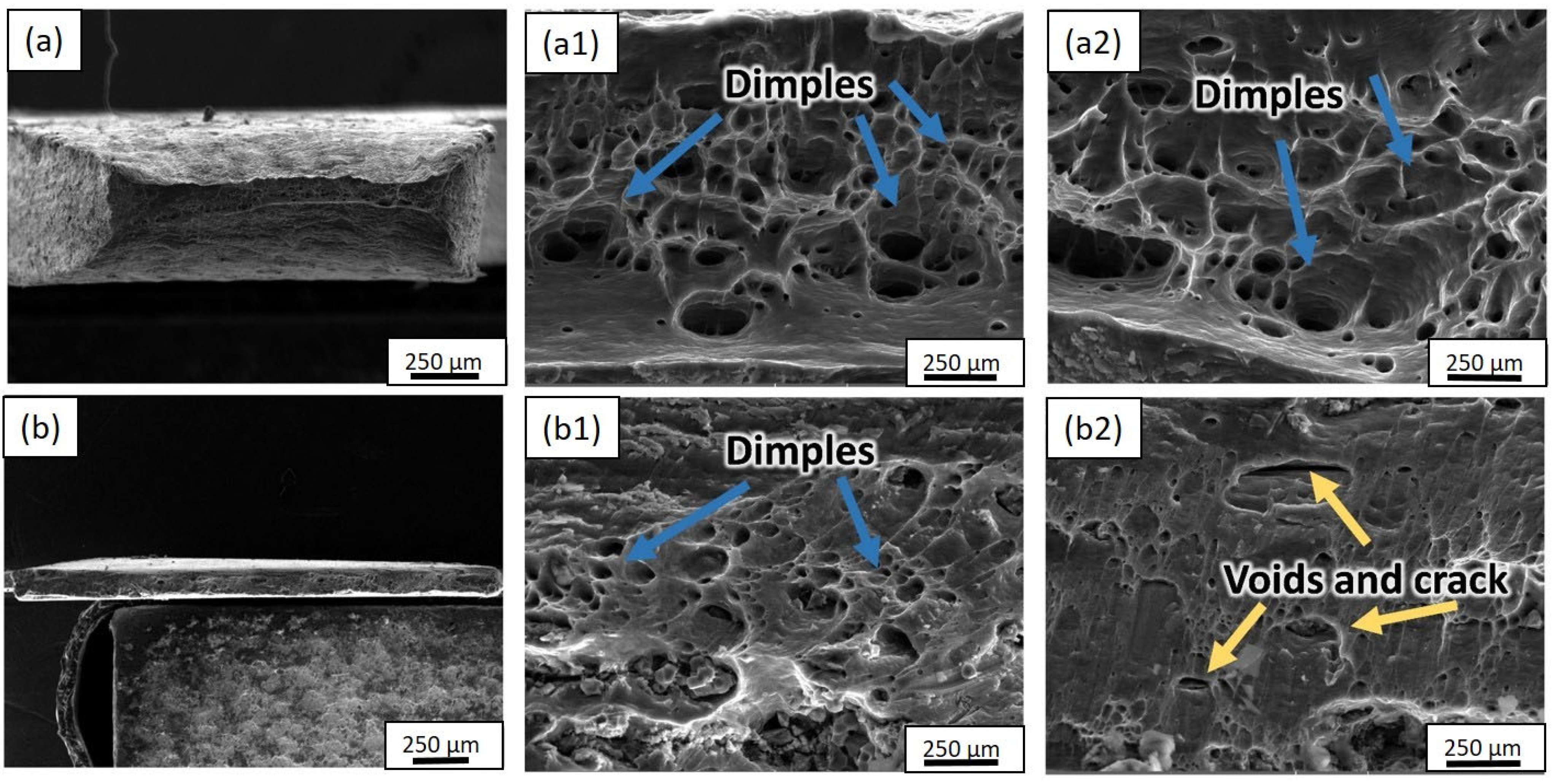
3.1. Microstructure
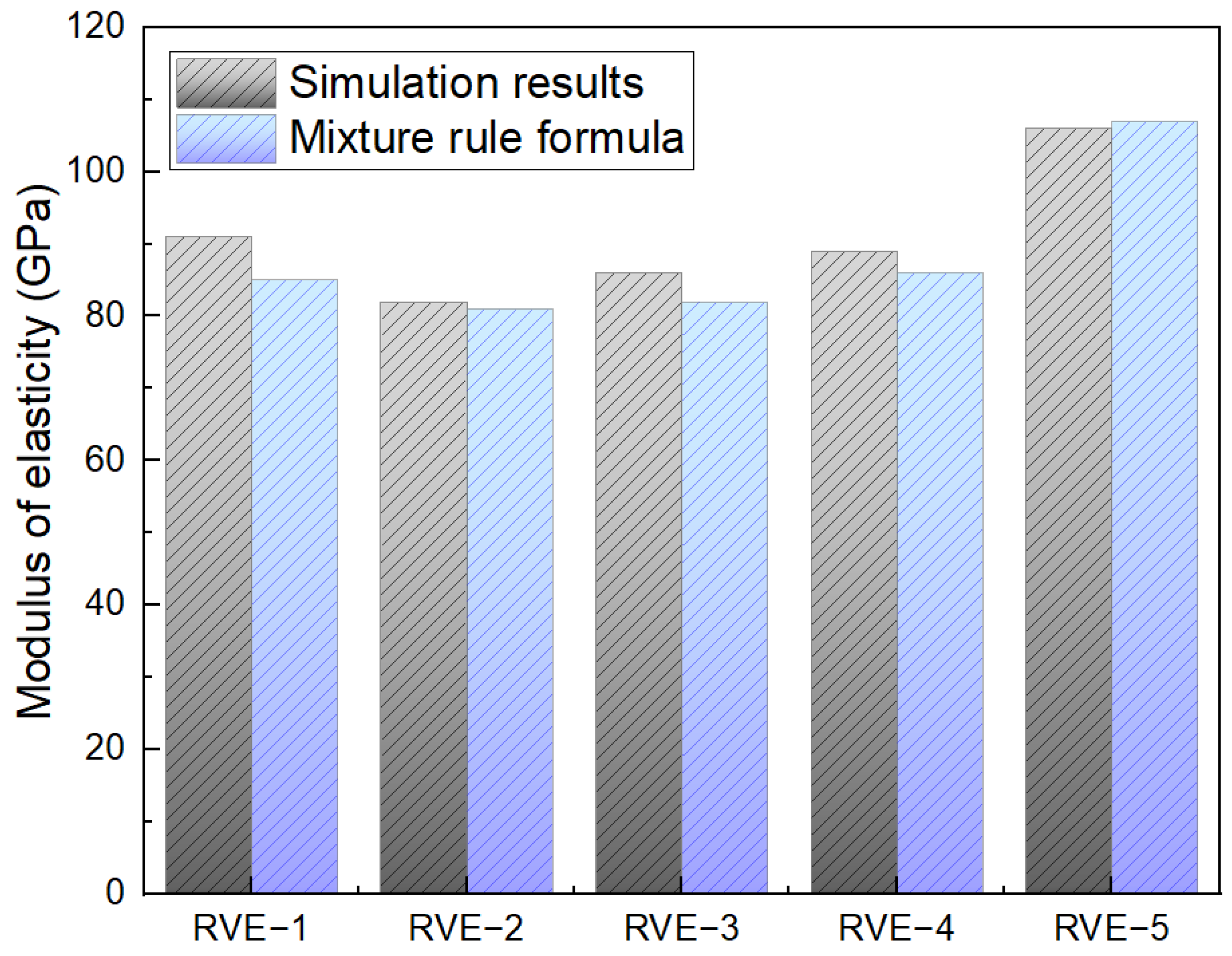
3.2. Modeling and Simulation
3.3. Experimental Case (RVE−1)
3.4. Effect of Particle Size and Shape
- E_comp is the overall Young’s modulus of the composite;
- E_al is the modulus of the aluminum matrix;
- E_TiC is the modulus of the titanium carbide reinforcement;
- V_al is the volume fraction of the aluminum matrix in the composite; and
- V_TiC is the volume fraction of the titanium carbide reinforcement in the composite.
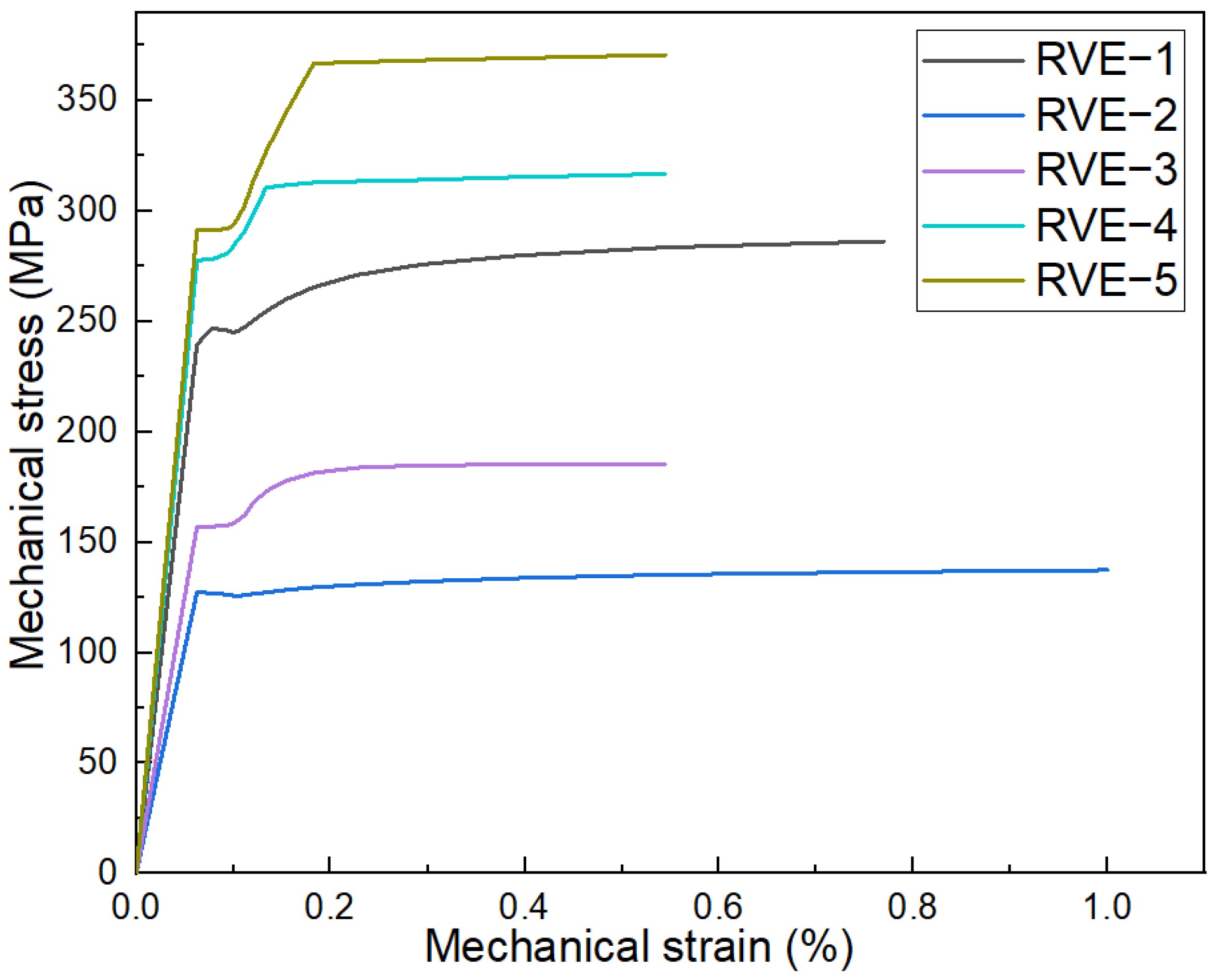
3.5. AMCs’ Microstructural and Mechanical Properties of Al–TiCp
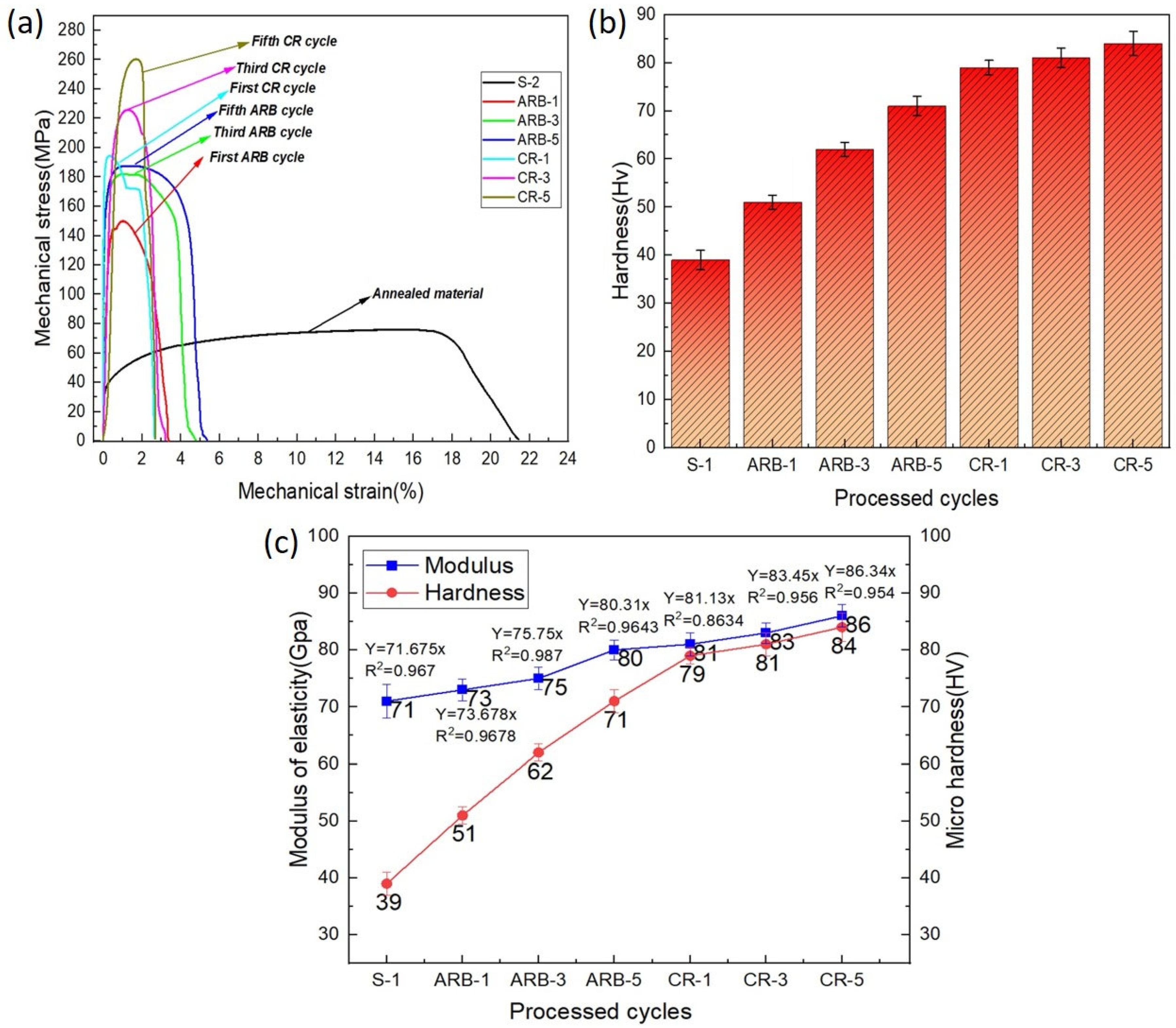
3.5.1. Microstructural Evolution
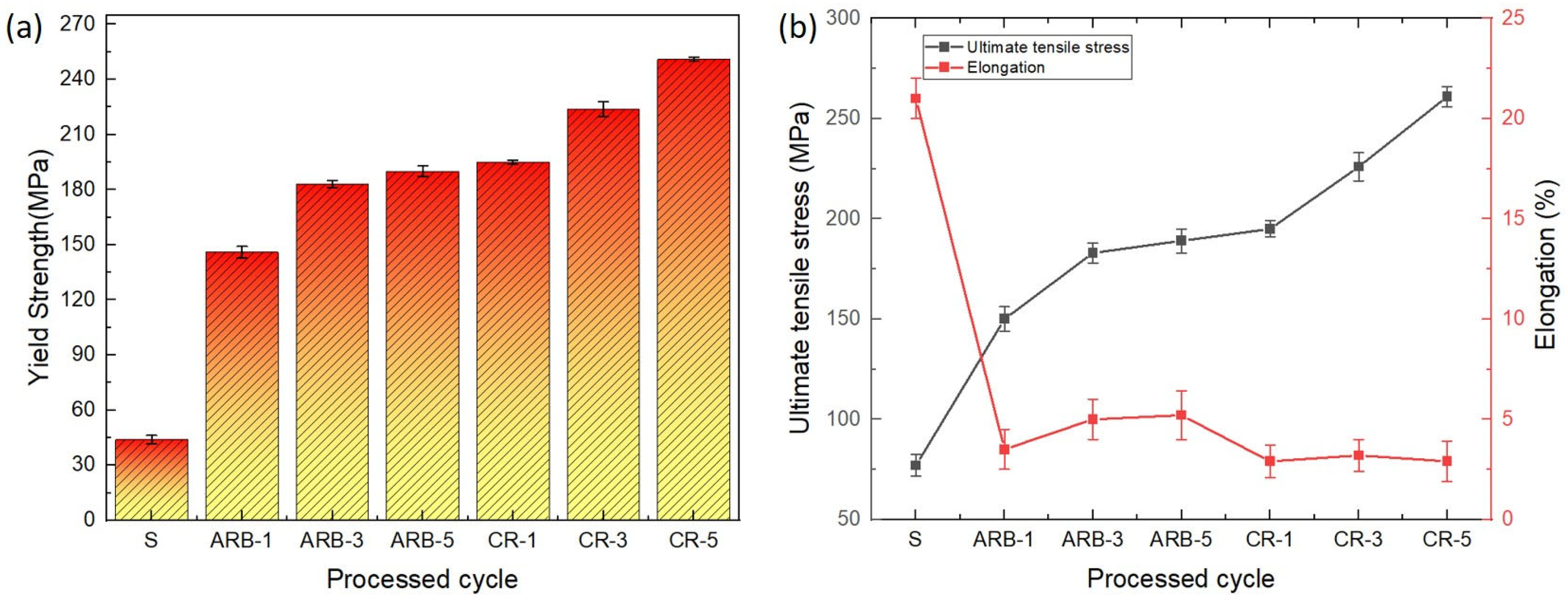
3.5.2. Mechanical Properties
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pradeep Kumar, J.; Robinson Smart, D.S.; Manova, S.; Akinwande, A.; Saravana Kumar, M. Mechanical and tribological assessment of AA7075 reinforced Si3N4/TaC/Ti hybrid metal matrix composites processed through stir casting process. Adv. Mater. Process. Technol. 2023, 1–23. [Google Scholar] [CrossRef]
- Deirmina, F.; Amirabdollahian, S.; Harris, L.; Bettini, E.; Siriki, R.; Pellizzari, M.; Bosetti, P.; Molinari, A. Laser-Directed Energy Deposition of Dissimilar Maraging Steels with a Defect-Free Interface: Design for Improved Surface Hardness and Fracture Toughness. Met. Mater. Int. 2023, 29, 2940–2954. [Google Scholar] [CrossRef]
- Farid, W.; Bah, T.A.; Kong, C.; Yu, H. A novel way to fabricate high elastic modulus and high strength of TiC reinforced aluminum matrix composite. Mater. Manuf. Process. 2023, 38, 1785–1797. [Google Scholar] [CrossRef]
- Baazamat, S.; Borhani, E.; Tajally, M. On the microstructure, recrystallization texture, and mechanical properties of Al/WO3/SiC hybrid nanocomposite during accumulative roll bonding (ARB) process. Int. J. Mater. Form. 2023, 16, 53. [Google Scholar] [CrossRef]
- Yu, H.; Lu, C.; Tieu, K.; Liu, X.; Sun, Y.; Yu, Q.; Kong, C. Asymmetric cryorolling for fabrication of nanostructural aluminum sheets. Sci. Rep. 2012, 2, 772. [Google Scholar] [CrossRef]
- Li, H.L.; Guo, A.H.; Kong, C.; Yu, H.L. Microstructure evolution and mechanical properties of Al/Mg-Li/Al laminate metallic composites via hot roll bonding and subsequent cryorolling. Mater. Sci. Eng. A 2024, 891, 146007. [Google Scholar] [CrossRef]
- Gao, H.T.; Kong, C.; Yu, H.L. Lightweight metal laminated plates produced via (hot, cold and cryogenic) roll bonding: A review. Trans. Nonferrous Met. Soc. China 2023, 33, 337–356. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Effective Mechanical Properties of Additive Manufactured Strut-Lattice Structures: Experimental and Finite Element Study. Adv. Eng. Mater. 2022, 24, 2100879. [Google Scholar] [CrossRef]
- Rogala, M.; Gajewski, J.; Gawdzińska, K. Crashworthiness analysis of thin-walled aluminum columns filled with aluminum–silicon carbide composite foam. Compos. Struct. 2022, 299, 116102. [Google Scholar] [CrossRef]
- Graça, A.; Vincze, G. A short review on the finite element method for asymmetric rolling processes. Metals 2021, 11, 762. [Google Scholar] [CrossRef]
- Ohguchi, K.I.; Sasaki, K.; Fukuchi, K.; Tsubota, Y.; Mita, T.; Nagai, W.; Ohsato, K.; Shinya, N. A material constants estimation method for efficient elastic–plastic–creep simulation of aluminum alloys by effective utilization of stored test data. Mech. Time-Depend. Mater. 2024, 28, 1–17. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Mahmoodi, M.J.; Ansari, R.; Mehdipour, H. Effects of adding CNTs on the thermo-mechanical characteristics of hybrid titanium nanocomposites. Mech. Mater. 2019, 131, 121–135. [Google Scholar] [CrossRef]
- Liu, C.; Ding, W.; Yu, T.; Yang, C. Materials removal mechanism in high-speed grinding of particulate reinforced titanium matrix composites. Precis. Eng. 2018, 51, 68–77. [Google Scholar] [CrossRef]
- Nie, C.; Wang, H.; He, J. Evaluation of the effect of adding carbon nanotubes on the effective mechanical properties of ceramic particulate aluminum matrix composites. Mech. Mater. 2020, 142, 103276. [Google Scholar] [CrossRef]
- Greco, A. FEM analysis of the elastic behavior of composites and nanocomposites with arbitrarily oriented reinforcements. Compos. Struct. 2020, 241, 112095. [Google Scholar] [CrossRef]
- Duongthipthewa, A.; Lu, M.; Du, K.; Ye, L.; Zhou, L. Experimental and numerical simulation of lightning damage development on composites with/without a carbon-based protection layer. Compos. Struct. 2021, 260, 113452. [Google Scholar] [CrossRef]
- Morovvati, M.; Mollaei-Dariani, B.; Angili, S.N.; Toghraie, D. The effects of single-walled carbon nanotubes dispersion and agglomeration in aluminum matrix: Fabrication and finite element simulation. Measurement 2023, 218, 113144. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Zhang, X.; Wang, Y.J.; Zhang, S.Y.; Yin, Y. Numerical simulation using in the preparation process of micron-sized silica–aluminium composite powders by high-energy alloying: Building visualisation and guiding preparation. Micro Nano Lett. 2023, 18, e12165. [Google Scholar] [CrossRef]
- Hullur, M.K.; Goudar, D.; Haider, J.; Kori, S.A. Microstructural, Mechanical and Wear behaviour of in-situ Al-TiB2 composites. Adv. Mater. Process. Technol. 2023, 1–16. [Google Scholar] [CrossRef]
- Gao, M.; Guo, E.; Chen, Z.; Kang, H.; Wang, T. Revealing the role of micropore defects in tensile deformation of a B4Cp/Al composite using an actual three-dimensional model. J. Mater. Res. Technol. 2023, 22, 3146–3155. [Google Scholar] [CrossRef]
- Rafique, M.M. Microstructural evolution in Zr based Bulk Metallic Glass Matrix Composites (BMGMC) in Additive Manufacturing-Modeling and simulation. SSRN 2023. [Google Scholar] [CrossRef]
- Polančec, T.; Lesićar, T.; Tonković, Z.; Glodež, S. Modelling of rolling-contact fatigue pitting phenomena by phase field method. Wear 2023, 532–533, 205068. [Google Scholar] [CrossRef]
- Anderson, C.; Ntala, C.; Ozel, A.; Reuben, R.L.; Chen, Y. Computational homogenization of histological microstructures in human prostate tissue: Heterogeneity, anisotropy and tension-compression asymmetry. Int. J. Numer. Method. Biomed. Eng. 2023, 39, e3758. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Du, C.; Friederichs, J.; Wang, Y.; Hu, J.; Leischner, S. Multiscale modelling and simulation for asphalt pavements under moving tire footprint loads. Int. J. Pavement Eng. 2023, 24, 2154349. [Google Scholar] [CrossRef]
- Daniyan, I.; Mpofu, K.; Ale, F.; Muvunzi, R. Finite Element Analysis of the Stress Distribution in a Novel Brake Beam of a Railcar. In Smart, Sustainable Manufacturing in an Ever-Changing World, Proceedings of the International Conference on Competitive Manufacturing (COMA’22); Springer International Publishing: Cham, Switzerland, 2023; pp. 825–837. [Google Scholar] [CrossRef]
- Mangal, A.; Holm, E.A. Applied machine learning to predict stress hotspots I: Face centered cubic materials. Int. J. Plast. 2018, 111, 122–134. [Google Scholar] [CrossRef]
- Wu, H.; Xu, W.; Shan, D.; Wang, X.; Guo, B.; Jin, B.C. Micromechanical modeling of damage evolution and fracture behavior in particle reinforced metal matrix composites based on the conventional theory of mechanism-based strain gradient plasticity. J. Mater. Res. Technol. 2023, 22, 625–641. [Google Scholar] [CrossRef]
- Elmoghazy, Y.H.; Safaei, B.; Sahmani, S. Finite element analysis for dynamic response of viscoelastic sandwiched structures integrated with aluminum sheets. FU Mech. Eng. 2023, 21, 591–614. [Google Scholar] [CrossRef]
- Phiri, R.; Rangappa, S.M.; Siengchin, S.; Marinkovic, D. Agro-waste natural fiber sample preparation techniques for bio-composites development: Methodological insights. FU Mech. Eng. 2023, 21, 631–656. [Google Scholar] [CrossRef]
- Goda, I.; Padayodi, E.; Raoelison, R.N. Recent advances in modeling and simulation approaches for fiber/matrix interface failure in FRP composites. Int. J. Mech. Sci. 2023, 108648. [Google Scholar] [CrossRef]
- Zeng, H.; Zhao, C.; Chen, S.; Xu, W.; Zang, M. Numerical Simulations of Tire-Soil Interactions: A Comprehensive Review. Arch. Comput. Methods Eng. 2023, 30, 4801–4829. [Google Scholar] [CrossRef]
- Zheng, W.; Airao, J.; Aghababaei, R. Phase transformation and incidental effects of metastable crystalline TiAlN on the material removal mechanism. Mech. Mater. 2024, 188, 104845. [Google Scholar] [CrossRef]
- Lu, Y.; Watanabe, M.; Miyata, R.; Nakamura, J.; Yamada, J.; Kato, H.; Yoshimi, K. Microstructures and mechanical properties of TiC-particulate-reinforced Ti–Mo–Al intermetallic matrix composites. Mater. Sci. Eng. A 2020, 790, 139523. [Google Scholar] [CrossRef]
- Farid, W.; Wang, Z.; Cui, H.; Kong, C.; Yu, H.L. Investigation on Various Ceramic Nanoparticles Reinforced Aluminum Matrix Composites via Accumulative Roll Bonding and Cryorolling. Adv. Eng. Mater. 2023, 25, 2300936. [Google Scholar] [CrossRef]
- Li, Z.D.; Gu, H.; Luo, K.G.; Kong, C.; Yu, H.L. Achieving High Strength and Tensile Ductility of Pure Nickel by Cryorolling with Subsequent Low-Temperature Short-Time Annealing. Engineering 2024, 33, 190–203. [Google Scholar] [CrossRef]
- Xie, H.; Lv, J. Dendrite Refinement and Improved Mechanical Properties of SiC/TiC/Al Hybrid Nanocomposites. Adv. Mater. Sci. Eng. 2022, 2022, 4985378. [Google Scholar] [CrossRef]
- Liu, S.L.; Luo, K.G.; Gu, H.; Gao, H.T.; Kong, C.; Yu, H.L. Phase reversion-induced heterogeneous structure in a ferrous medium entropy alloy via cryorolling and annealing. Scr. Mater. 2023, 222, 115004. [Google Scholar] [CrossRef]
- Gatea, S.; Jwad, T.; Chen, F.; Ou, H. Micromechanical Modeling of the Deformation and Damage Behavior of Al6092/SiC Particle Metal Matrix Composites. J. Mater. Eng. Perform. 2023, 32, 10680–10701. [Google Scholar] [CrossRef]
- Zhuang, W.; Huang, Z.; Hu, W.; Yu, Q.; Li, X.; Wang, H.; Wu, Y.; Zhou, Y. A multiscale elastoplastic tensive behavior of quasi-continuous network structured (Ti3AlC2-Al3Ti)/2024Al composite. Mater. Today Commun. 2023, 37, 107189. [Google Scholar] [CrossRef]
- Banerjee, N.; Sen, A.; Ghosh, P.S.; Biswas, A.R.; Sharma, S.; Kumar, A.; Singh, R.; Li, C.; Kaur, J.; Eldin, S.M. Prediction and simulation of mechanical properties of borophene-reinforced epoxy nanocomposites using molecular dynamics and FEA. Rev. Adv. Mater. Sci. 2023, 62, 20220322. [Google Scholar] [CrossRef]
- Talebsafa, V.; Yousefieh, M.; Borhani, E.; Gharibshahiyan, E. Numerical investigation of friction stir welding parameters on microstructure, thermal and mechanical properties of ultrafine-grained Al-0.2 wt% Sc alloy sheet. J. Cent. South Univ. 2023, 30, 61–73. [Google Scholar] [CrossRef]
- Zhou, C.; Zhan, L.; Liu, C.; Huang, M. Insights into electron wind force by a helical dislocation reconfiguration. iScience 2023, 26, 106870. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B.; Dang, X.; Zhao, T.; Xie, Y.; Cai, J.; Wang, K. Effect of Al2O3 particle content on microstructure and mechanical properties of 1060Al/Al–Al2O3 composites fabricated by cold spraying and accumulative roll bonding. J. Mater. Res. Technol. 2023, 26, 2941–2956. [Google Scholar] [CrossRef]
- Wu, H.; Fan, G.; Huang, M.; Geng, L.; Cui, X.; Xie, H. Deformation behavior of brittle/ductile multilayered composites under interface constraint effect. Int. J. Plast. 2017, 89, 96–109. [Google Scholar] [CrossRef]
- Song, L.; Gao, H.; Bhatt, L.; Kong, C.; Yu, H.L. Microstructure and mechanical properties of AA1050/AA6061 multilayer composites via accumulative roll bonding and cryorolling and subsequent aging. Mater. Sci. Eng. A 2023, 874, 145069. [Google Scholar] [CrossRef]
- Alsoruji, G.S.; Sadoun, A.M.; Abd Elaziz, M.; Al-Betar, M.A.; Abdallah, A.W.; Fathy, A. On the prediction of the mechanical properties of ultrafine grain Al-TiO2 nanocomposites using a modified long-short term memory model with beluga whale optimizer. J. Mater. Res. Technol. 2023, 23, 4075–4088. [Google Scholar] [CrossRef]
- Huang, Z.; Yan, H. Effect of Graphene on the Microstructure Evolution and Mechanical Properties of Al–10Si–2Cu–1.5Fe Aluminum Matrix Composites. Int. J. Met. 2023, 17, 2808–2817. [Google Scholar] [CrossRef]
- Alsoruji, G.S.; Sadoun, A.M.; Elmahdy, M. Microstructure-Based Modeling and Mechanical Characteristics of Accumulative Roll Bonded Al Nanocomposites with SiC Nanoparticles. Metals 2022, 12, 1888. [Google Scholar] [CrossRef]
- Fathy, A.; Ibrahim, D.; Elkady, O.; Hassan, M. Evaluation of mechanical properties of 1050-Al reinforced with SiC particles via accumulative roll bonding process. J. Compos. Mater. 2018, 53, 209–218. [Google Scholar] [CrossRef]
- Mazaheri, Y.; Meratian, M.; Emadi, R.; Najarian, A. Comparison of microstructural and mechanical properties of Al–TiC, Al–B4C and Al–TiC–B4C composites prepared by casting techniques. Mater. Sci. Eng. A 2013, 560, 278–287. [Google Scholar] [CrossRef]
- Raviraj, M.; Sharanprabhu, C.; Mohankumar, G. Experimental Analysis on Processing and Properties of Al-TiC Metal Matrix Composites. Procedia Mater. Sci. 2014, 5, 2032–2038. [Google Scholar] [CrossRef]
- Xing, Y.; Li, N.; Li, C.; Gao, P.; Guan, H.; Yang, C.; Pu, C.; Yi, J. Effects of size and oxidation treatment for SiC particles on the microstructures and mechanical properties of SiCp/Al composites prepared by powder metallurgy. Mater. Sci. Eng. A 2022, 851, 143664. [Google Scholar] [CrossRef]
- Bauri, R. Optimization of process parameters for friction stir processing (FSP) of Al–TiC in situ composite. Bull. Mater. Sci. 2014, 37, 571–578. [Google Scholar] [CrossRef]
- Reddy, M.P.; Himyan, M.; Ubaid, F.; Shakoor, R.; Vyasaraj, M.; Gururaj, P.; Yusuf, M.; Mohamed, A.; Gupta, M. Enhancing thermal and mechanical response of aluminum using nanolength scale TiC ceramic reinforcement. Ceram. Int. 2018, 44, 9247–9254. [Google Scholar] [CrossRef]
- Han, T.; Liang, S.; Zhu, X.; Wang, W.; Yang, J. An investigation of the flexural behaviour of large-span prestressed and steel-reinforced concrete slabs. Sci. Rep. 2023, 13, 10710. [Google Scholar] [CrossRef] [PubMed]
- Saadi, O.W.; Uddin, M.A.; Schiffer, A.; Kumar, S. Digital light processing of 2D lattice composites for tunable self-sensing and mechanical performance. Adv. Eng. Mater. 2023, 2300473. [Google Scholar] [CrossRef]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Fantuzzi, N. Thermomechanical characteristics of green nanofibers made from polylactic acid: An insight into tensile behavior via molecular dynamics simulation. Mech. Mater. 2023, 181, 104640. [Google Scholar] [CrossRef]
- Derakhshani Dastjerdi, M.; Carboni, M.; Hojjati, M. Mechanical Properties of Uncured Thermoset Tow Prepreg: Experiment and Finite Element Analysis. J. Compos. Sci. 2023, 7, 312. [Google Scholar] [CrossRef]
- Mohammed, S.; Nautiyal, P.; Paul, T.; Zhang, C.; Agarwal, A. A critique on boron nitride nanotube reinforced metal matrix composites. Crit. Rev. Solid State Mater. Sci. 2023. [Google Scholar] [CrossRef]






| Abbreviations | Explanation |
|---|---|
| AMMCs | Aluminum Metal Matrix Composites |
| ARB | Accumulative Roll Bonding |
| AMCs | Aluminum Matrix Composites |
| CR | Cryorolling |
| FEA | Finite Element Analysis |
| RVE | Representative Volume Element |
| SEM | Scanning Electron Microscopy |
| TEM | Transmission Electron Microscopy |
| OM | Optical microscope |
| XRD | X-ray diffraction |
| TiC | Titanium Carbide |
| σvm | Von Mises Stress |
| σxx | Normal Stress in the x-direction |
| σyy | Normal Stress in the y-direction |
| σxy | Shear Stress |
| εmax | Maximum Strain |
| Vf | Volume fraction |
| Elements | Al | Fe | Si | Cu | Mg | Mn | Ni | Ti | Zn |
|---|---|---|---|---|---|---|---|---|---|
| Wt% | 99.18 | 0.40 | 0.15 | 0.05 | 0.05 | 0.05 | 0.0014 | 0.05 | 0.07 |
| Materials | AA1050 | TiC |
|---|---|---|
| Elastic modulus (GPa) | 70 | 497 |
| Yield strength (MPa) | 105 | 20 × 103 |
| Poisson ratio | 0.33 | 0.21 |
| Density(kg/m3) | 2700 | 4930 |
| Thermal expansion coefficient (α)/°C | 23.1 × 10−6 | 6.6 × 10−6 |
| Thermal conductivity (k) W/(m·K) | 200 | 22 |
| Materials | Experimental | Simulation (RVE−1 Case Model) | Error Percentage (%) |
|---|---|---|---|
| Elastic modulus (GPa) | 86 ± 2 | 91 | 5.4 |
| Yield strength (MPa) | 260 ± 13 | 279 | 6.8 |
| Tensile strength (MPa) | 239 ± 15 | 246 | 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farid, W.; Li, H.; Wang, Z.; Cui, H.; Kong, C.; Yu, H. Integrating Experimental and Computational Analyses for Mechanical Characterization of Titanium Carbide/Aluminum Metal Matrix Composites. Materials 2024, 17, 2093. https://doi.org/10.3390/ma17092093
Farid W, Li H, Wang Z, Cui H, Kong C, Yu H. Integrating Experimental and Computational Analyses for Mechanical Characterization of Titanium Carbide/Aluminum Metal Matrix Composites. Materials. 2024; 17(9):2093. https://doi.org/10.3390/ma17092093
Chicago/Turabian StyleFarid, Waqas, Hailin Li, Zhengyu Wang, Huijie Cui, Charlie Kong, and Hailiang Yu. 2024. "Integrating Experimental and Computational Analyses for Mechanical Characterization of Titanium Carbide/Aluminum Metal Matrix Composites" Materials 17, no. 9: 2093. https://doi.org/10.3390/ma17092093
APA StyleFarid, W., Li, H., Wang, Z., Cui, H., Kong, C., & Yu, H. (2024). Integrating Experimental and Computational Analyses for Mechanical Characterization of Titanium Carbide/Aluminum Metal Matrix Composites. Materials, 17(9), 2093. https://doi.org/10.3390/ma17092093







