Deep Learning-Based Design Method for Acoustic Metasurface Dual-Feature Fusion
Abstract
1. Introduction
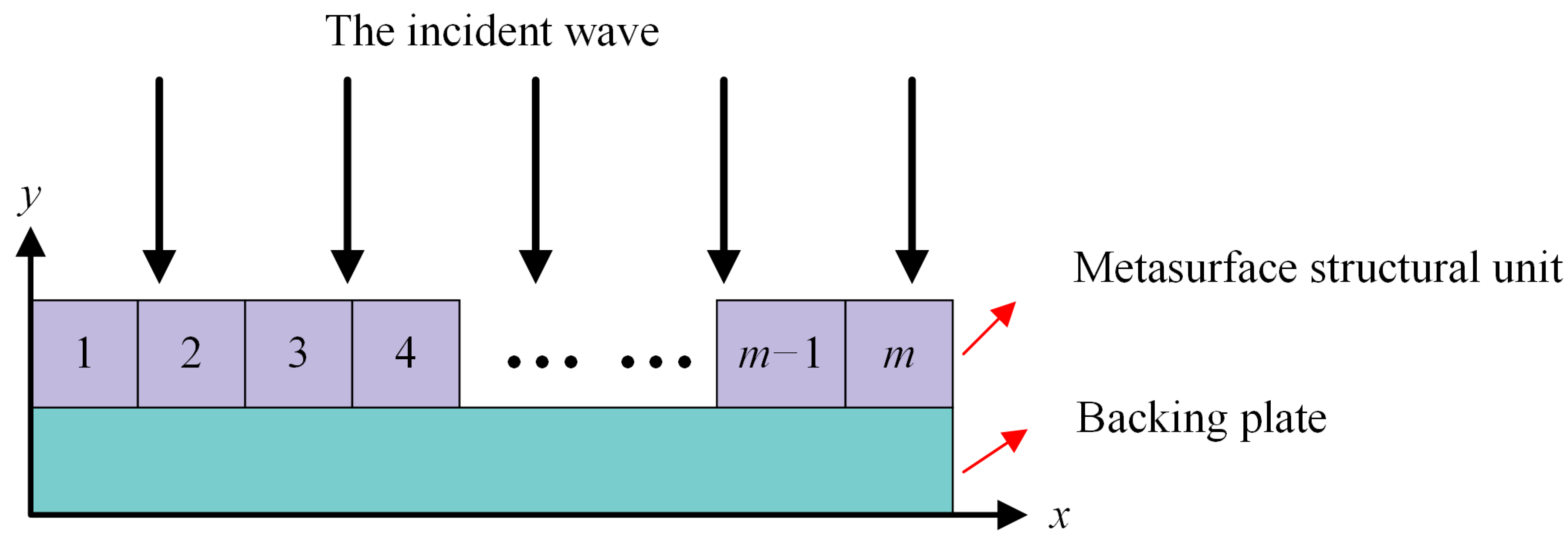
2. Physical Modeling of the Localized Acoustic Field on the Metasurfaces
3. Method
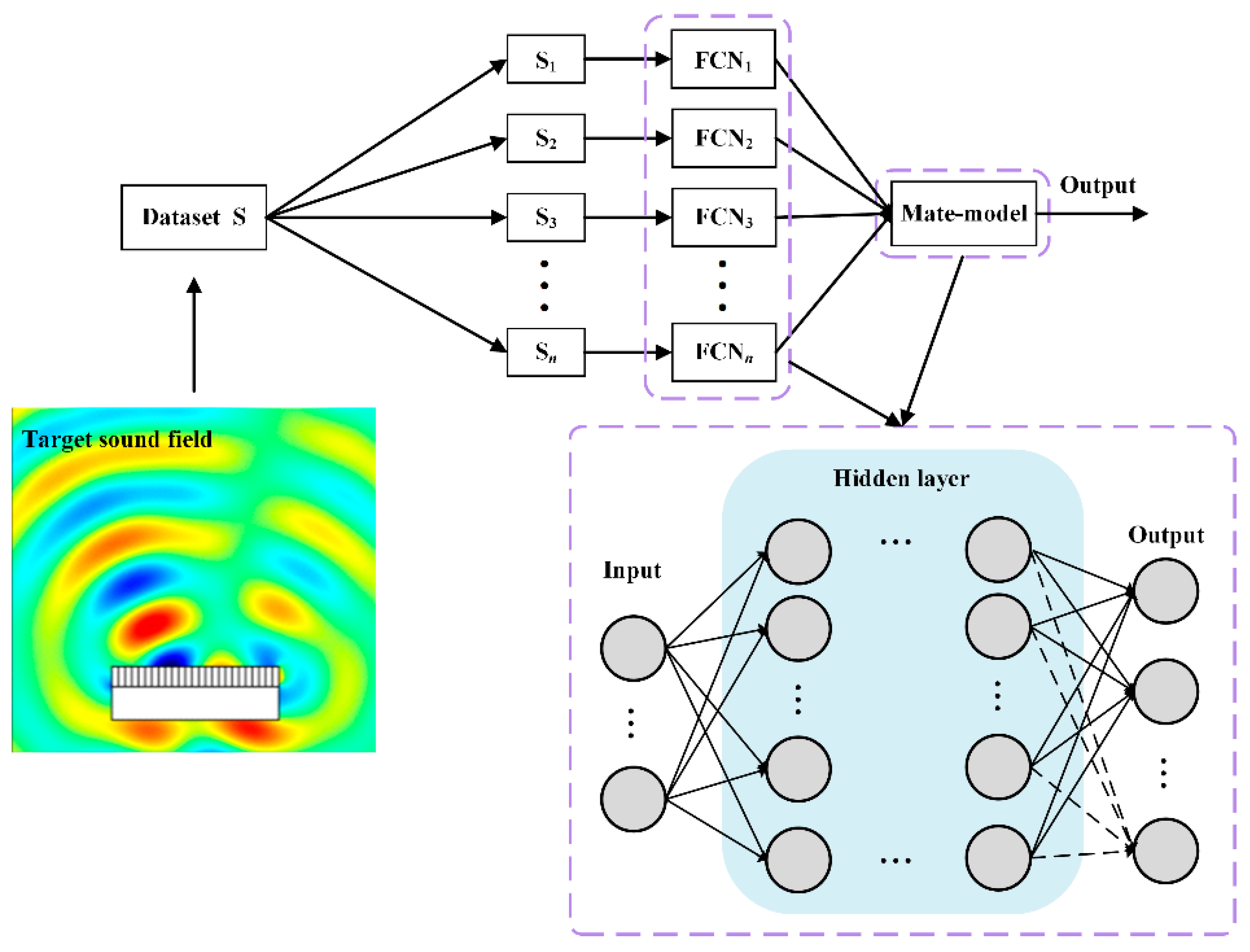
3.1. Forward Model Design Based on Ensemble Learning
3.1.1. Dataset Preparation
3.1.2. Ensemble Learning Models
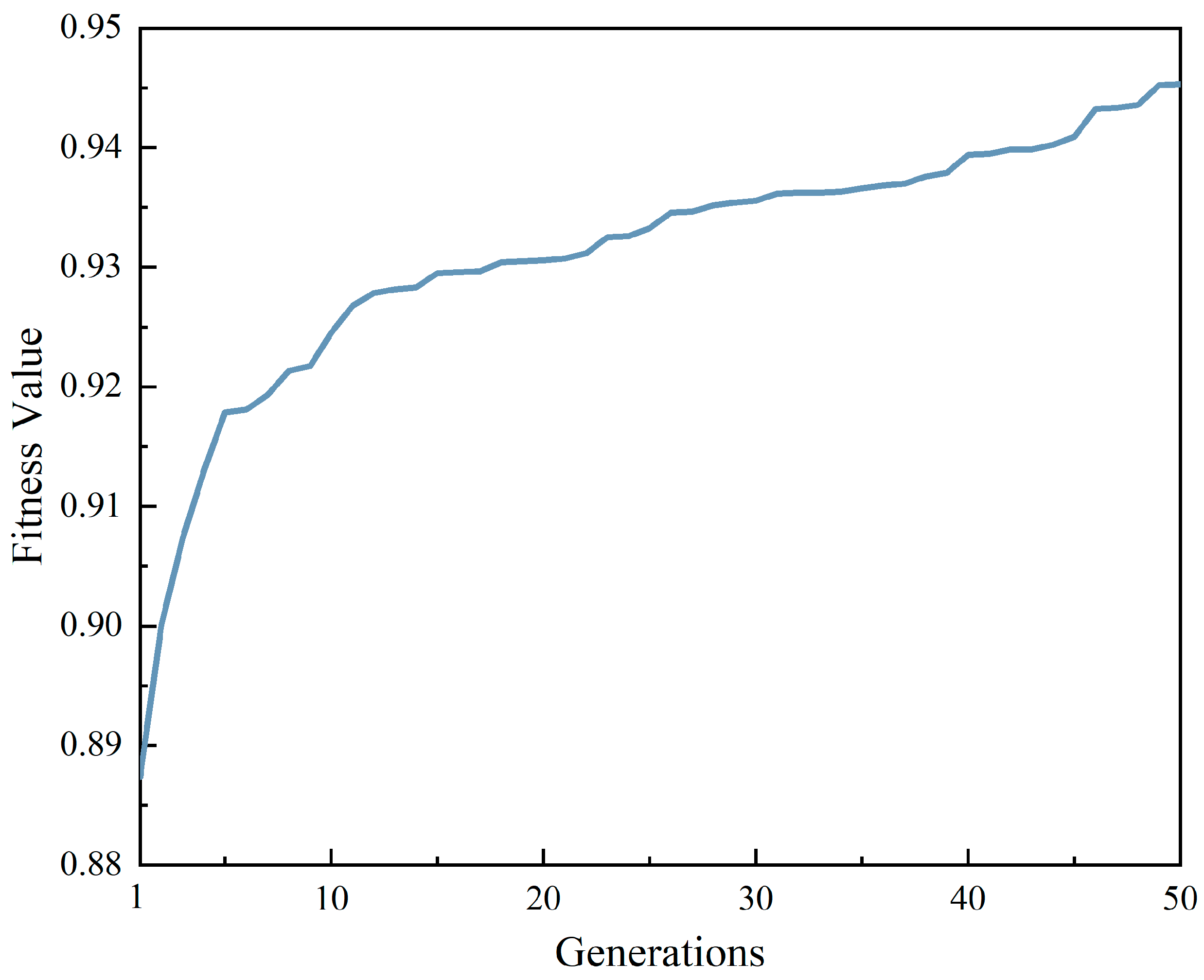
3.1.3. Algorithm Details and Discussion
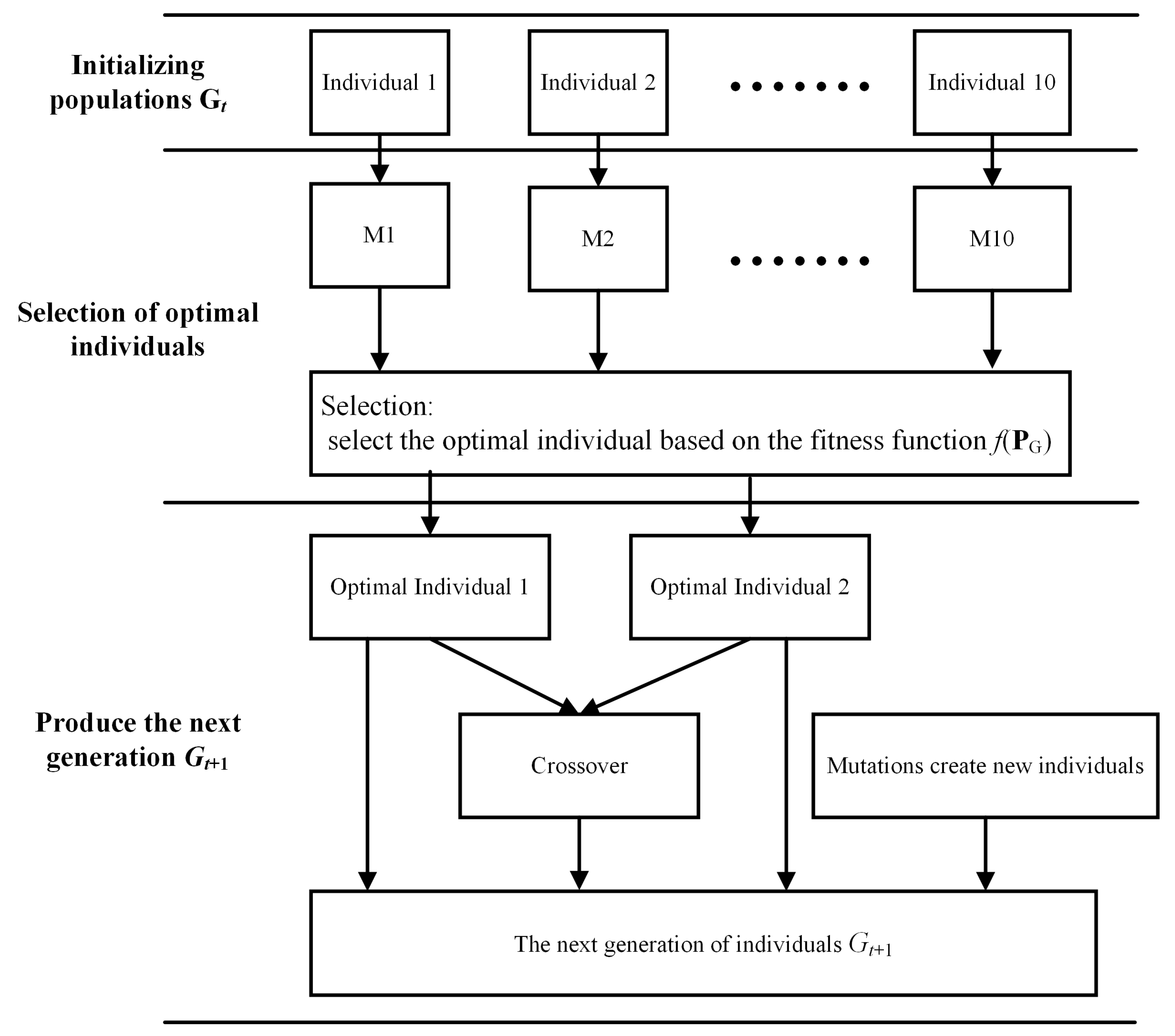
3.2. Reverse Design Method Based on DFCNN
3.2.1. Data Preprocessing
3.2.2. DFCNN Network
3.2.3. Algorithm Details
4. Discussion of Results
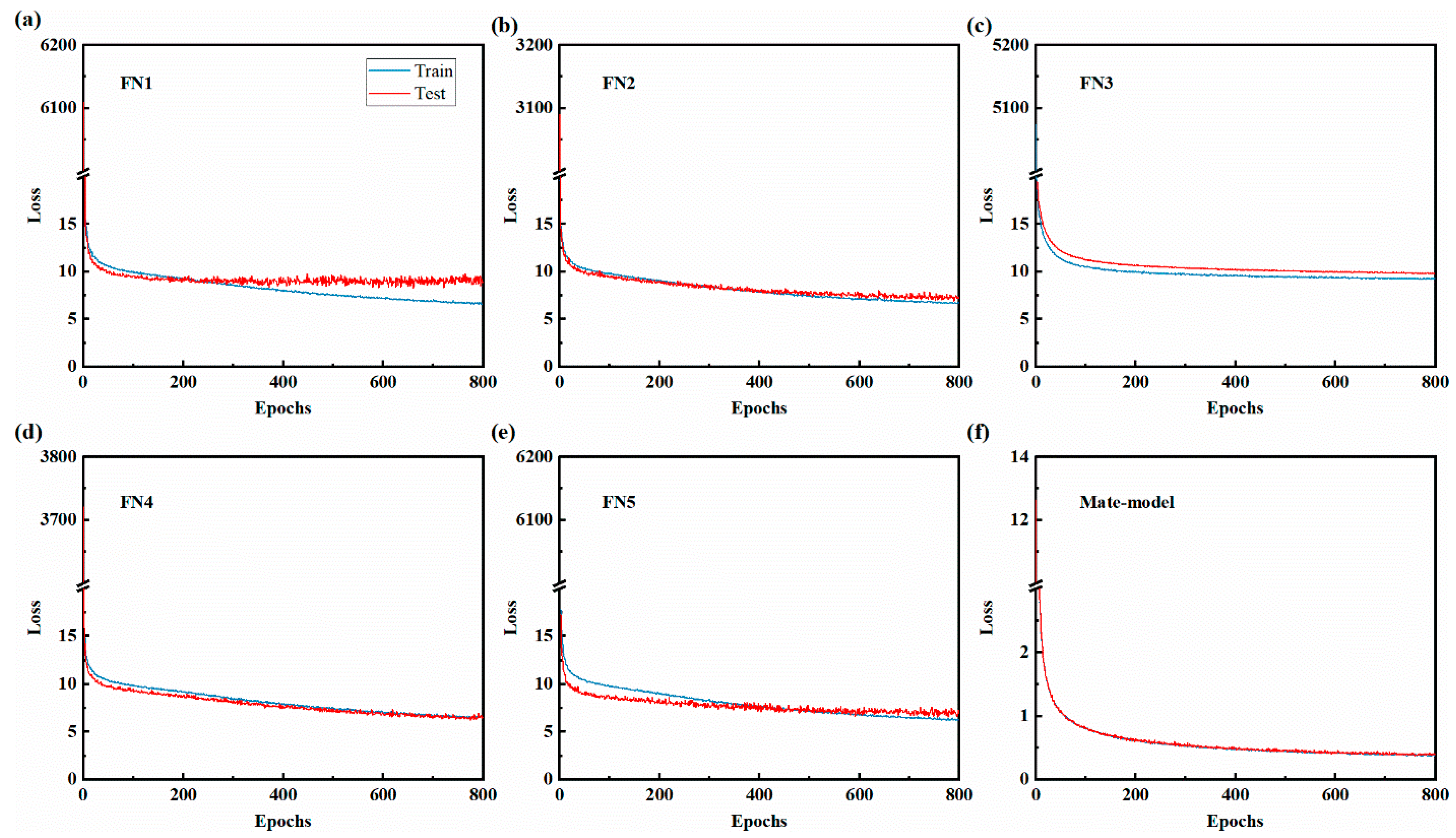
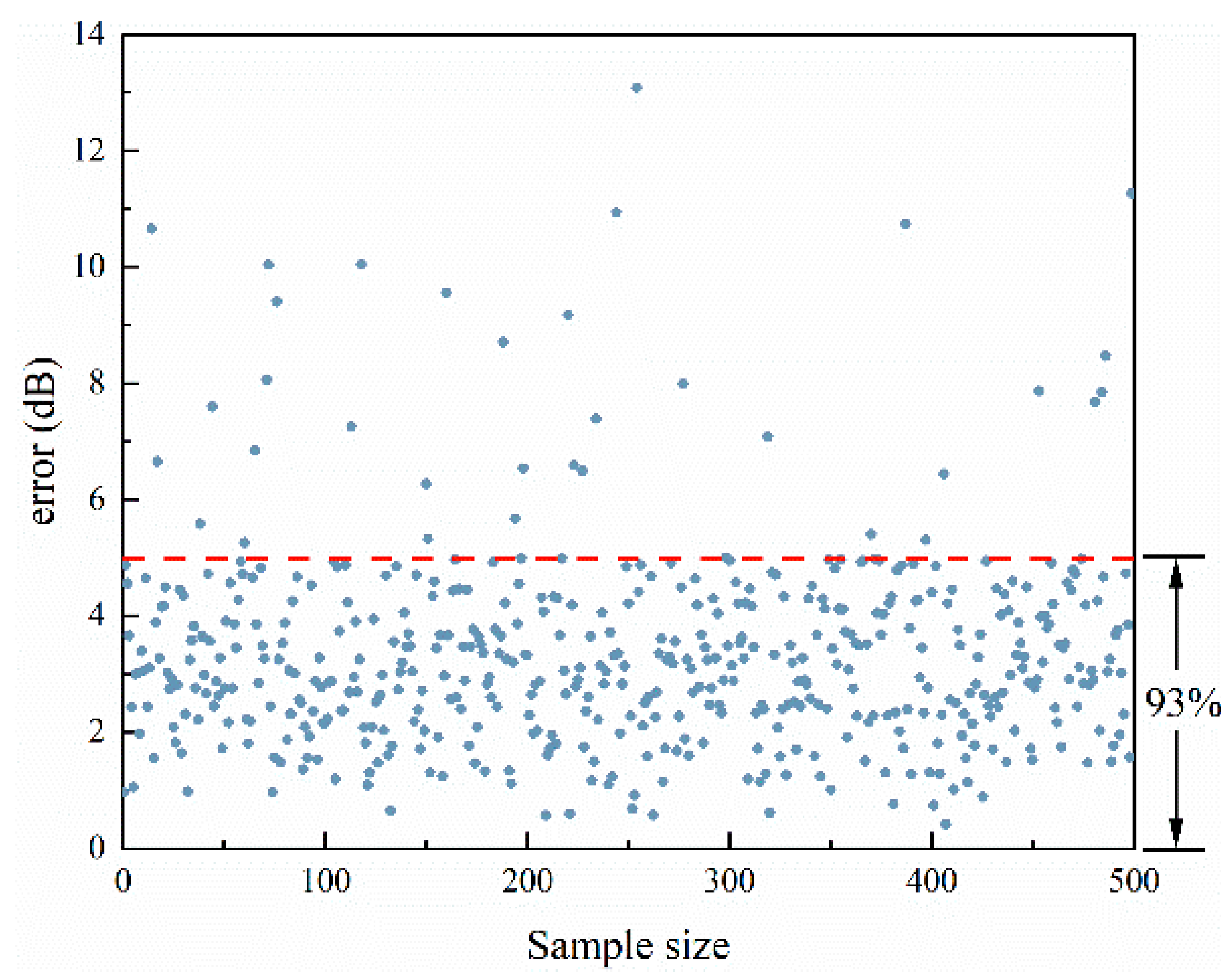
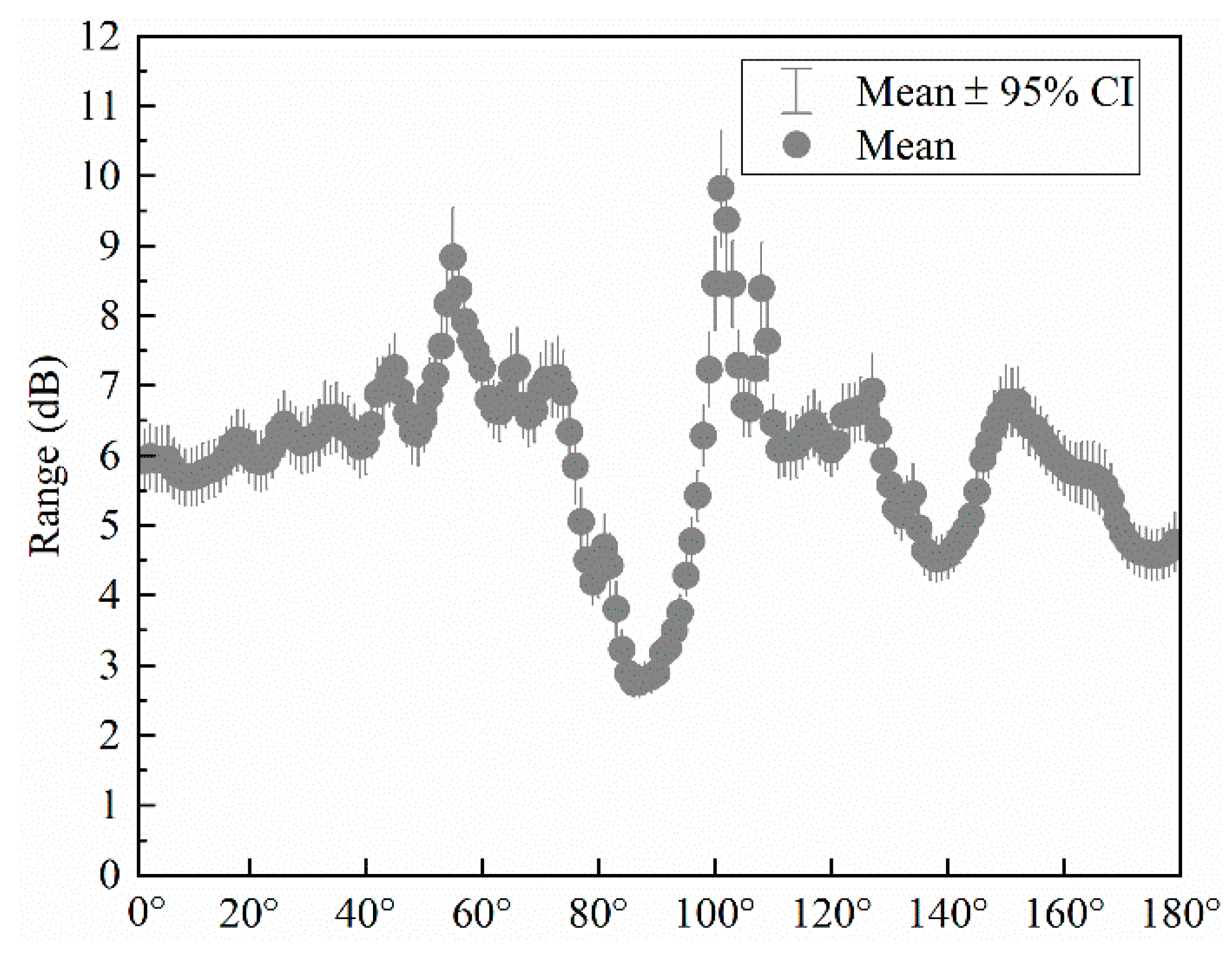
4.1. Ensemble Learning Model Results
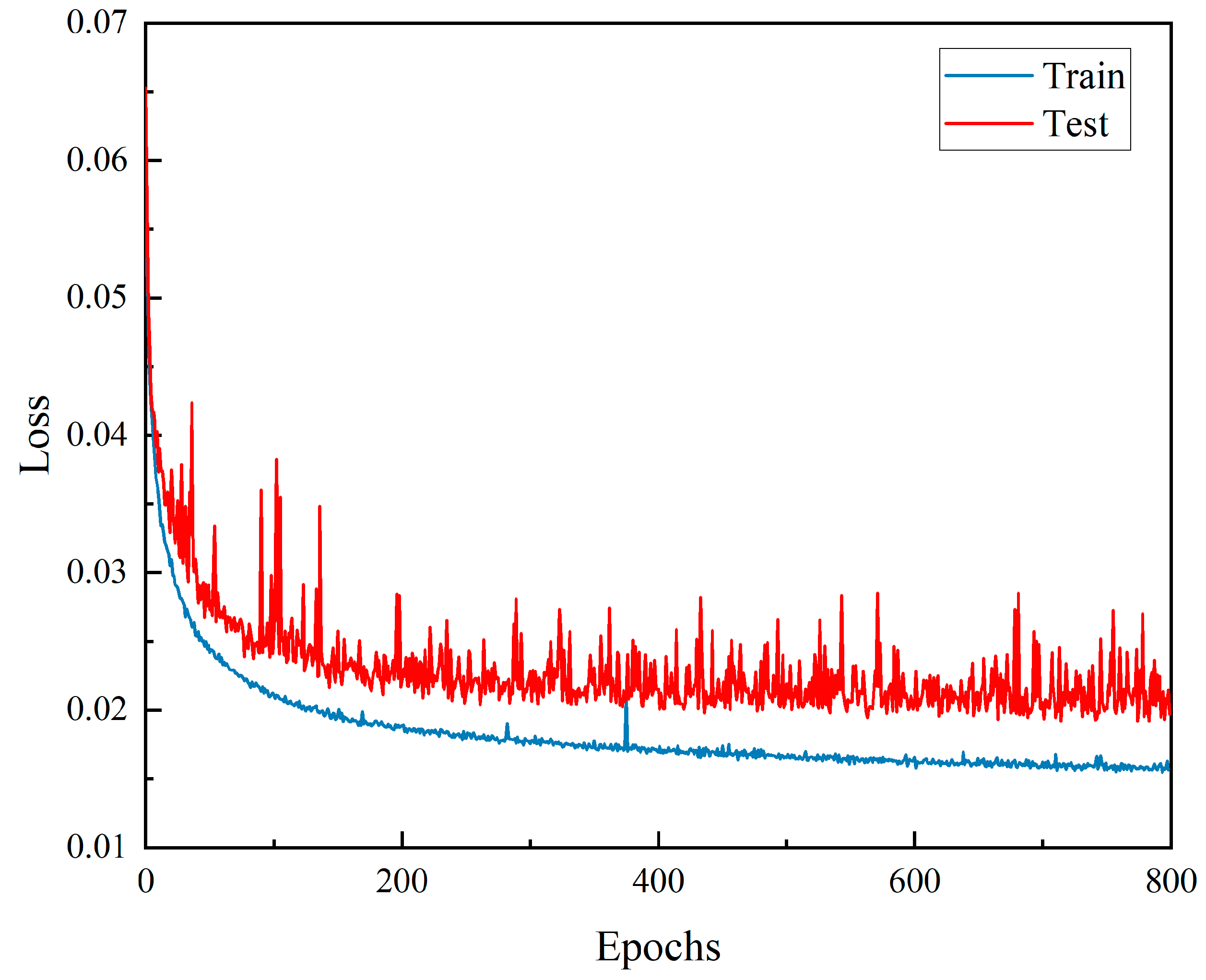
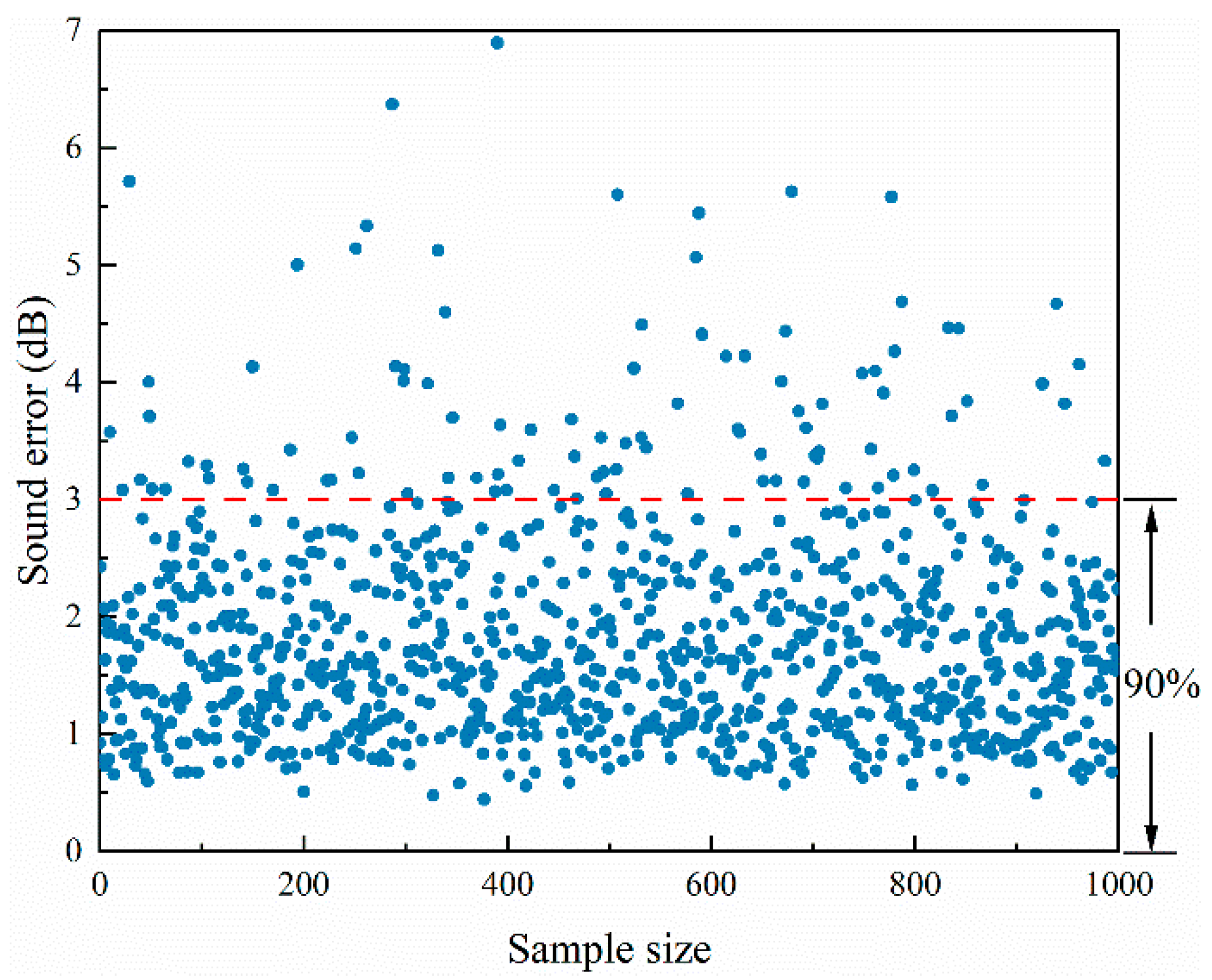
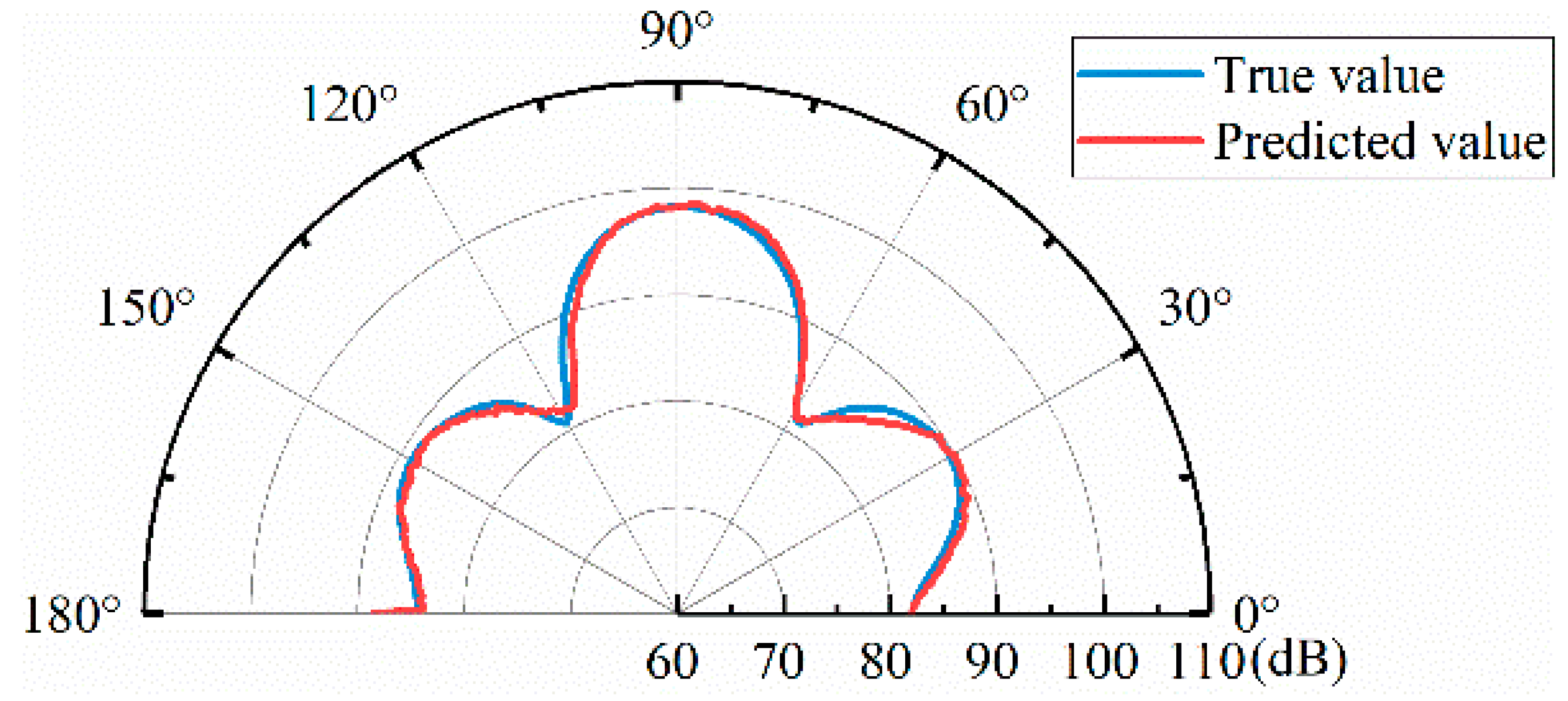
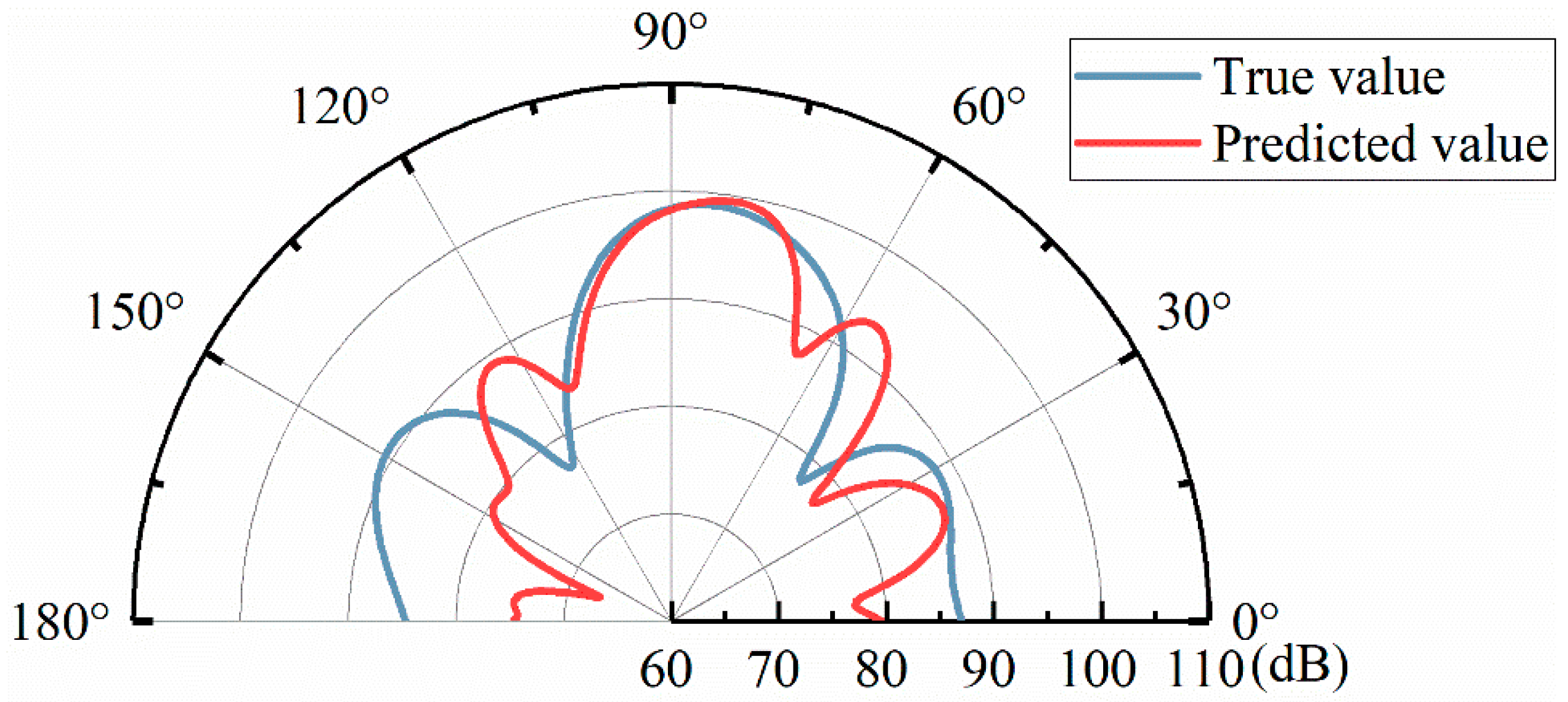
4.2. DFCNN Model Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Assouar, B.; Liang, B.; Wu, Y.; Li, Y.; Cheng, J.-C.; Jing, Y. Acoustic Metasurfaces. Nat. Rev. Mater. 2018, 3, 460–472. [Google Scholar] [CrossRef]
- Zabihi, A.; Ellouzi, C.; Shen, C. Tunable, Reconfigurable, and Programmable Acoustic Metasurfaces: A Review. Front. Mater. 2023, 10, 1132585. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Farhat, M.; Guenneau, S.; Enoch, S.; Alù, A. Acoustic Scattering Cancellation via Ultrathin Pseudo-Surface. Appl. Phys. Lett. 2011, 99, 191913. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, Z.; Zhao, S.; Cai, X.; Zhang, Y.; Cai, Z.; Li, H.; Li, Z.; Su, M.; Zhang, C.; et al. Lotus Metasurface for Wide-Angle Intermediate-Frequency Water–Air Acoustic Transmission. ACS Appl. Mater. Interfaces 2021, 13, 53242–53251. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Liu, J.-J.; Ding, Y.; Wang, W.; Liang, B.; Cheng, J.-C. Metamaterial-Based Real-Time Communication with High Information Density by Multipath Twisting of Acoustic Wave. Nat. Commun. 2022, 13, 5171. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Assouar, B.M. Acoustic Metasurface-Based Perfect Absorber with Deep Subwavelength Thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Eslamzadeh, S.; Ghaffari-Miab, M.; Abbasi-Arand, B. Design of a Broadband Metamaterial-Based Acoustic Lens Using Elaborated Carpet Cloak Strategy. Appl. Phys. A 2021, 127, 897. [Google Scholar] [CrossRef]
- Li, J.; Shen, C.; Díaz-Rubio, A.; Tretyakov, S.A.; Cummer, S.A. Systematic Design and Experimental Demonstration of Bianisotropic Metasurfaces for Scattering-Free Manipulation of Acoustic Wavefronts. Nat. Commun. 2018, 9, 1342. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, W.; Chen, H.; Konneker, A.; Popa, B.-I.; Cummer, S.A. Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 2014, 5, 5553. [Google Scholar] [CrossRef]
- Schnitzer, O.; Brandão, R. Absorption Characteristics of Large Acoustic Metasurfaces. Phil. Trans. R. Soc. A. 2022, 380, 20210399. [Google Scholar] [CrossRef]
- Moore, D.B.; Sambles, J.R.; Hibbins, A.P.; Starkey, T.A.; Chaplain, G.J. Acoustic Surface Modes on Metasurfaces with Embedded Next-Nearest-Neighbor Coupling. Phys. Rev. B 2023, 107, 144110. [Google Scholar] [CrossRef]
- Jiménez, N.; Groby, J.-P.; Romero-García, V. Spiral Sound-Diffusing Metasurfaces Based on Holographic Vortices. Sci. Rep. 2021, 11, 10217. [Google Scholar] [CrossRef] [PubMed]
- Palma, G.; Centracchio, F.; Burghignoli, L.; Cioffi, I.; Iemma, U. Numerical Optimization of Metasurface Cells for Acoustic Reflection. AIAA J. 2024, 62, 1136–1147. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Glynn Holt, R.; Anderson, S.; Zhang, X. Horn-like Space-Coiling Metamaterials toward Simultaneous Phase and Amplitude Modulation. Nat. Commun. 2018, 9, 1349. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jiang, X.; Li, R.; Liang, B.; Zou, X.; Yin, L.; Cheng, J. Experimental Realization of Full Control of Reflected Waves with Subwavelength Acoustic Metasurfaces. Phys. Rev. Appl. 2014, 2, 064002. [Google Scholar] [CrossRef]
- Lawrence, A.J.; Goldsberry, B.M.; Wallen, S.P.; Haberman, M.R. Numerical Study of Acoustic Focusing Using a Bianisotropic Acoustic Lens. J. Acoust. Soc. Am. 2020, 148, EL365–EL369. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.; Zhang, X.; Wu, Y. Ultrathin Metasurface with High Absorptance for Waterborne Sound. J. Appl. Phys. 2018, 123, 091710. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Zhang, X.; Li, L.; Chen, M.; Fang, D. Broadband Underwater Sound Absorbing Structure with Gradient Cavity Shaped Polyurethane Composite Array Supported by Carbon Fiber Honeycomb. J. Sound Vib. 2020, 479, 115375. [Google Scholar] [CrossRef]
- Fernández-Marín, A.A.; Jiménez, N.; Groby, J.-P.; Sánchez-Dehesa, J.; Romero-García, V. Aerogel-Based Metasurfaces for Perfect Acoustic Energy Absorption. Appl. Phys. Lett. 2019, 115, 061901. [Google Scholar] [CrossRef]
- Lissek, H.; Rivet, E.; Laurence, T.; Fleury, R. Toward Wideband Steerable Acoustic Metasurfaces with Arrays of Active Electroacoustic Resonators. J. Appl. Phys. 2018, 123, 091714. [Google Scholar] [CrossRef]
- He, J.; Liang, Q.; Lv, P.; Wu, Y.; Chen, T. Tunable Broadband Multi-Function Acoustic Metasurface by Nested Resonant Rings. Appl. Acoust. 2022, 197, 108957. [Google Scholar] [CrossRef]
- Yu, G.; Qiu, Y.; Li, Y.; Wang, X.; Wang, N. Underwater Acoustic Stealth by a Broadband 2-Bit Coding Metasurface. Phys. Rev. Appl. 2021, 15, 064064. [Google Scholar] [CrossRef]
- Long, H.; Zhu, Y.; Gu, Y.; Cheng, Y.; Liu, X. Inverse Design of an Ultrasparse Dissipated-Sound Metacage by Using a Genetic Algorithm. Phys. Rev. Appl. 2022, 18, 044032. [Google Scholar] [CrossRef]
- Li, R.; Jiang, Y.; Zhu, R.; Zou, Y.; Shen, L.; Zheng, B. Design of Ultra-Thin Underwater Acoustic Metasurface for Broadband Low-Frequency Diffuse Reflection by Deep Neural Networks. Sci. Rep. 2022, 12, 12037. [Google Scholar] [CrossRef] [PubMed]
- Ciaburro, G.; Iannace, G. Modeling Acoustic Metamaterials Based on Reused Buttons Using Data Fitting with Neural Network. J. Acoust. Soc. Am. 2021, 150, 51–63. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Li, Y.; Zuo, L.; Zhang, K. Machine-Learning Optimized Method for Regional Control of Sound Fields. Extrem. Mech. Lett. 2021, 45, 101297. [Google Scholar] [CrossRef]
- Gao, N.; Wang, M.; Cheng, B.; Hou, H. Inverse Design and Experimental Verification of an Acoustic Sink Based on Machine Learning. Appl. Acoust. 2021, 180, 108153. [Google Scholar] [CrossRef]
- Sajedian, I.; Lee, H.; Rho, J. Double-Deep Q-Learning to Increase the Efficiency of Metasurface Holograms. Sci. Rep. 2019, 9, 10899. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Meng, F.; Huang, X. Coding Metalens with Helical-Structured Units for Acoustic Focusing and Splitting. Appl. Phys. Lett. 2020, 117, 021901. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, W.; Xu, W.; Yang, T. Topology Optimization of Single-Groove Acoustic Metasurfaces Using Genetic Algorithms. Arch. Appl. Mech. 2022, 92, 961–969. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Liao, G.; Luan, C.; Wang, Z.; Liu, J.; Yao, X.; Fu, J. Acoustic Metamaterials: A Review of Theories, Structures, Fabrication Approaches, and Applications. Adv. Mater. Technol. 2021, 6, 2000787. [Google Scholar] [CrossRef]
- Zhen, W.; Xueqin, Y.; Zhigao, Z.; Min, S. Piecewise Design for a Pentamode Acoustic Metasurface and Its Analysis of Wave Manipulation Ability. J. Huazhong Univ. Sci. Technol. 2022, 50, 19–25. [Google Scholar] [CrossRef]
- Chu, Y.; Wang, Z.; Xu, Z. Broadband High-Efficiency Controllable Asymmetric Propagation by Pentamode Acoustic Metasurface. Phys. Lett. A 2020, 384, 126230. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H.; Zhao, Z.; Zhao, A.; Cai, X.; Wang, L. Experimental Demonstration of a Broadband Waterborne Acoustic Metasurface for Shifting Reflected Waves. J. Appl. Phys. 2020, 127, 174902. [Google Scholar] [CrossRef]
- Ding, H.; Fang, X.; Jia, B.; Wang, N.; Cheng, Q.; Li, Y. Deep Learning Enables Accurate Sound Redistribution via Nonlocal Metasurfaces. Phys. Rev. Applied 2021, 16, 064035. [Google Scholar] [CrossRef]
- Guo, M.-H.; Xu, T.-X.; Liu, J.-J.; Liu, Z.-N.; Jiang, P.-T.; Mu, T.-J.; Zhang, S.-H.; Martin, R.R.; Cheng, M.-M.; Hu, S.-M. Attention Mechanisms in Computer Vision: A Survey. Comp. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]



| Submodel | lr | Batch_Size | Epoch | Dropout | Optimizer | Number of Layers and Neurons Setting |
|---|---|---|---|---|---|---|
| FCN1 | 0.005 | 512 | 800 | 0.1 | Adam | 2→724→1000→650→400→200→181 |
| FCN2 | 0.005 | 256 | 800 | 0.1 | Adam | 2→724→1000→650→400→200→181 |
| FCN3 | 0.005 | 512 | 800 | 0.1 | SGD | 2→724→1000→600→400→300→181 |
| FCN4 | 0.01 | 512 | 800 | 0.1 | Adam | 2→700→1000→650→400→200→181 |
| FCN5 | 0.005 | 256 | 800 | 0.2 | Adam | 2→724→1000→650→400→200→181 |
| Name | Specific Settings |
|---|---|
| Dataset | 30,000 |
| Criteria for division | 80%, 20% |
| batch_size | 256 |
| epoch_GA | 150 |
| Number of iterations | 50 |
| Population size | 10 |
| mutation_rate | 0.4 |
| lr | 10 (−3, −1) |
| Activation function | ReLU, Leaky ReLU, PReLU |
| Optimizer | Adam, SGD, Nadam |
| epoch_DFCNN | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Q.; Zhao, H.; Huang, Z.; Hao, G.; Chen, W. Deep Learning-Based Design Method for Acoustic Metasurface Dual-Feature Fusion. Materials 2024, 17, 2166. https://doi.org/10.3390/ma17092166
Lv Q, Zhao H, Huang Z, Hao G, Chen W. Deep Learning-Based Design Method for Acoustic Metasurface Dual-Feature Fusion. Materials. 2024; 17(9):2166. https://doi.org/10.3390/ma17092166
Chicago/Turabian StyleLv, Qiang, Huanlong Zhao, Zhen Huang, Guoqiang Hao, and Wei Chen. 2024. "Deep Learning-Based Design Method for Acoustic Metasurface Dual-Feature Fusion" Materials 17, no. 9: 2166. https://doi.org/10.3390/ma17092166
APA StyleLv, Q., Zhao, H., Huang, Z., Hao, G., & Chen, W. (2024). Deep Learning-Based Design Method for Acoustic Metasurface Dual-Feature Fusion. Materials, 17(9), 2166. https://doi.org/10.3390/ma17092166






