Stripe Noise Removal in Blazed Grating Generation for Electrically Tunable Beam Deflector
Abstract
1. Introduction
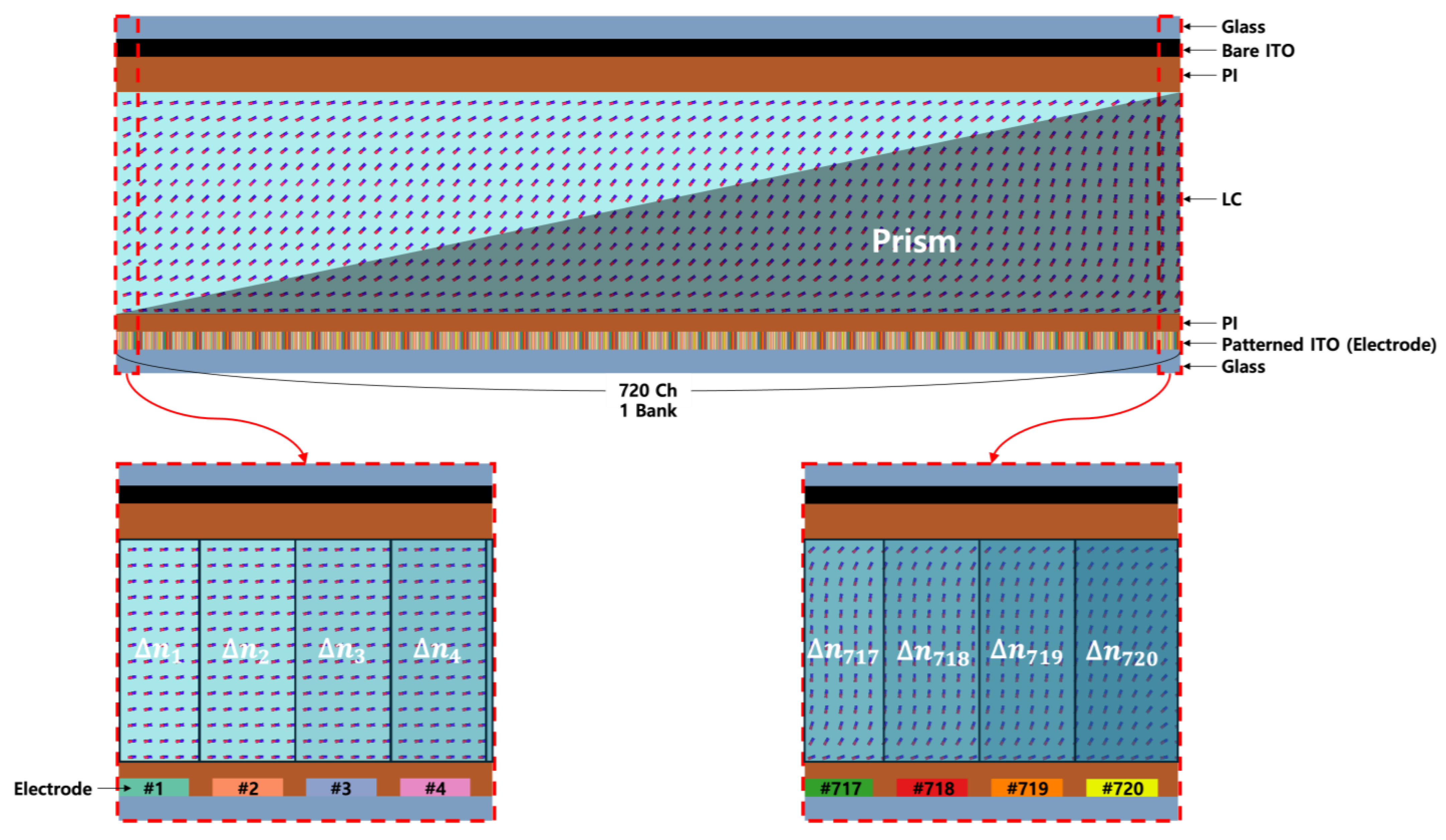
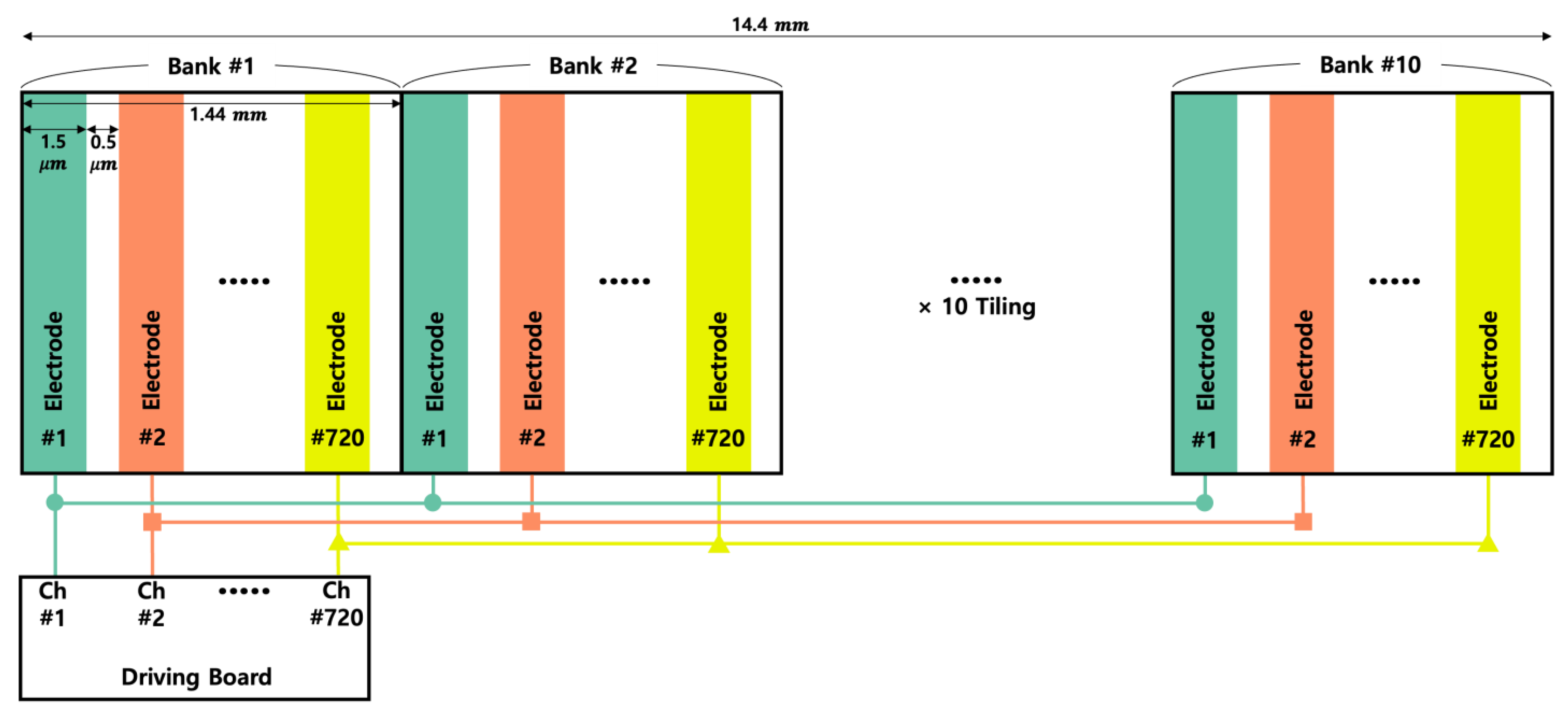
2. Materials and Methods
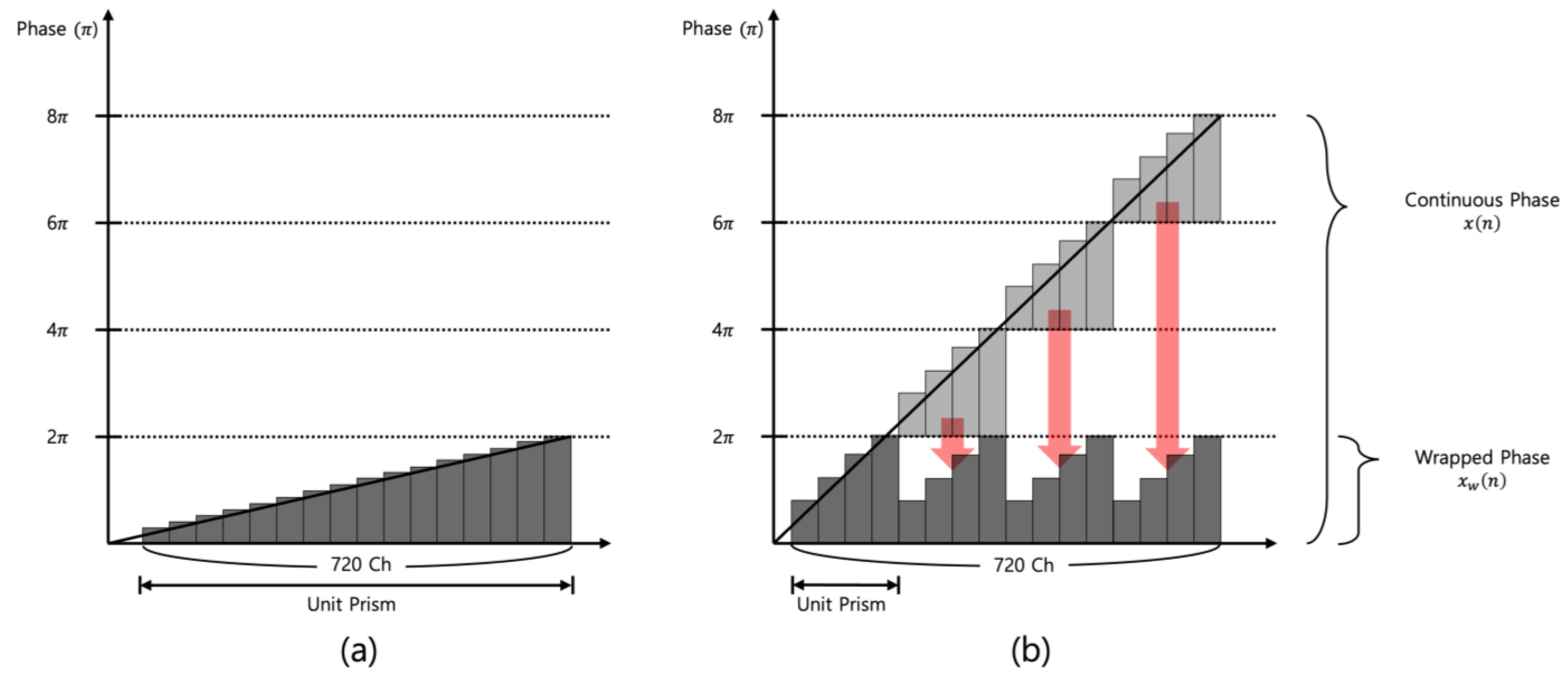
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Li, J.; Li, X.Y.; Wang, B.; Li, T.G. Image Stripe Noise Removal Based on Compressed Sensing. Int. J. Pattern Recognit. Artif. Intell. 2022, 36, 2254004. [Google Scholar] [CrossRef]
- Liu, C.W.; Sui, X.B.; Gu, G.H.; Chen, Q. Shutterless non-uniformity correction for the long-term stability of an uncooled long-wave infrared camera. Meas. Sci. Technol. 2018, 29, 025402. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, H.; Li, J.; Chi, M. A Neural Network-Based Method for Eliminating Stripe Noise. In Proceedings of the 2024 IEEE 4th International Conference on Electronic Communications, Internet of Things and Big Data (ICEIB), Taiwan, China, 19–21 April 2024; pp. 223–225. [Google Scholar]
- Cao, Y.P.; He, Z.W.; Yang, J.X.; Cao, Y.L.; Yang, M.Y. Spatially Adaptive Column Fixed-Pattern Noise Correction in Infrared Imaging System Using 1D Horizontal Differential Statistics. IEEE Photonics J. 2017, 9, 7803513. [Google Scholar] [CrossRef]
- Chen, B.Y.; Feng, X.; Wu, R.H.; Guo, Q.; Wang, X.; Ge, S.M. Adaptive Wavelet Filter With Edge Compensation for Remote Sensing Image Denoising. IEEE Access 2019, 7, 91966–91979. [Google Scholar] [CrossRef]
- Yan, F.; Wu, S.; Zhang, Q.; Liu, Y.; Sun, H. Destriping of Remote Sensing Images by an Optimized Variational Model. Sensors 2023, 23, 7529. [Google Scholar] [CrossRef]
- Song, Q.; Huang, Z.H.; Jiang, W.S.; Bai, K.; Liu, X.Y.; Hu, J.P. Remote Sensing Images Destriping via Nonconvex Regularization and Fast Regional Decomposition. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5646915. [Google Scholar] [CrossRef]
- Liu, Y.; Long, T.; Jiao, W.; Chen, B.; Cheng, B.; Du, Y.; He, G.; Huang, P. Leveraging “Night–Day” Calibration Data to Correct Stripe Noise and Vignetting in SDGSAT-1 Nighttime-Light Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5616923. [Google Scholar] [CrossRef]
- Li, J.; Zeng, D.; Zhang, J.J.; Han, J.G.; Mei, T. Column-Spatial Correction Network for Remote Sensing Image Destriping. Remote Sens. 2022, 14, 3376. [Google Scholar] [CrossRef]
- McManamon, P.F.; Bos, P.J.; Escuti, M.J.; Heikenfeld, J.; Serati, S.; Xie, H.K.; Watson, E.A. A Review of Phased Array Steering for Narrow-Band Electrooptical Systems. Proc. IEEE 2009, 97, 1078–1096. [Google Scholar] [CrossRef]
- Tolkachev, A.A.; Denisenko, V.V.; Shishlov, A.V.; Shubov, A.G. High gain antenna systems for millimeter wave radars with combined electronical and mechanical beam steering. In Proceedings of the 1996 IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 15–18 October 1996; pp. 266–271. [Google Scholar]
- Wu, G.B.; Qu, S.W.; Yang, S.W. Wide-Angle Beam-Scanning Reflectarray With Mechanical Steering. IEEE Trans. Antennas Propag. 2018, 66, 172–181. [Google Scholar] [CrossRef]
- Mcmanamon, P.F.; Watson, E.A.; Dorschner, T.A.; Barnes, L.J. Nonmechanical Beam-Steering for Active and Passive Sensors. Infrared Imaging Syst. Des. Anal. Model. Test. IV 1993, 1969, 2–10. [Google Scholar]
- Han, W.; Haus, J.W.; McManamon, P.; Heikenfeld, J.; Smith, N.; Yang, J. Transmissive beam steering through electrowetting microprism arrays. Opt. Commun. 2010, 283, 1174–1181. [Google Scholar] [CrossRef]
- Hornbeck, L.J. Digital light processing and MEMS: An overview. In Proceedings of the IEEE/Leos 1996 Summer Topical Meetings—Advanced Applications of Lasers in Materials and Processing, Digest, Keystone, CO, USA, 5–9 August 1996; pp. C7–C8. [Google Scholar]
- Berini, P. Optical Beam Steering Using Tunable Metasurfaces. Acs Photonics 2022, 9, 2204–2218. [Google Scholar] [CrossRef]
- Lin, S.; Chen, Y.; Wong, Z.J. High-performance optical beam steering with nanophotonics. Nanophotonics 2022, 11, 2617–2638. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Miroshnichenko, A.E. Beam Steering with Dielectric Metalattices. Acs Photonics 2018, 5, 1733–1741. [Google Scholar] [CrossRef]
- Ma, Z.; Tian, T.; Liao, Y.; Feng, X.; Li, Y.; Cui, K.; Liu, F.; Sun, H.; Zhang, W.; Huang, Y. Electrically switchable 2(N)-channel wave-front control for certain functionalities with N cascaded polarization-dependent metasurfaces. Nat. Commun. 2024, 15, 8370. [Google Scholar] [CrossRef]
- Resler, D.P.; Hobbs, D.S.; Sharp, R.C.; Friedman, L.J.; Dorschner, T.A. High-efficiency liquid-crystal optical phased-array beam steering. Opt. Lett. 1996, 21, 689–691. [Google Scholar] [CrossRef]
- Wang, X.; Wilson, D.; Muller, R.; Maker, P.; Psaltis, D. Liquid-crystal blazed-grating beam deflector. Appl. Opt. 2000, 39, 6545–6555. [Google Scholar] [CrossRef]
- Beeckman, J. Liquid-crystal photonic applications. Opt. Eng. 2011, 50, 081202. [Google Scholar] [CrossRef]
- Li, S.Q.; Xu, X.; Maruthiyodan Veetil, R.; Valuckas, V.; Paniagua-Dominguez, R.; Kuznetsov, A.I. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 2019, 364, 1087–1090. [Google Scholar] [CrossRef]
- Kim, Y.; Won, K.; Kim, Y.; An, J.; Song, H.; Kim, S.; Choi, C.S.; Lee, H.S. Electrically tunable transmission-type beam deflector using liquid crystal with high angular resolution. Appl. Opt. 2018, 57, 5090–5094. [Google Scholar] [CrossRef] [PubMed]
- de Blas, M.G.; Geday, M.A.; Otón, J.M.; Arregui, X.Q. Two-Dimensional Digital Beam Steering Based on Liquid Crystal Phase Gratings. Appl. Sci. 2021, 11, 3632. [Google Scholar] [CrossRef]
- Morris, R.; Jones, J.C.; Nagaraj, M. Liquid Crystal Devices for Beam Steering Applications. Micromachines 2021, 12, 247. [Google Scholar] [CrossRef] [PubMed]
- Inoue, Y.; Shikada, T.; Moritake, H. Enhancing steering angle in liquid crystal beam-steering devices with wideband performance. Opt. Lett. 2024, 49, 6081–6084. [Google Scholar] [CrossRef]
- Manko, A.; Kim, Y.; Morozov, A.; Palto, S.; Won, K.; Lee, H.S. Optimization of Optical Phase Profile in Beam Deflector with Advanced Simulation Method for High Diffraction Efficiency. Micromachines 2022, 13, 802. [Google Scholar] [CrossRef]
- Kim, Y.; Won, K.; An, J.; Hong, J.Y.; Kim, Y.; Choi, C.S.; Song, H.; Song, B.; Suk Kim, H.; Bae, K.D.; et al. Large-area liquid crystal beam deflector with wide steering angle. Appl. Opt. 2020, 59, 7462–7468. [Google Scholar] [CrossRef]
- Lee, H.-S.; An, J.; Seo, W.; Choi, C.-S.; Kim, Y.-T.; Sung, G.; Seo, J.; Song, H.; Kim, S.; Kim, H.; et al. 54–2: Invited paper: Holographic display and its applications. SID Symp. Dig. Tech. Pap. 2017, 48, 808–810. [Google Scholar] [CrossRef]
- Xu, D.; Tan, G.; Wu, S.T. Large-angle and high-efficiency tunable phase grating using fringe field switching liquid crystal. Opt. Express 2015, 23, 12274–12285. [Google Scholar] [CrossRef]
- Ji, X.X.; Wang, F.; Zhou, H.J.; Wang, K.F.; Yin, L.Q.; Zhang, J.H. 3400 PPI Active-Matrix Monolithic Blue and Green Micro-LED Display. IEEE Trans. Electron Devices 2023, 70, 4689–4693. [Google Scholar] [CrossRef]
- Sneck, A.; Ailas, H.; Gao, F.; Leppaniemi, J. Reverse-Offset Printing of Polymer Resist Ink for Micrometer-Level Patterning of Metal and Metal-Oxide Layers. ACS Appl. Mater. Interfaces 2021, 13, 41782–41790. [Google Scholar] [CrossRef]
- Itoh, K. Analysis of the phase unwrapping algorithm. Appl. Opt. 1982, 21, 2470. [Google Scholar] [CrossRef] [PubMed]
- Malacara, D. Optical Shop Testing; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley and Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- de Blas, M.G.; Garcia, J.P.; Andreu, S.V.; Arregui, X.Q.; Cano-Garcia, M.; Geday, M.A. High resolution 2D beam steerer made from cascaded 1D liquid crystal phase gratings. Sci. Rep. 2022, 12, 5145. [Google Scholar] [CrossRef] [PubMed]
- An, J.; Won, K.; Kim, Y.; Hong, J.Y.; Kim, H.; Kim, Y.; Song, H.; Choi, C.; Kim, Y.; Seo, J.; et al. Slim-panel holographic video display. Nat. Commun. 2020, 11, 5568. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.T.; Connelly, M.; Nickols, C.; Neville, K.A. Developmental Changes of Normal Pupil Size and Reactivity in Children. J. Pediatr. Ophthalmol. Strabismus 2015, 52, 147–151. [Google Scholar] [CrossRef]
- Kiel, M.; Grabitz, S.D.; Hopf, S.; Koeck, T.; Wild, P.S.; Schmidtmann, I.; Lackner, K.J.; Munzel, T.; Beutel, M.E.; Pfeiffer, N.; et al. Distribution of Pupil Size and Associated Factors: Results from the Population-Based Gutenberg Health Study. J. Ophthalmol. 2022, 2022, 9520512. [Google Scholar] [CrossRef]
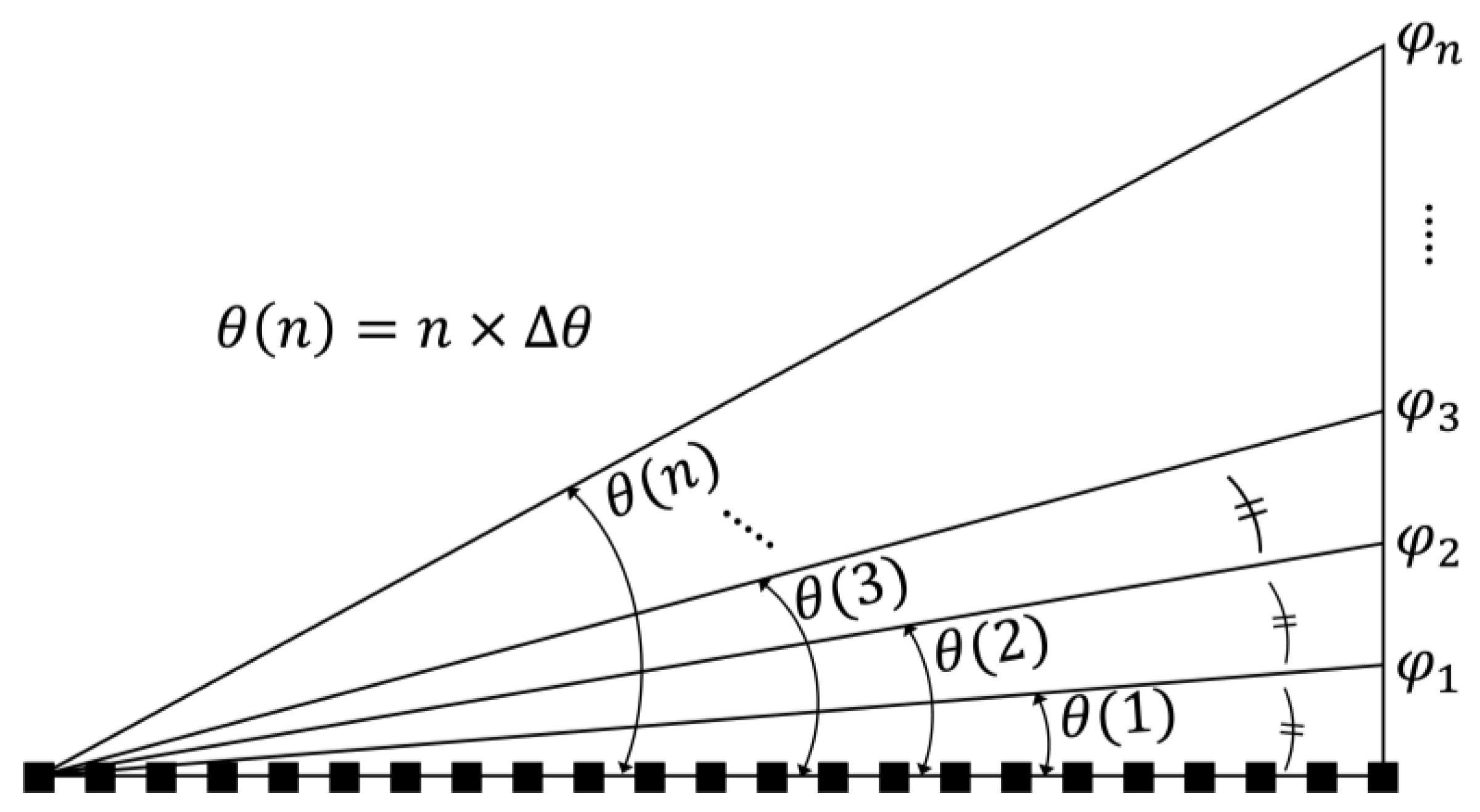
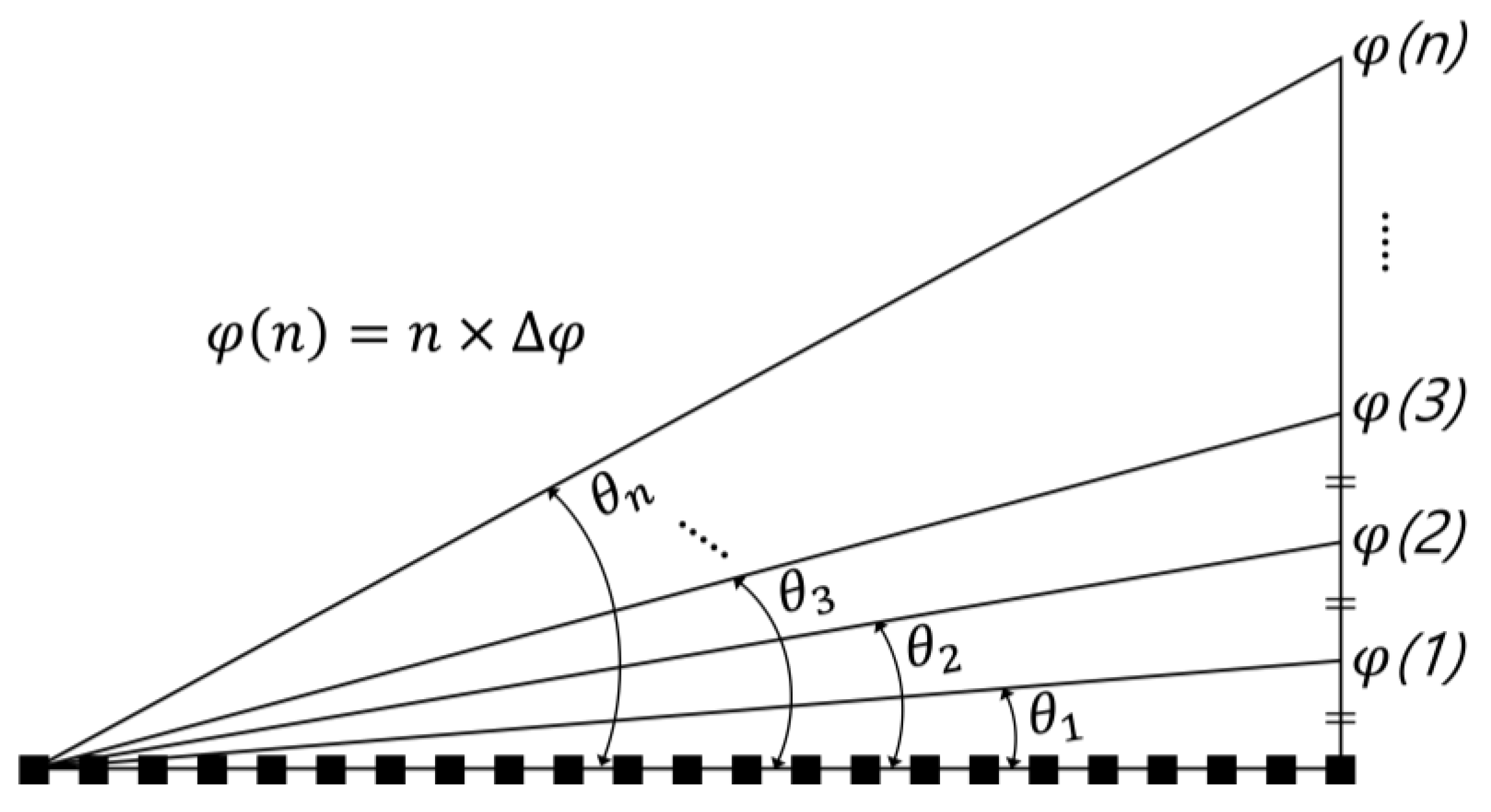
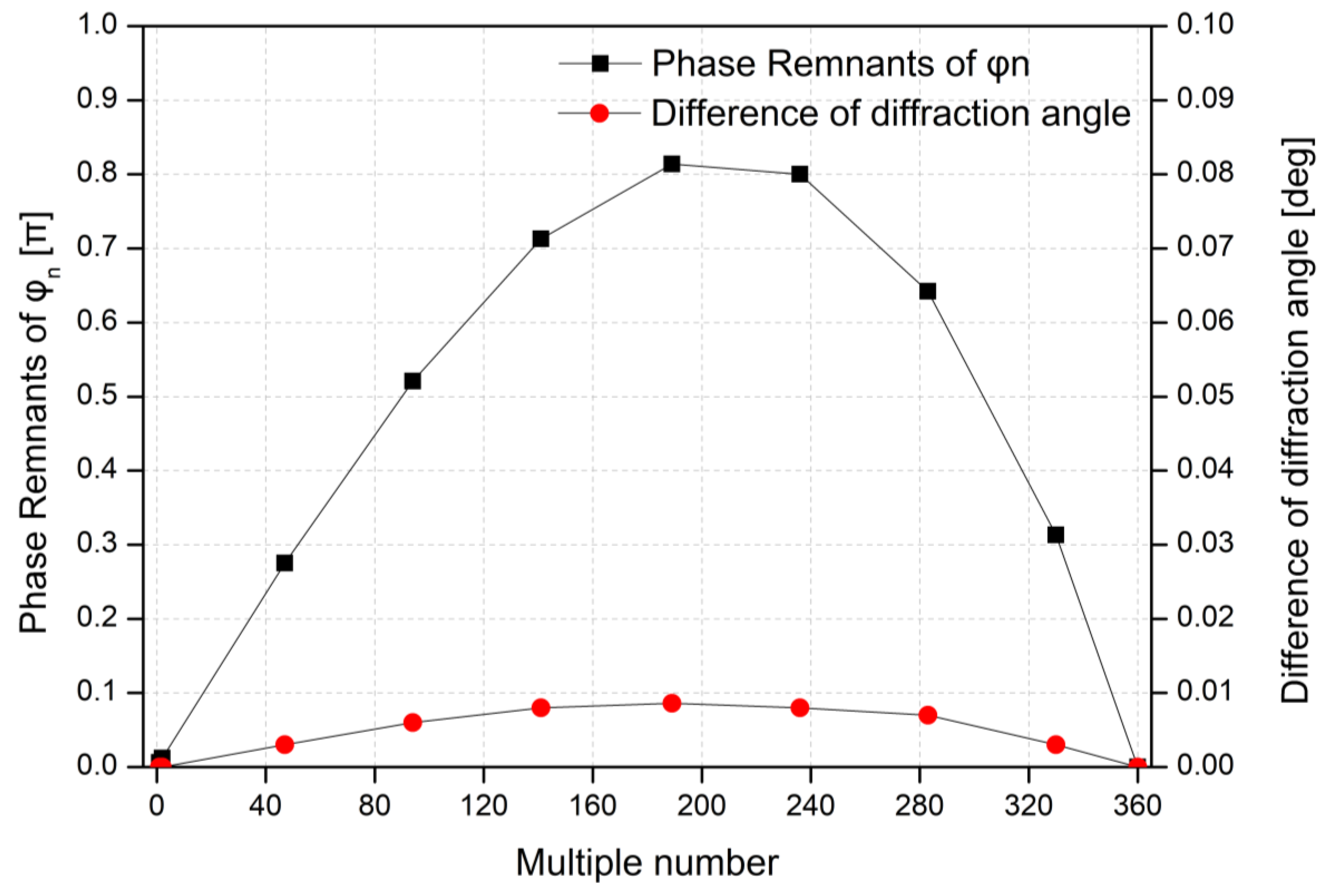
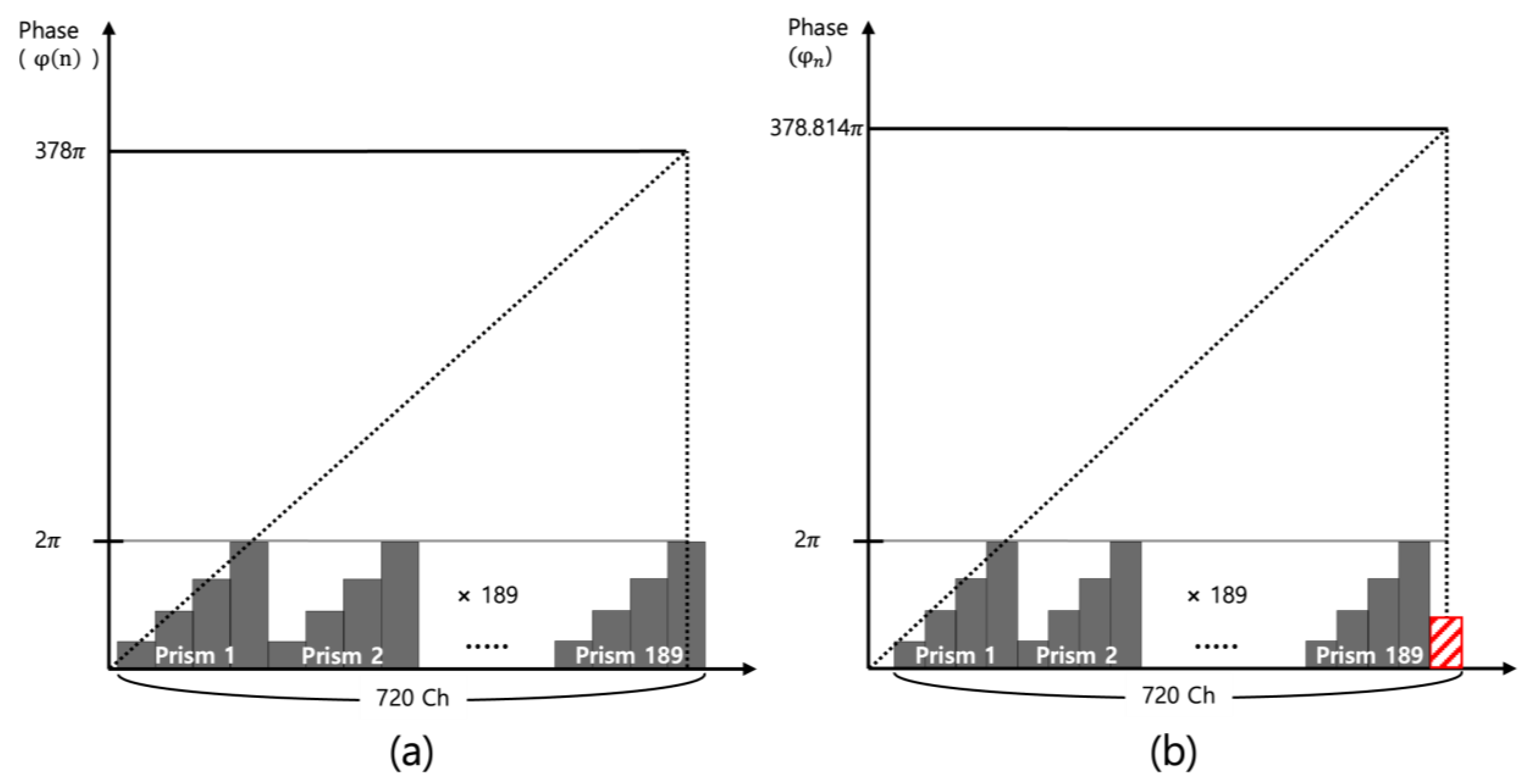

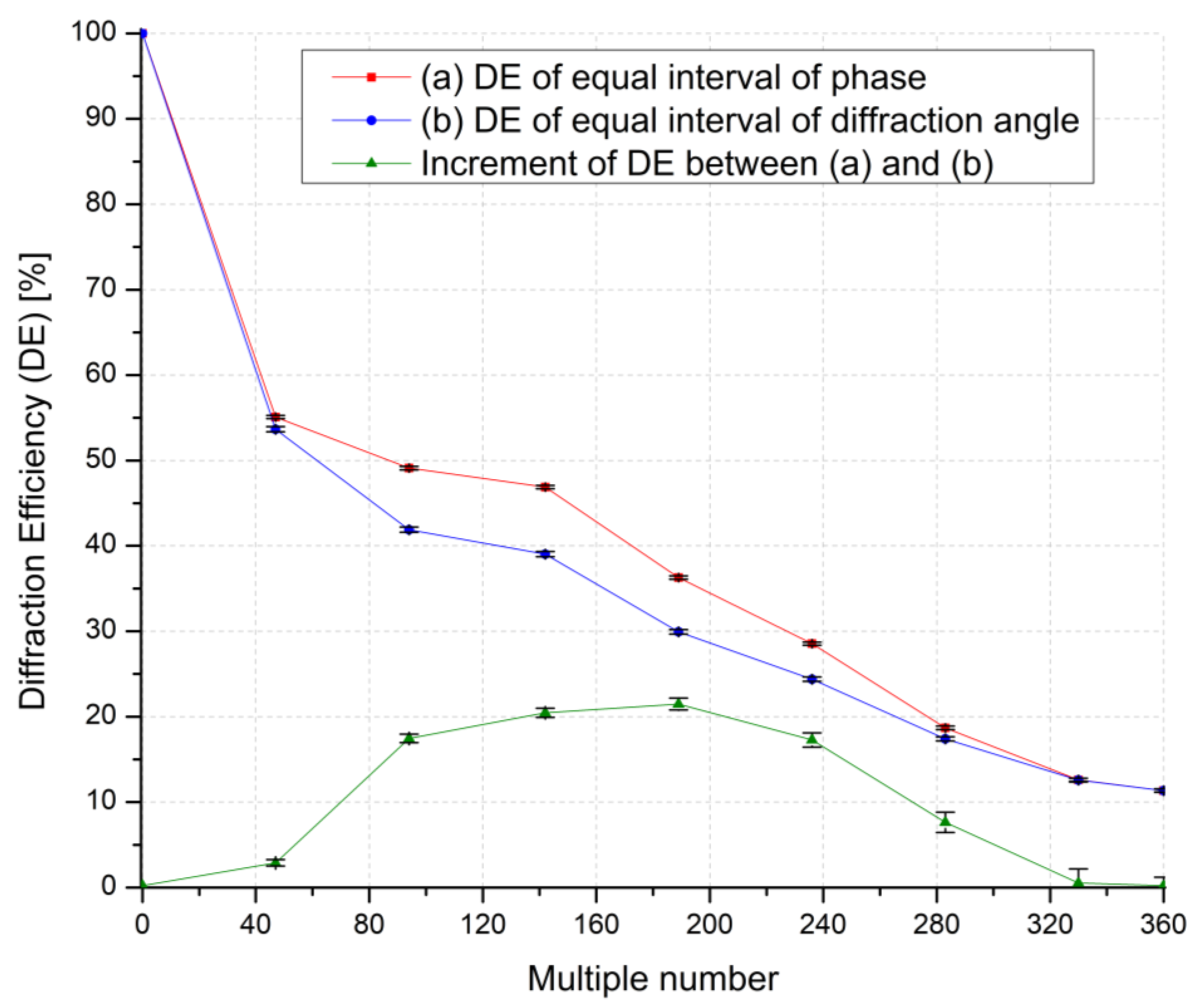
| Multiple Number (n) | Equal Interval of Diffraction Angle | Equal Interval of Phase | ||||
|---|---|---|---|---|---|---|
| θ(n) [°] | [π∙rad] | [π∙rad] | [°] | φ(n) [π∙rad] | Difference in Diffraction Angle [°] | |
| 1 | 0.026 | 2.009 | 0.009 | 0.026 | 2 | 0.000113 |
| 2 | 0.052 | 4.018 | 0.018 | 0.051 | 4 | 0.000225 |
| 47 | 1.211 | 94.405 | 0.405 | 1.206 | 94 | 0.005200 |
| 189 | 4.872 | 379.200 | 1.200 | 4.856 | 378 | 0.015457 |
| 330 | 8.506 | 660.462 | 0.462 | 8.500 | 660 | 0.005991 |
| 360 | 9.279 | 720.000 | 0.000 | 9.279 | 720 | 0.000000 |
| Multiple Number (n) | Equal Interval of Diffraction Angle | Equal Interval of Phase | ||||
|---|---|---|---|---|---|---|
| θ(n) [°] | [π∙rad] | Phase Remnants of [π∙rad] | [°] | φ(n) [π∙rad] | Difference in Diffraction Angle [°] | |
| 1 | 0.021 | 2.006 | 0.006 | 0.021 | 2 | 0.000063 |
| 2 | 0.042 | 4.012 | 0.012 | 0.042 | 4 | 0.000126 |
| 47 | 0.998 | 94.275 | 0.275 | 0.995 | 94 | 0.002907 |
| 189 | 4.013 | 378.814 | 0.814 | 4.004 | 378 | 0.008631 |
| 330 | 7.006 | 660.313 | 0.313 | 7.003 | 660 | 0.003338 |
| 360 | 7.643 | 720.000 | 0.000 | 7.643 | 720 | 0.000000 |
| Multiple Number (n) | Equal Interval of Diffraction Angle | Equal Interval of Phase | ||||
|---|---|---|---|---|---|---|
| θ(n) [°] | [π∙rad] | Phase Remnants of [π∙rad] | [°] | φ(n) [π∙rad] | Difference in Diffraction Angle [°] | |
| 1 | 0.019 | 2.005 | 0.005 | 0.019 | 2 | 0.000043 |
| 2 | 0.037 | 4.009 | 0.009 | 0.037 | 4 | 0.000087 |
| 47 | 0.881 | 94.214 | 0.214 | 0.879 | 94 | 0.002001 |
| 189 | 3.543 | 378.634 | 0.634 | 3.537 | 378 | 0.005938 |
| 330 | 6.186 | 660.244 | 0.244 | 6.183 | 660 | 0.002294 |
| 360 | 6.748 | 720.000 | 0.000 | 6.748 | 720 | 0.000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.; Kim, T.; Do, J.; Ma, H.; Yoon, H.; Won, K. Stripe Noise Removal in Blazed Grating Generation for Electrically Tunable Beam Deflector. Materials 2025, 18, 291. https://doi.org/10.3390/ma18020291
Kim W, Kim T, Do J, Ma H, Yoon H, Won K. Stripe Noise Removal in Blazed Grating Generation for Electrically Tunable Beam Deflector. Materials. 2025; 18(2):291. https://doi.org/10.3390/ma18020291
Chicago/Turabian StyleKim, Woosup, Taeyoung Kim, Jun Do, Heechang Ma, Heesun Yoon, and Kanghee Won. 2025. "Stripe Noise Removal in Blazed Grating Generation for Electrically Tunable Beam Deflector" Materials 18, no. 2: 291. https://doi.org/10.3390/ma18020291
APA StyleKim, W., Kim, T., Do, J., Ma, H., Yoon, H., & Won, K. (2025). Stripe Noise Removal in Blazed Grating Generation for Electrically Tunable Beam Deflector. Materials, 18(2), 291. https://doi.org/10.3390/ma18020291







