Enhancing Reverse Design Ability of Functional Materials Based on Data Quality Management: Taking Biomedical Zinc Alloy as an Example
Abstract
1. Introduction
2. Methods
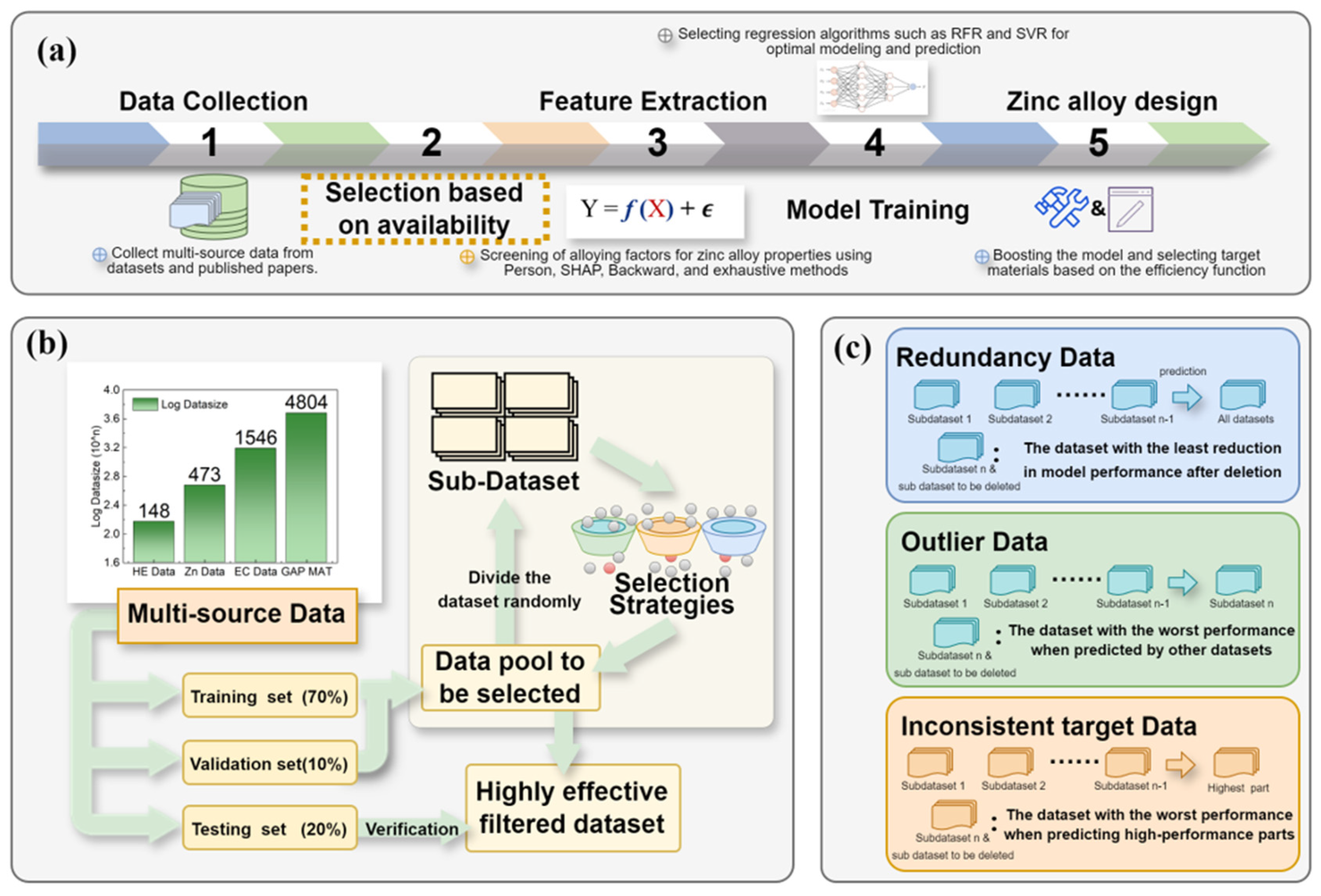
2.1. Workflow
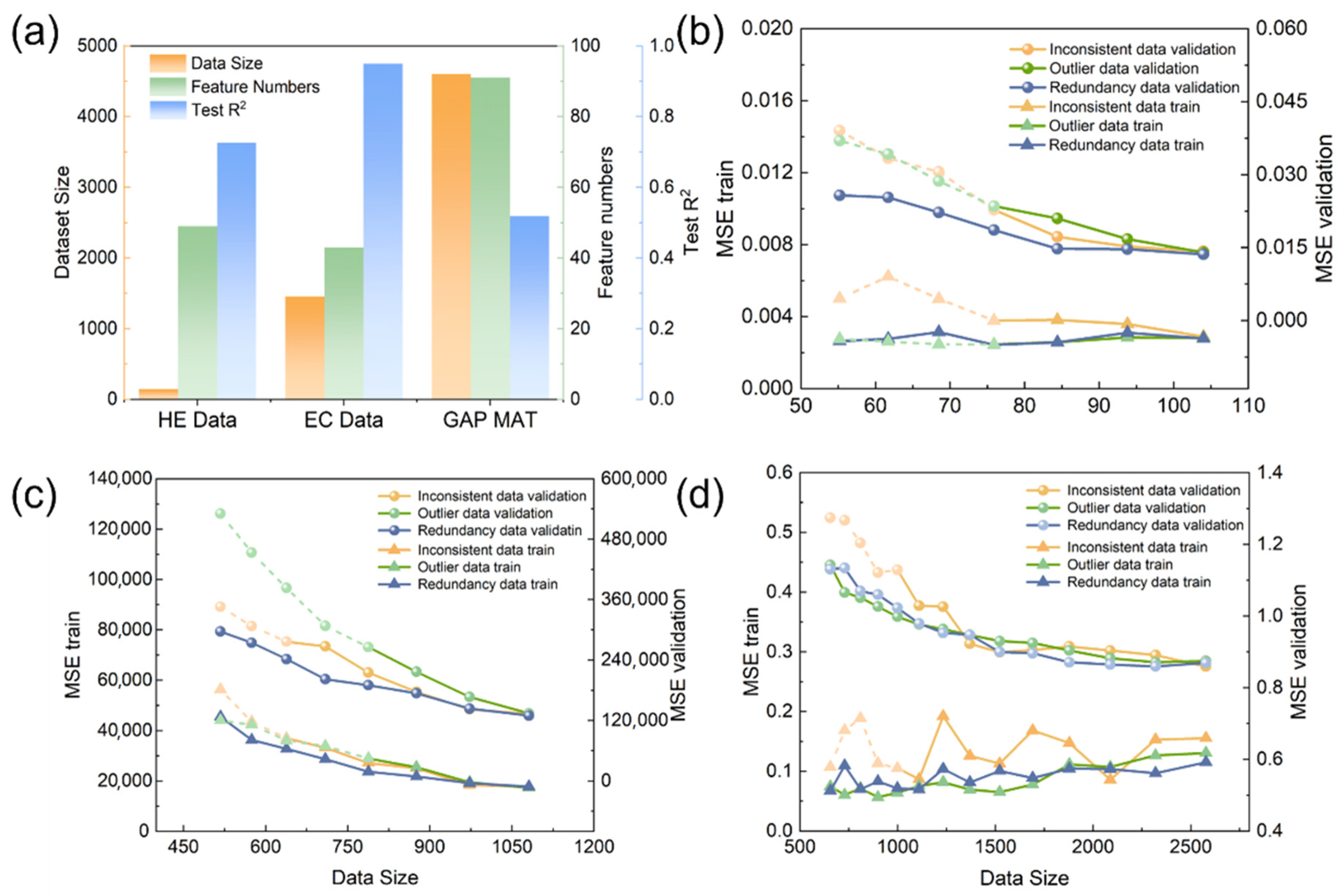
2.2. Method Validation
3. Results and Discussion
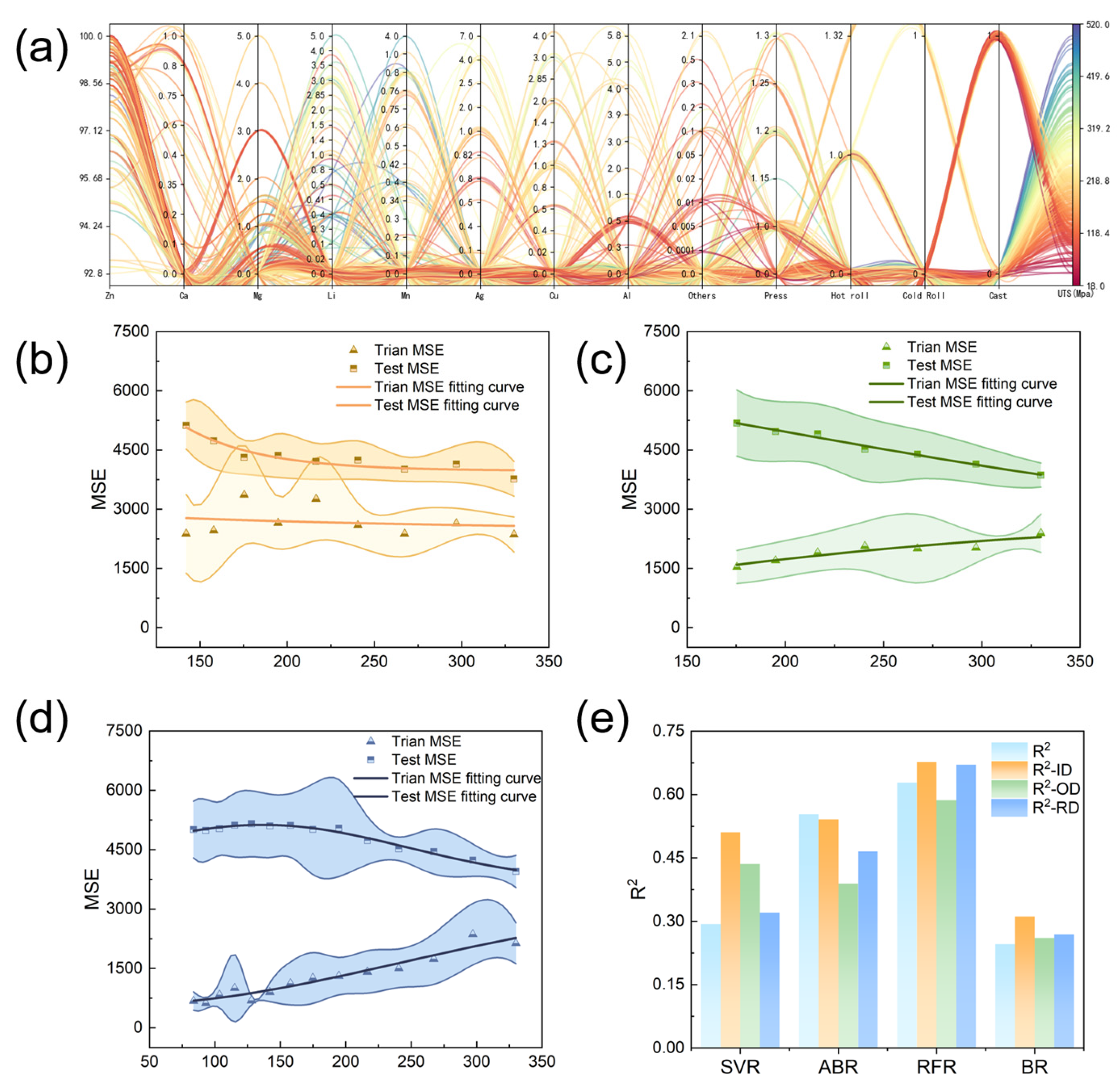
3.1. Degradable Zinc Alloy Dataset
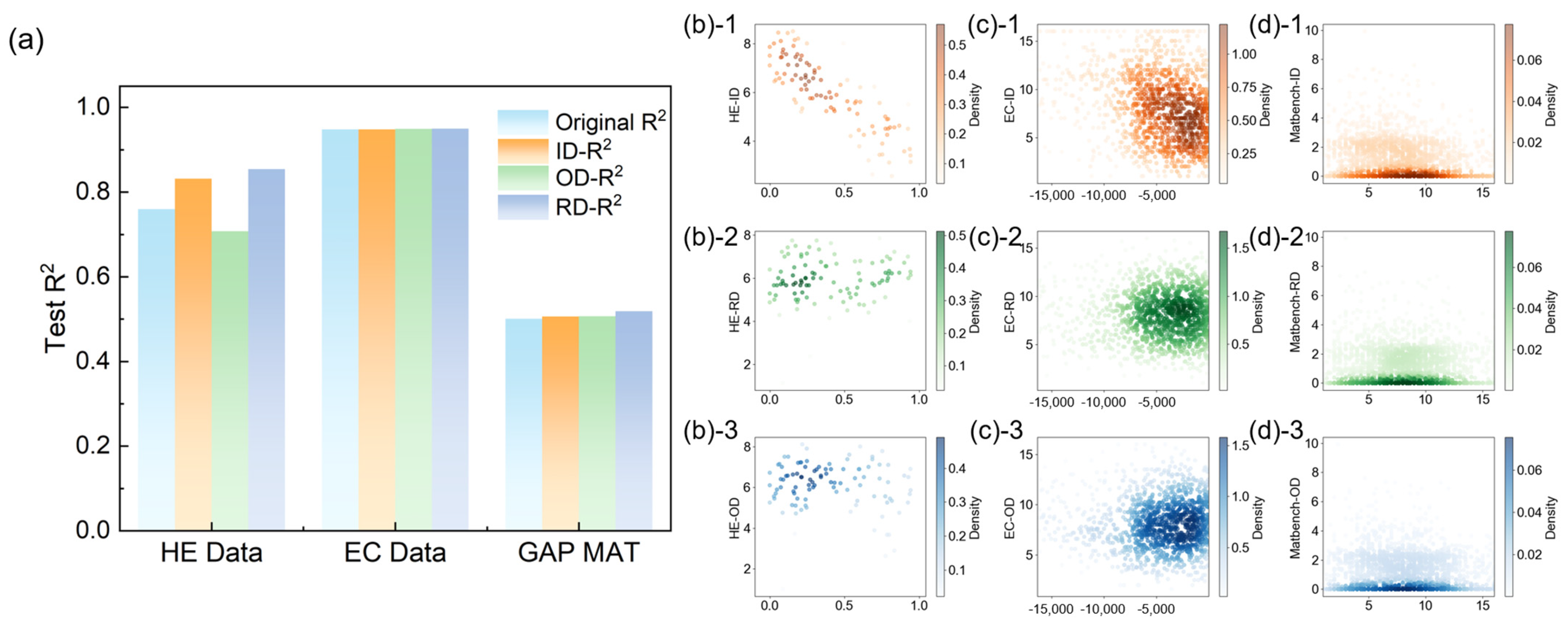
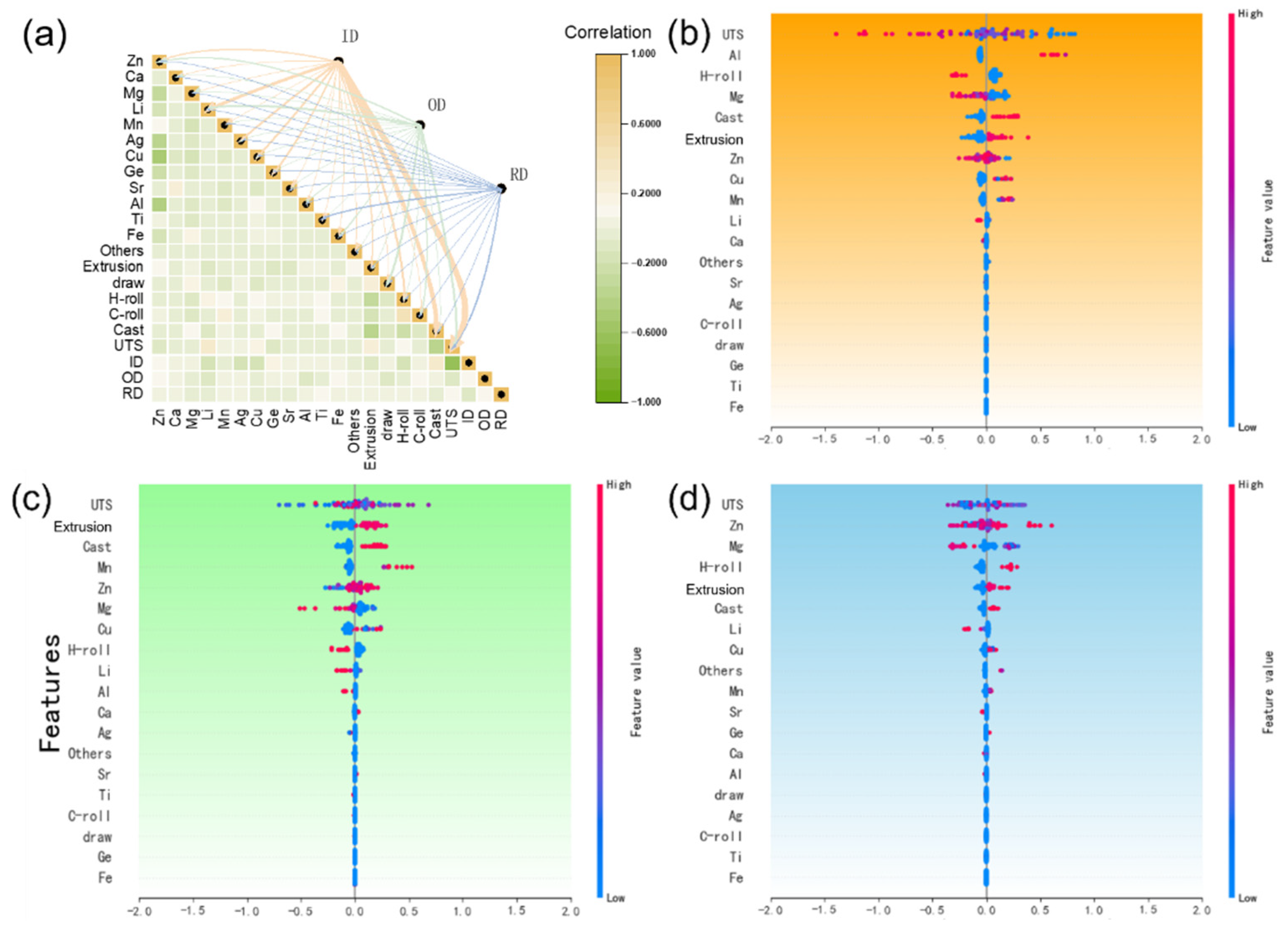
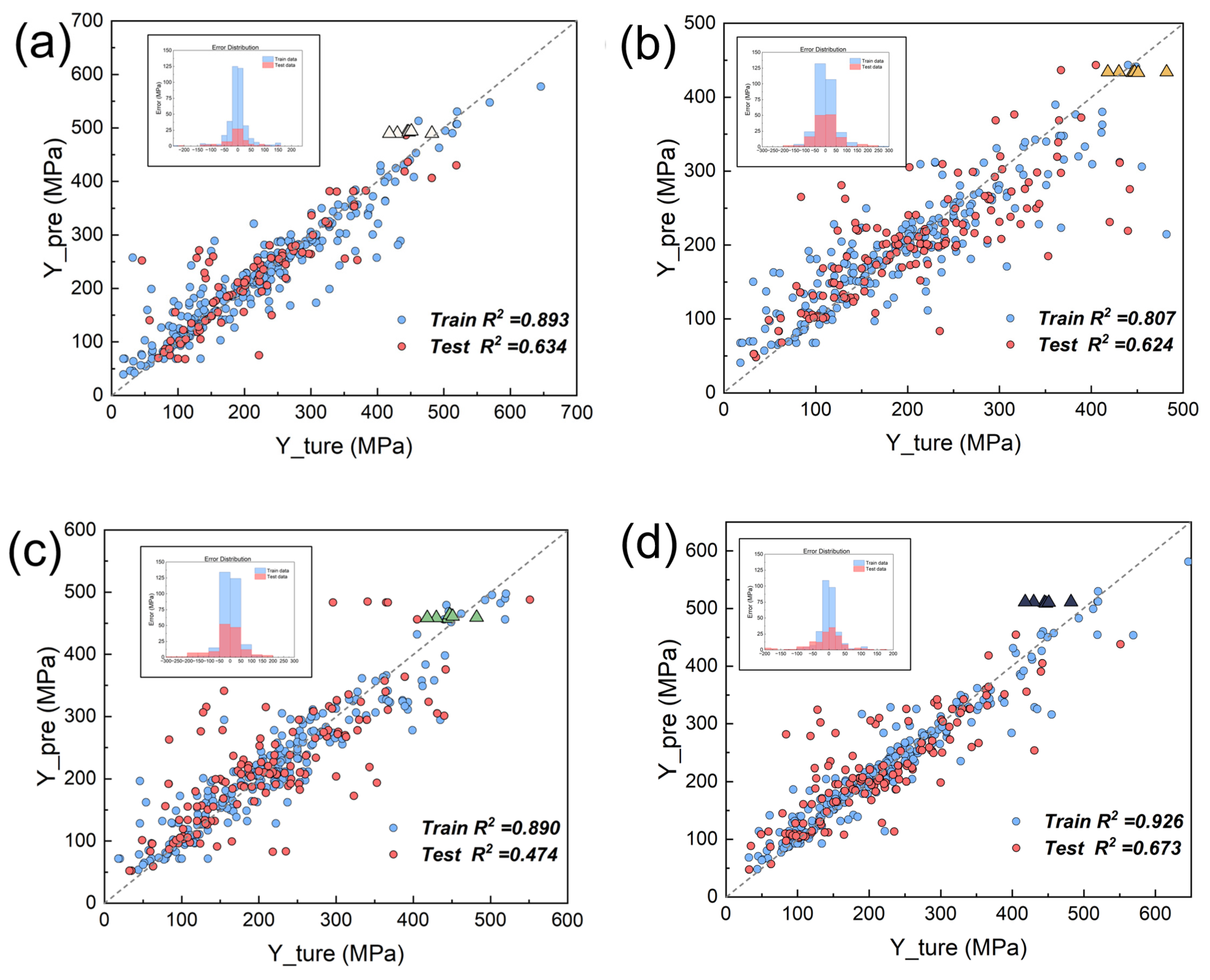
3.2. Analysis and Discussion
3.3. Material Reverse Design
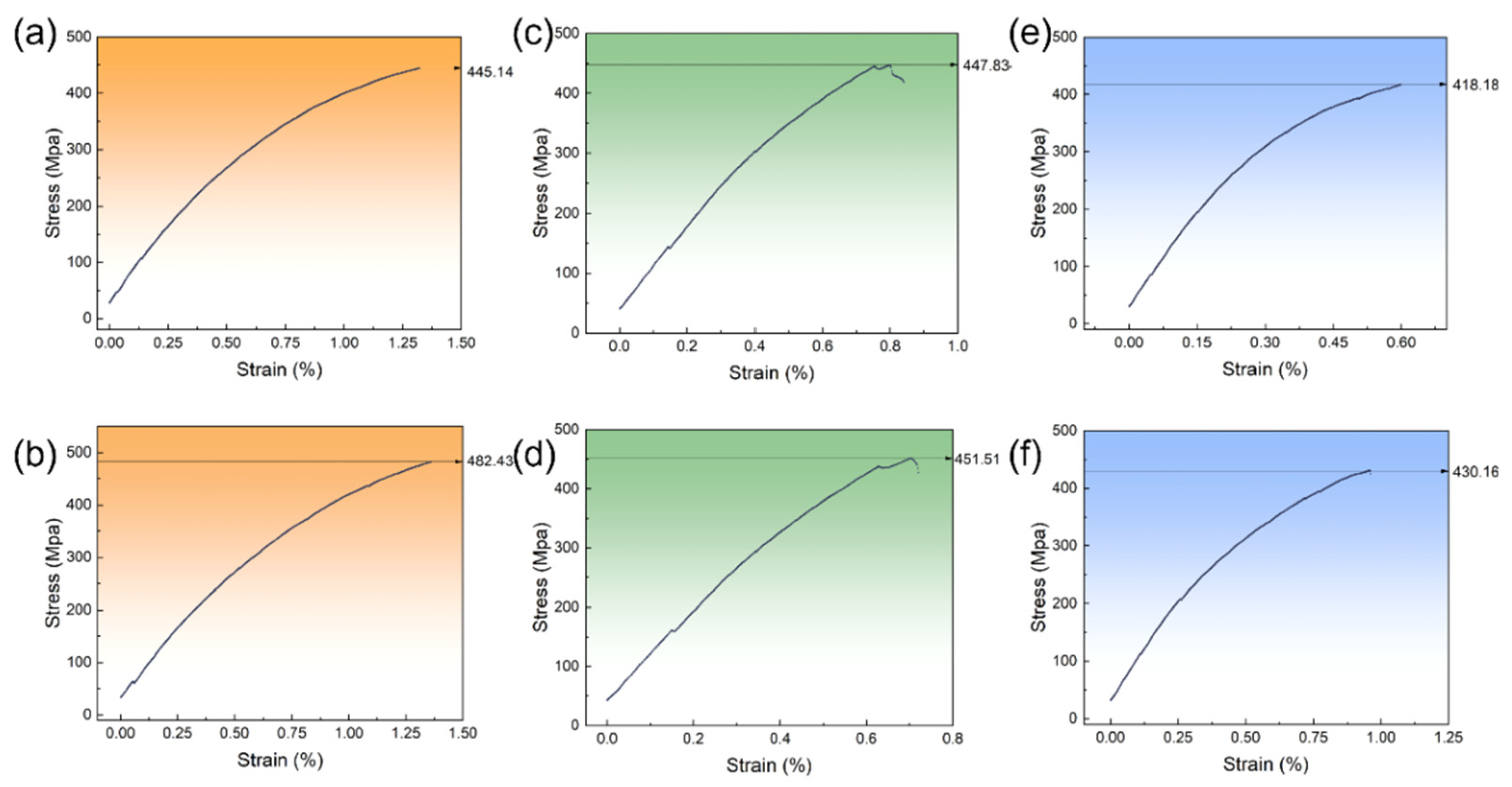
3.4. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, W.; Xia, D.; Wu, S.; Zheng, Y.; Guan, Z.; Rau, J.V. A review on current research status of the surface modification of Zn-based biodegradable metals. Bioact. Mater. 2022, 7, 192–216. [Google Scholar] [CrossRef]
- Meena, L.K.; Singh, A.K.; Malik, A.; Bisla, N. Manufacturing methods & characteristic analysis of zinc & its alloys for biomedical applications: A review. J. Alloys Compd. Commun. 2025, 6, 100068. [Google Scholar]
- Vojtěch, D.; Kubásek, J.; Šerák, J.; Novák, P. Mechanical and corrosion properties of newly developed biodegradable Zn-based alloys for bone fixation. Acta Biomater. 2011, 7, 3515–3522. [Google Scholar] [CrossRef] [PubMed]
- Oleksy, M.; Dynarowicz, K.; Aebisher, D. Advances in biodegradable polymers and biomaterials for medical applications—A review. Molecules 2023, 28, 6213. [Google Scholar] [CrossRef]
- Wu, C.C.; Lin, F.X.; Liu, H.; Pelletier, M.H.; Lloyd, M.; Walsh, W.R.; Nie, J.F. Stronger and coarser-grained biodegradable zinc alloys. Nature 2025, 638, 684–689. [Google Scholar] [CrossRef]
- Bowen, P.K.; Shearier, E.R.; Zhao, S.; Guillory, R.J.; Zhao, F.; Goldman, J.; Drelich, J.W. Biodegradable metals for cardiovascular stents: From clinical concerns to recent Zn-Alloys. Adv. Healthc. Mater. 2016, 5, 1121–1140. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Zhao, C.; Li, J.; Song, Y.; Xie, C.; Tao, H.; Zhang, Y.; He, Y.; Jiang, Y.; et al. Research on an Mg–Zn alloy as a degradable biomaterial. Acta Biomater. 2010, 6, 626–640. [Google Scholar] [CrossRef]
- Bowen, P.K.; Guillory, I.I.R.J.; Shearier, E.R.; Seitz, J.M.; Drelich, J.M.; Bocks, M.; Zhao, F.; Goldman, J. Metallic zinc exhibits optimal biocompatibility for bioabsorbable endovascular stents. Mater. Sci. Eng. C 2015, 56, 467–472. [Google Scholar] [CrossRef]
- Kong, L.; Heydari, Z.; Lami, G.H.; Saberi, A.; Baltatu, M.S.; Vizureanu, P. A comprehensive review of the current research status of biodegradable zinc alloys and composites for biomedical applications. Materials 2023, 16, 4797. [Google Scholar] [CrossRef]
- Su, Y.; Fu, J.; Zhou, J.; Georgas, E.; Du, S.; Qin, Y.X.; Wang, Y.; Zheng, Y.; Zhu, D. Blending with transition metals improves bioresorbable zinc as better medical implants. Bioact. Mater. 2023, 20, 243–258. [Google Scholar] [CrossRef]
- Yao, R.; Zhao, Y.; Han, S.; Shan, R.; Liu, L.; Sun, Y.; Yao, X.; Wang, X.; Hang, R. Microstructure, mechanical properties, in vitro degradation behavior and in vivo osteogenic activities of Zn-1Mg-β-TCP composites for bone defect repair. Mater. Des. 2023, 225, 111494. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Z.Z.; Hao, Y.; Li, H.F.; Liu, X.F.; Volinsky, A.A.; Zhang, H.J.; Wang, L.N. High-performance hot-warm rolled Zn-0.8 Li alloy with nano-sized metastable precipitates and sub-micron grains for biodegradable stents. J. Mater. Sci. Technol. 2019, 35, 2618–2624. [Google Scholar] [CrossRef]
- Li, G.; Chen, D.; Mine, Y.; Takashima, K.; Zhang, Y. Fatigue behavior of biodegradable Zn-Li binary alloys in air and simulated body fluid with pure Zn as control. Acta Biomater. 2023, 168, 637–649. [Google Scholar] [CrossRef] [PubMed]
- Lou, D.; Wang, L.; Ren, Y.; Li, H.; Qin, G. Textural evolution and improved ductility in Zn-0.2 Mg-0.8 Mn (wt%) alloys at different extrusion temperatures. J. Alloys Compd. 2021, 860, 158530. [Google Scholar] [CrossRef]
- Tang, Z.; Niu, J.; Huang, H.; Zhang, H.; Pei, J.; Ou, J.; Yuan, G. Potential biodegradable Zn-Cu binary alloys developed for cardiovascular implant applications. J. Mech. Behav. Biomed. Mater. 2017, 72, 182–191. [Google Scholar] [CrossRef]
- Xue, D.Z.; Xue, D.Q.; Yuan, R.; Zhou, Y.; Balachandran, P.V.; Ding, X.; Sun, J.; Lookman, T. An informatics approach to transformation temperatures of NiTi-based shape memory alloys. Acta Mater. 2017, 125, 532–541. [Google Scholar] [CrossRef]
- Xue, D.Z.; Balachandran, P.V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 532, 11241. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Dang, P.; Lookman, T.; Xue, D.; Su, Y. Toward ultra-high strength high entropy alloys via feature engineering. J. Mater. Sci. Technol. 2024, 200, 243–252. [Google Scholar] [CrossRef]
- Liu, P.; Huang, H.; Jiang, X.; Zhang, Y.; Omori, T.; Lookman, T.; Su, Y. Evolution analysis of γ′ precipitate coarsening in Co-based superalloys using kinetic theory and machine learning. Acta Mater. 2022, 235, 118101. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, H.; Zhu, S.; Yong, W.; Xie, J. Machine learning assisted composition effective design for precipitation strengthened copper alloys. Acta Mater. 2021, 215, 117118. [Google Scholar] [CrossRef]
- Hu, M.; Tan, Q.; Knibbe, R.; Xu, M.; Jiang, B.; Wang, S.; Li, X.; Zhang, M.X. Recent applications of machine learning in alloy design: A review. Mater. Sci. Eng. R Rep. 2023, 155, 100746. [Google Scholar] [CrossRef]
- Guo, C.; Shi, C.; Liu, P.; Gao, D.; Zhao, Y.; Qiao, Y. Prediction of mechanical properties of biodegradable zinc alloys based on machine learning. Acta Metall. Sin. 2024. Available online: https://www.ams.org.cn/EN/10.11900/0412.1961.2024.00332 (accessed on 30 June 2025).
- Chen, W.; Gou, W.; Li, Y.; Li, X.; Li, M.; Hou, J.; Zhang, X.; Shi, Z.; Wang, L. Machine learning design of 400 MPa grade biodegradable Zn-Mn based alloys with appropriate corrosion rates. Int. J. Miner. Metall. Mater. 2024, 31, 2727–2736. [Google Scholar] [CrossRef]
- Mukherjee, R.; Datta, S. Materials Informatics Driven Designing Mg Alloys for Biodegradable Short-Term Implants Using Machine Learning. JOM 2025, 77, 20–38. [Google Scholar] [CrossRef]
- Suh, J.S.; Suh, B.C.; Bae, J.H.; Kim, Y.M. Machine learning-based design of biodegradable Mg alloys for load-bearing implants. Mater. Des. 2023, 225, 111442. [Google Scholar] [CrossRef]
- Mi, X.; Dai, L.; Jing, X.; She, J.; Holmedal, B.; Tang, A.; Pan, F. Accelerated design of high-performance Mg-Mn-based magnesium alloys based on novel bayesian optimization. J. Magnes. Alloys 2024, 12, 750–766. [Google Scholar] [CrossRef]
- Ghorbani, M.; Boley, M.; Nakashima, P.N.H.; Birbilis, N. An active machine learning approach for optimal design of magnesium alloys using Bayesian optimisation. Sci. Rep. 2024, 14, 8299. [Google Scholar] [CrossRef]
- Shi, S.; Sun, S.; Ma, S.; Zou, X.; Qian, Q.; Liu, Y. Detection method on data accuracy incorporating materials domain knowledge. J. Inorg. Mater. 2022, 37, 1311. [Google Scholar] [CrossRef]
- Yue, L.; Shuchang, M.A.; Zhengwei, Y.; Zou, X.; Shi, S. A Data Quality and Quantity Governance for Machine Learning in Materials Science. J. Chin. Ceram. Soc. 2023, 51, 427–437. [Google Scholar]
- Li, K.; Persaud, D.; Choudhary, K.; Decost, B.; Greenwood, M.; Hattrick-Simpers, J. Exploiting redundancy in large materials datasets for efficient machine learning with less data. Nat. Commun. 2023, 14, 7283. [Google Scholar] [CrossRef]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep learning for anomaly detection: A review. ACM Comput. Surv. (CSUR) 2021, 54, 38. [Google Scholar] [CrossRef]
- Wang, B.; Liu, D.; Wu, Y.; Vasenko, A.S.; Prezhdo, O.V. Identifying Rare Events in Quantum Molecular Dynamics of Nanomaterials with Outlier Detection Indices. J. Phys. Chem. Lett. 2024, 15, 10384–10391. [Google Scholar] [CrossRef]
- Vazquez-Salazar, L.I.; Käser, S.; Meuwly, M. Outlier-detection for reactive machine learned potential energy surfaces. npj Comput. Mater. 2025, 11, 33. [Google Scholar] [CrossRef]
- Zhang, Y.; Xin, S.; Zhou, W.; Wang, X.; Xu, Y.; Su, Y. A multi-objective feature optimization strategy for developing high-entropy alloys with optimal strength and ductility. Mater. Genome Eng. Adv. 2025, 3, e70000. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Dang, P.; Jiang, X.; Xue, D.; Su, Y. Elemental numerical descriptions to enhance classification and regression model performance for high-entropy alloys. npj Comput. Mater. 2025, 11, 75. [Google Scholar] [CrossRef]
- Huang, S. Preparation and Characterization of Zinc-Copper Alloy with Tunable Degradation. Ph.D. Dissertation, Beijing University of Science and Technology, Beijing, China, 2023. [Google Scholar]
- Huang, S.; Wang, L.; Zheng, Y.; Qiao, L.; Yan, Y. In vitro degradation behavior of novel Zn–Cu–Li alloys: Roles of alloy composition and rolling processing. Mater. Des. 2021, 212, 110288. [Google Scholar] [CrossRef]
- Zhao, C.; Wen, M.; Wang, J.; Xu, D.; Zheng, Y.; Sheng, L. Regulating microstructure and mechanical properties of the as-cast Mg-4Zn-0.5 Y-0.5 Nd alloy by heat treatment. J. Alloys Compd. 2025, 1010, 177232. [Google Scholar] [CrossRef]
| Dataset Name | Target | Data Size | Data Sources |
|---|---|---|---|
| Hydrogen embrittlement dataset | Hydrogen-induced plasticity loss | 148 | http://mged.nmdms.ustb.edu.cn/task/#/ (accessed on 30 June 2025) |
| Phase-change refrigeration material (electrostriction) | Electrostriction | 473 | http://223.223.185.189:3010/#/ (accessed on 30 June 2025) |
| Matbench_expt_gap dataset | Gap expt | 4804 | https://matbench.materialsproject.org/ (accessed on 30 June 2025) |
| Feature Name | Max. Value | Min. Value | Variance | Non-Zero Ratio |
|---|---|---|---|---|
| Zn | 100 at% | 93 at% | 1.3559 | 100% |
| Ca | 1 at% | 0 | 0.1840 | 9.7% |
| Mg | 4 at% | 0 | 0.7052 | 42.7% |
| Li | 0.8 at% | 0 | 0.1753 | 17.5% |
| Mn | 1 at% | 0 | 0.2293 | 14.6% |
| Ag | 7 at% | 0 | 0.7223 | 6.5% |
| Cu | 4 at% | 0 | 0.8416 | 10.3% |
| Ge | 5 at% | 0 | 0.4714 | 2.3% |
| Ti | 1 at% | 0 | 0.0877 | 8.2% |
| Sr | 1.1 at% | 0 | 0.1990 | 6.1% |
| Al | 5.8 at% | 0 | 0.7244 | 7.8% |
| UTS | 513 MPa | 18 MPa | 12,289.03 | 100% |
| Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|
| ID | 63.88 | 0.293 | 60.02 | 0.554 | 52.47 | 0.586 | 72.78 | 0.246 |
| OD | 51.51 | 0.511 | 51.49 | 0.541 | 38.37 | 0.677 | 63.07 | 0.311 |
| RD | 55.47 | 0.436 | 57.98 | 0.389 | 41.23 | 0.628 | 66.24 | 0.260 |
| Baseline | 58.49 | 0.321 | 50.84 | 0.465 | 38.03 | 0.670 | 65.82 | 0.269 |
| ID Number | Zn (at%) | Al (at%) | Mg (at%) | Li (at%) | Mn (at%) |
|---|---|---|---|---|---|
| ID-1 | 97.5 | 1.2 | 0.6 | 0.4 | 0.3 |
| ID-2 | 97.25 | 1.2 | 0.8 | 0.45 | 0.3 |
| OD-1 | 98.65 | 0 | 0.6 | 0.45 | 0.3 |
| OD-2 | 98.5 | 0 | 0.8 | 0.4 | 0.3 |
| RD-1 | 97.9 | 0.8 | 0.6 | 0.4 | 0.3 |
| RD-2 | 97.8 | 0.8 | 0.6 | 0.4 | 0.4 |
| Sample Number | Zn (at%) | Al (at%) | Mg (at%) | Li (at%) | Mn (at%) | UTS (MPa) |
|---|---|---|---|---|---|---|
| ID-1-1 | 97.5 | 1.2 | 0.6 | 0.4 | 0.3 | 445 |
| ID-1-2 | 97.5 | 1.2 | 0.6 | 0.4 | 0.3 | 477 |
| ID-2-1 | 97.25 | 1.2 | 0.8 | 0.45 | 0.3 | 482 |
| ID-2-2 | 97.25 | 1.2 | 0.8 | 0.45 | 0.3 | 480 |
| OD-1-1 | 98.65 | 0 | 0.6 | 0.45 | 0.3 | 447 |
| OD-1-2 | 98.65 | 0 | 0.6 | 0.45 | 0.3 | 459 |
| OD-2-1 | 98.5 | 0 | 0.8 | 0.4 | 0.3 | 451 |
| OD-2-2 | 98.5 | 0 | 0.8 | 0.4 | 0.3 | 441 |
| RD-1-1 | 97.9 | 0.8 | 0.6 | 0.4 | 0.3 | 418 |
| RD-1-2 | 97.9 | 0.8 | 0.6 | 0.4 | 0.3 | 415 |
| RD-2-1 | 97.8 | 0.8 | 0.6 | 0.4 | 0.4 | 430 |
| RD-2-2 | 97.8 | 0.8 | 0.6 | 0.4 | 0.4 | 425 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Jiang, X.; Huang, S.; Wang, Y.; Ding, L.; Su, Y.; Yan, Y. Enhancing Reverse Design Ability of Functional Materials Based on Data Quality Management: Taking Biomedical Zinc Alloy as an Example. Materials 2025, 18, 4729. https://doi.org/10.3390/ma18204729
Gong X, Jiang X, Huang S, Wang Y, Ding L, Su Y, Yan Y. Enhancing Reverse Design Ability of Functional Materials Based on Data Quality Management: Taking Biomedical Zinc Alloy as an Example. Materials. 2025; 18(20):4729. https://doi.org/10.3390/ma18204729
Chicago/Turabian StyleGong, Xujie, Xue Jiang, Shiyu Huang, Yize Wang, Lishen Ding, Yanjing Su, and Yu Yan. 2025. "Enhancing Reverse Design Ability of Functional Materials Based on Data Quality Management: Taking Biomedical Zinc Alloy as an Example" Materials 18, no. 20: 4729. https://doi.org/10.3390/ma18204729
APA StyleGong, X., Jiang, X., Huang, S., Wang, Y., Ding, L., Su, Y., & Yan, Y. (2025). Enhancing Reverse Design Ability of Functional Materials Based on Data Quality Management: Taking Biomedical Zinc Alloy as an Example. Materials, 18(20), 4729. https://doi.org/10.3390/ma18204729







