Auger Recombination and Carrier-Surface Optical Phonon Interaction in Van Der Waals Heterostructures Composed of Graphene and 2D Transition Metal Chalcogenides
Abstract
:1. Introduction
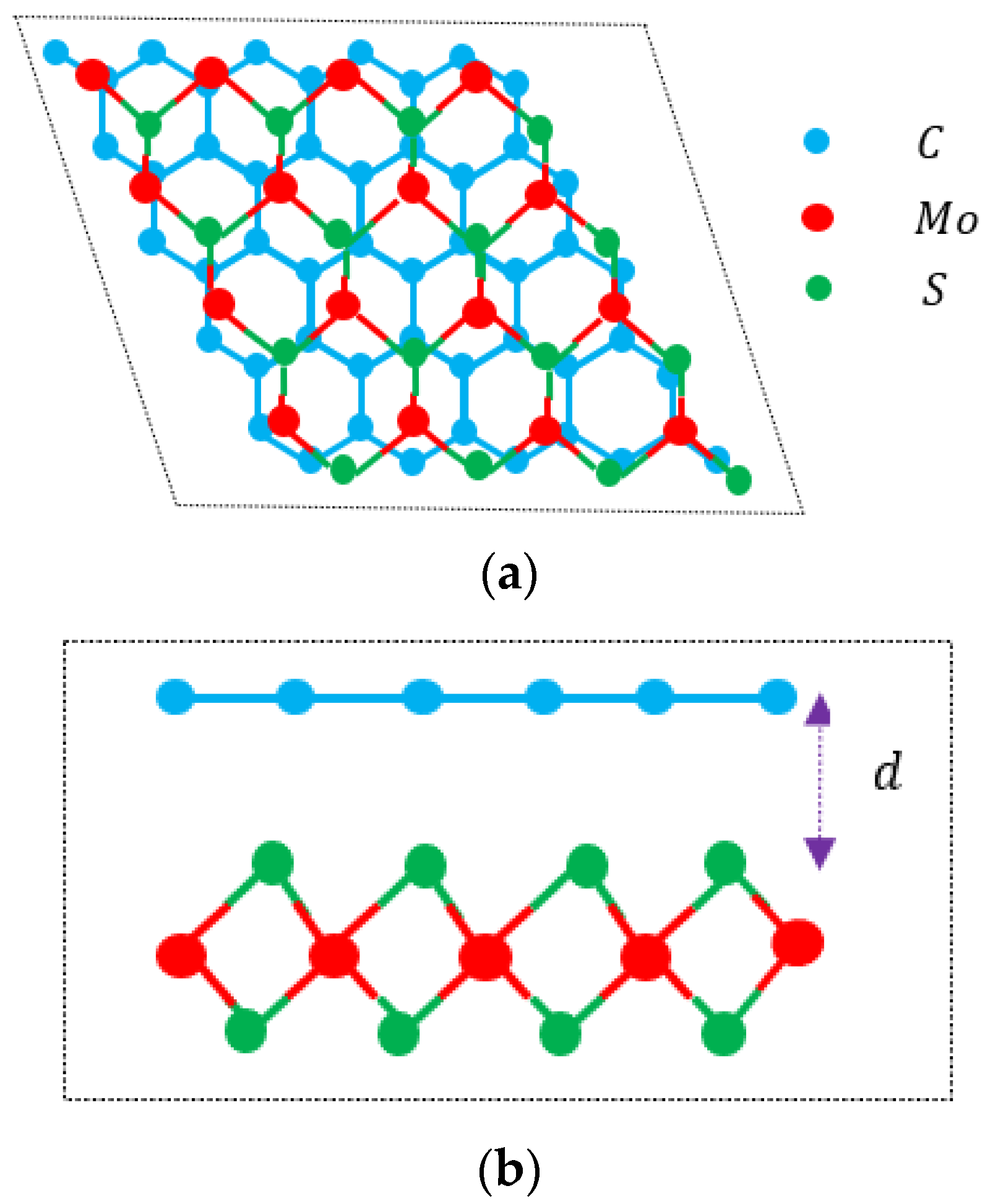
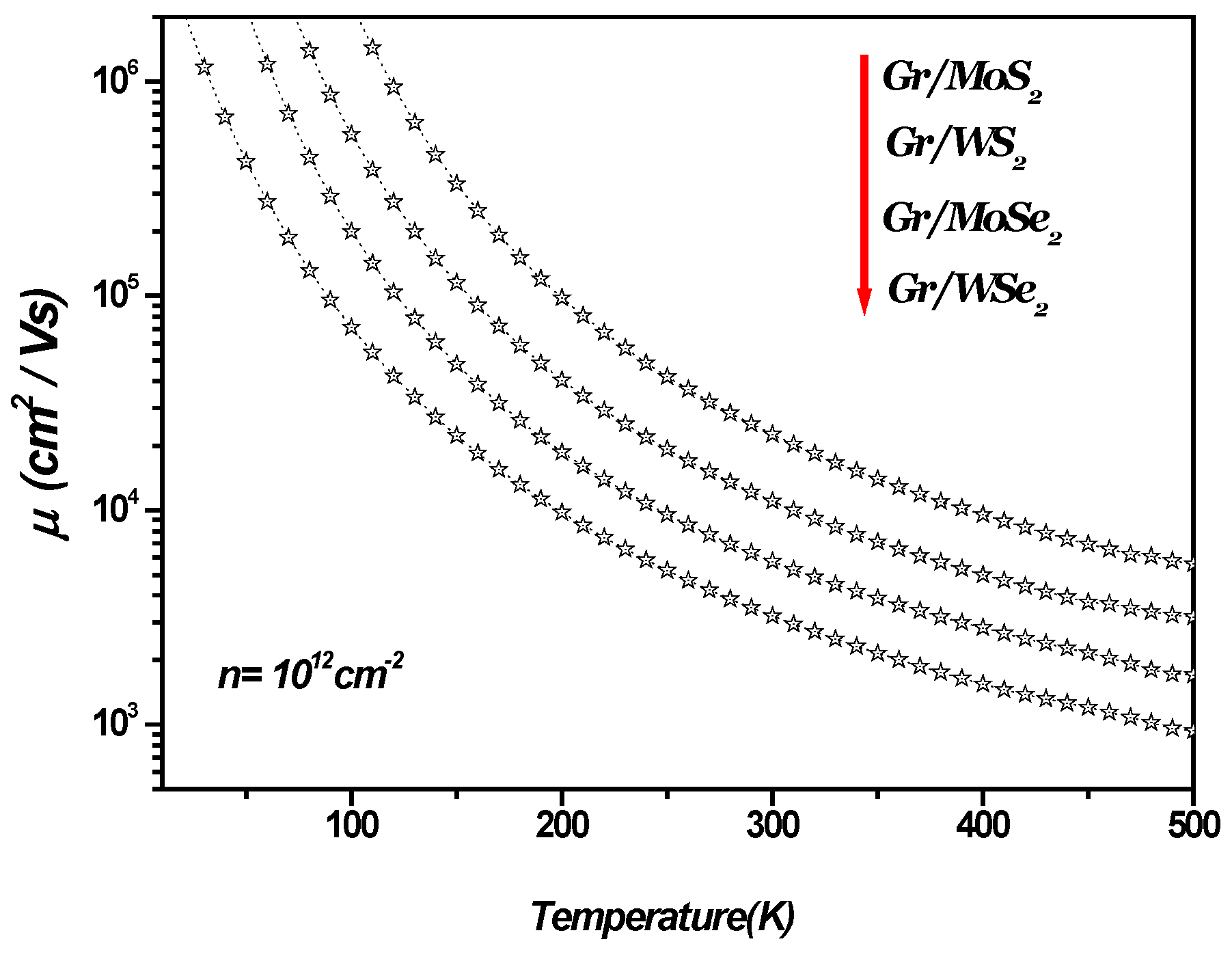
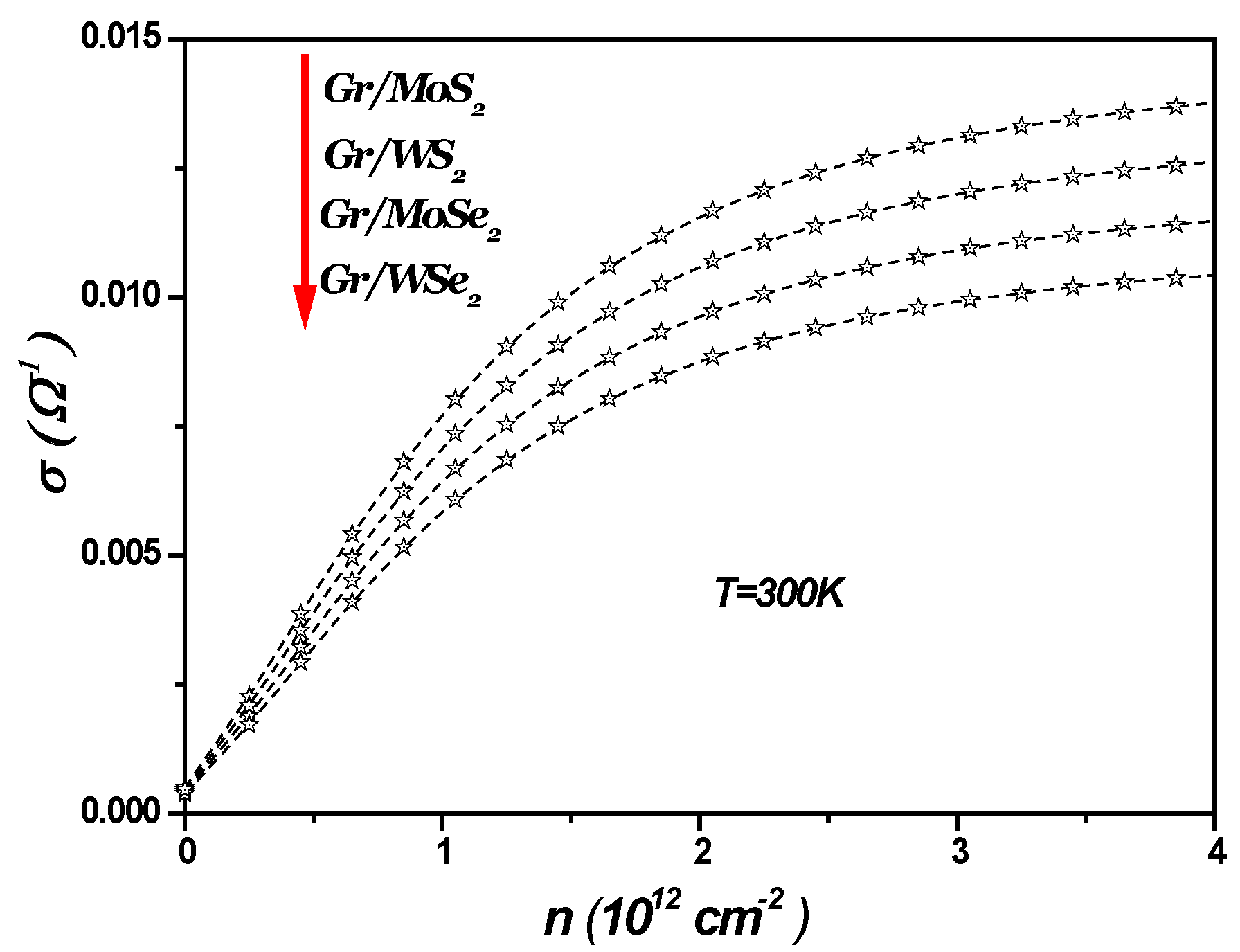
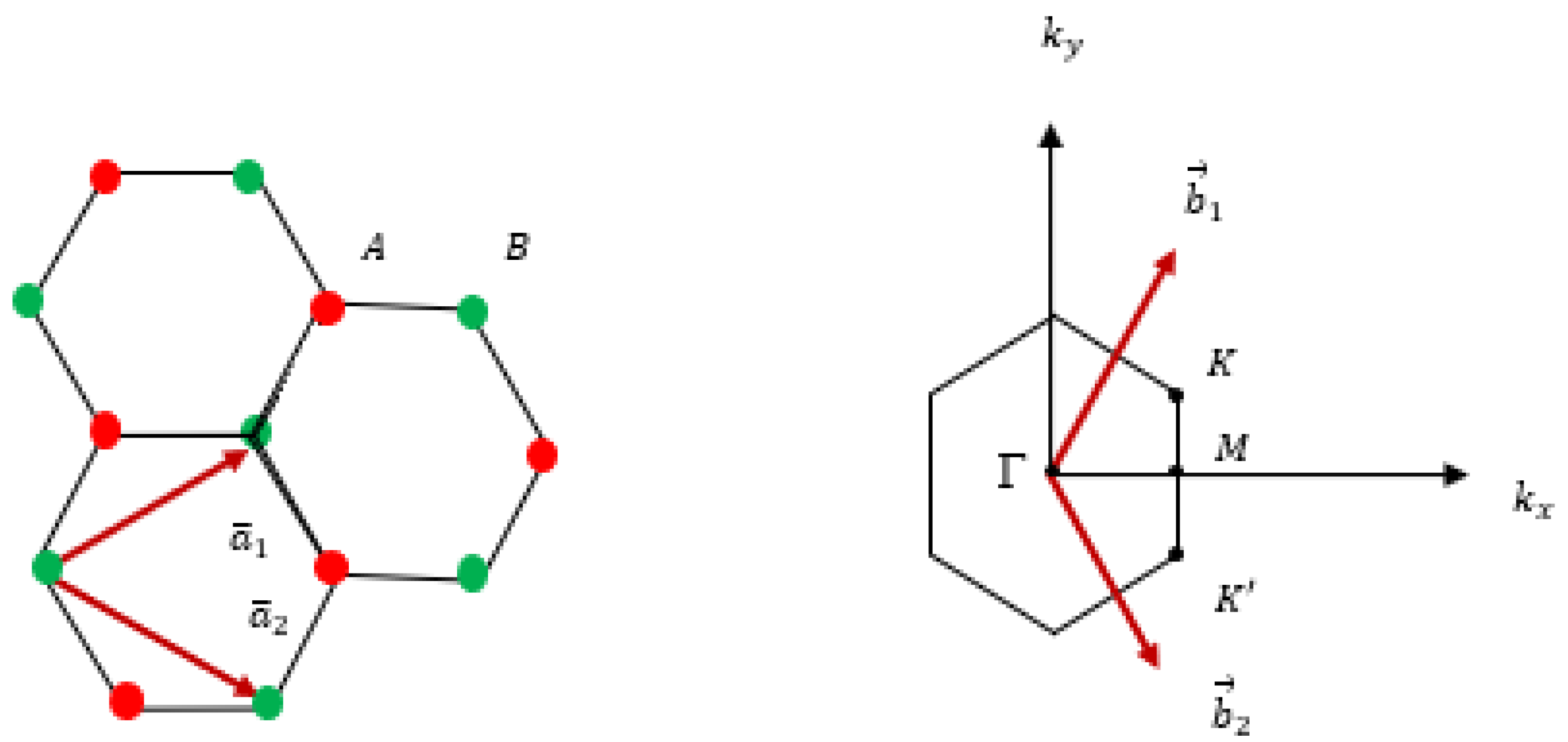
2. Electrical Transport in 1LG/ TMDC Interface
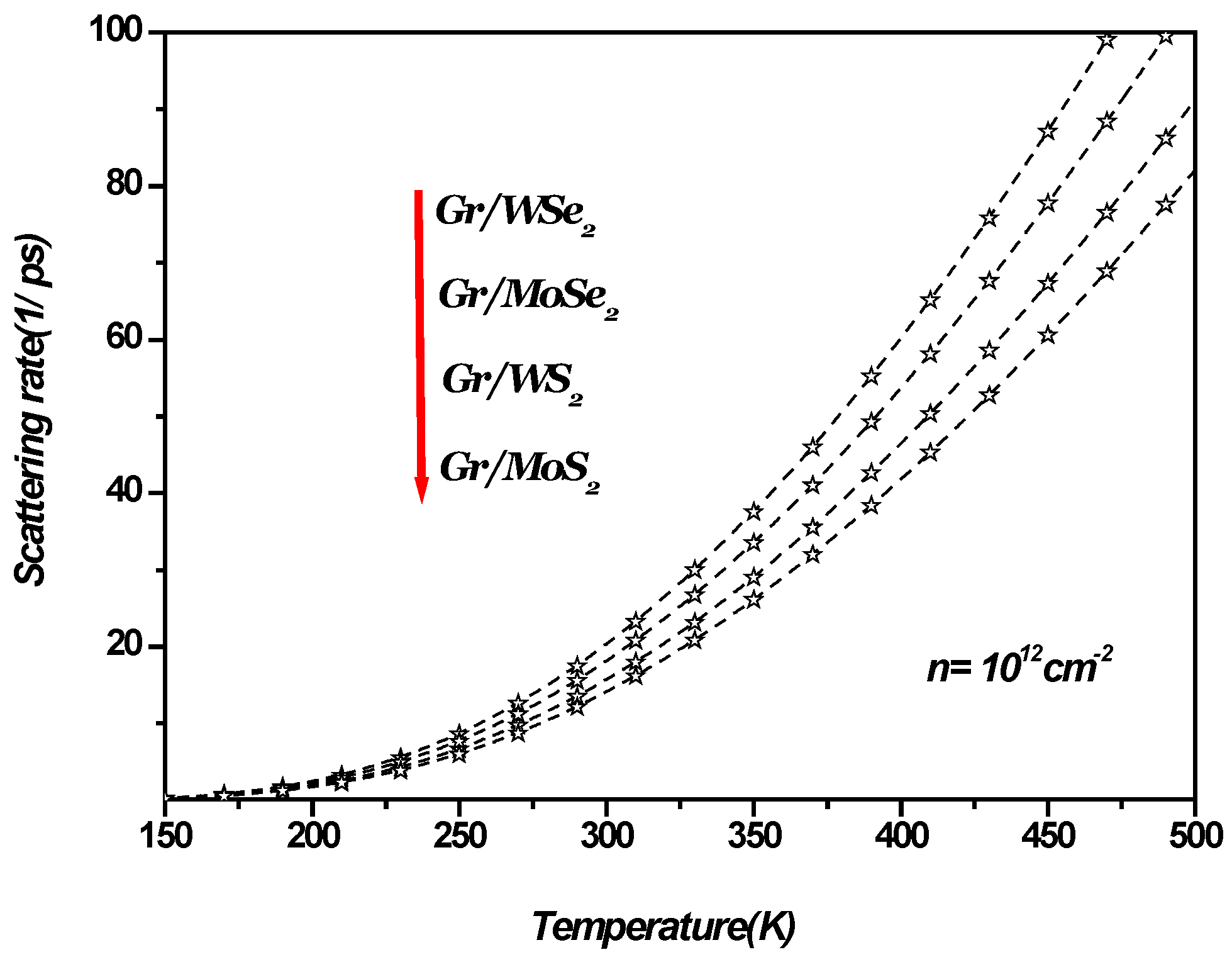
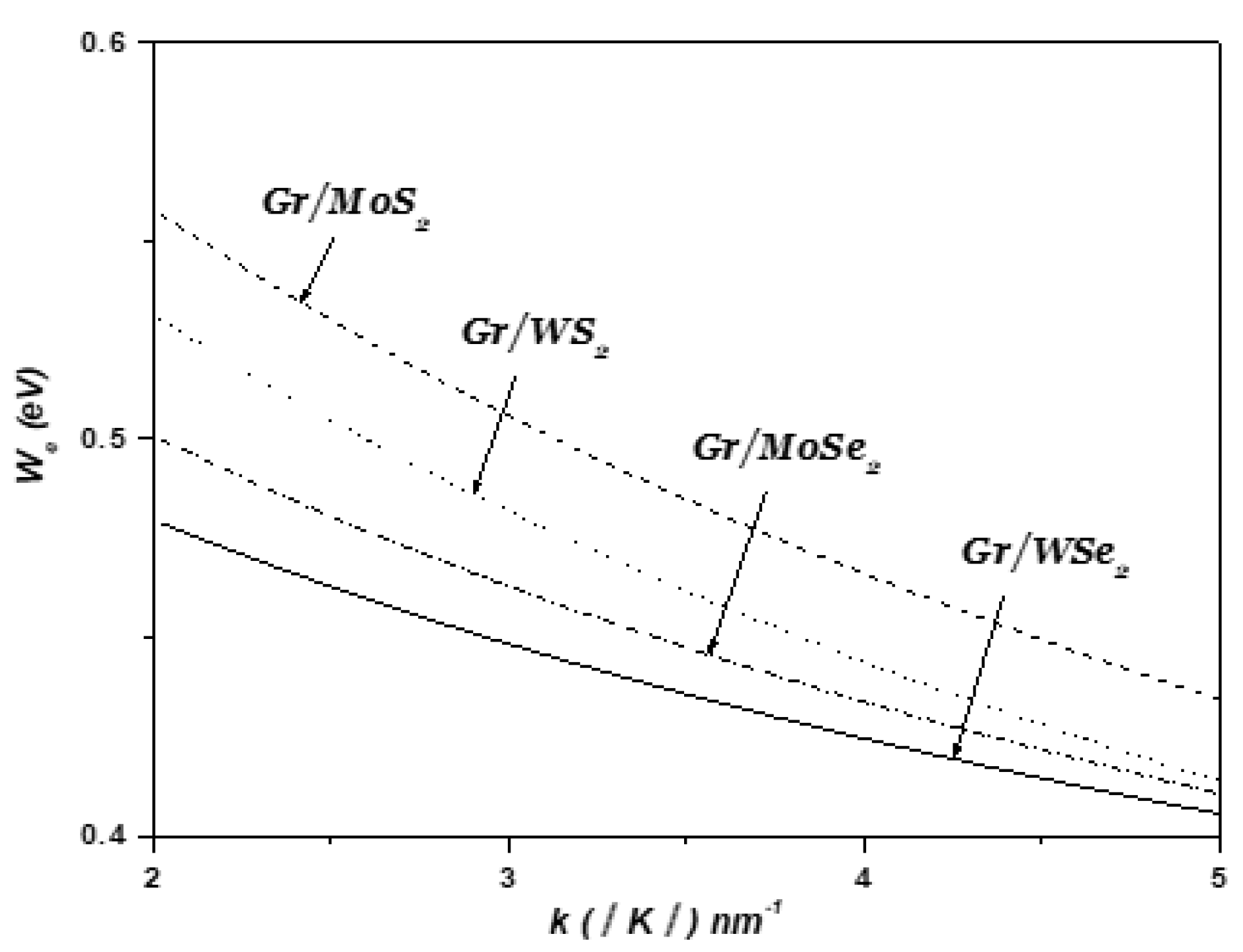
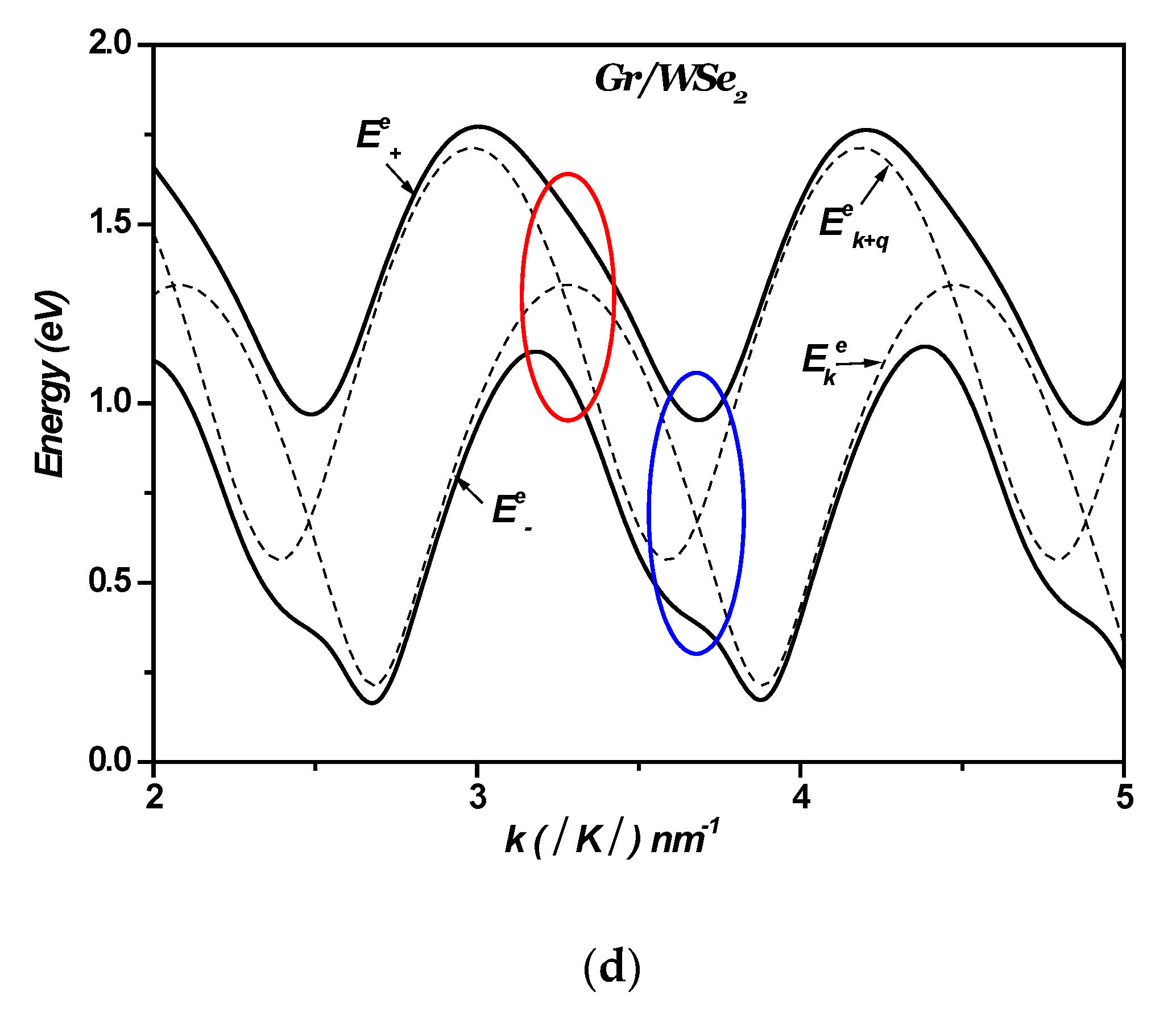
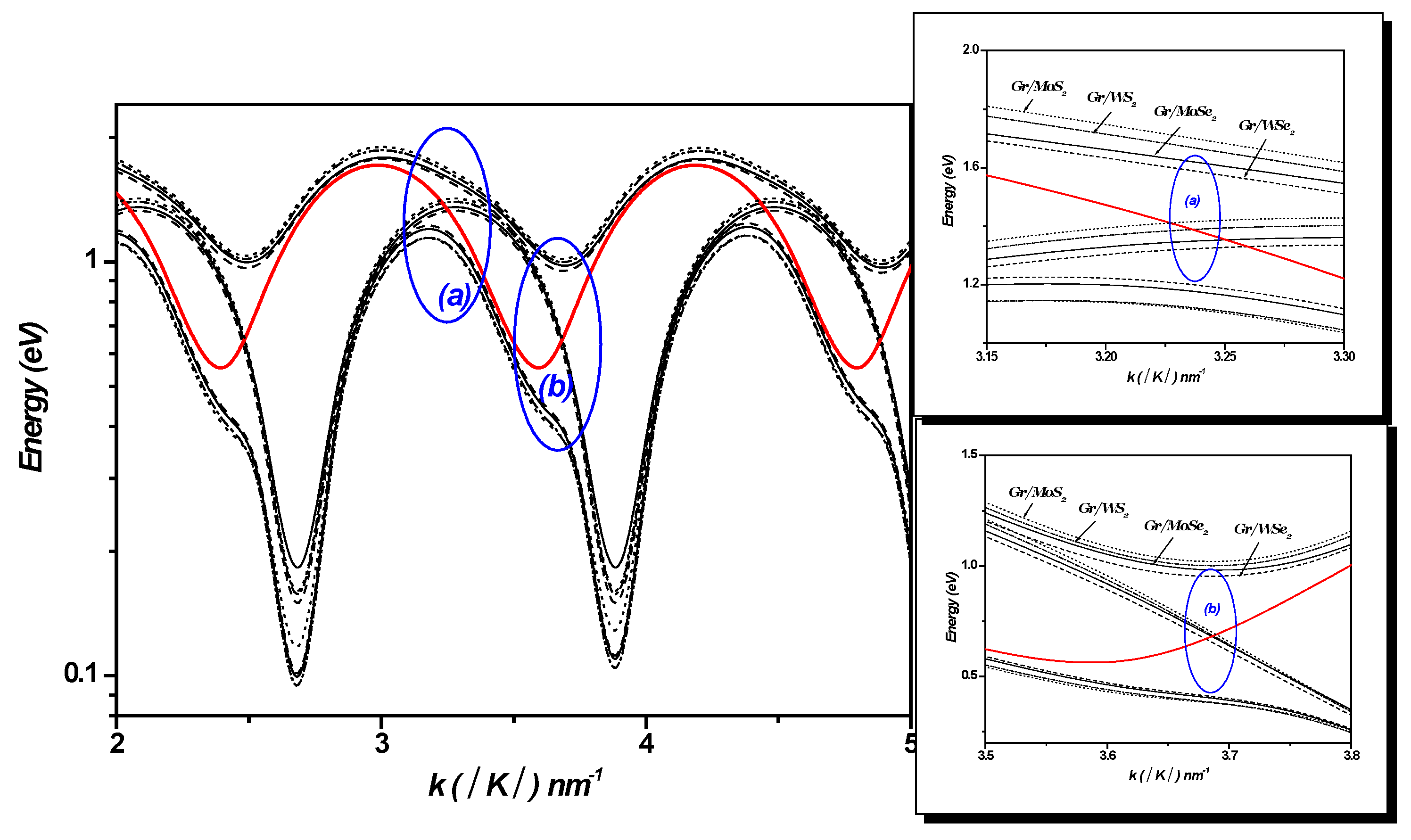
3. Electron–Surface Optical Phonon Interaction in 1LG/TMDC Interface
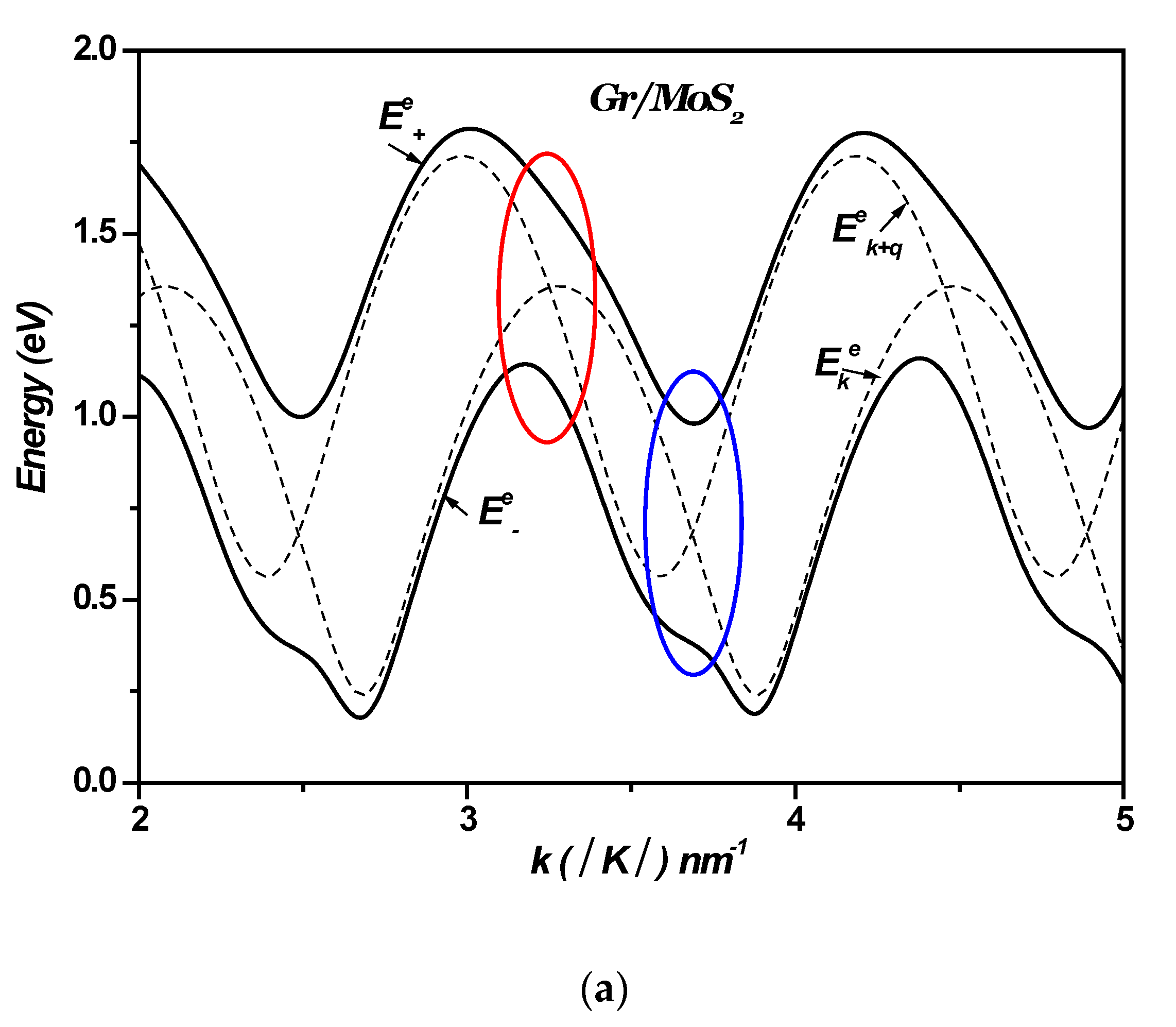
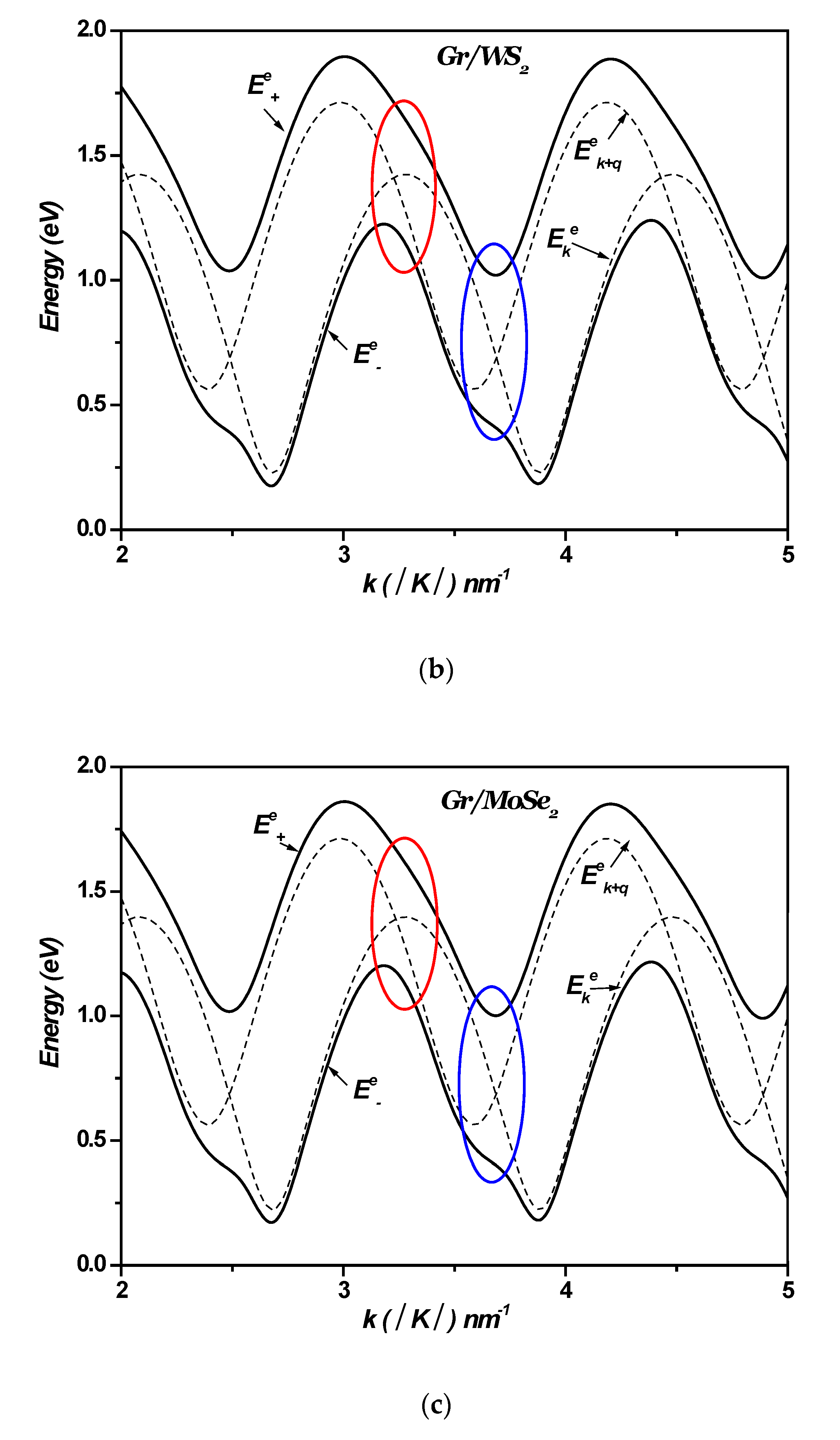
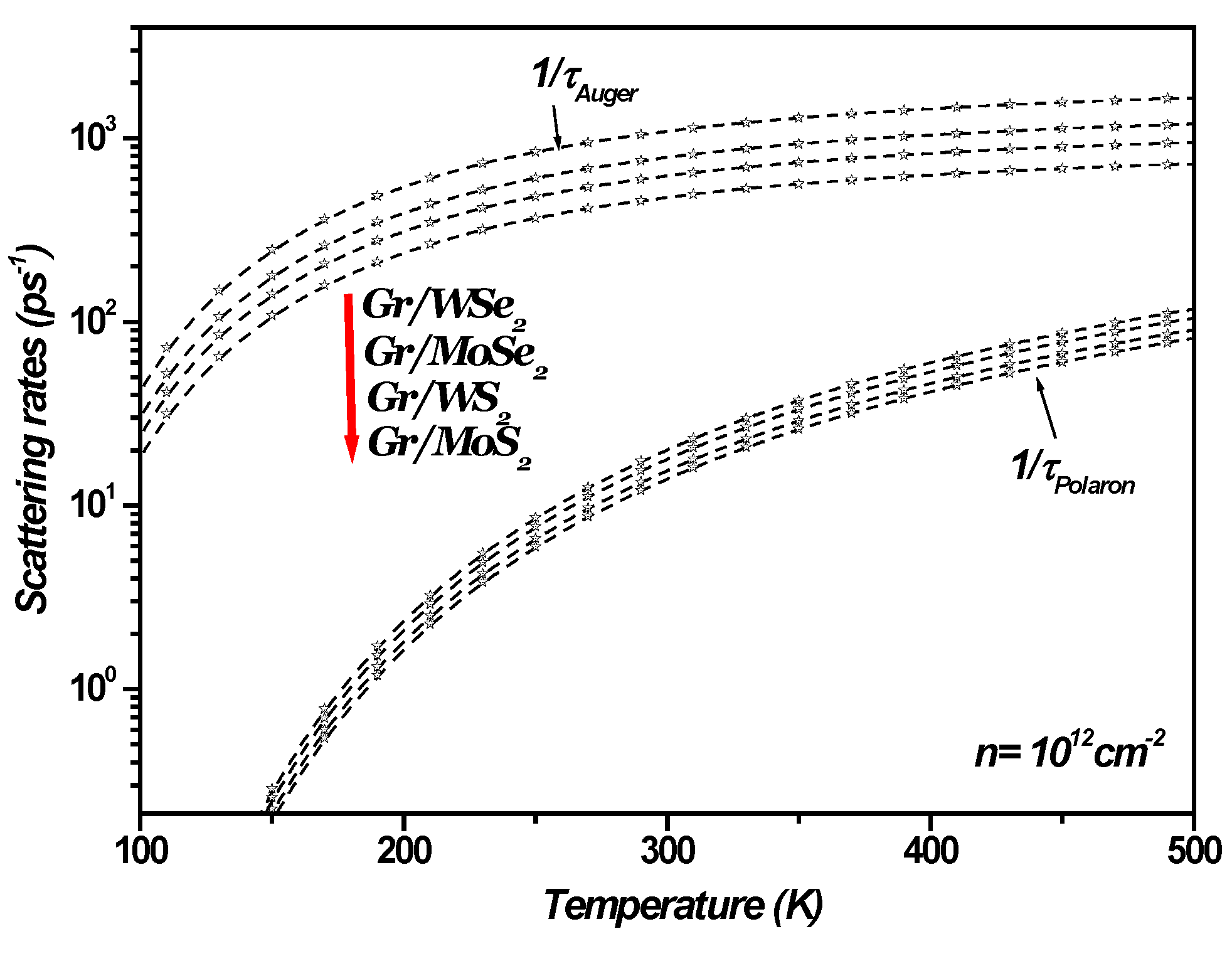
4. Auger Recombination in 1LG/TMDC Interfaces
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Tang, L.; Luo, W.; Feng, S.; Leng, C.; Shi, H.; Wei, X. Interface engineering of a silicon/graphene heterojunction photodetector via a diamond-like carbon interlayer. ACS Appl. Mater. Interfaces 2021, 13, 4692–4702. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Wang, H.; Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. Nat. Commun. 2014, 5, 4458. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Grigorieva, I.V. Van derWaals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Akinwande, D.; Huyghebaert, C.; Wang, C.-H.; Serna, M.I.; Goossens, S.; Li, L.-J.; Wong, H.-S.P.; Koppens, F.H.L. Graphene and two-dimensional materials for silicon technology. Nature 2019, 573, 507–518. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, X.; Shin, H.-J.; Park, S.; Huang, Y.; Duan, X. Promises and prospects of two-dimensional transistors. Nature 2021, 591, 43–53. [Google Scholar] [CrossRef]
- Huang, M.; Li, S.; Zhang, Z.; Xiong, X.; Li, X.; Wu, Y. Multifunctional high-performance van der Waals heterostructures. Nat. Nanotechnol. 2017, 12, 1148–1154. [Google Scholar] [CrossRef]
- Mao, L.; Stoumpos, C.C.; Kanatzidis, M.G. Two-dimensional hybrid halide perovskites: Principles and promises. J. Am. Chem. Soc. 2019, 141, 1171–1190. [Google Scholar] [CrossRef]
- Wei, K.; Sui, Y.; Xu, Z.; Kang, Y.; You, J.; Tang, Y.; Li, H.; Ma, Y.; Ouyang, H.; Zheng, X.; et al. Acoustic phonon recycling for photocarrier generation in graphene-WS2 heterostructures. Nat. Commun. 2020, 11, 3876. [Google Scholar] [CrossRef]
- Ng, H.K.; Xiang, D.; Suwardi, A.; Hu, G.; Yang, K.; Zhao, Y.; Liu, T.; Cao, Z.; Liu, H.; Li, S.; et al. Improving carrier mobility in two-dimensional semiconductors with rippled materials. Nat. Electron. 2022, 5, 489–496. [Google Scholar] [CrossRef]
- Aeschlimann, S.; Rossi, A.; Chávez-Cervantes, M.; Krause, R.; Arnoldi, B.; Stadtmüller, B.; Aeschlimann, M.; Forti, S.; Fabbri, F.; Coletti, C.; et al. Direct evidence for efficient ultrafast charge separation in epitaxial WS2/graphene heterostructures. Sci. Adv. 2020, 6, eaay0761. [Google Scholar] [CrossRef]
- Pandey, T.; Nayak, A.P.; Liu, J.; Moran, S.T.; Kim, J.-S.; Li, L.; Lin, J.-F.; Akinwande, D.; Singh, A.K. Pressure-Induced Charge Transfer Doping of Monolayer Graphene/MOS2 Heterostructure. Small 2016, 12, 4063–4069. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Dai, X.; Zhang, L.; Li, H. Electron transport properties of graphene/WS2 Van Der Waals heterojunctions. Molecules 2023, 28, 6866. [Google Scholar] [CrossRef]
- Mahdouani, M. Investigation of the electron-surface phonon interaction effects in graphene on a substrate made of polar materials. Phys. E 2017, 87, 192–198. [Google Scholar] [CrossRef]
- Mahdouani, M.; Gardelis, S.; Bourguiga, R. The effect of Si impurities on the transport properties and the electron-surface phonon interaction in single layer graphene deposited on polar substrates. Phys. B Condens. Matter 2018, 550, 171–178. [Google Scholar] [CrossRef]
- Mahdouani, M.; Bourguiga, R. Auger and carrier-surface phonon interaction processes in graphene on a substrate made of polar materials. Superlattices Microstruct. 2017, 102, 212–220. [Google Scholar] [CrossRef]
- Mahdouani, M.; Bourguiga, R.; Gardelis, S. A Theoretical Study of the Electron–Surface Optical Phonon Interaction in Monolayer Transition Metal Dichalcogenides Deposited on SiC and Hexagonal BN Dielectric Substrates in the Vicinity of the Points K+(K−) of the Brillouin Zone. Materials 2024, 17, 5552. [Google Scholar] [CrossRef]
- Mahdouani, M.; Gardelis, S.; Nassiopoulou, A.G. Role of surface vibration modes in Si nanocrystals within light emitting porous Si at the strong confinement regime. J. Appl. Phys. 2011, 110, 023527. [Google Scholar] [CrossRef]
- Gardelis, S.; Nassiopoulou, A.G.; Mahdouani, M.; Bourguiga, R.; Jaziri, S. Enhancement and red shift of photoluminescence (PL) of fresh porous Si under prolonged laser irradiation or ageing: Role of surface vibration modes. Phys. E 2009, 41, 986–989. [Google Scholar] [CrossRef]
- Mahdouani, M.; Bourguiga, R.; Jaziri, S. Polaronic states in Si nanocrystals embedded in SiO2 matrix. Phys. E 2008, 41, 228–234. [Google Scholar] [CrossRef]
- Lee, E.; Lee, S.G.; Lee, W.H.; Lee, H.C.; Nguyen, N.N.; Yoo, M.S.; Cho, K. Direct CVD growth of a graphene/MoS2 heterostructure with interfacial bonding for two-dimensional electronics. Chem. Mater. 2020, 32, 4544–4552. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, C.; Huang, X.; Zeng, S.; Liu, L.; Li, J.; Jiang, Y.-G.; Zhang, D.W.; Zhou, P. A steep-slope MoS2/graphene dirac-source field-effect transistor with a large drive current. Nano Lett. 2021, 21, 1758–1764. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Liu, Y.; Zhao, X.; Shen, Q.; Zhao, W.; Tan, Q.; Zhang, N.; Li, P.; Jiao, L.; Qu, X. Sandwich-like heterostructures of MoS2/graphene with enlarged interlayer spacing and enhanced hydrophilicity as high-performance cathodes for aqueous zinc-ion batteries. Adv. Mater. 2021, 33, 2007480. [Google Scholar] [CrossRef] [PubMed]
- Pomerantseva, E.; Gogotsi, Y. Two-dimensional heterostructures for energy storage. Nat. Energy 2017, 2, 17089. [Google Scholar] [CrossRef]
- Bag, A.; Lee, N.-E. Gas sensing with heterostructures based on two-dimensional nanostructured materials: A review. J. Mater. Chem. C 2019, 7, 13367–13383. [Google Scholar] [CrossRef]
- Choi, H.K.; Park, J.; Myoung, N.; Kim, H.-J.; Choi, J.S.; Choi, Y.K.; Hwang, C.-Y.; Kim, J.T.; Park, S.; Yi, Y.; et al. Gas molecule sensing of van der Waals tunnel field effect transistors. Nanoscale 2017, 9, 18644–18650. [Google Scholar] [CrossRef]
- Swager, T.M.; Mirica, K.A. Introduction: Chemical Sensors. Chem. Rev. 2019, 119, 1–2. [Google Scholar] [CrossRef]
- Li, Z.; Yao, Z.; Haidry, A.A.; Luan, Y.; Chen, Y.; Zhang, B.Y.; Xu, K.; Deng, R.; Hoa, N.D.; Zhou, J.; et al. Recent advances of atomically thin 2D heterostructures in sensing applications. Nano Today 2021, 40, 101287. [Google Scholar] [CrossRef]
- Shin, Y.; Kwon, J.; Jeong, Y.; Watanabe, K.; Taniguchi, T.; Im, S.; Lee, G.H. Graphene via Contact Architecture for Vertical Integration of vdW Heterostructure Devices. Small 2022, 18, e2200882. [Google Scholar] [CrossRef]
- Sun, X.; Li, X.; Zeng, Y.; Meng, L. Improving the stability of perovskite by covering graphene on FAPbI3surface. Int. J. Energy Res. 2021, 45, 10808–10820. [Google Scholar] [CrossRef]
- Wang, X.; Long, R. Rapid charge separation boosts solar hydrogen generation at the graphene–MoS2 junction: Time-domain ab initio analysis. J. Phys. Chem. Lett. 2021, 12, 2763–2769. [Google Scholar] [CrossRef]
- Wang, H.; Gao, S.; Zhang, F.; Meng, F.; Guo, Z.; Cao, R.; Zeng, Y.; Zhao, J.; Chen, S.; Hu, H.; et al. Repression of interlayer recombination by graphene generates a sensitive nanostructured 2D vdW heterostructure based photodetector. Adv. Sci. 2021, 8, 2100503. [Google Scholar] [CrossRef] [PubMed]
- Cong, C.; Shang, J.; Wang, Y.; Yu, T. Optical properties of 2D semiconductor WS2. Adv. Opt. Mater. 2018, 6, 1700767. [Google Scholar] [CrossRef]
- Zhen, J.; Huang, Q.; Liu, Y.; Zhang, S.; Dong, H.; Lv, K.; Qiu, J.; Liu, G. High carrier mobility and strong electron–phonon coupling in graphene–WS2 heterobilayers under pressure. J. Mater. Chem. C 2023, 11, 15555–15563. [Google Scholar] [CrossRef]
- Froehlicher, G.; Lorchat, E.; Berciaud, S. Charge versus Energy Transfer in Atomically Thin Graphene-Transition Metal Dichalcogenide van der Waals Heterostructures. Phys. Rev. X 2018, 8, 011007. [Google Scholar] [CrossRef]
- Noh, B.-I.; Reza, S.; Hardy, C.; Li, J.; Taba, A.; Mahjouri-Samani, M.; Edgar, J.H.; Dai, S. Low Dielectric Medium for Hyperbolic Phonon Polariton Waveguide in van der Waals Heterostructures. Nanomaterials 2024, 14, 1344. [Google Scholar] [CrossRef]
- Liao, W.; Zhao, S.; Li, F.; Wang, C.; Ge, Y.; Wang, H.; Wang, S.; Zhang, H. Interface engineering of two-dimensional transition metal dichalcogenides towards next-generation electronic devices: Recent advances and challenges. Nanoscale Horiz. 2020, 5, 787–807. [Google Scholar] [CrossRef]
- Martini, L.; Mišeikis, V.; Esteban, D.; Azpeitia, J.; Pezzini, S.; Paletti, P.; Ochapski, M.W.; Convertino, D.; Hernandez, M.G.; Jimenez, I.; et al. Scalable High-Mobility Graphene/hBN Heterostructures. ACS Appl. Mater. Interfaces 2023, 15, 37794–37801. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Chen, H.; Wang, R.; Mi, Y.; Zhang, C.; Du, W.; Zhang, S.; Liu, Z.; Zhang, Q.; et al. The Auger process in multilayer WSe2 crystals. Nanoscale 2018, 10, 17585–17592. [Google Scholar] [CrossRef]
- Tang, Y.; Li, H.; Mao, X.; Xie, J.; Lee, J.Y.; Fu, A. Bidirectional heterostructures consisting of graphene and lateral MoS2/WS2 composites: A first-principles study. RSC Adv. 2019, 9, 34986–34994. [Google Scholar] [CrossRef]
- Geng, H.; Yuan, D.; Yang, Z.; Tang, Z.; Zhang, X.; Yang, K.; Su, Y. Graphene van der Waals heterostructures for high-performance photodetectors. J. Mater. Chem. C 2019, 7, 11056–11067. [Google Scholar] [CrossRef]
- Perebeinos, V.; Avouris, P. Inelastic scattering and current saturation in graphene. Phys. Rev. B 2010, 81, 195442. [Google Scholar] [CrossRef]
- Fischetti, M.V.; Neumayer, D.A.; Cartier, E.A. Effective electron mobility in Si inversion layers in metal–oxide–semiconductor systems with a high-κ insulator: The role of remote phonon scattering. J. Appl. Phys. 2001, 90, 4587. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Nori, F. Exact wave functions for an electron on a graphene triangular quantum dot. Phys. Rev. B 2010, 81, 155401. [Google Scholar] [CrossRef]
- Antonius, G.; Louie, S.G. Theory of exciton-phonon coupling. Phys. Rev. B 2022, 105, 085111. [Google Scholar] [CrossRef]
- Sohier, T.; Calandra, M.; Mauri, F. Two-dimensional Fröhlich interaction in transition-metal dichalcogenide monolayers: Theoretical modeling and first-principles calculations. Phys. Rev. B 2016, 94, 085415. [Google Scholar] [CrossRef]
- Wang, Y.; He, C.; Tan, Q.; Tang, Z.; Huang, L.; Liu, L.; Yin, J.; Jiang, Y.; Wang, X.; Pan, A. Exciton–phonon coupling in two-dimensional layered (BA)2PbI4 perovskite microplates. RSC Adv. 2023, 13, 5893–5899. [Google Scholar] [CrossRef]
- Ma, J.; Xu, D.; Hu, R.; Luo, X. Examining two-dimensional Fröhlich model and enhancing the electron mobility of monolayer InSe by dielectric engineering. J. Appl. Phys. 2020, 128, 035107. [Google Scholar] [CrossRef]
- Hinsche, N.F.; Thygesen, K.S. Electron–phonon interaction and transport properties of metallic bulk and monolayer transition metal dichalcogenide TaS2. 2D Mater. 2017, 5, 015009. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, Z.-Q.; Wang, Z.-W. Polaron effect on the bandgap modulation in monolayer transition metal dichalcogenides. J. Phys. Condens. Matter 2017, 29, 485001. [Google Scholar] [CrossRef]
- Nguepnang, J.V.; Kenfack-Sadem, C.; Kenfack-Jiotsa, A.; Fobasso, M.F.C.; Sun, Y. Optical signature of bipolaron in monolayer transition metal dichalcogenides: All coupling approach. Opt. Quantum Electron. 2021, 53, 728. [Google Scholar] [CrossRef]
- Devreese, J.; Huybrechts, W.; Lemmens, L. On the optical absorption of free polarons at weak coupling. Phys. Status Solidi (B) 1971, 48, 77–86. [Google Scholar] [CrossRef]
- Mafra, D.L.; Araujo, P.T. Intra- and Interlayer Electron-Phonon Interactions in 12/12C and 12/13C BiLayer Graphene. Appl. Sci. 2014, 4, 207–239. [Google Scholar] [CrossRef]
- Wang, S.Q.; Mahan, G.D. Electron Scattering from Surface Excitations. Phys. Rev. B 1972, 6, 4517. [Google Scholar] [CrossRef]
- Van Tuan, D.; Jones, A.M.; Yang, M.; Xu, X.; Dery, H. Virtual Trions in the Photoluminescence of Monolayer Transition-Metal Dichalcogenides. Phys. Rev. Lett. 2019, 122, 217401. [Google Scholar] [CrossRef]
- Jin, Z.; Li, X.; Mullen, J.T.; Kim, K.W. Intrinsic Transport Properties of Electrons and Holes in Monolayer Transition-Metal Dichalcogenides. Phys. Rev. B 2014, 90, 045422. [Google Scholar] [CrossRef]
- Dery, H.; Song, Y. Polarization analysis of excitons in monolayer and bilayer transition-metal dichalcogenides. Phys. Rev. B 2015, 92, 125431. [Google Scholar] [CrossRef]
- Danovich, M.; Aleiner, I.L.; Drummond, N.D.; Falko, V.I. Fast relaxation of photo-excited carriers in 2-D transition Metal dichalcogenides. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 6000105. [Google Scholar] [CrossRef]
- Gopalan, S.; Van de Put, M.L.; Gaddemane, G.; Fischetti, M.V. Theoretical Study of Electronic Transport in Two-Dimensional Transition Metal Dichalcogenides: Effects of the Dielectric Environment. Phys. Rev. Appl. 2022, 18, 054062. [Google Scholar] [CrossRef]
- Silveira, J.F.R.V.; Besse, R.; Da Silva, J.L.F. Stacking Order Effects on the Electronic and Optical Properties of Graphene/Transition Metal Dichalcogenide van der Waals Heterostructures. ACS Appl. Electron. Mater. 2021, 3, 1671–1680. [Google Scholar] [CrossRef]
- Zhang, R.; Hao, G.; Ye, X.; Gao, S.; Li, H. Tunable electronic properties and Schottky barrier in a graphene/WSe2 heterostructure under out-of-plane strain and an electric field. Phys. Chem. Chem. Phys. 2020, 22, 23699–23706. [Google Scholar] [CrossRef] [PubMed]
- Benedict, L.X.; Louie, S.G.; Cohen, M.L. Static polarizabilities of single-wall carbon nanotubes. Phys. Rev. B 1995, 52, 8541. [Google Scholar] [CrossRef] [PubMed]
- Mahdouani, M.; Bourguiga, R.; Jaziri, S.; Gardelis, S.; Nassiopoulou, A. Investigation of Auger recombination in Ge and Si nanocrystals embedded in SiO2 matrix. Phys. E 2009, 42, 57–62. [Google Scholar] [CrossRef]
- Mahdouani, M.; Bourguiga, R.; Jaziri, S.; Gardelis, S.; Nassiopoulou, A.G. Auger recombination in silicon nanocrystals embedded in SiO2 wide band-gap lattice. Phys. Status Solidi (A) 2008, 205, 2630. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Peres, N.M.R. Colloquium: The transport properties of graphene: An introduction. Rev. Mod. Phys. 2010, 82, 2673. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407. [Google Scholar] [CrossRef]
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Guinea, F.; Neto, A.H.C. Electron-Electron Interactions in Graphene: Current Status and Perspectives. Rev. Mod. Phys. 2012, 84, 1067. [Google Scholar] [CrossRef]
- Tomadin, A.; Brida, D.; Cerullo, G.; Ferrari, A.C.; Polini, M. Nonequilibrium dynamics of photoexcited electrons in graphene. Phys. Rev. B 2013, 88, 035430. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdouani, M.; Bourguiga, R.; Gardelis, S. Auger Recombination and Carrier-Surface Optical Phonon Interaction in Van Der Waals Heterostructures Composed of Graphene and 2D Transition Metal Chalcogenides. Materials 2025, 18, 720. https://doi.org/10.3390/ma18030720
Mahdouani M, Bourguiga R, Gardelis S. Auger Recombination and Carrier-Surface Optical Phonon Interaction in Van Der Waals Heterostructures Composed of Graphene and 2D Transition Metal Chalcogenides. Materials. 2025; 18(3):720. https://doi.org/10.3390/ma18030720
Chicago/Turabian StyleMahdouani, Mounira, Ramzi Bourguiga, and Spiros Gardelis. 2025. "Auger Recombination and Carrier-Surface Optical Phonon Interaction in Van Der Waals Heterostructures Composed of Graphene and 2D Transition Metal Chalcogenides" Materials 18, no. 3: 720. https://doi.org/10.3390/ma18030720
APA StyleMahdouani, M., Bourguiga, R., & Gardelis, S. (2025). Auger Recombination and Carrier-Surface Optical Phonon Interaction in Van Der Waals Heterostructures Composed of Graphene and 2D Transition Metal Chalcogenides. Materials, 18(3), 720. https://doi.org/10.3390/ma18030720








