Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics
Abstract
:1. Introduction
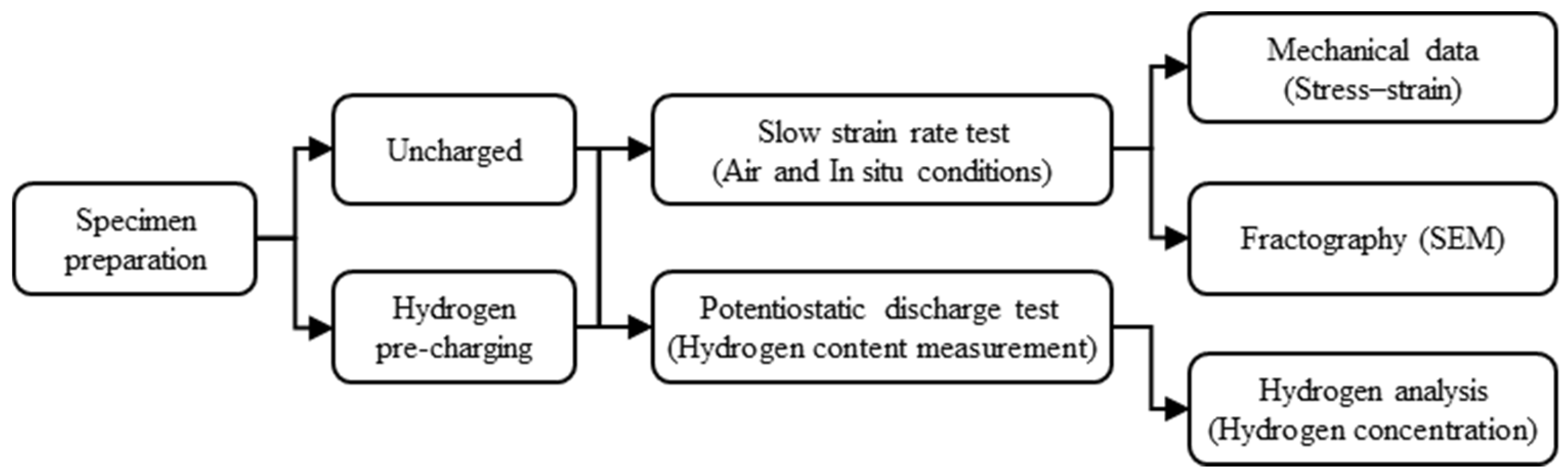
2. Experimental Preparations
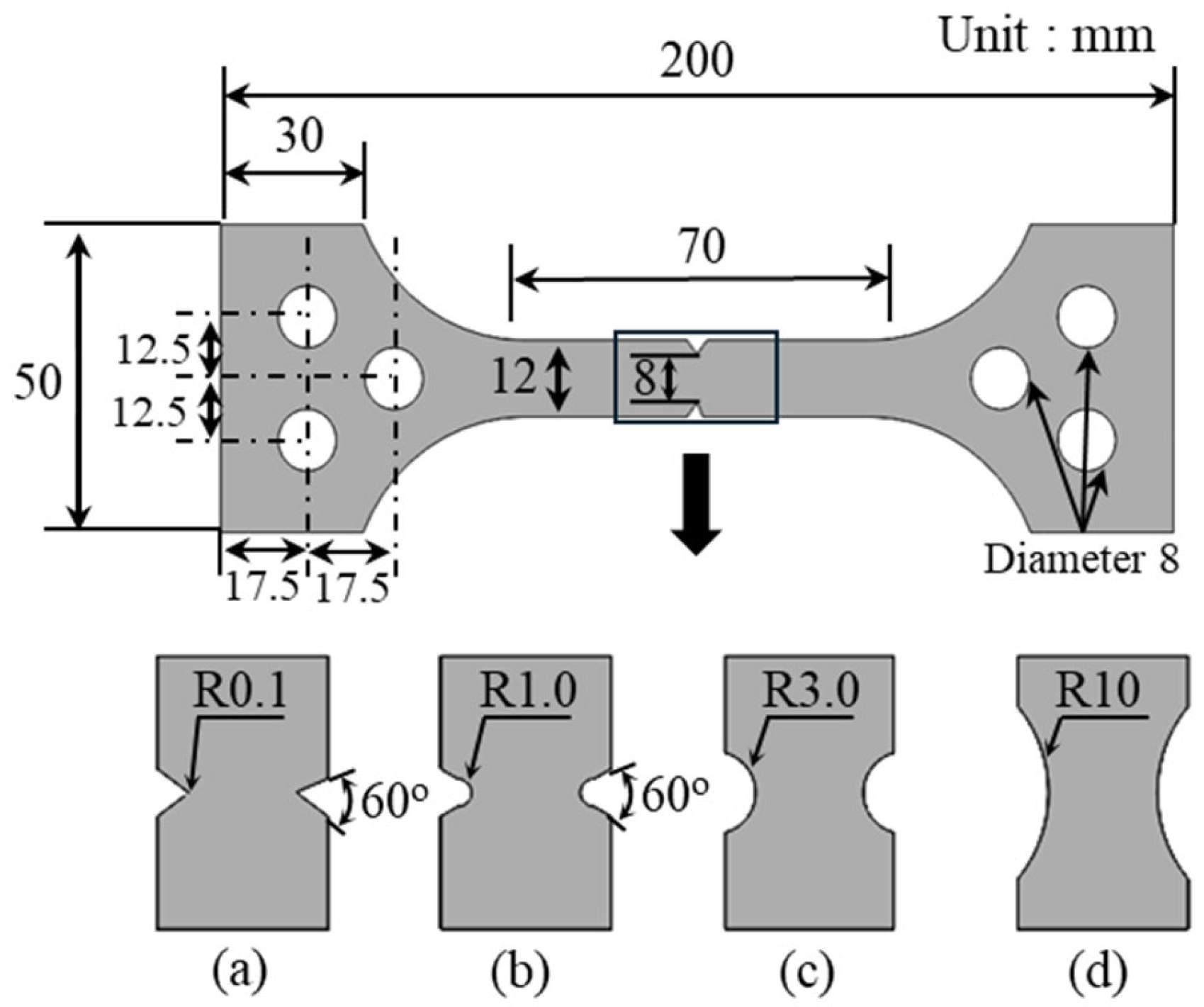
2.1. Experimental Setup and Specimen Preparation
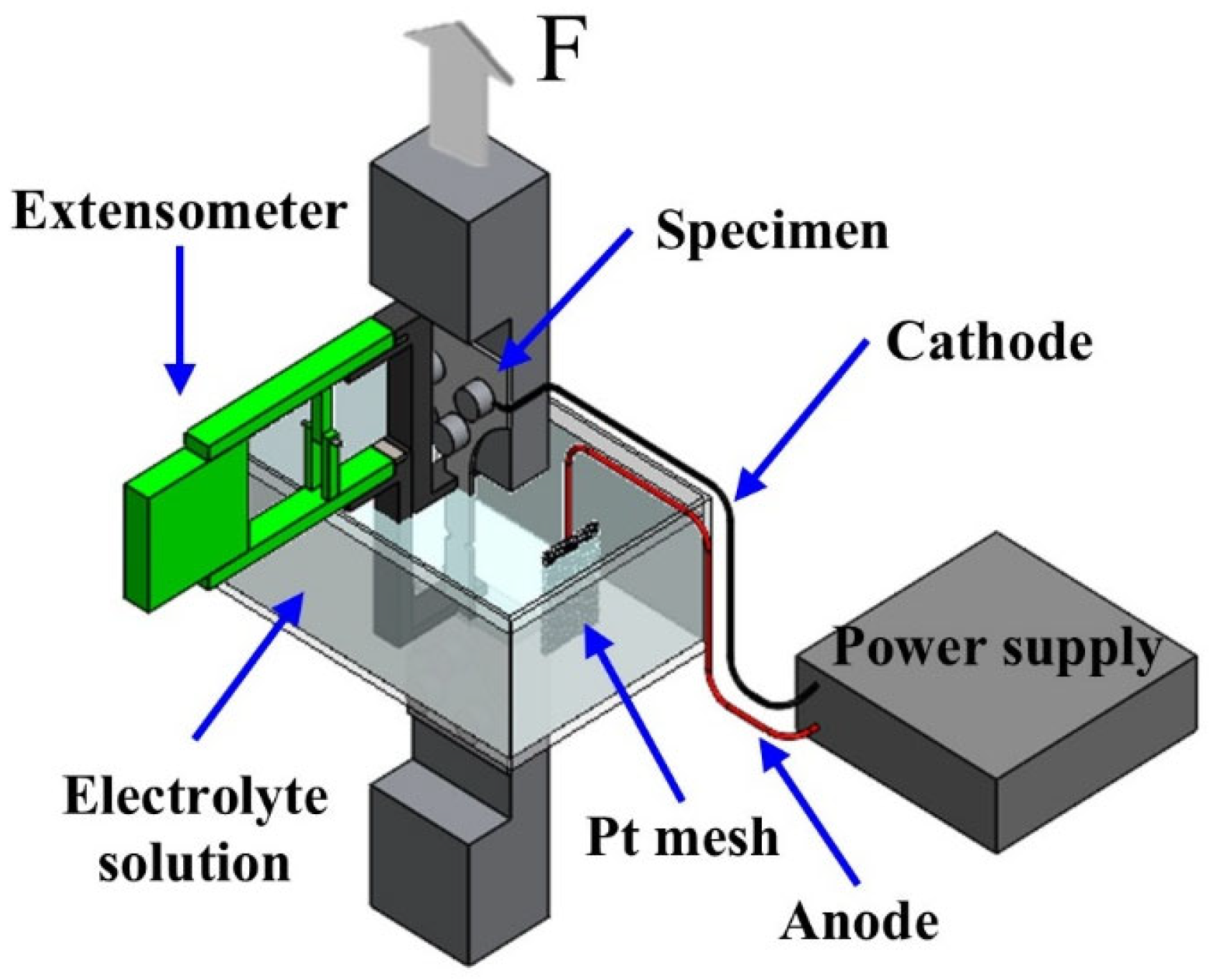
2.2. SSRT Under Cathodic Charging
2.3. Measurement of Hydrogen Concentration
2.4. Fractographic Feature Observations
3. Result and Discussion
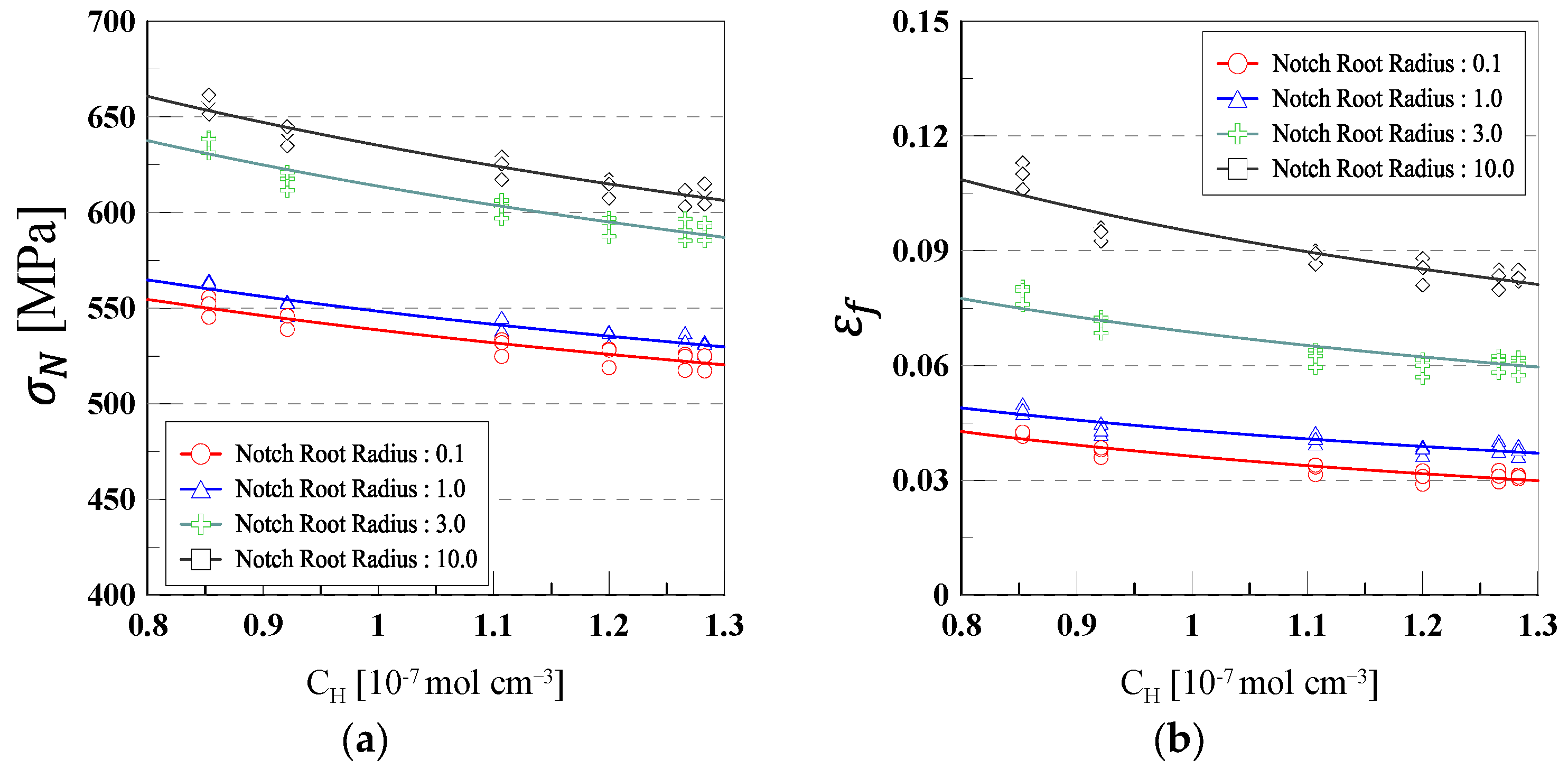
3.1. SSRT Results
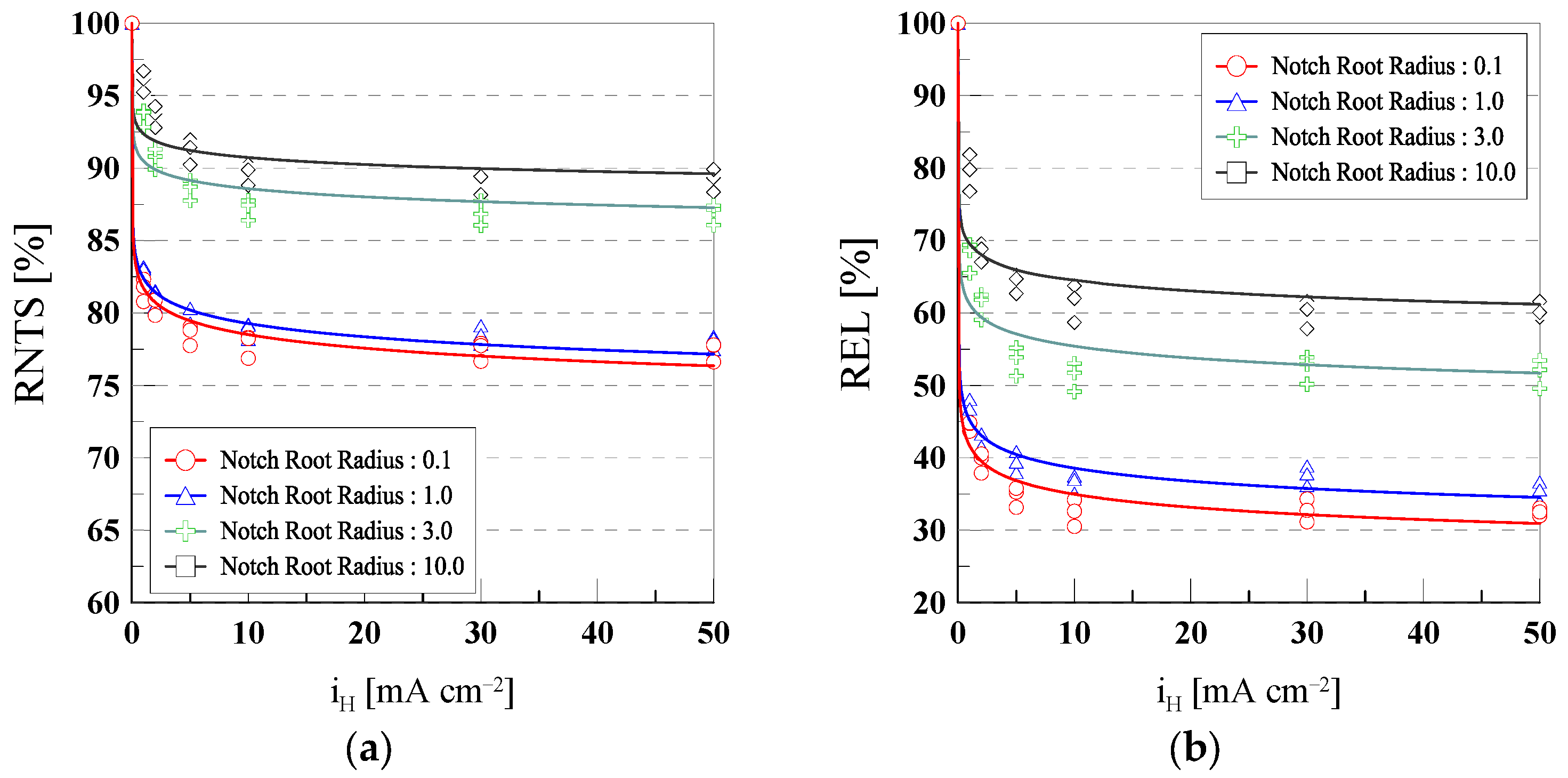
3.2. Hydrogen Embrittlement Susceptibility Index
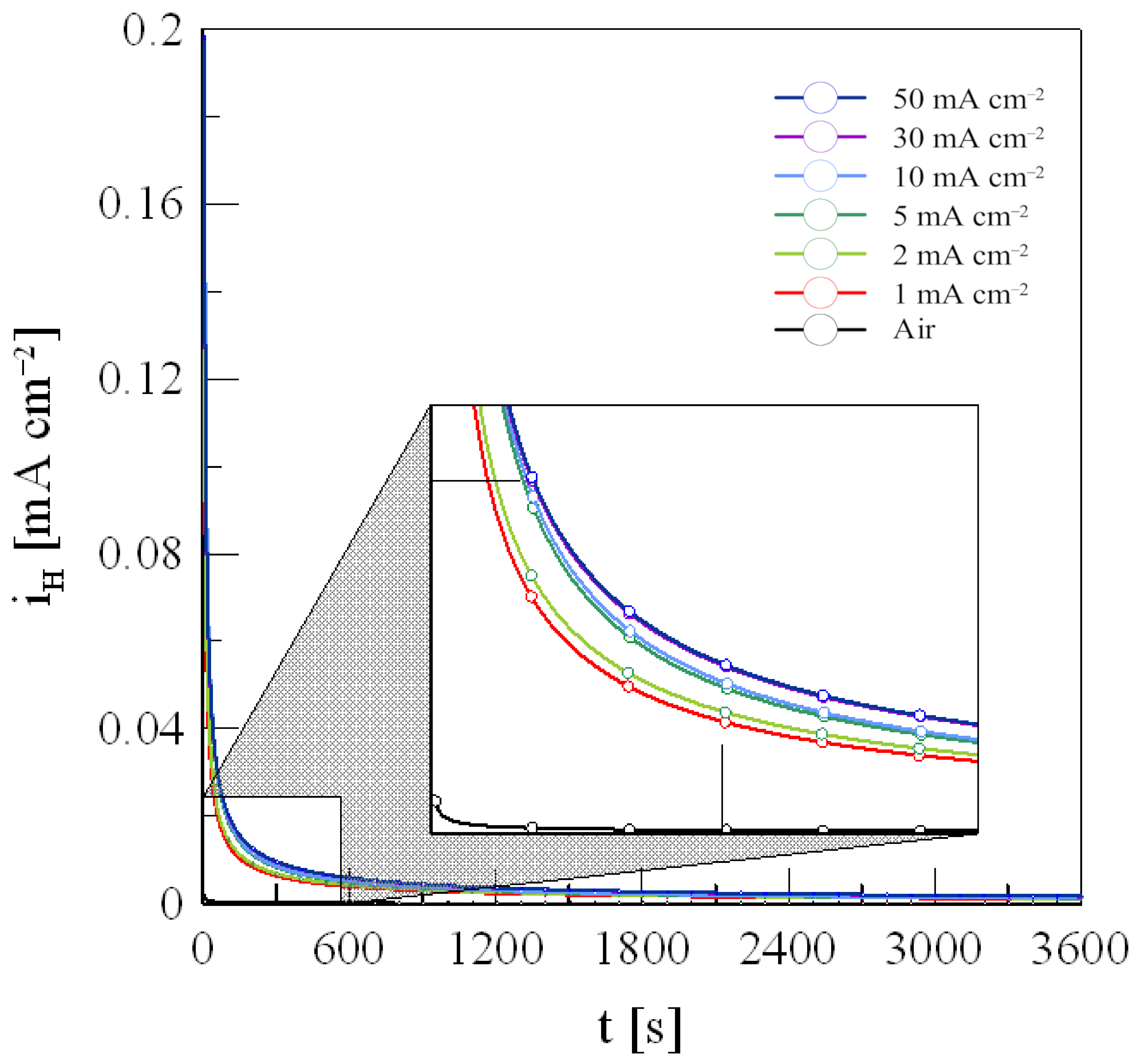
3.3. Hydrogen Concentration
3.4. Fractographic Analysis of the SSRT Specimens
4. Conclusions
- The hydrogen embrittlement of 316L stainless steel was mainly influenced by the notch radius and current density. As the current density increased, both tensile strength and elongation tended to decrease. This was attributed to the increased diffusion of hydrogen into the material at higher current densities, which promoted crack initiation and propagation through interactions with dislocations, grain boundaries, and microvoids.
- Experimental results indicated that the hydrogen embrittlement effect tended to saturate at current densities of 10 mA/cm2 or higher. This suggests that hydrogen saturation within grain boundaries and dislocation structures limits the additional impact of hydrogen charging on the mechanical properties.
- As the notch radius decreased (0.1 mm and 1.0 mm), local stress concentration increased, promoting hydrogen diffusion and trapping, which led to a significant reduction in RNTS and REL. In contrast, specimens with larger notch radii (3.0 mm and 10.0 mm) exhibited a more uniform stress distribution, resulting in relatively lower susceptibility to hydrogen embrittlement.
- As the current density increased, the hydrogen concentration inside the specimen also increased, showing a nonlinear increase at current densities above 30 mA/cm2. This indicates that additional hydrogen absorption is limited due to the saturation of hydrogen trapping sites, leading to a slowdown in changes in mechanical properties beyond a certain current density.
- In the hydrogen-charged specimens, a mixed fracture mode of ductile fracture (dimples) and brittle fracture (quasi-cleavage and intergranular fracture) was observed. Notably, specimens with smaller notches exhibited a higher tendency for brittle fractures. This suggests that local hydrogen accumulation and stress concentration are key factors in promoting brittle cracking.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations/Nomenclature
| RNTS | Relative Notch Tensile Strength |
| REL | Relative Elongation |
| SEM | Scanning Electron Microscopy |
| HE index | Hydrogen Embrittlement index |
| IG | Intergranular |
| QC | Quasi-Cleavage |
| Stress | |
| Strain | |
| Applied force | |
| Initial cross-sectional area of the specimen | |
| Measured displacement | |
| Initial gauge length of the specimen | |
| Critical force | |
| Notch strength | |
| Critical displacement | |
| Elongation | |
| Fitted parameters | |
| Current density | |
| Charge of diffusible hydrogen | |
| Valence number for hydrogen | |
| Faraday constant | |
| Effective volume | |
| Total hydrogen concentration | |
| Saturation level of hydrogen concentration | |
| Sensitivity coefficient and exponent for hydrogen traps |
References
- Wang, D.; Liao, B.; Zheng, J.; Huang, G.; Hua, Z.; Gu, C.; Xu, P. Development of regulations, codes and standards on composite tanks for on-board gaseous hydrogen storage. Int. J. Hydrogen Energy 2019, 44, 22643–22653. [Google Scholar] [CrossRef]
- Meda, U.S.; Bhat, N.; Pandey, A.; Subramanya, K.N.; Lourdu Antony Raj, M.A. Challenges associated with hydrogen storage systems due to the hydrogen embrittlement of high strength steels. Int. J. Hydrogen Energy 2023, 48, 17894–17913. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, M.; Rong, L. Overview of hydrogen-resistant alloys for high-pressure hydrogen environment: On the hydrogen energy structural materials. Clean Energy 2023, 7, 99–115. [Google Scholar] [CrossRef]
- Yan, Y.; Yan, Y.; He, Y.; Li, J.; Su, Y.; Qiao, L. Hydrogen-induced cracking mechanism of precipitation strengthened austenitic stainless steel weldment. Int. J. Hydrogen Energy 2015, 40, 2404–2414. [Google Scholar] [CrossRef]
- Köse, C. Fiber laser beam welding of additive manufactured 316L austenitic stainless steel with wrought 2507 super duplex and wrought 904L super austenitic stainless steels: Crystallographic texture, microstructure, and mechanical properties. Vacuum 2023, 215, 112347. [Google Scholar] [CrossRef]
- Khedr, M.; Hamada, A.; Abd-Elaziem, W.; Jaskari, M.; Elsamanty, M.; Komi, J.; Jarvenpaa, A. Effects of Wall Thickness Variation on Hydrogen Embrittlement Susceptibility of Additively Manufactured 316L Stainless Steel with Lattice Auxetic Structures. Materials 2023, 16, 2523. [Google Scholar] [CrossRef]
- Xing, X.; Pang, Z.; Zhang, H.; Liu, J.; Cui, G. Study of temperature effect on hydrogen embrittlement in X70 pipeline steel. Corros. Sci. 2024, 230, 111939. [Google Scholar] [CrossRef]
- Michler, T.; Wackermann, K.; Schweizer, F. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. [Google Scholar] [CrossRef]
- Toribio, J.; Lorenzo, M.; Aguado, L. Innovative Design of Residual Stress and Strain Distributions for Analyzing the Hydrogen Embrittlement Phenomenon in Metallic Materials. Materials 2022, 15, 9063. [Google Scholar] [CrossRef]
- Zhao, C.; Wu, W.; Deng, J.; Yu, M.; Peng, Y.; Wang, X.; Gong, J. Hydrogen-induced delayed fracture behavior of notched 316L austenitic stainless steel: Role of grain refinement. Eng. Fail. Anal. 2024, 166, 108880. [Google Scholar] [CrossRef]
- Song, E.J.; Baek, S.-W.; Nahm, S.H.; Baek, U.B. Notched-tensile properties under high-pressure gaseous hydrogen: Comparison of pipeline steel X70 and austenitic stainless type 304L, 316L steels. Int. J. Hydrogen Energy 2017, 42, 8075–8082. [Google Scholar] [CrossRef]
- Nietzke, J.; Konert, F.; Poka, K.; Merz, B.; Sobol, O.; Böllinghaus, T. Comparison of hydrogen effects on additively manufactured and conventional austenitic steels. Eng. Fail. Anal. 2025, 167, 109042. [Google Scholar] [CrossRef]
- Álvarez, G.; Harris, Z.; Wada, K.; Rodríguez, C.; Martínez-Pañeda, E. Hydrogen embrittlement susceptibility of additively manufactured 316L stainless steel: Influence of post-processing, printing direction, temperature and pre-straining. Addit. Manuf. 2023, 78, 103834. [Google Scholar] [CrossRef]
- Komatsu, A.; Fujinami, M.; Hatano, M.; Matsumoto, K.; Sugeoi, M.; Chiari, L. Straining-temperature dependence of vacancy behavior in hydrogen-charged austenitic stainless steel 316L. Int. J. Hydrogen Energy 2021, 46, 6960–6969. [Google Scholar] [CrossRef]
- Huang, S.; Ma, D.; Sheng, J.; Agyenim-Boateng, E.; Zhao, J.; Zhou, J. Effects of laser peening on tensile properties and martensitic transformation of AISI 316L stainless steel in a hydrogen-rich environment. Mater. Sci. Eng. A 2020, 788, 139543. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Park, J.; Nahm, S.H.; Baek, U.B. An experimental study for qualifying hydrogen compatibility of austenitic stainless steel under low temperature. J. Mech. Sci. Technol. 2022, 36, 157–165. [Google Scholar] [CrossRef]
- Toribio, J.; González, B.; Matos, J.C. Notch tip hydrogen diffusion assisted by stress and strain fields and its role in hydrogen assisted fracture. Procedia Struct. Integr. 2024, 59, 145–150. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, H.; Liu, C.; Wang, C.; Fan, X.; Cheng, Y.F.; Li, Y. Effects of defect on the hydrogen embrittlement behavior of X80 pipeline steel in hydrogen-blended natural gas environments. Int. J. Hydrogen Energy 2024, 58, 158–173. [Google Scholar] [CrossRef]
- Oh, D.K.; Kim, S.G.; Shin, S.H.; Hwang, B. Hydrogen Embrittlement Behavior of API X70 Linepipe Steel under Ex Situ and In Situ Hydrogen Charging. Materials 2024, 17, 4887. [Google Scholar] [CrossRef]
- Schmiedt-Kalenborn, A.; Lingnau, L.A.; Manka, M.; Tillmann, W.; Walther, F. Fatigue and Corrosion Fatigue Behaviour of Brazed Stainless Steel Joints AISI 304L/BAu-4 in Synthetic Exhaust Gas Condensate. Materials 2019, 12, 1040. [Google Scholar] [CrossRef]
- Dan, W.J.; Shi, H.; Tang, C.W.; Wang, X.Y. Effects of Electrochemical Hydrogen Charging Parameters on the Mechanical Behaviors of High-Strength Steel. Materials 2024, 17, 4290. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Huang, S.; Sheng, J.; Agyenim-Boateng, E.; Jiang, Y.; Liu, Q.; Zhu, M. Improvement of hydrogen embrittlement resistance of 2205 duplex stainless steel by laser peening. Int. J. Hydrogen Energy 2023, 48, 18930–18945. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Z.; Xu, X.; Li, Y.; Du, C.; Liu, X. Interaction between hydrogen and cyclic stress and its role in fatigue damage mechanism. Corros. Sci. 2019, 157, 146–156. [Google Scholar] [CrossRef]
- Yuan, S.; Zhu, Y.; Huang, M.; Zhao, L.; Liang, S.; Li, Z. A coupled diffusional-mechanical model accounting for hydrogen enhancements of strain-induced dislocations and vacancies. Mech. Mater. 2023, 186, 104781. [Google Scholar] [CrossRef]
- Arniella, V.; Álvarez, G.; Belzunce, J.; Rodríguez, C. Hydrogen embrittlement of 2205 duplex stainless steel in in-situ tensile tests. Theor. Appl. Fratc. Mec. 2023, 124, 103794. [Google Scholar] [CrossRef]
- Yang, X.; Sun, F.; Li, Q.; Zhu, R.; Liu, Z.; Du, C.; Li, X. Effect of Hydrogen Charging on the Stress Corrosion Cracking Behavior of X70 Steel in Simulated Deep Seawater Environment. Metals 2022, 12, 334. [Google Scholar] [CrossRef]
- Zhang, S.; An, T.; Zheng, S.; Li, J.; Li, S.; Chen, L. The effects of double notches on the mechanical properties of a high-strength pipeline steel under hydrogen atmosphere. Int. J. Hydrogen Energy 2020, 45, 23134–23141. [Google Scholar] [CrossRef]
- Lin, M.; Yu, H.; Wang, D.; Díaz, A.; Alvaro, A.; Olden, V.; Koren, E.; Ding, Y.; He, J.; Zhang, Z. Experimental and numerical study on hydrogen-induced failure of X65 pipeline steel. Mater. Sci. Eng. A. 2024, 894, 146175. [Google Scholar] [CrossRef]
- Shibata, A.; Yonemura, T.; Momotani, Y.; Park, M.-h.; Takagi, S.; Madi, Y.; Besson, J.; Tsuji, N. Effects of local stress, strain, and hydrogen content on hydrogen-related fracture behavior in low-carbon martensitic steel. Acta Mater. 2021, 210, 116828. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Z.; Hu, S.; Du, C.; Li, X. Effect of Hydrogen Charging on the Stress Corrosion Behavior of 2205 Duplex Stainless Steel Under 3.5 wt.% NaCl Thin Electrolyte Layer. J. Mater. Eng. Perform. 2017, 26, 2837–2846. [Google Scholar] [CrossRef]
- Weihrauch, M.; Patel, M.; Patterson, E.A. Measurements and predictions of diffusible hydrogen escape and absorption in catholically charged 316LN austenitic stainless steel. Sci. Rep. 2023, 13, 10545. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Tian, H.; Wang, Z.; He, K.; Wang, Y.; Zhang, Q.; Liu, D.; Cui, Z. Effect of Electrochemical Hydrogen Charging on Blistering and Mechanical Properties Behavior of Q690 Steel. Crystals 2023, 13, 918. [Google Scholar] [CrossRef]
- Shi, K.; Xiao, S.; Ruan, Q.; Wu, H.; Chen, G.; Zhou, C.; Jiang, S.; Xi, K.; He, M.; Chu, P.K. Hydrogen permeation behavior and mechanism of multi-layered graphene coatings and mitigation of hydrogen embrittlement of pipe steel. Appl. Surf. Sci. 2022, 573, 151529. [Google Scholar] [CrossRef]
- Christ, M.; Reisgen, U.; Sharma, R.; Mäde, K.; Angerhausen, M. Model description of hydrogen-induced damage evolution in high-strength steel weld metal based on results of a novel test method. Mater. Sci. Eng. A 2022, 840, 142905. [Google Scholar] [CrossRef]
- Yoo, J.; Jo, Y.; Lee, J.-J.; Kim, K.-W.; Lee, C.-H.; Kim, J.; Jung, S.-P.; Park, Y.-C.; Park, H. Microstructural aspect of hydrogen embrittlement in sheared edge of Zn-coated advanced high-strength steels. J. Mater. Res. Technol. 2025, 35, 5230–5241. [Google Scholar] [CrossRef]
- Qu, J.; Feng, M.; An, T.; Bi, Z.; Du, J.; Yang, F.; Zheng, S. Hydrogen-Assisted Crack Growth in the Heat-Affected Zone of X80 Steels during in Situ Hydrogen Charging. Materials 2019, 12, 2575. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J.; Liao, Z.; Yu, J.; Wang, R.; Sun, Y.; Yang, G. Hydrogen-Induced Ductility Loss of GH625 Superalloy Under Thermal Hydrogen Charging. Materials 2025, 18, 526. [Google Scholar] [CrossRef]
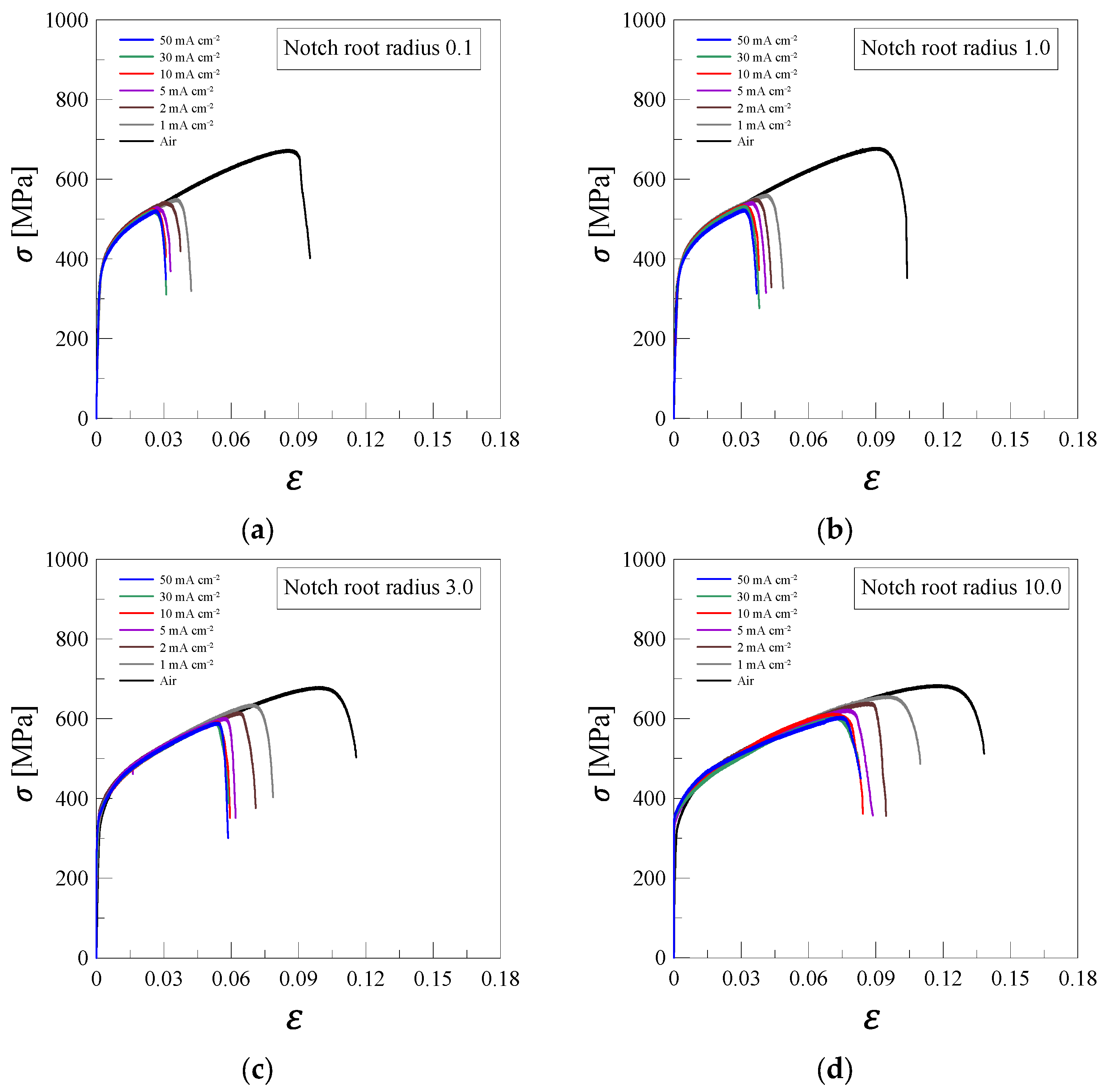



| Alloys | C | Si | Mn | P | S | Ni | Cr | Mo |
|---|---|---|---|---|---|---|---|---|
| Type 316L | 0.023 | 0.51 | 0.93 | 0.041 | 0.003 | 10.09 | 16.94 | 2.02 |
| Notch Root Radius | Current Density [ma cm−2] | [N] | [MPa] | [mm] | |
|---|---|---|---|---|---|
| 0.1 | 0 | 10,794 ± 55 | 675 ± 3 | 4.26 ± 0.11 | 0.095 ± 0.0030 |
| 1 | 8818 ± 83 | 551 ± 5 | 1.78 ± 0.08 | 0.042 ± 0.0006 | |
| 2 | 8699 ± 65 | 544 ± 4 | 1.52 ± 0.02 | 0.037 ± 0.0013 | |
| 5 | 8481 ± 74 | 530 ± 4 | 1.34 ± 0.03 | 0.033 ± 0.0014 | |
| 10 | 8403 ± 84 | 525 ± 5 | 1.25 ± 0.08 | 0.031 ± 0.0018 | |
| 30 | 8363 ± 70 | 523 ± 4 | 1.25 ± 0.06 | 0.031 ± 0.0015 | |
| 50 | 8358 ± 68 | 522 ± 4 | 1.25 ± 0.05 | 0.031 ± 0.0005 | |
| 1.0 | 0 | 10,870 ± 49 | 679 ± 3 | 4.50 ± 0.11 | 0.104 ± 0.0018 |
| 1 | 8992 ± 63 | 562 ± 4 | 2.06 ± 0.08 | 0.049 ± 0.0012 | |
| 2 | 8816 ± 65 | 551 ± 4 | 1.84 ± 0.06 | 0.043 ± 0.0015 | |
| 5 | 8688 ± 62 | 543 ± 4 | 1.73 ± 0.07 | 0.041 ± 0.0015 | |
| 10 | 8566 ± 63 | 535 ± 4 | 1.55 ± 0.08 | 0.038 ± 0.0013 | |
| 30 | 8527 ± 70 | 533 ± 4 | 1.55 ± 0.07 | 0.039 ± 0.0014 | |
| 50 | 8396 ± 72 | 530 ± 5 | 1.56 ± 0.06 | 0.038 ± 0.0014 | |
| 3.0 | 0 | 10,880 ± 63 | 680 ± 4 | 4.99 ± 0.14 | 0.116 ± 0.0030 |
| 1 | 10,178 ± 68 | 636 ± 4 | 3.47 ± 0.09 | 0.079 ± 0.0024 | |
| 2 | 9865 ± 74 | 617 ± 5 | 3.16 ± 0.10 | 0.071 ± 0.0021 | |
| 5 | 9634 ± 77 | 602 ± 5 | 2.85 ± 0.09 | 0.062 ± 0.0023 | |
| 10 | 9487 ± 78 | 593 ± 5 | 2.69 ± 0.10 | 0.059 ± 0.0023 | |
| 30 | 9451 ± 91 | 591 ± 6 | 2.68 ± 0.09 | 0.061 ± 0.0022 | |
| 50 | 9452 ± 77 | 591 ± 5 | 2.70 ± 0.08 | 0.060 ± 0.0023 | |
| 10.0 | 0 | 10,952 ± 70 | 684 ± 4 | 5.82 ± 0.12 | 0.138 ± 0.0035 |
| 1 | 10,510 ± 80 | 657 ± 5 | 4.78 ± 0.15 | 0.110 ± 0.0033 | |
| 2 | 10,246 ± 82 | 640 ± 5 | 4.26 ± 0.11 | 0.095 ± 0.0018 | |
| 5 | 9965 ± 92 | 623 ± 6 | 3.86 ± 0.12 | 0.089 ± 0.0019 | |
| 10 | 9810 ± 81 | 613 ± 5 | 3.55 ± 0.09 | 0.084 ± 0.0035 | |
| 30 | 9740 ± 80 | 609 ± 5 | 3.54 ± 0.08 | 0.082 ± 0.0027 | |
| 50 | 9762 ± 87 | 612 ± 5 | 3.55 ± 0.08 | 0.083 ± 0.0015 |
| Notch Root Radius | RNTS | REL | ||||
|---|---|---|---|---|---|---|
| m | n | R2 | m | n | R2 | |
| 0.1 | 78.06 | −0.021 | 0.93 | 49.16 | −0.143 | 0.80 |
| 1.0 | 84.60 | −0.035 | 0.85 | 64.49 | −0.209 | 0.77 |
| 3.0 | 94.53 | −0.033 | 0.96 | 79.03 | −0.182 | 0.85 |
| 10.0 | 95.60 | −0.034 | 0.88 | 82.99 | −0.143 | 0.83 |
| Sample | Total Hydrogen Concentration [10−7 mol cm−3] | |||||
|---|---|---|---|---|---|---|
| 1 mA cm−2 | 2 mA cm−2 | 5 mA cm−2 | 10 mA cm−2 | 30 mA cm−2 | 50 mA cm−2 | |
| 1 | 0.844 | 0.920 | 1.112 | 1.200 | 1.268 | 1.280 |
| 2 | 0.856 | 0.929 | 1.110 | 1.201 | 1.256 | 1.276 |
| 3 | 0.857 | 0.915 | 1.099 | 1.199 | 1.273 | 1.294 |
| Average | 0.853 | 0.921 | 1.107 | 1.200 | 1.266 | 1.283 |
| Standard deviation | 0.006 | 0.006 | 0.006 | 0.001 | 0.007 | 0.008 |
| Notch Root Radius | ||||||
|---|---|---|---|---|---|---|
| m | n | R2 | m | n | R2 | |
| 0.1 | 538.58 | −0.131 | 0.99 | 0.0363 | −0.737 | 0.95 |
| 1.0 | 548.39 | −0.132 | 0.97 | 0.0431 | −0.570 | 0.91 |
| 3.0 | 613.77 | −0.17 | 0.95 | 0.0687 | −0.540 | 0.93 |
| 10.0 | 635.11 | −0.177 | 0.98 | 0.095 | −0.598 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, B.-K.; Cha, S.-J.; Kim, H.-T.; Lee, S.-J.; Kim, J.-H.; Lee, J.-M. Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics. Materials 2025, 18, 1274. https://doi.org/10.3390/ma18061274
Hwang B-K, Cha S-J, Kim H-T, Lee S-J, Kim J-H, Lee J-M. Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics. Materials. 2025; 18(6):1274. https://doi.org/10.3390/ma18061274
Chicago/Turabian StyleHwang, Byeong-Kwan, Seung-Joo Cha, Hee-Tae Kim, Seung-Jun Lee, Jeong-Hyeon Kim, and Jae-Myung Lee. 2025. "Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics" Materials 18, no. 6: 1274. https://doi.org/10.3390/ma18061274
APA StyleHwang, B.-K., Cha, S.-J., Kim, H.-T., Lee, S.-J., Kim, J.-H., & Lee, J.-M. (2025). Notch Sensitivity of Hydrogen-Charged 316L Stainless Steel: Experimental Insights into Mechanical Degradation and Fracture Mechanics. Materials, 18(6), 1274. https://doi.org/10.3390/ma18061274







