Relationship Between Schmidt Hammer Rebound Hardness Test and Concrete Strength Tests for Limestone Aggregate Concrete Based on Experimental and Statistical Study
Abstract
:1. Introduction
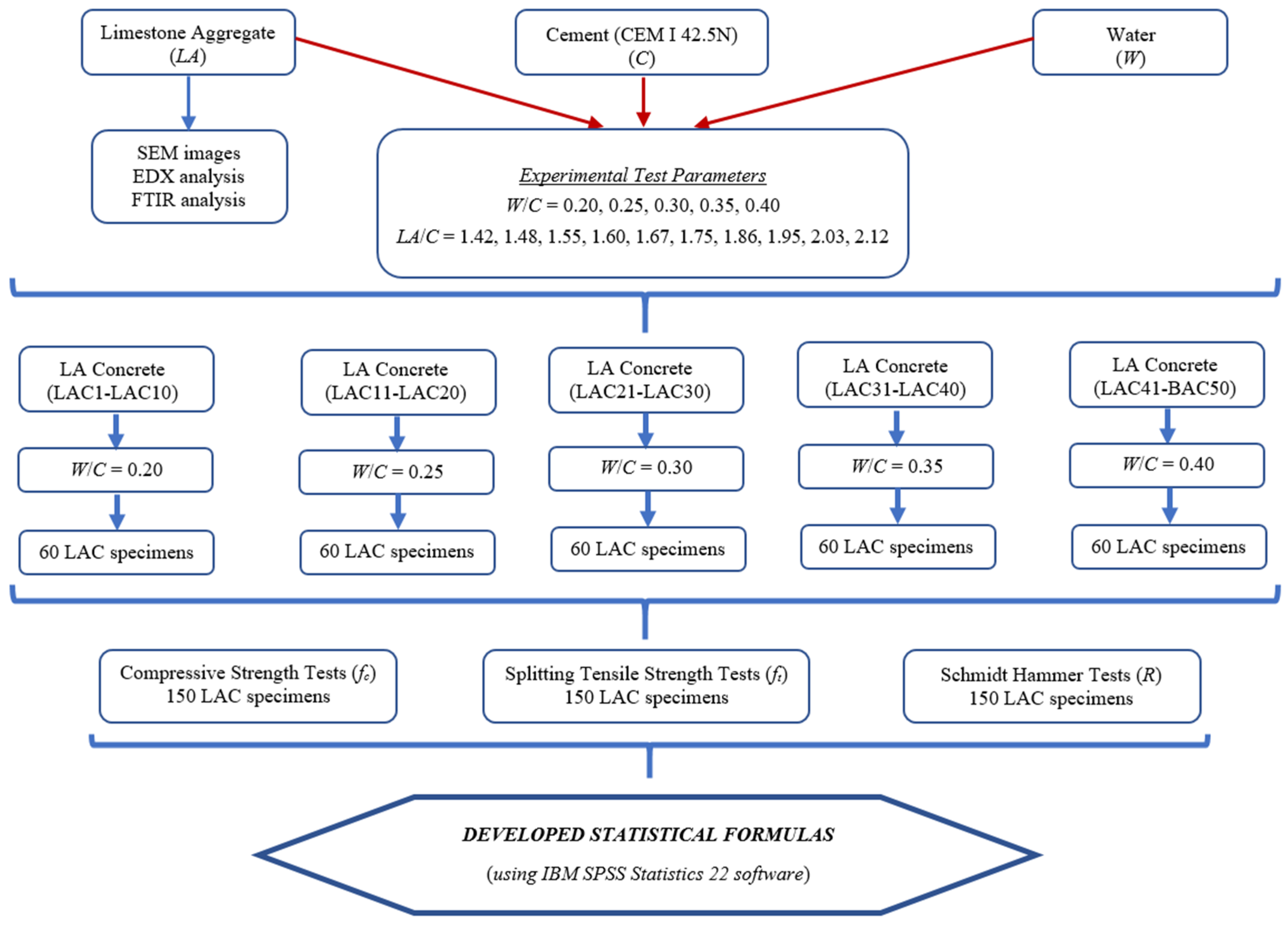
2. Materials and Methods
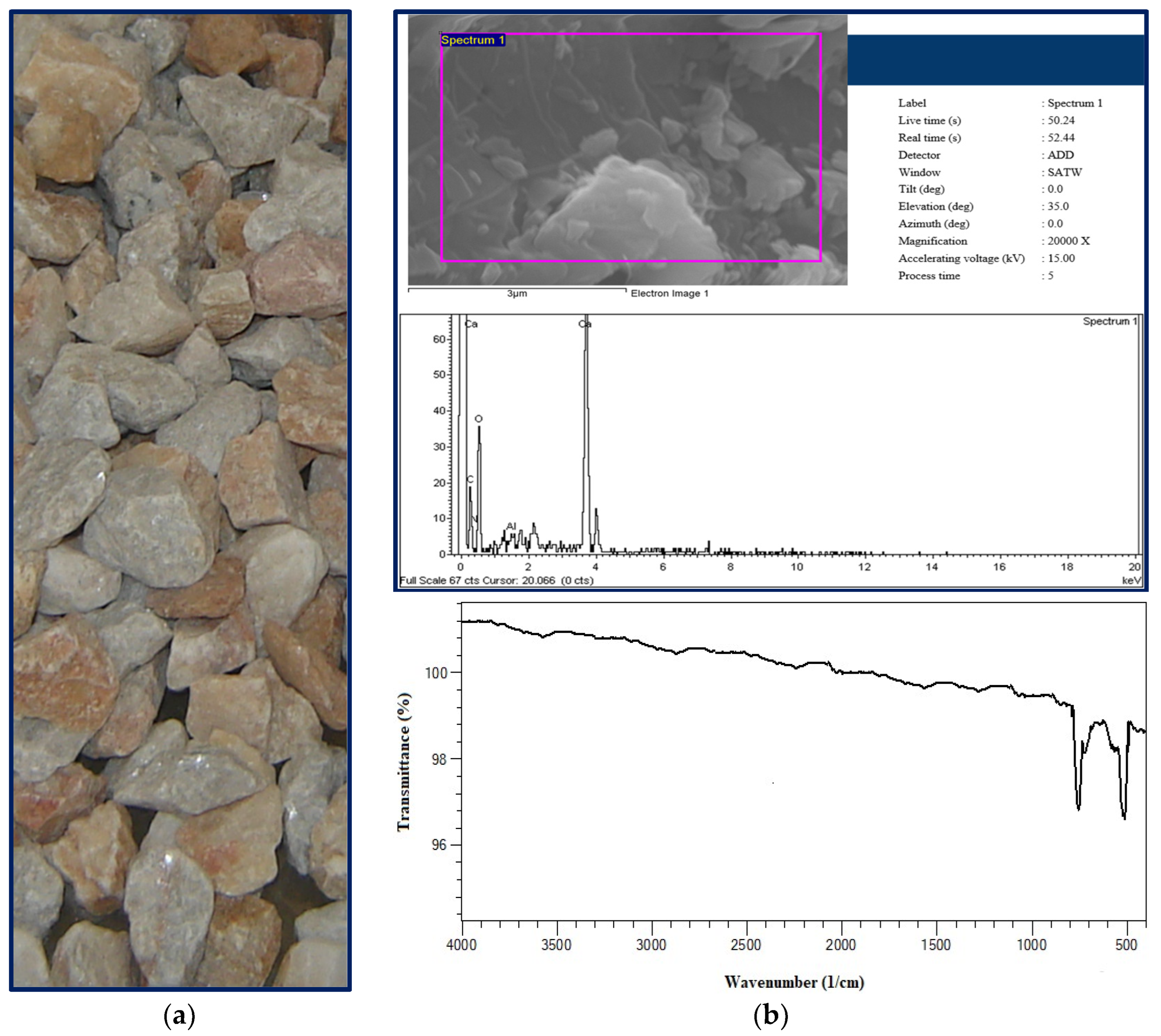
2.1. Materials
2.2. Experimental Method
2.2.1. Concrete Compressive Strength Test
2.2.2. Concrete Splitting Tensile Strength Test
2.2.3. Schmidt Hammer Rebound Hardness Test
2.3. Statistical Analysis
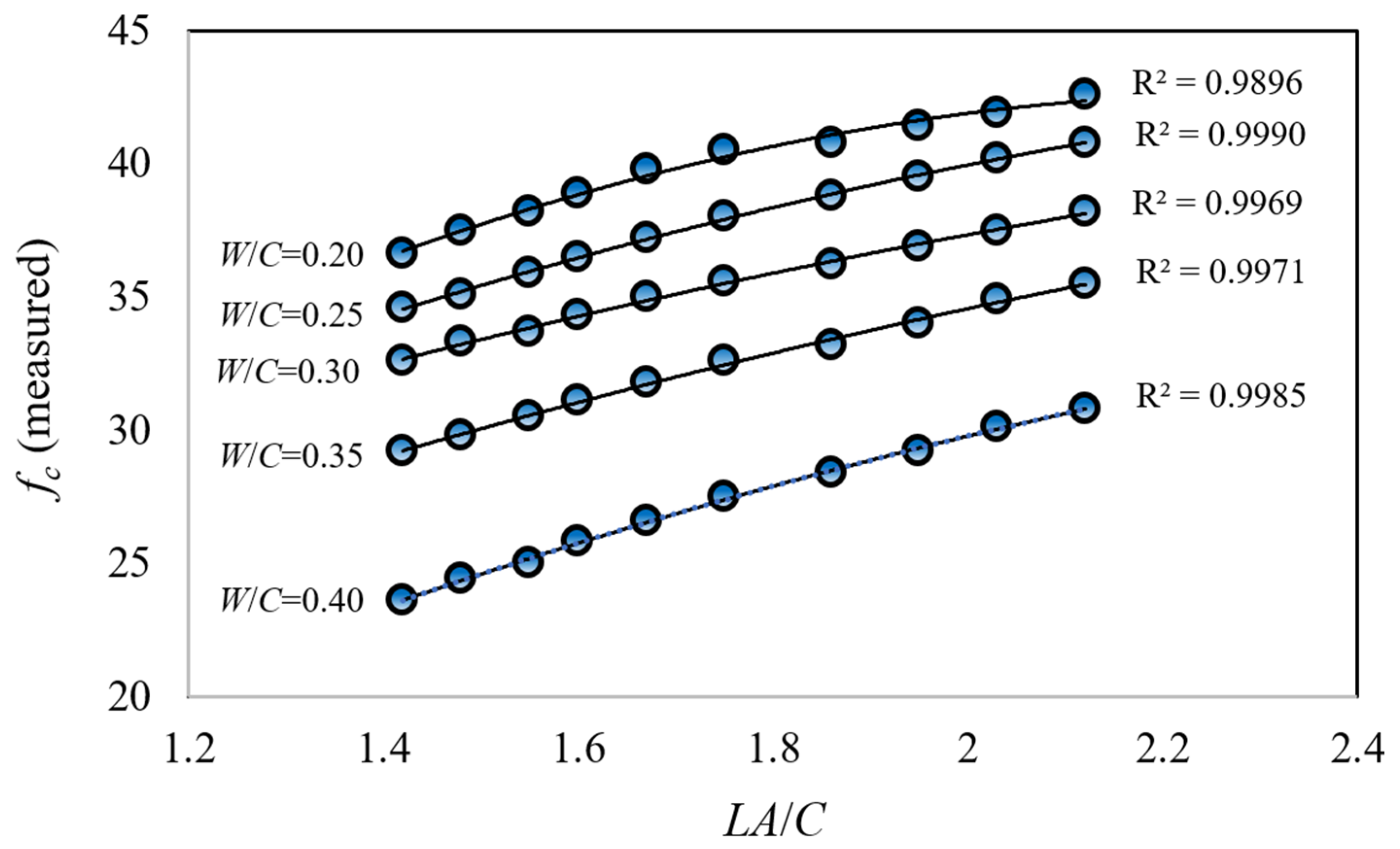
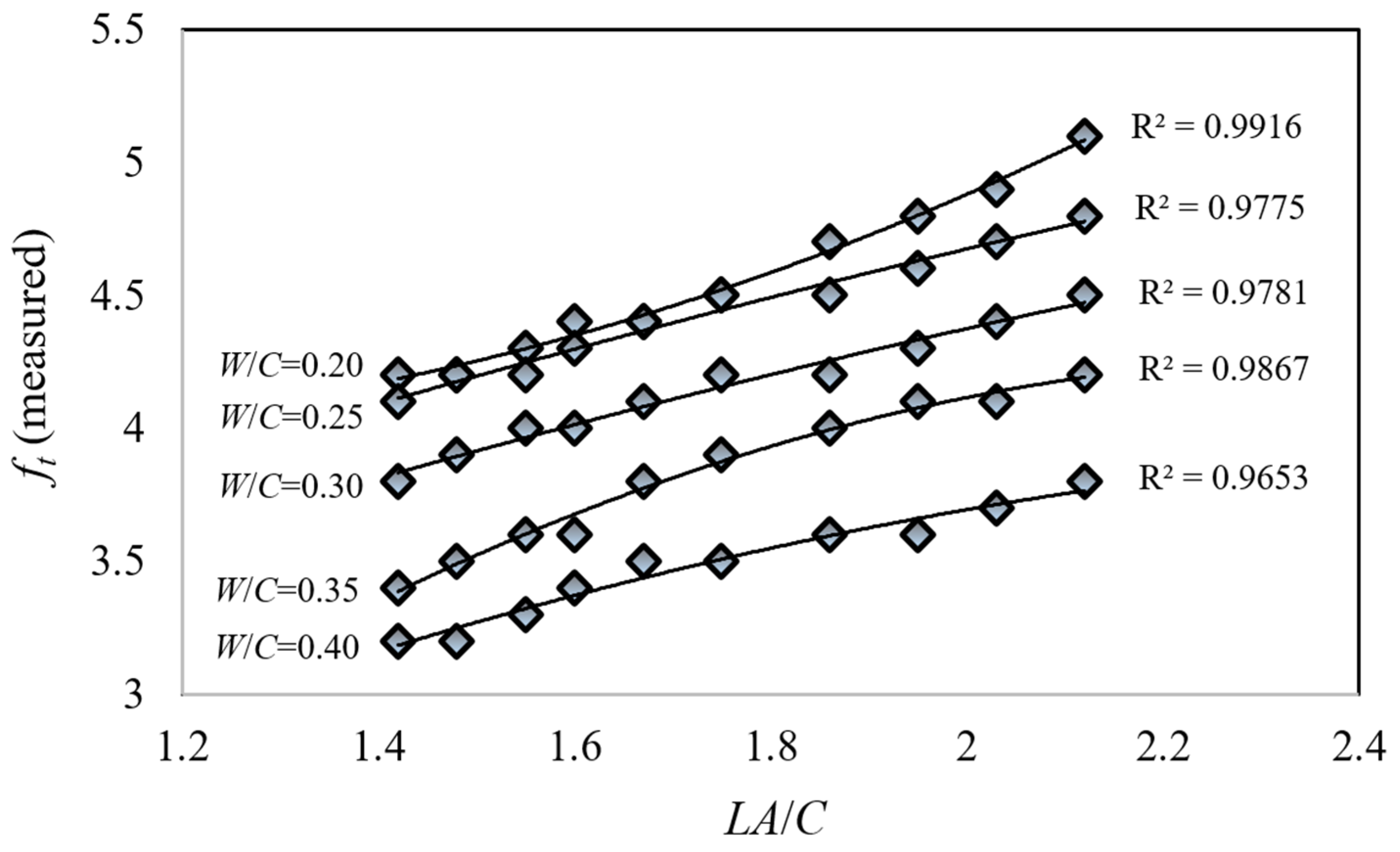
3. Experimental Results
4. Statistical Analysis Results
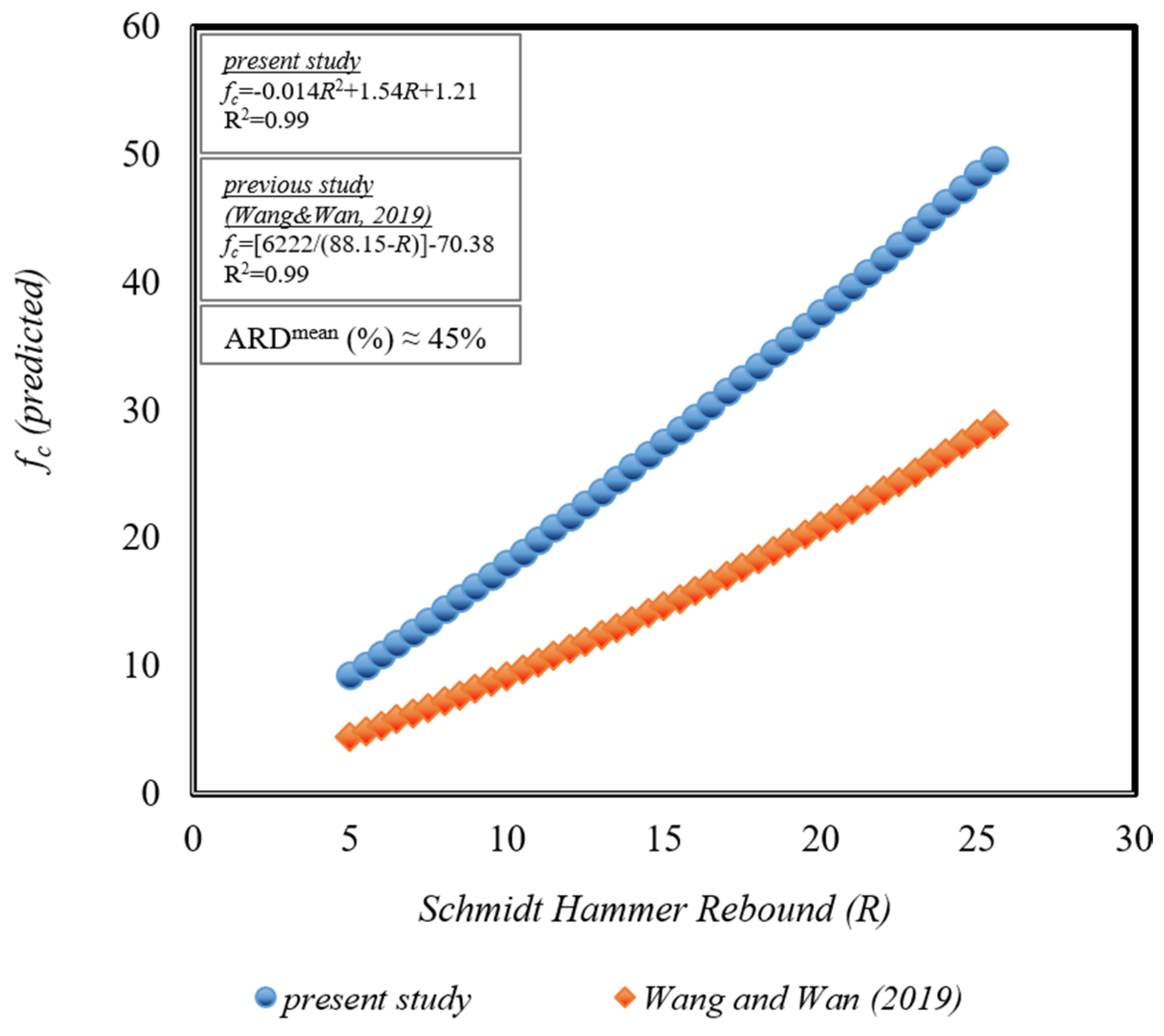
5. Discussion of Statistical Methods Developed from Previous Study from the Literature and Present Study
6. Conclusions
- An investigation revealed that increasing the water-to-cement ratio (W/C) from 0.20 to 0.40 resulted in a mean reduction of approximately 31.8% in concrete compressive strength (fc) and a mean reduction of approximately 23.5% in concrete splitting tensile strength (ft). These findings underscore the significant influence of the water-to-cement ratio on concrete strength development.
- Variations in Schmidt hammer rebound values, ranging from R = 18 N to 43 N, correlated with changes in the compressive strength (fc) of limestone aggregate concrete within the range of from 23.6 MPa to 42.6 MPa. Concurrently, the splitting tensile strength (ft) of the concrete specimens exhibited variations within the range of from 3.2 MPa to 5.1 MPa.
- An approximately 2.4-fold increase in Schmidt hammer rebound (R) values was observed, corresponding to an approximately 1.8-fold increase in compressive strength (fc) and an approximately 1.6-fold increase in splitting tensile strength (ft).
- A strong correlation was observed between compressive strength (fc) and Schmidt hammer rebound (R) values, as evidenced by a coefficient of determination (R2) of approximately 0.99. Similarly, a strong correlation was found between splitting tensile strength (ft) and R values, with an R2 of approximately 0.96.
- This study aims to develop an empirical formulation for predicting concrete strength based on Schmidt hammer rebound (R) values, applicable to both fresh concrete production and existing structural concrete assessment.
- The high-accuracy empirical formulas developed in this study, for predicting concrete compressive strength and splitting tensile strength based on Schmidt hammer rebound (R) values, offer a novel contribution and demonstrate the potential impact of this research on the existing literature.
- This study employed an experimental and statistical approach, comparing the results of destructive concrete tests with those obtained from the non-destructive Schmidt hammer rebound test. It is recommended that future research expand upon this work by incorporating multiple non-destructive testing methodologies.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koc, A.B.; Erberik, M.A.; Askan, A.; Karimzadeh, S. The Sensitivity of Global Structural Parameters for Unreinforced Masonry Buildings Subjected to Simulated Ground Motions. Buildings 2023, 13, 2060. [Google Scholar] [CrossRef]
- Sayın, E.; Yön, B.; Onat, O.; Gör, M.; Öncü, M.E.; Tunç, E.T.; Bakır, D.; Karaton, M.; Calayır, Y. 24 January 2020 Sivrice-Elazığ, Turkey earthquake: Geotechnical evaluation and performance of structures. Bull. Earthq. Eng. 2021, 19, 657–684. [Google Scholar] [CrossRef]
- Eslamlou, A.D.; Ghaderiaram, A.; Schlangen, E.; Fotouhi, M. A review on non-destructive evaluation of construction materials and structures using magnetic sensors. Constr. Build. Mater. 2023, 397, 132460. [Google Scholar] [CrossRef]
- Tešić, K.; Baričević, A.; Serdar, M. Non-destructive corrosion inspection of reinforced concrete using ground-penetrating radar: A review. Materials 2021, 14, 975. [Google Scholar] [CrossRef]
- Hafiz, A.; Schumacher, T.; Raad, A. A self-referencing non-destructive test method to detect damage in reinforced concrete bridge decks using nonlinear vibration response characteristics. Constr. Build. Mater. 2022, 318, 125924. [Google Scholar] [CrossRef]
- Schabowicz, K. Non-destructive testing of materials in civil engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef] [PubMed]
- Keshmiry, A.; Hassani, S.; Mousavi, M.; Dackermann, U. Effects of environmental and operational conditions on structural health monitoring and non-destructive testing: A systematic review. Buildings 2023, 13, 918. [Google Scholar] [CrossRef]
- Wang, J.; Xia, Y.; Zhang, C.; Wang, C.; Xue, B.; Sun, R.; Pan, Y.; Chen, J.; Li, P.; Shi, M.; et al. Evaluation of compressive strength of concrete durability degradation in dry and wet environments using destructive and non-destructive testing. Measurement 2023, 223, 113702. [Google Scholar] [CrossRef]
- Saint-Pierre, F.; Philibert, A.; Giroux, B.; Rivard, P. Concrete quality designation based on ultrasonic pulse velocity. Constr. Build. Mater. 2016, 125, 1022–1027. [Google Scholar] [CrossRef]
- Balayssac, J.P.; Garnier, V. (Eds.) Non-Destructive Testing and Evaluation of Civil Engineering Structures; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Silva, M.I.; Malitckii, E.; Santos, T.G.; Vilaça, P. Review of conventional and advanced non-destructive testing techniques for detection and characterization of small-scale defects. Prog. Mater. Sci. 2023, 138, 101155. [Google Scholar] [CrossRef]
- Gupta, M.; Khan, M.A.; Butola, R.; Singari, R.M. Advances in applications of Non-Destructive Testing (NDT): A review. Adv. Mater. Process. Technol. 2022, 8, 2286–2307. [Google Scholar] [CrossRef]
- Misokefalou, D.; Papoutsidakis, P.; Priniotakis, P. Non-destructive testing for quality control in automotive industry. Int. J. Eng. Appl. Sci. Technol. 2022, 7, 349–355. [Google Scholar] [CrossRef]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Hashim, K.; Yeboah, D. Recent advancements in non-destructive testing techniques for structural health monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Zarei, A.; Pilla, S. Laser ultrasonics for nondestructive testing of composite materials and structures: A review. Ultrasonics 2023, 136, 107163. [Google Scholar] [CrossRef] [PubMed]
- Hassani, S.; Dackermann, U. A systematic review of advanced sensor technologies for non-destructive testing and structural health monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Krentowski, J.R.; Knyziak, P.; Pawłowicz, J.A.; Gavardashvili, G. Historical masonry buildings’ condition assessment by non-destructive and destructive testing. Eng. Fail. Anal. 2023, 146, 107122. [Google Scholar] [CrossRef]
- Breysse, D. Nondestructive evaluation of concrete strength: An historical review and a new perspective by combining NDT methods. Constr. Build. Mater. 2012, 33, 139–163. [Google Scholar] [CrossRef]
- Selek, I.; Wijte, S.N.; Swinkels, M. Reliability of Non-destructive Testing Methods by Detecting the Presence of Reinforcement in Existing Concrete Structures. In High Tech Concrete: Where Technology and Engineering Meet: Proceedings of the 2017 fib Symposium, Held in Maastricht, The Netherlands, June 12–14, 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 1858–1866. [Google Scholar] [CrossRef]
- Gdoutos, E.; Konsta-Gdoutos, M. Nondestructive Testing (NDT). Mechanical Testing of Materials 201–225; Springer Nature: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Breysse, D.; Elachachi, S.M.; Balayssac, J.P.; Laurens, S. Méthodologie de qualification des observables issus du contrôle non destructif pour diagnostiquer l’état du béton. Eur. J. Environ. Civ. Eng. 2008, 12, 459–472. [Google Scholar] [CrossRef]
- Hou, X.; Wang, N.; He, T.; Chen, C. Compressive stress-strain relationship of steam free reactive powder concrete at ultra-low temperatures. Cem. Concr. Compos. 2024, 152, 105655. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Li, C.; Yang, Q.; Jiang, J. Biaxial compressive failure criteria and constitutive model of high-strength geopolymer concrete after high temperature. Constr. Build. Mater. 2024, 426, 136165. [Google Scholar] [CrossRef]
- Jiang, N.; Ge, Z.; Wang, Z.; Gao, T.; Zhang, H.; Ling, Y.; Šavija, B. Size effect on compressive strength of foamed concrete: Experimental and numerical studies. Mater. Des. 2024, 240, 112841. [Google Scholar] [CrossRef]
- Díaz, E.; Salamanca-Medina, E.L.; Tomás, R. Assessment of compressive strength of jet grouting by machine learning. J. Rock Mech. Geotech. Eng. 2024, 16, 102–111. [Google Scholar] [CrossRef]
- Chu, Y.; Guo, L.-P.; Dai, G.-Z.; Wu, J.-D.; Lyu, B.-C.; Fei, X.-P.; Chen, H.-T.; Chen, B. Effects of the early curing regime on the properties and pore structure of concrete in an environment with high altitudes and low atmospheric pressures. J. Build. Eng. 2024, 82, 108195. [Google Scholar] [CrossRef]
- Prem, P.R.; Bharatkumar, B.H.; Iyer, N.R. Influence of curing regimes on compressive strength of ultra high performance concrete. Sadhana 2013, 38, 1421–1431. [Google Scholar] [CrossRef]
- Ozcelikci, E.; Kul, A.; Gunal, M.F.; Ozel, B.F.; Yildirim, G.; Ashour, A.; Sahmaran, M. A comprehensive study on the compressive strength, durability-related parameters and microstructure of geopolymer mortars based on mixed construction and demolition waste. J. Clean. Prod. 2023, 396, 136522. [Google Scholar] [CrossRef]
- Piro, N.S.; Mohammed, A.S.; Hamad, S.M. Electrical resistivity measurement, piezoresistivity behavior and compressive strength of concrete: A comprehensive review. Mater. Today Commun. 2023, 36, 106573. [Google Scholar] [CrossRef]
- Tugrul Tunc, E. An experimental study based on the strength properties of concrete containing chemical admixture. Eur. J. Sci. Technol. 2019, 17, 901–908. [Google Scholar] [CrossRef]
- Bensaber, A.; Boudaoud, Z.; Seghir, N.T.; Czarnecki, S.; Sadowski, Ł. The assessment of concrete subjected to compressive and flexural preloading using nondestructive testing methods, correlation between concrete strength and combined method (SonReb). Measurement 2023, 222, 113659. [Google Scholar] [CrossRef]
- Badarloo, B.; Lehner, P. Practical Aspects of Correlation Analysis of Compressive Strength from Destructive and Non-Destructive Methods in Different Directions. Infrastructures 2023, 8, 155. [Google Scholar] [CrossRef]
- Waqar, M.; Memon, A.M.; Sabih, M.; AlHems, L.M. Composite pipelines: Analyzing defects and advancements in non-destructive testing techniques. Eng. Fail. Anal. 2023, 157, 107914. [Google Scholar] [CrossRef]
- Malhotra, V.M.; Carino, N.J. Handbook on Nondestructive Testing of Concrete; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Schmidt, E. A Non-Destructive Concrete Tester. Concrete 1951, 59, 34–35. [Google Scholar]
- Katman, H.Y.B.; Khai, W.J.; Kırgız, M.S.; Nehdi, M.L.; Benjeddou, O.; Thomas, B.S.; Papatzani, S.; Rambhad, K.; Kumbhalkar, M.A.; Karimipour, A. Transforming conventional construction binders and grouts into high-performance nanocarbon binders and grouts for today’s constructions. Buildings 2022, 12, 1041. [Google Scholar] [CrossRef]
- Kırgız, M.S. Fresh and hardened properties of green binder concrete containing marble powder and brick powder. Eur. J. Environ. Civ. Eng. 2016, 20, 64–101. [Google Scholar] [CrossRef]
- İlhan, İ. Beton (Schmidt) çekici ne işe yarar. TMH Türkiye Mühendislik Haberleri Derg. 2000, 6, 27–29. (In Turkish) [Google Scholar]
- Mutlu, E. Kalıp ve başlıklama tipinin beton basınç dayanımına ve tahribatsız yöntemlerle dayanım tahmini üzerine etkisi. Master’s Thesis, Kocaeli Üniversitesi, Fen Bilimleri Enstitüsü, Kabaoğlu, Türkiye, 2019. (In Turkish). [Google Scholar]
- Kong, F.; Xue, Y.; Shang, J.; Zhu, C.; Han, M.; Qu, Z.; Wang, B.; Yang, K. Predicting uniaxial compressive strength of building stone based on index tests: Correlations, validity, reliability, and unification. Constr. Build. Mater. 2024, 438, 137227. [Google Scholar] [CrossRef]
- Rucka, M. Non-destructive testing of structures. Materials 2020, 13, 4996. [Google Scholar] [CrossRef]
- Işık, N.; Halifeoğlu, F.M.; Ipek, S. Nondestructive testing techniques to evaluate the structural damage of historical city walls. Constr. Build. Mater. 2020, 253, 119228. [Google Scholar] [CrossRef]
- Deer, D.U.; Miller, R. Engineering Classification and Index Properties for Intact Rock. Deformation Curve AFNL-TR; Air Force Weapons Lab., Kirtland Air Force Buse: New Mexico, NW, USA, 1966; pp. 65–116. [Google Scholar]
- Aufmuth, E.R. A systematic determination of engineering criteria for rocks. Bull. Assoc. Eng. Geol. 1973, 11, 235–245. [Google Scholar]
- Beverly, B.E.; Schoenwolf, D.A.; Brierly, G.S. Correlations of Rock Index Values with Engineering Properties and the Classification of Intact Rock; FHWA: Washington, DC, USA, 1979. [Google Scholar]
- ISRM. Suggested Methods for Determining Hardness and Abrasiveness of Rocks; ISRM: Lisbon, Portugal, 1981; Part 3, pp. 101–102. [Google Scholar]
- Sachpazis, C. Correlating Schmidt hardness with compressive strength and Young’s modulus of carbonate rocks. Bull. Eng. Geol. Environ. 1990, 42, 75–83. [Google Scholar] [CrossRef]
- Sheorey, P.; Barat, D.; Das, M.; Mukherjee, K.; Sigh, B. Schmidt hammer rebound data for estimation of large scale in situ coal strength. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1984, 1, 39–42. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Amin, M.F.M.; Yagiz, S.; Faradonbeh, R.S.; Abdullah, R.A. Prediction of the uniaxial compressive strength of sandstone using various modeling techniques. Int. J. Rock Mech. Min. Sci. 2016, 85, 174–186. [Google Scholar] [CrossRef]
- Fattahi, H. Applying soft computing methods to predict the uniaxial compressive strength of rock from schmidt hammer rebound values. Comput. Geosci. 2017, 21, 665–681. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W.; Zhao, Y. Prediction of the uniaxial compressive strength of rocks from simple index tests using a random forest predictive model. Comptes Rendus Mécanique 2020, 348, 3–32. [Google Scholar] [CrossRef]
- Davila, J.M.; Sarmiento, A.M.; Grande, J.A.; Luís, A.T. Different evolution of tensile and compressive strength in concrete affected by acid mine drainage. Constr. Build. Mater. 2023, 397, 132351. [Google Scholar] [CrossRef]
- Tugrul Tunc, E.; Alyamac, K.E.; Ince, R.; Ulucan, Z.C. Relationship between Reinforcement Diameter and Bond Stress in High Performance Lightweight Concrete. Eur. J. Sci. Technol. 2021, 23, 851–860. [Google Scholar] [CrossRef]
- De Hosson, J.T.M.; De Haas, M.; Teeuw, D.H.J. High resolution scanning electron microscopy observations of nano-ceramics. In Impact of Electron and Scanning Probe Microscopy on Materials Research; Springer: Dordrecht, The Netherlands, 1999; pp. 109–134. [Google Scholar] [CrossRef]
- Tugrul Tunc, E. An experimental investigation on the abrasion strength of aggregate: Elazığ province calcareous aggregate. Bitlis Eren Univ. J. Sci. Technol. 2018, 8, 75–80. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Wan, J.; Yi, Z. Study on microstructure and mechanical property of interfacial transition zone between limestone aggregate and Sialite paste. Constr. Build. Mater. 2009, 23, 3393–3397. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ardani, A.; Barrett, T.; Jones, S.Z.; Lootens, D.; Peltz, M.A.; Sato, T.; Stutzman, P.E.; Tanesi, J.; Weiss, W.J. Multi-scale investigation of the performance of limestone in concrete. Constr. Build. Mater. 2015, 75, 1–10. [Google Scholar] [CrossRef]
- TS EN 1008; Mixing Water Forconcrete—Specifications for Sampling, Testing and Assessing Thesuitability of Water, Including Water Recovered from Processesin the Concrete Industry, as Mixing Water for Concrete. Turkish Standards Institution: Ankara, Turkey, 2003.
- Tugrul Tunc, E.T. Effects of basalt aggregates on concrete properties. Qual. Stud. 2018, 13, 68–79. [Google Scholar] [CrossRef]
- ASTM C 192/C 192M-95; Standard Practice for Making and Curing Test Specimens in the Laboratory (1996) Annual Book of ASTM Standards. ASTM: West Conshohocken, PA, USA, 1996; Volume 04.02.
- TSEN 12390-3; Concrete-Hardened Concrete Tests-Part 3: Determination of Compressive Strength in Test Samples. Turkish Standards Institute: Ankara, Türkiye, 2003.
- TS EN 12390-6; Concrete-Hardened Concrete Tests-Part 3: Determination of Splitting Tensile Strength of Test Samples. Turkish Standards Institute: Ankara, Türkiye, 2010.
- TS EN 12504-2; Yapılarda Beton Deneyleri, Bölüm 2: Tahribatsız Deneyler-Geri Sıçrama Değerinin Tayini. Türk Standartları Enstitüsü: Ankara, Türkiye, 2004. (In Turkish)
- ASTM C805M; Standard Test Method for Rebound Number of Hardened Concrete. ASTM: West Conshohocken, PA, USA, 2003.
- Aydin, A. ISRM suggested method for determination of the schmidt hammer rebound hardness: Revised version. In The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 25–33. [Google Scholar] [CrossRef]
- Martireni, A.P. Comparative Analysis and Evaluation of the Conversion Formula for Rebound Number of Schmidt Hammer Test and Unconfined Compressive Strength Test–Case Study: Andesite Rock Slope in Graha Puspa, Lembang Fault. Rud.-Geološko-Naft. Zb. 2024, 39, 45–54. [Google Scholar] [CrossRef]
- Tugrul Tunc, E. Strength and Durability of Superplasticizer Concrete Based on Different Component Parameters: An Experimental and Statistical Study. Arab. J. Sci. Eng. 2024, 50, 1649–1664. [Google Scholar] [CrossRef]
- García-Avalos, E.M.; Gómez-Oliván, L.M.; Hernández-Navarro, M.D.; Saleem, M.H.; San Juan-Reyes, N.; Elizalde-Velázquez, G.A.; Rosales-Pérez, K.E. Dietary solutions for aluminum embryotoxicity: A study in Danio rerio using spirulina and okra-spirulina diets. Sci. Total Environ. 2024, 910, 168510. [Google Scholar] [CrossRef]
- Tugrul Tunc, E.; Alyamac, K.E. Determination of the relationship between the Los Angeles abrasion values of aggregates and concrete strength using the Response Surface Methodology. Constr. Build. Mater. 2020, 260, 119850. [Google Scholar] [CrossRef]
- Luo, X.; Xing, G.; Qiao, L.; Miao, P.; Yu, X.; Ma, K. Multi-objective optimization of the mix proportion for dune sand concrete based on response surface methodology. Constr. Build. Mater. 2023, 366, 129928. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W. A new empirical formula for evaluating uniaxial compressive strength using the Schmidt hammer test. Int. J. Rock Mech. Min. Sci. 2019, 123, 104094. [Google Scholar] [CrossRef]

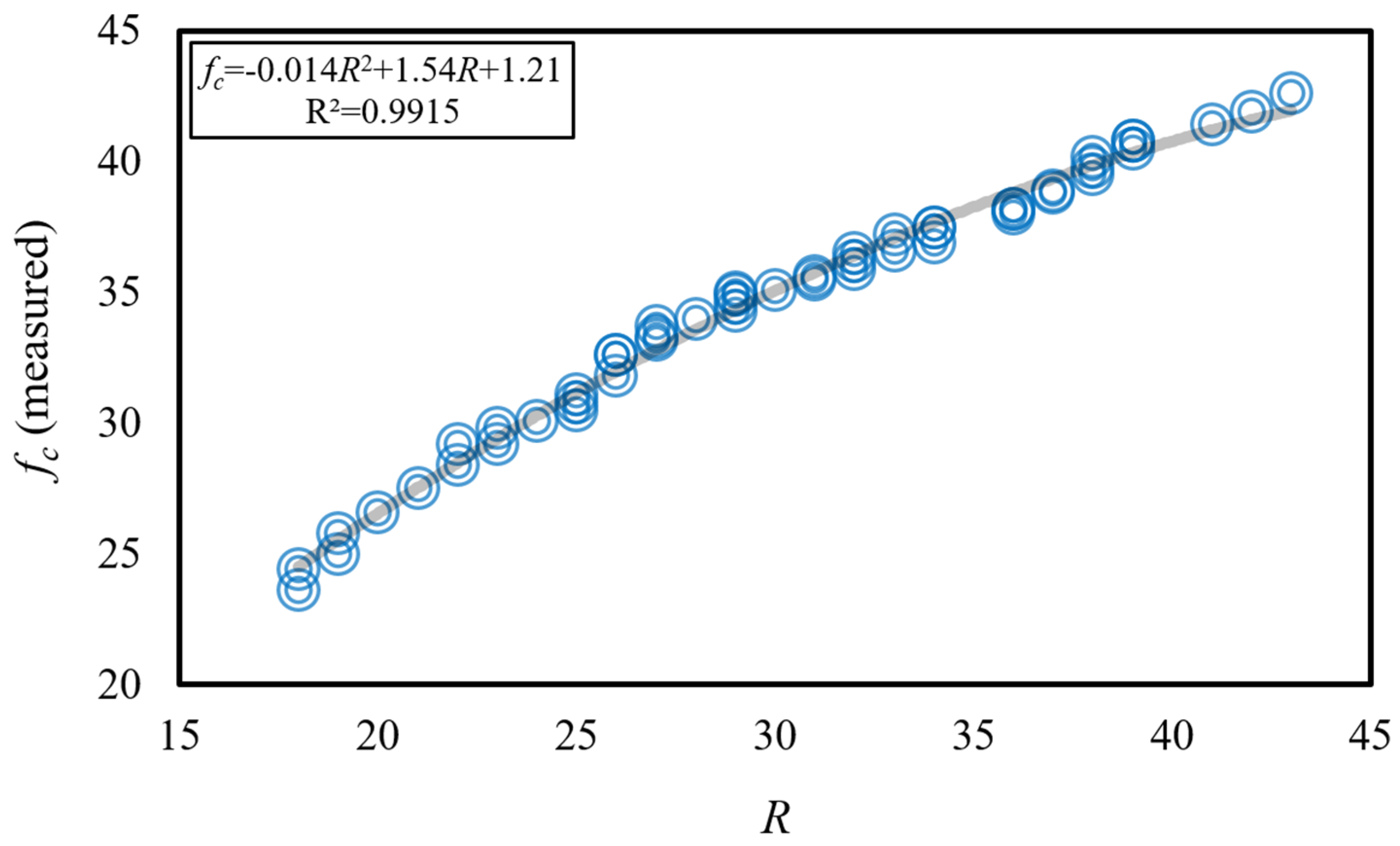
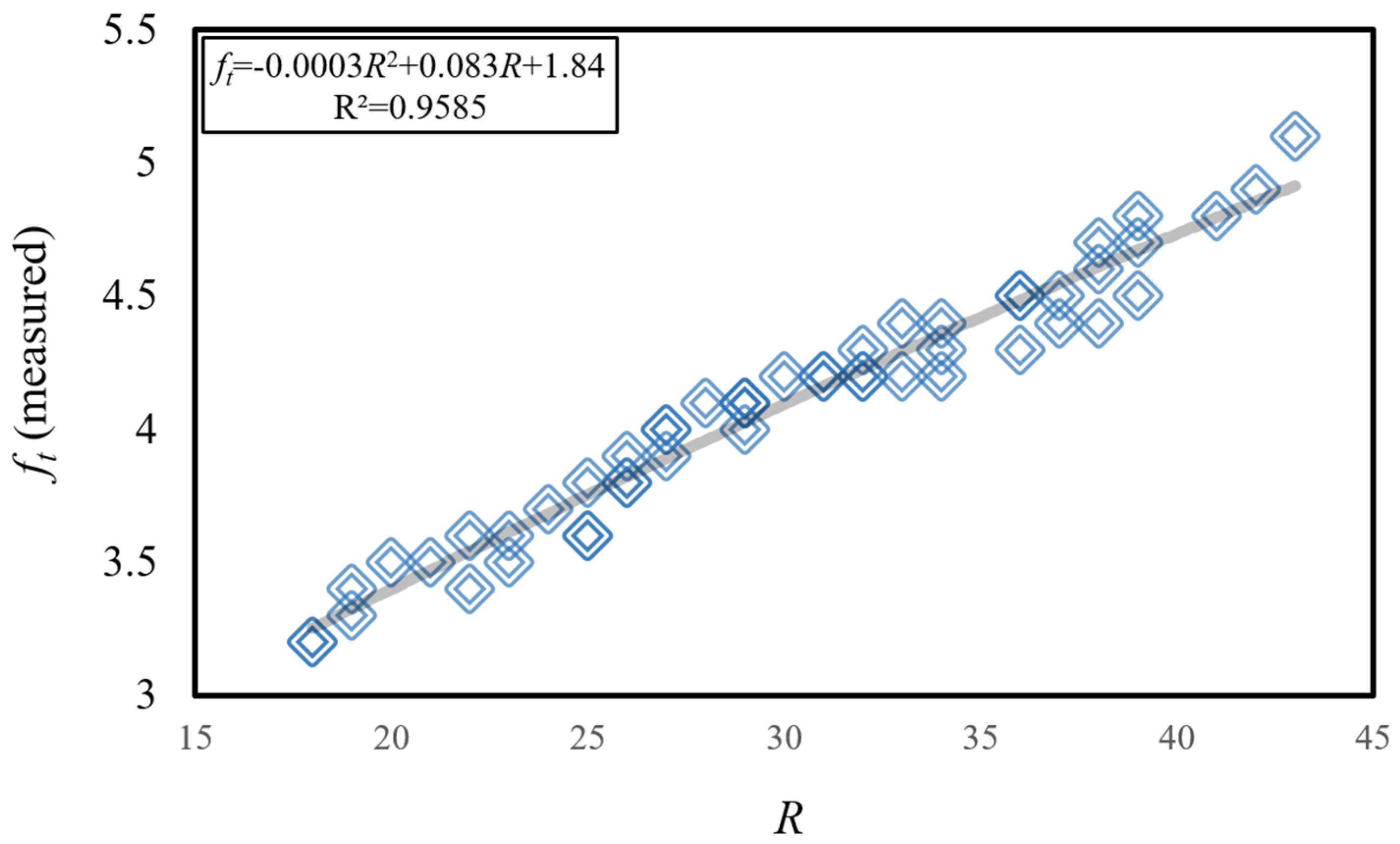
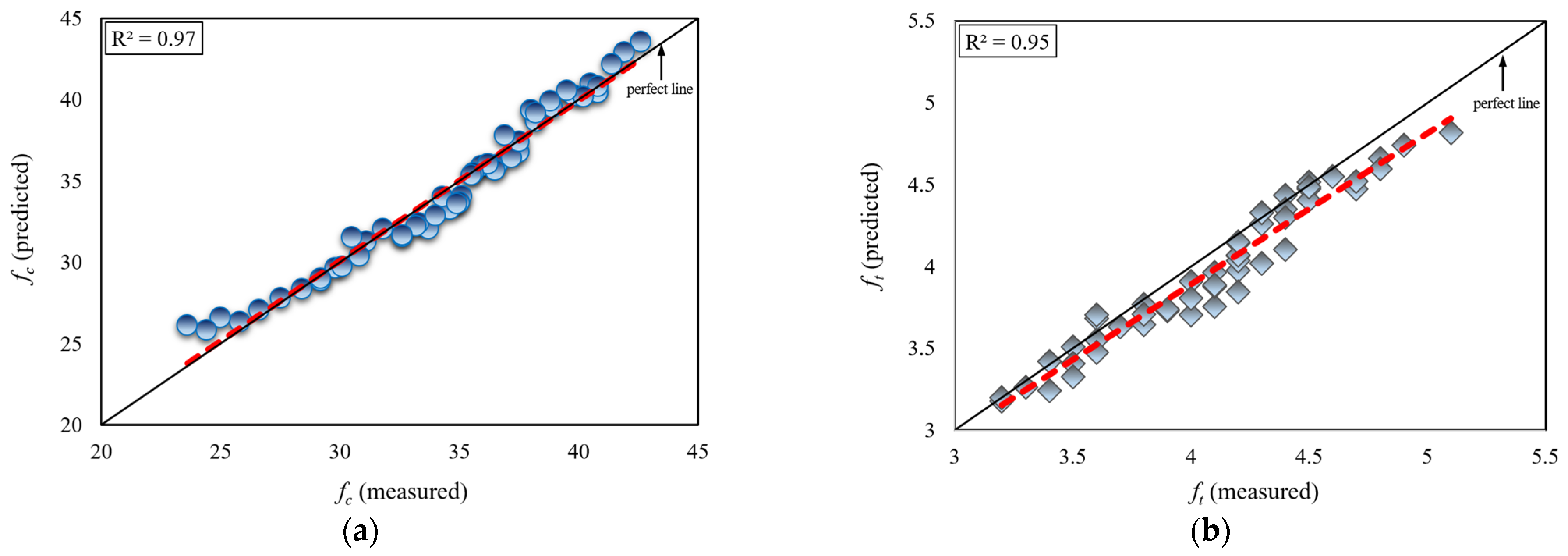
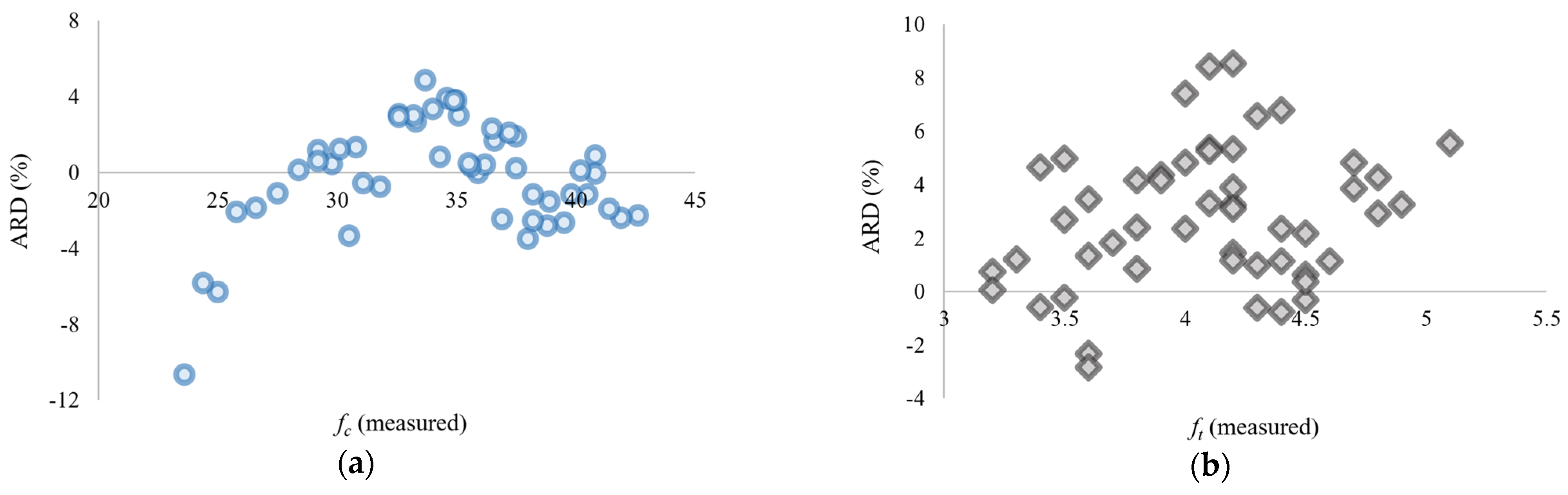
| Specimen Code | W/C (-) | LA/C (-) | R | fc | ft | |||
|---|---|---|---|---|---|---|---|---|
| Measured (N) | ARD (%) | Measured (N) | ARD (%) | Measured (N) | ARD (%) | |||
| LAC1 | 0.2 | 2.12 | 43 | 4.6 | 42.6 | 3.0 | 5.1 | 5.8 |
| LAC2 | 0.2 | 2.03 | 42 | 3.6 | 41.9 | 0.6 | 4.9 | 5.2 |
| LAC3 | 0.2 | 1.95 | 41 | 0.6 | 41.4 | 2.8 | 4.8 | 0.5 |
| LAC4 | 0.2 | 1.86 | 39 | 2.9 | 40.8 | 2.1 | 4.7 | 0.4 |
| LAC5 | 0.2 | 1.75 | 39 | 7.3 | 40.5 | 4.9 | 4.5 | 6.7 |
| LAC6 | 0.2 | 1.67 | 38 | 6.8 | 39.8 | 7.8 | 4.4 | 4.0 |
| LAC7 | 0.2 | 1.6 | 37 | 10.1 | 38.9 | 8.9 | 4.4 | 1.7 |
| LAC8 | 0.2 | 1.55 | 36 | 8.5 | 38.2 | 8.0 | 4.3 | 5.8 |
| LAC9 | 0.2 | 1.48 | 34 | 11.6 | 37.5 | 9.1 | 4.2 | 0.5 |
| LAC10 | 0.2 | 1.42 | 33 | 6.3 | 36.6 | 7.6 | 4.2 | 1.2 |
| LAC11 | 0.25 | 2.12 | 39 | 1.6 | 40.8 | 1.6 | 4.8 | 1.0 |
| LAC12 | 0.25 | 2.03 | 38 | 3.4 | 40.2 | 0.7 | 4.7 | 4.1 |
| LAC13 | 0.25 | 1.95 | 38 | 2.8 | 39.5 | 0.3 | 4.6 | 0.3 |
| LAC14 | 0.25 | 1.86 | 37 | 0.4 | 38.8 | 8.6 | 4.5 | 2.4 |
| LAC15 | 0.25 | 1.75 | 36 | 5.7 | 38.0 | 0.7 | 4.5 | 8.2 |
| LAC16 | 0.25 | 1.67 | 33 | 6.3 | 37.2 | 1.6 | 4.4 | 6.7 |
| LAC17 | 0.25 | 1.6 | 32 | 4.1 | 36.5 | 7.3 | 4.3 | 1.8 |
| LAC18 | 0.25 | 1.55 | 32 | 7.3 | 35.9 | 9.1 | 4.2 | 1.2 |
| LAC19 | 0.25 | 1.48 | 30 | 9.7 | 35.1 | 7.4 | 4.2 | 3.6 |
| LAC20 | 0.25 | 1.42 | 29 | 6.7 | 34.6 | 0.2 | 4.1 | 0.4 |
| LAC21 | 0.3 | 2.12 | 36 | 11.0 | 38.2 | 6.7 | 4.5 | 2.2 |
| LAC22 | 0.3 | 2.03 | 34 | 7.5 | 37.5 | 6.9 | 4.4 | 2.6 |
| LAC23 | 0.3 | 1.95 | 34 | 5.1 | 36.9 | 4.9 | 4.3 | 0.3 |
| LAC24 | 0.3 | 1.86 | 32 | 10.1 | 36.2 | 1.0 | 4.2 | 1.0 |
| LAC25 | 0.3 | 1.75 | 31 | 3.1 | 35.6 | 6.0 | 4.2 | 2.0 |
| LAC26 | 0.3 | 1.67 | 29 | 2.6 | 35.0 | 7.7 | 4.1 | 2.8 |
| LAC27 | 0.3 | 1.6 | 29 | 5.3 | 34.3 | 5.3 | 4.0 | 3.3 |
| LAC28 | 0.3 | 1.55 | 27 | 2.7 | 33.7 | 5.5 | 4.0 | 5.0 |
| LAC29 | 0.3 | 1.48 | 27 | 3.4 | 33.3 | 3.5 | 3.9 | 3.7 |
| LAC30 | 0.3 | 1.42 | 26 | 4.5 | 32.6 | 3.1 | 3.8 | 5.2 |
| LAC31 | 0.35 | 2.12 | 31 | 6.0 | 35.5 | 6.1 | 4.2 | 2.0 |
| LAC32 | 0.35 | 2.03 | 29 | 1.2 | 34.9 | 5.5 | 4.1 | 0.1 |
| LAC33 | 0.35 | 1.95 | 28 | 2.1 | 34.0 | 3.1 | 4.1 | 1.1 |
| LAC34 | 0.35 | 1.86 | 27 | 0.4 | 33.2 | 4.1 | 4.0 | 3.3 |
| LAC35 | 0.35 | 1.75 | 26 | 0.1 | 32.6 | 7.7 | 3.9 | 4.2 |
| LAC36 | 0.35 | 1.67 | 26 | 0.8 | 31.8 | 4.5 | 3.8 | 7.6 |
| LAC37 | 0.35 | 1.6 | 25 | 0.6 | 31.1 | 2.1 | 3.6 | 0.2 |
| LAC38 | 0.35 | 1.55 | 25 | 1.6 | 30.5 | 2.9 | 3.6 | 5.4 |
| LAC39 | 0.35 | 1.48 | 23 | 1.2 | 29.8 | 2.7 | 3.5 | 6.9 |
| LAC40 | 0.35 | 1.42 | 22 | 0.1 | 29.2 | 0.8 | 3.4 | 2.2 |
| LAC41 | 0.4 | 2.12 | 25 | 0.2 | 30.8 | 5.4 | 3.8 | 0.9 |
| LAC42 | 0.4 | 2.03 | 24 | 2.3 | 30.1 | 1.0 | 3.7 | 1.1 |
| LAC43 | 0.4 | 1.95 | 23 | 0.8 | 29.2 | 0.7 | 3.6 | 0.3 |
| LAC44 | 0.4 | 1.86 | 22 | 2.4 | 28.4 | 4.1 | 3.6 | 0.7 |
| LAC45 | 0.4 | 1.75 | 21 | 1.2 | 27.5 | 3.3 | 3.5 | 1.1 |
| LAC46 | 0.4 | 1.67 | 20 | 0.5 | 26.6 | 1.6 | 3.5 | 2.3 |
| LAC47 | 0.4 | 1.6 | 19 | 0.2 | 25.8 | 2.6 | 3.4 | 3.1 |
| LAC48 | 0.4 | 1.55 | 19 | 0.7 | 25.0 | 4.0 | 3.3 | 3.6 |
| LAC49 | 0.4 | 1.48 | 18 | 0.8 | 24.4 | 0.5 | 3.2 | 0.8 |
| LAC50 | 0.4 | 1.42 | 18 | 0.2 | 23.6 | 1.5 | 3.2 | 0.6 |
| Parameter Estimates | |||||
| For Equation (3) | For Equation (4) | ||||
| Parameter | Estimate | Std. Error | Parameter | Estimate | Std. Error |
| x1 | 33.15 | 2.548 | x1 | 4.36 | 0.305 |
| x2 | −4.89 | 0.948 | x2 | −0.37 | 0.114 |
| x3 | 1.10 | 0.033 | x3 | 0.11 | 0.004 |
| ANOVA a | |||||
| For Equation (3) | For Equation (3) | ||||
| Source | Sum of Squares | df | Source | Sum of Squares | df |
| Regression | 60,459.954 | 3 | Regression | 844.021 | 3 |
| Residual | 38.996 | 47 | Residual | 0.559 | 47 |
| Uncorrected Total | 60,498.950 | 50 | Uncorrected Total | 844.580 | 50 |
| Corrected Total | 1186.382 | 49 | Corrected Total | 10.627 | 49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tugrul Tunc, E. Relationship Between Schmidt Hammer Rebound Hardness Test and Concrete Strength Tests for Limestone Aggregate Concrete Based on Experimental and Statistical Study. Materials 2025, 18, 1388. https://doi.org/10.3390/ma18061388
Tugrul Tunc E. Relationship Between Schmidt Hammer Rebound Hardness Test and Concrete Strength Tests for Limestone Aggregate Concrete Based on Experimental and Statistical Study. Materials. 2025; 18(6):1388. https://doi.org/10.3390/ma18061388
Chicago/Turabian StyleTugrul Tunc, Esra. 2025. "Relationship Between Schmidt Hammer Rebound Hardness Test and Concrete Strength Tests for Limestone Aggregate Concrete Based on Experimental and Statistical Study" Materials 18, no. 6: 1388. https://doi.org/10.3390/ma18061388
APA StyleTugrul Tunc, E. (2025). Relationship Between Schmidt Hammer Rebound Hardness Test and Concrete Strength Tests for Limestone Aggregate Concrete Based on Experimental and Statistical Study. Materials, 18(6), 1388. https://doi.org/10.3390/ma18061388






