Thermo-Mechanical Analysis for Composite Cylindrical Shells with Temperature-Dependent Material Properties Under Combined Thermal and Mechanical Loading
Abstract
:1. Introduction
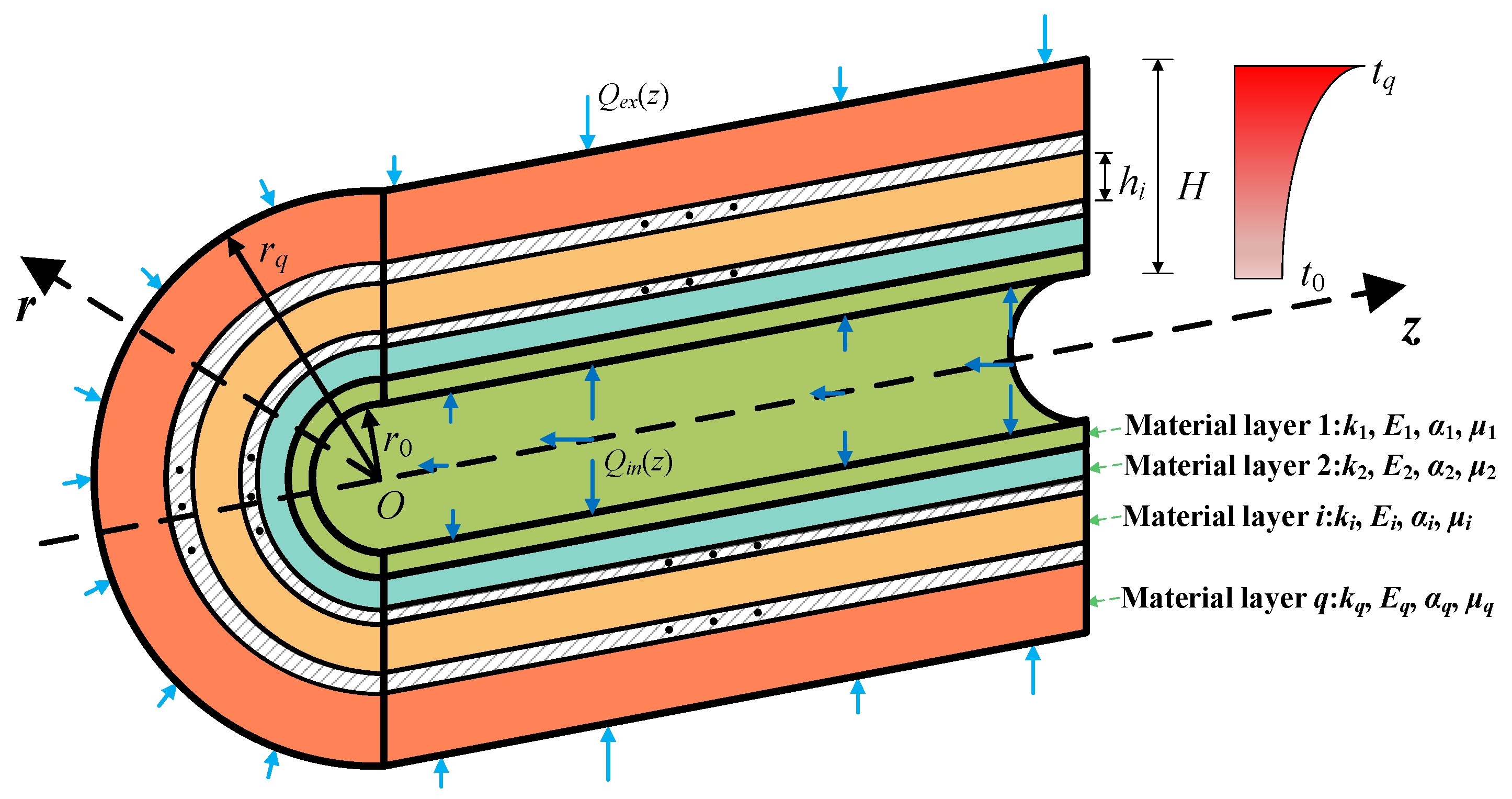
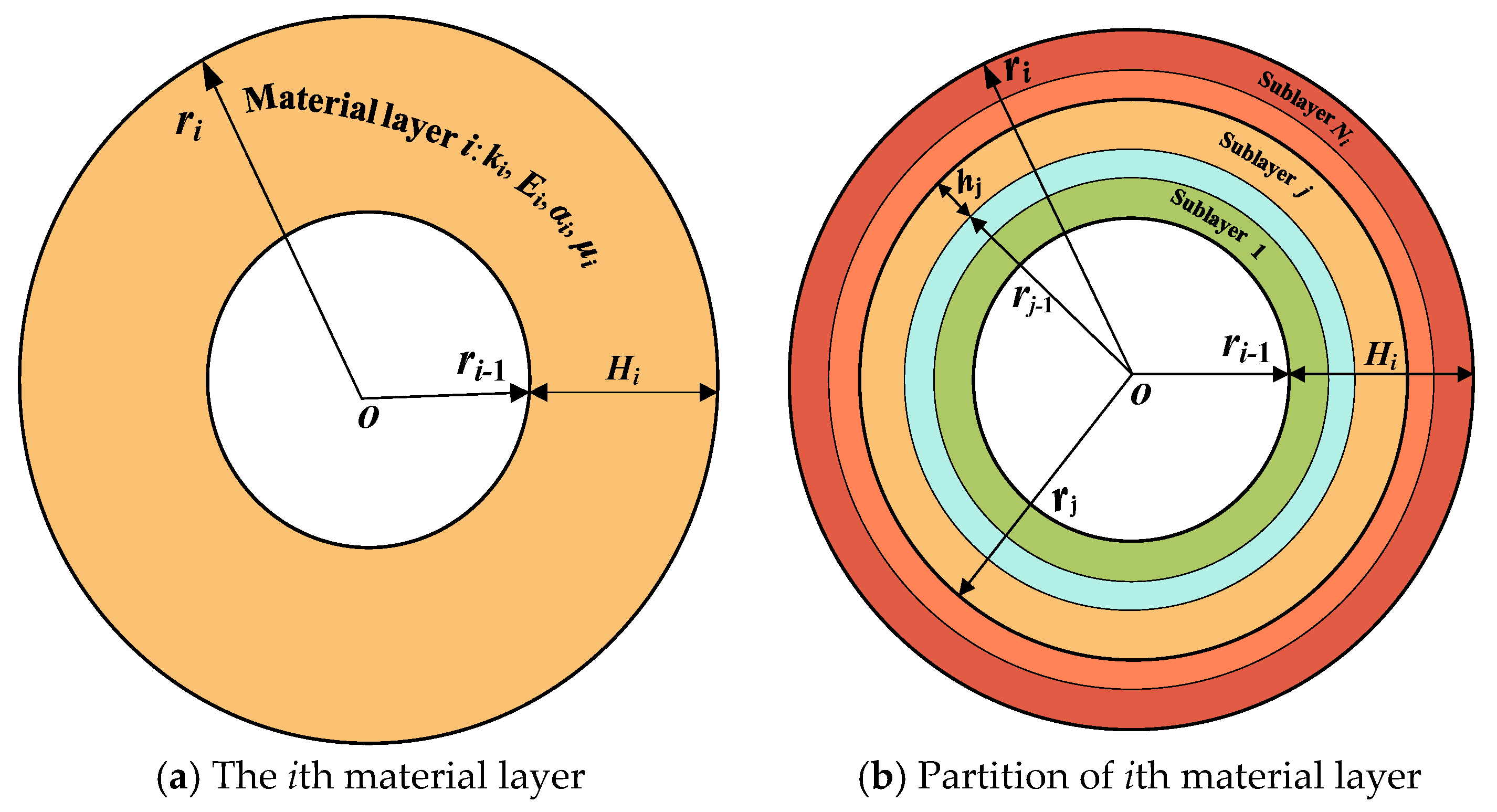
2. Geometrical Model
3. Analysis of the Temperature Field
3.1. Temperature Solutions for Temperature Independence
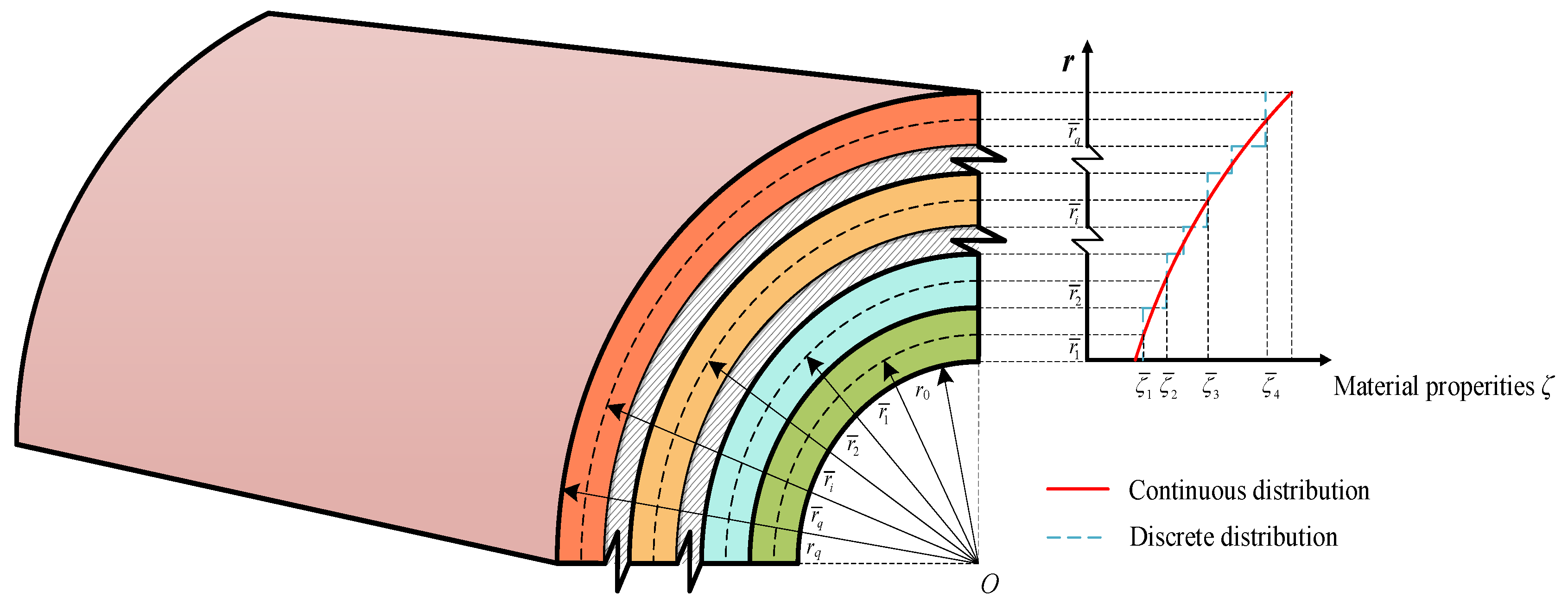
3.2. Temperature Analysis for Temperature Dependence
3.2.1. The Slice Model
3.2.2. The Iterative Method
4. Solutions for Stresses and Displacements
4.1. Basic Equations
4.2. Solutions for Stresses and Displacements Within the Single-Layer Shell
4.3. Recursive Formulas for Stresses and Displacements
4.4. Exact Solutions for Stresses and Displacements
5. Convergence and Comparison Studies
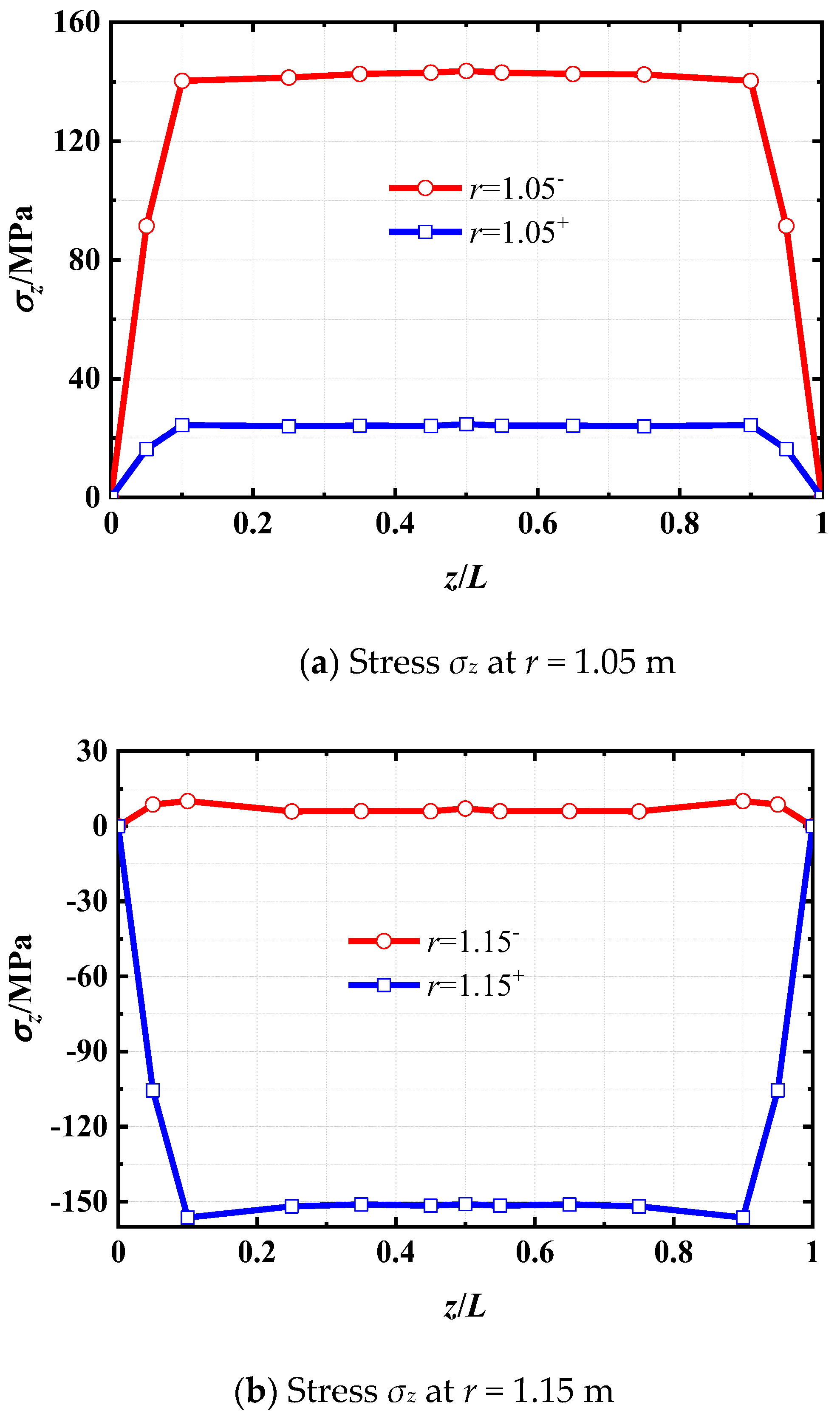
6. Parametric Analysis
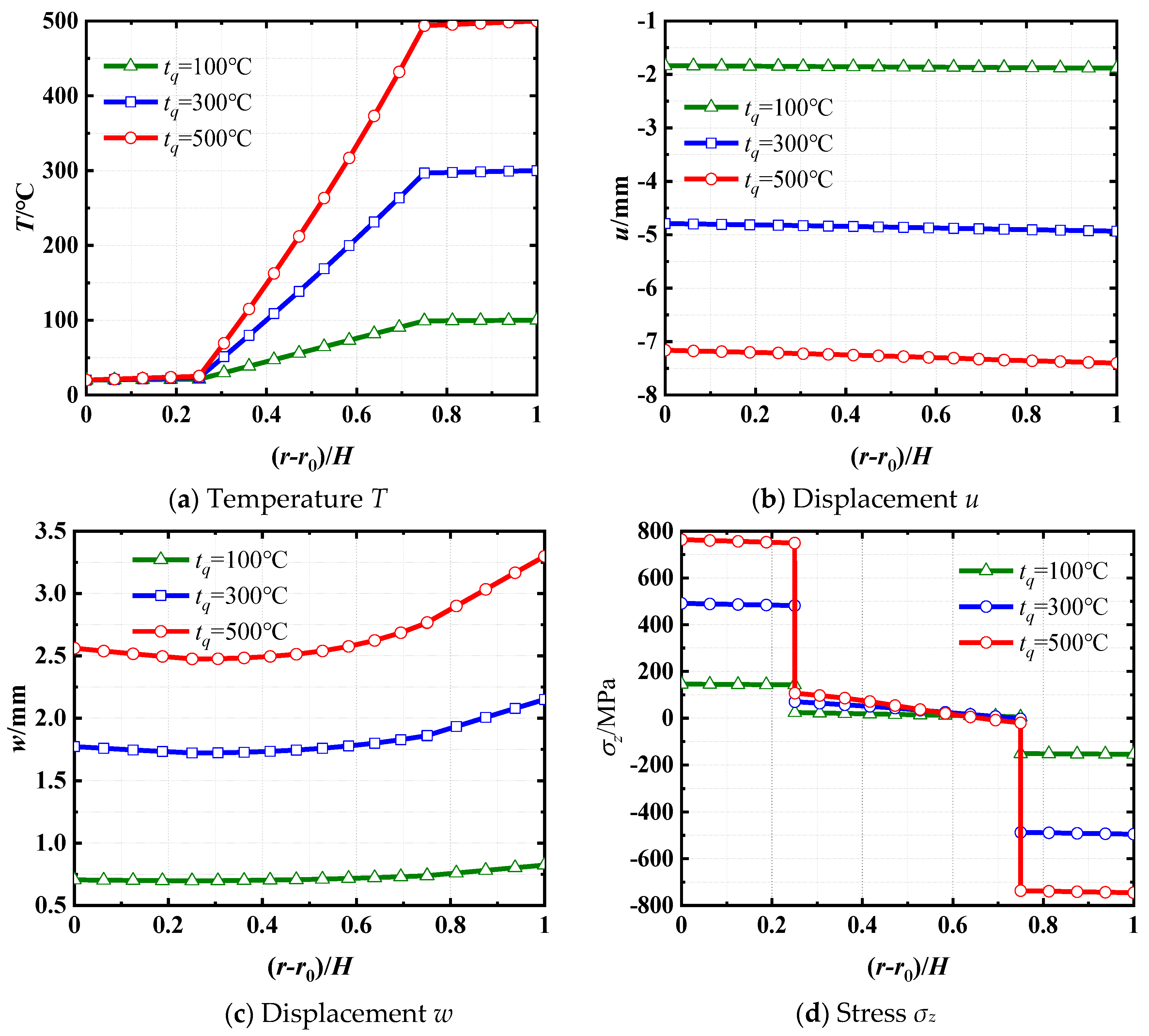
6.1. Influence of Surface Temperature
6.2. Influence of Thickness-to-Radius Ratios H/r0
6.3. Influence of Layer Numbers and Component Materials
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, D.; Shi, D.; Wang, Q.; Ma, C. A unified power series method for vibration analysis of composite laminate conical, cylindrical shell and annular plate. Structures 2021, 29, 305–327. [Google Scholar] [CrossRef]
- Hastie, J.C.; Guz, I.A.; Kashtalyan, M. Effects of thermal gradient on failure of a thermoplastic composite pipe (TCP) riser leg. I. Int. J. Press. Vessel. Pip. 2019, 172, 90–99. [Google Scholar] [CrossRef]
- He, Y.Y.; Vaz, M.A.; Caire, M. Stress and failure analyses of thermoplastic composite pipes subjected to torsion and thermomechanical loading. Mar. Struct. 2021, 79, 103024. [Google Scholar] [CrossRef]
- Duong, V.; Tran, N.D.; Luat, D.T.; Thom, D. Static analysis and boundary effect of FG-CNTRC cylindrical shells with various boundary conditions using quasi-3D shear and normal deformations theory. Structures 2022, 44, 828–850. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, K.; Yun, J.; Kim, S.; Ri, P. Free vibration analysis of laminated closed conical, cylindrical shells and annular plates with a hole using a meshfree method. Structures 2021, 34, 3070–3086. [Google Scholar] [CrossRef]
- Rafiee, M.; Hejazi, M.; Amoushahi, H. Buckling response of composite cylindrical shells with various stiffener layouts under uniaxial compressive loading. Structures 2021, 33, 4514–4537. [Google Scholar] [CrossRef]
- Qian, H.; Cui, J.W.; Lu, C.H.; Yang, Y.; Wang, Z.T. Thermo-elastic analysis for clamped laminated arches subjected to non-uniform temperature boundary conditions. Mech. Adv. Mater. Struct. 2025. [Google Scholar] [CrossRef]
- Qian, H.; Zhou, D.; Lu, C. Elasticity solutions of clamped laminated arches.with temperature-dependent material properties under thermo-mechanical loading. J. Therm. Stress. 2024, 47, 1330–1346. [Google Scholar] [CrossRef]
- Qian, H.; Wang, Z.T.; Lu, C.H.; Cai, D.S.; Yang, Y. Thermal analysis for laminated plates with arbitrary supports under non-uniform temperature boundary conditions. Thin-Walled Struct. 2024, 197, 111595. [Google Scholar] [CrossRef]
- Qian, H.; Qiu, Y.X.; Lu, C.H.; Yang, Y.; Sha, X. Thermal analysis for clamped laminated beams with non-uniform temperature boundary conditions. Thin-Walled Struct. 2022, 179, 109693. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Vu, M.D.; Cao, V.D.; Vu, H.N. Nonlinear torsional buckling of functionally graded graphene-reinforced composite (FG-GRC) laminated cylindrical shells stiffened by FG-GRC laminated stiffeners in thermal environment. Polym. Compos. 2021, 42, 3051–3063. [Google Scholar] [CrossRef]
- Xia, L.; Ding, K. Three-dimensional thermoelastic solution for laminated cantilever cylindrical shell. Aerosp. Sci. Technol. 2001, 5, 339–346. [Google Scholar] [CrossRef]
- Moayedi, H.; Ebrahimi, F.; Habibi, M.; Safarpour, H.; Foong, L.K. Application of nonlocal strain-stress gradient theory and GDQEM for thermo-vibration responses of a laminated composite nanoshell. Eng. Comput. 2021, 37, 3359–3374. [Google Scholar] [CrossRef]
- Zhen, W.; Yang, C.; Zhang, H.G.; Zheng, X.T. Stability of laminated composite and sandwich beams by a Reddy-type higher-order zig-zag theory. Mech. Adv. Mater. Struct. 2019, 26, 1622–1635. [Google Scholar] [CrossRef]
- Ahmadi, I. Edge stresses analysis in laminated thick sandwich cylinder subjected to distributed hygrothermal loading. J. Sandw. Struct. Mater. 2018, 20, 425–461. [Google Scholar] [CrossRef]
- Carrera, E. An assessment of mixed and classical theories on global and local response of multilayered orthotropic plates. Compos. Struct. 2000, 50, 183–198. [Google Scholar] [CrossRef]
- Mirzavand, B.; Pourmohammad, H. Post-buckling analysis of non-uniformly heated functionally graded cylindrical shells enhanced by shape memory alloys using classical lamination theory. J. Intell. Mater. Syst. Struct. 2019, 30, 2421–2435. [Google Scholar] [CrossRef]
- He, X.Q.; Ng, T.Y.; Sivashanker, S.; Liew, K.M. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]
- Ghasemi, N.; Kordbacheh, A.A.; Berahman, M. Electronic, magnetic and transport properties of zigzag silicene nanoribbon adsorbed with Cu atom: A first-principles calculation. J. Magn. Magn. Mater. 2019, 473, 306–311. [Google Scholar] [CrossRef]
- Topal, U.; Uzman, Ü. Thermal buckling load optimization of angle-ply laminated cylindrical shells. Mater. Des. 2009, 30, 532–536. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Inman, D.J. 2-D differential quadrature solution for vibration analysis of functionally graded conical, cylindrical shell and annular plate structures. J. Sound Vibr. 2009, 328, 259–290. [Google Scholar] [CrossRef]
- Bouderba, B.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R. Thermal stability of functionally graded sandwich plates using a simple shear deformation theory. Struct. Eng. Mech. 2016, 58, 397–422. [Google Scholar] [CrossRef]
- Reddy, J.N. A refined nonlinear theory of plates with transverse shear deformation. Int. J. Solids Struct. 1984, 20, 881–896. [Google Scholar] [CrossRef]
- Zine, A.; Tounsi, A.; Draiche, K.; Sekkal, M.; Mahmoud, S.R. A novel higher-order shear deformation theory for bending and free vibration analysis of isotropic and multilayered plates and shells. Steel Compos. Struct. 2018, 26, 125–137. [Google Scholar] [CrossRef]
- Ramezani, M.; Rezaiee-Pajand, M.; Tornabene, F. Nonlinear thermomechanical analysis of GPLRC cylindrical shells using HSDT enriched by quasi-3D ANS cover functions. Thin-Walled Struct. 2022, 179, 109582. [Google Scholar] [CrossRef]
- Safarpour, M.; Ghabussi, A.; Ebrahimi, F.; Habibi, M.; Safarpour, H. Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin-Walled Struct. 2020, 150, 106683. [Google Scholar] [CrossRef]
- Murakami, H. Laminated Composite Plate Theory With Improved In-Plane Responses. J. Appl. Mech.-Trans. ASME 1986, 53, 661–666. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Liu, X.L.; Hu, L.Y.; Wang, Y.; Chen, W.Q.; Xu, R.Q. Zig-zag theory for concrete beams with corrugated steel webs. Eng. Struct. 2022, 258, 114100. [Google Scholar] [CrossRef]
- Padhi, A.; Pandit, M.K. Behaviour of sandwich laminates subjected to thermal loading using higher-order zig-zag theory. J. Sandw. Struct. Mater. 2016, 18, 174–199. [Google Scholar] [CrossRef]
- Ghalami-Choobar, M.; Liaghat, G.; Sadighi, M.; Ahmadi, H.; Razmkhah, O.; Aboutorabi, A. Static analysis of highly anisotropic laminated beam using unified zig-zag theory subjected to mechanical and thermal loading. Int. J. Mech. Sci. 2018, 141, 491–501. [Google Scholar] [CrossRef]
- Icardi, U. Applications of zig-zag theories to sandwich beams. Mech. Adv. Mater. Struct. 2003, 10, 77–97. [Google Scholar] [CrossRef]
- Reddy, J.N. A generalization of two-dimensional theories of laminated composite plates. Commun. Numer. Methods Eng. 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Tornabene, F. General higher-order layer-wise theory for free vibrations of doubly-curved laminated composite shells and panels. Mech. Adv. Mater. Struct. 2016, 23, 1046–1067. [Google Scholar] [CrossRef]
- Saini, R.; Pradyumna, S. A layer-wise theory for the dynamic analysis of functionally graded composite nanobeams under thermal environment using nonlocal boundary conditions and Chebyshev collocation technique. J. Vib. Control 2024, 30, 4591–4611. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R. Static Analysis of Anisotropic Doubly-Curved Shell Subjected to Concentrated Loads Employing Higher Order Layer-Wise Theories. CMES-Comp. Model. Eng. Sci. 2022, 134, 1393–1468. [Google Scholar] [CrossRef]
- Fares, M.E.; Elmarghany, M.K.; Atta, D.; Salem, M.G. Bending and free vibration of multilayered functionally graded doubly curved shells by an improved layerwise theory. Compos. Pt B-Eng. 2018, 154, 272–284. [Google Scholar] [CrossRef]
- Huang, X.; Yang, J.; Yang, Z. Thermo-elastic analysis of functionally graded graphene nanoplatelets(GPLs) reinforced closed cylindrical shells. Appl. Math. Model. 2021, 97, 754–770. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- EN 1992-1-2:2005; Eurocode 2: Design of Concrete Structures-Part 1-2: General Rules-Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1993-1-2:2005; Eurocode 3: Design of Steel Structures-Part 1-2: General Rules-Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2005.





| Materials | ki [W/(m°C)] | μi | αi (°C−1) |
|---|---|---|---|
| Steel | −3.33 × 10−2 T + 54 | 0.3 | 4 × 10−9 T2 + 1.208 × 10−5 |
| Concrete | 5.7 × 10−7 T2 − 1.36 × 10−3 T + 1.36 | 0.2 | 1.4 × 10−11 T2 + 2.8 × 10−10 T + 6.0056 × 10−6 |
| T (°C) | Steel (GPa) | Concrete (GPa) |
|---|---|---|
| 20 | 210 | 30 |
| 100 | 210 | 30 |
| 200 | 189 | - |
| 300 | 169 | - |
| 400 | 147 | - |
| 500 | 126 | - |
| 600 | 65.1 | - |
| 700 | 27.3 | 0 |
| Position | N1 | N2 | N3 | N | Iterative Step s | ||||
|---|---|---|---|---|---|---|---|---|---|
| s = 1 | s = 2 | s = 3 | s = 4 | s = 5 | |||||
| r = 1.15 m | 3 | 6 | 3 | 12 | 20.7171 | 20.6889 | 20.6892 | 20.6892 | 20.6892 |
| 4 | 8 | 4 | 16 | 20.7171 | 20.6889 | 20.6893 | 20.6893 | 20.6893 | |
| 5 | 10 | 5 | 20 | 20.7171 | 20.6889 | 20.6893 | 20.6893 | 20.6893 | |
| 6 | 12 | 6 | 24 | 20.7171 | 20.6889 | 20.6893 | 20.6893 | 20.6893 | |
| r = 1.45 m | 3 | 6 | 3 | 12 | 43.7626 | 43.1245 | 43.1275 | 43.1276 | 43.1276 |
| 4 | 8 | 4 | 16 | 43.7626 | 43.0994 | 43.1029 | 43.1030 | 43.1030 | |
| 5 | 10 | 5 | 20 | 43.7626 | 43.1083 | 43.1116 | 43.1117 | 43.1117 | |
| 6 | 12 | 6 | 24 | 43.7626 | 43.0993 | 43.1115 | 43.1117 | 43.1117 | |
| r = 1.60 m | 3 | 6 | 3 | 12 | 63.9704 | 63.1830 | 63.1818 | 63.1819 | 63.1818 |
| 4 | 8 | 4 | 16 | 63.9704 | 63.1827 | 63.1815 | 63.1816 | 63.1816 | |
| 5 | 10 | 5 | 20 | 63.9704 | 63.1826 | 63.1814 | 63.1815 | 63.1815 | |
| 6 | 12 | 6 | 24 | 63.9704 | 63.1825 | 63.1813 | 63.1815 | 63.1815 | |
| r = 1.75 m | 3 | 6 | 3 | 12 | 82.3660 | 81.8424 | 81.8384 | 81.8385 | 81.8385 |
| 4 | 8 | 4 | 16 | 82.3660 | 81.8244 | 81.8200 | 81.8200 | 81.8200 | |
| 5 | 10 | 5 | 20 | 82.3660 | 81.8243 | 81.8199 | 81.8199 | 81.8199 | |
| 6 | 12 | 6 | 24 | 82.3660 | 81.8242 | 81.8198 | 81.8199 | 81.8199 | |
| r = 2.05 m | 3 | 6 | 3 | 12 | 99.6377 | 99.6338 | 99.6336 | 99.6336 | 99.6336 |
| 4 | 8 | 4 | 16 | 99.6377 | 99.6337 | 99.6335 | 99.6335 | 99.6335 | |
| 5 | 10 | 5 | 20 | 99.6377 | 99.6337 | 99.6335 | 99.6335 | 99.6335 | |
| 6 | 12 | 6 | 24 | 99.6377 | 99.6337 | 99.6335 | 99.6335 | 99.6335 | |
| Displacements or Stresses | Sublayer Number N | M = 10 | M = 20 | M = 30 | M = 40 | M = 50 |
|---|---|---|---|---|---|---|
| u (mm) | 12 | −0.814 | −0.811 | −0.810 | −0.810 | −0.810 |
| 16 | −0.814 | −0.811 | −0.810 | −0.810 | −0.810 | |
| 20 | −0.814 | −0.811 | −0.810 | −0.810 | −0.810 | |
| 24 | −0.814 | −0.811 | −0.810 | −0.810 | −0.810 | |
| σr (MPa) | 12 | 16.4 | 15.4 | 14.7 | 15.3 | 15.3 |
| 16 | 16.7 | 15.7 | 15.0 | 15.6 | 15.6 | |
| 20 | 16.7 | 15.7 | 15.0 | 15.5 | 15.5 | |
| 24 | 16.7 | 15.7 | 15.0 | 15.5 | 15.5 | |
| W (mm) | 12 | 0.815 | 0.815 | 0.815 | 0.815 | 0.815 |
| 16 | 0.815 | 0.815 | 0.815 | 0.815 | 0.815 | |
| 20 | 0.815 | 0.815 | 0.815 | 0.815 | 0.815 | |
| 24 | 0.815 | 0.815 | 0.815 | 0.815 | 0.815 | |
| τrz (MPa) | 12 | −10.2 | −10.2 | −10.1 | −10.0 | −10.0 |
| 16 | −10.2 | −10.2 | −10.1 | −10.0 | −10.0 | |
| 20 | −10.2 | −10.2 | −10.1 | −10.0 | −10.0 | |
| 24 | −10.2 | −10.2 | −10.1 | −10.0 | −10.0 |
| Position | Method | T (°C) | u (mm) | w (mm) | σz (MPa) | τrz (MPa) |
|---|---|---|---|---|---|---|
| r = 1.15 m | FE | 20.7 | −0.733 | 0.823 | 76.0 | −9.77 |
| present | 20.7 | −0.733 | 0.823 | 75.8 | −9.72 | |
| r = 1.45 m | FE | 43.1 | −0.920 | 0.955 | 19.5 | −13.5 |
| present | 43.1 | −0.920 | 0.955 | 19.5 | −13.3 | |
| r = 1.60 m | FE | 63.2 | −1.08 | 1.09 | 18.8 | −12.8 |
| present | 63.2 | −1.08 | 1.09 | 18.8 | −12.7 | |
| r = 1.75 m | FE | 81.8 | −1.22 | 1.24 | 18.4 | −12.1 |
| present | 81.8 | −1.22 | 1.24 | 18.3 | −12.1 | |
| r = 2.05 m | FE | 99.6 | −1.38 | 1.64 | −72.5 | −7.61 |
| present | 99.6 | −1.38 | 1.64 | −72.7 | −7.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Qian, H.; Lu, C. Thermo-Mechanical Analysis for Composite Cylindrical Shells with Temperature-Dependent Material Properties Under Combined Thermal and Mechanical Loading. Materials 2025, 18, 1391. https://doi.org/10.3390/ma18071391
Li J, Qian H, Lu C. Thermo-Mechanical Analysis for Composite Cylindrical Shells with Temperature-Dependent Material Properties Under Combined Thermal and Mechanical Loading. Materials. 2025; 18(7):1391. https://doi.org/10.3390/ma18071391
Chicago/Turabian StyleLi, Junjie, Hai Qian, and Chunhua Lu. 2025. "Thermo-Mechanical Analysis for Composite Cylindrical Shells with Temperature-Dependent Material Properties Under Combined Thermal and Mechanical Loading" Materials 18, no. 7: 1391. https://doi.org/10.3390/ma18071391
APA StyleLi, J., Qian, H., & Lu, C. (2025). Thermo-Mechanical Analysis for Composite Cylindrical Shells with Temperature-Dependent Material Properties Under Combined Thermal and Mechanical Loading. Materials, 18(7), 1391. https://doi.org/10.3390/ma18071391





