Computationally Efficient p-Version Finite Element Analysis of Composite-Reinforced Thin-Walled Cylindrical Shells with Circumferential Cracks
Abstract
1. Introduction
2. Materials and Methods
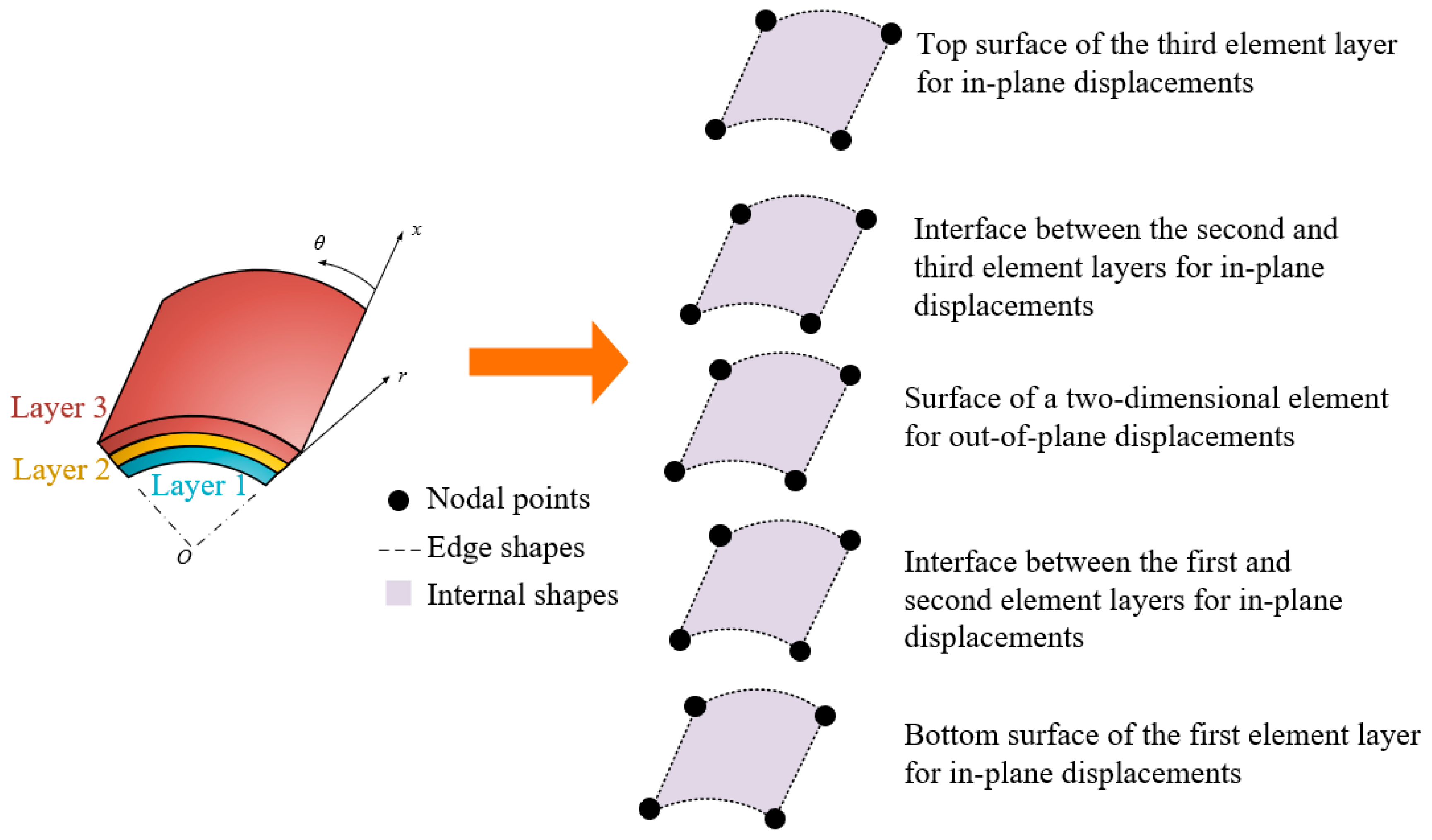
2.1. Construction of Polynomical Shape Functions for p-Version FEM
2.2. Geometry and Displacement Fields
2.3. Constitutive Equations
2.4. The Formulation of the Element Stiffness Matrix for the Proposed Model
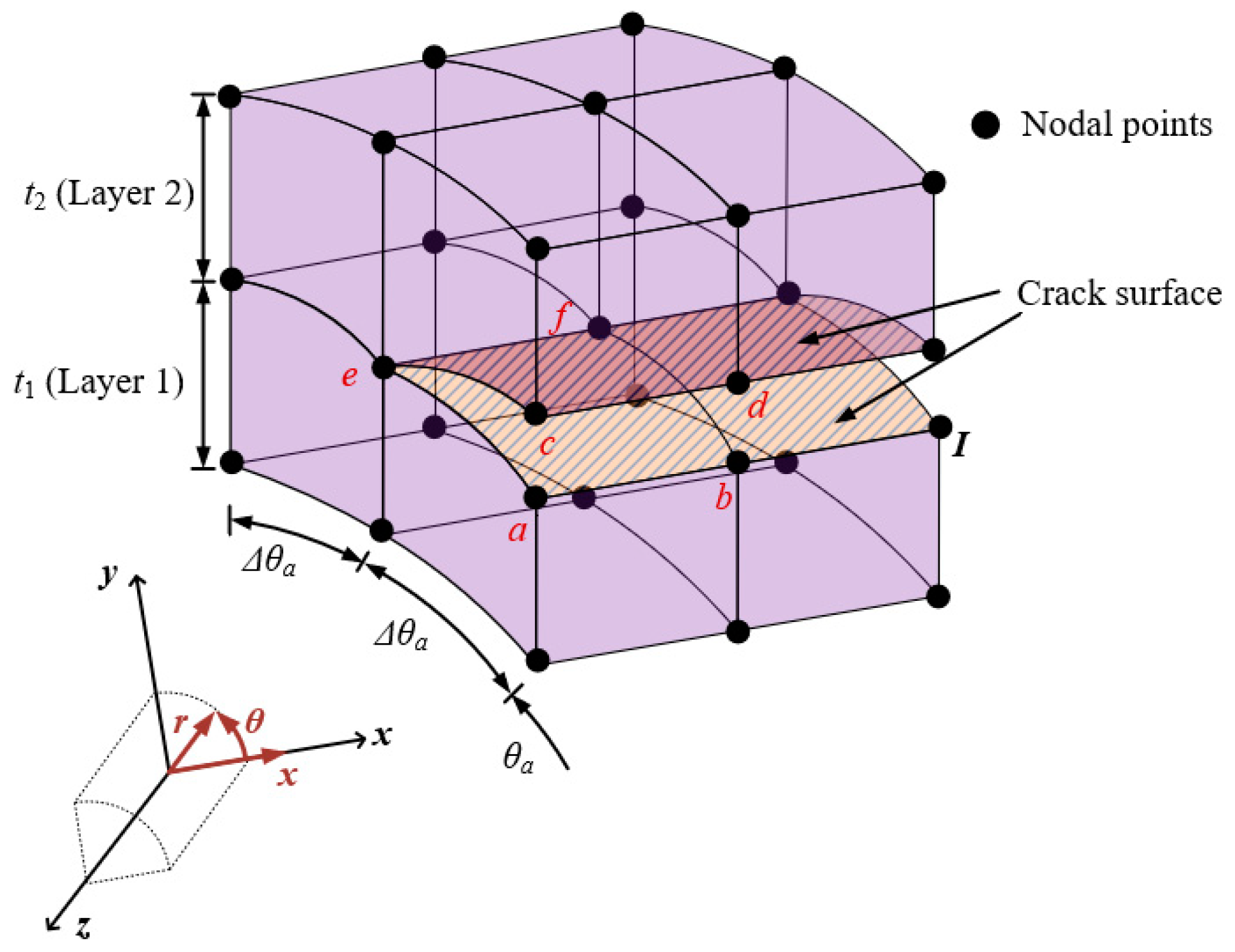
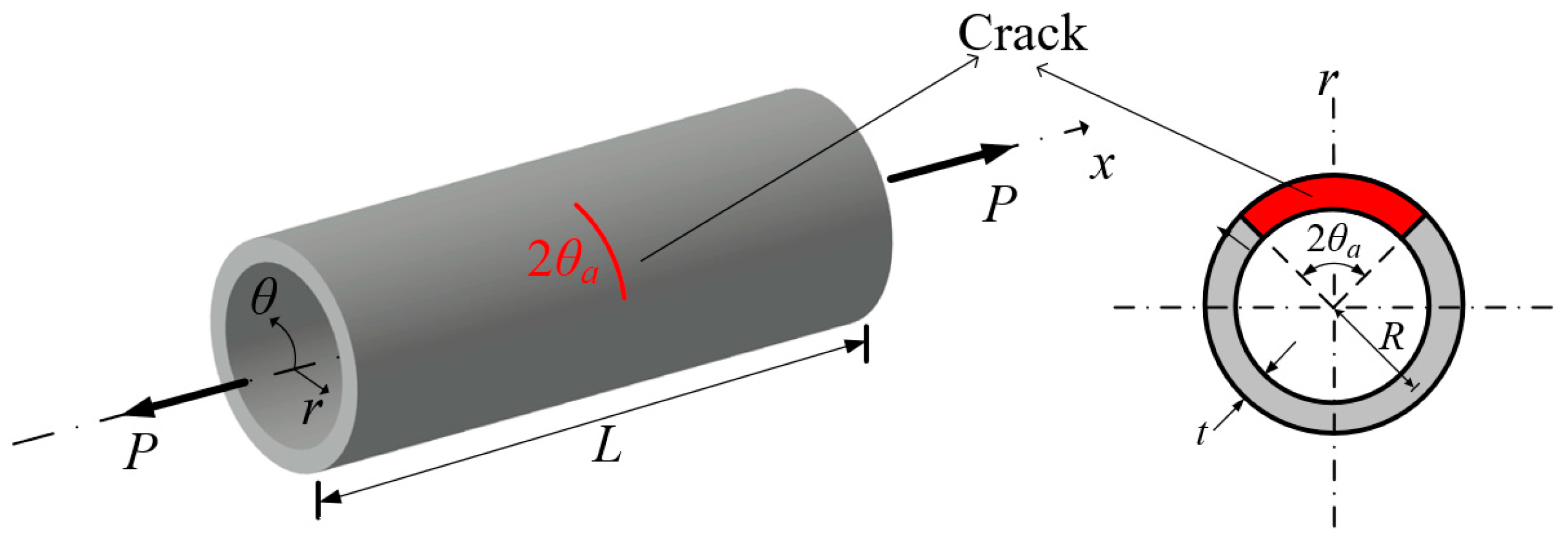
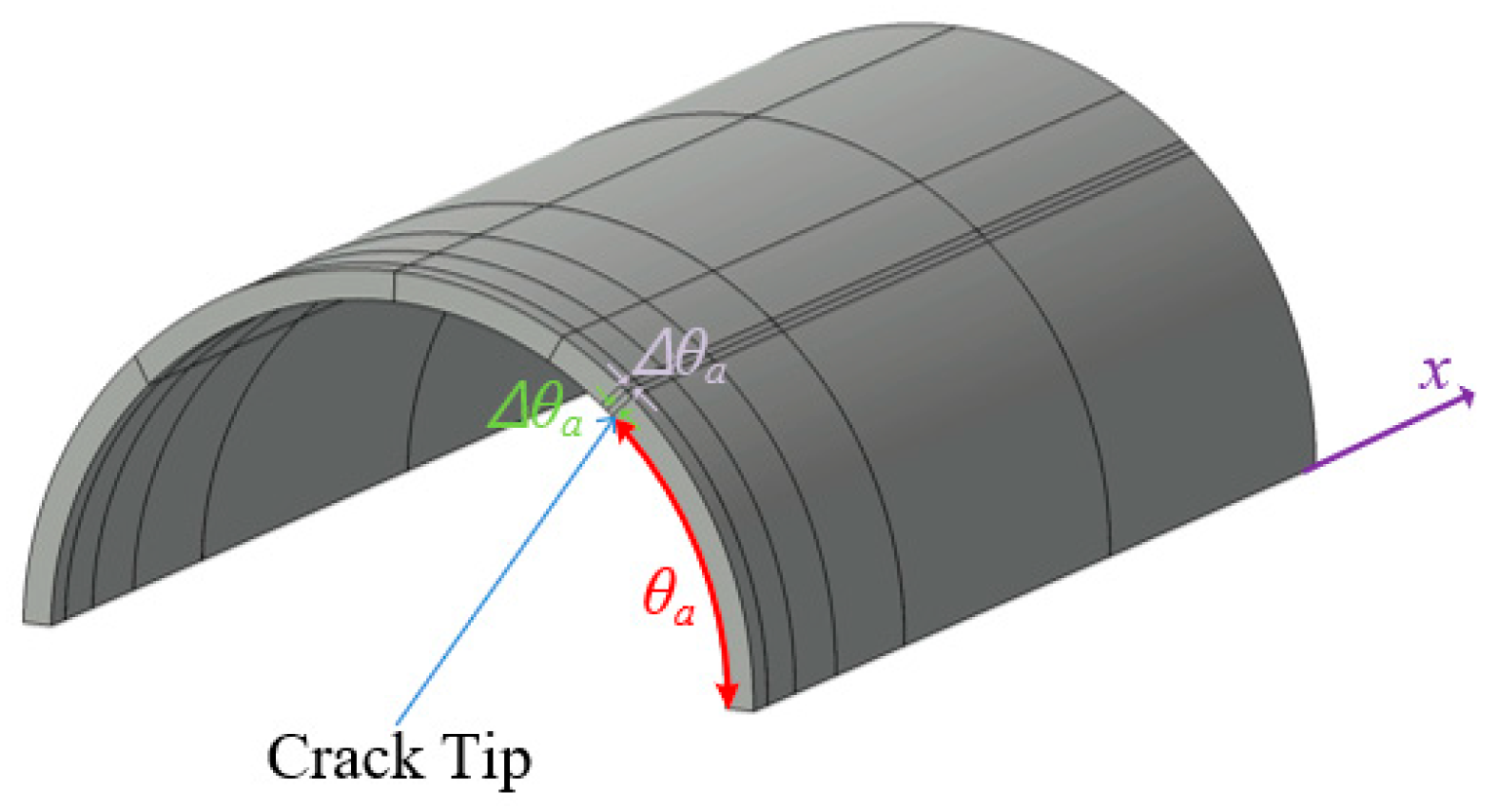
2.5. VCCT for the Proposed Model for Cylindrical Shells with a Circumferential Crack
3. Results
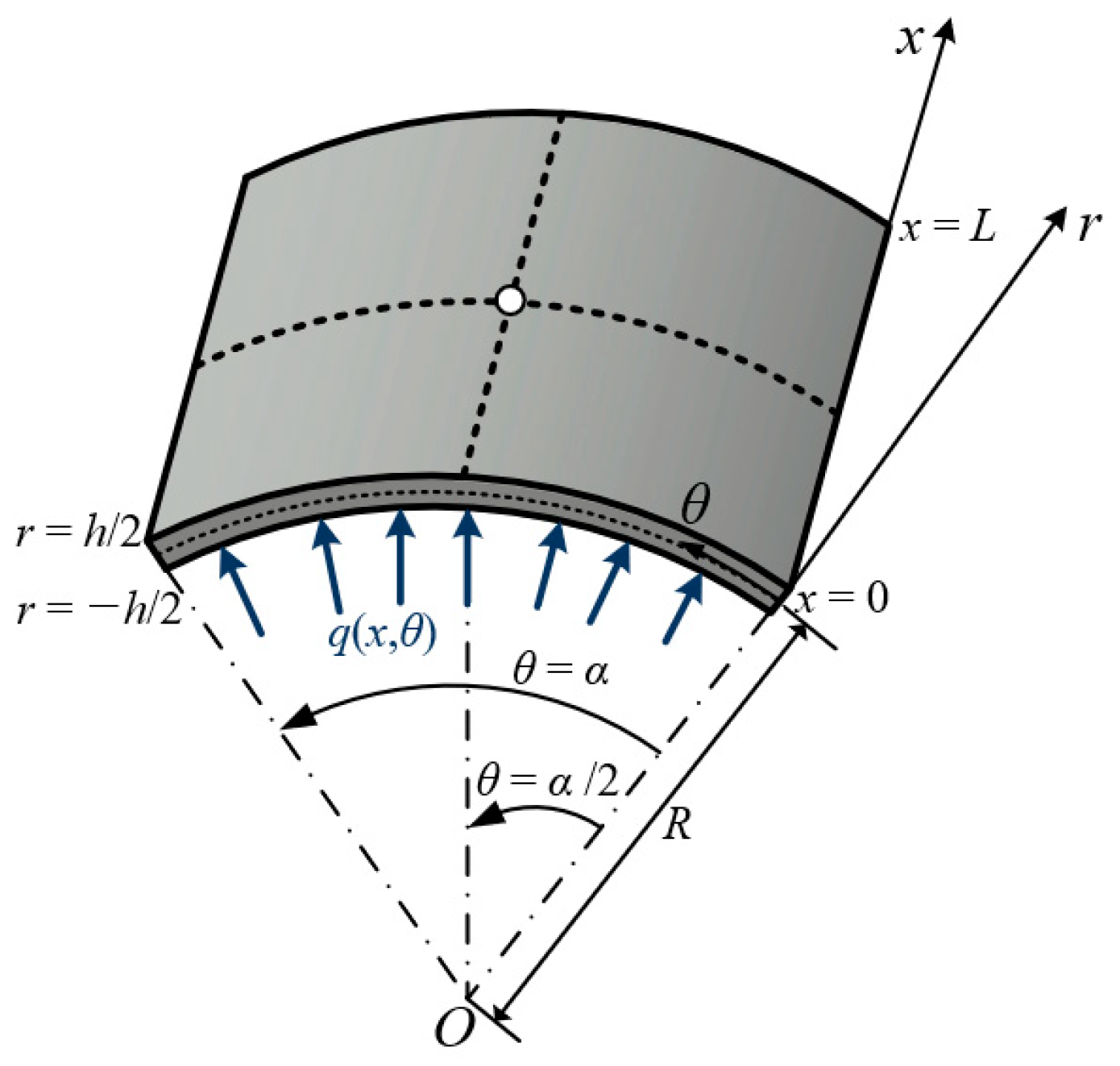
3.1. Cylindrical Panel with Simply Boundary Condtions
3.2. Thin-Walled Cylindrical Shells with Circumferential Cracks
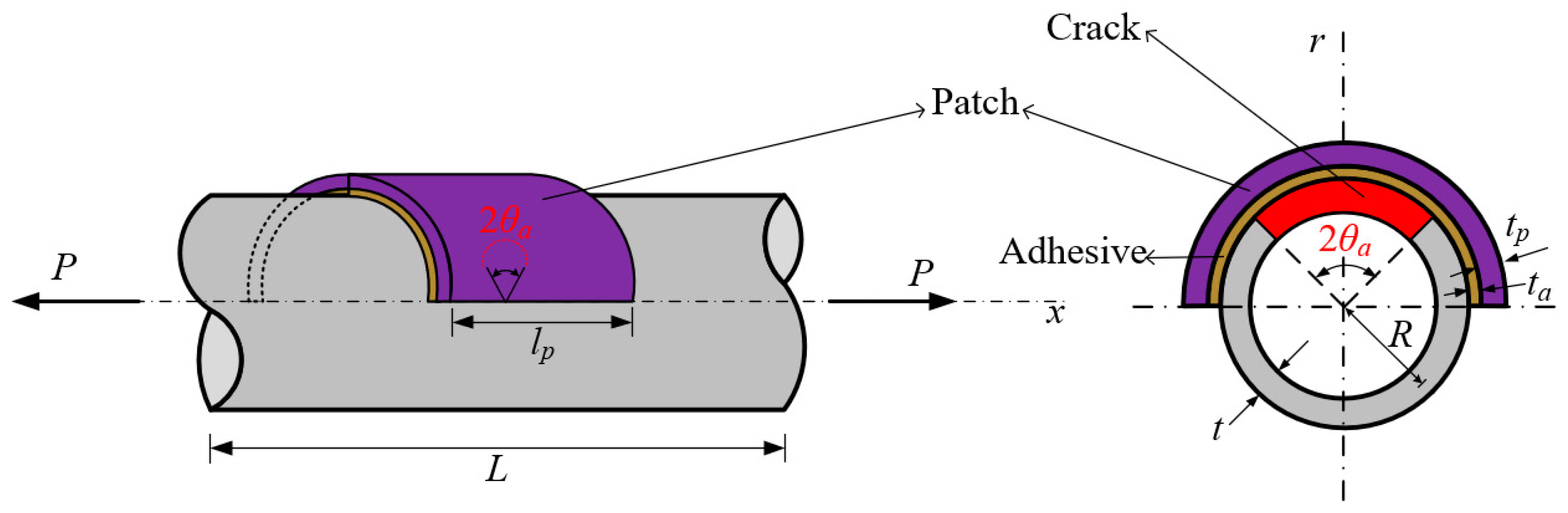
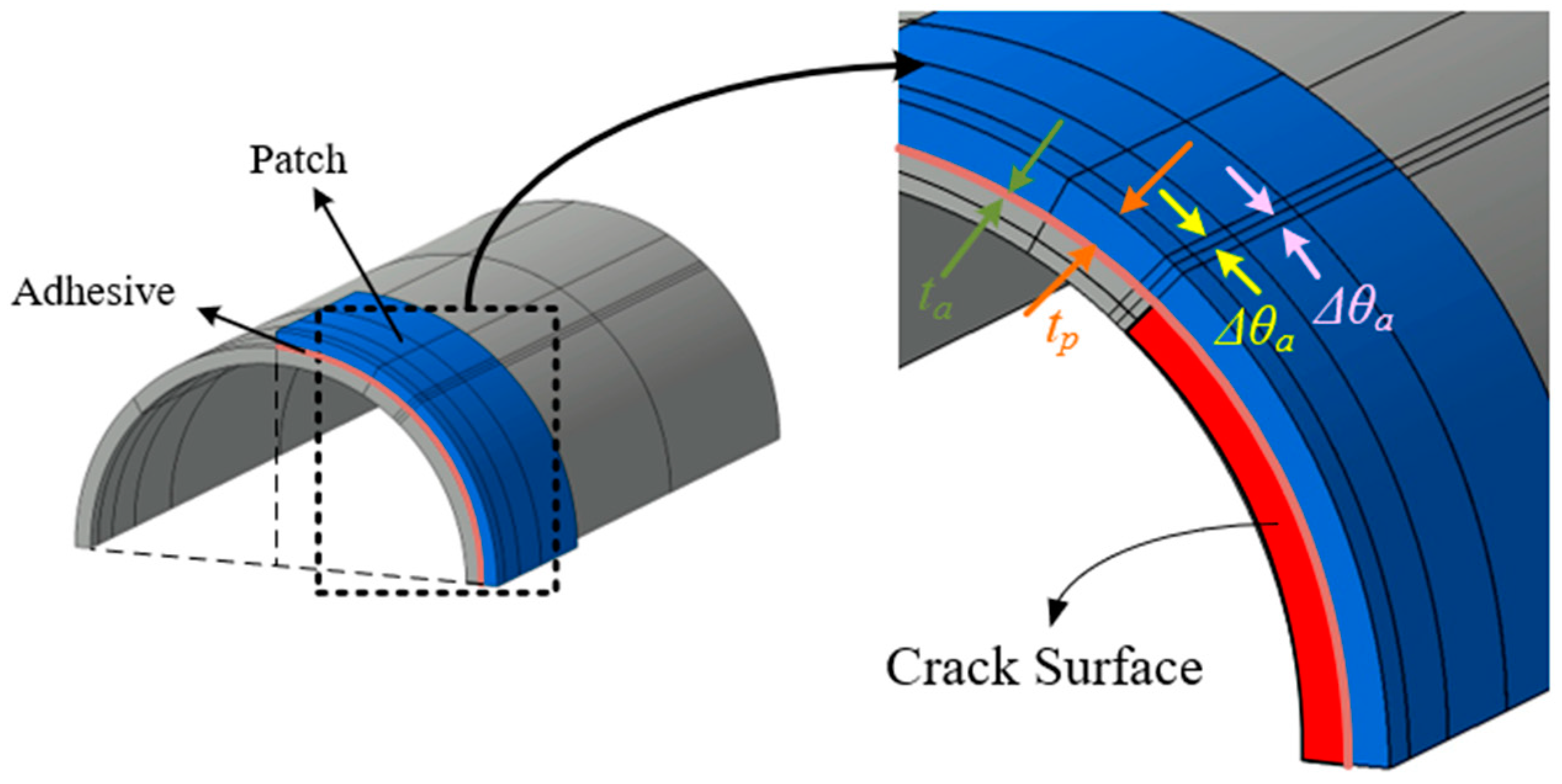
3.3. Circumferentially Cracked Shells with Composite Patches
4. Discussion
5. Conclusions
- The proposed p-version finite element model integrating ESL and LW theories significantly improves computational efficiency while maintaining high accuracy in analyzing composite-reinforced cylindrical shells.
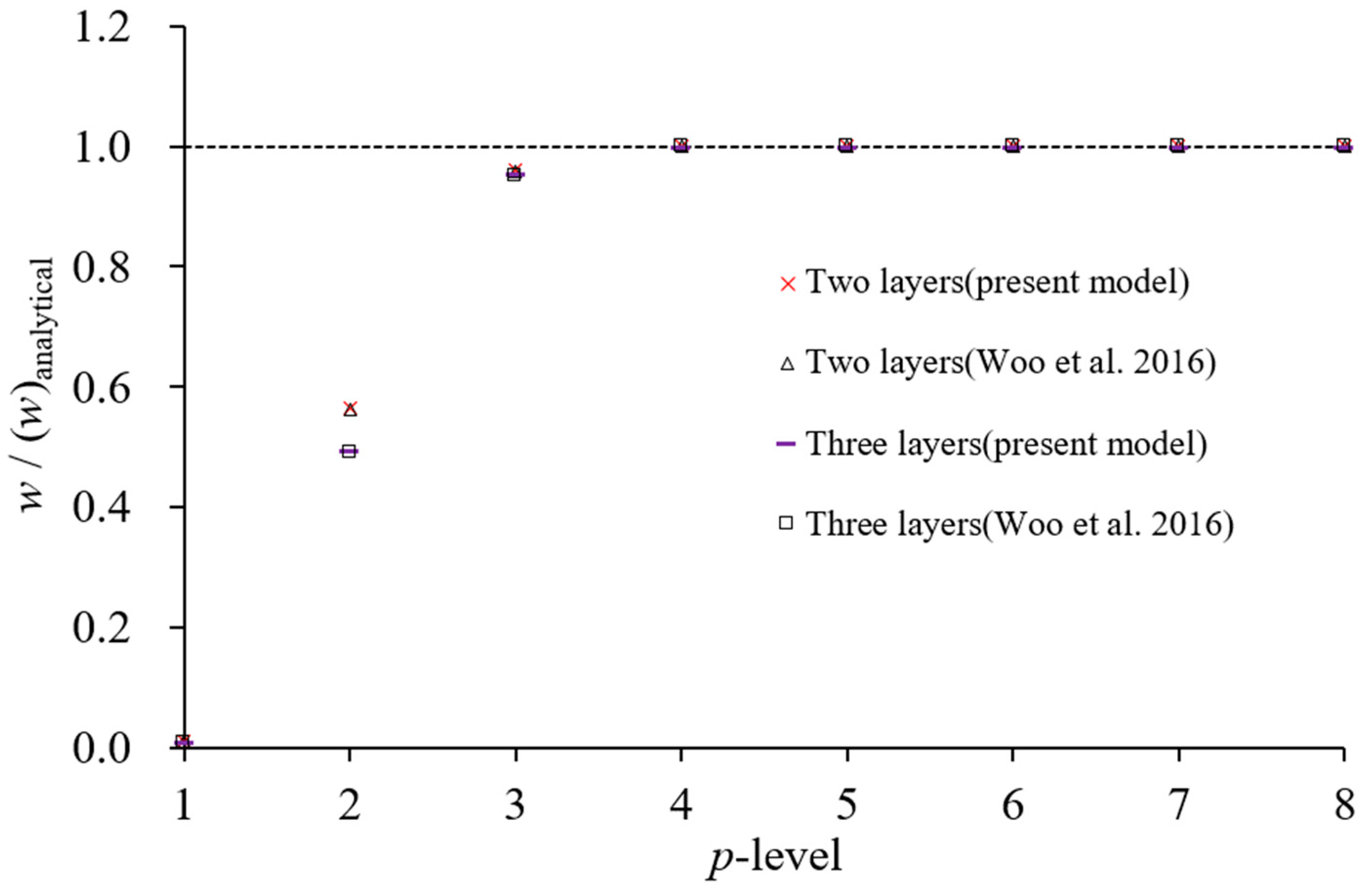
- Displacement and stress convergence studies confirmed that the proposed model reduces the need for excessive mesh refinement, achieving accurate results with fewer DOFs compared to conventional LW models.
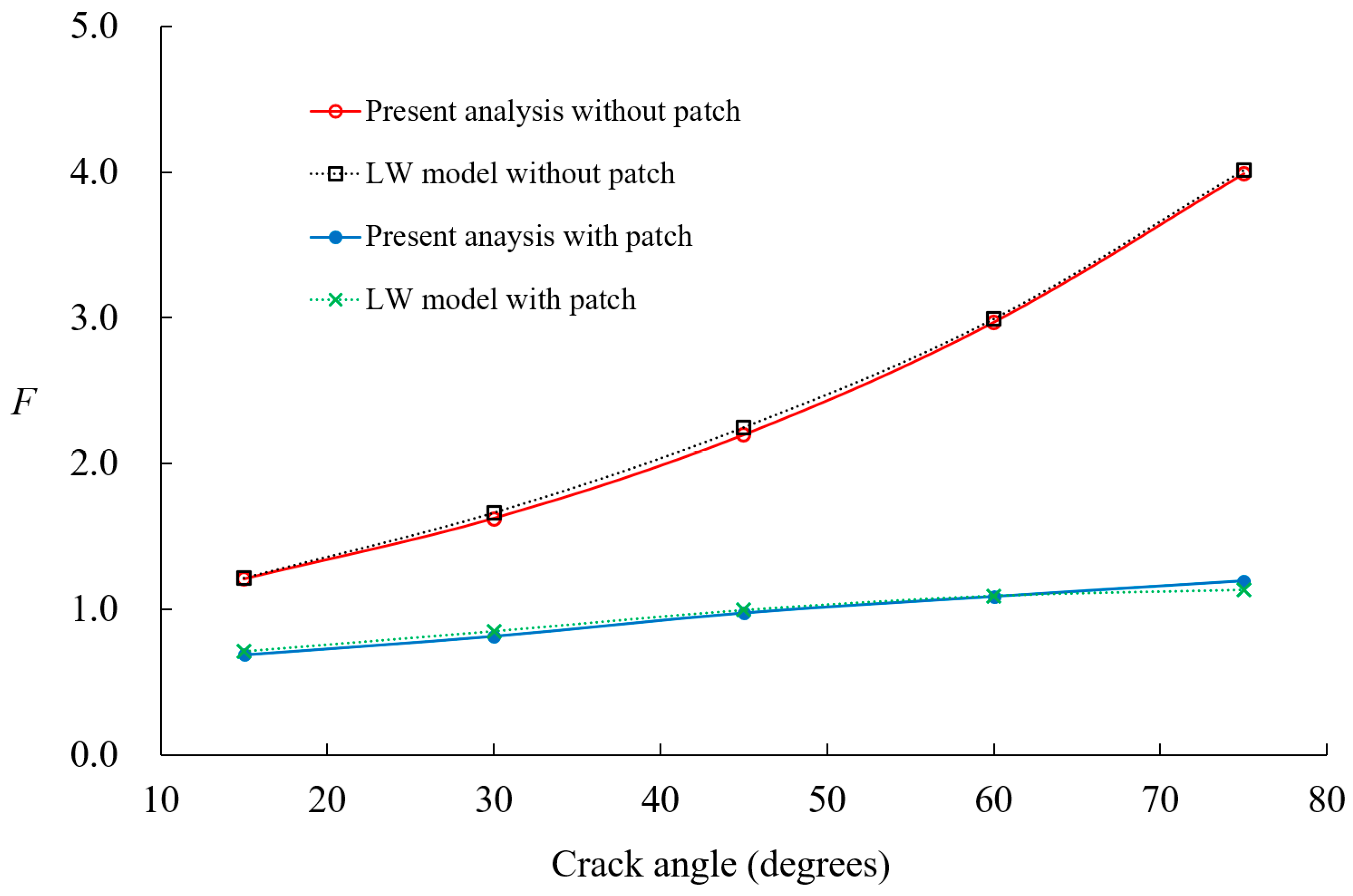
- The model effectively predicts SIF values for circumferential cracks, with relative errors within 10%, validating its accuracy against existing solutions.
- Composite patch reinforcement effectively reduces SIFs, and its effectiveness for larger cracks, particularly when the crack angle exceeds 45°, is significant.
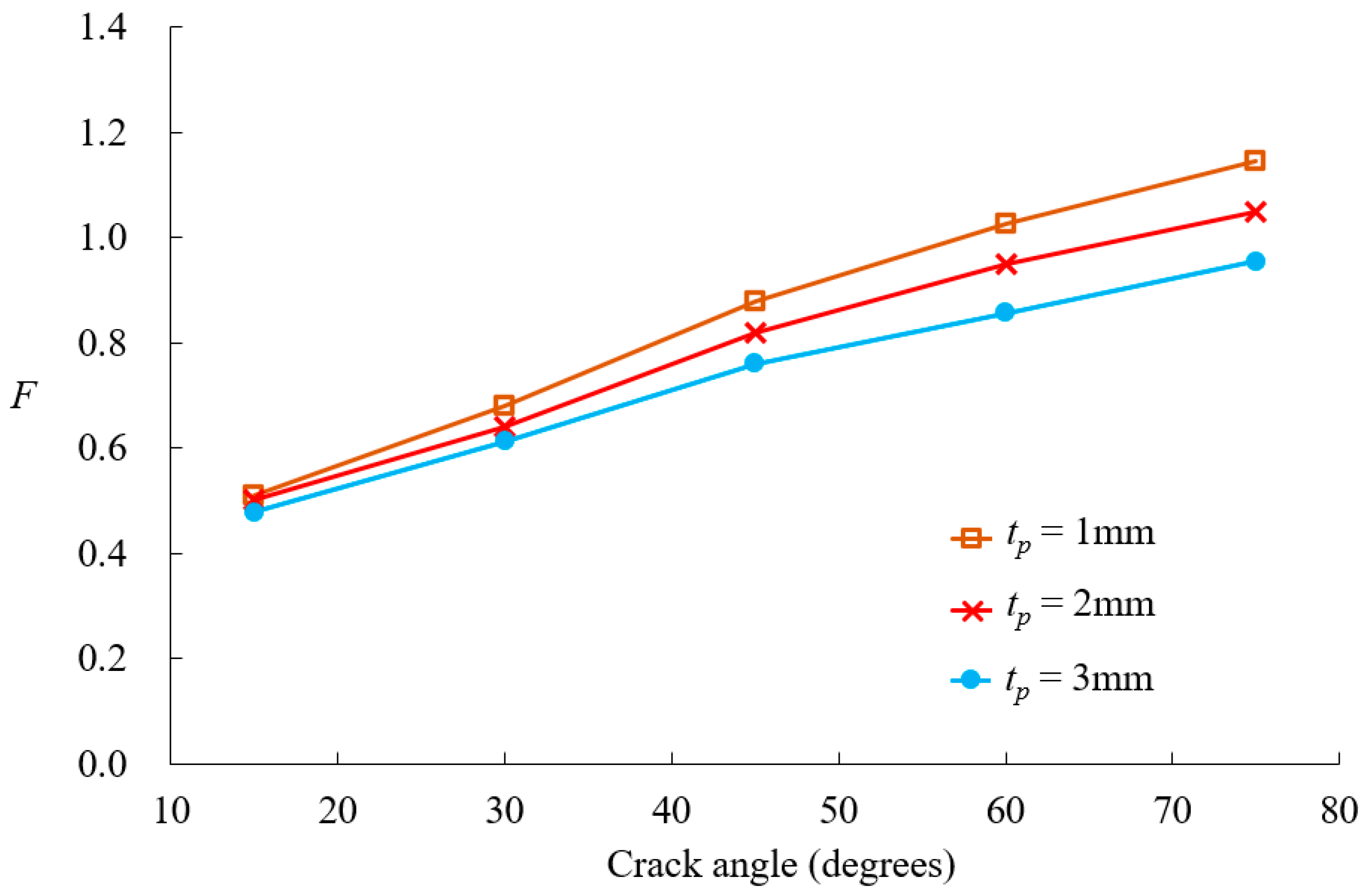
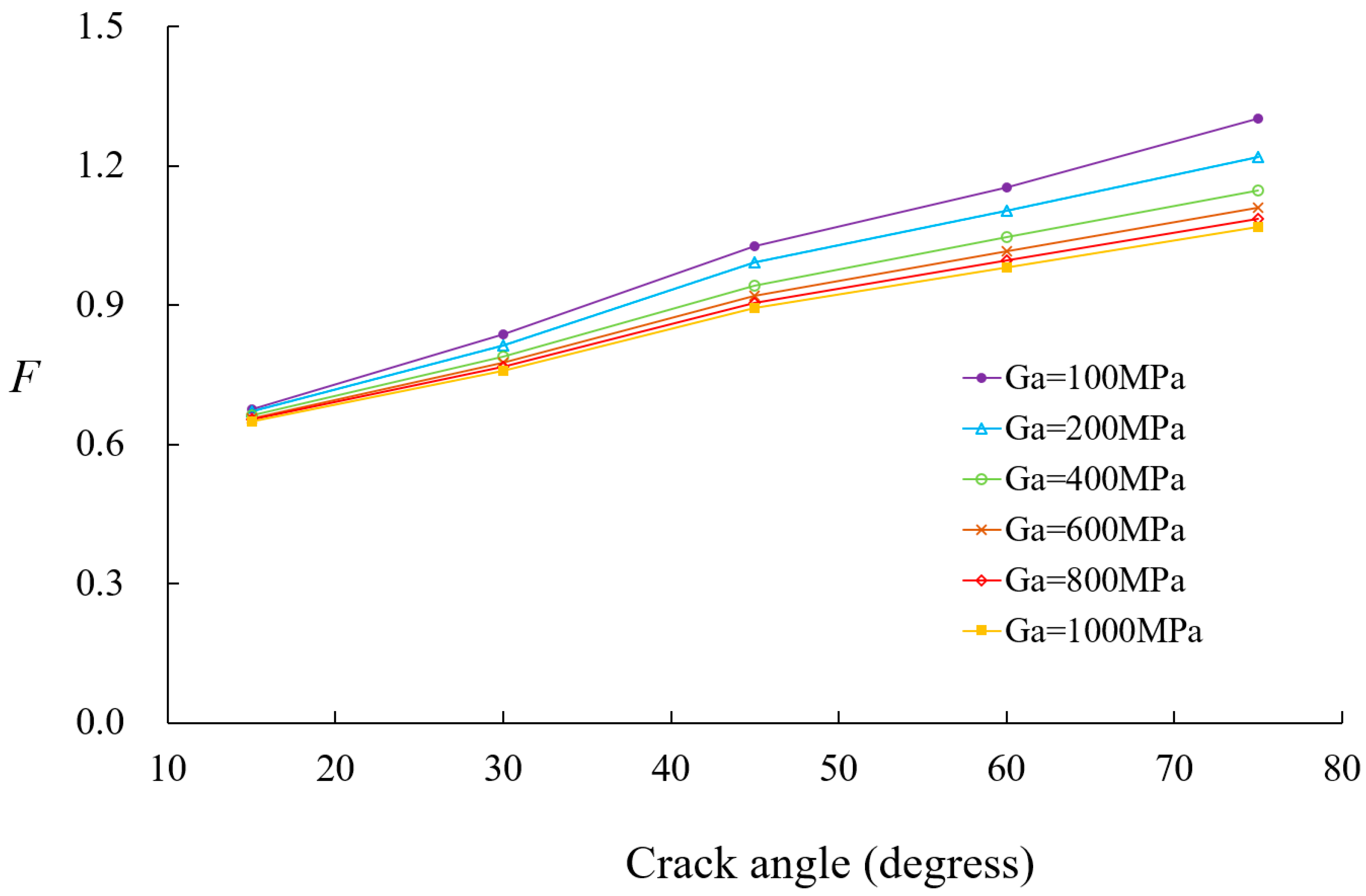
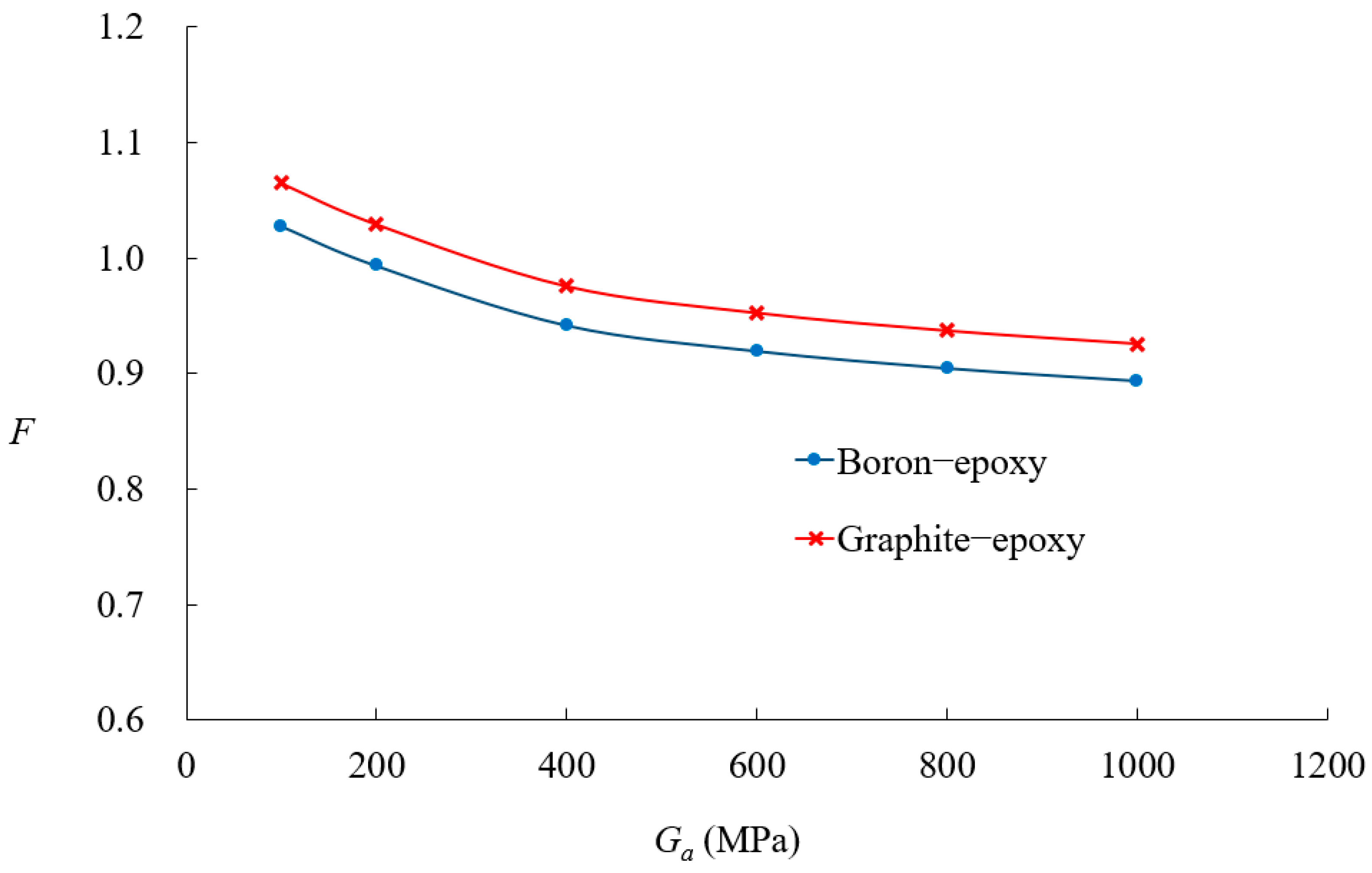
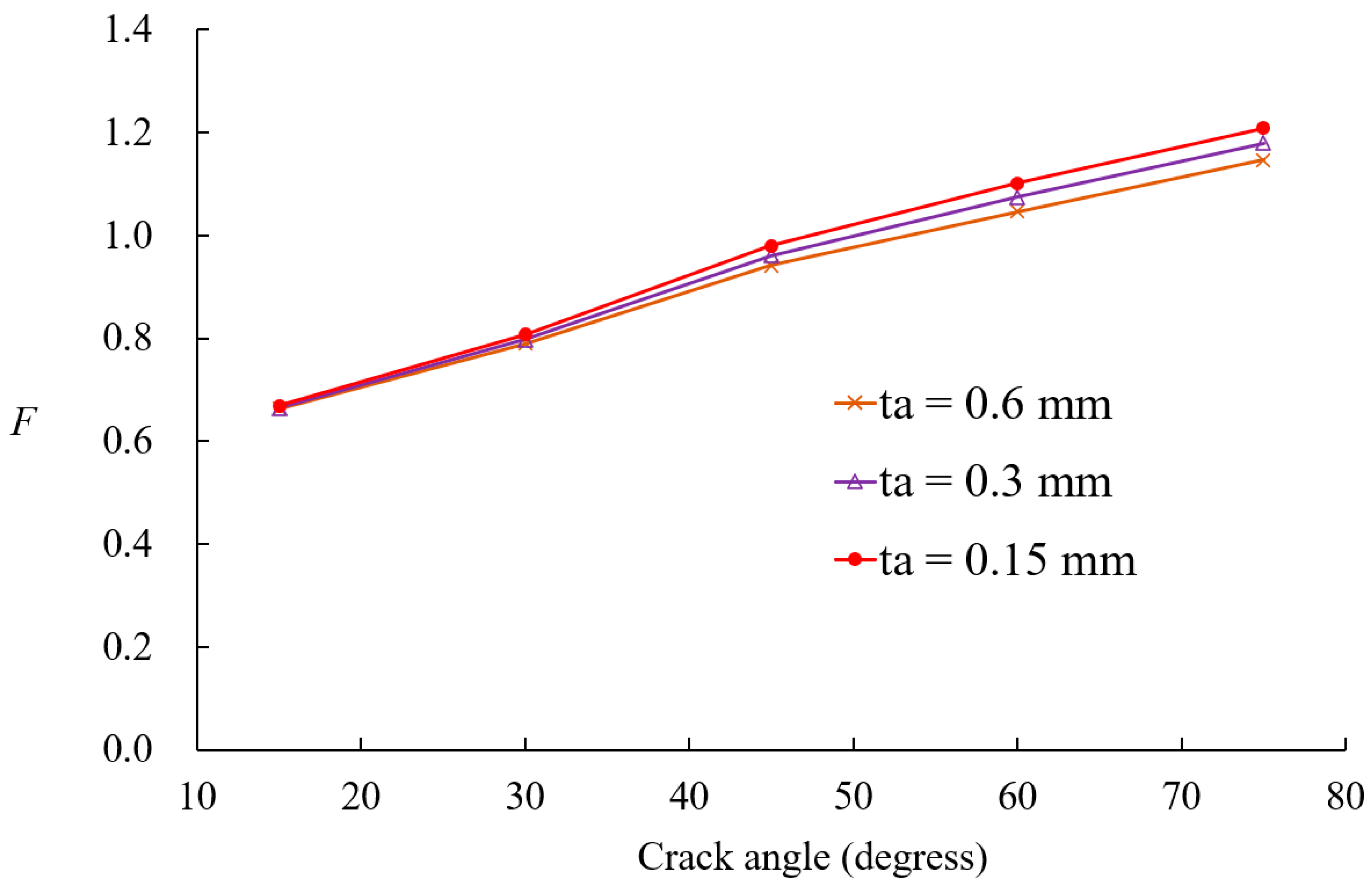
- Material stiffness has a significant impact on SIFs for large cracks, whereas patch thickness and adhesive properties have minimal influence on small cracks but become critical as crack size increases.
- Optimal adhesive properties were identified, with higher shear modulus improving reinforcement effects, but beyond 300 MPa, further increases provide diminishing benefits. Thinner adhesives were found to be more effective in reducing excessive bending effects.
- The proposed method provides a computationally efficient and robust framework for analyzing composite-reinforced cracked cylindrical shells, with applications in aerospace, marine, and pipeline engineering.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOF | Degrees of freedom |
| FEM | Finite element method |
| ESL | Equivalent single-layer |
| LW | Layer-wise |
| SIF | Stress intensity factors |
| VCCT | Virtual crack closure technique |
References
- Erdogan, F.; Ezzat, H. Fracture of Pipelines and Cylinders Containing a Circumferential Crack. Weld. Res. Counc. Bull. 1983, 288, 1–23. Available online: http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=9531116 (accessed on 10 March 2025).
- Baker, A.A. Repair of Cracked or Defective Metallic Aircraft Components With Advanced Fibre Composites—An Overview of Australian Work. Compos. Struct. 1984, 2, 153–181. [Google Scholar] [CrossRef]
- Oterkus, E.; Barut, A.; Madenci, E.; Ambur, D.R. Nonlinear Analysis of a Composite Panel With a Cutout Repaired by a Bonded Tapered Composite Patch. Int. J. Solids Struct. 2005, 42, 5274–5306. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Hashemi, R. Mixed-Mode Fracture in an Inclined Center Crack Repaired by Composite Patching. Compos. Struct. 2007, 81, 264–273. [Google Scholar] [CrossRef]
- Ellyin, F.; Ozah, F.; Xia, Z. 3-D Modelling of Cyclically Loaded Composite Patch Repair of a Cracked Plate. Compos. Struct. 2007, 78, 486–494. [Google Scholar] [CrossRef]
- Iváñez, I.; Braun, M. Numerical Analysis of Surface Cracks Repaired With Single and Double Patches of Composites. J. Compos. Mater. 2018, 52, 1113–1120. [Google Scholar] [CrossRef]
- Salem, M.; Berrahou, M.; Mechab, B.; Bouiadjra, B.B. Analysis of the Adhesive Damage for Different Patch Shapes in Bonded Composite Repair of Corroded Aluminum Plate Under Thermo-Mechanical Loading. J. Fail. Anal. Prev. 2021, 21, 1274–1282. [Google Scholar] [CrossRef]
- Benzineb, H.; Berrahou, M.; Belkaddour, L. Analysis of the Effect of Localized Corrosion Shape on a Cracked and Notched 2024 AL Plate Repaired With Composite Patch Under Thermo-Mechanical Loading. Lat. Am. J. Solids Struct. 2023, 20, e476. [Google Scholar] [CrossRef]
- Berrahou, M.; Demmouche, N. Study of the Effects of Adhesive Damage and Plasticity on the Repair of Cracked Aluminum Structures. J. Fail. Anal. Prev. 2023, 23, 1597–1607. [Google Scholar] [CrossRef]
- Bouchkara, N.H.M.; Albedah, A.; Benyahia, F.; Khan, S.M.A.; Bouiadjra, B.B. Experimental and Numerical Analyses of the Effects of Overload on the Fatigue Life of Aluminum Alloy Panels Repaired With Bonded Composite Patch. Int. J. Aeronaut. Space Sci. 2022, 22, 1075–1084. [Google Scholar] [CrossRef]
- Achour, A.; Albedah, A.; Benyahia, F.; Bouiadjra, B.A.B.; Ouinas, D. Analysis of Repaired Cracks With Bonded Composite Wrap in Pipes Under Bending. J. Press. Vessel Technol. 2016, 138, 060909. [Google Scholar] [CrossRef]
- Rashed, G.; Eskandari, H.; Savari, A. Investigating the Effectiveness of a Composite Patch on Repairing Pipes Subjected to Circumferential Cracks Under Combined Loadings. Iran. J. Oil Gas Sci. Technol. 2019, 8, 92–106. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.D.; de Barros, S. Analysis of Failure Pressure of Defective Pipes Repaired With Composite Systems Considering the Plastic Deformation of Pipe. J. Inst. Eng. (India) Ser. C 2020, 101, 929–936. [Google Scholar] [CrossRef]
- Jamal-Omidi, M.; Nabavi, S.M.; Parsania, A.H.P. The Repair of Circumferential Through-Wall Cracked Pipe by Using Local Composite Patch. J. Mar. Eng. 2020, 15, 41–51. [Google Scholar] [CrossRef]
- Yu, D.; Hossain, A.; Huang, H.; Coker, D.; Turchet, S.; Alexander, C.; Whalen, C. Composite Repair of Large-Size Diameter Pipe With Severe Metal Loss Defects. Int. Pipeline Conf. 2024, 88544, V02AT03A050. [Google Scholar] [CrossRef]
- Savari, A. Crack Assessment in Spiral-Welded Pipelines Repaired by Composite Patch: A Smart and Failure Assessment Diagram Approach. J. Pipeline Sci. Eng. 2025, 5, 100222. [Google Scholar] [CrossRef]
- Khode, A.P.; Nimje, S.V. Numerical Simulation for Stress Analysis of Functionally Graded Adhesively Bonded Composite Patch Repair System. Discov. Mech. Eng. 2023, 2, 15. [Google Scholar] [CrossRef]
- Shouman, A.; Taheri, F. Compressive Strain Limits of Composite Repaired Pipelines Under Combined Loading States. Compos. Struct. 2011, 93, 1538–1548. [Google Scholar] [CrossRef]
- Djahida, D.; Tewfik, G.; Witek, M.; Abdelghani, M. Analytical Model and Numerical Analysis of Composite Wrap System Applied to Steel Pipeline. Materials 2021, 14, 6393. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, Z.; Xin, J.; Yao, W. The Failure Mechanism Analysis of Corroded Pipelines Repaired With CFRP Under Bending Loads Using FEM. Ships Offshore Struct. 2024, 19, 549–556. [Google Scholar] [CrossRef]
- Yu, W. A Review of Modeling of Composite Structures. Materials 2024, 17, 446. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Carrera, E. Theories and Finite Elements for Multilayered Plates and Shells: A Unified Compact Formulation With Numerical Assessment and Benchmarking. Arch. Comput. Methods Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Ahn, J.S.; Basu, P.K.; Woo, K.S. Hierarchic Layer Models for Anisotropic Laminated Plates. KSCE J. Civ. Eng. 2011, 15, 1067–1080. [Google Scholar] [CrossRef]
- Carrera, E. Historical Review of Zig-Zag Theories for Multilayered Plates and Shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Li, D. Layerwise Theories of Laminated Composite Structures and Their Applications: A Review. Arch. Comput. Methods Eng. 2021, 28, 577–600. [Google Scholar] [CrossRef]
- Ahmed, N.U.; Basu, P.K. Higher-Order Finite Element Modelling of Laminated Composite Plates. Int. J. Numer. Methods Eng. 1994, 37, 123–139. [Google Scholar] [CrossRef]
- Ahn, J.S.; Basu, P.K. Locally Refined P-FEM Modeling of Patch Repaired Plates. Compos. Struct. 2011, 93, 1704–1716. [Google Scholar] [CrossRef]
- Woo, K.S.; Ahn, J.S.; Yang, S.H. Cylindrical Discrete-Layer Model for Analysis of Circumferential Cracked Pipes With Externally Bonded Composite Materials. Compos. Struct. 2016, 143, 317–323. [Google Scholar] [CrossRef]
- Wu, Y.; Xing, Y.; Liu, B. Hierarchical p-Version C1 Finite Elements on Quadrilateral and Triangular Domains With Curved Boundaries and Their Applications to Kirchhoff Plates. Int. J. Numer. Methods Eng. 2019, 119, 177–207. [Google Scholar] [CrossRef]
- Winterscheidt, D. Improved P-Version Finite Element Matrix Conditioning Using Semi-Orthogonal Modal Approximation Functions. Int. J. Numer. Methods Eng. 2022, 123, 5394–5415. [Google Scholar] [CrossRef]
- Szabó, B.; Düster, A.; Rank, E. The P-Version of the Finite Element Method. In Encyclopedia of Computational Mechanics; Stein, E., de Borst, R., Hughes, T.J.R., Eds.; Wiley: New York, NY, USA, 2004; Volume 1, pp. 119–139. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method, 3rd ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Solin, P.; Segeth, K.; Dolezel, I. Higher-Order Finite Element Methods, 1st ed.; Chapman & Hall/CRC: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A Finite Element Calculation of Stress Intensity Factors by a Modified Crack Closure Integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Varadan, T.K.; Bhaskar, K. Bending of Laminated Orthotropic Cylindrical Shells—An Elasticity Approach. Compos. Struct. 1991, 17, 141–156. [Google Scholar] [CrossRef]
- Cheng, Z.Q.; He, L.H.; Kitipornchai, S. Influence of Imperfect Interfaces on Bending and Vibration of Laminated Composite Shells. Int. J. Solids Struct. 2000, 37, 2127–2150. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook; ASME: New York, NY, USA, 2000. [Google Scholar]
- Zahoor, A. Closed Form Expressions for Fracture Mechanics Analysis of Cracked Pipes. J. Press. Vessel Technol. Trans. ASME 1985, 107, 203–205. [Google Scholar] [CrossRef]
- Sanders, J.L.; Lyell, J. Circumferential Through-Cracks in Cylindrical Shells Under Tension. J. Appl. Mech. Trans. ASME 1982, 49, 103–107. [Google Scholar] [CrossRef]
- Ting, T.; Jones, R.; Chiu, W.K.; Marshall, I.H.; Greer, J.M. Composites Repairs to Rib-Stiffened Panels. Compos. Struct. 1999, 47, 737–743. [Google Scholar] [CrossRef]



| Variables | R/h | Present | Reference [18] | Reference [23] | Reference [24] |
|---|---|---|---|---|---|
| w | 50 | 2.2398 | 2.2419 | 2.2420 | 2.2372 |
| 100 | 1.3668 | 1.3669 | 1.3670 | 1.3666 | |
| 500 | 0.1005 | 0.1005 | 0.1005 | 0.1005 | |
| σx-top | 50 | 0.2188 | 0.2189 | 0.2189 | 0.2187 |
| 100 | 0.1871 | 0.1871 | 0.1871 | 0.1871 | |
| 500 | 0.0449 | 0.0449 | 0.0449 | 0.0449 | |
| σx-bot | 50 | 1.6087 | 1.6099 | 1.6100 | 1.6051 |
| 100 | 2.2984 | 2.2998 | 2.3000 | 2.2979 | |
| 500 | 0.9436 | 0.9436 | 0.9436 | 0.9436 | |
| σθ-top | 50 | 8.9421 | 8.9368 | 8.9370 | 8.9543 |
| 100 | 5.5630 | 5.5603 | 5.5600 | 5.5643 | |
| 500 | 0.4345 | 0.4345 | 0.4345 | 0.4346 | |
| σθ-bot | 50 | −0.9656 | −0.9668 | −0.9670 | −0.9615 |
| 100 | −0.5755 | −0.5758 | −0.5759 | −0.5750 | |
| 500 | −0.03389 | −0.0339 | −0.0339 | −0.0339 | |
| τtop | 50 | 0.0783 | 0.0783 | 0.0784 | 0.0784 |
| 100 | 0.1819 | 0.1819 | 0.1819 | 0.1819 | |
| 500 | 0.0925 | 0.0925 | 0.0925 | 0.0925 | |
| τbot | 50 | 0.3444 | 0.3444 | 0.3444 | 0.3444 |
| 100 | 0.3414 | 0.3414 | 0.3414 | 0.3414 | |
| 500 | 0.1045 | 0.1045 | 0.1045 | 0.1045 |
| Variables | R/h | Present | Reference [29] | Reference [36] | Reference [37] |
|---|---|---|---|---|---|
| w | 50 | 0.5490 | 0.5494 | 0.5495 | 0.5486 |
| 100 | 0.4712 | 0.4715 | 0.4715 | 0.4711 | |
| 500 | 0.1027 | 0.1027 | 0.1027 | 0.1027 | |
| σx-top | 50 | 0.0711 | 0.0712 | 0.0712 | 0.0710 |
| 100 | 0.0838 | 0.0838 | 0.0838 | 0.0837 | |
| 500 | 0.0559 | 0.0559 | 0.0559 | 0.0559 | |
| σx-bot | 50 | −0.0220 | −0.0223 | −0.0225 | −0.0217 |
| 100 | 0.0019 | 0.0018 | 0.0018 | 0.0020 | |
| 500 | 0.0379 | 0.0379 | 0.0379 | 0.0379 | |
| σθ-top | 50 | 3.9287 | 3.9299 | 3.9300 | 3.9265 |
| 100 | 3.5068 | 3.5070 | 3.5070 | 3.5048 | |
| 500 | 0.7896 | 0.7895 | 0.7895 | 0.7897 | |
| σθ-bot | 50 | −3.9869 | −3.9869 | −3.9870 | −3.9870 |
| 100 | −3.5069 | −3.5069 | −3.5070 | −3.5063 | |
| 500 | −0.7543 | −0.7543 | −0.7542 | −0.7545 | |
| τtop | 50 | 0.0120 | 0.0119 | 0.0118 | 0.0123 |
| 100 | 0.0479 | 0.0478 | 0.0478 | 0.0480 | |
| 500 | 0.0766 | 0.0766 | 0.0766 | 0.0766 | |
| τbot | 50 | 0.0761 | 0.0760 | 0.0760 | 0.0764 |
| 100 | 0.1038 | 0.1038 | 0.1038 | 0.1039 | |
| 500 | 0.0889 | 0.0889 | 0.0889 | 0.0889 |
| Types | Crack Angles (Degrees) | ||||
|---|---|---|---|---|---|
| 15 | 30 | 45 | 60 | 75 | |
| Present analysis | 1.2064 | 1.6221 | 2.1954 | 2.9667 | 3.9847 |
| Reference [29] | 1.2167 | 1.664 | 2.2484 | 2.9913 | 4.0102 |
| Reference [39] | 1.1915 | 1.5564 | 2.075 | 2.8002 | 3.8295 |
| Reference [40] | 1.1854 | 1.4961 | - | - | - |
| Materials | E1 | E2, E3 | G12, G13 | G23 | ν12, ν13 | ν23 |
|---|---|---|---|---|---|---|
| Boron-epoxy | 208 | 25.4 | 7.24 | 4.94 | 0.168 | 0.035 |
| Graphite-epoxy | 172 | 10.3 | 4.83 | 3.10 | 0.300 | 0.180 |
| Adhesive | 0.965 | - | - | - | 0.32 | - |
| Types | p-Level | |||||
| 2 | 3 | 4 | 5 | 6 | 7 | |
| Present model | 1371 | 2922 | 5053 | 7764 | 11,055 | 14,926 |
| p-version LW model [29] | 4122 | 8760 | 15,126 | 23,220 | 33,042 | 44,592 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, J.S. Computationally Efficient p-Version Finite Element Analysis of Composite-Reinforced Thin-Walled Cylindrical Shells with Circumferential Cracks. Materials 2025, 18, 1404. https://doi.org/10.3390/ma18071404
Ahn JS. Computationally Efficient p-Version Finite Element Analysis of Composite-Reinforced Thin-Walled Cylindrical Shells with Circumferential Cracks. Materials. 2025; 18(7):1404. https://doi.org/10.3390/ma18071404
Chicago/Turabian StyleAhn, Jae S. 2025. "Computationally Efficient p-Version Finite Element Analysis of Composite-Reinforced Thin-Walled Cylindrical Shells with Circumferential Cracks" Materials 18, no. 7: 1404. https://doi.org/10.3390/ma18071404
APA StyleAhn, J. S. (2025). Computationally Efficient p-Version Finite Element Analysis of Composite-Reinforced Thin-Walled Cylindrical Shells with Circumferential Cracks. Materials, 18(7), 1404. https://doi.org/10.3390/ma18071404






