Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body
Abstract
1. Introduction
2. Methodology
- (1)
- The FE model of the complete vehicle was required to be positively validated in accordance with the reference standard EN 12663-1:2015 [19]. Although loading conditions were consistently applied to the entire vehicle, it was essential for the reference car body to exhibit adequate mechanical performance, particularly regarding stress concentrations and modal behavior. Therefore, a comprehensive analysis of the vehicle was conducted for both materials.
- (2)
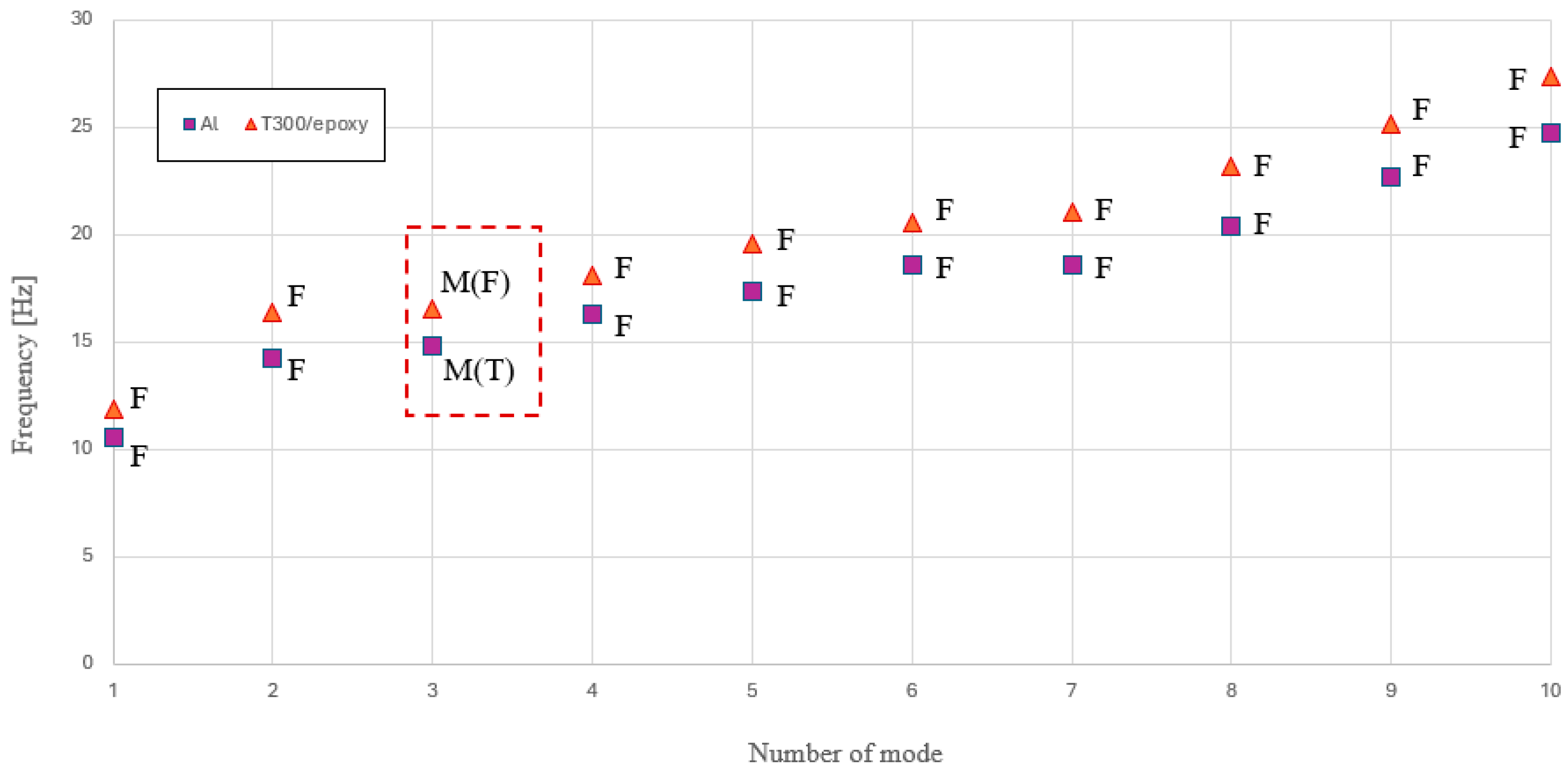
- The reference car body was then isolated, incorporating all relevant components influencing the system’s dynamic behavior, like suspended equipment, modeled as concentrated masses. A modal analysis was conducted to assess its dynamic characteristics under free-free boundary conditions, observing potential differences in terms of eigenvalues and eigenvectors of the system. The first vibration frequency was subsequently considered as a constraint in the optimization process.
- (3)
- The optimization approach was implemented on the reference car body with the aim of minimizing mass while ensuring the required dynamic performance, specifically in terms of the minimum vibration frequency.
- (4)
- In order to complete the verification process, the innovative structure was subsequently subjected to a complete static analysis according to the reference standard.
3. Light Rail Vehicle Description
Structural Materials in Comparison
4. FE Dynamic Optimization: Results and Discussion
4.1. FE Model and Analysis Settings
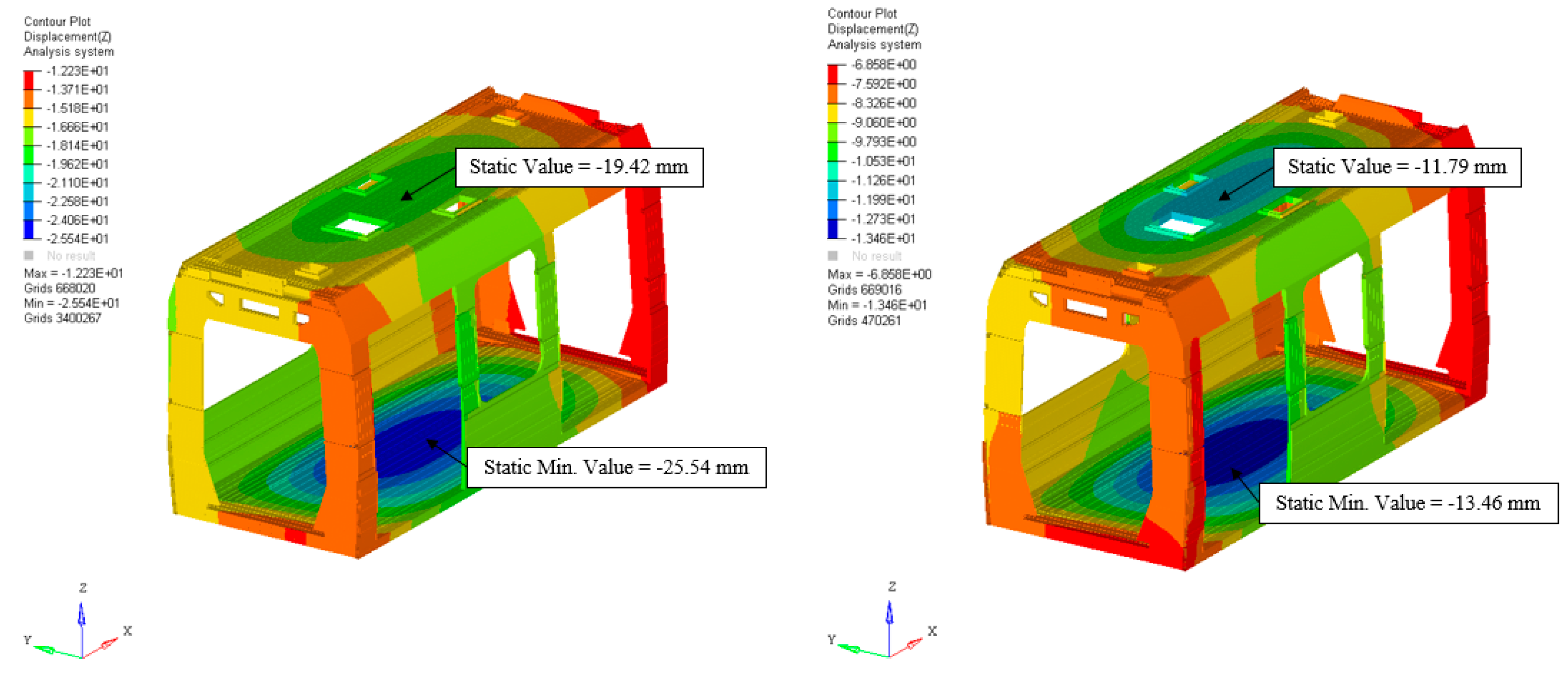
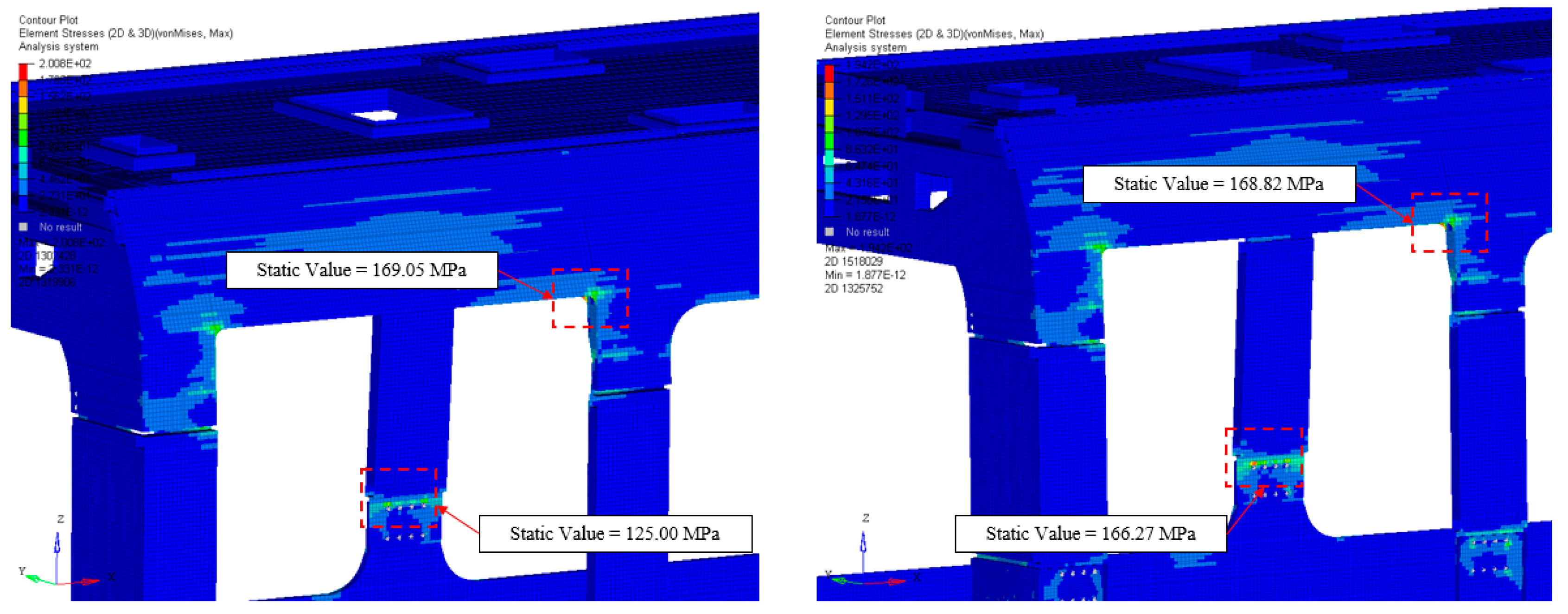
4.2. Static Analysis of the Complete Vehicle
4.3. Modal Analysis of the Single Car Body
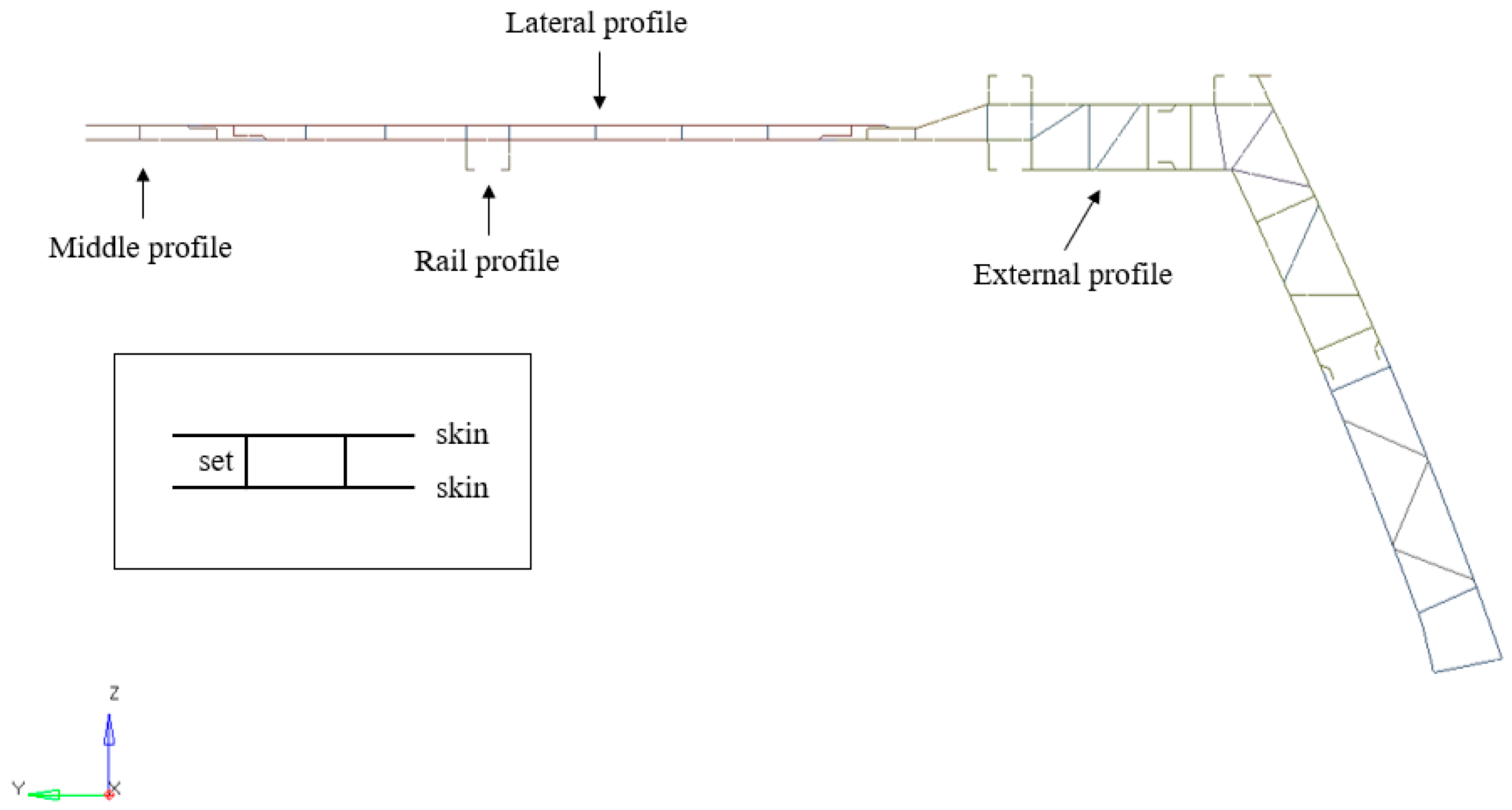
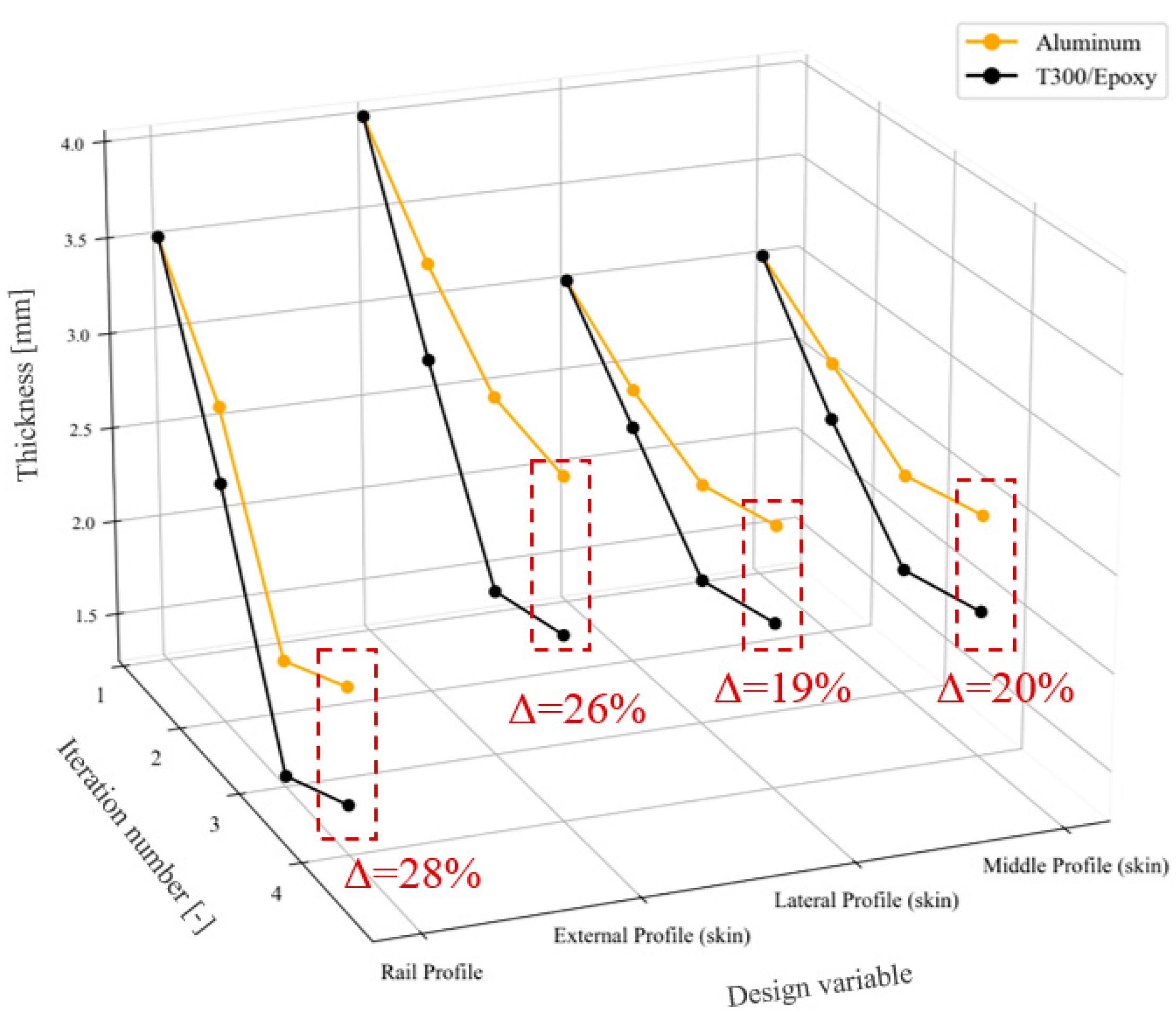
4.4. Dynamic Size Optimization of the Single Car Body
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faruk, D.; Tolga, E. Estimating national exhaust emissions from railway. Sci. Total Environ. 2007, 374, 127–134. [Google Scholar]
- Mayer, R.M.; Poulikakos, L.D.; Lees, A.R. Reducing the environmental impact of road and rail vehicles. Environ. Impact Assess. Rev. 2012, 32, 25–32. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M. Current Trends in Metallic Materials for Body Panels and Structural Members Used in the Automotive Industry. Materials 2024, 17, 590. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chevali, V.S.; Wang, H.; Wang, C.-H. Current status of carbon fibre and carbon fibre composites recycling. Compos. Part B Eng. 2020, 193, 108053. [Google Scholar] [CrossRef]
- Saeedi, A.; Motavalli, M.; Shahverdi, M. Recent advancements in the applications of fiber-reinforced polymer structures in railway industry—A review. Polym. Compos. 2024, 45, 77–97. [Google Scholar] [CrossRef]
- Muhammad, A.; Rahman, M.R.; Baini, R.; Bakri, M.K.B. Advances in Sustainable Polymer Composites; Woodhead Publishing: Sawston, UK, 2021; ch. 8. [Google Scholar]
- Arifurrahman, F.; Budiman, B.A.; Aziz, M. On the lightweight structural design for electric road and railway vehicles using fiber reinforced polymer composites—A review. Int. J. Sustain. Transp. 2018, 1, 21–29. [Google Scholar]
- Jagadeesh, P.; Puttegowda, M.; Oladijo, O.P.; Lai, C.W.; Gorbatyuk, S.; Matykiewicz, D.; Rangappa, S.M.; Siengchin, S. A comprehensive review on polymer composites in railway applications. Polym. Compos. 2022, 43, 1238. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. Development of a Design Procedure Combining Topological Optimization and a Multibody Environment: Application to a Tram Motor Bogie Frame. Vehicles 2024, 6, 1843–1856. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints. Eng 2024, 5, 1485–1498. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A New Strategy for Railway Bogie Frame Designing Combining Structural–Topological Optimization and Sensitivity Analysis. Vehicles 2024, 6, 651–665. [Google Scholar] [CrossRef]
- Grasso, M.; Gallone, A.; Genovese, A.; Macera, L.; Penta, F.; Pucillo, G.; Strano, S. Composite material design for rail vehicle innovative lightweight components. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2015. [Google Scholar]
- Yang, C.; Ying, G.; Guo, W.; Yang, Y.; Xu, P.; Alqahtani, M.S. High-velocity impact behaviour of curved GFRP composites for rail vehicles: Experimental and numerical study. Polym. Test. 2022, 116, 107774. [Google Scholar]
- Harte, A.M.; McNamara, J.F.; Roddy, I.D. A multilevel approach to the optimization of a composite light rail vehicle bodyshell. Compos. Struct. 2004, 63, 447–453. [Google Scholar]
- Hudson, C.W.; Carruthers, J.J.; Robinson, A.M. Multiple objective optimisation of composite sandwich structures for rail vehicle floor panels. Compos. Struct. 2010, 92, 2077–2082. [Google Scholar]
- Miao, B.; Luo, Y.; Peng, Q.; Qiu, Y.; Chen, H.; Yang, Z. Multidisciplinary design optimization of lightweight car body for fatigue assessment. Mater. Des. 2020, 194, 108910. [Google Scholar]
- Cascino, A.; Meli, E.; Rindi, A. Dynamic size optimization approach to support railway carbody lightweight design process. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2023, 237, 871–881. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A strategy for lightweight designing of a railway vehicle car body including composite material and dynamic structural optimization. Rail. Eng. Sci. 2023, 31, 340–350. [Google Scholar] [CrossRef]
- EN 12663-1:2015; Railway Applications—Structural Requirements of Railway Vehicle Bodies—Part 1: Locomotives and Passenger Rolling Stock (and Alternative Method for Freight Wagons). Deutsches Institut für Normung: Berlin, Germany, 2015.
- UNI EN 1999-1-1:2014; Eurocode 9: Design of Aluminium Structures—Part 1-1: General Rules—General Rules and Rules for Buildings. Ente Nazionale Italiano di Unificazione: Roma, Italy, 2014.
- Fantuzzi, N.; Dib, A.; Babamohammadi, S.; Campigli, S.; Benedetti, D.; Agnelli, J. Mechanical analysis of a carbon fibre composite woven composite laminate for ultra-light applications in aeronautics. Compos. Part C Open Access 2024, 14, 100447, ISSN 2666-6820. [Google Scholar]
- Bradley, A. Newcomb, Processing, structure, and properties of carbon fibers. Compos. Part A Appl. Sci. Manuf. 2016, 91, 262–282, ISSN 1359-835X. [Google Scholar]
- UNI EN 15663:2019; Railway Applications—Vehicle Reference Masses. Ente Nazionale Italiano di Unificazione: Roma, Italy, 2019.
- Park, G.J. Analytic Methods for Design Practice; Springer: Berlin, Germany, 2007. [Google Scholar]



| Material | Density | Young’s Modulus | Proof Strength (0.2%) | Ultimate Tensile Strength | Proof Strength (0.2%) | Ultimate Tensile Strength | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Base Material | Weld Material | ||||||
| [kg/m3] | [N/mm2] | [N/mm2] | [N/mm2] | [-] | |||
| EN AW 6005 T6 | 2700 | 70,000 | 215 | 255 | 115 | 165 | 0.30 |
| EN AW 6106 T6 | 2700 | 70,000 | 200 | 250 | 95 | 160 | 0.30 |
| Material | Density | Young’s Modulus | Ultimate Tensile Strength | Ultimate Compressive Strength | Elongation at Break |
|---|---|---|---|---|---|
| [kg/m3] | [N/mm2] | [N/mm2] | [N/mm2] | [%] | |
| T300/epoxy | 1760 | 135,000 | 1860 | 1460 | 1.5–2.0 |
| Index | Type of Load | Load Formula |
|---|---|---|
| 1 | Vertical | Vertical load = 1.3 × g × C4 |
| 2 | Compressive on buffers, C0 condition | Vertical load = C0 × g Longitudinal force = 200,000 N |
| 3 | Compressive on buffers, C4 condition | Vertical load = C4 × g Longitudinal force = 200,000 N |
| 4 | Tensile on drawbar, C0 condition | Vertical load = C0 × g Longitudinal force = 55,000 N |
| 5 | Compressive on drawbar, C0 condition | Vertical load = C0 × g Longitudinal force = 100,000 N |
| Design Variable | Starting Thickness | Range of Thickness Variation (Max–Min) | Optimized Thickness (Aluminum) | Optimized Thickness (T300/Epoxy) | |
|---|---|---|---|---|---|
| [-] | [mm] | [mm] | [mm] | [mm] | |
| Middle profile | skin | 3.0 | 3.0–1.0 | 2.5 | 2.0 |
| rib | 3.0 | 3.0–1.0 | 1.5 | 1.2 | |
| Lateral profile | skin | 3.0 | 3.0–1.0 | 2.6 | 2.1 |
| rib | 3.0 | 3.0–1.0 | 2.6 | 2.0 | |
| External profile | skin | 4.0 | 4.0–1.0 | 3.0 | 2.2 |
| rib | 3.0 | 3.0–1.0 | 2.2 | 1.6 | |
| Rail profile | 3.5 | 3.5–1.0 | 2.1 | 1.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cascino, A.; Meli, E.; Rindi, A. Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body. Materials 2025, 18, 1501. https://doi.org/10.3390/ma18071501
Cascino A, Meli E, Rindi A. Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body. Materials. 2025; 18(7):1501. https://doi.org/10.3390/ma18071501
Chicago/Turabian StyleCascino, Alessio, Enrico Meli, and Andrea Rindi. 2025. "Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body" Materials 18, no. 7: 1501. https://doi.org/10.3390/ma18071501
APA StyleCascino, A., Meli, E., & Rindi, A. (2025). Comparative Analysis and Dynamic Size Optimization of Aluminum and Carbon Fiber Thin-Walled Structures of a Railway Vehicle Car Body. Materials, 18(7), 1501. https://doi.org/10.3390/ma18071501








