Electric Field-Defined Superlattices in Bilayer Graphene: Formation of Topological Bands in Two Dimensions
Abstract
1. Introduction and Model Description
2. Computational Methods
3. Results and Discussion
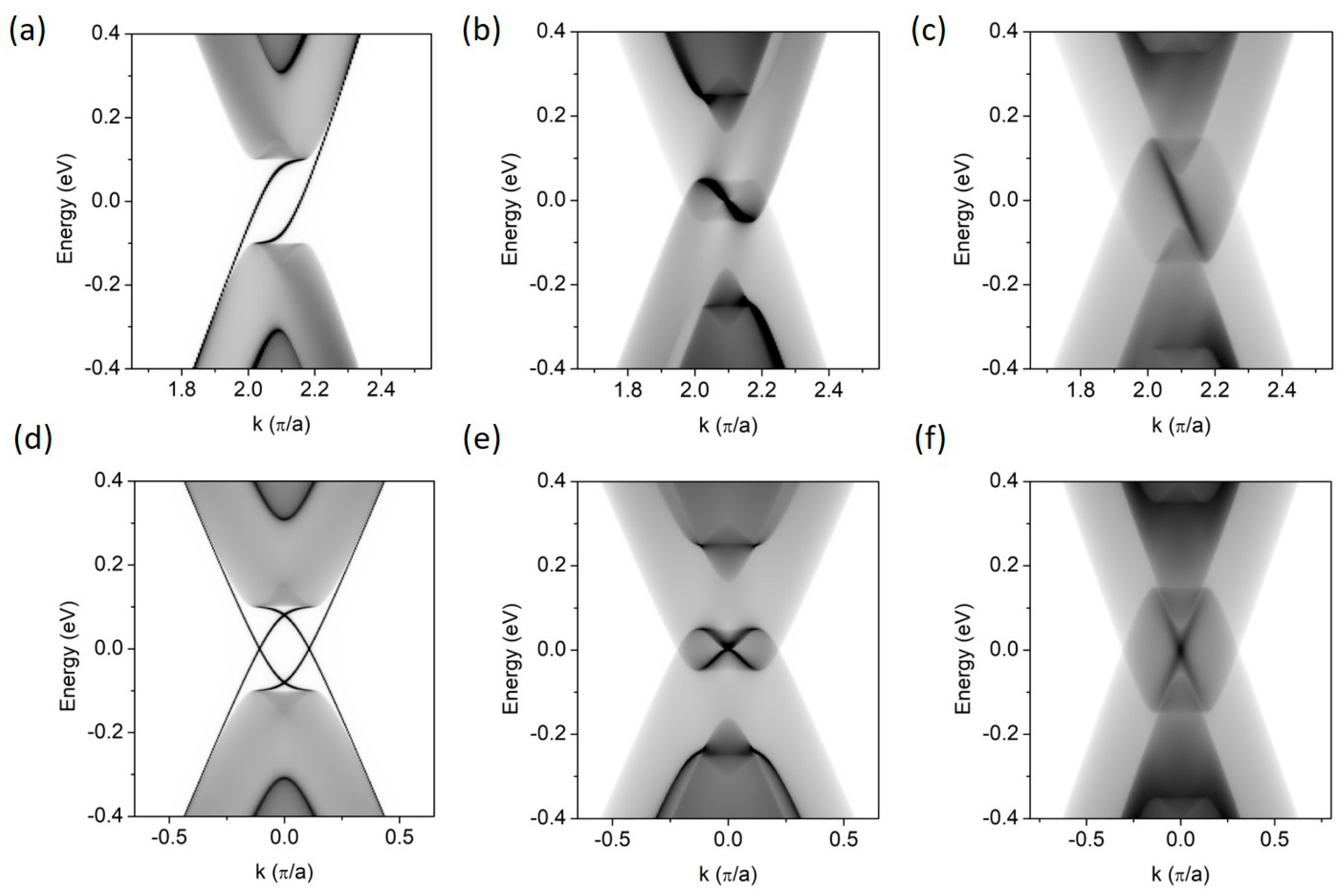
3.1. Single EFW
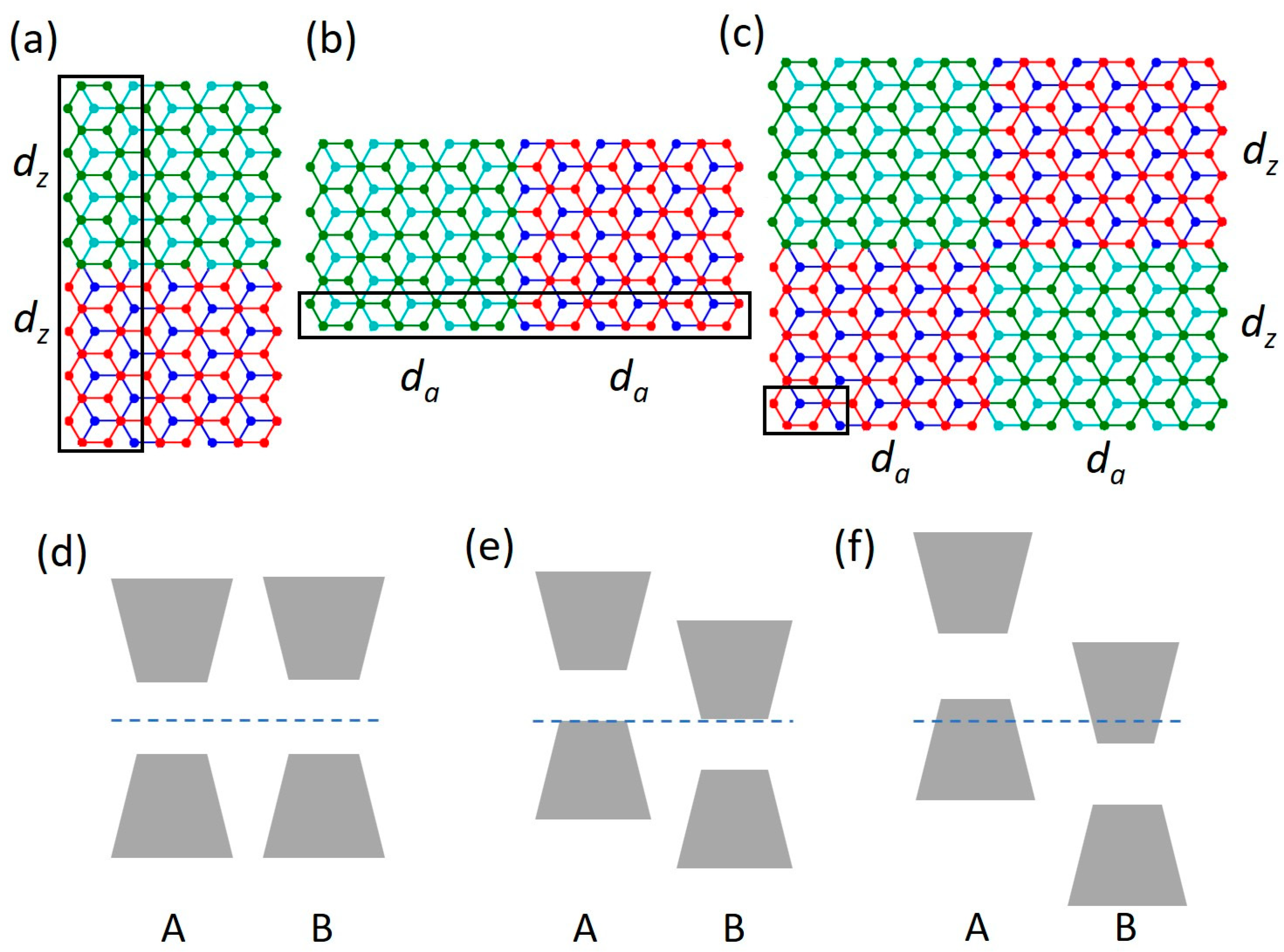
3.2. One-Dimensional Superlattices
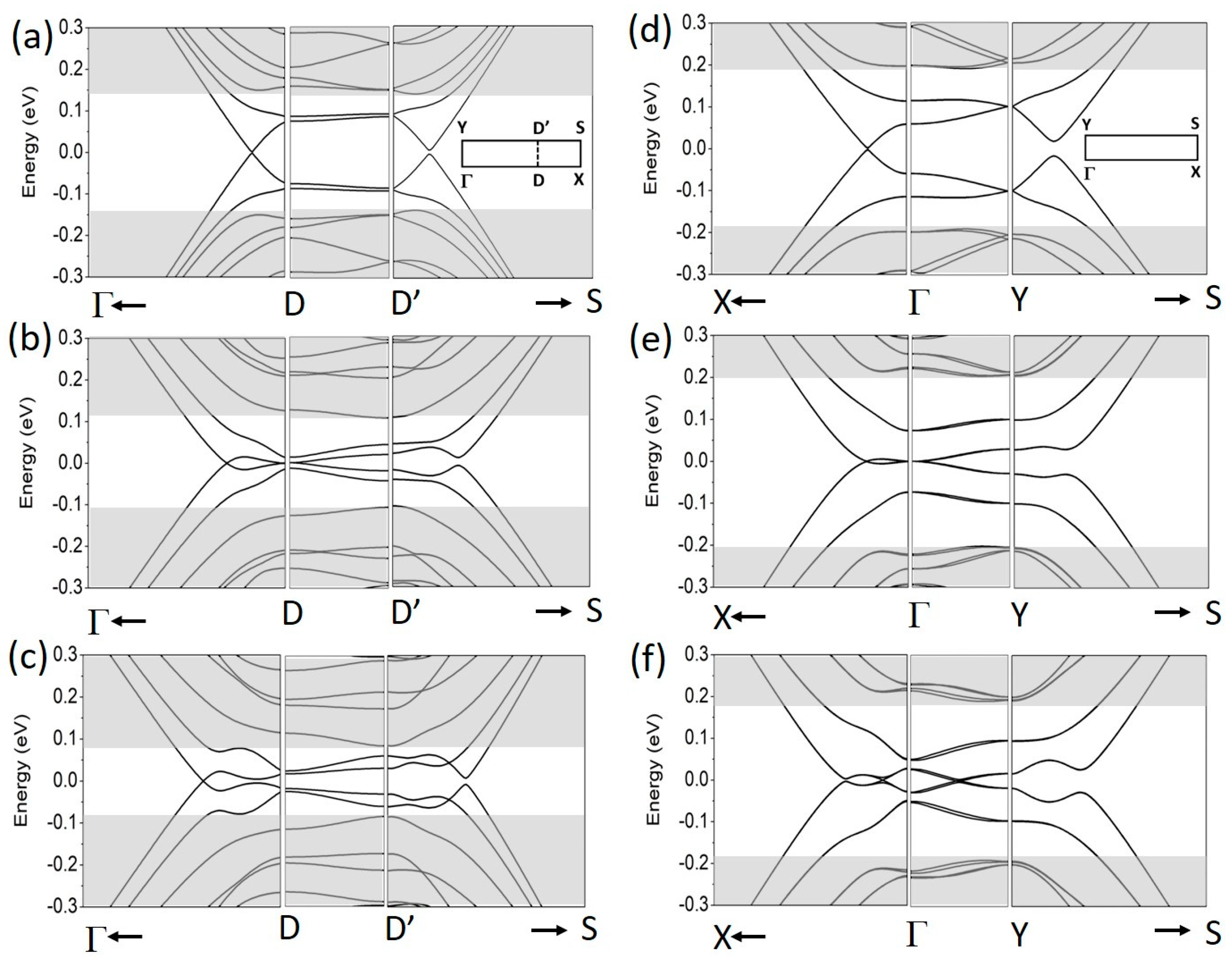
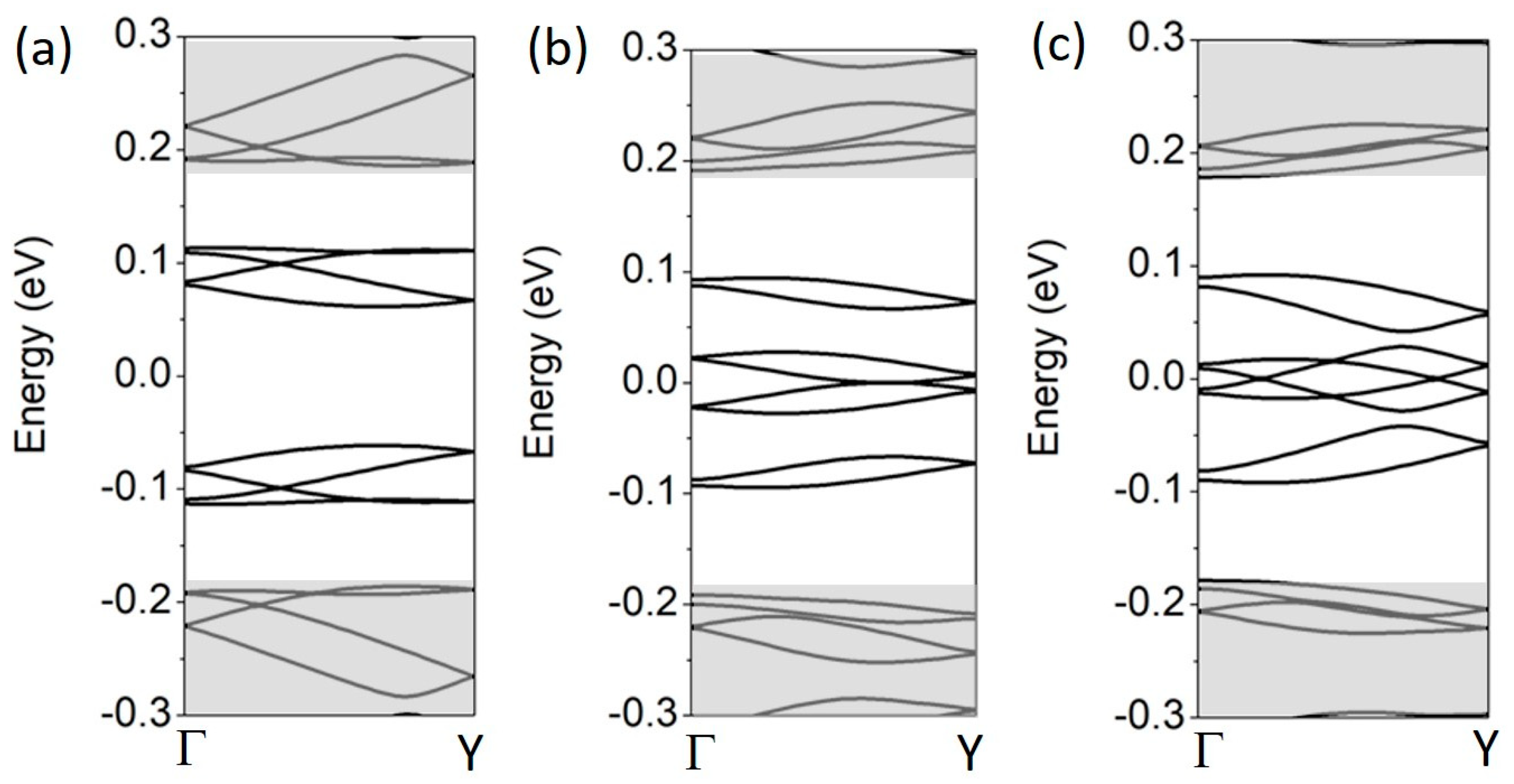
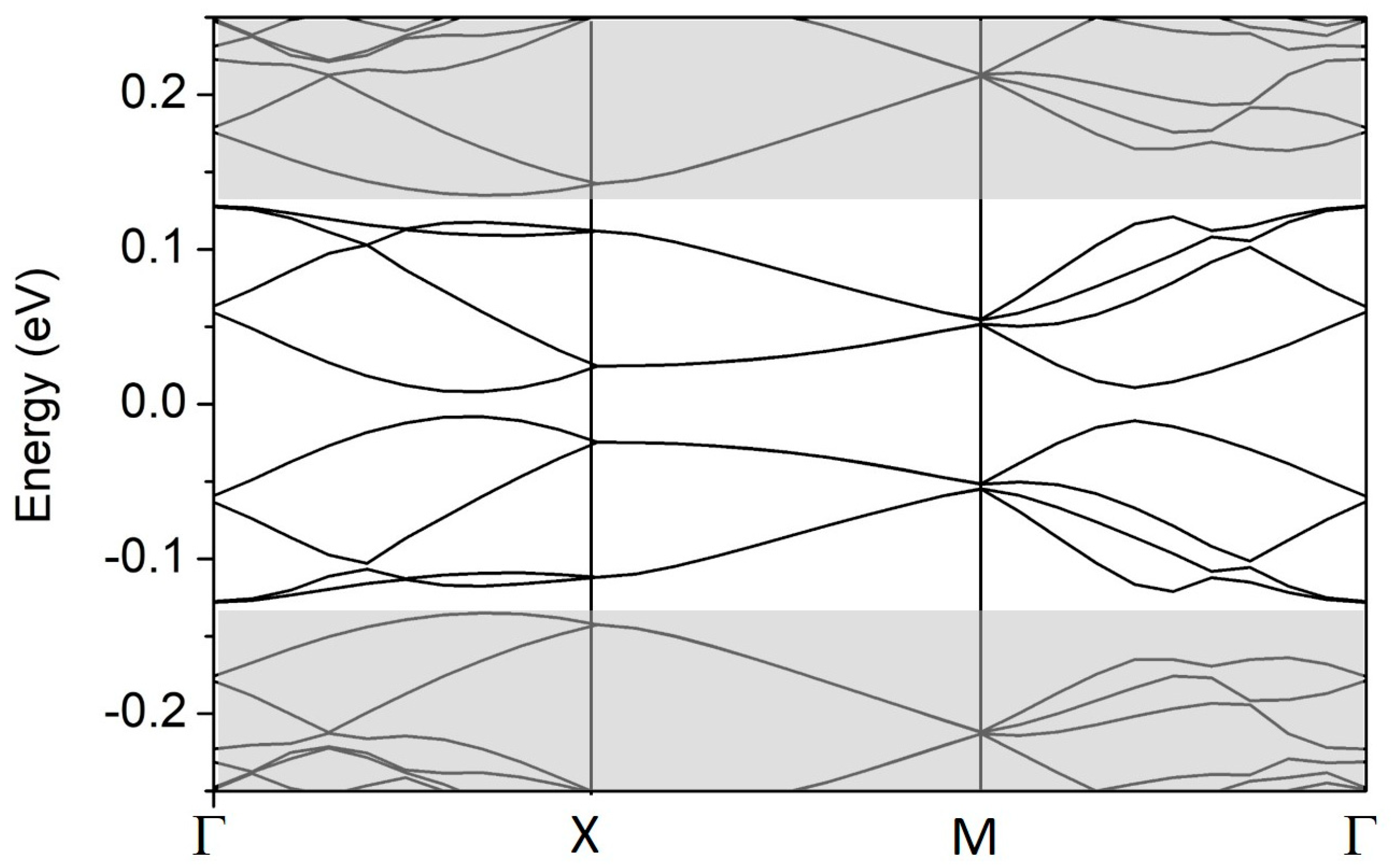
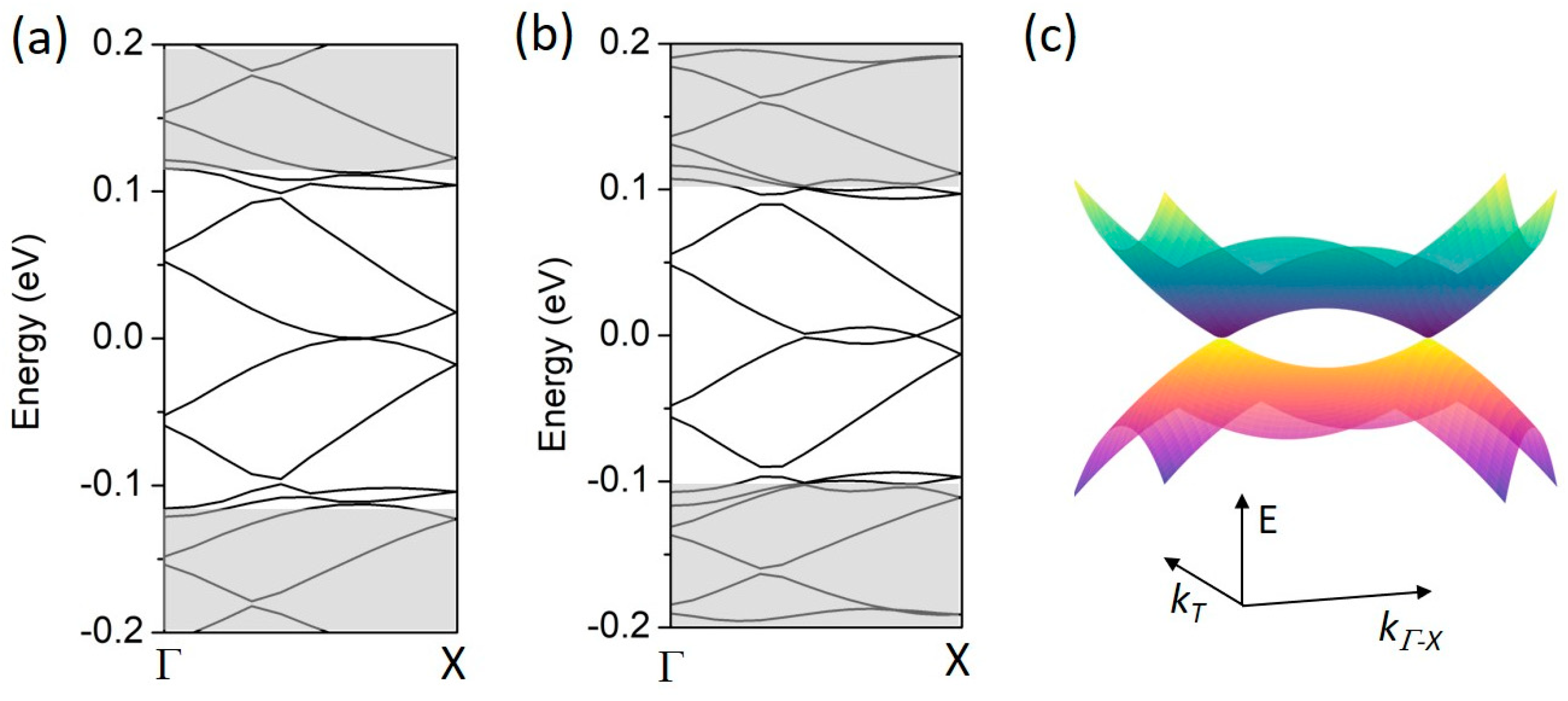
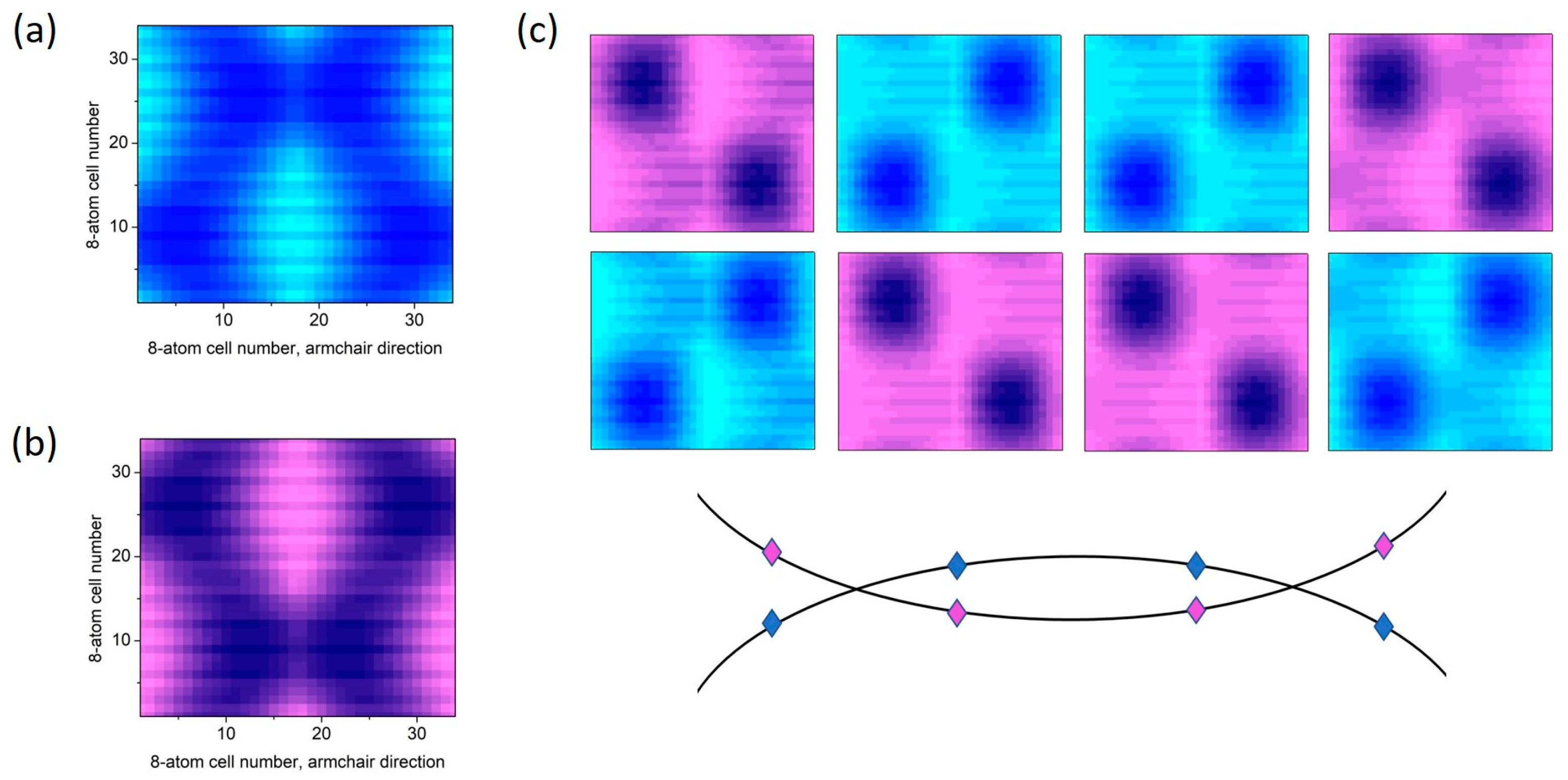
3.3. Two-Dimensional Superlattices
4. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; MacDonald, A.H.; Mele, E.J. Valley Chern numbers and boundary modes in gapped bilayer graphene. Proc. Natl. Acad. Sci. USA 2013, 110, 10546. [Google Scholar] [CrossRef] [PubMed]
- San-Jose, P.; Gorbachev, R.V.; Geim, A.K.; Novoselov, K.S.; Guinea, F. Stacking Boundaries and Transport in Bilayer Graphene. Nano Lett. 2014, 14, 2052. [Google Scholar] [CrossRef] [PubMed]
- Vaezi, A.; Liang, Y.; Ngai, D.H.; Yang, L.; Kim, E.-A. Topological Edge States at a Tilt Boundary in Gated Multilayer Graphene. Phys. Rev. X 2013, 3, 021018. [Google Scholar] [CrossRef]
- Pelc, M.; Jaskólski, W.; Ayuela, A.; Chico, L. Topologically confined states at corrugations of gated bilayer graphene. Phys. Rev. B 2015, 92, 085433. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; McFaul, K.J.; Zern, Z.; Ren, Y.; Watanabe, K.; Taniguchi, T.; Qiao, Z.; Zhu, J. Gate-controlled topological conducting channels in bilayer graphene. Nat. Nanotechnol. 2016, 11, 1060. [Google Scholar] [CrossRef] [PubMed]
- Jaskolski, W.; Pelc, M.; Bryant, G.W.; Chico, L.; Ayuela, A. Controlling the layer localization of gapless states in bilayer graphene with a gate voltage. 2D Mater. 2018, 5, 025006. [Google Scholar] [CrossRef]
- Koshino, M. Electronic transmission through AB-BA domain boundary in bilayer graphene. Phys. Rev. B 2013, 88, 115409. [Google Scholar] [CrossRef]
- Jung, J.; Zhang, F.; Qiao, Z.; MacDonald, A.H. Valley-Hall kink and edge states in multilayer graphene. Phys. Rev. B 2011, 84, 075418. [Google Scholar] [CrossRef]
- Ju, L.; Shi, Z.; Nair, N.; Lv, Y.; Jin, C.; Velasco, J., Jr.; Ojeda-Aristizabal, C.; Bechtel, H.A.; Martin, M.C.; Zettl, A.; et al. Topological valley transport at bilayer graphene domain walls. Nature 2015, 520, 650–655. [Google Scholar] [CrossRef]
- Alden, J.S.; Tsen, A.W.; Huang, P.Y.; Hovden, R.; Brown, L.; Park, J.; Muller, D.A.; McEuen, P.L. Strain solitons and topological defects in bilayer graphene. Proc. Natl. Acad. Sci. USA 2013, 110, 11256. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, S.; Zhao, S.; Crommie, M.; Wang, F. Soliton-Dependent Electronic Transport across Bilayer Graphene Domain Wall. Nano Lett. 2020, 20, 5936. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Blanter, Y.M.; Morpurgo, A.F. Topological Confinement in Bilayer Graphene. Phys. Rev. Lett. 2008, 100, 036804. [Google Scholar] [CrossRef] [PubMed]
- Klinovaja, J.; Ferreira, G.J.; Loss, D. Helical states in curved bilayer graphene. Phys. Rev. B 2012, 86, 235416. [Google Scholar] [CrossRef]
- Zarenia, M.; Pereira, J.M.; Farias, G.A.; Peeters, F.M. Chiral states in bilayer graphene: Magnetic field dependence and gap opening. Phys. Rev. B 2011, 84, 125451. [Google Scholar] [CrossRef]
- de Sena, S.H.R.; Pereira, J.M.; Peeters, F.M.; Farias, G.A. Topological confinement in trilayer graphene. Phys. Rev. B 2014, 89, 035420. [Google Scholar] [CrossRef]
- Mazo, V.; Huang, C.-W.; Shimshoni, E.; Carr, S.T.; Fertig, H.A. Superfluid-insulator transition of quantum Hall domain walls in bilayer graphene. Phys. Rev. B 2014, 89, 121411. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Chittari, B.L.; Chen, G.; Zhang, L.; Wang, F.; Jung, J. Gate-Tunable Topological Flat Bands in Trilayer Graphene Boron-Nitride Moiré Superlattices. Phys. Rev. Lett. 2019, 122, 016401. [Google Scholar] [CrossRef]
- Yin, L.-J.; Yang, L.-Z.; Zhang, L.; Wu, Q.; Fu, X.; Tong, L.-H.; Yang, G.; Tian, Y.; Zhang, L.; Qin, Z. Imaging of nearly flat induced atomic-scale negative differential conductivity in ABC-stacked trilayer graphene. Phys. Rev. B 2020, 102, 241403. [Google Scholar] [CrossRef]
- Pons, R.; Mielke, A.; Stauber, T. Flat-band ferromagnetism in twisted bilayer graphene. Phys. Rev. B 2020, 102, 235101. [Google Scholar] [CrossRef]
- Culchac, F.J.; Del Grande, R.R.; Capaz, R.B.; Chico, L.; Suárez Morell, E. Flat bands and gaps in twisted double bilayer graphene. Nanoscale 2020, 12, 5014. [Google Scholar] [CrossRef] [PubMed]
- Suárez Morell, E.; Correa, J.D.; Vargas, P.; Pacheco, M.; Barticevic, Z. Flat bands in slightly twisted bilayer graphene: Tight-binding calculations. Phys. Rev. B 2010, 82, 121407. [Google Scholar] [CrossRef]
- Morell, E.S.; Pacheco, M.; Chico, L.; Brey, L. Electronic properties of twisted trilayer graphene. Phys. Rev. B 2013, 87, 125414. [Google Scholar] [CrossRef]
- Chen, E.; Sharpe, A.L.; Gallagher, P.; Rosen, I.T.; Fox, E.J.; Jiang, L.; Lyou, B.; Li, H.; Watanabe, K.; Taniguchi, T.; et al. Signatures of tunable superconductivity in a trilayer graphene moire superlattice. Nature 2019, 572, 215. [Google Scholar] [CrossRef]
- Liu, X.; Hao, Z.; Khalaf, E.; Lee, J.Y.; Ronen, Y.; Yoo, H.; Najafabadi, D.H.; Watanabe, K.; Taniguchi, T.; Vishwanath, A.; et al. Tunable spin-polarized correlated states in twisted double bilayer graphene. Nature 2020, 583, 221. [Google Scholar] [CrossRef]
- Shen, C.; Chu, Y.; Wu, Q.; Li, N.; Wang, S.; Zhao, Y.; Tang, J.; Liu, J.; Tian, J.; Watanabe, K.; et al. Correlated states in twisted double bilayer graphene. Nat. Phys. 2020, 16, 520. [Google Scholar] [CrossRef]
- Zeng, J.; Xue, R.; Hou, T.; Han, Y.; Qiao, Z. Formation of topological domain walls and quantum transport properties of zero-line modes in commensurate bilayer graphene systems. Front. Phys. 2022, 17, 63503. [Google Scholar] [CrossRef]
- Ghorashi, S.A.A.; Dunbrack, A.; Abouelkomsan, A.; Sun, J.; Du, X.; Cano, J. Topological and Stacked Flat Bands in Bilayer Graphene with a Superlattice Potential. Phys. Rev. Lett. 2023, 130, 196201. [Google Scholar] [CrossRef]
- Ghorashi, S.A.A.; Cano, J. Multilayer graphene with a superlattice potential. Phys. Rev. B 2023, 107, 195423. [Google Scholar] [CrossRef]
- Killi, M.; Wu, S.; Paramekanti, A. Band Structures of Bilayer Graphene Superlattices. Phys. Rev. Lett. 2011, 107, 086801. [Google Scholar] [CrossRef]
- Sun, J.; Ghorashi, S.A.A.; Watanabe, K.; Taniguchi, T.; Camino, F.; Cano, J.; Du, X. Signature of Correlated Insulator in Electric Field Controlled Superlattice. Nano Lett. 2024, 24, 13600–13606. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Wolf, T.M.R.; Huang, C.; Wei, N.; Ghorashi, S.A.A.; MacDonald, A.H.; Cano, J. Gate-tunable topological phases in superlattice modulated bilayer graphene. Phys. Rev. B 2024, 109, 195406. [Google Scholar] [CrossRef]
- Tan, T.; Reddy, A.P.; Fu, L.; Devakul, T. Designing Topology and Fractionalization in Narrow Gap Semiconductor Films via Electrostatic Engineering. Phys. Rev. Lett. 2024, 133, 206601. [Google Scholar] [CrossRef] [PubMed]
- Crepel, V.; Cano, J. Efficient Prediction of Superlattice and Anomalous Miniband Topology from Quantum Geometry. Phys. Rev. X 2025, 15, 011004. [Google Scholar] [CrossRef]
- Jaskolski, W. Controlling spin polarization of gapless states in defected trilayer graphene with a gate voltage. Physica E 2024, 157, 115878. [Google Scholar] [CrossRef]
- Castro, E.V.; Novoselov, K.S.; Morozov, S.V.; Peres, N.M.R.; Lopes dos Santos, J.M.B.; Nilsson, J.; Guinea, F.; Geim, A.K.; Castro Neto, A.H. Biased Bilayer Graphene: Semiconductor with a Gap Tunable by the Electric Field Effect. Phys. Rev. Lett. 2007, 99, 216802. [Google Scholar] [CrossRef]
- Otha, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the Electronic Structure of Bilayer Graphene. Science 2006, 313, 951. [Google Scholar] [CrossRef]
- Freitas, R.R.Q.; de Brito Mota, F.; Rivelino, F.; de Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Spin-orbit-induced gap modification in buckled honeycomb XBi and XBi3 (X = B, Al, Ga, and In) sheets. J. Phys. Condens. Matter 2015, 27, 485306. [Google Scholar] [CrossRef]
- Nardelli, M.B. Electronic transport in extended systems: Application to carbon nanotubes. Phys. Rev. B 1999, 60, 7828–7833. [Google Scholar] [CrossRef]
- Santos, H.; Ayuela, A.; Jaskólski, W.; Pelc, M.; Chico, L. Interface states in carbon nanotube junctions: Rolling up graphene. Phys. Rev. B 2009, 80, 035436. [Google Scholar] [CrossRef]
- Jaskolski, W.; Ayuela, A.; Pelc, M.; Santos, H.; Chico, L. Edge states and flat bands in graphene nanoribbons with arbitrary geometries. Phys. Rev. B 2011, 83, 235424. [Google Scholar] [CrossRef]
- Jaskolski, W. Single-layer graphene with electronic properties of a gated bilayer. Phys. Rev. B 2019, 100, 035436. [Google Scholar] [CrossRef]
- Lee, C.; Kim, G.; Jung, J.; Min, H. Zero-line modes at stacking faulted domain walls in multilayer graphene. Phys. Rev. B 2016, 94, 125438. [Google Scholar] [CrossRef]
- Naselli, G.; Konye, V.; Das, S.K.; Angilella, G.G.N.; Isaeva, A.; van den Brink, J.; Fulga, C. Nontrivial gapless electronic states at the stacking faults of weak topological insulators. Phys. Rev. B 2022, 106, 094105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaskólski, W. Electric Field-Defined Superlattices in Bilayer Graphene: Formation of Topological Bands in Two Dimensions. Materials 2025, 18, 1521. https://doi.org/10.3390/ma18071521
Jaskólski W. Electric Field-Defined Superlattices in Bilayer Graphene: Formation of Topological Bands in Two Dimensions. Materials. 2025; 18(7):1521. https://doi.org/10.3390/ma18071521
Chicago/Turabian StyleJaskólski, Włodzimierz. 2025. "Electric Field-Defined Superlattices in Bilayer Graphene: Formation of Topological Bands in Two Dimensions" Materials 18, no. 7: 1521. https://doi.org/10.3390/ma18071521
APA StyleJaskólski, W. (2025). Electric Field-Defined Superlattices in Bilayer Graphene: Formation of Topological Bands in Two Dimensions. Materials, 18(7), 1521. https://doi.org/10.3390/ma18071521





