Compressive Response and Damage Distribution of Fiber-Reinforced Concrete with Various Saturation Degrees
Abstract
:1. Introduction
2. Raw Materials and Test Scheme
2.1. Raw Materials
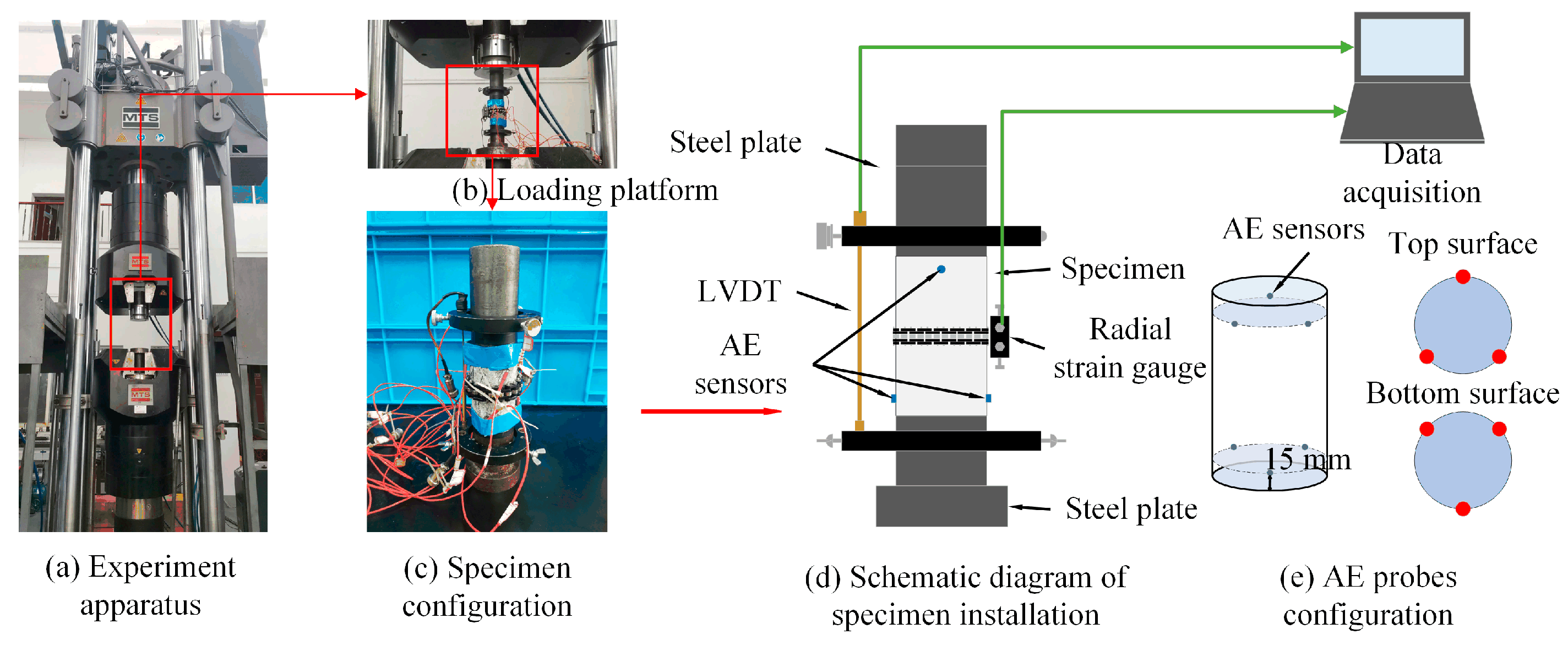
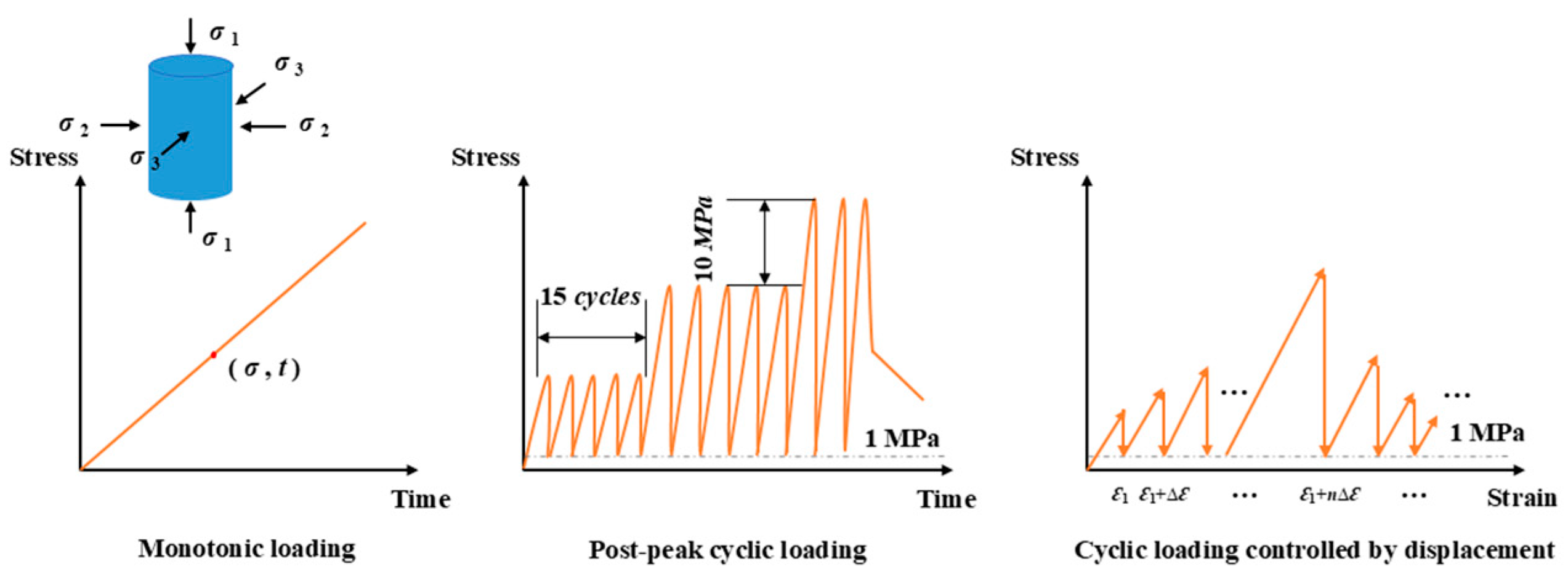
2.2. Experimental Program
3. Mechanical Response Under Different Loading Paths
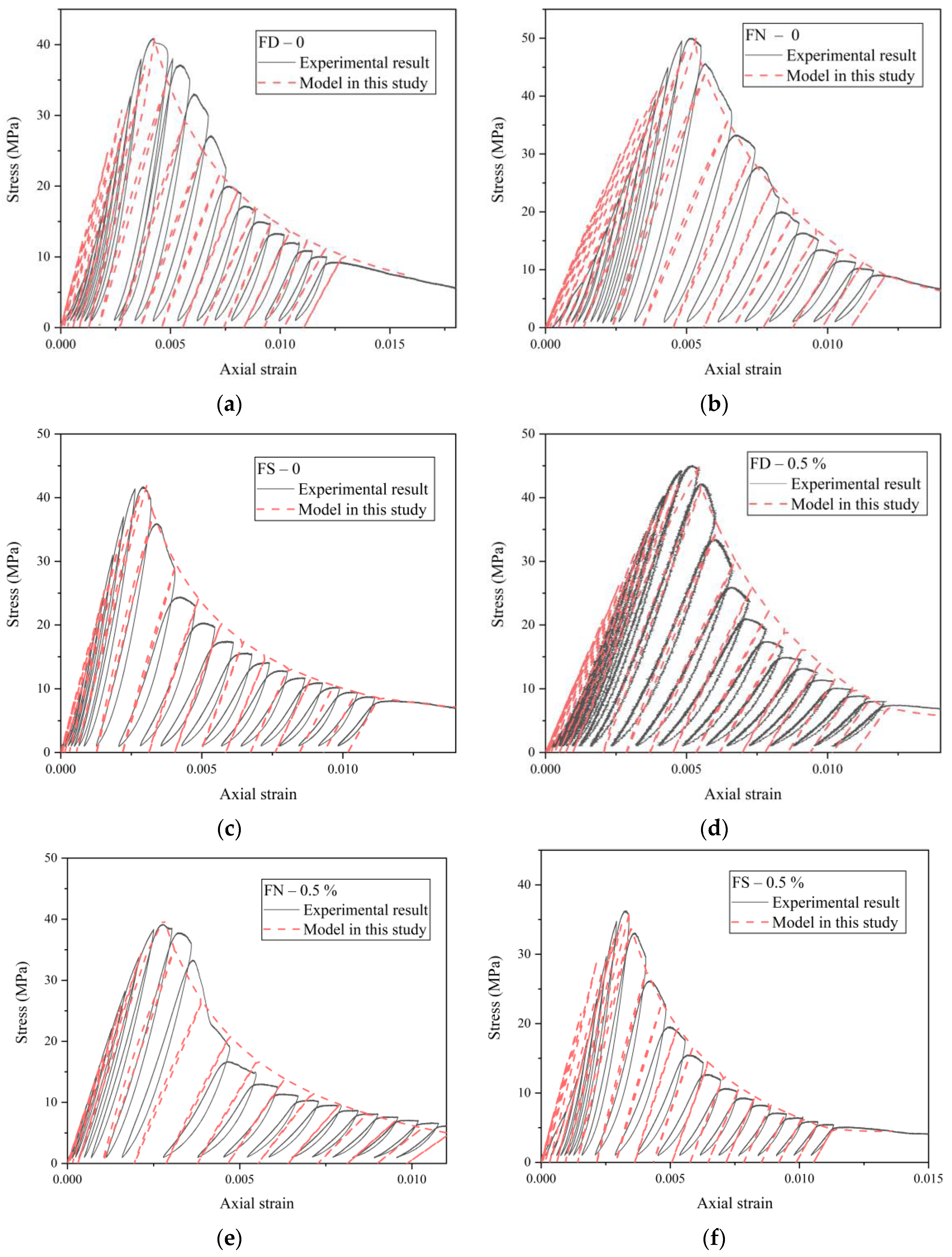
3.1. Stress–Strain Behavior
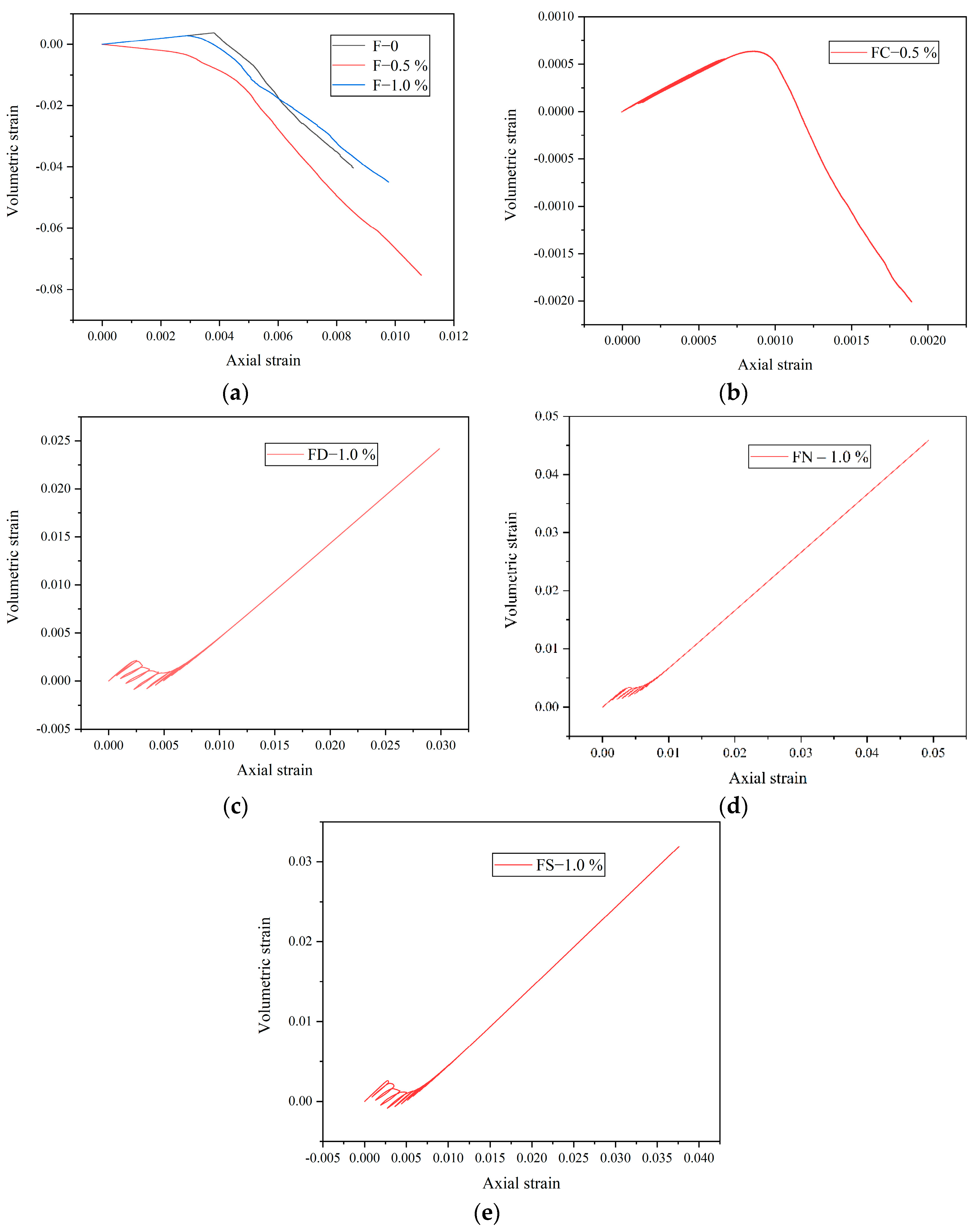
3.2. Volumetric Strain Characteristics
3.3. Elastic Modulus
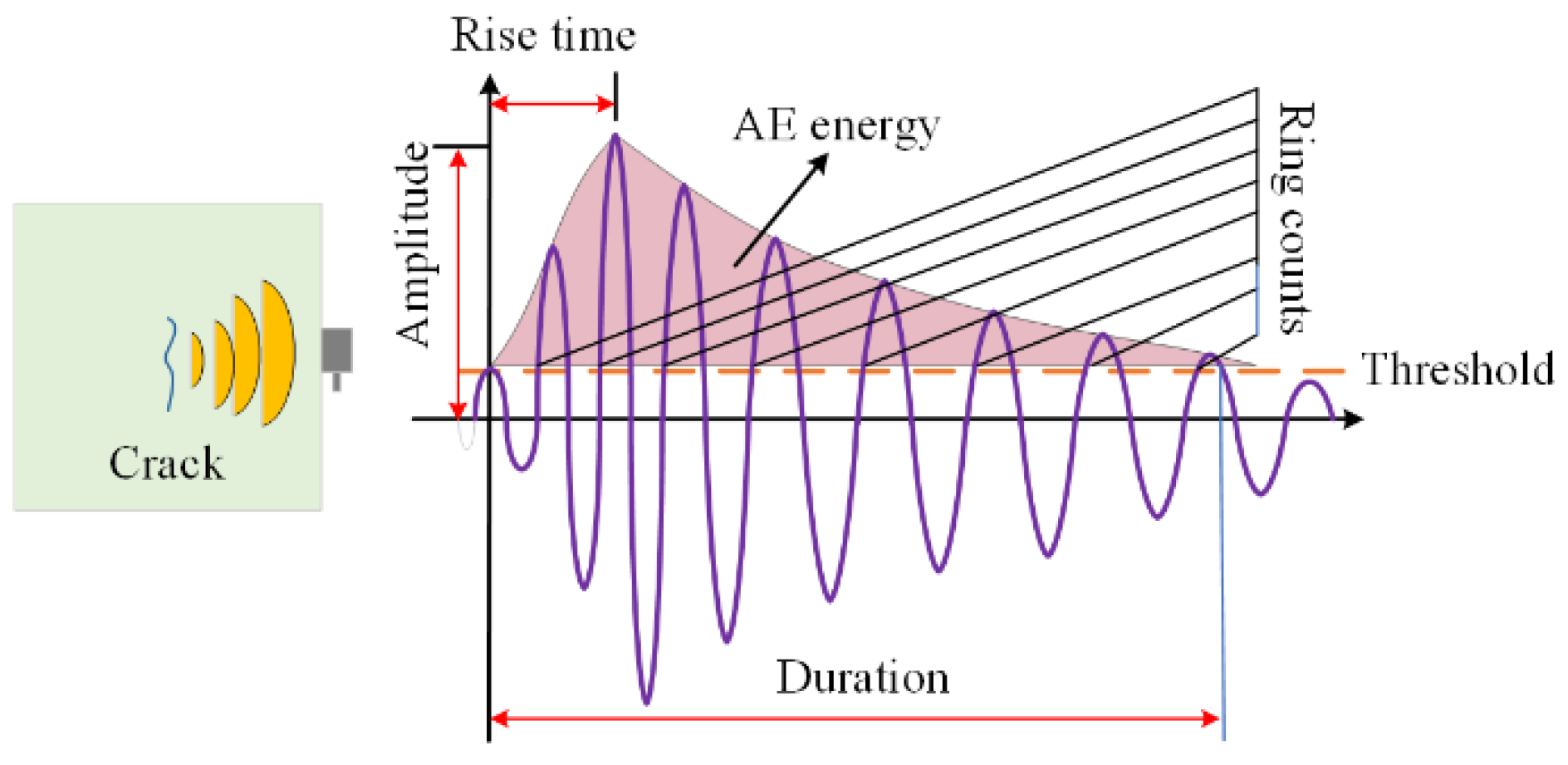
4. Damage Distribution Mechanism Based on AE
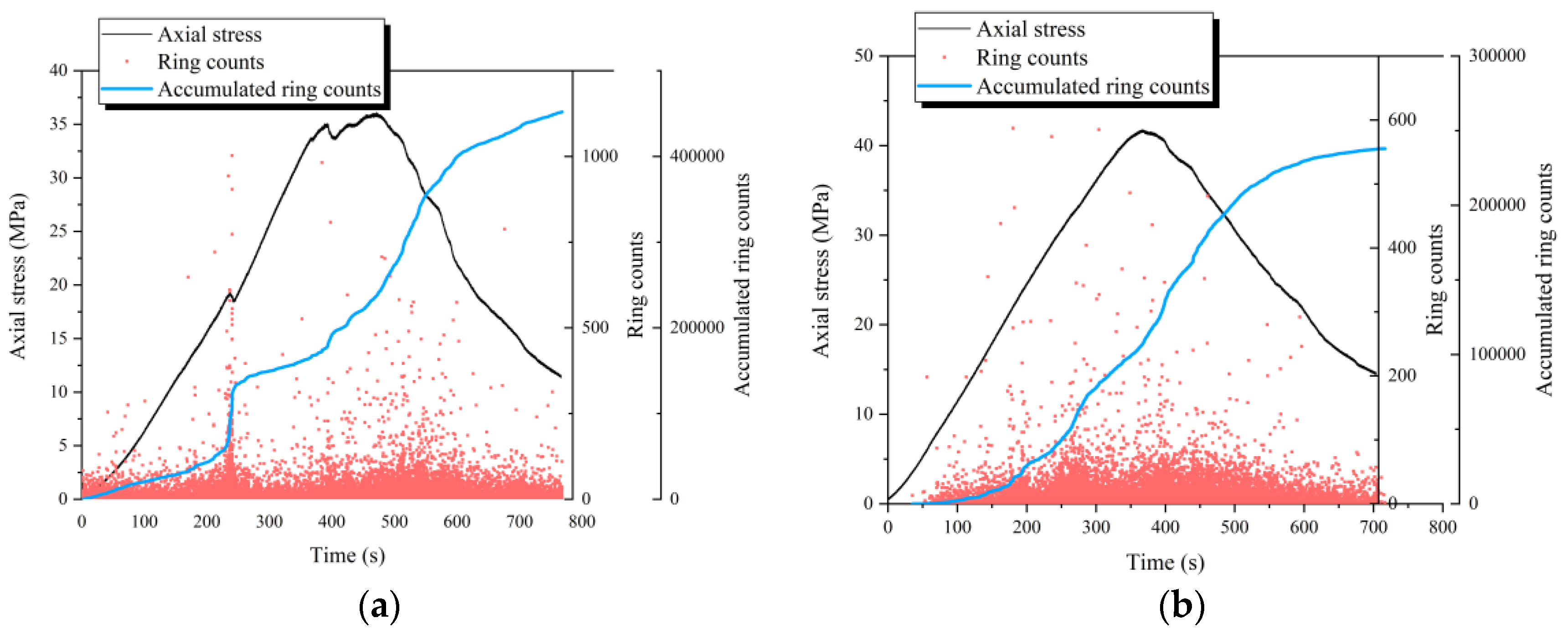
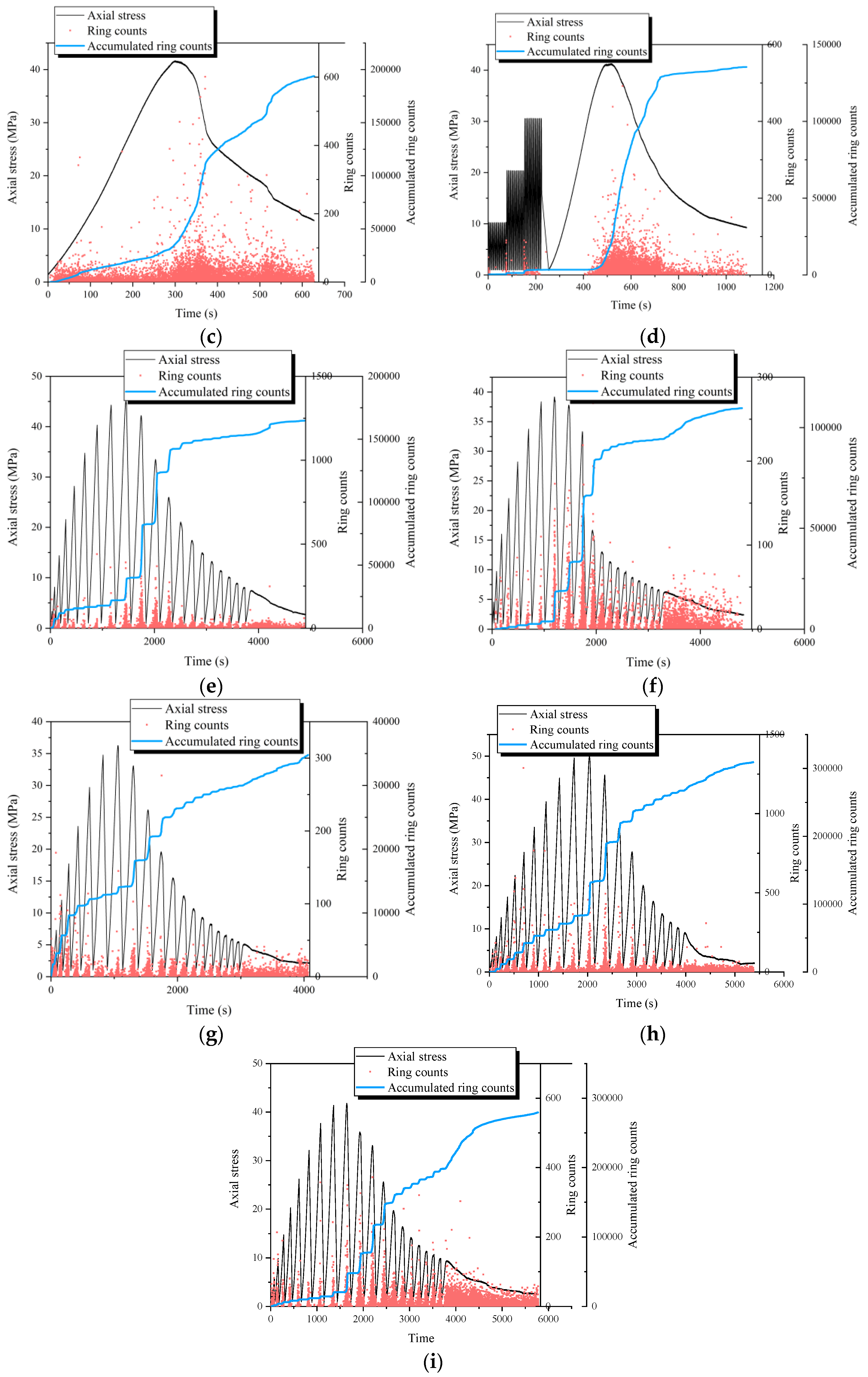
4.1. Cumulative Ring Counts
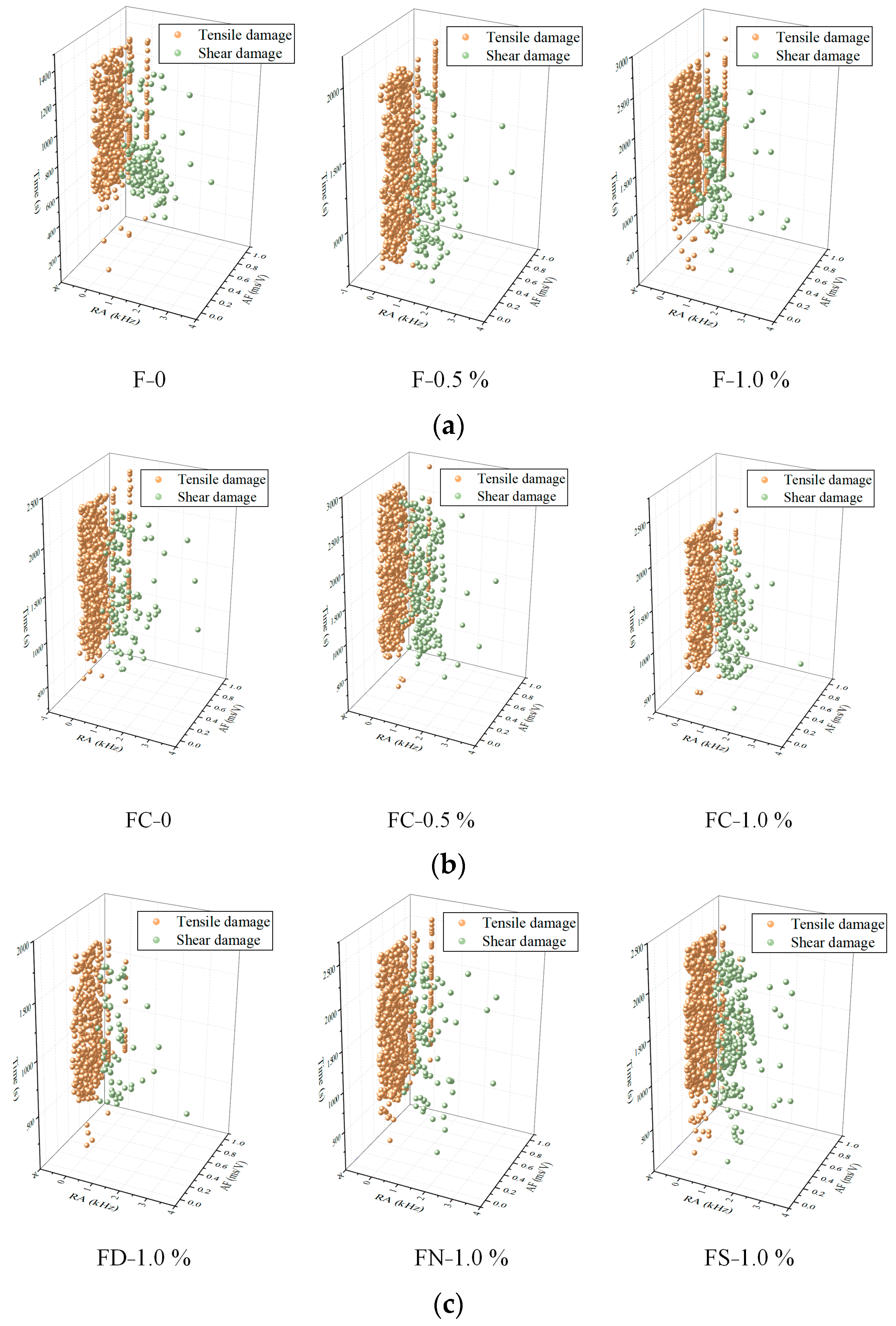
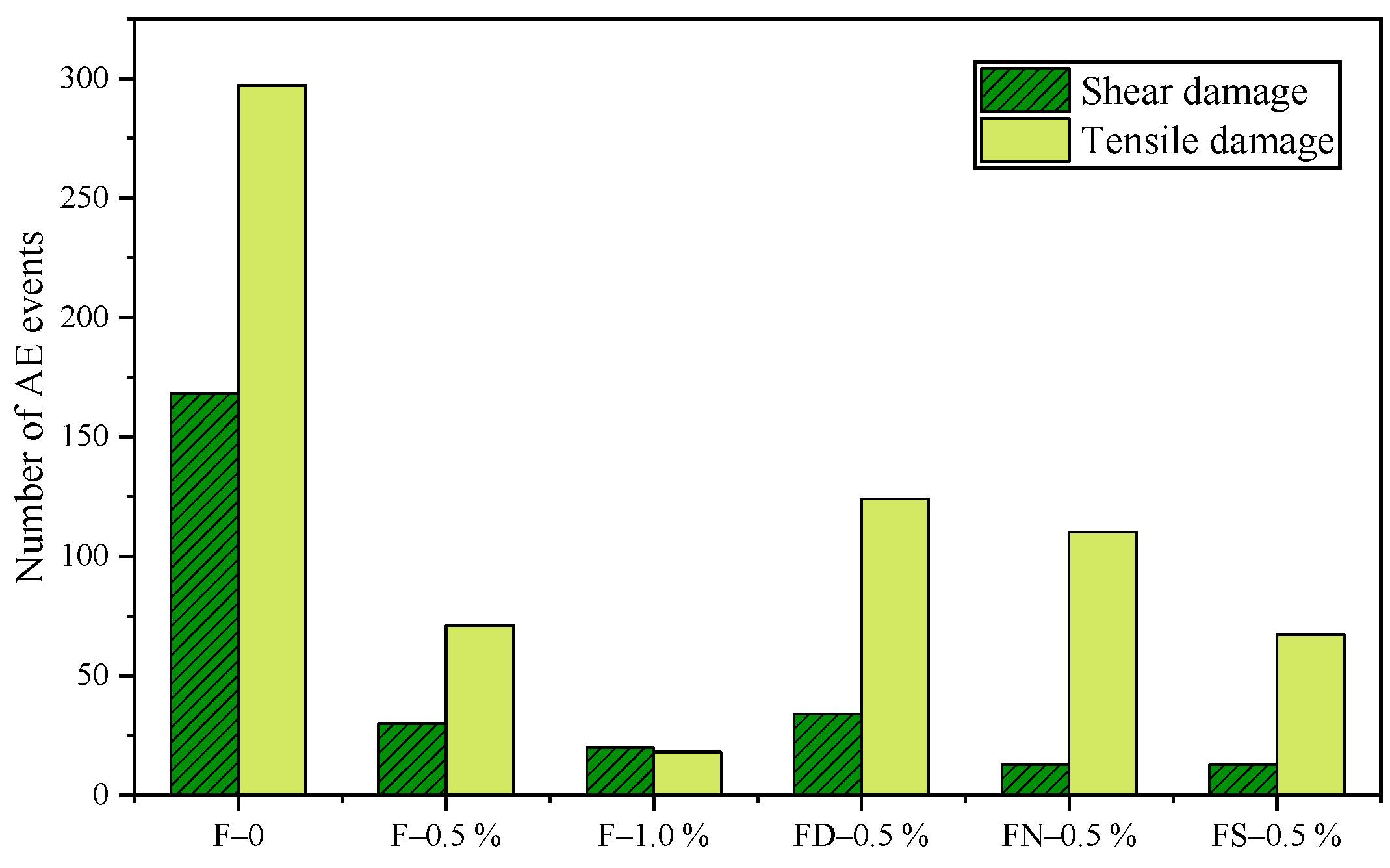
4.2. Spatial Distribution of Fracture Damage Based on Logistic Regression
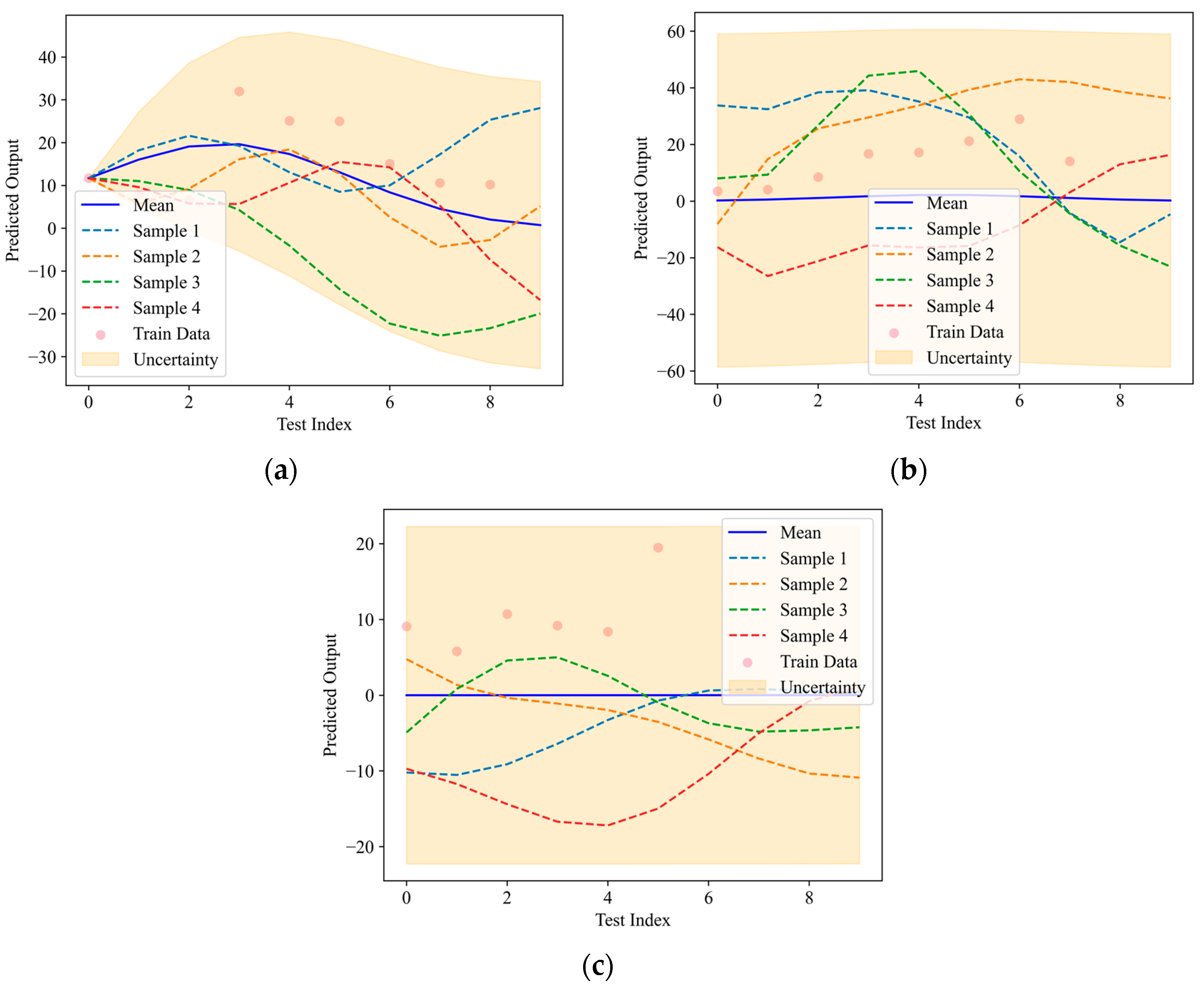
4.3. Gaussian Process Regression of AE Multi-Parameters
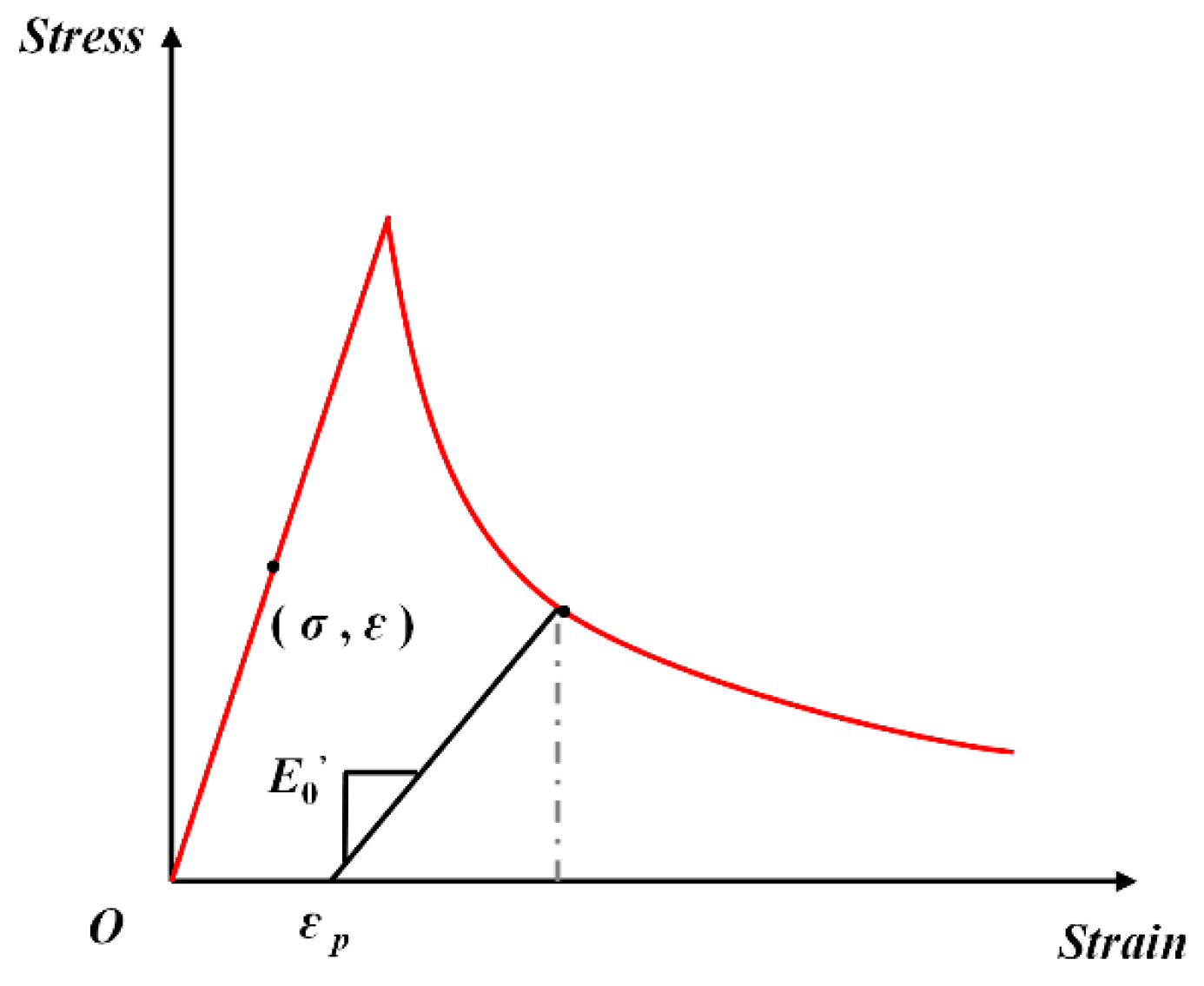
5. Damage Constitutive Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cakiroglu, C.; Ahadian, F.; Bekdaş, G.; Geem, Z.W. Tensile Strength Predictive Modeling of Natural-Fiber-Reinforced Recycled Aggregate Concrete Using Explainable Gradient Boosting Models. J. Compos. Sci. 2025, 9, 119. [Google Scholar] [CrossRef]
- Golewski, G.L. Determination of Fracture Mechanic Parameters of Concretes Based on Cement Matrix Enhanced by Fly Ash and Nano-Silica. Materials 2024, 17, 4230. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.; Daskalakis, P.; Hosseini, S.; Furtado, A. Parametric Numerical Analysis of Factors Influencing the Shear Strength of Precast Concrete Walls with Dry Connections. Available online: https://openurl.ebsco.com/contentitem/doi:10.3390%2Fapp15041959?sid=ebsco:plink:crawler&id=ebsco:doi:10.3390%2Fapp15041959 (accessed on 12 March 2025).
- Chen, J.; Chen, W.; Deng, C.; Deng, R.; Xiao, M.; Su, D. Study on Torsional Shear Deformation Characteristics of Segment Joints Under the Torque Induced by Tunnel Boring Machine Construction. Appl. Sci. 2025, 15, 1104. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Mix Design and Properties Assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC). Cem. Concr. Res. 2014, 56, 29–39. [Google Scholar] [CrossRef]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C.; Álvarez, C. Using Polyolefin Fibers with Moderate-Strength Concrete Matrix to Improve Ductility. J. Mater. Civ. Eng. 2019, 31, 04019170. [Google Scholar] [CrossRef]
- Farooq, M.A.; Fahad, M.; Ali, B.; Ullah, S.; El Ouni, M.H.; Elhag, A.B. Influence of Nylon Fibers Recycled from the Scrap Brushes on the Properties of Concrete: Valorization of Plastic Waste in Concrete. Case Stud. Constr. Mater. 2022, 16, e01089. [Google Scholar] [CrossRef]
- Wille, K.; El-Tawil, S.; Naaman, A.E. Properties of Strain Hardening Ultra High Performance Fiber Reinforced Concrete (UHP-FRC) under Direct Tensile Loading. Cem. Concr. Compos. 2014, 48, 53–66. [Google Scholar] [CrossRef]
- Najm, H.M.; Nanayakkara, O.; Sabri, M.M.S. Destructive and Non-Destructive Evaluation of Fibre-Reinforced Concrete: A Comprehensive Study of Mechanical Properties. Materials 2022, 15, 4432. [Google Scholar] [CrossRef]
- Yan, L.; Kasal, B.; Huang, L. A Review of Recent Research on the Use of Cellulosic Fibres, Their Fibre Fabric Reinforced Cementitious, Geo-Polymer and Polymer Composites in Civil Engineering. Compos. Part B Eng. 2016, 92, 94–132. [Google Scholar] [CrossRef]
- Mastali, M.; Dalvand, A. The Impact Resistance and Mechanical Properties of Self-Compacting Concrete Reinforced with Recycled CFRP Pieces. Compos. Part B Eng. 2016, 92, 360–376. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, A.; Yu, Y.; Yang, B.; Yu, B.; Xie, C. Freeze–Thaw Damage Degradation Model and Life Prediction of Air-Entrained Concrete in Multi-Year Permafrost Zone. Materials 2023, 16, 7703. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Tan, K.-H. Experimental and Numerical Investigation on Progressive Collapse Resistance of Reinforced Concrete Beam Column Sub-Assemblages. Eng. Struct. 2013, 55, 90–106. [Google Scholar] [CrossRef]
- Blanco, A.; Pujadas, P.; De la Fuente, A.; Cavalaro, S.H.P.; Aguado, A. Influence of the Type of Fiber on the Structural Response and Design of FRC Slabs. J. Struct. Eng. 2016, 142, 04016054. [Google Scholar] [CrossRef]
- Li, B.; Jiang, J.; Xiong, H.; Zhan, Y.; Wu, Z.; Cunningham, L.S. Improved Concrete Plastic-Damage Model for FRP-Confined Concrete Based on True Tri-Axial Experiment. Compos. Struct. 2021, 269, 114051. [Google Scholar] [CrossRef]
- Khabaz, A. Assessment of Frictional-Bond Strength at the Interface of Single SSF in Cementitious Composite and Prediction of Accompanying Pressure of Surrounding Matrix. Compos. Interfaces 2022, 29, 765–793. [Google Scholar] [CrossRef]
- Ranjbarian, M.; Ma, X.; Mechtcherine, V. Influence of Crack Width in Alternating Tension–Compression Regimes on Crack-Bridging Behaviour and Degradation of PVA Microfibres Embedded in Cement-Based Matrix. Materials 2020, 13, 4189. [Google Scholar] [CrossRef]
- Jin, Z.; Li, S.; Song, H.; Li, Z.; Zhu, D. Experimental and Simulative Study of Bonding Properties on Fiber/Epoxy Interfaces by Digital Image Correlation (DIC) Technique and Molecular Dynamics. Cem. Concr. Compos. 2022, 131, 104569. [Google Scholar] [CrossRef]
- Medeiros, A.; Zhang, X.; Ruiz, G.; Yu, R.C.; Velasco, M.d.S.L. Effect of the Loading Frequency on the Compressive Fatigue Behavior of Plain and Fiber Reinforced Concrete. Int. J. Fatigue 2015, 70, 342–350. [Google Scholar] [CrossRef]
- Poveda, E.; Ruiz, G.; Cifuentes, H.; Yu, R.C.; Zhang, X. Influence of the Fiber Content on the Compressive Low-Cycle Fatigue Behavior of Self-Compacting SFRC. Int. J. Fatigue 2017, 101, 9–17. [Google Scholar] [CrossRef]
- Li, B.; Xu, L.; Chi, Y.; Huang, B.; Li, C. Experimental Investigation on the Stress-Strain Behavior of Steel Fiber Reinforced Concrete Subjected to Uniaxial Cyclic Compression. Constr. Build. Mater. 2017, 140, 109–118. [Google Scholar] [CrossRef]
- Hubert, M.; Desmettre, C.; Charron, J.-P. Influence of Fiber Content and Reinforcement Ratio on the Water Permeability of Reinforced Concrete. Mater. Struct. 2015, 48, 2795–2807. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Peng, G. Effect of Water Pressure on Mechanical Behavior of Concrete under Dynamic Compression State. Constr. Build. Mater. 2016, 125, 501–509. [Google Scholar] [CrossRef]
- Stamati, O.; Roubin, E.; Andò, E.; Malecot, Y. Tensile Failure of Micro-Concrete: From Mechanical Tests to FE Meso-Model with the Help of X-Ray Tomography. Meccanica 2019, 54, 707–722. [Google Scholar] [CrossRef]
- Sadowski, Ł.; Mathia, T.G. Multi-Scale Metrology of Concrete Surface Morphology: Fundamentals and Specificity. Constr. Build. Mater. 2016, 113, 613–621. [Google Scholar] [CrossRef]
- Naoum, M.C.; Papadopoulos, N.A.; Sapidis, G.M.; Voutetaki, M.E. Efficacy of PZT Sensors Network Different Configurations in Damage Detection of Fiber-Reinforced Concrete Prisms under Repeated Loading. Sensors 2024, 24, 5660. [Google Scholar] [CrossRef]
- van der Heijden, G.H.A.; van Bijnen, R.M.W.; Pel, L.; Huinink, H.P. Moisture Transport in Heated Concrete, as Studied by NMR, and Its Consequences for Fire Spalling. Cem. Concr. Res. 2007, 37, 894–901. [Google Scholar] [CrossRef]
- Tayfur, S.; Alver, N.; Abdi, S.; Saatcı, S.; Ghiami, A. Characterization of Concrete Matrix/Steel Fiber de-Bonding in an SFRC Beam: Principal Component Analysis and k-Mean Algorithm for Clustering AE Data. Eng. Fract. Mech. 2018, 194, 73–85. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.; Ning, Y. Identification of Fracture Damage Characteristics in Ultra-High Performance Cement-Based Composite Using Digital Image Correlation and Acoustic Emission Techniques. Compos. Struct. 2022, 291, 115612. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, X.; Tang, Y.; Wu, J. Visual Damage Identification of Concrete Cylinders with Steel-Fiber-Reinforced Composite Bars Based on Acoustic Emission. Struct. Control Health Monit. 2022, 29, e2880. [Google Scholar] [CrossRef]
- Li, W.; Ho, S.C.M.; Patil, D.; Song, G. Acoustic Emission Monitoring and Finite Element Analysis of Debonding in Fiber-Reinforced Polymer Rebar Reinforced Concrete. Struct. Health Monit. 2017, 16, 674–681. [Google Scholar] [CrossRef]
- Wu, S.; Chen, X.; Zhou, J. Influence of Strain Rate and Water Content on Mechanical Behavior of Dam Concrete. Constr. Build. Mater. 2012, 36, 448–457. [Google Scholar] [CrossRef]
- Vu, X.H.; Malecot, Y.; Daudeville, L.; Buzaud, E. Experimental Analysis of Concrete Behavior under High Confinement: Effect of the Saturation Ratio. Int. J. Solids Struct. 2009, 46, 1105–1120. [Google Scholar] [CrossRef]
- Golewski, G.L. The Phenomenon of Cracking in Cement Concretes and Reinforced Concrete Structures: The Mechanism of Cracks Formation, Causes of Their Initiation, Types and Places of Occurrence, and Methods of Detection—A Review. Buildings 2023, 13, 765. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, D.; Liu, W. Mechanical Behavior of Sandstone under Uniaxial Constant Cyclical Compressive and Tensile Loading. Arab. J. Geosci. 2018, 11, 490. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Zhang, Q.; Chen, C.; Chen, Y. Experimental Study on the Damage Evolution of Tuff under Different Containing Moisture States. J. Min. Saf. Eng. 2021, 38, 1189–1197, 1209. [Google Scholar]
- Noorsuhada, M.N. An Overview on Fatigue Damage Assessment of Reinforced Concrete Structures with the Aid of Acoustic Emission Technique. Constr. Build. Mater. 2016, 112, 424–439. [Google Scholar] [CrossRef]
- RILEM Technical Committee (Masayasu Ohtsu). Recommendation of RILEM TC 212-ACD: Acoustic Emission and Related NDE Techniques for Crack Detection and Damage Evaluation in Concrete. Mater. Struct. 2010, 43, 1183–1186. [Google Scholar] [CrossRef]
- LaValley, M.P. Logistic Regression. Circulation 2008, 117, 2395–2399. [Google Scholar] [CrossRef]
- Chen, Z. Gaussian Process Regression Methods and Extensions for Stock Market Prediction. Ph.D. Thesis, University of Leicester, Leicester, UK, 2017. [Google Scholar]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. ISBN 978-3-540-28650-9. [Google Scholar]
- Sidoroff, F. Description of Anisotropic Damage Application to Elasticity. In Physical Non-Linearities in Structural Analysis; Hult, J., Lemaitre, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 237–244. [Google Scholar]
- Ghrib, F.; Tinawi, R. Nonlinear Behavior of Concrete Dams Using Damage Mechanics. J. Eng. Mech. 1995, 121, 513–527. [Google Scholar] [CrossRef]









| Number | Cement (kg/m3) | Coarse Aggregates (kg/m3) | Sand (kg/m3) | Fiber (kg/m3) | Water (kg/m3) | Superplasticizer (kg/m3) |
|---|---|---|---|---|---|---|
| FRC-0 | 430 | 705 | 1015 | 0 | 215 | 1.14 |
| FRC-0.5% | 430 | 700 | 1007 | 4.55 | 215 | 1.14 |
| FRC-1.0% | 430 | 694 | 999 | 9.1 | 215 | 1.14 |
| Material | Shape | Nominal Length (mm) | Equivalent Diameter (mm) | Density (g/cm3) | Fracture Strength (MPa) | Initial Modulus (GPa) | Origin Place |
|---|---|---|---|---|---|---|---|
| Polypropylene | Oblate | 30 | 0.81 | 0.91 | 474 | 6.0 | Jiangsu |
| Water Reducing Rate (%) | Solid Content (%) | Water Bleeding Ratio (%) | Gas Content (%) | Setting Time - Difference (min) | Compressive Strength Ratio (%) | ||
|---|---|---|---|---|---|---|---|
| Initial Set | Final Set | 3d | 28d | ||||
| 29.5 | 24.5 | 30.0 | 1.4 | +120 | +197 | 29.5 | 24.5 |
| Specific Surface Area (m2/kg) | Setting Time (min) | Compressive Strength (MPa) | Flexural Strength (MPa) | |||
|---|---|---|---|---|---|---|
| Initial Set | Final Set | 3d | 28d | 3d | 28d | |
| 359 | 217 | 322 | 26.7 | 47.4 | 5.9 | 8.9 |
| Water Absorption (%) | Voidage (%) | Apparent Density (kg/m3) | Silt Content (%) | Lump Content (%) |
|---|---|---|---|---|
| 0.86 | 43.0 | 2720 | 0.9 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Chen, X. Compressive Response and Damage Distribution of Fiber-Reinforced Concrete with Various Saturation Degrees. Materials 2025, 18, 1555. https://doi.org/10.3390/ma18071555
Feng L, Chen X. Compressive Response and Damage Distribution of Fiber-Reinforced Concrete with Various Saturation Degrees. Materials. 2025; 18(7):1555. https://doi.org/10.3390/ma18071555
Chicago/Turabian StyleFeng, Lu, and Xudong Chen. 2025. "Compressive Response and Damage Distribution of Fiber-Reinforced Concrete with Various Saturation Degrees" Materials 18, no. 7: 1555. https://doi.org/10.3390/ma18071555
APA StyleFeng, L., & Chen, X. (2025). Compressive Response and Damage Distribution of Fiber-Reinforced Concrete with Various Saturation Degrees. Materials, 18(7), 1555. https://doi.org/10.3390/ma18071555






